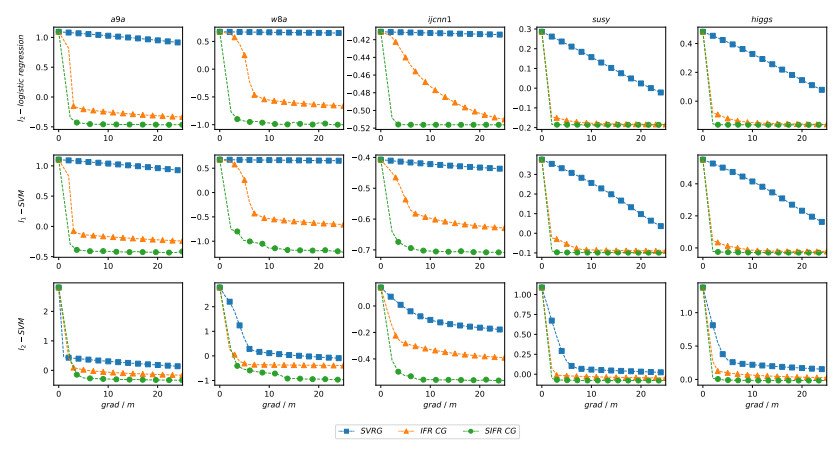
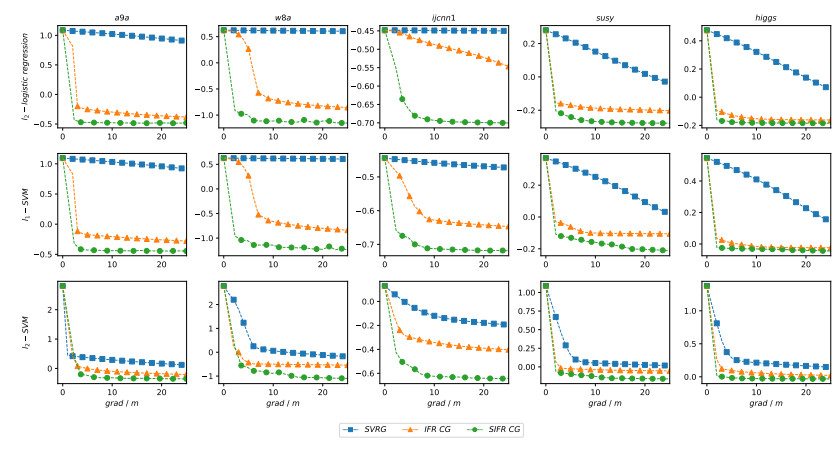
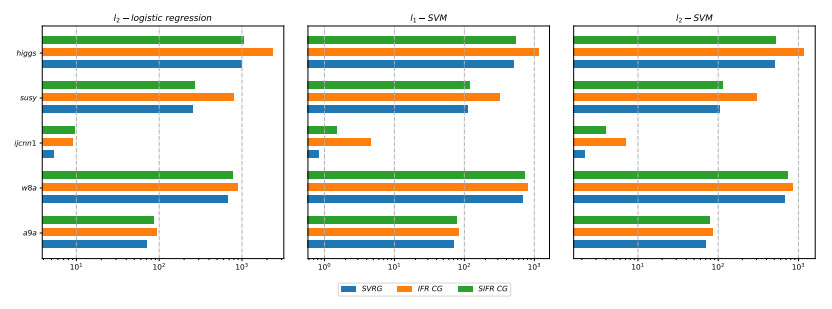
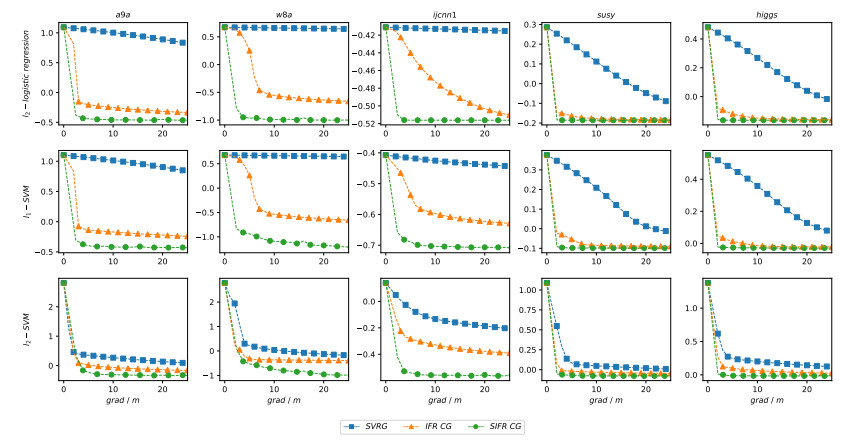
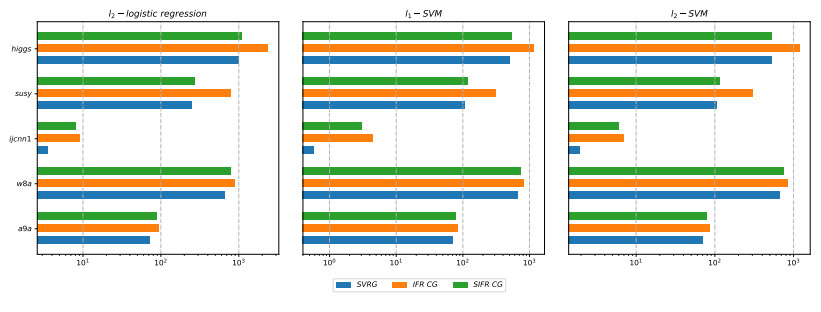
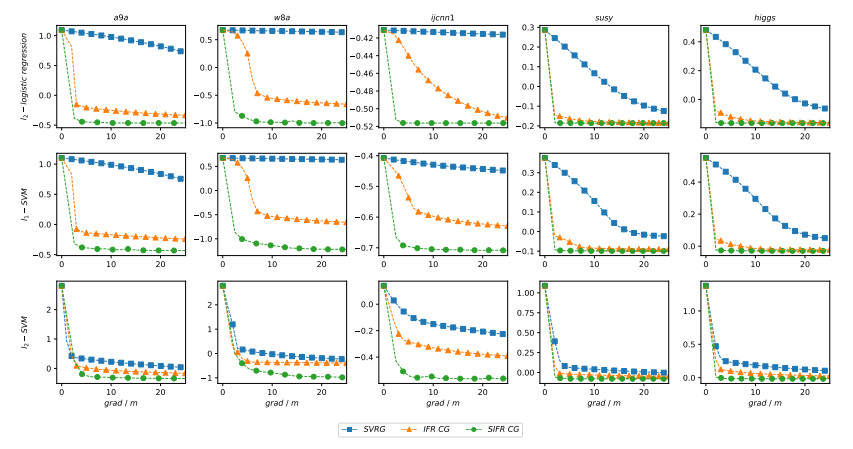
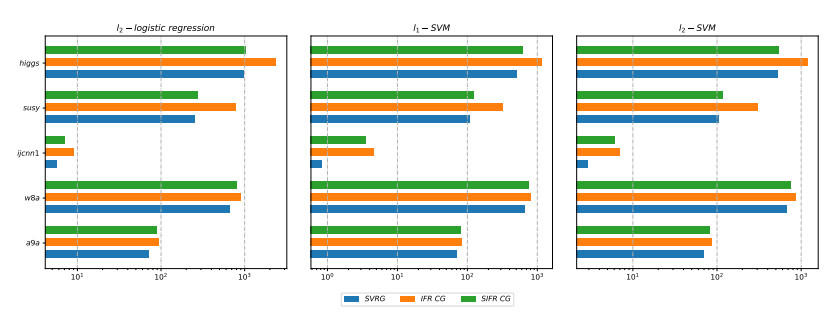
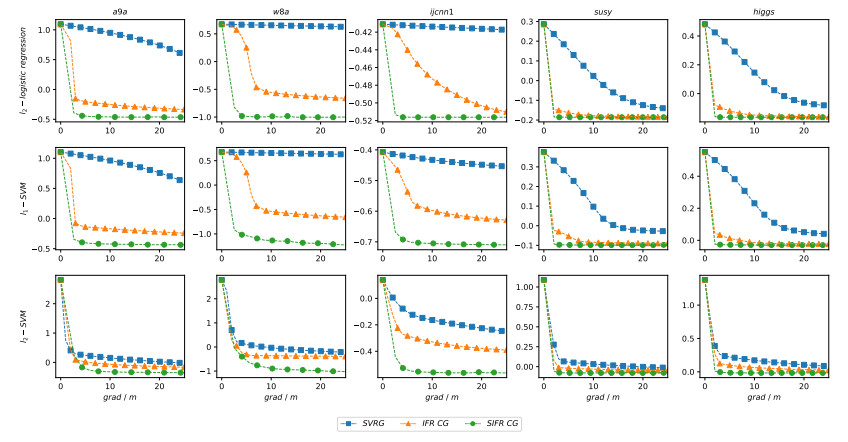
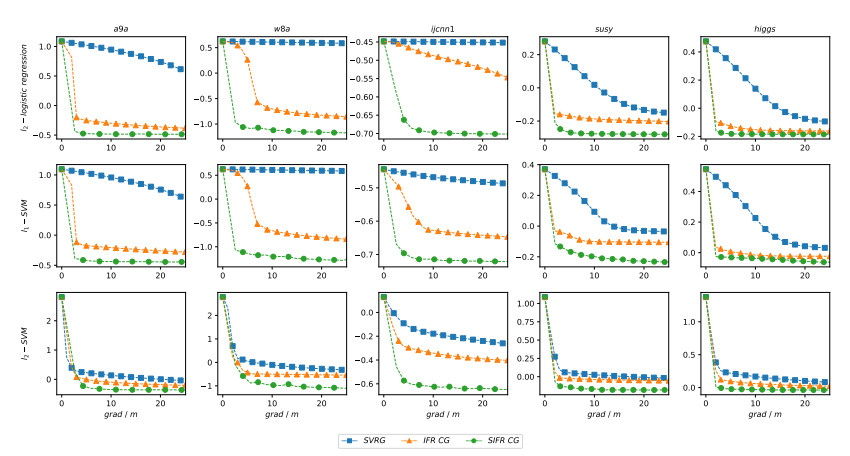
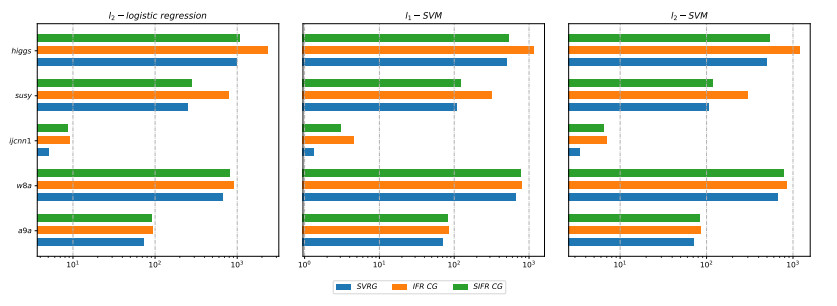
In recent years, the amount of available data is growing exponentially, and large-scale data is becoming ubiquitous. Machine learning is a key to deriving insight from this deluge of data. In this paper, we focus on the large-scale data analysis, especially classification data, and propose an online conjugate gradient (CG) descent algorithm. Our algorithm draws from a recent improved Fletcher-Reeves (IFR) CG method proposed in Jiang and Jian[13] as well as a recent approach to reduce variance for stochastic gradient descent from Johnson and Zhang [15]. In theory, we prove that the proposed online algorithm achieves a linear convergence rate under strong Wolfe line search when the objective function is smooth and strongly convex. Comparison results on several benchmark classification datasets demonstrate that our approach is promising in solving large-scale machine learning problems, viewed from the points of area under curve (AUC) value and convergence behavior.
1.
Introduction
Ostrowski's Inequality. Let f:I⊂[0,+∞)→R be a differentiable function on int(I), such that f′∈L[a,b], where a,b∈I with a<b. If |f′(x)|≤M for all x∈[a,b], then the inequality:
holds for all x∈[a,b]. This inequality was introduced by Alexander Ostrowski in [26], and with the passing of the years, generalizations on the same, involving derivatives of the function under study, have taken place. It is playing a very important role in all the fields of mathematics, especially in the theory approximations. Thus such inequalities were studied extensively by many researches and numerous generalizations, extensions and variants of them for various kind of functions like bounded variation, synchronous, Lipschitzian, monotonic, absolutely continuous and n-times differentiable mappings etc.
For recent results and generalizations concerning Ostrowski's inequality, we refer the reader to the recent papers [1,3,4,31,32]. The convex functions play a significant role in many fields, for example in biological system, economy, optimization and so on [2,16,19,24,29,34,39]. And many important inequalities are established for these class of functions. Also the evolution of the concept of convexity has had a great impact in the community of investigators. In recent years, for example, generalized concepts such as s-convexity (see[10]), h-convexity (see [30,33]), m-convexity (see [7,15]), MT-convexity (see[21]) and others, as well as combinations of these new concepts have been introduced.
The role of convex sets, convex functions and their generalizations are important in applied mathematics specially in nonlinear programming and optimization theory. For example in economics, convexity plays a fundamental role in equilibrium and duality theory. The convexity of sets and functions have been the object of many studies in recent years. But in many new problems encountered in applied mathematics the notion of convexity is not enough to reach favorite results and hence it is necessary to extend the notion of convexity to the new generalized notions. Recently, several extensions have been considered for the classical convex functions such that some of these new concepts are based on extension of the domain of a convex function (a convex set) to a generalized form and some of them are new definitions that there is no generalization on the domain but on the form of the definition. Some new generalized concepts in this point of view are pseudo-convex functions [22], quasi-convex functions [5], invex functions [17], preinvex functions [25], B-vex functions [20], B-preinvex functions [8], E-convex functions [38], Ostrowski Type inequalities for functions whose derivatives are (m,h1,h2)-convex [35], Féjer Type inequalities for (s,m)-convex functions in the second sense [36] and Hermite-Hadamard-Féjer Type inequalities for strongly (s,m)-convex functions with modulus C, in the second sense [9]. In numerical analysis many quadrature rules have been established to approximate the definite integrals. Ostrowski inequality provides the bounds of many numerical quadrature rules [13].
In this paper we have established new Ostrowski's inequality given by Badreddine Meftah in [23] for s-φ-convex functions with f∈Cn([a,b]) such that f(n)∈L([a,b]) and we give some applications to some special means, the midpoint formula and some examples for the case n=2.
2.
Preliminaries
Recall that a real-valued function f defined in a real interval J is said to be convex if for all x,y∈J and for any t∈[0,1] the inequality
holds. If inequality 2.1 is strict when we say that f is strictly convex, and if inequality 2.1 is reversed the function f is said to be concave. In [37] we introduced the notion of s-φ-convex functions as a generalization of s-convex functions in first sense.
Definition 1. Let 0<s≤1. A function f:I⊂R→R is called s-φ-convex with respect to bifunction φ:R×R→R (briefly φ-convex), if
for all x,y∈I and t∈[0,1].
Example 1. Let f(x)=x2, then f is convex and 12-φ- convex with φ(u,v)=2u+v, indeed
On the other hand;
Hence,
Example 2. Let f(x)=xn and 0<s≤1, then f is convex and s-φ- convex with φ(u,v)=∑nk=1(nk)v1−kn(u1n−v1n)n, indeed
Remark 1. If f is increasing monotone in [a,b], then f is s-φ- convex for φ(x,y)=K, where K∈[0,+∞) and s∈(0,1].
3.
Main results
In this section, we give some integral approximation of f∈Cn([a,b]) such that f(n)∈L([a,b]), for n≥1 using the following lemma as the main tool (see [11]).
Lemma 1. Let f:[a,b]→R be a differentiable mapping such that f(n−1) is absolutely continuous on [a,b]. Then for all x∈[a,b] we have the identity
where the kernel Kn:[a,b]2→R is given by
with x∈[a,b] and n is natural number, n≥1.
Theorem 1. Let f:I→R be n-times differentiable on [a,b] such that f(n)∈L([a,b]) with n≥1 and 0<s≤1. If |f(n)| is s-φ-convex, then the following inequality
holds for all x∈[a,b].
Proof. From Lemma 1, properties of modulus, making the changes of variables u=(1−t)a+tx in the first integral and u=(1−t)x+tb in the second integral we have that,
Since |f(n)| is s-φ- convex (2.2) gives
which is the desired result. The proof is completed.
Remark 2. If we take s=1 then obtain a result of Meftah B. (see Theorem 2.1 in [23]).
Corollary 1. Let f:I→R be n-times differentiable on [a,b] such that f(n)∈L([a,b]) with n≥1 and 0<s≤1. If |f(n)| is s-convex in the first sense, we have the following estimate
Proof. Taking φ(u,v)=v−u in Theorem 1.
Remark 3. It is important to notice that if s=1 we have that |f(n)| is convex and then obtain the corollary 2.2 of Meftah see [23].
Theorem 2. Let f:I→R be n-times differentiable on [a,b] such that f(n)∈L([a,b]) with n≥1, 0<s≤1 and let q>1 with 1p+1q=1. If |f(n)|q is s-φ-convex, then the following inequality holds
Proof. From Lemma 1, properties of modulus, and Holder's inequality, we have
Since |f(n)|q is s-φ-convex, we deduce
Corollary 2. Let f:I→R be n-times differentiable on [a,b] such that f(n)∈L([a,b]) with n≥1, 0<s≤1 and let q>1 with 1p+1q=1. If |f(n)|q is s-convex in the first sense, then the following inequality holds
Proof. Taking φ(u,v)=v−u in Theorem 1.
Corollary 3. Let f:I→R be n-times differentiable on [a,b] such that f(n)∈L([a,b]) with n≥1, 0<s≤1 and let q>1 with 1p+1q=1. If |f(n)|q is s-convex in the first sense, then the following inequality holds
Proof. Taking φ(u,v)=v−u in Theorem 1, we obtain 3.1. Then using the following algebraic inequality for all a,b≥0, and 0≤α≤1 we have (a+b)α≤aα+bα, we get the desired result.
Theorem 3. Let q>1 and f:I→R be n-times differentiable on [a,b] such that f(n)∈L([a,b]) with n≥1, 0<s≤1. If |f(n)|q is s-φ−convex, then the following inequality
holds for all x∈[a,b].
Proof. From Lemma 1, properties of modulus, and power mean inequality, we have
Since |f(n)|q is s-φ-convex, we deduce
The proof is completed.
Remark 4. If we take s=1 then obtain a result of Meftah B. (see Theorem 2.6 in [23]).
Corollary 4. Let f:I→R be n-times differentiable on [a,b] such that f(n)∈L([a,b]) with n≥1, 0<s≤1 and let q>1. If |f(n)|q is s-convex in the first sense, then the following inequality
holds for all x∈[a,b].
Proof. Taking φ(u,v)=v−u in Theorem 3.
Theorem 4. Let f:I→R be n-times differentiable on [a,b] such that f(n)∈L([a,b]) with n≥1, 0<s≤1 and let q>1. If |f(n)|q is s-φ-convex, then the following inequality
holds for all x∈[a,b].
Proof. From Lemma 1, properties of modulus, and power mean inequality, we have
Since |f(n)|q is s-φ-convex, we deduce
which in the desired result.
Remark 5. If we take s=1 then obtain a result of Meftah B. (see Theorem 2.9 in [23]).
Corollary 5. Let f:I→R be n-times differentiable on [a,b] such that f(n)∈L([a,b]) with n≥1, 0<s≤1 and let q>1. If |f(n)|q is s-convex in the first sense, then the following inequality
holds for all x∈[a,b].
Proof. Taking φ(u,v)=v−u in Theorem 4.
4.
s-φb-convex function
In this section, using [12] we define s-φb-convex function as generalized form of s-φ convex functions [37] and give some results.
Definition 2. Let R+ be the set of nonnegative real numbers and b:R×R×[0,1]→R+ be a function with tsb(x,y,t)∈[0,1] for all x,y∈R, t∈[0,1] and s∈(0,1]. A function f:I→R is called s-φb-convex if
for all x,y∈R and t∈[0,1].
Remark 6. If b(x,y,z)=1 then the definition of s-φb-convex function matches the definition of s-φ-convex function.
Theorem 5. Consider a function f:I→R and b:R×R×[0,1]→R+ be a function with tsb(x,y,t)∈[0,1] for all x,y∈R and s,t∈[0,1]. Then the following assertions are equivalent:
(i) f is s-φb-convex for some b and s∈[0,1].
(ii) f is φ-quasiconvex.
Proof. (i)→(ii) For any x,y∈I and t∈[0,1],
(ii)→(i) For x,y∈I and t∈[0,1], define
Notice that tsb(x,y,t)∈[0,1]. For a such function b we have
Remark 7. Let f:I→R be a s-φ-convex function. For x1,x2∈I and α1+α2=1, we have f(α1x1+α2x2)≤f(x2)+αs1φ(f(x1),f(x2)). Aso when n>2, for x1,x2,...,xn∈I, ∑ni=1αi=1 and Ti=∑ij=1αj, we have
Theorem 6. Let f:I→R be a s-φ-convex function and φ be nondecreasing nonnegatively sublinear in first variable. If Ti=∑ij=1αj for i=1,2,...,n such that Tn=1, then
where φf(xi,xi+1,...,xn)=φ(φf(xi,xi+1,...,xn−1),f(xn)) and φf(x)=f(x) for all x∈I.
Proof. Since φ is nondecreasing nonnegatively sublinear on first variable, so from (4.1) it follows that:
Example 3. Consider f(x)=x2 and φ(x,y)=2x+y for x,y∈R+=[0,+∞). The function φ is nondecreasing nonnegatively sublinear in first variable and f is 12-φ-convex (see Example 1). Now for x1,x2,...,xn∈R+ and α1,α2,...,αn with ∑ni=1αi=1 according to Theorem 6 we have
5.
Applications for some particular mappings
In this section we give some applications for the special case where n=2 and the function φ(f(x),f(y))=f(y)−f(x), in this case we have that f is s-convex in the first sense.
Example 4. Let s∈(0,1) and p,q,r∈R, we define the function f:[0,+∞)→R as
we have that if q≥0 and r≤p, then f is s-convex in the first sense (see [18]). If we do φ(f(x),f(y))=f(x)−f(y), then f is s-φ-convex, but is not φ-convex because f is not convex.
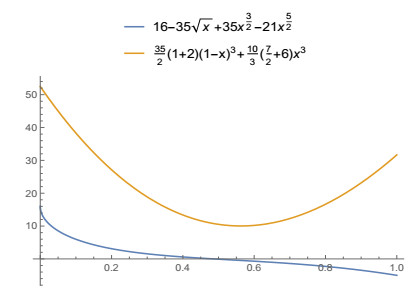
Example 5. In the previous example if s=12, p=1, q=2 and r=1 we have that f:[0,+∞)→R,f(t)=2t12+1 is 12-φ-convex. Then if we define g:[0,+∞)→R, g(t)=815t52+t22, we have to g″ is \frac{1}{2} - \varphi -convex in [0, +\infty) with \varphi(f(x), f(y)) = f(x)-f(y) . Using Theorem 1, for a, b\in [0, +\infty) with a < b and x\in [a, b] , we get
Remark 6. In particular if we choose a = 0 and b = 1 , we have for x\in [0, 1] , we get a graphic representation of the Example 5.
Example 6. If we define g(t) = \frac{t^4}{12} we have that g''(t) is \frac{1}{2} - \varphi - convex with \varphi(u, v) = 2u+v (see example 1) and by Theorem 1, for a, b\in \mathbb{R} with a < b and x\in [a, b] , we have that
Moreover, if choose x = \frac{a+b}{2} , we obtain that
Then
Therefore
Example 7. If we define g(t) = \frac{36}{91}\sqrt[3]{2} \ t^{\frac{13}{6}} we have that |g''(t)|^3 is \frac{1}{2} - \varphi -convex with \varphi(u, v) = 2u+v (see example 1) and by Theorem 4, for a, b\in \mathbb{R} with a < b and x\in [a, b] , we have
6.
Conclusions
In this paper we have established new Ostrowski's inequality given by Badreddine Meftah in [23] for s-\varphi- convex functions with f\in C^n([a, b]) such that f^{(n)}\in L([a, b]) with n\ge 1 and we give some applications to some special means, the midpoint formula and some examples for the case n = 2 . We expect that the ideas and techniques used in this paper may inspire interested readers to explore some new applications of these newly introduced explore some new applications of these newly introduced functions in various fields of pure and applied sciences.
Acknowledgments
The authors want to give thanks to the Dirección de investigación from Pontificia Universidad Católica del Ecuador for technical support to our research project entitled: "Algunas desigualdades integrales para funciones convexas generalizadas y aplicaciones".
Conflict of interest
The authors declare that they have no conflicts of interest.

















 DownLoad:
DownLoad: