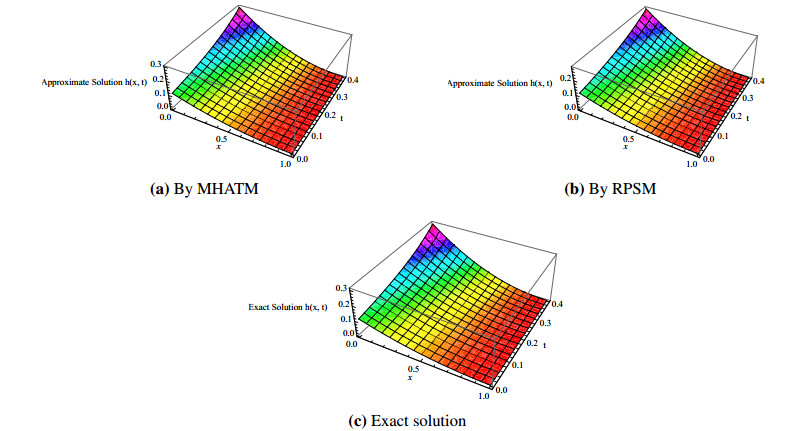
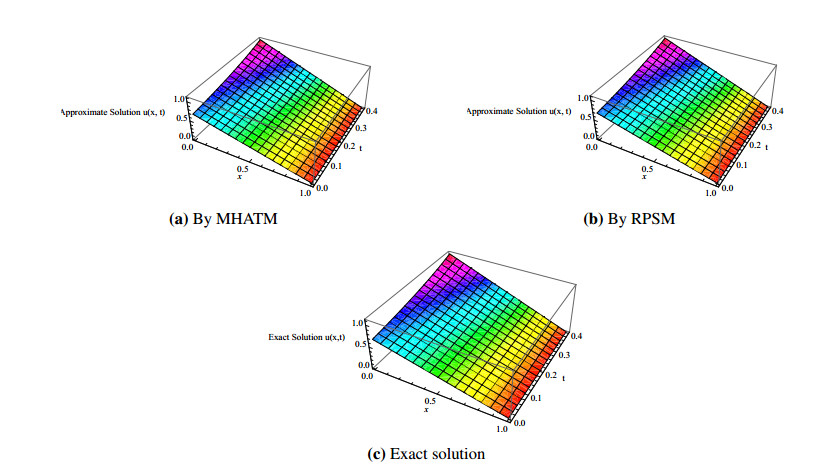
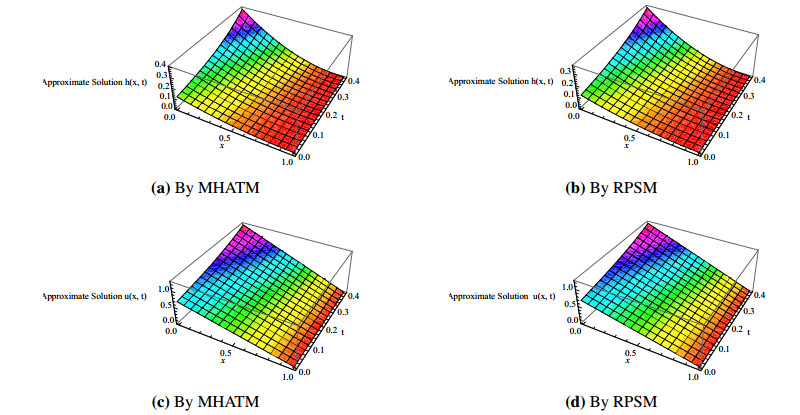
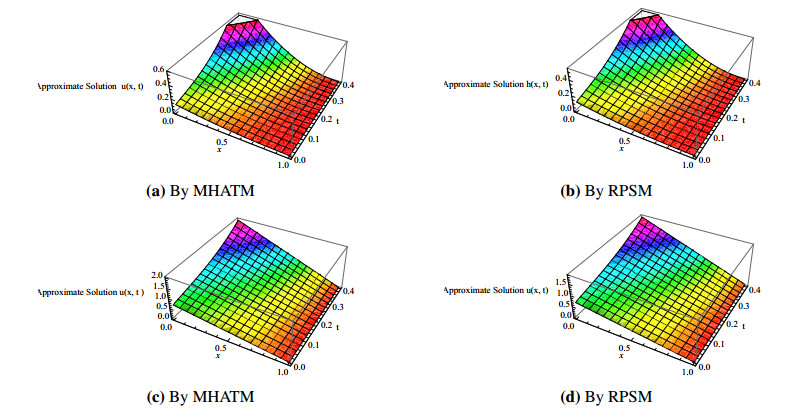
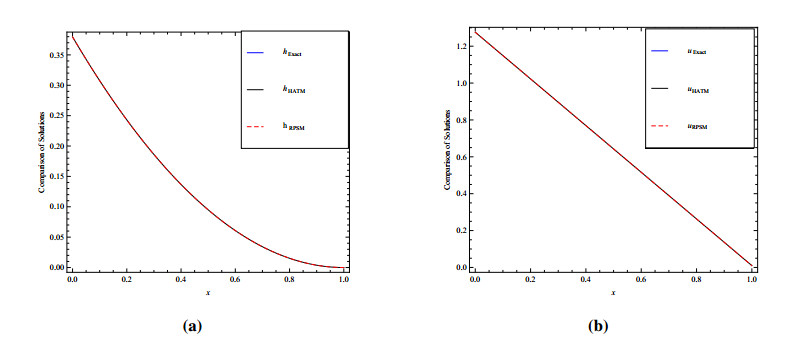
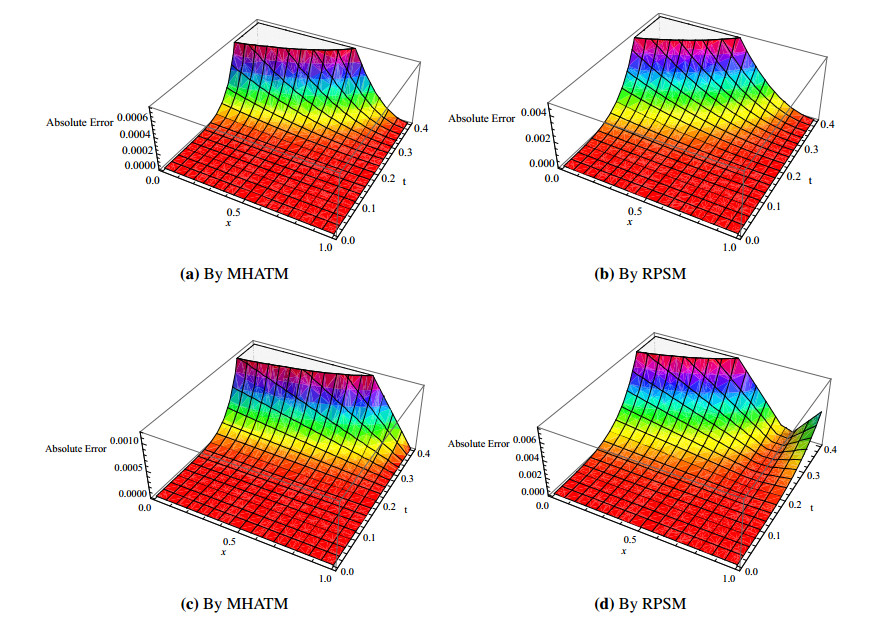
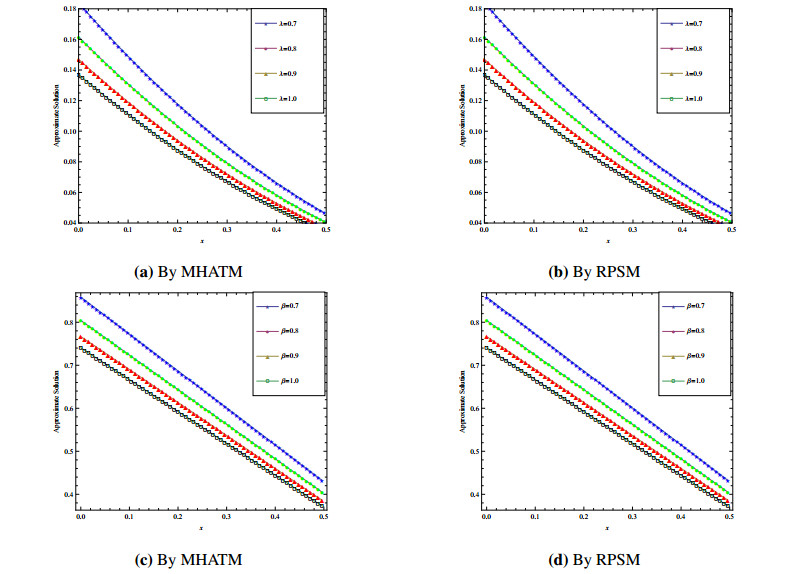
In this study, a comparison between the modified homotopy analysis transform method (MHATM) and residual power series method (RPSM) have been given for solving time-fractional coupled shallow water equations (SWEs). The time-fractional coupled SWEs are a system of PDEs that describe the flow below a pressure surface in a fluid is considered. Rigorous convergence analysis and error estimated have been exhibited for both the featured methods. The results obtained by MHATM and RPSM are then compared with well-known exact solutions. To show the effectiveness and advantage of the featured techniques the numerical simulation of coupled SWEs has been represented graphically with tabulated data. However, the results indicate that MHATM provides more accurate value than RPSM for solving fractional coupled SWEs.
1.
Introduction
Nonlinear evolution equations are essential to applied mathematics, applied science, and engineering because of their wide range of practical applications. Many models have drawn a lot of attention, including those related to fluid dynamics, fluid mechanics, neurons, optical fibers, electrical circuits, waves in water, plasma oscillations, capillary-gravity waves, physics of plasma, chemical kinetics, and chemical physics. To gain a greater understanding of the dynamics of these real-world components, methods for solving fractional nonlinear partial differential equations (PDEs) must be investigated. To further study and understand the complex behaviors that are inherent in the aforementioned systems, this exploration is essential. Solutions to fractional nonlinear PDEs are of academic interest because of the increased detail and generality they provide, which outperforms traditional solutions in terms of descriptive power. Additionally, graphs representing the physical solutions of various fractional orders can be compared. To investigate new findings for the exact traveling wave solutions, mathematicians have developed and implemented innovative and reliable techniques. Some of these methods are the Khater Ⅱ method [1], generalized Khater method [2], modified Khater method [3], simple equation method [4], Poincare-Lighthill-Kuo method [5], generalized Kudryashov method [6], modified Kudryashov method [7], fractional sub-equation method [8] and (G′/G)-expansion method [9]. Recent studies have used a variety of techniques to investigate solutions for solitary waves, revealing a wide range of approaches to comprehending intricate physical phenomena. Scholars have conscientiously employed several techniques, all of which have added significant value to our understanding of the nature and dynamics of isolated waves [10,11,12,13,14]. These joint efforts have improved our knowledge of nonlinear dynamics and provided a wide range of solitary wave solutions, which have enhanced the scientific discourse [15,16,17,18,19].
Numerous mathematical strategies have been developed to solve the difficulties involved in solving fractional partial differential equations (FPDEs) analytically. Through the revelation of the exact behavior of the modeled system, these strategies seek to overcome the inherent complexity of FPDEs and provide benefits over numerical methods. The knowledge obtained from analytical solutions advances our understanding of basic physical processes more thoroughly. As such, the study of analytical solutions in the field of FPDEs is an important and constantly developing field of research [20,21,22,23,24]. The scientific literature demonstrates the wide range of mathematical techniques used to analytically solve FPDEs, highlighting the complexity of the methods used by experts in this area. Interestingly, a range of approaches [25,26,27,28,29,30,31,32,33] have been included, highlighting their importance in the variety of strategies that are being examined.
Furthermore, within the parameters of the suggested methodology [34,35,36], which is known for its skillful management of complex algebraic calculations, the extraction of solutions for a wide range of phenomena, such as fluid dynamics and transport phenomena, offers a potential pathway for applications in a variety of scientific and engineering fields. The intended application in biological systems, industrial processes, and environmental flows has the potential to provide insightful knowledge about the complexities of fluid behavior, leading to improved prediction and optimization techniques. The given partial differential equations are converted into an algebraic system of equations by using the Riccati-Bernoulli equation in conjunction with the Backlund transformation. This approach makes it easier to retrieve important information from the complex behaviors these dynamic systems display, which improves our understanding of the underlying physical processes. Most notably, the method guarantees the derivation of finite solutions, guaranteeing the accuracy and effectiveness of solutions for the examined equations. One important aspect of this method is its ability to produce a wide range of single-wave solutions.
In addition, the current study attempts to apply this analytical approach to clarify the complex dynamics found in the Estevez-Mansfield-Clarkson (EMC) equation. The 1997 study by Mansfield and Clarkson on pattern dispersion in liquid drops provided the basis for this fourth-order nonlinear evolution equation. The EMC equation poses a difficult set of complications and is mostly used to examine wave behavior in shallow water. By putting the suggested technique to use, this study hopes to further our understanding of these complexities and promote improvements in the field of complex phenomenon analysis. The goals that have been mentioned are intended to improve our comprehension of the behavior of the EMC equation and further our collective efforts to address the difficulties presented by very complex mathematical models.
The EMC equation was developed as a result of research into the dispersion patterns found in liquid droplets. This specific equation, which is utilized in the research, is essential for deciphering the complex dynamics of waves in shallow water. The particular form under examination is a fourth-order fractional nonlinear space-time EMC equation, which may be stated as follows [4]:
where F=F(x,y,t) and (λ≠0) is a constant. The EMC equation is a key equation in the vast field of nonlinear science. It has applications in fluid dynamics, optics, image processing, and plasma physics. The importance of the EMC equation has been highlighted by recent studies [37,38,39], which highlight how vital it is to comprehending intricate physical processes. For higher-dimensional nonlinear evolution equations, the investigations use novel approaches like the Sine-Gordon expansion method to find steady soliton solutions for non-linear equations that have not been solved before. Furthermore, the dynamics of important equations are investigated, such as the fractional Ablowitz-Kaup-Newell-Segur equation and the non-linear space-time fractional EMC equation. These investigations offer important insights into wave propagation in many scientific fields. Continuing this direction, the studies explore linked sine-Gordon equations and solitary wave solutions for the EMC equation, two essential mathematical models for studying shape development in many physical contexts. All of these discoveries highlight how important the EMC equation is to improve our comprehension of complex systems and how they materialize in the actual world.
The operator that represents the derivatives of order α adheres to the definition provided in [40].
2.
Methodology
Consider the following fractional partial differential equation (FPDE) that we have presented:
Polynomial P1 is a function of f(ζ1,ζ2,ζ3,⋯,t). This polynomial includes the fractional order derivatives as well as the nonlinear terms. The primary stages of this method are then thoroughly covered. The wave transformations that follow are our suggestions for looking into possible solutions for Eq (1.1):
where
A universal variable denoting the transformation of propagating waves is represented by the symbol (ψ). Three non-zero constants, (p), (q) and (ω), give different features to the travelling wave dynamics. More specifically, for ω>0, the wave travels in a positive direction and for ω<0, the wave travels in a negative direction. We apply a transformation to Eq (2.1) that results in the formation of a nonlinear ordinary differential equation (NODE) and, as a result, assumes a modified mathematical expression. This change reflects an intrinsic change in the nature of the equation, which goes from its original form to a non-linear one. This introduces new dynamics and behaviors, which call for an improved mathematical representation.
Consider the formal solution for Eq (2.4):
Under the restriction that both bm≠0 and b−m≠0 simultaneously, the bi constants must be determined. Concurrently, the function is generated via the subsequent Backlund transformation.
With the requirement that B≠0, let (τ), (A) and (B) be constants. Furthermore, suppose that ϕ(ψ) is a function that has the following definition:
It is commonly acknowledged that the following are the solutions to Eq (2.7):
Under the framework of Eq (2.5), the positive integer (N) can be found by using homogeneous balancing principles, which entail finding equilibrium between the highest order derivatives and the nonlinear variables in Eq (2.4). f(ψ) degree can be expressed more precisely as D[f(ψ)]=N. Therefore, this enables us to perform the following computation of the degree of linked expressions:
Algebraic equations are established by combining Eq (2.4) with Eqs (2.5) and (2.7), grouping terms with the same powers of f(ψ), and then equating them to zero. Applying Maple software to deduce the pertinent values for various parameters will result in an efficient resolution of this system. Thus, this makes it easier to compute the soliton wave-propagating solutions to Eq (2.1) with accuracy by computational analysis.
3.
Execution of the problem
Using the approach outlined in Section 2, we methodically solve the fractional EMC equation (1.1), concentrating on solutions for single waves. Using the wave transformation described in Eq (2.3), our analysis is simplified inside the EMC equation framework. We then show the resulting equation, a derived nonlinear ordinary differential equation (ODE), that captures the nonlinear dynamics after this transformation step. This new equation is a concise expression derived from the original fractional partial differential equation (PDE) and represents a breakthrough in our comprehension of the fundamental dynamics in the frictional EMC framework.
Equation (3.1) as well as Eqs (2.7) and (2.6) all incorporate the replacement given in Eq (2.5). After collecting coefficients for ϕi(ψ) in a methodical manner, we create an algebraic system of equations that equals zero. By utilizing the computing power of Maple, we can solve this system of algebraic equations and obtain the following answers. This methodology guarantees a methodical and effective extraction of the solutions, revealing insights into the interrelationships between variables in the specified mathematical context:
Case 1.
Case 2.
Case 3.
The solution set for the values of (ψ) that follow is obtained by assuming Case 1:
Solution Set 1: When τ<0, then Eq (1.1) brings about the resulting single-wave solutions:
or
Solution Set 2: When τ>0, then Eq (1.1) brings about the resulting single-wave solutions:
or
Solution Set 3: When τ=0, then Eq (1.1) brings about the resulting single-wave solutions:
The solution set for the values of (ψ) that follow is obtained by assuming Case 2:
Solution Set 1: When τ<0, then Eq (1.1) brings about the resulting single-wave solutions:
or
Solution Set 2: When τ>0, then Eq (1.1) brings about the resulting single-wave solutions:
or
Solution Set 3: When τ=0, then Eq (1.1) brings about the resulting single-wave solutions:
The solution set for the values of (ψ) that follow is obtained by assuming Case 3:
Solution Set 1: When τ<0, then Eq (1.1) brings about the resulting single-wave solutions:
or
Solution Set 2: When τ>0, then Eq (1.1) brings about the resulting single-wave solutions:
or
Solution Set 3: When τ=0, then Eq (1.1) brings about the resulting single-wave solutions:
4.
Results and discussion
When used in conjunction with the Backlund transformation, the Riccati-Bernoulli sub-ODE technique becomes a powerful analytical tool for studying complex dynamic systems, including shallow water waves, tsunami modeling, coastal engineering, environmental impact assessment, river and estuary dynamics, and biophysical applications. This method is well-known for its flexibility in a wide range of physical systems and its capacity to produce a large number of periodic and single traveling wave solutions, each with unique properties. Interestingly, this is accomplished without using the discretization and linearization steps that are frequently used in problem-solving techniques. This highlights the Riccati-Bernoulli sub-ODE technique's intrinsic effectiveness and wide applicability as a sophisticated analytical framework in the investigation of complicated dynamic systems.
The results obtained with this approach provide exact solutions for systems representing the physical phenomena outlined above, which contributes to our comprehension of the complex dynamics involved in these processes. The flexibility of the approach is crucial for capturing complex behaviors, yielding a wide range of solutions with different parameters. Moreover, the analytical solutions that are obtained are used as standards, which makes it easier to thoroughly assess accuracy and strengthen stability analyses, which are essential for guaranteeing the dependability of computer models. One notable feature of this approach is its ability to produce self-reinforcing solitary waves with solitons with the least amount of energy loss. Because soliton formation is a complex process resulting from a fine balance between linear and nonlinear mechanisms, it opens up new possibilities for investigating and understanding the dynamics of complex physical systems. The recently found exact solutions to this equation exhibit a high degree of variation compared to the previously reported results in the literature. We visualize these solutions as part of our thorough investigation, and the results show a broad spectrum including shock-type, periodic, kink, and anti-kink structures. Each wave has unique applications and significance. Shock waves are used in fluid dynamics, especially in supersonic flows and explosive events. They are characterized by abrupt and fast changes in the physical properties. Periodic waves can be thought of as steady, recurring perturbations in the domain of solitary waves. Kink waves can be seen in a variety of systems, including some plasma waves. They are characterized by a sudden change in amplitude that frequently has a discernible bend. In contrast, the anti-kink waves imply non-linear optics and plasma physics due to their abrupt amplitude change in the opposite direction.
The graphical discussion delves into the interpretation of the figures presented in the study. Each figure showcases variations in the real and imaginary parts of specific solutions, providing insights into their behavior and characteristics.
Figure 1 illustrates the variations in the real and imaginary parts of the solution F1(x,y,t), highlighting any oscillatory patterns, amplitude changes, or spatial distribution of the solution. Figure 2 presents similar variations for the solution F5(x,y,t), allowing for comparisons with Figure 1 and potentially revealing differences in behavior or dynamics. In Figure 3, the focus shifts to the solution F10(x,y,t), offering further insights into its real and imaginary components, potentially uncovering unique features or phenomena. Figure 4 provides additional perspectives on the solution F11(x,y,t), enabling a comprehensive analysis of its behavior and interaction with the underlying system dynamics. Finally, Figure 5 offers insights into the solution F15(x,y,t), potentially highlighting any distinct characteristics or noteworthy phenomena compared to the previous solutions.
In Table 1, comparison of the current approach with the alternative approaches, the simple equation approach [4] and G′/G-expansion method [9]. Through a detailed examination of these graphical representations, the study aims to enhance understanding of the soliton solutions within the context of the investigated equations, providing valuable insights for further analysis and interpretation.
5.
Conclusions
Through the use of Backlund transformation techniques, we have improved the application of the Riccati Bernoulli sub-ODE method in this work. The fractional EMC equation stable solitary wave solutions have been successfully derived using this extension. The results validate the flexibility of our suggested method, which may now be used to solve a larger class of nonlinear evolution equations. Future research avenues and intriguing applications can be pursued with the kink, anti-kink, and periodic solutions obtained by using our proposed approach. These results have the potential to improve the communications systems by employing solitary wave stability for long-distance transmission. Investigating the behavior of kink, anti-kink, and periodic solutions provides important insights for manipulating nonlinear optical phenomena and creating cutting-edge optical devices in the fields of material sciences and non-linear optics. Moreover, energy transmission in periodic structures can be studied using periodic solutions, which might advance knowledge of energy propagation and possibly enhance energy harvesting technology. Our analysis demonstrates the effectiveness of the technique, establishing it as a useful resource for theoretical physicists and mathematicians, especially when dealing with discrete nonlinear dynamics. Systems that can be solved analytically or that admit explicit solutions are given preference. This work is important not only for theoretical biologists looking for insights into physical applications but also for fluid dynamics engineers.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Funding
This work was supported by the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia (Grant No. 6158).
Acknowledgments
This work was supported by the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia (Grant No. 6158).
Conflict of interest
The authors declare that they have no conflicts of interest.










 DownLoad:
DownLoad: