An impulsive system with a linear continuous-time part and a nonlinear discrete-time part is considered. A criterion for exponential orbital stability of its periodic solutions is obtained. The proof is based on linearization by the first approximation of an auxiliary discrete-time system. The formulation of the criterion depends significantly on a number of impulses per period of the solution. The paper provides a mathematical rationale for some results previously examined in mathematical biology by computer simulations.
1.
Introduction
The system considered in this paper is a generalization of a hormonal regulation model introduced in [1] and later developed in a number of publications (see, among others, [2,3,4,5,6,7,8,9,10]). This system belongs to the class of impulsive differential equations widely addressed in mathematical literature (see, e. g., [11,12,13,14,15,16,17]). An impulsive release of some hormones results from the fact that it is controlled by neurons of the brain. The amplitudes and frequencies of this release are governed by other hormones secreted in certain organs or tissues. The working regimes of such a hormonal system are periodic oscillations.
Following [14], an impulsive system can be seen as a special class of hybrid systems that includes both continuous-time and discrete-time dynamics. We are interested in the case when the times between impulses are variable and depend on the state vector and the previous impulse moments. In electrical engineering and biology such systems are called pulse-frequency modulated [18].
It is well known, that the conventional stability concept [19,20] is unsuitable for systems with impulses, since their solutions are discontinuous in time and even for close initial values, solutions may differ significantly in some vicinities of jumping times. Definitions of stability of solutions taking into account specifity of impulsive systems can be found, e. g., in [11,13,16]. An alternative approach is an adoption of the orbital stability concept to impulsive systems, see [21,22,23,24,25,26,27].
In the present paper we provide a criterion for some kind of exponential orbital stability of periodical solutions. The stability concept pursued here is different from that was addressed in previous works. Its analogues for non-impulsive systems can be found in [28,29].
When compared with [1], the result of this paper is novel in several aspects. Firstly, in [1] an orbital stability was considered, and here we obtain a more powerful result that ensures some kind of exponential orbital stability. Secondly, in [1] the statement on orbital stability was formulated, however its proof was only sketched because of the lack of space. In the present paper we provide a detailed and rigorous mathematical proof. Additionally, the system treated here is more general than that in [1]. Thirdly, in most publications on impulsive systems the initial impulse moment is considered fixed and common for all the solutions. However it is not suitable for some applications, e. g., when we address synchronization problems [2]. In this paper we examine stability in the augmented phase space including continuous-time and discrete-time coordinates.
The paper is organized as follows. Firstly, a special class of linear systems with a nonlinear impulsive impact is described. Then a characterization of its periodic solutions with the help of an auxiliary discrete-time system is given. We also prove some results on stability of discrete-time systems. Based on these results, a criterion for exponential orbital stability of periodic solutions of the initial impulsive system is established. Finally, a numerical example is provided.
2.
Impulsive system
2.1. System description
Consider a system with impulses that describes dynamics of an unknown p-dimensional vector function x(t) and a discrete-time sequence {tn}∞n=0:
n≥0, t≥t0. Here A is a nonzero constant p×p matrix, tn is an increasing scalar sequence and Λn is a sequence of p-dimensional vectors. The notation x(t−), x(t+) is used for left-sided and right-sided limits of the function x(⋅) at the point t. The system's solutions have jumps Λn at times tn, and Tn is the duration of the interval between consecutive jumping times tn, tn+1. The sequences Tn and Λn are defined by (2.4), where Φ(⋅), F(⋅) are nonlinear continuous maps, Φ:Rp↦R,F:Rp↦Rp.
Assume that Φ(⋅) has finite lower and upper bounds:
for all x∈Rp, where Φ1, Φ2 are some constants. Additionally, suppose that Φ(⋅), F(⋅) are Lipschitz with some Lipschitz constants LΦ, LF, respectively:
Here ‖⋅‖ is the Euclidean vector norm.
The state space systems (2.1)–(2.4) is (p+1)-dimensional, since it encompasses dynamics not only of x(t), but also of tn. Initial values for its solutions are given by points (t0,x(t−0)).
2.2. Existence and uniqueness of solutions
Integrating (2.1) and taking (2.2) into account, we obtain
Hence, if we know a solution at a point tn, namely the pair (tn,x(t−n)), we can uniquely extend x(t) to the whole interval (tn,tn+1) and thus obtain the pair (tn+1,x(t−n+1)). Moreover, from (2.5) it follows that tn+1−tn≥Φ1>0, so the sequence {tn}, n=0,1,… is strictly increasing, has no accumulation points, and tn→+∞ as n→∞.
Thus we conclude that for any initial value (t0,x(t−0)) there exists a unique solution (tn,x(t)) of (2.1)–(2.4) for t∈[t0,+∞) and n=0,1,2,….
2.3. Reduction to a discrete-time system
For brevity, let us introduce notation xn=x(t−n). From (2.7) it follows that for any solution of (2.1)–(2.4) and for all n≥0
(see, e. g., [30]).
Then any solution (tn,x(t)) of (2.1)–(2.4) obeys a system of discrete-time (difference) equations
Notice that (2.10) does not influence (2.9), so the dynamics of (2.9) can be studied independently of (2.10). Discrete-time system (2.9) is p-dimensional, while the augmented system (2.9), (2.10) is (p+1)-dimensional. Further (2.9), (2.10) will be called the discrete-time system related to (2.1)–(2.4).
Observe that if some sequences {xn}, {tn} satisfy (2.9), (2.10), then there exists a unique solution (tn,x(t)) of (2.1)–(2.4) with x(t−n)=xn, n=0,1,…. Indeed, between the sampling times tn, tn+1 the function x(t) can be uniquely recovered as
Thus there is one-to-one correspondence between solutions of discrete-time systems (2.9), (2.10) and of impulsive systems (2.1)–(2.4).
3.
Periodic solutions
3.1. Periodic solutions of the discrete-time system
Let us inroduce a map Q:Rp↦Rp,
Then (2.9) can be rewritten as
Consider the discrete-time equation (2.9), where the map Q(⋅) is defined by (3.1). Solutions of (2.9) are infinite sequences {xn}∞n=0={x0,…,xk,…}.
For an integer k≥1 consider the kth iteration of the map Q:
Then any solution of (2.9) can be found as xn=Q(n)(x0), n≥1, where x0 is an initial value.
A solution {xn} of (2.9) is called 1-periodic or 1-cycle, if xn≡x0 for all n≥0. The initial value x0 of a 1-cycle is a fixed point of the map Q, i. e., Q(x0)=x0.
A solution {xn} of (2.9) is called m-periodic (m>1) or m-cycle, if xn+m=xn for all n≥0, and the vectors x0,…,xm−1 are all different. Obviously, the initial value x0 of an m-cycle is a fixed point of the mth iterate, but not a fixed point of lower iterates:
Let {xn,tn} be a solution of discrete-time systems (2.9), (2.10), where the sequence {xn} is m-periodic (m≥1). Then
with
The second equality (3.4) follows from periodicity of xn and the relationships
3.2. Periodic solutions of the continuous-time impulsive system
Let T be some positive real number. The solution (tn,x(t)) of impulsive systems (2.1)–(2.4) will be called T-periodic if the function x(t) is T-periodic for t≥t0 with the least period T.
Theorem 1. Establish a correspondence between periodic solutions (tn,x(t)) of impulsive systems (2.1)–(2.4) and periodic solutions {xn} of discrete-time system (2.9).
(i) Let a solution {xn} of (2.9) be an m-cycle with some integer m≥1. Then the solution (x(t),tn) of the systems (2.1)–(2.4) with an arbitrary initial value t0 and the initial condition x(t−0)=x0 is periodic with the least period T defined by (3.5).
(ii) Let (tn,x(t)) be a T-periodic soluton of (2.1)–(2.4) with some initial values t0 and x(t−0)=x0. Take the solution {xn} of (2.9) with the same initial value x0. Then there exists an integer m≥1 such that {xn} is an m-cycle and (3.5) is satisfied.
Proof. Consider a solution of (2.1)–(2.4) with the initial condition x(t−0)=x0. Then x(t−n) satisfies (2.9) and Tn, Λn are defined by (2.4). Thus
Since {xn} is an m-cycle, we have
Let tn<t<tn+1 for some n≥0. From (3.4) we obtain tn+m<t+T<tn+m+1, hence
This evidently implies x(t+T)=x(t) for t+n≤t<tn+1. Since n is taken arbitrarily, x(t) is T-periodic.
Let us prove that T is the least period of x(t). Assume that there exists some number 0<˜T<T such that x(t+˜T)=x(t) for t≥t−0. Then
Thus t0+˜T is a jumping point of the vector function x(t). Since x(t) has no jumping points but t0,t1,t2,…, there exists some k≥1 such that t0+˜T=tk. Hence xk=x0 and k<m that contradicts the supposition that m is the least period for the sequence {xn}. Thus statement (ⅰ) is proved.
Consider a T-periodic soluton (tn,x(t)) of (2.1)–(2.4) with some initial values t0 and x(t−0)=x0. then the sequences {xn}, {tn}, where xn=x(t−n), satisfy (2.9), (2.10) and Tn=Φ(xn), Λn=F(xn).
As it was shown above, then t0+T is a jumping point and there exists some m≥1 such that t0+T=tm. Here
so (3.5) holds. Moreover, due to T-periodicity of x(t) we have
Hence Q(m)(x0)=x0 and the sequence {xn} is m-periodic.
Let us prove that m is the least period of {xn}. If there exists some integer k such that 0<k<m and {xn} is k-periodic, then from the first part of Theorem 1 we obtain that the corresponding solution of (2.1)–(2.4) has a period ˜T=T0+…+Tk−1 and ˜T<T. This contradicts the supposition that T is the least period.
In particular, Theorem 1 claims that for every periodic solution of a least period T there exists an integer m such that any interval [tn,tn+T) contains exactly m jumping times. Such a solution will also be called an m-cycle.
4.
General statements on stability of discrete-time systems
We will follow the definitions from [31]. Consider a discrete-time system
where xn is a p-dimentional vector and Q is a continuous map, Q:Rp↦Rp. (Here we do not require that Q(⋅) be of form (3.1).)
Let us take a solution {xn}∞n=0 of (4.1) with some initial value x0.
The solution {xn}∞n=0 is called stable if for any given ε>0 there exists δ>0 such that all solutions {˜xn}∞n=0 of (4.1) with ‖x0−˜x0‖<δ are such that ‖xn−˜xn‖<ε for all n≥0.
A solution {˜xn}∞n=0 with perturbed initial data will be called a perturbed solution.
The solution {xn}∞n=0 is called exponentially stable if there exist numbers δ>0, M≥1 and 0<r<1 such that all solutions {˜xn}∞n=0 of (4.1) with ‖x0−˜x0‖<δ satisfy
for all n≥0.
We will need the following auxiliary statement on stability by the first approximation (see Theorem 2.10 [31] for the proof).
Lemma 1. Consider system (4.1) and let its solution {xn}∞n=0 be a 1-cycle, i. e., xn≡x0 and x0 is a fixed point of the map Q(⋅): Q(x0)=x0. Assume that Q(⋅) is continuously differentiable in a neighborhood of x0 and its Jacobian matrix J(x0) is Schur stable [32], i. e., all its eigenvalues are within the unit circle of the complex plane. Then this 1-cycle is exponentially stable.
Let us extend the previous statement to the case of an m-cycle with m>1. Again, let J(x) be the Jacobian matrix of Q(⋅) at a point x.
Lemma 2. Consider a solution {xn} that is an m-cycle, m>1. Assume that the vector valued function Q(⋅) is continuously differentiable in some neighborhoods of the points x0,…xm−1. If the matrix product of Jacobian matrices J(xm−1)⋯J(x0) is Schur stable, then the m-cycle is exponentially stable.
Proof. For brevity, denote Jn=J(xn). Since the sequence xn is m-periodic, Jn is also m-periodic and Jn+m=Jn for all n≥0.
Consider the m-cycle {xn}∞n=0 and a perturbed solution {˜xn}∞n=0. Define the sequences yn=xmn and ˜yn=˜xmn, n=0,1,…. Obviously yn and ˜yn satisfy the discrete-time equations
with the initial values y0=x0, ˜y0=˜x0. Here Q(m) is the mth iteration of the map Q.
As it was mentioned previously, an initial value x0 of an m-cycle is a fixed point of the iteration Q(m), i. e., Q(m)(x0)=x0. By the chain rule, the Jacobian matrix of Q(m) at the point x0 is the product Jm−1⋯J0. By the supposition, this product is Schur stable. Thus {yn} is a 1-cycle of (4.3) with a Schur stable Jacobian matrix. From Lemma 1, this 1-cycle is exponentially stable. Hence there exist numbers M0≥1, 0<r0<1 and h0>0 such that if ‖x0−˜x0‖<h0 then ‖xnm−˜xnm‖≤M0rn0‖x0−˜x0‖ for all n≥0.
It is easily seen that for any two square matrices A1, A2 of the same sizes the products A1A2 and A2A1 are simultaneously Schur stable or unstable. If the product Jm−1⋯J0 is Schur stable, from the previous statement we get that any matrix product obtained from Jm−1⋯J0 by a cyclic permutation will be also Schur stable. Then from m-periodicity of Jn it follows that the matrix product Jn+m−1⋯Jn is Schur stable for any n≥0.
Let us fix some integer s, 1≤s<m, and define the sequences yn=xmn+s and ˜yn=˜xmn+s, n=0,1,…. They satisfy the same equations (4.3), (4.4), however with the initial data y0=xs, ˜y0=˜xs. Moreover, yn is a 1-cycle of (4.3). Since the product Jm+s−1⋯Js is Schur stable, arguing as above we conclude that there exist there exist Ms≥1, 0<rs<1 and hs>0 such that if ‖xs−˜xs‖<hs then ‖xnm+s−˜xnm+s‖≤Msrns‖xs−˜xs‖ for all n≥0. Define
Thus, if max0≤s≤m−1‖xs−˜xs‖<h, then
for all n≥0.
Continuous differentiability implies that Q(⋅) is locally Lipschitz. Then for every xk, 0≤k≤m−1, there exist a sufficiently small number δk> and a number Lk>0 such that if ‖˜xk−xk‖<δk, then
Let us take
Hence if ‖˜x0−x0‖<δ then
Combining (4.5) and (4.6) we obtain that if ‖˜x0−x0‖<min{δ,h} then
Thus we arrive at the exponential stability of the m-cycle {xn}∞n=0.
5.
Stability of cycles of the augmented discrete-time system
Augment discrete-time system (4.1) with system (2.10). This results in system
that is considered in the (p+1)-dimensional space Rp+1. As in the previous section, the function Q(⋅) may be rather general, not only of form (3.1).
Equation (5.1) (a reduced system) can be treated independently of (5.2). If Q(⋅) is continuously differentiable, Lemmas 1, 2 provide conditions for exponential stability of periodic solutions of (5.1).
However, if we consider augmented system (5.1), (5.2) it is easily seen that its solutions cannot be exponentially stable. Indeed, let {tn,xn} and {˜tn,˜xn} be two solutions of (5.1), (5.2) such that ˜x0=x0, but ˜t0≠t0. Then ˜tn−tn≡˜t0−t0 and ˜tn−tn does not vanish as n→∞. Nevertheless, solutions of the augmented system can be just stable.
Theorem 2. Assume that the function Φ(⋅) is Lipschitz with some Lipschitz constant LΦ. Suppose that {tn,xn}∞n=0 is a solution of systems (5.1), (5.2) such that {xn} is an m-cycle of (5.1). Let {xn} be exponentially stable, i. e., there exist numbers δ>0, M≥1 and 0<r<1 such that all solutions {˜xn} of (5.1) with ‖x0−˜x0‖<δ satisfy (4.2) for all n≥0. Then inequality ‖x0−˜x0‖<δ also implies
Proof. From (2.6) we get
for all k≥0. Then ‖x0−˜x0‖<δ implies
We have
hence
If ‖x0−˜x0‖<δ then from (5.4), (5.5) we come to (5.3).
Obviously, (4.2) and (5.3) imply (non-exponential) stability of {tn,xn}∞n=0 considered in Rp+1.
6.
Orbital stability of periodic solutions of the impulsive system
In this section we will introduce a "hybrid" approach to exponential orbital stability for periodic solutions of (2.1)–(2.4) (for a non-impulsive case see [28,29]). This approach is slightly different from the "geometrical" one [21,22,23,24,26].
As previously, let ‖⋅‖ denote the Euclidean norm for vectors and its induced (spectral) norm for matrices [33]. Let {tn,x(t)} be a periodic solution of impulsive system (2.1)–(2.4) defined for t≥t0, n=0,1,…. Assume that O is a periodic orbit of x(t), namely the set
For any point x∈Rp define the distance between x and O as
Assume that the functions Φ(⋅), F(⋅) are continuously differentiable and Lipschitz, satisfying (2.6). Let J(x) be the Jacobian matrix of the right-hand side of (3.1) at a point x and estimates (2.5) be valid. For brevity, we will use notation xn=x(t−n), ˜xn=x(˜t−n), n=0,1,… for solutions {tn,x(t)}, {˜tn,˜x(t)} of (2.1)–(2.4).
Theorem 3. Consider a solution {tn,x(t)} of (2.1)–(2.4) with initial values {t0,x(t−0)=x0} that is an m-cycle for some m≥1. Let the matrix product J(xm−1)⋯J(x0) be Schur stable. Then their exist constant numbers C0>0, C>0, 0<r<1, Δ0>0, Δ>0 such that for any other solution {˜tn,˜x(t)} of (2.1)–(2.4) with initial values {˜t0,˜x(˜t−0)=˜x0} satisfying inequalities
it follows that
for all n≥0.
Proof. Consider discrete-time systems (2.9), (2.10) related to (2.1)–(2.4). From Lemmas 1, 2 we conclude that the sequence {xn} is an exponentially stable solution of (2.9).
Thus there exist numbers δ>0, M≥1 and 0<r<1 such that all solutions {˜xn} of (2.9) with ‖x0−˜x0‖<δ satisfy (4.2) for all n≥0. Then from Theorem 2 we get that inequality (6.3) is valid with
Let us choose Δ, Δ0 so small that
If inequalities (6.2) are valid, the second inequality (6.5) implies 2|˜tn−tn|≤Φ1 for all n≥0. It follows
for all n≥0. Inequality (6.6) can be also rewritten as
which implies
Let n be an arbitrarily integer, n≥0 and t is a number, ˜tn<t<˜tn+1. The following two cases will be considered.
(i) Firstly, let ˜tn<t<tn+1−tn+˜tn, which follows
Thus
and
Hence
(ii) Let ˜tn+1+tn−tn+1<t<˜tn+1. Then
and
Hence
and
Since 0<r<1, estimates (6.9), (6.10) and (4.2) imply (6.4) with
The proof is complete.
Notice that (6.4) implies
7.
Example
Periodic solutions of dynamical systems are of major interest for characterization of physiological rhythms [34,35,36,37]. Many of these rhythms result from regulatory processes in biological organs. If neurons of the brain are involved into this mechanism, the processes become impulsive (see, e. g., [38,39]) and impulsive differential equations seem to be an adequate mathematical tool for describing them. To reduce the model's complexity and to elucidate regulatory mechanisms lying behind the model, an ensemble of synchronized neurons is sometimes replaced by a consolidated impulsive oscillator [38,40]. This idea was realized in a endocrinological model proposed in [1].
Consider a mathematical model of a hypothalamus-driven hormonal system that is given by impulsive equations [1]
where x1(t), x2(t), x3(t) are scalar functions. Assume that the functions x2(t), x3(t) are continuous and x1(t) has jumps at some times {tn}∞n=0 with
Here F0(⋅), Φ0(⋅) are Hill functions [41]
all the parameters k1, k2, k3, k4, h, q are positive, q is integer.
The biological sense of this model is the following. The function x1(t) describes the concentration in the blood of a hypothalamic hormone, which is released impulsively from an ensemble of neurons of hypothalamus. The function x2(t) is the concentrations of a pituitary hormone, and x3(t) is the concentration of a hormone released from a controlled gland involved in regulation (such as liver, pancreas or gonads). The coefficients α, β, γ characterize hormonal clearance rates, g1, g2 — secretion rates. All the parameters are positive. The hypothalamic hormone stimulates the secretion of the pituitary hormone, the pituitary hormone stimulates the secretion of the controlled gland's hormone. The latter hormone inhibits the neural activity and the impulsive release of the hypothalamic hormone — the impulses become sparser and their amplitudes decrease. (The inhibitory effect is seen from the fact that F0(y) is decreasing and Φ0(y) is increasing for y>0.) Thus the system attains a dynamical equilibrium (homeostasis) that is characterized by some periodic oscillation.
Equations (7.1), (7.2) can be rewritten in the form of (2.1)–(2.4) with
Thus the map Q(x) defined by (3.1) becomes
with the Jacobian matrix
(Here I is the identity matrix of order 3.) For a 1-cycle we have
i. e., the initial value is a fixed point of the map Q(⋅), while for a 2-cycle we obtain two equations
Let us consider a numerical example with
Assume that
Then Eqs. (7.4) have a solution
and
The product of the Jacobian matrices J(x1)J(x0) is Schur stable with the eigenvalues
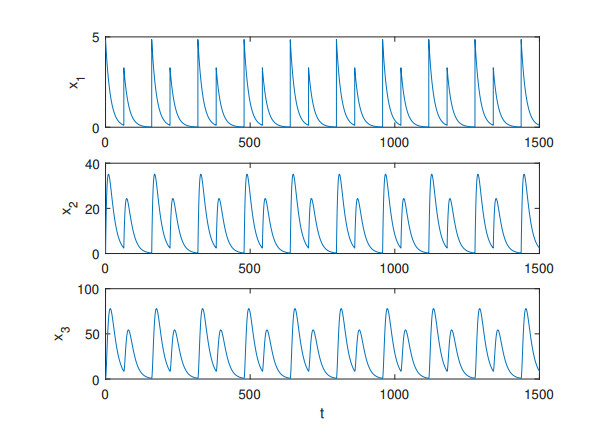
Thus we arrived at an orbitally stable 2-cycle that is visualized in Figure 1. This type of dynamical behavior is observed, e. g., in growth hormone's profiles [42].
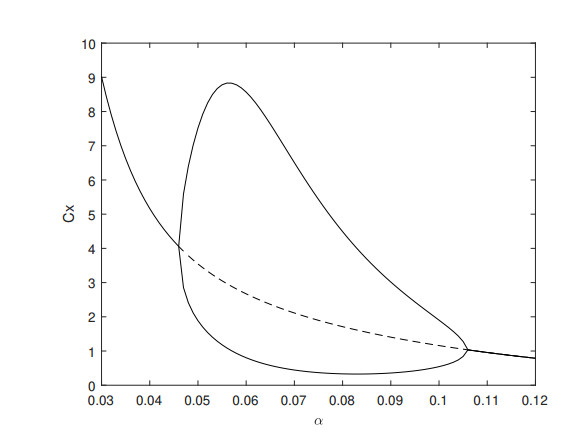
When α varies in the range 0<α<0.12 we get a one-parametric bifurcation diagram shown in Figure 2 [1]. For α<0.045 and α>0.11 we obtain an orbitally stable 1-cycle (the value Cx=Cx0), while for 0.05<α<0.10 there exists an orbitally stable 2-cycle (the values Cx correspond to Cx0 and Cx1). The dashed line indicates an unstable 1-cycle. Thus when α increases, it passes through two bifurcation points — for period doubling and for period halving. Such bubble-type diagrams seem to be conventional for physiological oscillations (see [36]). In [43] it was demonstrated that with a suitable choice of parameters, system (7.1)–(7.3) can possess m-cycles for higher values of m and attain a deterministic chaos.
An understanding of hormonal rhythms opens the way to their administration. In review [37] this problem was named one of the main challenges for the interaction between nonlinear dynamics and medicine.
8.
Conclusion
The paper considers a stability problem for an impulsive system with a linear dynamics between impulses. The magnitudes and times of jumps are variable and depend on the system's states. We are interested in stable periodical solutions of these impulsive systems. The main characteristic of such a solution is a number of jumps per period, which can be obtained by the study of fixed points of auxiliary discrete-time maps. In this paper we propose a new notion of exponential orbital stability that combines the known stability notions for impulsive and discrete-time systems. An easily verifiable criterion for such a stability is provided.
Acknowledgments
A. N. Churilov was supported by the Russian Foundation for Basic Research, grant 17-01-00102-a.
Conflict of interest
The author declares that there is no conflict of interests regarding the publication of this paper.









 DownLoad:
DownLoad: