The averaging method is developed for periodic piecewise-smooth systems. We discuss the behavior of solutions intersecting the discontinuity boundary and the problems it introduces. We illustrate these difficulties on specific examples. In the case of transversal and sliding solutions, we introduce conditions that allow us to prove averaging theorems for piecewise-smooth periodic differential equations.
1.
Introduction
Averaging method has many applications and it is well-developed for ordinary and partial differential equations [4,8], for impulsive and differential inclusions [7], and for more general types of differential equations as well [6,5]. Non-smooth dynamical systems also possess many applications [2]. The goal of this paper is to extend the tool set available for analyzing periodic piecewise-smooth differential equations by generalizing the averaging method. Several intrinsic problems surfaced while trying to generalize the results to the piecewise-smooth setting. We focus on the cases of transversal and sliding solutions of the piecewise-smooth systems. In these cases, we discuss the problems and try to shed some light on their nature and causes by considering concrete examples. Several conditions are introduced which allow us to prove results analogous to the averaging theorem for smooth systems.
Section 2 is a brief introduction to the theory of averaging for smooth systems and contains an averaging theorem whose statement serves as a prototype for statements of our generalizations for piecewise-smooth systems. Section 3 introduces piecewise-smooth systems and our main definitions. Section 4 provides examples that motivated us for these definitions. Section 5 presents some auxiliary results concerning the discontinuity boundary and its intersection with a solution that are used in the next sections. Sections 6 and 7 deal with the proofs of our main results. The final Section 8 summarizes our results with a possible outline for further study.
Throughout the paper, we shall denote u⋅v the inner product of vectors u,v∈Rn and |u| the Euclidean norm of u∈Rn. Furthermore, the distance of sets A,B⊂Rn is defined as dist(A,B)=inf{|a−b|∣a∈A,b∈B}.
2.
Averaging for smooth systems
Let Ω⊂Rn be a domain and a∈Ω. We consider the initial value problem
defined for x∈Ω, ϵ∈[0,1] and t∈R where f(x,t,ϵ) is a continuously differentiable periodic function in the time variable t with the period T.
Definition 2.1. Let f be the right-hand side of initial value problem (2.1). Denote
The averaged system associated with (2.1) is the system
and the guiding system associated with (2.1) is the system
Initial value problem (2.1) gives naturally a rise to the initial value problem for the averaged system (2.2) with z(0)=a, and for the guiding system (2.3) with w(0)=a. The guiding system is only a rescaled averaged system.
The following theorem from [8,Theorem 2.8.1] is the key result we need and it will be used throughout the whole paper.
Theorem 2.2. Consider initial value problem (2.1). Suppose that f is Lipschitz continuous and w:[0,L]→Ω is solution of the associated guiding system. Then there exist positive constants ϵ0, C such that for all ϵ∈(0,ϵ0] there exists a unique solution xϵ:[0,Lϵ]→Ω such that
for 0≤t≤Lϵ.
To simplify some of the statements in the rest of the paper, we collect some of the common assumptions on the right-hand side f in the following definition.
Definition 2.3. We say, that a function f:Ω×R×[0,1]→Rn is T-PCDLB if it is T-periodic in the second argument, continuously differentiable, Lipschitz continuous and bounded.
The following lemma is an extension of the averaging theorem for smooth systems which will be useful in the next sections.
Lemma 2.4. Let f be a T-PCDLB function, w:[L1,L2]→Ω be a solution of the guiding system ˙w=ˉf(w) with w(L1)=a and A≥0 be a constant. Let ϵ∈(0,1]. Consider the local solution of initial value problem ˙x=ϵf(x,t,ϵ), x(L1ϵ+A)=bϵ for bϵ∈Ω such that |a−bϵ|≤Dϵ for some constant D>0.
Then there exist ϵ0,C>0 and a unique solution xϵ:[L1ϵ+A,L2ϵ]→Ω of ˙x=ϵf(x,t,ϵ), x(L1ϵ+A)=bϵ for all ϵ∈(0,ϵ0] such that for all t∈[L1ϵ+A,L2ϵ] it holds
Proof. Let us at first assume the existence of xϵ for sufficiently small ϵ>0 and prove estimate (2.4). Let Aϵ be such that Aϵ≥A, |Aϵ−A|≤T, L1ϵ+Aϵ=kϵT for some kϵ∈Z. The existence of such Aϵ for all ϵ is obvious. Let ϵ0>0 be so small that L1ϵ+Aϵ≤L2ϵ for all ϵ∈(0,ϵ0]. Let M be a bound of |f|.
First, we prove inequality (2.4) for t∈[L1ϵ+A,L1ϵ+Aϵ]. Using the assumption |a−bϵ|≤Dϵ and the Lipschitz continuity of solutions xϵ and w, we obtain
Next, we prove inequality (2.4) for t∈[L1ϵ+Aϵ,L2ϵ]. Since the solution w is defined on interval [L1,L2], we will use the averaging theorem for smooth systems for function ˜w(τ)=w(τ+L1). Hence there exists some C>0 such that for all ϵ>0 sufficiently small, there is a solution yϵ:[0,L2−L1ϵ]→Ω of the initial value problem ˙y=ϵf(y,t,ϵ), y(0)=a, and for all t∈[0,L2−L1ϵ] it holds
Using yϵ we can define a function uϵ:[L1ϵ+Aϵ,L2ϵ+Aϵ]→Ω by uϵ(t)=yϵ(t−(L1ϵ+Aϵ)). The function uϵ satisfies the equation
since L1ϵ+Aϵ=kϵT and f is T-periodic in the second argument.
Now, let t∈[L1ϵ+Aϵ,L2ϵ]. Using (2.5) we estimate
The functions uϵ, xϵ satisfy the same equation (2.1) (however, with possibly different initial values), hence it holds
Using the Lipschitz continuity of f and the Gronwall lemma, we obtain
for some constant C>0. The estimates (2.4), (2.6) for t=L1ϵ+Aϵ imply
Thus the proof of the estimate (2.4) for t∈[L1ϵ+Aϵ,L2ϵ] is finished.
Now we prove the existence and uniqueness. The uniqueness and the local existence of xϵ are consequences of the Lipschitz continuity. The only issue for global existence of xϵ would be if xϵ approaches the boundary ∂Ω.
Denote d=dist(∂Ω,w([L1,L2])). Let ϵ0>0 be such small that Cϵ0≤d2. Then we have
for any ϵ∈(0,ϵ0] and t∈[L1ϵ+A,L2ϵ]. Consequently,
which means that dist(∂Ω,xϵ(t))≥d2 for all t∈[L1ϵ+A,L2ϵ]. Hence, xϵ exists globally on interval [L1ϵ+A,L2ϵ].
3.
Definition of a piecewise-smooth system
We start with a definition of a discontinuity boundary.
Definition 3.1. We say that a function G:Ω→R is a boundary function if G is continuously differentiable and ∇G(x)≠0 for every x∈Ω such that G(x)=0.
For a boundary function G, let us define
The set Ω0 is a C1-manifold and is called a discontinuity boundary or a discontinuity surface. The notation introduced above will be used throughout our paper.
Definition 3.2. Let Ω⊂Rn be an open set, let f−,f+:Ω×R×[0,1]→Rn and G:Ω→R be functions. We say that the tuple (Ω,G,f−,f+) is a piecewise-smooth system if f− and f+ are continuously differentiable and G is a boundary function. We say that the tuple (Ω,G,f−,f+) is a well-behaved piecewise-smooth system if f− and f+ are T-PCDLB and G is a boundary function.
A shorthand ˙x=f±(x,t,ϵ) will be often used instead of the tuple (Ω,G,f−,f+) while talking about a piecewise-smooth system, implicitly including a set Ω and a boundary function G.
Definition 3.3. An absolutely continuous function x:[a,b]→Ω is called a solution of the piecewise-smooth system (Ω,G,f−,f+) if for almost all t∈[a,b],
Furthermore, we say that a solution of the piecewise-smooth system is a solution of an initial value problem ˙x=ϵf±(x,t,ϵ), x(a)=xa∈Ω if x(a)=xa.
The formalism that we just introduced is called the Filippov regularization of a piecewise-smooth system (see [1,2]).
Next we define two properties for which we will prove the averaging theorem.
Definition 3.4. We say that a well-behaved piecewise-smooth system (Ω,G,f−,f+) is uniformly transversal at the point x0∈Ω0 if there exists a positive constant m such that
for all t∈R and ϵ∈[0,1].
The uniform transversality at x0 also implies that ¯f±(x0)⋅∇G(x0)≥m.
Definition 3.5. We say that a well-behaved piecewise-smooth system (Ω,G,f−,f+) is uniformly sliding, if there exists a positive constant m such that
for all x∈Ω0, t∈R and ϵ∈[0,1].
The condition of uniform sliding itself is not sufficient to prove an averaging theorem. We need to reformulate the guiding system in a following way. Suppose that the condition of uniform sliding is true for every x∈Ω0. This implies, that any solution sliding at t0 has to stay on Ω0 up to some t1>t0. Hence the derivative of the solution is tangent to the manifold Ω0 or, equivalently, it is orthogonal to ∇G(x). A short calculation shows that for a given (x,t,ϵ) such that the piecewise smooth system is sliding at (x,t,ϵ), there is a unique element of conv({f−(x,t,ϵ),f+(x,t,ϵ)}), which is orthogonal to ∇G(x). We define function g:Ω0×R×[0,1]→Rn,
where
The function g can be used to define an induced differential equation on some neighborhood of (x,t,ϵ) in the set Ω0×R×[0,1]. The smoothness of g depends on the smoothness of f−, f+ and ∇G; see [1] for details. We can apply averaging to this function to get
which serves as a right-hand side of the guiding system ˙u=ˉg(u) for the equation induced on the discontinuity surface.
Definition 3.6. Let (Ω,G,f−,f+) be a well-behaved piecewise-smooth system that is uniformly sliding. Let ˉg be defined as in (3.3). The sliding adjusted guiding system associated with the initial value problem ˙x=ϵf±(x,t,ϵ), x(0)=a∈Ω− is given by
An absolutely continuous function w:[0,L]→Ω is a solution of the sliding adjusted guiding system, if it satisfies the above equality almost everywhere.
Suppose that we are given an initial value problem for a piecewise-smooth system (Ω,G,ϵf−,ϵf+),
such that both f− and f+ are T-periodic. Our goal is to generalize the averaging theorem, Theorem 2.2, to this setting. Akin to Definition 2.1, we can define
and also define a guiding system associated with (3.4) as
Given a solution w:[0,T]→Ω of the guiding system (3.5), it is clear that if (Im w)∩Ω0=∅, we can use the result for smooth systems by restricting ourselves to a neighborhood of Im w that entirely lies inside Ω− or inside Ω+.
That is the reason why we will be concerned only with solutions of the guiding system (3.5), which intersect Ω0. Furthermore, we will assume that w(0)=a∈Ω−. It is easy to see that if a∈Ω+, it suffices to exchange G for −G and all the results hold. We are not going to explicitly consider a∈Ω0, but such an initial condition is a special case that can usually be easily inferred from presented results.
4.
Some useful examples
Let us start with an example, which shows that we cannot simply adapt the averaging theorem by adding the word `piecewise' to the statement. More specifically, we construct a well-behaved piecewise-smooth system and a transversal solution of the associated initial value problem and we show that the result of the averaging theorem does not hold.
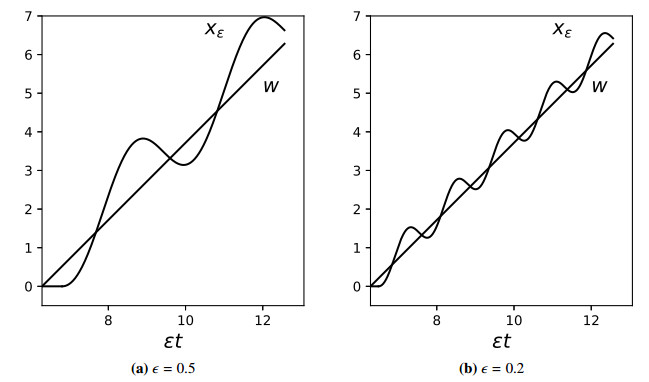
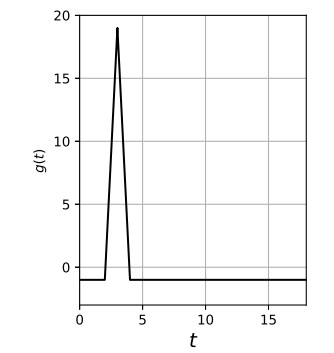
Example 4.1. Let us define g as a periodic function with period 18, which is defined on the interval [0,18] by the following formula (see Figure 1):
We can calculate that
We will use the standard mollifier as defined in [3,p.629],
For each δ>0, we set
and we define
By [3,p.630,Theorem 6(ⅰ)], gδ∈C∞(R). Let 0<δ<2 be fixed such that
and ∫180gδ(t)dt>0, which can be done due to [3,p.630,Theorem 6(ⅲ)]. We can immediately see that
We will show that gδ has exactly two zeros in [0,18]. The derivative of gδ is
where h is the periodic continuation of
This implies that (gδ)′(t)>0 for t∈(2−δ,3) and (gδ)′(t)<0 for t∈(3,4+δ). Hence, by (4.1), gδ has on [0,18] just two zeros: r1∈(2,3), r2∈(3,4).
Consider ˙x=ϵf±(x,t), x∈R, t∈R with a boundary function G(x)=x and
Such a system is well-behaved. The corresponding averaged version of these functions is
and the guiding system is ˙w=I. Consider the initial value problem w(0)=−C whose solution is w:[0,L]→R, w(t)=−C+It where C∈R+ and L>CI.
We will show that although the averaged system has a transversal solution for all choices of C and L satisfying the conditions above, the original system has no solution that begins in R− and then crosses over to R+.
Suppose that xϵ(t) is such a solution, meaning that xϵ(0)<0 and there is a t∗ such that xϵ(t∗)=0 (that is, it intersects the boundary Ω0={0}).
Let t0=sup{t∣∀s∈[0,t):xϵ(s)<0}. The definition of t0 and existence of t∗ imply that xϵ(t0)=0. Since for all s<t0 we have xϵ(s)<0, for each m∈N there is tm∈(t0−1m,t0) such that ϵgδ(tm)=˙xϵ(tm)>0. This implies that t0∈[r1+18l,r2+18l] for some l∈Z. Consequently, for all t∈[t0,r2+18l] it holds that ϵf−(t)≥0, ϵf+(t)<0 implying that xϵ(t)=0.
For all t∈(r2+18l,(18−r2)+18l) it holds that ϵf−(t)<0, ϵf+(t)<0 which means that ˙xϵ(t)<0. Thus, xϵ(t)<0 and also xϵ((18−r2)+18l)<0.
For all t∈[(18−r2)+18l,r1+18(l+1)], ϵf−(t)<0 which implies
Since
there is t1∈(r1+18(l+1),r2+18(l+1)) such that xϵ(t1)=0 and t1=sup{t∣∀s∈(r2+18l,t):xϵ(s)<0}.
The same analysis as for t0 can be repeated for t1, etc. The solution can be extended up to infinity, but does not cross the boundary. However, the solution of the guiding system crosses the boundary without a problem. The problem is that the guiding system does not reflect the behavior of the original equation at the discontinuity boundary.
Now, we provide an example of an initial value problem for a well-behaved piecewise-smooth system. The solution of the associated guiding system is transversal, while there is a solution of the original system for which the estimate from the averaging theorem holds and this solution is not transversal.
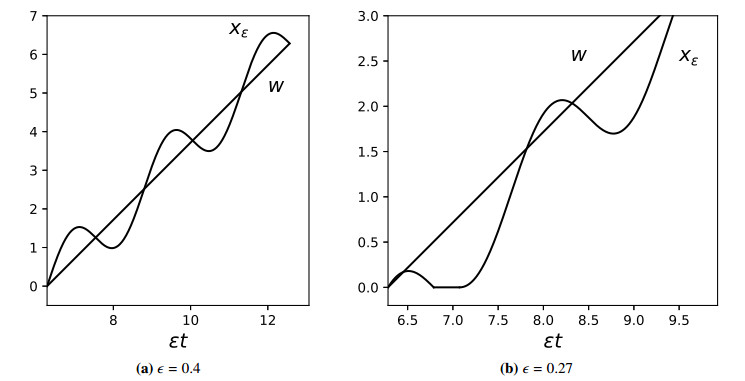
Example 4.2. Let G(x)=x be the boundary function and consider a system ˙x=ϵf±(x,t), x∈R, t∈R with
and an initial condition x(0)=−2π.
The guiding system is ˙w=1, which is transversal at x=0 and we can immediately write the solution of the guiding system as
which means that
The solution of the original system up to the intersection with the discontinuity, that is for t∈[0,2πϵ], is given by
The solution xϵ can cross Ω0 transversally at t=2πϵ only if f+(0,2πϵ)>0. That implies
Let ϵk>0 be such that 1ϵk∈(−16+k,16+k) for some k∈Z (see Figure 2). For such ϵk, the solution xϵk makes the first contact with the boundary at t=2πϵk∈(−π3+2kπ,π3+2kπ). However, since f+(t)≤0 up to π3+2kπ, we can say that the solution "sticks" to x=0 up to t=π3+2kπ.
By solving the system ˙x=ϵkf+(x,t), x(π3+2kπ)=0 we obtain a continuation of the solution xϵk, namely
where Ck=2ϵksin(π3+2kπ)−ϵk(π3+2kπ).
Such a solution does not make a contact with the boundary again. To see that, it only suffices to look at the values of t−2sint−π3+2sin(π3) for t>π3.
Now, we show that condition (2.4) is satisfied. For t∈[2πϵk,2kπ+π3],
For t>2kπ+π3,
because
The analysis for other values of ϵ is a bit more tricky. The solution crosses Ω0 transversally, but it can make a contact with the boundary again. If it makes the second contact with the boundary, it will continue with the same motion as we just analyzed (see Figure 3).
However, the difference in values of wϵ and xϵ will be less than C|ϵ| for some C>0. That means that the averaging estimate still holds on an interval [0,T] for any T.
Note that the condition that the solution of the guiding system w is transversal translates to a condition that the system ˙w=ˉf±(w) is transversal at x0. However, that does not imply that the original system ˙x=ϵf(x,t,ϵ) is transversal at x0 for all t∈R,ϵ∈[0,1]. This means that the behavior of the original system near x0∈Ω0 is not reflected by the guiding system and can be more complex. For this reason, we introduce the notion of uniform transversality of the system ˙x=ϵf(x,t,ϵ) at x0 (uniform in t and ϵ).
Now consider the guiding system ˙w=ˉf±(w) associated with ˙x=ϵf±(x,t,ϵ). The right-hand side of the differential equation induced by this guiding system on the discontinuity boundary is given by
where β is given by
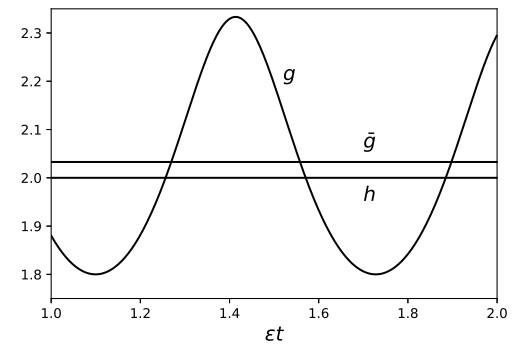
The sliding solution of the guiding system ˙w=ˉf±(w) is governed by h, but ˉg of (3.1) is the true right-hand side of the guiding system for the sliding motion on Ω0.
A question that naturally arise is: What is the relationship between ˉg and h? We could hope that these two functions are equal. However, this is not the case in general. The function ˉg is a result of first inducing an equation on Ω0 and then averaging. For h, those operations are reversed. That is, we first average and induce an equation on Ω0 afterwards. Their relationship is not that simple.
The following example shows a specific system, where ˉg and h are not equal.
Example 4.3. Let the discontinuity surface be defined by G:R2→R, G(x)=x1 and consider the system ˙x=ϵf±(x,t), x∈R2, t∈R with
along with the initial condition x(0)=(−1,−1).
The differential equation induced on Ω0={0}×R is ˙x=ϵg(x,t), where g depends only on t, and is given by
The function α is defined by the equality
By solving for α and substituting into the previous equality, we get
By averaging over the period, we obtain
The guiding system for this example is given by the right-hand side
which induces a differential equation on Ω0, ˙x=ϵh(x), where
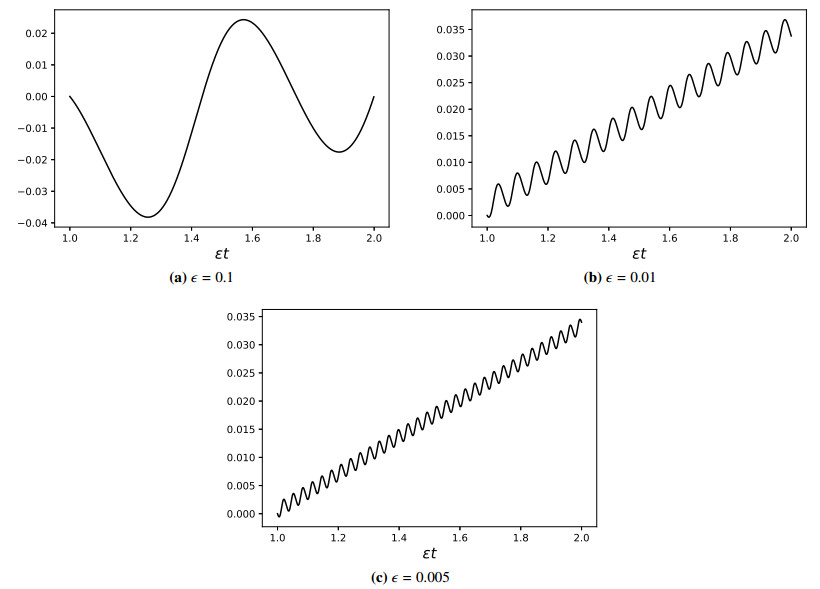
Let us compare the solution of the original initial value problem xϵ and wϵ obtained from the guiding system for τ∈[0,2] (that is, t∈[0,2ϵ]).
For t∈[0,1ϵ] we have
and the solutions make contact with the boundary at t=1ϵ in x=(0,0). After that time, both solutions slide along the discontinuity boundary Ω0. The motion of xϵ is given by the differential equation ˙xϵ=ϵg(xϵ,t), while the motion of wϵ is given by ˙wϵ=ϵh(wϵ)=ϵ(0,2) (see Figure 4).
To analyze the behavior of xϵ on the boundary for sufficiently small ϵ, we can employ the averaging theorem for smooth systems. In the following, let us drop the first coordinate (which is constant and equal to 0).
The guiding system for the equation on the boundary has the right-hand side equal to ˉg0. Using Lemma 2.4 (an extension of the averaging theorem), there is ϵ0>0, C>0 such that for all ϵ∈(0,ϵ0] and t∈[1ϵ,2ϵ],
In particular, at t=2ϵ we have
On the other side,
which means that it cannot be true that there exists a constant ˜C>0 such that for all t∈[1ϵ,2ϵ] and all ϵ>0 sufficiently small,
Indeed, otherwise one would get a contradiction from
(see Figure 5).
5.
Analysis of the discontinuity boundary Ω0
For the purpose of this section, we denote Br(a)={x∈Rn∣|x−a|<r}. The next theorem shows that the function G can be thought of as a distance function on some neighborhood of a point x0∈Ω0.
Theorem 5.1. Let Ω⊂Rn be an open set and G:Ω→R a continuously differentiable function. Suppose that x0∈Ω0={x∈Ω∣G(x)=0} and that ∇G(x0)≠0. Then there exist positive numbers d,α,β∈R, such that ¯Bd(x0)⊂Ω, and for each x∈¯Bd(x0),
Proof. Since the functions (x,y)↦∇G(x)⋅∇G(y) defined on Ω×Ω and x↦|∇G(x)| defined on Ω are continuous and ∇G(x0)⋅∇G(x0)>0, |∇G(x0)|>0, there are positive constants d, a, A, b, B such that ¯B2d(x0)⊂Ω and for all x,y∈¯B2d(x0),
Suppose that x∈¯Bd(x0) and z∈Ω0 is such that |x−z|=dist(x,Ω0). Since x0∈Ω0 and |x−x0|≤d, it follows that |x−z|≤d. Hence |x0−z|≤2d, i.e., z∈¯B2d(x0). Consequently, ∇G(z)≠0. It follows from the geometry that x−z=k∇G(z) where k=sgn G(x)|x−z||∇G(z)|=sgn G(x)dist(x,Ω0)|∇G(z)|. Hence, it holds
Using the inequalities (5.1), we arrive at
and the statement easily follows.
In the next lemma, we consider a system with C1-smooth right-hand side but included in Ω=Ω+∪Ω0∪Ω−. So, we can estimate the time and position of the contact with Ω0.
Lemma 5.2. Let f be T-PCDLB and G be a boundary function. Let w:[0,L]→Ω be a solution of the initial value problem ˙w=ˉf(w), w(0)=a∈Ω− and xϵ:[0,Lϵ]→Ω be a solution to ˙x=ϵf(x,t,ϵ), x(0)=a. Assume that w intersects Ω0 in exactly one point x0 at τ0∈(0,L) and ˉf(x0)⋅∇G(x0)>0.
Then there exist positive constants ϵ0,A,B such that for all ϵ∈(0,ϵ0], the solution xϵ intersects Ω0 in some point and if we define tϵ to be the smallest t such that xϵ(t)∈Ω0, then
Proof. Let M be a bound of |f|. Due to the smooth averaging, Lemma 2.4 can be used to show that there exist C>0 and ϵ0>0 sufficiently small such that for all ϵ∈(0,ϵ0] and t∈[0,Lϵ], it holds
In the rest of the proof, ϵ0 may decrease.
Since w(L)∈Ω+, we have G(w(L))>0. Then the estimate (5.2) and the continuity of G imply that G(xϵ(Lϵ))>0 for all ϵ∈(0,ϵ0]. Since G(xϵ(0))=G(a)<0, the solution xϵ crosses Ω0 in some point.
Due to the continuity of mapping x↦ˉf(x)⋅∇G(x) and Theorem 5.1, there exist positive constants d, m, α, β such that ¯Bd(x0)⊂Ω, and for all x∈¯Bd(x0), it holds
Let A be a constant such that A>Cmα where C is from (5.2). Let ϵ0 be such that τ0−ϵ0A>0, τ0+ϵ0A<L and MAϵ0≤d. If we choose ϵ∈(0,ϵ0], then for all τ∈[τ0−Aϵ,τ0+Aϵ]⊂[0,L], it holds
i.e., w(τ)∈¯Bd(x0). Since w(τ0+Aϵ)∈Ω+, we have G(w(τ0+Aϵ))>0 and we obtain
due to the first inequality of (5.3). Now, we can use the other inequality of (5.3) to get
Observe that the set w([τ0+Aϵ0,L]) is compact and lies in Ω+. Therefore, dist(w([τ0+Aϵ0,L],Ω0)>0. Consequently, for some ϵ0>0 and all ϵ∈(0,ϵ0], we obtain
The estimate (5.2) implies that for any ϵ∈(0,ϵ0],
Due to our choice of A, we deduce that xϵ(t)∈Ω+ for all t∈[τ0+Aϵϵ,Lϵ], ϵ∈(0,ϵ0].
Using similar arguments, we can show that
for all ϵ∈(0,ϵ0] for some (possibly smaller than before) ϵ0>0. Hence, there exists tϵ∈(τ0−Aϵϵ,τ0+Aϵϵ) such that xϵ(tϵ)∈Ω0. Furthermore, the following estimate is valid:
6.
Uniformly transversal systems
In this section, we prove an averaging theorem for uniformly transversal systems. First we prove an auxiliary result.
Lemma 6.1. Let (Ω,G,f−,f+) be a well-behaved piecewise-smooth system that is uniformly transversal at x0∈Ω0. Let w:[0,L]→Ω be a solution of the guiding system ˙w=¯f±(w),w(0)=a∈Ω− which intersects the boundary Ω0 in exactly one point w(τ0)=x0 at τ0∈(0,L).
Suppose that there is ϵ1∈(0,1] such that for all ϵ∈(0,ϵ1] there is a unique solution xϵ:[0,Lϵ]→Ω of the problem ˙xϵ=ϵf±(xϵ,t,ϵ), xϵ(0)=a intersecting the boundary Ω0 at exactly one point in time.
Then there are ϵ0∈(0,ϵ1] and C>0 such that for all ϵ∈(0,ϵ0] and all t∈[0,Lϵ],
Proof. We know that w is a solution of ˙w(τ)=ˉf−(w(τ)) for τ∈[0,τ0], satisfying w(0)=a. Since the right-hand side ˉf− is defined on the whole Ω, there is a solution w−:[0,L−]→Ω of the same problem for some L−>τ0. This solution is equal to w on [0,τ0]. The uniform transversality at x0 implies that ˙w−(τ0)≠0. Hence the solution w− intersects Ω0 exactly once if L− is sufficiently close to τ0.
In what follows, the constants ϵ0 and C may vary from step to step. By Theorem 2.2, for every ϵ∈(0,ϵ0], there is a unique solution x−ϵ:[0,L−ϵ]→Ω of the initial value problem ˙x=ϵf−(x,t,ϵ), x(0)=a such that
for all t∈[0,L−ϵ]. The assumption of uniform transversality at x0 and Lemma 5.2 imply that there are positive constants A, B such that for all ϵ∈(0,ϵ1], the solution x−ϵ intersects Ω0 and it holds
where tϵ is the earliest time of intersection. Our assumption on f− implies that tϵ is the time of the only intersection. Clearly, the solution x−ϵ is equal to xϵ on [0,tϵ] and x−ϵ(t)∈Ω+ for t∈(tϵ,L].
Since the functions f± are bounded, the solutions xϵ, w are Lipschitz continuous. For t∈[τ0ϵ−A,τ0ϵ+A], we estimate
Since x−ϵ(τ0ϵ−A)=xϵ(τ0ϵ−A) and w−(τ0−ϵA)=w(τ0−ϵA), using Lipschitz continuity of xϵ, w and inequality (6.2), we arrive at (6.1) for t∈[τ0ϵ−A,τ0ϵ+A].
Now, let t∈[τ0ϵ+A,Lϵ]. For all such t we have that w(t),xϵ(t)∈Ω+. Hence xϵ is a solution of equation ˙x=ϵf+(x,t,ϵ) and w is a solution of the corresponding guiding system. Lemma 2.4 with L1=τ0, a=w(τ0) and bϵ=xϵ(τ0ϵ+A) implies the existence of ϵ0,C>0 such that for all ϵ∈(0,ϵ0], it holds
for all t∈[τ0ϵ+A,Lϵ]. This estimate concludes the proof.
Theorem 6.2. Let (Ω,G,f−,f+) be a well-behaved piecewise-smooth system that is uniformly transversal at x0∈Ω0. Let w:[0,L]→Ω be a solution of the guiding system ˙w=¯f±(w), w(0)=a∈Ω− which intersects the boundary Ω0 in exactly one point w(τ0)=x0 at time τ0∈(0,L).
Then there are ϵ0>0 and C>0 such that for all ϵ∈(0,ϵ0] there exists a unique solution xϵ of the problem ˙xϵ=ϵf±(x,t,ϵ), xϵ(0)=a, intersecting Ω0 exactly once, the intersection is transversal, and for all t∈[0,Lϵ], it holds
Proof. The main idea of the proof is to use the averaging theorem, Theorem 2.2, for smooth systems in Ω− and Ω+ separately and to construct a solution of the piecewise-smooth system ˙x=ϵf±(x,t,ϵ) that crosses Ω0 only once.
The proof is divided into two parts. Lemma 6.1 shows that, given a transversal solution of ˙x=ϵf±(x,t,ϵ), the averaging estimate (6.4) holds for all sufficiently small ϵ>0.
Now, it only remains to show that there exists a unique transversal solution for all sufficiently small ϵ. The uniform transversality at x0 implies the existence of d,m>0 such that ¯B2d(x0)⊂Ω and
for all x∈¯B2d(x0), t∈R, ϵ∈[0,1].
Let M be a bound of both |f+| and |f−|. Analogously to the proof of Lemma 6.1, there is L−>τ0 and a solution w−:[0,L−]→Ω of ˙w=ˉf−(w), w(0)=a that intersects Ω0 exactly once and w−(τ)=w(τ) for τ∈[0,τ0]. Due to the averaging theorem for smooth systems, there is ϵ1∈(0,1] and C>0 such that for any ϵ∈(0,ϵ0], there is a unique solution x−ϵ:[0,L−ϵ]→Ω of the initial value problem ˙x=ϵf−(x,t,ϵ), x(0)=a such that it holds
for all t∈[0,L−ϵ]. In the following again, the constants ϵ0 and C may vary from step to step. By Lemma 5.2, there are constants A, B such that for all ϵ∈(0,ϵ0] the solution x−ϵ intersects Ω0 and it holds
where tϵ is the time of the first contact. Let ϵ0 be so small that the following inequalities are true
The first inequality of (6.5) implies
for all ϵ∈(0,ϵ0].
Now, let ϵ∈(0,ϵ0] be fixed. Denote x+ϵ(t):[tϵ,s]→Ω the unique local solution of the initial value problem ˙x=ϵf+(x,t,ϵ), x(tϵ)=x−(tϵ) for some s>tϵ. This solution can be extended until it approaches ∂Ω. For t∈[tϵ,s], we estimate
Denote Δ=min{d2M,L−τ0}. From the third inequality of (6.5) we deduce that
Assume that s≤τ0+Δϵ. The inequality tϵ≥τ0−ϵAϵ together with (6.5) imply
Combining this estimate with (6.6), we get
for any t∈[tϵ,s]. This means that the solution x+ϵ is separated from the boundary ∂Ω on [tϵ,s] for arbitrary s≤τ0+Δϵ. Hence, it exists on [tϵ,τ0+Δϵ]. Moreover, since x+ϵ(t)∈¯B2d(x0) for all t∈[tϵ,τ0+Δϵ], it holds
for all t∈[tϵ,τ0+Δϵ], and so x+ϵ(t)∈Ω+.
For ϵ∈[0,ϵ0], define xϵ:[0,τ0+Δϵ]→Ω as follows:
This is a solution of the initial value problem ˙x=f±(x,t,ϵ), x(0)=a, which intersects Ω0 exactly once and the intersection is transversal. Lemma 6.1 implies validity of estimate (6.4) for ϵ∈(0,ϵ0] and t∈[0,τ0+Δϵ].
If τ0+Δ=L the proof is done. Thus assume that τ0+Δ<L. Let
Since ˙w(τ)=ˉf+(w(τ)) for τ∈(τ0,L), we can use Lemma 2.4 with L1=τ0+Δ, a=w(L1), bϵ=xϵ(τ0+Δϵ) and A=0. Hence, there is a unique solution x++ϵ:[τ0+Δϵ,Lϵ]→Ω such that
for all t∈[τ0+Δϵ,Lϵ] and ϵ∈(0,ϵ0]. Observe that x++ϵ(t)∈Ω+ for all t∈[τ0+Δϵ,Lϵ] and ϵ∈(0,hC].
Finally for ϵ∈[0,ϵ0], we define the desired solution xϵ:[0,Lϵ]→Ω as
and estimate (6.4) is valid.
The uniqueness of the solution xϵ follows from the smoothness of f−, f+ and the transversality.
7.
Uniformly sliding systems
Notice that ∇G is used in the definition of the function g. To ensure that the function g is Lipschitz continuous, which is needed to use the averaging theorem for smooth systems, we will need to impose some further conditions on ∇G. One can see that we deal with a differential equation defined on (n−1)-dimensional surface. We will show that it can be analyzed using the techniques available for differential equations defined on open subsets of Rn by extending the equation to an open set in Ω.
Lemma 7.1. Let (Ω,G,f−,f+) be a well-behaved piecewise-smooth system that is uniformly sliding and let g be defined by (3.1). Let M be a compact subset of Ω0 and let ∇G be continuously differentiable and Lipschitz continuous on some open neighborhood V of M. Then there exists an open set U⊂V such that M⊂U, g can be defined by the formula (3.1) on U×R×[0,1], and the function g:U×R×[0,1]→Rn is T-PCDLB.
Proof. We define a function ϕ:Ω→R as
The uniform sliding implies that ϕ(x)≥2m for all x∈Ω0, where m is a positive constant from the definition of uniformly sliding systems. For every x∈M, there is a radius d>0 such that ¯Bd(x)⊂V and ϕ(y)≥m for all y∈Bd(x). Since the compact set M is covered by these balls, there exists a finite open subcover of M. Let U be the union of the balls from the finite open subcover of M. It is clear that ¯U⊂V and ϕ(x)≥m for all x∈U.
This implies that for all x∈U, t∈R and ϵ∈[0,1],
Hence, the function g can be extended to ¯U and one can prove that it has the desired properties.
We are now ready to formulate and prove an averaging theorem for sliding solutions of piecewise-smooth systems.
Theorem 7.2. Let (Ω,G,f−,f+) be a well-behaved piecewise-smooth system that is uniformly sliding. Let w:[0,L]→Ω be a solution of the sliding adjusted guiding system
associated with the initial value problem ˙x=ϵf±(x,t,ϵ), x(0)=a∈Ω−, where g is given by (3.1). Let τ0 be such that 0<τ0<L, w(τ)∈Ω− for τ∈[0,τ0) and w(τ)∈Ω0 for τ∈[τ0,L]. Furthermore, let there be an open set V such that w([τ0,L])⊂V⊂Ω and ∇G is continuously differentiable and Lipschitz continuous on V.
Then there is a constant ϵ0>0 such that for all ϵ∈(0,ϵ0], there is a unique solution xϵ of the problem ˙x=ϵf±(x,t,ϵ), x(0)=a∈Ω− defined on [0,Lϵ] and sliding from time tϵ. In addition, there are constants C,A>0 such that |tϵ−τ0ϵ|≤A and
for all t∈[0,Lϵ].
Proof. The uniform sliding condition implies that
Hence there is a solution w− of ˙w=ˉf−(w), w(0)=a defined on [0,L−] for some L−>τ0 such that w−(τ)∈Ω+ for all τ∈(τ0,L−].
The averaging theorem for smooth systems implies that there exist ϵ0,C>0 such that for all ϵ∈(0,ϵ0], there is a unique solution x−ϵ of ˙x=ϵf−(x,t,ϵ), x(0)=a defined on [0,L−ϵ] and it holds
for every t∈[0,L−ϵ]. Lemma 5.2 implies that there are constants A, B such that for all ϵ∈(0,ϵ0], the solution x−ϵ crosses Ω0 and we have
where tϵ is the time of the first contact of x−ϵ with Ω0.
For τ∈[τ0,L], we define w0(τ)=w(τ). Thus the function w0 is the solution of the initial value problem ˙w=ˉg(w), w(τ0)=x0.
Due to Lemma 7.1, there is an open set U⊂V such that g is T-PCDLB on U. The uniform sliding condition implies that the solution x−ϵ can be uniquely extended as a solution x0ϵ of the initial value problem ˙x=ϵg(x,t,ϵ), x(tϵ)=x−ϵ(tϵ). Trajectories of solutions of this system lie in Ω0 and the local solution x0ϵ can be extended at least as long as the solution does not approach the boundary of U. Suppose that x0ϵ can be defined at least up to some s>tϵ.
Assume that s≤τ0ϵ+A. For every t∈[tϵ,s], we estimate
Using estimate (7.1) and the Lipschitz continuity of solutions x0ϵ, x−ϵ and w−, w0, we arrive at
for tϵ≤t≤s≤τ0ϵ+A. Observe that C does not depend on s, if s≤τ0ϵ+A and x0ϵ is separated from ∂U for ϵ0 sufficiently small. Since s was arbitrary, the solution x0ϵ can be defined up to τ0ϵ+A.
At this point, we can use Lemma 2.4 on the initial value problem ˙x=ϵg(x,t,ϵ), x(τ0ϵ+A)=x0ϵ(τ0ϵ+A) with w0:[τ0,L]→Ω and L1=τ0, a=w0(τ0), L2=L. The assumptions of Lemma 2.4 are satisfied since
Hence for all ϵ∈(0,ϵ0], the solution x0ϵ can be extended to the interval [τ0ϵ,Lϵ], and it holds
for all t∈[τ0ϵ+A,Lϵ]. It is clear that the function
is the desired unique solution.
8.
Conclusion
We have contributed to the study of piecewise-smooth differential equations by extending the results of averaging methods for periodic systems to the piecewise-smooth setting. Our main contribution is the analysis of how the boundary behavior influences averaging, especially in case of sliding. We have also proposed some sufficient conditions that allowed us to prove results on averaging in case of transversal crossing and sliding. Moreover, we demonstrated how to achieve results for solutions of piecewise-smooth systems by dividing them into solutions of smooth systems and patching together results from the smooth setting. Future opportunities for study include weakening of the assumptions in the transversal and sliding case and extension of the results to situations, in which f+⋅∇G or f−⋅∇G vanish, which includes grazing solutions. Moreover, it would be interesting to develop an averaging method for differential equations with impacts [2].
Acknowledgments
We thank the referee for valuable comments. The paper was supported in part by the Slovak Research and Development Agency under the contract No. APVV-18-0308 and by the Slovak Grant Agency VEGA No. 2/0153/16 and No. 1/0078/17.
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: