1.
Introduction
Phononic crystals (PnCs) [1] display bandgap properties, wherein the transmission of elastic waves is prohibited. This property can be artificially controlled and manipulated by tailoring the geometrical configurations of PnCs to achieve maximum bandgap widths or target low-frequency regimes. Such tailored designs enable the generation of desired functionalities for waveguiding of sound and elastic waves [2,3], vibration attenuation [4,5] and wave filtering [6,7]. Therefore, the bandgap design of PnCs to satisfy the requirements of various applications has been a significant and compelling area of research. For decades, a large portion of published work has been devoted to the design of one-dimensional (1D) [8] or two-dimensional (2D) PnC structures [9,10,11,12,13,14,15,16]. In comparison to 1D and 2D PnCs, three-dimensional (3D) porous PnCs are of more practical significance due to their all-angle absorbability to acoustic waves, aligning with the 3D propagation characteristics of such waves and their light-weight–high-strength merit. Thereby, concentration has also been directed towards the bandgap design of 3D porous PnCs. It is widely acknowledged that both large mass of lumps and small stiffness of connectors within the PnC facilitate the generation of desirable PnC structures. With this principle in mind, Zhang et al. [17] proposed a 3D PnC with a centered sphere served as a mass lump and four connectors linking to the lump. Ultra-wide low-frequency bandgaps can be acquired by adding ellipsoids to the sphere to raise the mass of the lump and adjusting the shape of connectors to decrease their stiffness. Luca et al. [18] also developed a 3D PnC structure with box-like connections in the center to link spheres and, as a result, the ultra-wide bandgap was achieved when increasing the radii of spheres to raise the lumped mass and decreasing the dimension of connectors to reduce their stiffness. A thin-walled hollow truss-based structure was designed by Delpero et al. [19], in which each truss was attached to the neighboring trusses with two different types of connectors, one made of a solid metal as a heavy mass and one composed of a hollow plastic as a light mass. Elmadih et al. [20] described a 3D metamaterial comprising internal resonators that consist of six struts, each connecting one side of a cubic mass to the inner walls of the unit cell. Increasing the strut diameter would increase the stiffness of the resonator, and increasing the strut length would alter its volume fraction, thus directly influencing the total mass. McGee et al. [21] designed an architected hollow sphere foam consisting of spheres and binders. As expected, by increasing the sphere thickness and thus the lumped mass of the system, a larger bandgap was observed, and a weak connection among hollow spheres also led to the same result.
Manual attempts relying on the empirical knowledge of the designer were the main routine to initialize the geometrical structures of the unit cells in the abovementioned designs of the 3D PnCs. This heavy intuition-reliance design may be far from the desired performances, with outcomes highly dependent on the designers' knowledge. To further improve the performance of the proposed structures, parametric or shape optimizations are usually employed. For example, based on the independent continuous mapping topology method, Zhang et al. [22] initiated a metamaterial microstructure with an extremely narrow bandgap width (nearly zero) and subsequently conducted a parametric optimization design to achieve a microstructure with 42.7% bandgap width. Similarly, Dong et al. [23] conducted parametric optimization on a PnC structure with an initial bandgap width of 21.99% and eventually enlarged the ratio to 37.7%. Utilizing the bidirectional evolutionary structural optimization, Luca et al. [24] performed shape optimization on the initial hole-shape structure lacking full bandgaps and enlarged a maximum bandgap width to 76%. Although the proposed initializing PnC structures can be optimized to their best performance by using parametric or shape optimizations, ultimately optimized performance is deeply affected by initial geometrical topology. In this regard, topology optimization methods have a distinct advantage in overcoming the restriction of predefined microstructures and attaining the desired structures effectively. It is well known that the complicated 3D microstructure poses challenges in formulating the optimization problems of acoustic wave propagation. Accordingly, establishing the explicit relations between the design variables and the targeting properties of the PnC structures is usually difficult. This inherent complexity makes heuristic optimization methods more appealing and suitable than gradient-based topology optimization approaches for bandgap designs of PnCs. Thus, genetic algorithms (GAs) have emerged as the most popular technique employed for the optimization design of PnC bandgaps.
This work conducts geometric-constrained topology optimization to search novel PnC structures and reveal the underlying features among excellent structures. Topology optimization typically involves a high dimensionality of design variables arising from the discretization of the unit cell. This causes computational challenges for both topology optimization and numerical analysis of bandgaps, as finer discretization requires higher computational effort. To handle high-dimensional design variables, pyramid symmetry is proposed to maximize the deduction of variable number and meanwhile broaden the bandgap, as highly symmetrical 3D PnC unit cells tend to open the ultrawide bandgaps [21,25,26,27,28,29] compared with those with less symmetry, as evidenced in previously reported works on 3D PnC designs [19,30,31]. The performance of PnCs depends heavily on the mesh dimension of the unit cell in conventional topology optimization, as discrete elements of the unit cell can only be connected face-to-face in six directions (named 6 connectivity). Specifically, a 3D single-phase PnC usually relies on a mass connector–based structure to generate bandgaps, where large masses of lumps and small stiffness of connectors contribute to superior performance. The stiffness of connectors is directly affected by connection dimension, which is determined by the mesh size. To address this limitation, 26 connectivity is considered where elements can be connected in node-to-node and edge-to-edge manners from 26 possible directions and, accordingly, cylinders are inserted to ensure the stability of node-to-node and edge-to-edge connections. It is expected that 26 connectivity can not only facilitate the diversity of structure patterns but also alleviate the restriction of mesh dependence. Finally, extra geometric constraints are utilized to filter unstable PnC structures.
The remainder of the paper is organized as follows. Section 2 elaborates on the design domain with pyramid symmetry, 26 connectivity for 3D single-phase PnCs, and the exclusion of unstable PnC structures. Section 3 introduces the bandgap calculation and the two-stage genetic algorithm. Section 4 presents the results and discussions regarding the optimized PnC structures. Finally, Section 5 summarizes the research findings.
2.
Materials and methods
2.1. Design domain with pyramid symmetry
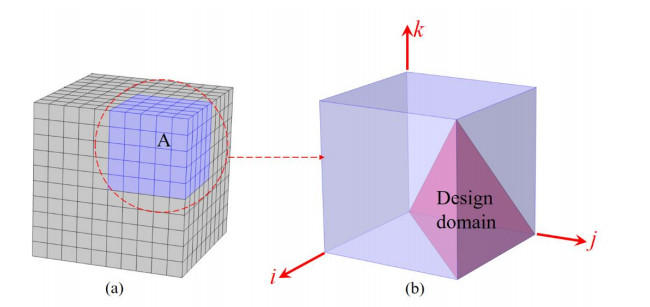
In this paper, the 3D PnC unit cell is discretized into 2N × 2N × 2N elements, including both empty elements and non-empty elements. Each element is assigned with a design variable Xi, where Xi = 0 or 1 represents empty or non-empty status for the ith element. A topology can be determined by a vector X = [X1, X2, ……, Xi, ……, X8N3]. When 2N = 10 (or 20), there would be 1000 (or 8000) design variables corresponding to a search space of 21000 (or 28000). The number of design variables will exponentially climb as N increases. It is well known that the search space for optimization algorithms is determined by the number of design variables. A larger number of variables will cause a larger search space, leading to a slimmer chance and higher computational burden to search the PnC structures with desirable performance. Although 1/8 of the total number of elements (see Figure 1a) is considered as design variables in [32,33], there are still 125 (or 1000) design variables for 2N = 10 (or 20) [with a search space of 2125 (or 21000)]. To further cut down variable dimensions, a novel geometric constraint (pyramid symmetry) for 3D PnC structures is proposed. As shown in Figure 1b, the pyramid-shaped domain serves as the design domain, and the remaining domains are produced by symmetrical operation on the design domain. Thus, only ∑Ni=1(i×(N−(i−1))) variables are required to be designed for a unit cell with 2N × 2N × 2N elements. Specifically, only 35 (or 220) variables for 2N = 10 (or 20) are required in the design, which is much less than 125 (or 1000) variables from the 1/8 symmetry.
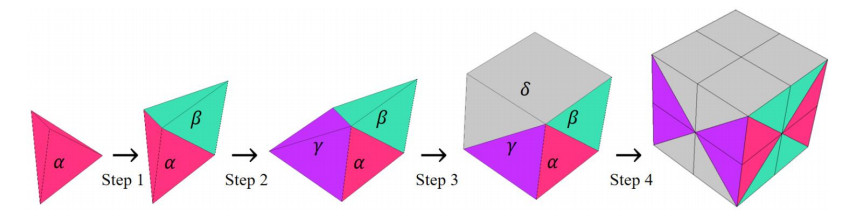
To gain a clear understanding of pyramid symmetry, the details for obtaining the entire unit cell are illustrated in Figure 2. Here, X(j, i, k) represents material assignment (0 for empty or 1 for non-empty) for the element located at the jth column, the ith row, and the kth layer. Thus, the material assignments of all elements in the design domain αcan be denoted by X(j1, k1:j1, k1), where k1∈[1, N], j1∈[k1, N], k1∈Z, j1∈Z. In step 1, the domain β is attained by conducting symmetry operation on the design domain αand the corresponding operation is mathematically expressed in Eq 1:
A similar symmetry operation is carried out on the design domain α to obtain the domain γ, and its material assignments can be stated in Eq 2:
Based on the domains α, β and γ, the material assignments of the domain δ are acquired as shown in Eq 3:
Until now, the 1/8 portion of the unit cell has been completed, which is usually considered as the design domain in the previous scientific research. The entire unit cell is obtained by performing symmetry operations on the 1/8 portion as shown in step 4, and the related mathematical expression is not reiterated.
2.2. 26 connectivity for 3D single-phase PnCs
The term "26 connectivity" (comprising node-to-node + edge-to-edge + face-to-face connections) means that a non-empty element can be connected in 26 possible directions; accordingly, "6 connectivity" (face-to-face connection) indicates connections in only 6 directions. It is noted that there are also other connection scenarios, such as 8 connectivity (node-to-node connection), 12 connectivity (edge-to-edge connection), 14 connectivity (node-to-node + face-to-face connections), 18 connectivity (edge-to-edge + face-to-face connections), and 20 connectivity (node-to-node + edge-to-edge connections). Among them, node-to-node and edge-to-edge connections contribute to reducing the stiffness of connections, rather than enlarging mass of lumps, while only face-to-face connections contribute to forming large lumps. Therefore, a combination of node-to-node and face-to-face connections (14 connectivity) or edge-to-edge and face-to-face connections (18 connectivity) is preferable for generating a potential PnC with flexible connectors and large mass lumps. Therefore, 26 connectivity is chosen, which is a combination of 14 and 18 connectivity, with 6 connectivity serving as a reference.
In 26 connectivity, hinges are common, which are characterized by non-empty elements connected in edge-to-edge and node-to-node manners, as shown in Figure 3a, b. These hinges do not occur in 6 connectivity, as each non-empty element is connected only in a face-to-face manner (see Figure 3c).
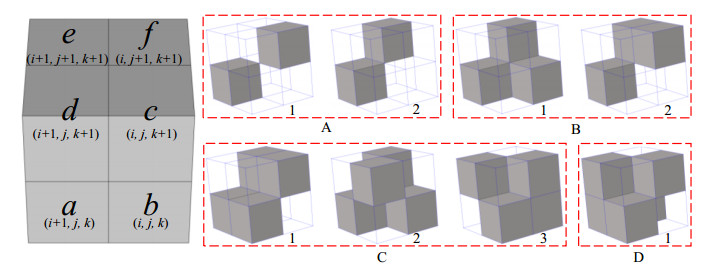
Hinges often adversely affect the stability of the unit cell structures, and therefore cylinders with a certain diameter (d) are inserted to mitigate the adverse effects. Specifically, cylinders are used to connect the centers of two non-empty elements linked in node-to-node or edge-to-edge manners under specified circumstances. For convenient description, eight adjacent elements are represented by labels (a, b, c, d, e, f, g, h) with each one's value denoted by 1 (non-empty) or 0 (empty), as displayed in Figure 4. By summing the values of these elements, the number (N) of non-empty elements can be determined as shown in Eq 4. The relative distance between elements m and n is defined as dmn in Eq 5.
For N = 2, two non-empty elements are assumed to be denoted by m, n∈{a, b, c, d, e, f, g, h}. Distribution patterns of the two non-empty elements are illustrated in Figure 4 (A1) with dmn = 3 and Figure 4 (A2) with dmn = 2. Cylinders are used to connect the centers of these non-empty elements.
For N = 3, three non-empty elements are labeled by m, n, s∈{a, b, c, d, e, f, g, h}. Each two of their centers are connected by cylinders if [dmn dms dns] = [2 2 2] [see Figure 4 (B1)], and only edge-to-edge connected non-empty elements are connected by a cylinder for {dmn dms dns} = {1 2 3}, as shown in Figure 4 (B2).
For N = 4, four non-empty elements are denoted by m, n, s, t∈{a, b, c, d, e, f, g, h}. Only edge-to-edge connected non-empty elements are linked by cylinders if the distributed pattern is as illustrated in Figure 4 (C1), characterized by [dmn dms dmt dns dnt dst] = [1 1 2 2 3 3]. If the distribution pattern is [dmn dms dmt dns dnt dst] = [2 2 2 2 2 2], every two of non-empty elements are linked with cylinders [Figure 4 (C2)]. As for the arrangement represented by [dmn dms dmt dns dnt dst] = [1 1 2 2 2 3] in Figure 4 (C3), only two non-empty elements with a relative distance equal to 3 are joined with a cylinder.
For N = 5, five non-empty elements are represented by m, n, s, t, w∈{a, b, c, d, e, f, g, h}. Only one type of material layout needs to be addressed [see Figure 4 (D1)] where two non-empty elements with a relative distance of 3 are connected by a cylinder. This kind of material distribution can be determined by: [dmn dms dmt dmw dns dnt dnw dst dsw dtw] = [1 1 1 2 2 2 2 2 2 3].
2.3. Exclusion of unstable PnC structures
Aside from the pyramid symmetry and cylinder insertion for the unit cell, additional essential geometric constraints must be introduced to render the optimization progress smoothly. First, all existing non-empty elements in the unit cell of a PnC must be interconnected, and no isolated ones are allowed in the unit cell structure. For instance, the structures in Figure 5 illustrate examples of stable and unstable unit cells for 6 and 26 connectivity. An unstable unit cell with isolated non-empty elements is incapable of generating a stable PnC structure and therefore should be filtered during optimization.
A filtering scheme [34,35] is employed to evaluate the connecting conditions within the unit cells. This method assigns a label to each non-empty element and ensures that their neighboring non-empty elements share the same label. Non-empty elements will be labeled accordingly after the filtering scheme is completed. No isolated non-empty element exists within a unit cell if all labels of non-empty elements are identical.
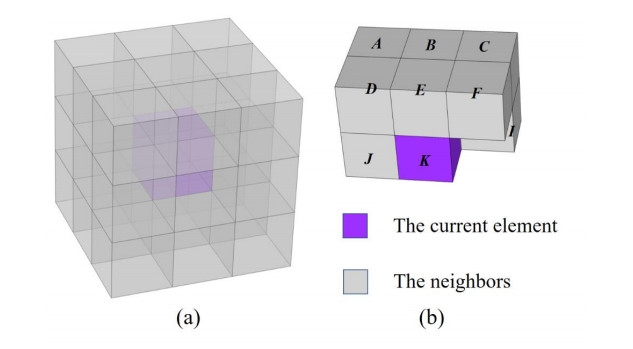
For 26 connectivity, the current element being examined is marked as K and the 10 neighbors in the scanning mask are designated as A–J as shown in Figure 6. All non-empty elements will be given a label when the scanning mask is scanned from top to bottom, left to right, and front to back. Specifically, for the current element K, if it is an empty element, no action is taken. If there is no non-empty element in the mask other than the current element K, the element K is given a new label. Otherwise, it is assigned the minimal label in the mask, and all different labels (if any) in the mask are replaced by this minimal label. For the first scan, the assignment of a provisional label for K can be described as Eq 6. In the second scan, the larger labels are replaced by smaller labels as described by Eq 7.
where L1(K) and L2(K) are the labels of the element K in the first and second scan, V(K) and V(m) denote the element value (0 for empty or 1 for non-empty) of the current element K and neighbor m (m∈{A, B, C, D, E, F, G, H, I, J}), Z is defined as an integer variable initialized to one. If all labels in L2 equate to 1, it means all non-empty elements within the PnC unit cell are interconnected and the corresponding structure satisfies structure stability.
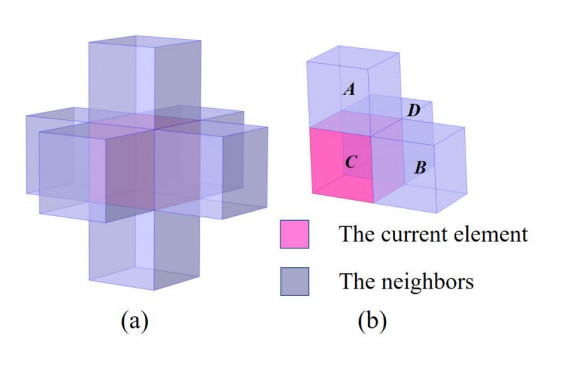
As for 6 connectivity, the current element being examined is marked as C and the three neighbors in the scanning mask are designated as A, B and D, as shown in Figure 7. The corresponding filtering procedure for 6 connectivity follows a similar approach to that for 26 connectivity.
Second, at least one non-empty element should exist in each face of the 3D unit cell. This requirement can be satisfied if there exists at least one non-empty element located in each boundary face of the design domain, and corresponding constraints are expressed as Eqs 8–11:
where X(i, j, k) represents element assignments in domain A (see Figure 1b). The 3D single-phase PnC unit cells that fail to meet the geometric constraints are excluded before numerical calculation.
2.4. Bandgap calculation theory
The propagation of waves can be expressed by using Bloch's theorem and the governing equation can be formulated as Eq 12:
where u = (ux, uy, uz) is the displacement vector, r = (x, y, z) is the coordinate vector, λ and μ are the Lame's constants, and ρ is the mass density.
Based on the boundary conditions, the displacement field can be written as Eqs 13 and 14:
where k is the wave vector, uk(r) is the wave amplitude function, and R is the translation periodicity of the unit cell. Coupling the periodic boundary condition and the governing equation, the dispersion equation can be obtained by Eq 15:
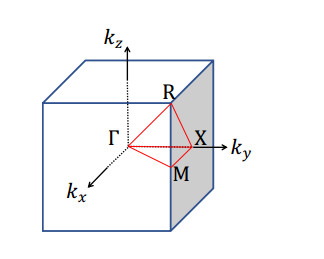
where K, M and U are the stiffness, mass, and displacement matrix, respectively. The energy level diagram of the metamaterials can be established by varying the wave vector along the boundary (Γ-X-M-Γ-R-X/M-R) of the first irreducible Brillouin zone (see Figure 8) based on the finite element numerical calculation.
2.5. Topology optimization scheme
The genetic algorithm is adopted to maximize the relative bandgap width (RBGW) between two adjacent bands, and the related objective function is expressed in Eq 16:
where W is the relative bandgap width; X represents the topology of a PnC unit cell; n denotes the number of the energy band, and m is the number of design variables (m=∑Ni=1(i×(N−(i−1)))).
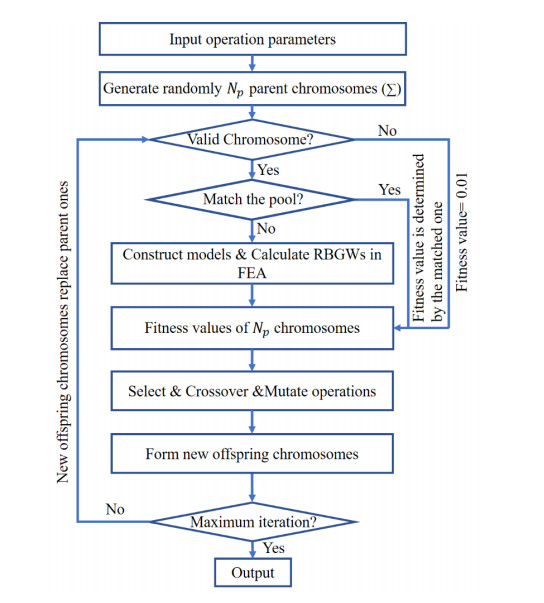
Each topology is encoded as a chromosome with genes featured by 0 (empty) or 1 (non-empty). The survival probability of every chromosome is proportional to their fitness value associated with maximum RBGW. Due to the enormous search space for the genetic algorithm, a two-stage strategy is used in the optimization procedure. For stage one, the genetic algorithm is performed on a unit cell of N × N × N elements, and then the optimal topology from stage one is mapped onto a unit cell with 2N × 2N × 2N elements as the initial structure of a new round of optimization search in stage two. In general, the initial parent chromosomes with population size Np are created randomly or given certain chromosomes, and the maximum RBGW of every chromosome is calculated. Chromosomes with large fitness values are more likely to survive according to roulette wheel selection [36]. In cross operation process, if t1 ≤ Pc (cross probability), a two-point operation is applied on any given pair of chromosomes and t1 is a random number (t1∈[0, 1]). Followed by a mutation operation, t2∈[0, 1] is randomly generated for each chromosome. If t2 ≤ Pm (mutation probability), one of the genes in the chromosome will mutate from 1 to 0 or vice versa. After all these operations are completed, we will obtain a new population of offspring chromosomes. These chromosomes will replace the parent chromosomes. The workflow will be repeated within a prescribed maximum iteration (see Figure 9).
It is worth noting that invalid chromosomes (representing unstable PnC structures) cannot be completely excluded from the search space. Although as coarse as 10 × 10 × 10 meshes and pyramid symmetry are employed, there are still 235 (≈3.4×107) chromosomes in total. Let's assume that each chromosome requires 1 second to be checked and filtered if invalid, then a total of 393 days are needed to do so, which is nearly unapproachable. Hence, invalid chromosomes will be unavoidably generated and searched, but they will be excluded from the simulation analysis. Considering that their presence may contribute to the evolution of the optimization process, the fitness value of each invalid chromosome is assigned a relatively low value (0.01). This can be unreasonable, however, as the RBGWs for some valid chromosomes may be lower than 0.01. As a result, the fitness value for each valid chromosome is set to be the sum of their RBGW and a positive constant θ (θ = 2). In addition, a single chromosome may be reproduced many times in the process of topology optimization. To avoid a repeated simulation analysis like this, all previously appeared chromosomes and their fitness values are stored in a pool. Before being calculated in the FEA, each newly generated chromosome is examined based on the pool. If it matches one of the chromosomes from the pool, its fitness value is determined directly by this one in the pool.
3.
Results and discussion
The lattice constant of the unit cell is set as a = 50 mm, with a cross probability Pc = 0.9, mutation probability Pm = 0.1, and the population size Np = 20. The diameter of the cylinders is considered as a/25 [27,37] to meet the manufacturing requirement. Nylon PA12 is used with a Young's modulus E = 1.586 Gpa, density ρ = 1000 kg/m3, and Poisson's ratio ν = 0.4. A coarse mesh of 10 × 10 × 10 elements is used at stage one with a maximum iteration of 300. The optimized structure from stage one is mapped onto a unit cell with 20 × 20 × 20 elements as the initial structure for stage two, and the corresponding maximum iteration is set as 400. It should be noted that other symmetry shapes can be used, such as diamond symmetry and 1/8 symmetry, but these symmetries have been proven to fail to obtain desirable structures: the former lacks high symmetry and the latter causes a high dimensionality of design variables. One can imagine that optimizing a desired structure is unapproachable if no symmetry is used. By contrast, the pyramid symmetry strategy can confine the search space to a promising space, which can help the optimization procedure to search for desired solutions efficiently. Therefore, only the optimization examples using pyramid symmetry are illustrated in the following work.
3.1. The effectiveness of the adopted algorithm
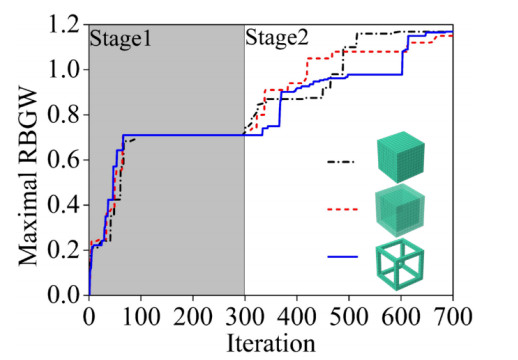
To demonstrate the effectiveness of the adopted algorithm, the optimization procedure is initiated from three different initial settings based on 6 connectivity. As bandgaps between many pairs of bands cannot be opened, inappropriate goal setting of bandgap rank may lead to significant time consumption. Considering previous man-made structures in [18,27,28,37], it appears feasible to open a wide bandgap between the 18th and 19th bands. Accordingly, the objective of the topology optimization is set to maximize the bandgap between the 18th and 19th bands. The optimization task for each initial structure setting is repeated multiple times, and the optimized structures obtained from the same initial structure setting are found to be identical or similar to each other; therefore, only one of the results for each initial structure setting is displayed here. Figure 10 illustrates that topology optimization begins from the three initial structure settings, each with zero bandgaps. It progresses and converges to the same value of 71% within 100 iterations at stage one, and the final structures attained show a similar bandgap width of 117% and a similar optimized structure at stage two, demonstrating the effectiveness of the adopted topology algorithm. It is noteworthy that the ultimately optimized structure remains unaffected by the initial structure settings.
3.2. Topology optimization based on 6 connectivity
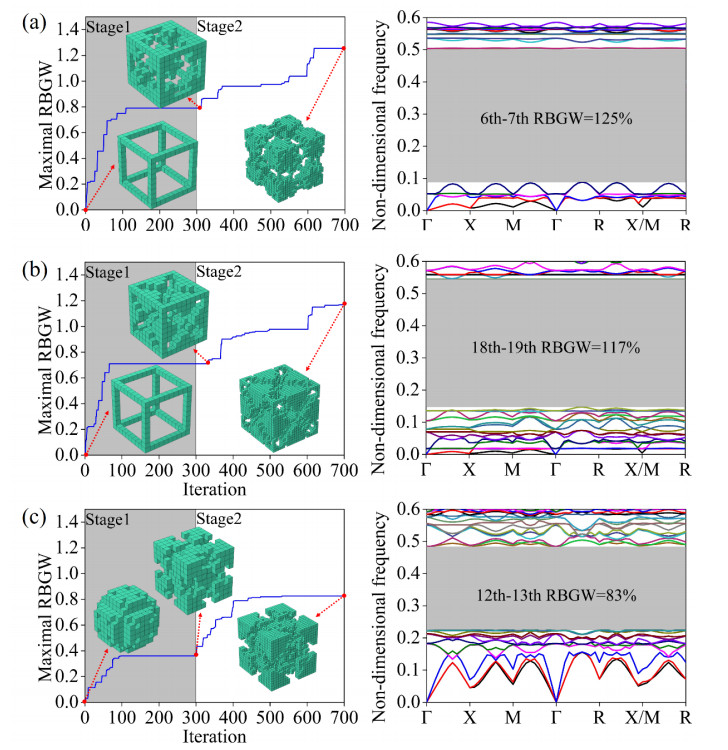
To explore various optimized structures, topology optimization is conducted to maximize the bandgap between certain pairs of adjacent bands within the first 30 bands based on 6 connectivity. Optimization calculation shows that it is impossible to open any bandgaps from the first five bands, and only a few pairs of adjacent bands show promising potential to open relatively wide bandgaps. The evolution history of the 6th–7th, 12th–13th, and 18th–19th bandgap widths and corresponding band structures are displayed in Figure 11. Topology optimization starts from the initial settings with zero bandgaps and converges rapidly within 100 iterations at values of 79%, 36%, and 71% for the 6th–7th, 12th–13th, and 18th–19th bandgaps at stage one. These bandgaps are enlarged by 58.2%, 130.6%, and 64.8% with much more iterations required at stage two. Approximate 15 (25) min and 20 (35) GB float type data are consumed for each iteration at stage one (two). This indicates that the lower dimensionality of design variables at stage one can facilitate the RBGW convergence with less computational effort and time, although potentially compromising the performance of the resulting structures. In comparison, high-dimensional design variables at stage two can improve the performance of the optimized structures, but a large amount of computational effort and time are inevitably required. Therefore, it is important to strike a balance between resource consumption and structural performance.
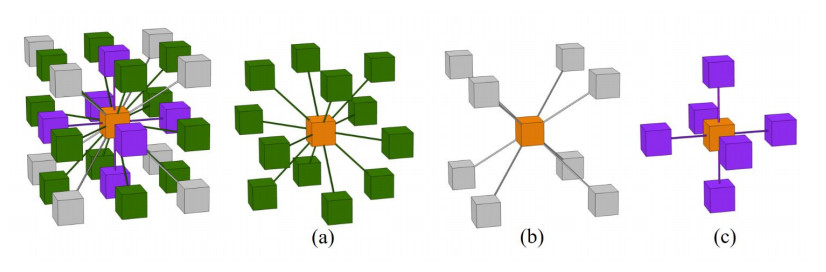
Among the three optimized unit cells, the simple lattice shown in Figure 11a illustrates the broadest bandgap in the lowest frequency spectrum. That is why the traditional simple lattice is typically selected to construct PnC structures with superior bandgap properties. Interestingly, although the optimal configuration in Figure 11b does not fall into the traditional lattice, it displays outstanding performance with a broad bandgap in a low-frequency domain. Its unit cell topology is characterized by twelve identical masses of lumps. The body-centered unit cell in Figure 11c displays a narrower bandgap in a higher-frequency domain compared to the other two structures. When examining the PnC structure formed by the repetition of the unit cell while disregarding the connections, it is observed that there is only one type of mass lump present within the configurations depicted in Figure 11a, b, whereas the one in Figure 11c displays a configuration containing two types of mass lumps. This implies that structures comprised solely of one type of mass lump (ignoring the tiny mass lump) are more inclined to yield favorable performance than those incorporating multiple types of masses.
3.3. Topology optimization based on 26 connectivity
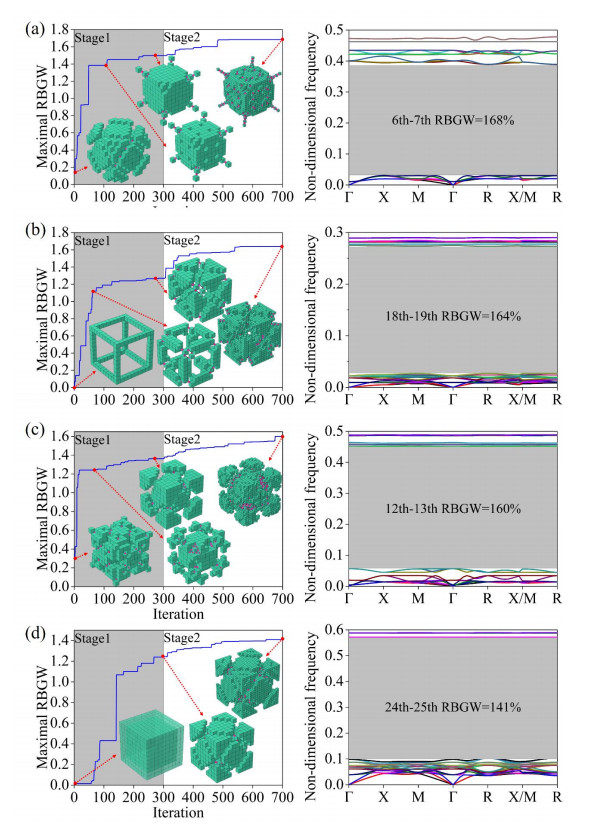
In this section, topology optimization is carried out on 26 connectivity to explore the novel structures with the maximized bandgap within the first thirty bands. Besides the bandgaps opened under 6 connectivity, the 24th–25th bandgap is found to be promising under 26 connectivity. The evolution history of the maximum RBGWs between different adjacent bands and corresponding band structures is displayed in Figure 12. It is evident that topology optimization starts from the initial settings featuring narrow or zero bandgaps and progresses towards the desired configurations with broad bandgaps. Specifically, the rapid convergence speed for maximum RBGWs occurs at stage one with values converging at 148%, 127%, 136%, and 124%, followed by a slow pace at stage two with values at 168%, 164%, 160%, and 141%. 25 (45) min/35 (60) GB float type data is required for each iteration at stage one (two).
The performance of resulting structures under 26 connectivity at stage one (or two) is superior to 6 connectivity. Even the optimized structures with a mesh of 103 elements under 26 connectivity demonstrate significantly superior performance compared to those with 203 elements under 6 connectivity, according to Figures 11 and 12. This is mainly because the performance of optimized structures under 6 connectivity is highly mesh dependent. Specifically, it is more difficult to produce small stiffness of connectors than large masses of lumps, as the minimum size of connections is restricted by the mesh size. This explains why the bandgap widths are increased considerably when using a fine mesh at stage two, according to Figure 11. For the structures under 26 connectivity, the insertion of cylinders mitigates the restriction of mesh dependence and contributes to forming various connections. This sheds light on why the 24th–25th bandgap can be opened under 26 connectivity other than 6 connectivity. Compared to 6 connectivity, however, topology optimization under 26 connectivity demands significant time and computational effort.
According to Figure 12, the simple lattice in Figure 12a demonstrates its dominant advantage in generating excellent performance. The optimized structure in Figure 12b, comprised of 12 identical mass lumps, presents the second broadest bandgap in the low-frequency domain. The body-centered lattice in Figure 12c, characterized by eight small lumps and one large lump, shows a slightly narrower bandgap in the relatively higher-frequency spectrum. Among the four optimized structures, the face-centered lattice in Figure 12d possesses the narrowest bandgap in the highest frequency domain. The same conclusion can also be drawn for 26 connectivity: the PnC configurations containing only one type of large mass lump (ignoring the tiny mass lump) possess greater potential to produce excellent performance, as shown in Figure 12a, b. This interesting finding can also be witnessed in the existing man-made structures exhibiting ultrawide bandgaps in [18,27,28,37], where these PnC structures coincidentally feature only one type of mass lump.
Aside from the geometrical features of the optimized structures, it is also of interest to investigate the relationship between the bandgap rank and the corresponding structure. According to Figures 11 and 12, it is obvious that the 6th–7th, 12th–13th, and 24th–25th bandgaps correspond to the simple, body-centered, and face-centered lattices, and the 18th–19th bandgap relates to a brand-new lattice featured by identical mass lumps. It reveals that geometric patterns of the ultimately optimized structures are closely associated with the specific rank of the bandgap. It is recommended for other researchers to optimize the bandgaps between the 6th and 7th, 12th and 13th, 18th and 19th, and 24th and 25th bands separately, as these ranks of the bandgaps have been demonstrated to be capable of generating broad bandgaps. Meanwhile, it is not advisable to optimize the bandgaps between adjacent bands in the first specific number of bands simultaneously, as the structures associated with the 6th–7th and 18th–19th bandgaps are prone to be searched compared with other counterparts. This operation is counterproductive to exploring various structures.
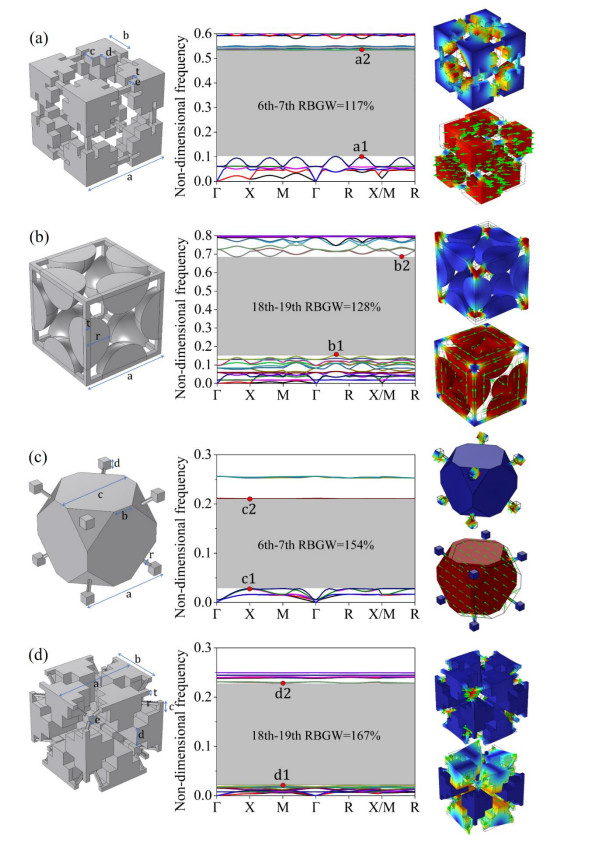
3.4. Parameterized structures
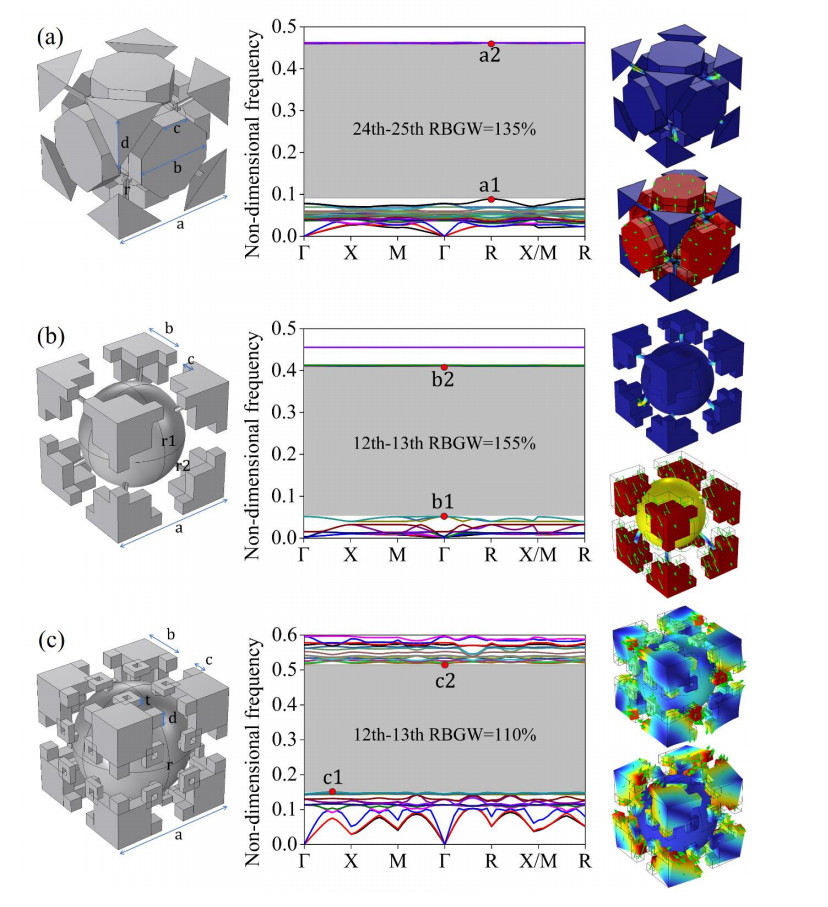
Although various novel structures have been attained, these irregular and discretized structures do not lend themselves well to being utilized by other researchers for remodeling purposes. Therefore, the optimized structures are parameterized as shown in Figures 13 and 14. It is worth noting that these parameterized structures are not completely identical to the original discretized structures, hence there will be potential differences in band structures. To get an insight into the mechanism of bandgap generation, typical vibration modes are calculated based on the parameterized structures. For the face-centered lattice structure in Figure 13a, its bandgap opens because of the vibration of centered lumps and closes with the vibration of connectors. For the body-centered lattice in Figure 13b, its bandgap starts with eight cornered lumps moving to and from the centered lump. Although the structures in Figure 13b, c fall to the same topology pattern (the body-centered lattice) and open the bandgap at the same rank, their mechanisms of bandgap formation are quite different. For vibration modes at the opening and closing frequency in Figure 13c, cornered lumps contribute to the rotational deformation while the centered lump remains almost unchanged.
As discussed in sections 3.2 and 3.3, the optimal structures corresponding to the 6th–7th and 18th–19th bandgaps exhibit significant potential for excellent performance. Therefore, it is of interest to investigate how their bandgaps are generated. For vibration modes at the opening frequency in Figure 14a–c, the lumps exhibit considerable deformation as opposed to a significantly small deformation of connectors. Based on the spring-mass vibration theory, the opening frequency of bandgaps is associated with the value of √k/m, where k indicates the stiffness of the spring (connector) and m means the mass of the lump. The PnC structure in Figure 14c possesses relatively long connectors with the largest mass of lumps involved in the vibration, while the one in Figure 14b has the shortest connectors and the smallest mass of vibrating lumps. That explains why the opening frequency of the maximum bandgap in Figure 14c is the lowest while that in Figure 14b is the highest. As for vibration mode shapes at the closing frequency, different from the structure in Figure 14a where deformation mainly occurs at some portion of lumps, only connectors vibrate while lumps remain still for the structures in Figure 14b, c. Similar to most mode shapes at the closing frequency, only connectors of the structure in Figure 14d produce displacement. However, for the opening frequency, eight lumps undergo rotational deformation while the remaining lumps do not move. Generally, the bandgaps are opened because of the vibration of lumps and closed with the deformation of connectors. This indicates the great importance of both large masses of lumps and small stiffness of connections to the formation of the bandgaps.
4.
Conclusions
Geometric-constrained topology optimization is performed on 3D single-phase phononic crystals to explore innovative and excellent structures. This approach proposes pyramid symmetry to deduct design variables, inserts cylinders to enhance connection stability, and applies additional geometric constraints to filter out unstable structures. The effectiveness of the optimization algorithm has been demonstrated and main conclusions are drawn from this work as follows.
The optimized structures under 26 connectivity exhibit more advantages than those under 6 connectivity in terms of diverse connections and superior performance. Specifically, using the same mesh of elements, the performance of resulting structures under 26 connectivity is significantly superior to those under 6 connectivity. Even the optimized structures with a coarse mesh under 26 connectivity exhibit significantly larger bandgaps in lower-frequency domains compared to those counterparts with a fine mesh under 6 connectivity. Because of high mesh dependence, the minimum dimension of connections is determined by the mesh size of the unit cell under 6 connectivity. This explains why the bandgaps of the optimized structures under 6 connectivity are enlarged more considerably when using a fine mesh than 26 connectivity. For the optimal structures under 26 connectivity, however, the insertion of cylinders lessens the restriction of mesh dependence and facilitates the generation of flexible connections.
The simple lattice structures have obvious advantages in exhibiting low-frequency ultrawide bandgaps over other conventional lattices, such as body-centered and face-centered configurations. Aside from conventional structures, a brand-new structure characterized by several identical mass lumps also shows excellent bandgap properties. The structures comprised of only one type of mass lump are inclined to exhibit a greater opportunity to generate desirable performance. The conclusion can be extended to the manually designed structures displaying ultrawide bandgaps in the previously published work, where these PnC structures incidentally showcase only one category of mass lump.
The geometrical configurations of the ultimately optimized structures are intimately connected with the rank of the bandgaps. Researchers are encouraged to optimize the bandgaps between the aforementioned bands, as they have demonstrated the potential to exhibit broad bandgaps. In the meantime, optimizing the bandgaps between adjacent bands in the first certain number of bands simultaneously is not advised. This operation hinders the exploration of diverse structures, as optimal structures related to the 6th–7th and 18th–19th bandgaps are more likely to be discovered than others.
Although the two structures fall to the same topology lattice and open the bandgap at the same rank, their mechanisms of bandgap formation can be different. Generally, the bandgaps are opened as a result of the vibration of large lumps and closed with the deformation of flexible connectors. This highlights the significant importance of both large lumps and flexible connections in the formation of the bandgaps. The findings of this work provide a variety of novel geometrical topologies and valuable guidance for researchers to design structures with excellent performance.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
CRediT authorship contribution statement
Cheng Xiong: methodology, formal analysis, writing—original draft. Xiao Yi: supervision, revision. Qing-Hua Qin: supervision, revision, comment. Hui Wang: comment. Zhuo-Ran Zeng: comment.
Conflict of interest
Qing-Hua Qin is editor in chief for AIMS Materials Science and was not involved in the editorial review or the decision to publish this article. The authors declare no conflict of interest.
Acknowledgement
The authors are grateful for the financial support from National Natural Science Foundation of China (Grant No. 12272239), special projects in key fields of ordinary universities from Guangdong Provincial Department of Education (Grant No. 2022ZDZX3037), 2022 Stable Support Plan Program of Shenzhen Natural Science Fund, and the China Scholarship Council (Grant No. 202008440523).









 DownLoad:
DownLoad: