1. Introduction
Since the announcement in 1984 by Shechtman et al. [1] of the exciting discovery of the new class of novel alloys that are now known as quasicrystals, there has been an enormous concerted effort by especially the exponents of materials science, solid mechanics and solid state physics to investigate their behaviour both theoretically and experimentally. They have desirable properties that are now widely exploited in, for example, engine surface coatings in the aerospace industry and nuclear fuel containers.
However, with the increasing maturity of the technological applications of quasicrystals, it is crucial that their behaviour should continue to be fully researched and particularly that their intrinsic piezoelectric coupling effects are incorporated. Piezoelectric materials are utilized extensively in signal processing in, for example, transducers, sensors and attenuators and piezoelectric quasicrystals can play a vital role in the design of intelligent systems and structures. It is vital that fundamental solutions of all types of boundary value problems and particularly those involving various configurations of inclusions and cracks are made available, as experiments have demonstrated that quasicrystals are quite brittle and thus can experience premature failure.
Fan [2,3] and Ding et al. [4], for example, have most conveniently comprehensively referenced and reviewed the growing literature of mathematical theories and analyses of physical problems in quasicrystals. But encouragingly, more recently relevant techniques have begun to be developed for studying the corresponding situations within piezoelectric quasicrystals.
The fundamental equations that govern the behaviour of three-dimensional piezoelectric quasicrystals were developed by Altay and Dökmeci [5] in both differential and variational invariant forms. Using the theory of group representation, Li and Liu [6] derived the matrix forms of the thermal-expansion coefficients and piezoelectric coefficient tensors for all 31 point-groups of one-dimensional quasicrystals. These provided the starting point for Wang and Pan [7] to produce elementary expressions for the induced fields of a uniformly moving screw dislocation within a one-dimensional hexagonal piezoelectric quasicrystal. Thereafter, the generalized formalism of Stroh was used by Yang et al. [8] to give the piezoelectric fields created in a one-dimensional piezoelectric quasicrystal by a motionless straight dislocation that is parallel to its axis of periodicity.
By introducing two functions of displacement and rigorously applying the theory of operators, a set of general solutions of static problems in three-dimensions for hexagonal piezoelectric quasicrystals was obtained by Li et al. [9]. Yu et al. [10] proposed a method of complex variables for an elliptical anti-plane cavity to derive explicit solutions for the elastic-electric fields in a one-dimensional hexagonal piezoelectric quasicrystal. Further, Yu et al. [11] used operator and complex variable function methods to rigorously deduce general solutions of piezoelasticity plane problems for quasicrystals and considered an antiplane, constantly-loaded, stationary crack in a hexagonal piezoelastic quasicrystal by the semi-inverse method. Zhang et al. [12] introduced four potential functions in terms of which solutions of the equations governing plane problems in one-dimensional orthorhombic quasicrystals having piezoelectric effects are expressed.
Most recently, in 2016, methods of complex variable functions and techniques of conformal mappings assisted Yang and Li [13] in studying a circular hole with a straight crack and Guo et al. [14] in considering an elliptical inclusion embedded in composites of one-dimensional hexagonal piezoelectric quasicrystals. Fan et al. [15] presented basic solutions of three-dimensional cracks in such media using Green's functions, Hankel transforms and methods of boundary integral equations and Tupholme [16] derived closed-form expressions for the stress and electric fields created by a moving uniformly-loaded shear crack in one-dimensional hexagonal piezoelectric quasicrystals.
The continuing wider interest in quasicrystals is further demonstrated by, for example, the proposal and analysis by Guo and Pan [17] of a three-phase model of one-dimensional hexagonal piezoelectric quasicrystal composites and a study of two-dimensional thermoelastic deformations of a conductive elliptical hole embedded within a two-dimensional decagonal quasicrystal by Guo et al. [18], and the references therein.
However, there has been no analysis whatsoever presented previously using any technique of a row of moving, anti-plane cracks in quasicrystals with piezoelectric effects. The focus of the current investigation is to demonstrate that the continuous dislocation layers method, that was devised originally for purely elastic isotropic solids, can be extended most conveniently to yield expressions for the components of the fields induced by such cracks.
In Section 2, a summary is provided of the underlying basic three-dimensional equations which govern the deformation of piezoelectric quasicrystals and the fundamental constitutive equations of one-dimensional hexagonal piezoelectric quasicrystals with point group 6 mm are stated. A formulation is then given of the problem being studied here. The required components of the phonon and phason displacement and stress field and the electric potential of a moving screw dislocation are presented in Section 3, before an extension of the classical dislocation layer method is described and adapted in Section 4 to yield closed-form representations for the fields around the cracks. Illustrative numerical results are displayed graphically for the variation of the stress component ahead of a crack tip for a range of values of the geometric parameters. The results for the situation that has not been presented previously of a stationary row of cracks are deduced. As observed in the concluding Section 5, the solutions are also provided by this analysis to the problems of a moving single central crack within a finite plate and a finite plate having a moving edge crack in a piezoelectric quasicrystal.
2. Fundamental Equations of Piezoelectric Quasicrystals and Problem Formulation
The deformation fields within the linear theory of piezoelectric quasicrystals have components that are governed by the general three-dimensional equations which Altay and Dökmeci [5] have presented in both differential and variational invariant forms. In the absence of body forces and an electric charge density, the quasistatic equilibrium equations and the constitutive equations can be written compactly, relative to a fixed system of rectangular Cartesian coordinates (x1,x2,x3), using a suffix notation where i, j, k, l = 1, 2, 3 with the adoption of the repeated suffices summation convention, as
|
σij,i=0,Hij,i=0,Dij,i=0
|
(1)
|
|
σij=cijkl(uk,l+ul,k)/2+Rijklwk,l−ekijEk
|
(2)
|
|
Hij=Rklij(uk,l+ul,k)/2+Kijklwk,l−e′kijEk
|
(3)
|
|
Di=ekij(uj,k+uk,j)/2+e′kijwj,k−εijEj
|
(4)
|
with a comma followed by p denoting partial differentiation with respect to xp for p = i, j, k, l.
The components of the phonon stress and displacement, the phason stress and displacement and the electric displacement and field are denoted by σij,ui,Hij,wi,Di and Ei, respectively, and cijkl,Rijkl,Kijkl,eijk,e′ijk and εij are the phonon elastic constants, the phonon-phason coupling constants, the phason elastic constants, the phonon and phason piezoelectric constants and the dielectric constants, respectively.
Here an infinite homogeneous one-dimensional hexagonal piezoelectric quasicrystal of point group 6 mm is considered that has a constant density, ρ, and is initially in an undisturbed reference state which is free of stress and at rest everywhere. It is oriented, with reference to a system of fixed rectangular Cartesian coordinates (x, y, z), so that its periodic plane is the x-y plane and its quasiperiodic direction is that of the positive z-axis.
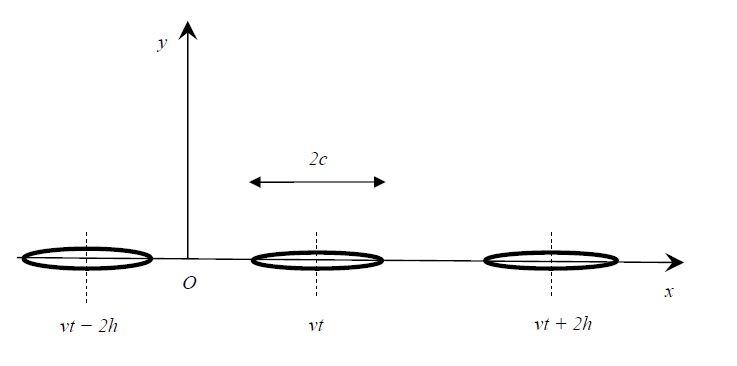
A problem of mode III fracture is addressed in which a periodic infinite array of collinear, plane Griffith-type, moving, strip cracks of equal constant width 2c is embedded in such a material that is subjected to remote uniform phonon, phason and electrical loads.
Within the piezoelectric quasicrystal, the created components σXY, εXY and uX of the phonon stress and strain tensors and displacement vector, HzX , wzX and wX of the phason stress and strain tensors and displacement vector, and DX and EX of the electric displacement and field vectors, for X and Y = x, y or z, are linked by the matrix constitutive equations
|
[σxxσyyσzzσyzσxzσxyHzzHzxHzy]=[c11c12c13000R100c12c11c13000R100c13c13c33000R2000002c440000R300002c4400R3000000c11−c12000R1R1R2000K10000002R300K200002R30000K2][εxxεyyεzzεyzεxzεxywzzwzxwzy]−[00e3100e3100e330e150e150000000e′33e′15000e′150][ExEyEz]
|
(5)
|
|
[DxDyDz]=[00002e1500e′1500002e150000e′15e31e31e33000e′3300][εxxεyyεzzεyzεxzεxywzzwzxwzy]+[ε11000ε11000ε33][ExEyEz].
|
(6)
|
with
|
εXY=12(∂uX∂Y+∂uY∂X),wzX=∂wz∂X
|
(7)
|
The constants involved are the phonon elastic moduli, cij, the phason elastic moduli, Ki, the phonon-phason coupling elastic moduli, Ri, the piezoelectric moduli, eij and e′ij, and the dielectric moduli, εij, where i and j take integer values and the customary Voigt's contracted notation is being used.
At time t, it is assumed that the cracks are moving uniformly parallel to their axes in their own planes with a speed v and occupy the regions Rt of the y=0 plane, where
|
Rt={(x,y,z):vt−c+2nh<x<vt+c+2nh,y=0,−∞<z<∞}
|
(8)
|
for n = 0, ±1, ±2, ... , with their centres at x = vt, vt ± 2h, vt ± 4h, ... , as illustrated in Figure 1.
It is appropriate to utilize a moving coordinate, ξ, defined by
and an electric potential, Φ, which is related to the electric field vector, E, by
The field variables in the antiplane deformation under consideration here are independent of z. Thus the required relations between the phonon and phason displacements' components, and , and the strain components involved become
|
εxz=12∂uz∂x,εyz=12∂uz∂y,
|
(11)
|
|
wzx=∂wz∂x,wzy=∂wz∂y,
|
(12)
|
and the corresponding components of the phonon and phason stresses and electric displacement are given by Eqs. (5) and (6) in the forms.
|
σyz=2c44εyz+Rwzy−e15Ey,σxz=2c44εxz+Rwzx−e15Ex
|
(13)
|
|
Hzy=2Rεyz+Kwzy−e′15Ey,Hzx=2Rεxz+Kwzx−e′15Ex
|
(14)
|
|
Dy=2e15εyz+e′15wzy+ε11Ey,Dx=2e15εxz+e′15wzx+ε11Ex
|
(15)
|
Here, and subsequently, R and K are used as abbreviations for the constants R3 and K2 for the sake of brevity of presentation.
With the solid subjected to phonon, phason and electrical loading such that
|
σyz→T,Hzy→H,Dy→Datinfinity,
|
(16)
|
where the constants T, H and D are specified, an antiplane mode III deformation is induced.
Similarly, an interested reader could develop the corresponding analyses to that given below if analogously any desired combination of three of the phonon, phason and electrical components σyz,εyz,Hzy,wzy,Dy, or Ey are prescribed instead.
3. Moving Screw Dislocation in a Piezoelectric Quasicrystal
The stimulus is provided for the current study by the fundamental properties of the fields of a moving “piezoelectric quasicrystal screw dislocation”. This has a generalized Burgers vector which is extended from that of a traditional purely elastic screw dislocation. Across its slip plane, such a dislocation has discontinuities of finite magnitudes b in the component uz of the phonon displacement, d in the component wz of the phason displacement and b4 in Φ, the electric potential.
Expressions have been derived explicitly by Wang and Pan [7] for the components of the fields created around a dislocation at the origin of this type, which is parallel to the z-axis and moves in a one-dimensional hexagonal piezoelectric quasicrystal with point group 6 mm with a speed v along the x-axis. These can be written, after appropriate rearrangement and some renaming of the terms and moduli of the medium as
|
uIIIz(ξ,y)=12π(α2+¯R2)[b{α2tan−1(β1yξ)+¯R2tan−1(β2yξ)}+dα¯R{tan−1(β1yξ)−tan−1(β2yξ)}]
|
(17)
|
|
wIIIz(ξ,y)=12π(α2+¯R2)[bα¯R{tan−1(β1yξ)−tan−1(β2yξ)}+d{¯R2tan−1(β1yξ)+α2tan−1(β2yξ)}]
|
(18)
|
|
φIII(ξ,y)=12π{b[1ε11(α2+¯R2){α(e15α+e′15¯R)tan−1(β1yξ)−¯R(e′15α−e15¯R)tan−1(β2yξ)}+d[1ε11(α2+¯R2){¯R(e15α+e′15¯R)tan−1(β1yξ)+α(e′15α−e15¯R)tan−1(β2yξ)}−e′15ε11tan−1(yξ)]+b4tan−1(yξ)}
|
(19)
|
where, here and henceforth, the superscript III indicates that the terms are related to the antiplane mode III deformation.
It is convenient to put
|
α={¯c44−¯K+√(¯c44−¯K)2+4¯R2}/2
|
(20)
|
where the piezoelectrically stiffened elastic constants, ¯c44 and ¯K, in the phonon and phason fields, and the piezoelectrically stiffened phonon-phason coupling elastic constant, , are defined by
|
¯c44=c44+e152ε11,¯K=K+e′152ε11,¯R=R+e15e′15ε11,
|
(21)
|
and
|
βi=√1−v2si2fori=1and2
|
(22)
|
Under antiplane shear conditions, the piezoelectrically stiffened wave speeds, s1 and s2, are given by
where
|
ε1={¯c44+¯K+√(¯c44−¯K)2+4¯R2}/2,ε2={¯c44+¯K−√(¯c44−¯K)2+4¯R2}/2.
|
(24)
|
Then the phonon and phason stresses and electric displacement have non-zero components which can be deduced, using the constitutive equations (5) and (6), from Eqs. (17)-(19) in the forms.
|
σIIIxz(ξ,y)=−y2π{b[1(α2+¯R2){β1α(¯c44α+¯R2)ξ2+β12y2+β2¯R2(¯c44−α)ξ2+β22y2}−e152ε11(ξ2+y2)]+d[¯R(α2+¯R2){β1(¯c44α+¯R2)ξ2+β12y2−β2α(¯c44−α)ξ2+β22y2}−e15e′15ε11(ξ2+y2)]+b4e15ξ2+y2}
|
(25)
|
|
σIIIyz(ξ,y)=ξ2π{b[1(α2+¯R2){β1α(¯c44α+¯R2)ξ2+β12y2+β2¯R2(¯c44−α)ξ2+β22y2}−e152ε11(ξ2+y2)]+d[¯R(α2+¯R2){β1(¯c44α+¯R2)ξ2+β12y2−β2α(¯c44−α)ξ2+β22y2}−e15e′15ε11(ξ2+y2)]+b4e15ξ2+y2}
|
(26)
|
|
HIIIzx(ξ,y)=−y2π{b[¯R(α2+¯R2){β1α(α+¯K)ξ2+β12y2−β2(α¯K−¯R2)ξ2+β22y2}−e15e′15ε11(ξ2+y2)]+d[1(α2+¯R2){β1¯R2(α+¯K)ξ2+β12y2+β2α(α¯K−¯R2)ξ2+β22y2}−e′152ε11(ξ2+y2)]+b4e′15ξ2+y2}
|
(27)
|
|
HIIIzy(ξ,y)=ξ2π{b[¯R(α2+¯R2){β1α(α+¯K)ξ2+β12y2−β2(α¯K−¯R2)ξ2+β22y2}−e15e′15ε11(ξ2+y2)]+d[1(α2+¯R2){β1¯R2(α+¯K)ξ2+β12y2+β2α(α¯K−¯R2)ξ2+β22y2}−e′152ε11(ξ2+y2)]+b4e′15ξ2+y2}
|
(28)
|
|
DIIIx(ξ,y)=−y2πbe15+de′15−b4ε11ξ2+y2
|
(29)
|
|
DIIIy(ξ,y)=ξ2πbe15+de′15−b4ε11ξ2+y2
|
(30)
|
If required, the corresponding components of the phonon and phason strain and electric field can be deduced analogously using Eqs. (17)-(19) together with Eqs. (10)-(12).
4. Solution by Extending the Technique of Dislocation Layers
The realization that an equivalent continuous planar array of elastic dislocations usefully models a strip crack in classical elastic materials inspired the development of the so-called “dislocation layer method”, as conveniently summarized, for example, by Bilby and Eshelby [19] and Lardner [20]. This fundamental method is suitably extended here to represent the moving row of shear cracks in piezoelectric quasicrystals by appropriately spreading a distribution of moving piezoelectric quasicrystal screw dislocations of the kind introduced in Section 3 above.
To the right of each crack the screws are positive and they are negative to the left. The distributions of the components of the phonon and phason displacements and the electric potential therefore have discontinuities with densities f(ξ), g(ξ) and f4(ξ), respectively, which are stipulated as being odd functions of ξ.
The corresponding phonon and phason stresses and electric displacement then have relevant components at a point on the ξ-axis given by Eqs. (26), (28) and (30) as
|
σIIIyz(ξ,0)=b2π[{β1α(¯c44α+¯R2)+β2¯R2(¯c44−α)α2+¯R2}−e152ε11]∫∞−∞f(ξ′)ξ−ξ′dξ′+d2π[¯R{β1(¯c44α+¯R2)−β2α(¯c44−α)α2+¯R2}−e15e′15ε11]∫∞−∞g(ξ′)ξ−ξ′dξ′+b4e152π∫∞−∞f4(ξ′)ξ−ξ′dξ′,
|
(31)
|
|
HIIIzy(ξ,0)=b2π[¯R{β1α(α+¯K)−β2(α¯K−¯R2)α2+¯R2}−e15e′15ε11]∫∞−∞f(ξ′)ξ−ξ′dξ′+d2π[{β1¯R2(α+¯K)+β2α(α¯K−¯R2)α2+¯R2}−e′152ε11]∫∞−∞g(ξ′)ξ−ξ′dξ′+b4e′152π∫∞−∞f4(ξ′)ξ−ξ′dξ′,
|
(32)
|
|
DIIIy(ξ,0)=be152π∫∞−∞f(ξ′)ξ−ξ′dξ′+de′152π∫∞−∞g(ξ′)ξ−ξ′dξ′−b4ε112π∫∞−∞f4(ξ′)ξ−ξ′dξ′
|
(33)
|
The Plemelj formulae indicate that a Cauchy principal value interpretation must be assigned to the improper integrals in Eqs. (31)-(33).
To satisfy the imposed conditions (16), the dislocation array must fulfil the equilibrium equations that
|
σIIIyz(ξ,0)=−T,HIIIzy(ξ,0)=−H,DIIIy(ξ,0)=−DinRt
|
(34)
|
The system of three simultaneous equations which follows by substituting the representations (31)-(33) into Eqs. (34) can be solved to yield three singular integral equations for the densities f(ξ), g(ξ) and f4(ξ) that, after considerable, intricate manipulation and algebraic simplification, can be written concisely as
|
∫∞−∞f(ξ′)ξ−ξ′dξ′=−2πbβ1β2ε11(¯c44¯K−¯R2)(α2+¯R2)×[ε11{β1¯R2(α+¯K)+β2α(α¯K−¯R2)}T−ε11¯R{β1(¯c44α+¯R2)−β2α(¯c44−α)}H[ε11{β1¯R2(α+¯K)+β2α(α¯K−¯R2)}T−ε11¯R{β1(¯c44α+¯R2)−β2α(¯c44−α)}H−[e′15¯R{β1(¯c44α+¯R2)−β2α(¯c44−α)}−e15{β1¯R2(α+¯K)+β2α(α¯K−¯R2)}]D]
|
(35)
|
|
∫∞−∞g(ξ′)ξ−ξ′dξ′=−2πdβ1β2ε11(¯c44¯K−¯R2)(α2+¯R2)×[−ε11¯R{β1α(α+¯K)−β2(α¯K−¯R2)}T+ε11{β1α(¯c44α+¯R2)+β2¯R2(¯c44−α)}H+[e′15{β1α(¯c44α+¯R2)+β2¯R2(¯c44−α)}−e15¯R{β1α(α+¯K)−β2(α¯K−¯R2)}]D]
|
(36)
|
|
∫∞−∞f4(ξ′)ξ−ξ′dξ′=−2πb4β1β2ε11(¯c44¯K−¯R2)(α2+¯R2)×{−[e′15¯R{β1α(α+¯K)−β2(α¯K−¯R2)}−e15{β1¯R2(α+¯K)+β2α(α¯K−¯R2)}]T+[e′15{β1α(¯c44α+¯R2)+β2¯R2(¯c44−α)}−e15¯R{β1(¯c44α+¯R2)−β2α(¯c44−α)}]H−[β1β2(¯c44¯K−¯R2)(α2+¯R2)−e152ε11{β1¯R2(α+¯K)+β2α(α¯K−¯R2)}−e′152ε11{β1α(¯c44α+¯R2)+β2¯R2(¯c44−α)}+e15e′15ε11¯R(β1{α(α+¯K)+(¯c44α+¯R2)}−β2{α(¯c44−α)+(α¯K−¯R2)})]D}
|
(37)
|
However, the infinite integrals arising in Eqs. (35)-(37) can be rewritten as the summation of the separate contributions from the individual cracks.
For example, by recalling the stipulation that the density functions must be odd, so that f(ξ)=−f(−ξ), and observing that f(ξ+2nh)=f(ξ), it follows using the relationship
|
∞∑n=11z2−n2=−12z2+π2zcotπz
|
(38)
|
together with partial fractions, that the left-hand side of Eq. (35) can be expressed alternatively (cf. Leibfried [21]) as
|
π2h∫c−ccos(πξ′/2h)sin(πξ/2h)−sin(πξ′/2h)f(ξ′)dξ′.
|
(39)
|
Further, this can be more concisely rewritten in terms of new variables given by
|
ξ1=sin(πξ/2h),c1=sin(πc/2h),ξ′1=sin(πξ′/2h),
|
(40)
|
so that finally the integral equation (35) for is converted into the convenient form
|
∫c1−c1f1(ξ′1)ξ1−ξ′1dξ′1=−2πbβ1β2ε11(¯c44¯K−¯R2)(α2+¯R2)×[ε11{β1¯R2(α+¯K)+β2α(α¯K−¯R2)}T−ε11¯R{β1(¯c44α+¯R2)−β2α(¯c44−α)}H−[e′15¯R{β1(¯c44α+¯R2)−β2α(¯c44−α)}−e15{β1¯R2(α+¯K)+β2α(α¯K−¯R2)}]D]for|ξ1|<c1
|
(41)
|
with f1(ξ1)=f1(sin(πξ/2h))≡f(ξ). The relevant solution of this is readily deducible by the classical methods of Muskhelishvili [22], and Gakhov [23], for example, to be
|
f1(ξ1)=−2πbβ1β2ε11(¯c44¯K−¯R2)(α2+¯R2)×[ε11{β1¯R2(α+¯K)+β2α(α¯K−¯R2)}T−ε11¯R{β1(¯c44α+¯R2)−β2α(¯c44−α)}H−[e′15¯R{β1(¯c44α+¯R2)−β2α(¯c44−α)}−e15{β1¯R2(α+¯K)+β2α(α¯K−¯R2)}]D]×−[e′15¯R{β1(¯c44α+¯R2)−β2α(¯c44−α)}−e15{β1¯R2(α+¯K)+β2α(α¯K−¯R2)}]D]×
|
(42)
|
|
1(c12−ξ12)1/2∫c1−c1(c12−ξ′12)1/2ξ′1−ξ1dξ′1=2bβ1β2ε11(¯c44¯K−¯R2)(α2+¯R2)×[ε11{β1¯R2(α+¯K)+β2α(α¯K−¯R2)}T−ε11¯R{β1(¯c44α+¯R2)−β2α(¯c44−α)}H−[e′15¯R{β1(¯c44α+¯R2)−β2α(¯c44−α)}−e15{β1¯R2(α+¯K)+β2α(α¯K−¯R2)}]D]×ξ1(c12−ξ12)1/2,
|
(43)
|
which, by reverting to the original variables using Eqs. (40), becomes
|
f(ξ)=2bβ1β2ε11(¯c44¯K−¯R2)(α2+¯R2)×[ε11{β1¯R2(α+¯K)+β2α(α¯K−¯R2)}T−ε11¯R{β1(¯c44α+¯R2)−β2α(¯c44−α)}H−[e′15¯R{β1(¯c44α+¯R2)−β2α(¯c44−α)}−e15{β1¯R2(α+¯K)+β2α(α¯K−¯R2)}]D]×sin(πξ/2h)[sin2(πc/2h)−sin2(πξ/2h)]1/2.
|
(44)
|
The phason and electric densities satisfying the Eqs. (36) and (37) can be deduced analogously to be
|
g(ξ)=2dβ1β2ε11(¯c44¯K−¯R2)(α2+¯R2)×[−ε11¯R{β1α(α+¯K)−β2(α¯K−¯R2)}T+ε11{β1α(¯c44α+¯R2)+β2¯R2(¯c44−α)}H[−ε11¯R{β1α(α+¯K)−β2(α¯K−¯R2)}T+ε11{β1α(¯c44α+¯R2)+β2¯R2(¯c44−α)}H+[e′15{β1α(¯c44α+¯R2)+β2¯R2(¯c44−α)}−e15¯R{β1α(α+¯K)−β2(α¯K−¯R2)}]D]×sin(πξ/2h)[sin2(πc/2h)−sin2(πξ/2h)]1/2
|
(45)
|
and
|
f4(ξ)=2b4β1β2ε11(¯c44¯K−¯R2)(α2+¯R2)×{−[e′15¯R{β1α(α+¯K)−β2(α¯K−¯R2)}−e15{β1¯R2(α+¯K)+β2α(α¯K−¯R2)}]T+[e′15{β1α(¯c44α+¯R2)+β2¯R2(¯c44−α)}−e15¯R{β1(¯c44α+¯R2)−β2α(¯c44−α)}]H−[β1β2(¯c44¯K−¯R2)(α2+¯R2)−e152ε11{β1¯R2(α+¯K)+β2α(α¯K−¯R2)}−e′152ε11{β1α(¯c44α+¯R2)+β2¯R2(¯c44−α)}+e15e′15ε11¯R(β1{α(α+¯K)+(¯c44α+¯R2)}−β2{α(¯c44−α)+(α¯K−¯R2)})]D}sin(πξ/2h)[sin2(πc/2h)−sin2(πξ/2h)]1/2.
|
(46)
|
With the necessary densities f(ξ), g(ξ) and f4(ξ)now determined, explicit expressions for any of the components of the phonon and phason stress and electric fields which are required can be deduced from Eqs. (25)-(30) and (44)-(46). These generally depend not only upon the values of the loads T, H and D which are applied and the geometric constants c and h, but also upon the piezoelectric quasicrystal material moduli and the speed v of the cracks.
However, in considering practical criteria for the fracture of materials, traditionally there is especial interest in the components’ magnitudes directly in front of the tip of a crack.
The component of the phonon shear stress on the y = 0 plane, for example, is obtained as the sum of the contributions from all the image cracks. Using a summation of finite integrals as a replacement for the resulting infinite integral and recalling Eqs. (38) and (39) gives
|
σyz(ξ,0)=T+b2π[{β1α(¯c44α+¯R2)+β2¯R2(¯c44−α)α2+¯R2}−e152ε11]∫c1−c1f1(ξ′1)ξ1−ξ′1dξ′1+d2π[¯R{β1(¯c44α+¯R2)−β2α(¯c44−α)α2+¯R2}−e15e′15ε11]∫c1−c1g1(ξ′1)ξ1−ξ′1dξ′+b4e152π∫c1−c1f41(ξ′)ξ−ξ′dξ′
|
(47)
|
where g1(ξ1)=g1(sin(πξ/2h))≡g(ξ), f41(ξ1)=f41(sin(πξ/2h))≡f4(ξ). The substitution into this of the expressions (44)-(46) for f1, g1 and f41 appears to yield extremely unwieldy terms, but extensive rearrangement and manipulation leads to
|
σyz(ξ,0)=T+Tπ∫c1−c1ξ′1(c12−ξ′12)1/2dξ′1ξ1−ξ′1.
|
(48)
|
Evaluation of the involved integral using the method of contour integration in complex variable analysis and the relationships (40) ultimately gives
|
σyz(ξ,0)=Tsin(πξ/2h)[sin2(πξ/2h)−sin2(πc/2h)]1/2.
|
(49)
|
Analogously, the components of the phason stress and electric displacement on the y = 0 plane are found to be
|
Hzy(ξ,0)=H+b2π[¯R{β1α(α+¯K)−β2(α¯K−¯R2)α2+¯R2}−e15e′15ε11]∫c1−c1f1(ξ′1)ξ1−ξ′1dξ′+d2π[{β1¯R2(α+¯K)+β2α(α¯K−¯R2)α2+¯R2}−e′152ε11]∫c1−c1g1(ξ′1)ξ1−ξ′1dξ′]+b4e′152π∫c1−c1f41(ξ′1)ξ1−ξ′1dξ′=Hsin(πξ/2h)[sin2(πξ/2h)−sin2(πc/2h)]1/2
|
(50)
|
|
Dy(ξ,0)=D+be152π∫c1−c1f1(ξ′1)ξ1−ξ′1dξ′+de′152π∫c1−c1g1(ξ′1)ξ1−ξ′1dξ′−b4ε112π∫c1−c1f41(ξ′1)ξ1−ξ′1dξ′=Dsin(πξ/2h)[sin2(πξ/2h)−sin2(πc/2h)]1/2.
|
(51)
|
It is appropriate to extend the classical notion of a stress intensity factor for a stationary crack within a purely elastic material to moving cracks in piezoelectric quasicrystals. The phonon and phason stress and electric displacement intensity factors, KT, KH and KD, respectively, can thus be defined and evaluated, from Eqs. (49)-(51), in the forms
|
KT=limξ→c+(ξ−c)1/2σyz(ξ,0)=T[hπtan(πc2h)]12,
|
(52)
|
|
KH=limξ→c+(ξ−c)1/2Hzy(ξ,0)=H[hπtan(πc2h)]12,
|
(53)
|
|
KD=limξ→c+(ξ−c)1/2Dy(ξ,0)=D[hπtan(πc2h)]12,
|
(54)
|
As observed above, the density functions given by Eqs. (44)-(46) depend upon the values of the piezoelectric quasicrystal material constants, as well as the loads applied and the parameters c, h and v. However, it is of interest to note that on the otherhand the stress intensity factors, KT, KH and KD, given by Eqs. (52)-(54), each depend only upon c and h and the respective applied loads T, H, D.
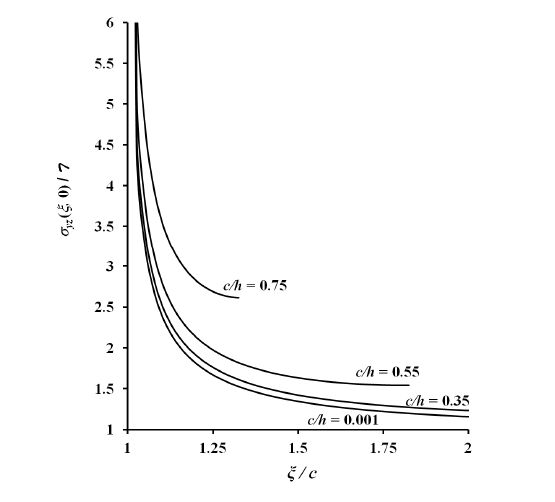
Curves are depicted in Figure 2 to representatively illustrate graphically the variation with ξ/c of the non-dimensional, scaled phonon stress component σyz(ξ,0)/T (and likewise those of Hzy(ξ,0)/H and Dy(ξ,0)/D) for various values of c/h. The curves display the same basic shapes for different values of c/h. But as the ratio c/h increases in magnitude the intensity of σyz(ξ,0)/T also increases.
It is apparent, from Eqs. (44)-(46), that the analysis above is invalid when ¯c44¯K−¯R2=0 or β1=0 or β2=0. From the definition (22), the value of is zero when the crack speed, v, is equal to the wave speed si, for i = 1, 2, under antiplane shear conditions given by Eq. (23).
The reported data for the values of the material constants of one-dimensional hexagonal piezoelectric quasicrystals are still somewhat variable. However, typically Li et al. [9] report c44=5.0×1010Nm−2, R=1.2×109Nm−2, K=3.0×108Nm−2, e15=−0.138Cm−2, e′15=−0.160Cm−2, ε11=82.6×10−12C2N−1m−2, which, with representatively ρ=5.1×103kgm−3, give these wave speeds to be s1≈3139ms−1 and s2≈333ms−1. Moreover, it is clear that ¯c44¯K−¯R2 does not vanish, since the value of ¯c44¯K is much greater than that of ¯R2.
Finally, an analysis of a row of stationary cracks in piezoelectric quasicrystals has not been presented previously and therefore it is worthwhile highlighting briefly the considerably simplified results as a special case of the current analysis. When , from Eq. (22), β1=β2=1 and then the densities given by Eqs. (44)-(46) simply become
|
f(x)=−2bε11(¯c44¯K−¯R2){−ε11¯KT+ε11¯RH+(e′15¯R−e15¯K)D}sin(πx/2h)[sin2(πc/2h)−sin2(πx/2h)]1/2
|
(55)
|
|
g(x)=−2dε11(¯c44¯K−¯R2){ε11¯RT−ε11¯c44H−(e′15¯c44−e15¯R)D}sin(πx/2h)[sin2(πc/2h)−sin2(πx/2h)]1/2
|
(56)
|
|
f4(x)=−2b4ε11(¯c44¯K−¯R2){(e′15¯R−e15¯K)T−(e′15¯c44−e15¯R)H+(¯c44¯K−¯R2−e152ε11¯K−e′152ε11¯c44+2e15e′15ε11¯R)D}sin(πx/2h)[sin2(πc/2h)−sin2(πx/2h)]1/2
|
(57)
|
and these enable any of the components of the phonon, phason and electric fields around the stationary cracks to be derived as desired.
5. Conclusions
The analysis is focussed on adapting and extending the traditional dislocation layer method of elastic media for studying cracks in one-dimensional piezoelectric quasicrystals.
Explicit expressions for the phonon, phason and electric field components of an infinite row of mode III, moving Yoffe-type constant-width cracks in piezoelectric quasicrystals are derived. Illustrative graphs of the variation of the components of the field along the axis ahead of a crack tip are displayed for a range of the geometric parameters.
The phonon, phason and electric densities are distributed antisymmetrically about the planes and thus clearly by an image construction the components of the phonon and phason stress and the electric displacement, σxz, Hzx and Dx vanish on these planes. Therefore the analysis above also describes the piezoelectric quasicrystal fields around a moving single crack originally occupying the region −c<x<c of a finite piezoelectric quasicrystalline plate −h<x<h, with load-free surfaces x=±h.
Further, the solution for an edge crack 0<x<c moving in a finite plate 0<x<h is also provided, since the distributions are odd about .
Conflict of Interest
The author declares that there is no conflict of interest regarding the publication of this paper.









 DownLoad:
DownLoad: