Reliability analysis of bistable composite laminates

1.   Introduction

Advanced composites are being employed for many industrial applications ^[1,2]. Bistable composite laminates are excellent candidates for their applications in morphing structures due to their unique features. They can change shapes and remain in natural equilibrium configuration without any external force. One of their most important applications is in aerospace structures such as airfoil section, air inlet demonstrator, morphing aerofoil and winglet and solar tracking device ^[3,4,5,6,7]. Moreover, they have considerable applications in energy harvesting fields, robotic gripper ^[8,9,10,11]. In order to use them effectively, different factors that affect their two stable states must be examined.

However, there are a wide range of undesirable uncertainties related to the design parameters in the composite laminate structures. They are random in nature due to their manufacturing or measuring errors. A probabilistic analysis can determine safer and reliable predictor of their structural response.

A large number of previous researches relating to bistable composite laminates have been published over the past 30 years ^[12]. It can be said that if the thermal load is applied to the unsymmetric composite laminates, they will have two cylindrical stable states in addition to an unstable saddle shape. This cannot be predicted with the classical lamination theory with these two configurations ^[13]. The analytical model, used in various reports, was based on the total potential energy and the Rayleigh–Ritz method using a geometrical nonlinearity ^[14,15]. In the theoretical approach, the displacement fields have a notable effect on the accuracy of the achieved results. A wide range of functions have been used for this aim, so far. Pirrera et al. studied the behavior of bistable composite shells by proposing the high-order polynomials and using a combination of the Ritz model with the path-following algorithm ^[16]. Lamacchia et al. estimated the transverse displacements by using Legendre polynomials and presented a new method based on the Rayleigh–Ritz approach for analyzing static and thermal behaviors of the multistable composite shells ^[17]. Material properties, geometry and environmental conditions have a considerable effect on the behavior of bistability of composite laminates. Vidoli and Maurini analyzed the tristability of orthotropic shallow shells with uniform initial curvature and investigated the range of initial curvatures and material parameters leading to tristability ^[18]. Brampton et al. used the total potential energy and the Rayleigh–Ritz methods and determined the influences of material properties, geometry and environmental conditions uncertainties on the curvature of the bistable composite laminate. The sensitivity of the stable shape was determined by considering a ±5% change in these parameters ^[19]. Che et al. studied the effect of the side length and stacking sequence on the stable configurations of the fiber metal laminates with different initial curvatures under thermal load using the analytical model, finite element and experimental methods ^[20]. Carey at el. studied the bistable helical structures by introducing an analytical method and investigated the variation of curvature respect to change in length for two different lay-ups ^[21].

The character of bistable laminates depends on the variation in temperature as well. Giddings et al. studied the impact of variation of laminate angle on the cured shape of bistable laminates under a range of temperature situations ^[22]. Eckstein et al. presented a model to estimate the cured shape of multistable plate subject to linear through-thickness temperature variation and for temperature-dependent material properties ^[23]. Zhang et al. presented an experimental study on the bistable behaviour of anti-symmetric laminated cylindrical shell at various temperatures. Based on the results, as the temperature rises, the snap-back load and curvatures increase but the snap-through force falls ^[24]. Fujioka et al. made bistable composite rods by the woven carbon fabrics composites and studied the influence of temperature on the deployment force of these structures. According to the result, the increase of temperature can significantly fall the deployment forces of bi-stable rods ^[25]. Chai et al. systematically analyzed the impact of moisture and temperature on bistable anti-symmetric composite shells and variable stiffness composite structures. The results showed that the temperature and moisture of bistable anti-symmetric composite shells are sensitive for different plies ^[26].

The aim of this study is to conduct reliability and sensitivity analysis with respect to random variables, involving material properties, geometrical features, which are studied by the combination of minimum potential energy, Rayleigh–Ritz and Monte Carlo methods. The equations of bistable composite laminates are derived by using the principle of minimizing potential energy and the Rayleigh–Ritz method. The limit state function is expressed via the context of bistability. The appropriate distribution is applied to variables and then the bistability probability is evaluated for cross-ply bistable composite by MCS method. Also, the uncertainty effect of the input parameters on out-off-plane displacement at the corner is studied using sensitivity analysis. In this work, FEM is employed to confirm these results as well.

2.   Theoretical formulation

2.1.   Bistable composite plate

The principle of minimum potential energy is used to establish the equations of the bistable composite plate. The total potential energy $\mathit{\Pi}$ of the composite laminate is expressed by Eq 1.

where $v$ is the volume of the plate, σ is the stress tensor, the superscript "T" illustrates the transpose operator and the $ϵ$ demonstrates the strain terms. According to the Classic Laminate Analysis (CLA), the stress tensor is given in Eq 2.

where $\stackrel{-}{Q}$ is the reduced stiffness matrix, the superscript "t" illustrates the contribution of thermal deformations and ${ϵ}^{t}$ is the thermal strain terms (${ϵ}^{t} = \alpha \mathrm{ \Delta} T$). By substituting Eq 2 into Eq 1, total potential energy is defined in Eq 3.

with $i, j = \left(1, 2, 6\right),$ where ${ \alpha }_{i}$ thermal expansion coefficients, ΔΤ is temperature difference between the cure and ambient temperatures.

By considering the assumption of small strains and moderate rotations, the strain field $\in$ of bistable composite plates are described by the Von-Karman formulation in Eq 4.

where $z$ is the distance from the mid-plane of laminate. Also, $\epsilon$ is the mid-plane strains as $\epsilon { = \left\{\begin{array}{ccc}{\epsilon }_{xx}& {\epsilon }_{yy}& {\epsilon }_{xy}\end{array}\right\}}^{T}$ and $\kappa$ is the mid-plane curvatures as $\kappa { = \left\{\begin{array}{ccc}{\kappa }_{xx}& {\kappa }_{yy}& {\kappa }_{xy}\end{array}\right\}}^{T}$, which are expressed by Eq 5.

where ${W}_{0}{, U}_{0}, {V}_{0}$ illustrate the out-of-plane and in-plane displacements in the z, x and y and directions. In Eq 6, these displacement fields are provided.

where ${t}_{ij}$, ${s}_{ij}$ and ${r}_{ij}$ are unknown coefficients. Displacement fields proposed in Eq 3 can satisfy boundary conditions of the plate, which is fixed at center and has free edges.

By substituting Eq 6 in Eq 4 and then in Eq 3, the potential energy will turn into Eq 7.

where ${L}_{x}$ and ${L}_{y}$ are the side lengths and h is the thickness of plate.

By integrating Eq 7, the total potential energy is obtained as a function of the coefficients of displacement fields. According to the principle of minimizing potential energy, to determine the equilibrium states, it is enough that its variations with respect to the unknown parameters obtained and the resulting expressions are set to zero, which is stated in Eq 8.

Eq 8 is a system of nonlinear equations that are solved by using the Newton-Raphson numerical method in MATLAB software. There three types of solutions for this equation, which two of them are stable equilibrium states and other is an unstable equilibrium state. The equilibrium configuration of a plate will stable if the Jacobin matrix J of the potential energy of it be definite positive, according to Eq 9.

where $X = {\left\{{t}_{ij}, {s}_{ij}, {r}_{ij}\right\}}^{T}$ is the unknown coefficients vector.

In the next section, the reliability and sensitivity analysis using Monte Carlo Simulation (MCS) are presented.

2.2.   Reliability analysis

The uncertainty sources may lead to inappropriate behaviour of the engineering systems. The probabilistic evolution of engineering system may include a significant number of uncertainties in their behavior ^[27]. To implement probabilistic assessment for an engineering system, the number of identified issues such as correlation between random variables (RVs), high dimension problems, information about rare event scenarios and many interactive responses in the statement of performance criteria could be addressed ^[28].

Reliability analysis has been extensively used in engineering applications to evaluate the risk caused by such uncertainties ^[29]. In addition, it has a specific place in the process design of composite materials which leads to design more reliable laminated structures ^{[30,31,32,33,34]}.

Generally, there are three approaches to estimate the failure probability, namely approximation (first and second order reliability method), simulation (MCS, subset simulation, important sampling, etc.) and adaptive surrogate-modeling-based (Adoptive kriging-MCS, Adaptive polynomial chaos kriging-MCS, etc. ^[35]. MCS is a robust tool for analyzing complex system. In the reliability problems with small failure probability, the computational cost is high but it is more accurate. The MCS failure probability ${P}_{f}$ is defined in Eq 10.

where $f\left(\boldsymbol{x}\right)$ is the joint density function of ${x}_{1}, \dots , {x}_{n}$. If the limit state function $g\left(\boldsymbol{x}\right)<0$, then the failure is occurred. The integral failure probability ${P}_{f}$ of Eq 10 using indicator function ${I}_{g\left(\boldsymbol{x}\right)\le 0}\left(\boldsymbol{x}\right)$ can be express by Eq 11.

where ${I}_{g\left(\boldsymbol{x}\right)\le 0}\left(\boldsymbol{x}\right) = 1$ if $g\left(\boldsymbol{x}\right)\le 0$, otherwise ${I}_{g\left(\boldsymbol{x}\right)\le 0}\left(\boldsymbol{x}\right) = 0$. The parameter $N$ is the total number of simulations and ${N}_{f}$ is number of simulation when $g\left(\boldsymbol{x}\right)<0$. To enhance the efficiency of MCS analysis, some state-of-the-art methodologies can be applied as an alternative to estimate ${P}_{f}$ such as stochastic finite element method (SFEM) based on stochastic perturbation ^[36] which is not under the scope of this study.

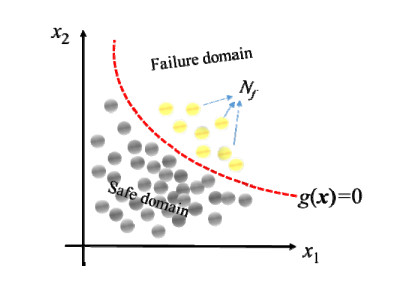
Figure 1 shows the schematic exhibition of the safe and failure domains in 2D reliability problem.

To investigation the accuracy of ${P}_{f}$ can be used the coefficient of variation (COV) as Eq 12.

Sensitivity is applied to explore the rate of change in a model output due to changes in the model inputs in deterministic design, which is frequently calculated by partial derivative analytically or numerically. The sensitivity analysis provides a different meaning for random uncertainty.

The reliability sensitivity analysis is to investigate the rate of change in the probability characteristics of the response, especially P_f, due to the probability characteristics of a basic RV x_i, such as $\frac{\partial {P}_{f}}{\partial {\mu }_{{x}_{i}}}$ and $\frac{\partial {P}_{f}}{\partial {\sigma }_{{x}_{i}}}$ ^[37]. Eq 13 defines the MCS sensitivity analysis.

where ${\xi }_{i}$ indicated the probability characteristics of RVs, ${\mu }_{{x}_{i}}$ and ${\sigma }_{{x}_{i}}$, and ${D}_{F}$ is the domain of failure. The Eq 13 could be written as Eq 14 using the Lebesgue dominated convergence theorem ^[38].

where $\frac{\partial lnf\left(\boldsymbol{x}\right)}{\partial {\xi }_{i}}$ is introduced as a score function ${S}_{{\xi }_{i}}$. Hence, the Eq 14 be converted into Eq 15.

In the current research, the bistability probability of cross-ply bistable composites plate is studied. So, the limit state function g(x) is presented by Eq 16.

The limit state function in Eq 16 illustrates that $g\left(\boldsymbol{x}\right)\le 0$ is the unstable configuration or failure while $g\left(\boldsymbol{x}\right)$ > 0 is the stable configuration or non-failure.

3.   Results

The bistable composite plate is composed of Graphite/Epoxy (T300/5208) in the unsymmetric stacking sequences [0/90] with 150 mm × 150 mm side length. The means and the Coefficients of Variation (COV) of the geometry and material properties are listed in Table 1. In this work, nine independent random variables are considered. The uncertain material properties, laminate dimensions are considered as random variables which the distribution type is normal ^[39,40].

3.1.   Stable configurations

To study the different behaviors of bistable composite laminates, the first step is to determine the static stable states. There are two cylindrical stable configurations for [0/90] bistable composite laminates so that they are identical and perpendicular to each other and have opposite directions. In other words, each state has two transverse curvatures which are the opposite. For cross-ply laminate one of them is much more than other and the twisting curvature is close to zero. These stable states obtained from analytical and finite element methods are presented in Figure 2.

The numerical results for the corner displacement obtained from analytical and finite element methods are listed in Table 2.

These results show that the analytical method has acceptable accuracy. The ABAQUS software is employed to study the bistable composite plate by finite element method, the simulated plate is meshed with the S4R element, which consists of 2500 elements and 2601 nodes. The "Static, General" step is used and "Nlgeom" is selected for static analysis due to there is geometric nonlinearity. Figure 3 illustrates the stable states of the desired cross-ply bistable plate after the curing process in the room temperature. The bistability characteristic depends on the geometry dimensions and material properties. In the next section, the effect of these parameters on bistability behavior will be investigated.

3.2.   Reliability and sensitivity analysis

According to Table 1, the bistability probability is estimated about 0.0152 through MCS. The MCS is an accurate method which helps the experts to recognize the different factors on the reliability analysis and future behavior of complex problems. The bistability probability is estimated by 10000 samples and the COV is achieved about 0.080.

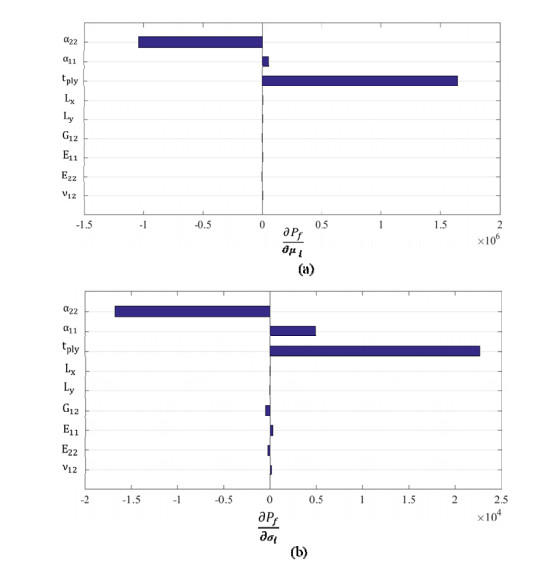
The sensitivities of bistability probability are shown in Figure 4. It is observed from Figure 4a that the mean values of the basic random variables ${\alpha }_{22}$, ${G}_{12}$, ${E}_{22}$, ${L}_{x}$ and ${L}_{y}$ have positive influences on reliability, i.e., the reliability improves with increase in mean values of these parameters. In fact, by increasing the mean value of these parameters the bistability probability is increased. However, the reliability reduces with the increase as mean values of ${t}_{ply}$, ${\alpha }_{11}$, ${E}_{11}$ and ${\nu }_{12}$. The mean values of ${t}_{ply}$, ${\alpha }_{11}$ have the most effect on decreasing as well as ${\alpha }_{22}$ has the most impact on the increasing bistability probability. According to Figure 4b, standard deviations have the same effects as the mean values on the probability bistability, of course, their values are different.

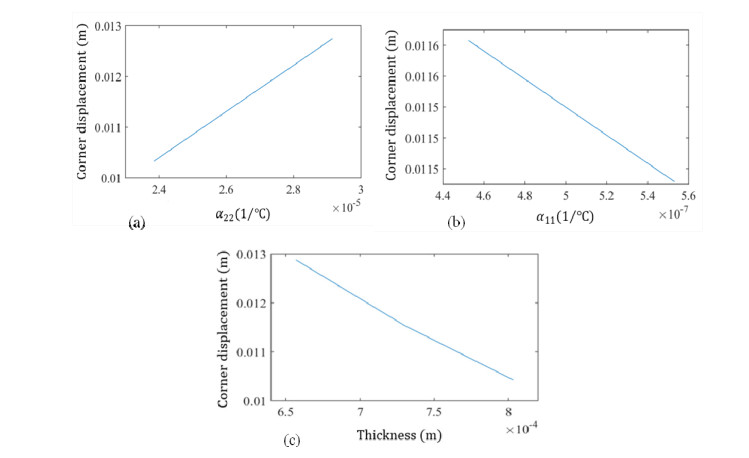
The sensitivity of the corner displacement in the stable configuration to a ±10% change in each parameter is shown in Figure 5. According to that, ${\alpha }_{22}$ has the most influence upon stable shape. In other words, ±10% variation in ${\alpha }_{22}$ makes a 23.3% increase in the amount of maximum displacement at the corner. ±10% variation in ${t}_{ply}$ and ${\alpha }_{11}$, however, lead to decrease in the amount of maximum displacement at the corner by 18.98% and 0.43% in maximum displacement, respectively.

4.   Conclusions

The bistable composite laminates structure is affected by the design parameters such as their material properties and dimensions in practical application. In this paper, the reliability and sensitivity of the cross-ply composite plate were analyzed. The principle conclusions of this work are:

1.Reliability analysis estimates the bistable probability about 0.0152.

2.Sensitivity analysis indicates that thickness and coefficient of thermal expansions have the most important effect on bistability character of the composite laminates.

3.The transverse displacement at the corner increases with the rise of the transverse coefficient of thermal expansion. However, it decreases with the rise of the longitudinal coefficient of thermal expansion and the thickness of the plate.

Moreover, the finite element model of the bistable composite plate was established using ABAQUS software. It could be seen that the finite element analysis results were consistent with the theoretical analysis results. The impact of inter-dependency between RVs can be investigated in future studies. In addition, it's strongly recommended that probability analysis of multi-stable composite structures will be studied in the next work.

Conflict of interest

There is no conflict of interest.