Search Advanced

AIMS Materials Science

2020, Volume 7, Issue 6: 772-787. doi: 10.3934/matersci.2020.6.772
Previous Article Next Article
Review

A review on characteristics and recent advances in piezoelectric thermoset composites

  • 1.
    Department of Mechanical Engineering, Cochin University of Science and Technology, India
  • 2.
    Department of Mechanical Engineering, Mar Baselios College of Engineering and Technology, India
  • 3.
    Indian Space Research Organisation, India
  • Received: 07 August 2020 Accepted: 11 November 2020 Published: 25 November 2020

  • Piezoelectric thermoset composites (PTCs) are the class of material having the ability of transformation between mechanical energy and electric energy. In addition to having the advantages of high strength, easier processing, lower temperature, pressure requirement and unlimited storage, PTCs also have high stiffness, high elastic modulus and high strain coefficients. This review presents the advances and approaches used in PTCs and their applications. Various techniques, such as analytical, finite element and experimental methods for analyzing the coupled piezoelectric responses, are also reviewed. This paper also includes current applications of PTCs in strain sensing, vibration control, actuation, energy harvesting, structural health monitoring and biomedical fields. The studies of PTCs and its applications are in the emerging phase, and the review permits to find new notions for interface studies and modelling progresses for PTCs. In addition to that, these reviews pave the way for various research potentials towards the flourishing pertinent application zones of PTCs. Also, this review highlights the relevance of the particular research area and preliminary work under its different approaches, necessitates the need for more researches.

    Citation: Ruby Maria Syriac, A.B. Bhasi, Y.V.K.S Rao. A review on characteristics and recent advances in piezoelectric thermoset composites[J]. AIMS Materials Science, 2020, 7(6): 772-787. doi: 10.3934/matersci.2020.6.772

    Related Papers:

    [1] Okechukwu Okafor, Abimbola Popoola, Olawale Popoola, Samson Adeosun . Surface modification of carbon nanotubes and their nanocomposites for fuel cell applications: A review. AIMS Materials Science, 2024, 11(2): 369-414. doi: 10.3934/matersci.2024020
    [2] Hendra Suherman, Yovial Mahyoedin, Edi Septe, Roni Rizade . Properties of graphite/epoxy composites: the in-plane conductivity, tensile strength and Shore hardness. AIMS Materials Science, 2019, 6(2): 165-173. doi: 10.3934/matersci.2019.2.165
    [3] Ahmed Ali Farhan Ogaili, Ehsan S. Al-Ameen, Mohammed Salman Kadhim, Muhanad Nazar Mustafa . Evaluation of mechanical and electrical properties of GFRP composite strengthened with hybrid nanomaterial fillers. AIMS Materials Science, 2020, 7(1): 93-102. doi: 10.3934/matersci.2020.1.93
    [4] Adel M Bash, Sulaiman E. Mnawe, Salim A. Salah . Numerical buckling analysis of carbon fibre-epoxy composite plates with different cutouts number by finite element method. AIMS Materials Science, 2020, 7(1): 46-59. doi: 10.3934/matersci.2020.1.46
    [5] Mohd Shahneel Saharudin, Rasheed Atif, Syafawati Hasbi, Muhammad Naguib Ahmad Nazri, Nur Ubaidah Saidin, Yusof Abdullah . Synergistic effects of halloysite and carbon nanotubes (HNTs + CNTs) on the mechanical properties of epoxy nanocomposites. AIMS Materials Science, 2019, 6(6): 900-910. doi: 10.3934/matersci.2019.6.900
    [6] Suman Chhetri, Pranab Samanta, Naresh Chandra Murmu, Suneel Kumar Srivastava, Tapas Kuila . Electromagnetic interference shielding and thermal properties of non-covalently functionalized reduced graphene oxide/epoxy composites. AIMS Materials Science, 2017, 4(1): 61-74. doi: 10.3934/matersci.2017.1.61
    [7] Chaitra Srikanth, G.M. Madhu, Shreyas J. Kashyap . Enhanced structural, thermal, mechanical and electrical properties of nano ZTA/epoxy composites. AIMS Materials Science, 2022, 9(2): 214-235. doi: 10.3934/matersci.2022013
    [8] DavidWood, Dale K. Hensley, Nicholas Roberts . Enhanced thermal conductance of polymer composites through embeddingaligned carbon nanofibers. AIMS Materials Science, 2016, 3(3): 851-861. doi: 10.3934/matersci.2016.3.851
    [9] Dorel Feldman . Poly(vinyl alcohol) nanocomposites: Recent contributions to engineering and medicine. AIMS Materials Science, 2021, 8(1): 119-129. doi: 10.3934/matersci.2021008
    [10] Omar Hassan Mahmood, Mustafa Sh. Aljanabi, Farouk M. Mahdi . Effect of Cu nanoparticles on microhardness and physical properties of aluminum matrix composite prepared by PM. AIMS Materials Science, 2025, 12(2): 245-257. doi: 10.3934/matersci.2025013
  • Piezoelectric thermoset composites (PTCs) are the class of material having the ability of transformation between mechanical energy and electric energy. In addition to having the advantages of high strength, easier processing, lower temperature, pressure requirement and unlimited storage, PTCs also have high stiffness, high elastic modulus and high strain coefficients. This review presents the advances and approaches used in PTCs and their applications. Various techniques, such as analytical, finite element and experimental methods for analyzing the coupled piezoelectric responses, are also reviewed. This paper also includes current applications of PTCs in strain sensing, vibration control, actuation, energy harvesting, structural health monitoring and biomedical fields. The studies of PTCs and its applications are in the emerging phase, and the review permits to find new notions for interface studies and modelling progresses for PTCs. In addition to that, these reviews pave the way for various research potentials towards the flourishing pertinent application zones of PTCs. Also, this review highlights the relevance of the particular research area and preliminary work under its different approaches, necessitates the need for more researches.


    1.   Introduction

    Bipolar plates are the main components of polymer electrolyte membrane (PEM) fuel cells, constituting 80% of PEM fuel cells by weight [1,2]. Conductive polymer composites (CPCs) are potential bipolar plate materials, because these materials can be produced according to the desired shape at relatively inexpensive prices [3,4,5]. However, these materials have low electrical conductivity.

    Several attempts have been made by researchers to improve the electrical conductivity of CPCs by adding conductive fillers of various shapes, sizes and contents. Expanded graphite (EG), graphite (G), carbon black (CB), carbon fibres (CF), and carbon nanotubes (CNTs) have been frequently used to improve the electrical conductivity of CPCs [6,7,8,9,10,11,12,13,14]. However, if higher contents of these conductive fillers are not well dispersed in the matrix (forming agglomerations), then the electrical conductivity of the resulting CPC material decreases [15]. The Department of Energy of the United States has provided requirements for CPCs as bipolar plate materials, namely, that the electrical conductivity must be > 100 S/cm, and the flexural strength must be > 25 MPa.

    Du et al. [16] conducted research on the properties of CPCs using thin epoxy resin as a binder and expanded graphite as a conductive filler. The optimum electrical conductivity for the bipolar plate composite is obtained from an expanded graphite content of 70 wt%, that is, 119.8 S/cm. Suherman et al. [14] used hybrid fillers, with graphite as the main conductive filler, carbon nanotubes as a second conductive filler, and epoxy resin as a binder at a content of 20 weight percent (wt%). These researchers obtained an optimum composition of (75/5/20 wt%), respectively. The moulding parameters that significantly influence the bipolar plate composite properties are the moulding temperature, moulding time, and moulding pressure. San et al. [17] used a thermosetting material as a matrix and synthetic graphite and carbon as conductive materials. These researchers used response surface methodology (RSM) to optimize the parameters to produce a bipolar plate material. These researchers found that the maximum electrical conductivity of the bipolar plate composite was 107.4 S/cm. Akhtar et al. [18] used multifillers of multiwall carbon nantube (MWCNT) and natural graphite (NG) to produce bipolar plates, by using epoxy resins as a matrix. The electrical conductivity of the bipolar plate composite material produced was 126 S/cm. Selamat et al. [19] conducted a study using the Taguchi method to optimize the multiple responses of the compression moulding parameters of a polypropylene–graphite composite. These researchers found that the Taguchi method obtained a balance between the flexural strength and electrical conductivity. However, the electrical conductivity and flexural strength were still low at 16.61 S/cm and 19.82 MPa, respectively, and it did not meet the U.S. Department of Energy requirements.

    Previous research shows that very few researchers use an optimization method to obtain optimum properties for CPC materials. Therefore, the orthogonal array (OA)-Taguchi method and signal to noise ratio (SNR) analysis were used [20,21,22] to obtain the optimal electrical conductivity while reducing the time and cost [20,23,24]. Thus, the optimization of the compression moulding parameters of MWCNT/SG/epoxy nanocomposites for bipolar plates with respect to electrical conductivity was investigated using the Taguchi method.

    2.   Materials and methods

    2.1.   Materials

    Synthetic graphite (SG) and multiwalled carbon nanotubes (MWCNTs) were used as the primary and secondary fillers in this study, respectively. SG with particle size of 74 μm and surface area of 1.5 m2/g was obtained from Asbury Carbons, New Jersey. MWCNTs with surface area of 300 m2/g, diameter of 9.5 nm, length of 1.5 mm, and purity of 90% were obtained from Nanocyl Carbon, Belgium. The 635 thin epoxy resin at a viscosity of 6 Poise and the hardener (4-Aminophenylsulphone) were obtained from US Composites. The ratio between the epoxy resin and hardener was 3:1; these properties were based on the manufacturer descriptions.

    2.2.   Nanocomposite manufacturing process

    The composition in weight percentage (wt%) used was 75/5/20 synthetic graphite (SG), multiwalled carbon nanotubes (MWCNTs), and epoxy, respectively. There are three stages in the manufacturing process of the MWCNT/SG/epoxy nanocomposites. (1) SG and MWCNTs were mixed using a stainless steel ball mill (ball diameter, 10 mm) at 200 rpm for one hour. The ball to powder (graphite and MWCNTs) ratio was 4:1. (2) Hardener and epoxy resin were mixed using a mixer (model RM 20-KIKA-WERK) for 40 seconds at 1200 rpm. An epoxy resin mixture with a ratio of 3:1 was used as suggested by the manufacturer. (3) The filler and epoxy resin were mixed using a Haake Rheomix internal mixer at 20 rpm for 15 minutes at 35 ℃. Next, the mixture of MWCNTs/SG/epoxy was poured into steel moulds at various moulding parameters: moulding temperature (A) = 110, 130, and 150 ℃, moulding pressure (B) = 1200, 1500, and 1800 psi, and moulding time (C) = 60, 75, and 90 minutes.

    2.3.   Characterization

    The electrical conductivity of the nanocomposites was tested by a Jandel four-point probe with a RM3 test unit, and the fracture surface was measured using an FESEM (field emission scanning electron microscope), Model Supra 55/55VP. The FESEM sample was fractured from a sample with dimensions of 100 × 12.7 × 2.5 mm3. The bottom of the fault was cut to 4 mm (thickness) to observe the scattering of the conductive fillers in the matrix. The voltage and magnifications used for observation were 3 kV and 200 to 10, 000 times, respectively.

    2.4.   Selection of control factors

    The compression moulding parameters varied in this study were the moulding time, moulding temperature, and moulding pressure. Table 1 shows the levels and control factors of these moulding parameters. Each control factor consisted of three levels, moulding temperature (A) = 110, 130, and 150 ℃, moulding pressure (B) = 1200, 1500, and 1800 psi, and moulding time (C) = 60, 75, and 90 minutes. Each moulding parameter used was first tested to ensure that the specimens produced using these parameters were well formed. For example, the shortest moulding time selected was 60 minutes because the 45 minutes moulding time used in the preliminary experiments did not produce CPC material well. Therefore, 60 minutes was selected as the lowest moulding time.

    Table 1.  Control factors and levels of compression molding parameters.
    Control factor Level
    1 2 3
    A Moulding temperature (℃) 110 130 150
    B Moulding pressure (psi) 1200 1500 1800
    C Moulding time (min) 60 75 90
     | Show Table
    DownLoad: CSV

    The influence of each compression moulding parameter on the electrical conductivity of the nanocomposites was estimated. Three different temperatures of 110, 130 and 150 ℃ were used to obtain the optimum moulding temperature for the electrical conductivity. The moulding pressure was limited by the viscosity of the mixture of resin and conductive filler at 1800 psi. Therefore, the compression moulding pressures applied were 1200, 1500, and 1800 psi to obtain the optimum combination. Compression moulding pressures exceeding 1800 psi caused the mixture of resin and conductive filler to overflow from the mould. Three different compression moulding times (60, 75 and 90 minutes) were used to obtain the optimal moulding time to produce nanocomposites. The levels of the parameters were set to obtain the optimum electrical conductivity, customized with the Taguchi orthogonal array (OA) L9 (33) design. Analysis of variance (ANOVA) was conducted for the electrical conductivity for each compression moulding parameter in each replicate experiment.

    2.5.   Nanocomposite orthogonal array (OA) L9 (33)

    The optimization of the compression moulding parameters was conducted by producing nine nanocomposite plates with dimensions of 100 mm × 100 mm × 2.5 mm. The number of nanocomposite plates produced was based on the factors and levels of the compression moulding parameters (Table 2). The electrical conductivity was measured at three different points: the middle, far right, and left side of each sample.

    Table 2.  OA L9 (33) for compression moulding parameters of nanocomposites.
    Experiment Number Control Factor and Level
    A B C
    1 110 1200 60
    2 110 1500 75
    3 110 1800 90
    4 130 1200 75
    5 130 1500 90
    6 130 1800 60
    7 150 1200 90
    8 150 1500 60
    9 150 1800 75
     | Show Table
    DownLoad: CSV

    The OA with L9 (33) with nine experiment runs was used to obtain optimum compression moulding parameters. Although this number of experiments is the minimum number of runs for an OA with three control factors and three levels, the minimum number of runs successfully produced the optimum combination parameters for this study [22,25,26].

    2.6.   Analysis of Variance (ANOVA)

    ANOVA is a statistical technique for comparing datasets, or it can be used as an exploratory tool to explain observations. In this study, the analysis of variance was used to determine whether the compression moulding parameters significantly affect the electrical conductivity and to obtain the percentage contribution of each parameter through certain steps (Eq 1 to Eq 8) [27,28] as follows:

    1. The electrical conductivity data from the experimental results are separated by the influences of the control factors and levels, namely, the moulding temperature (A1, A2, and A3), moulding pressure (B1, B2, and B3), and moulding time (C1, C2, and C3).

    2. The sum of squares for each factor control (Sn(i)), total sum of squares(SST), and sum of squares error (SSE) is calculated using the following formula:

    Sn(i)=1N∑ij(X(i,1)−X(i,2))2+(X(i,1)−X(i,3))2+(X(i,2)−X(i,3))2 (1)
    SST=∑ki=1∑nj=1(X2i,j)−(∑X)2N (2)
    SSe=SST−∑Sn(i) (3)

    where X is the experimental data, N is the total number of experiments, and i is the control factors (A, B, and C) at levels of j (level 1, 2, and 3).

    3. The variance (Vn) of each control factor is obtained from Sn divided by DoFn:

    Vn=Sn(i)DoFn (4)

    The variance error (Ve) is obtained from the results of the SS error (SSe) divided by the DoF errors (DoFe) according to the following formula:

    Ve=SSeDoFe (5)

    The number of DoF (degrees of freedom) of the control factors is the number of data points in the collection minus one. The total number of DoF is obtained from the total of the experiments minus one, while the DoF error is the total number of DoF minus the number of DoF of the control factors of A, B, and C.

    4. The variance ratio (Fn) test examines the combined effect of the control factors and is obtained by dividing the variance of each control factor by the variance error:

    Fn=VnVe (6)

    5. The critical value (F) is obtained from the distribution of F (α, d1, and d2), where α is the level of significance, d1 is the numerator (number of degrees of freedom of the control factors), and d2 is the denominator (number of degrees of freedom of the error). This study uses a significance level of 99.5%, so α is 0.005. The critical value (F) is necessary to determine whether the control factors significantly influence the electrical conductivity produced.

    6. Pn is the contribution percentage of each control factor and is calculated using the formula:

    Pn=SSn−(DoFn×VeSSe)×100 (7)

    Because the total contribution percentage (Pt) is 100, the error contribution percentage (Pe) is the total contribution percentage minus the contribution percentages of all the control factors.

    Pe=Pt−(PA+PB+PC) (8)

    2.7.   Signal to noise ratio (SNR) analysis

    The SNR calculates how the response varies relative to the nominal value or target in various noise conditions. In this study, the SNR for the electrical conductivity was maximized; therefore, Eqs 9 and 10 are used [27] as follows:

    SNR=−10log(MSD) (9)

    The MSD is the squared deviation of the average value, as in the following equation:

    MSD=1n∑ni=11yi2 (10)

    where n is the number of experimental replications, carried out for each control factor combination, while yi is the electrical conductivity of the nanocomposite for test repetition.

    3.   Results and discussion

    3.1.   Electrical conductivity of nanocomposites

    The electrical conductivity and SNR of each experiment are shown in Table 3. The electrical conductivity of the MWCNT/SG/epoxy nanocomposites is the major focus of this study. The Taguchi method with orthogonal arrays (OA) of L9 (33) was used. The significant level, influence of each factor, and bilateral reliability was determined using analysis of variance (ANOVA).

    Table 3.  Electrical conductivity of MWCNT/SG/epoxy nanocomposites.
    Number of Experiments Orthogonal Array L9 (33) Electrical Conductivitiy (S/cm) SNR
    A B C σ1 σ2 σ3 ˉσ [dB]
    1 110 1200 60 122.31 118.10 119.28 119.90 41.55
    2 110 1500 75 113.12 116.04 117.00 115.39 41.11
    3 110 1800 90 109.98 113.98 111.87 111.94 40.94
    4 130 1200 75 113.03 111.89 113.06 112.66 41.65
    5 130 1500 90 130.07 127.99 128.19 128.75 42.11
    6 130 1800 60 162.00 159.04 160.49 160.51 44.10
    7 150 1200 90 112.56 113.10 111.63 112.43 41.02
    8 150 1500 60 132.04 134.00 130.98 132.34 42.43
    9 150 1800 75 121.65 120.03 123.01 121.56 41.70
    Avg 123.94
    Max 162.00
    Min 109.98
     | Show Table
    DownLoad: CSV

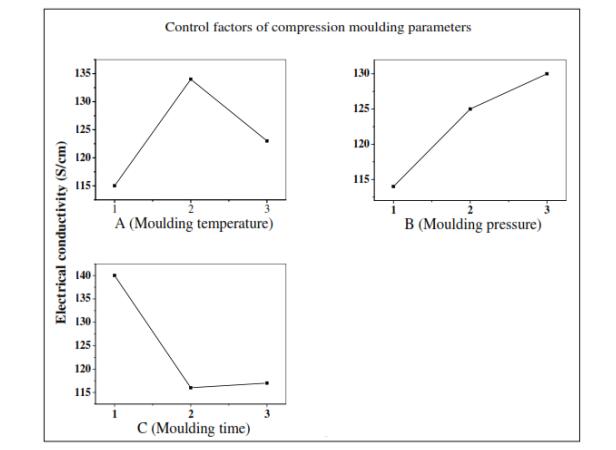
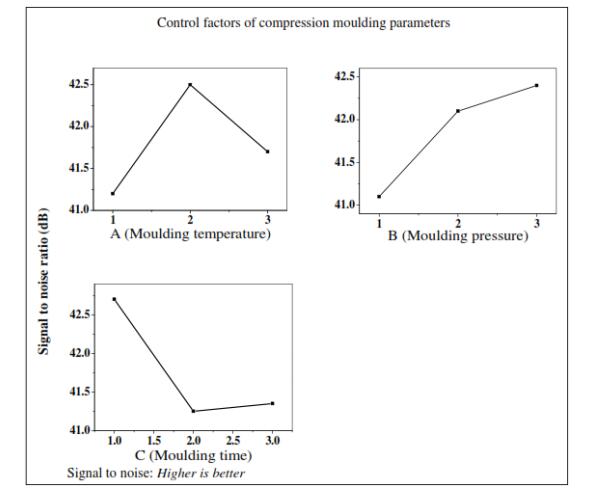
    The average electrical conductivity and signal to noise ratio (SNR) for the different compression moulding parameters are shown in Figures 1 and 2.

    Figure 1.  Electrical conductivity for different compression moulding parameters.
    DownLoad: Full-Size Img PowerPoint
    Figure 2.  SNR of the electrical conductivity for different compression moulding parameters.
    DownLoad: Full-Size Img PowerPoint

    Increasing the moulding temperature from 110 to 130 ℃ improves the electrical conductivity of the MWCNT/SG/epoxy nanocomposites produced. The epoxy resin viscosity decreases as the moulding temperature increases, facilitating the formation of an electrical conductivity network between the flake shaped primary conductive filler (SG) and the micro sized and tubular elongated shaped (nano sized) secondary conductive filler (MWCNTs) [12,29]. Increasing the moulding pressure from 1200 to 1500 to 1800 psi effectively increases the electrical conductivity of nanocomposites. This effect is due to the decrease in the number of voids produced during the manufacturing process with increasing moulding pressure. The electrical conductivity increases as the number of voids decreases [30]. Figures 1 and 2 show that the optimum combination of compression moulding parameters for the electrical conductivity based on the highest SNR is the moulding temperature (A2), moulding pressure (B3) and moulding time (C1).

    3.2.   Analysis of variance (ANOVA) of the nanocomposite electrical conductivity

    The ANOVA of the nanocomposite electrical conductivity is shown in Table 4. The table shows that the variance ratio (Fn) is higher than the critical value (F) at the highest significant level of α = 0.005 (99.5% confidence level) for the moulding temperature (A), moulding pressure (B), and moulding time (C). This result proves that the predetermined compression moulding parameters significantly affect the electrical conductivity of the nanocomposites produced.

    Table 4.  ANOVA of the nanocomposite electrical conductivity.
    Factor Degree of freedom [DoF] Sum of Square [Sn] Variance [Vn] Variance Ratio [Fn] Critical Value [F] Percentage Contribution [Pn]
    A 2 1541.15 770.57 28.53 F(0.005;2;20): 6.9865 25.49
    B 2 1234.15 617.07 22.85 F(0.005;2;20): 6.9865 20.23
    C 2 2517.77 1258.88 46.61 F(0.005;2;20): 6.9865 42.24
    Error 20 540.13 27.00 12.04
    Sum 26 5833.20 100
     | Show Table
    DownLoad: CSV

    The moulding time (C) provides the highest percentage contribution to the electrical conductivity at 42.24%, followed by the moulding temperature (A) at 25.49%. The moulding pressure (B) contributes a percentage of 20.23% to the electrical conductivity. Bin et al. [31] and Hui et al. [32] reported that the moulding temperature, moulding time, and moulding pressure effectively affect the electrical conductivity of the composite produced.

    The highest percentage contribution (Pn) of the moulding time to the electrical conductivity of the nanocomposites is 42.24% due to the decrease in the contact resistance between the conductive filler particles during the compression moulding process [31]. The ANOVA error, at 12.4%, shows that almost all the significant factors were covered in the Taguchi approach. This result has a much smaller error than that reported by Zakaria et al. [33] for a CB/G/EP composite of 80/20, namely, 44%.

    3.3.   Nanocomposite verification tests

    The optimum electrical conductivity for the nanocomposites was obtained through the forecast equation (σforecast ) and verification testing (experimental study). The optimum parameters were obtained from the average SNR, namely, parameters A2, B3, and C1. The forecast equation was used to predict the SNR and electrical conductivity with the optimum compression moulding parameters, using Eq 11 [22].

    σforecast optimum =J+(A2−J)+(B3−J)+(C1−J) (11)

    J = the average SNR of the electrical conductivity from the experiments. The SNR is maximized (Figure 2) with A2 (moulding temperature, 130 ℃), B3 (moulding pressure, 1800 psi), and C1 (moulding time, 60 minutes).The average predictive values for the electrical conductivity and SNR of the nanocomposites using Eq 11 are 155 S/cm and 43.73 dB, respectively. Then, the optimum combination obtained from the average of the compression moulding parameters and SNR was confirmed through experiments. The experiments were carried out by preparing samples with the optimum combination of compression moulding parameters, that is, 130 ℃ moulding temperature, 1800 psi moulding pressure, and 60 minutes moulding time.

    The summary of the results of the initial combination of parameters, optimum combination of parameters and σforecast  are shown in Table 5. The average value of the electrical conductivity and SNR for the initial combination parameters of A1, B1, and C1 are 120 S/cm and 41.55 dB, respectively. Meanwhile, the electrical conductivity and SNR for the optimum combination of factors and levels of A2, B3, and C1 are 163 S/cm and 44.26 dB, respectively. Compared with the initial combination, the confirmation test of the optimum combination shows an increase in the electrical conductivity of the nanocomposites as high as 36.21%. This result occurs because the optimum combination of compression moulding parameters is capable of producing a more even dispersion of the conductive filler material in the polymer matrix. Therefore, the optimum combination of parameters for the nanocomposites produces electrical conductivity higher than that of the initial combination of parameters. Thus, the higher average SNR for each optimum compression moulding parameter effectively increases the electrical conductivity of the nanocomposites. The differences between the average electrical conductivity and SNR of the optimum combination and those of the optimum σforecast  are only 5.37% and 1.21%, respectively, which shows that the prediction equation appropriately predicted the electrical conductivity and SNR of the optimum nanocomposites.

    Table 5.  The optimization of electrical conductivity on nanocomposites.
    Level Electrical conductivity (S/cm) SNR
    σ1 σ2 σ3 ˉσ (dB)
    Initial combination A1, B1, C1 122.31 118.10 119.28 120 41.55
    Optimum combination A2, B3, C1 166.22 161.32 162.43 163 44.26
    Optimum σforecast  A2, B3, C1 155 - - - 43.73
    * Molding temperature 130 ℃ (A2); molding pressure, 1800 psi (B3); molding time 60 minutes (C1).
     | Show Table
    DownLoad: CSV

    3.4.   Nanocomposite microstructures

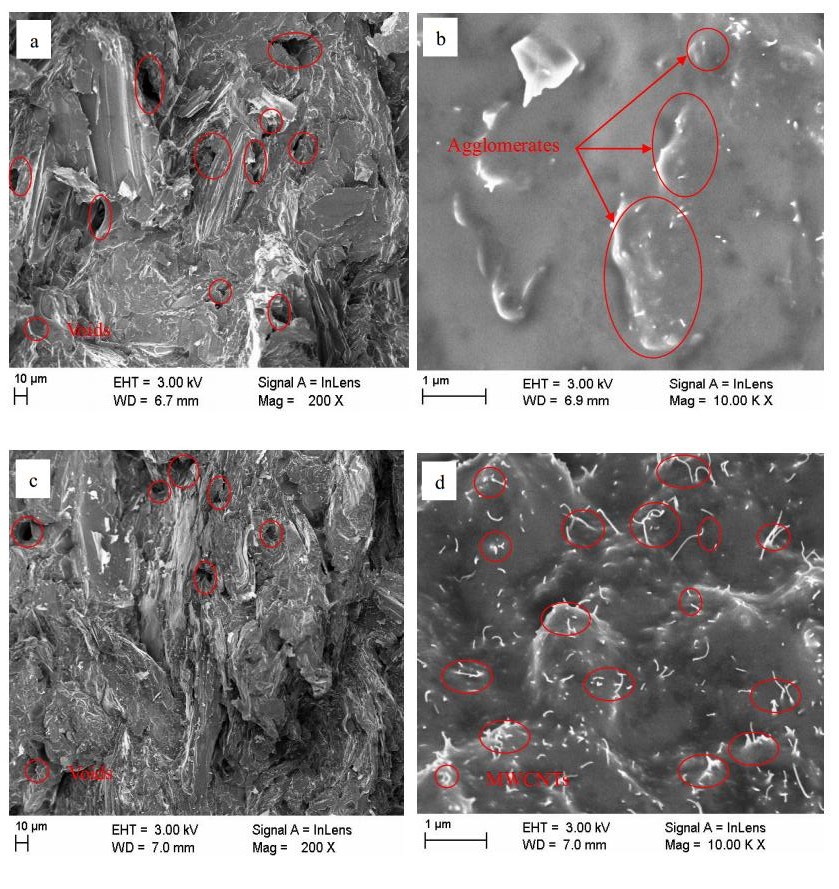
    The primary conductive filler (synthetic graphite) and secondary conductive filler (MWCNT) dispersions in the epoxy matrix were observed by a scanning electron microscope (SEM). Figure 3 shows the microstructure of the MWCNT/SG/epoxy nanocomposites with optimized compression moulding parameters. The microstructure contains a conductive filler dispersion within a polymer matrix. The MWCNTs have tubular geometry and are a brighter colour (white) than the synthetic graphite particles (SG), which have flake geometries.

    Figure 3.  SEM images of the fracture surfaces of the MWCNT/SG/epoxy nanocomposites from the initial tests (a and b) and confirmation tests (c and d) of the compression moulding parameters with magnifications of 200 and 10, 000 times.
    DownLoad: Full-Size Img PowerPoint

    The microstructure of both optimization processes showed voids between the SG as the primary conductive filler material (Figure 3a, c) in the initial fracture surface testing. These voids reduce the electrical conductivity of the nanocomposite generated. The number of voids decreased in the confirmation test (Figure 3c) due to the MWCNTs, which exhibited an elongated tube geometry, effectively filling the voids and conducting electricity between the larger SG particles. The increasing contact between the conductive filler particles increased the electrical conductivity of the nanocomposites produced.

    Agglomeration occurred in the initial testing of the epoxy matrix for both optimization compression moulding parameters that used MWCNTs as a secondary filler, as shown in Figure 3b. The agglomeration increased the distance between the conductive filler materials, decreasing the electrical conductivity of the MWCNT/SG/epoxy nanocomposites produced. The electrical conductivity network formation occurred not only by direct contact between the conductive filler particles but also by distances of a few micrometres between particles, thus enabling electrons to jump across the gaps between the conductive filler materials [28]. The optimization of the compression moulding parameters effectively reduced the agglomeration of the MWCNTs within the polymer matrix, so that the MWCNTs could be dispersed more evenly in the epoxy. An even dispersion of the conductive filler in the matrix produces a higher electrical conductivity in MWCNT/SG/epoxy nanocomposites compared with an uneven dispersion of the conductive filler material [12,34,35]. This situation was observed in the confirmation tests (Figure 3c, d).

    4.   Conclusions

    The compression moulding parameters of MWCNT/SG/epoxy nanocomposites were investigated with respect to electrical conductivity. Based on the results, certain conclusions can be drawn:

    1. The moulding temperature (A), moulding pressure (B), and moulding time (C) were selected as control factors using the Taguchi method. Experimental trials based on an L9 (33) orthogonal array were carried out.

    2. The analysis of variance (ANOVA) results show that all the control factors significantly influence the electrical conductivity produced. The moulding time (C) provides the highest percentage contribution to the resulting electrical conductivity at 42.24%, the moulding temperature (A) at 25.49% and the moulding pressure (B) at 20.23%.

    3. The electrical conductivity of the initial combination at factors and levels of A1, B1, C1 is 120 S/cm. The optimum combination at factors and levels of A2, B3, C1 is 163 S/cm.

    4. The optimum electrical conductivity of the MWCNT/SG/epoxy nanocomposites is 163 S/cm. This value meets the U.S. Department of Energy requirements for bipolar plate applications.

    Acknowledgements

    The authors gratefully acknowledge the financial assistance of the Directorate General of Higher Education for this research, with contract number: SP DIPA-042.06.1.401516/2019, 5 December 2018.

    Conflicts of interest

    The authors have no conflicts of interest.



    [1] Khan AA, Zahid N, Zafar S, et al. (2014) History, current status and challenges of structural health monitoring in aviation. J Space Technol 4: 67-74.
    [2] Galea SC, Powlesland IG, Moss SD, et al. (2001) Development of structural health monitoring systems for composite bonded repairs on aircraft structures, Smart Structures and Materials 2001: Smart Structures and Integrated Systems, 4327: 246-257.
    [3] Shahinpoor M (2020) Review of piezoelectric materials, Fundamentals of Smart Materials, The Royal Society of Chemistry, 13.
    [4] Yousefi-Koma A (2018) Piezoelectric ceramics as intelligent materials, Fundamentals of Smart Materials, The Royal Society of Chemistry, 233.
    [5] Das S, Biswal AK, Roy A (2017) Fabrication of flexible piezoelectric PMN-PT based composite films for energy harvesting. IOP Conf Ser: Mater Sci Eng 178: 012020.
    [6] Kao KC (2014) Dielectric Phenomena in Solids with Emphasis on Physical Concepts of Electronic Processes, Elsevier Academic Press.
    [7] Nunes-Pereira J, Costa P, Lanceros-Mendez S (2018) Piezoelectric energy production, In: Dincer I, Comprehensive Energy Systems, Elsevier, 3: 381-415.
    [8] Blackwoodt GH, Ealey MA (1999) Electrostrictive behaviour in lead magnesium niobate (PMN) actuators. Part Ⅰ: materials perspective. Smart Mater Struct 2: 124-133.
    [9] Kim SK, Komarneni S (2011) Synthesis of PZT fine particles using Ti3+ precursor at a low hydrothermal temperature of 110 º C. Ceram Int 37: 1101-1107.
    [10] Hadjiloizi DA, Georgiades AV, Kalamkarov AL (2012) Dynamic modeling and determination of effective properties of smart composite plates with rapidly varying thickness. Int J Eng Sci 56: 63-85.
    [11] Akdogan EK, Allahverdi M, Safari A (2005) Piezoelectric composites for sensor and actuator applications. IEEE T Ultrason Ferr 52: 746-775.
    [12] Lin XJ, Zhou KC, Zhang XY, et al. (2013) Development, modeling and application of piezoelectric fibre composites. T Nonferr Metal Soc 23: 98−107.
    [13] Mishra S, Unnikrishnan L, Nayak SK, et al. (2019) Advances in piezoelectric polymer composites for energy harvesting applications: A systematic review. Macromol Mater Eng 304: 1800463.
    [14] Sundar U, Banerjee S, Cook-C K (2018) Piezoelectric and dielectric properties of PZT-epoxy composite thick films. Academ J Polym Sci 1: 555574.
    [15] Hadjiloizi DA, Georgiades AV, Kalamkarov AL (2012) Dynamic modeling and determination of effective properties of smart composite plates with rapidly varying thickness. Int J Eng Sci 56: 63-85.
    [16] Elshafei MA, Ajala MR, Riad AM (2014) Modeling and analysis of smart timoshenko beams with piezoelectric materials. Int J Eng Innovative Technol 3: 21-33.
    [17] Jain A, Prashanth KJ, Sharma, AK, et al. (2015) Dielectric and piezoelectric properties of PVDF/PZT composites: A review. Polym Eng Sci 55: 1589-1616.
    [18] Li Y, Lu G, Chen JJ, et al. (2019) PMN-PT/epoxy 1-3 composite based ultrasonic transducer for dual-modality photoacoustic and ultrasound endoscopy. Photoacoustics 15: 100138.
    [19] Leadbetter J, Brown JA, Adamson RB (2013) The design of ultrasonic lead magnesium niobate-lead titanate (PMN-PT) composite transducers for power and signal delivery to implanted hearing aids. POMA 19: 030029.
    [20] Osman KI (2011) Synthesis and characterization of BatiO3 ferroelectric material [PhD thesis], Egypt: Cairo University.
    [21] Jaffe B, Cook WR, Jaffe H (1971) Piezoelectric Ceramics, London: Academic Press, 326.
    [22] Lupeiko TG, Lopatin SS (2004) Old and new problems in piezoelectric materials research and materials with high hydrostatic sensitivity. Inorg Mater 40: S19-S32.
    [23] Lopatin SS, Medvedev BS, Fainrider DE (1986) Properties of piezoceramics based on solid solutions of BiTiMO6 (M = Nb, Sb) in orthorhombic lead metaniobate. Inorg Mater 21: 1757-1762.
    [24] Bhalla S, Yang YW, Annamdas VGM, et al. (2012) Impedance models for structural health monitoring using piezo-impedance transducers, In: Soh CK, Yang YW, Bhalla S, Smart Materials in Structural Health Monitoring, Control and Biomechanics, Berlin, Heidelberg: Springer, 53-128.
    [25] Xu TB (2016) Energy harvesting using piezoelectric materials in aerospace structures, In: Yuan FG, Structural Health Monitoring (SHM) in Aerospace Structures, Elsevier.
    [26] Green DG (1989) Assurance of structural reliability in ceramics, In: Mostaghaci H, Processing of Ceramic and Metal Matrix Composites, Elsevier, 349-366.
    [27] Ivan IA, Agnus J, Lambert P (2012) PMN-PT (lead magnesium niobate-lead titanate) piezoelectric material micromachining by excimer laser ablation and dry etching (DRIE). Sensor Actuat A-Phys 177: 37-47.
    [28] Swallow LM, Siores E, Dodds D (2010) Self-powered medical devices for vibration suppression, In: Anand SC, Kennedy JF, Miraftab M, et al., Medical and Healthcare Textiles, Woodhead Publishing, 415-422.
    [29] Liu T, Pei JZ, Xu J (2019) Analysis of PZT/PVDF composites performance reinforced by aramid fibres. Mater Res Express 6: 066303.
    [30] Banerjee S, Cook-Chennault KA (2011) Influence of Al particle size and lead zirconate titanate (PZT) volume fraction on the dielectric properties of PZT-epoxy-aluminum composites. J Eng Mater-T ASME 133: 04016.
    [31] Banerjee S, Cook-Chennault KA (2011) An analytical model for the effective dielectric constant of a 0-3-0 composite. J Eng Mater-T ASME 133: 041005.
    [32] Banerjee S, Cook-Chennault KA (2012) An investigation into the influence of electrically conductive particle size on electro-mechanical coupling and effective dielectric strain coefficients in three-phase composite piezoelectric polymers. Compos Part A-Appl S 43: 1612-1619.
    [33] Banerjee S, Du W, Wang L, et al. (2013) Fabrication of dome-shaped PZT-epoxy actuator using modified solvent and spin coating technique. J Electroceram 31: 148-158.
    [34] Banerjee S, Cook-Chennault KA (2011) An analytical model for the effective dielectric constant of a 0-3-0 composite. J Eng Mater-T ASME 133: 041005.
    [35] Nguyen TT, Phan TTM, Chu NC, et al. (2016) Elaboration and dielectric property of modified PZT/epoxy nanocomposites. Polym Composite 37: 455-461.
    [36] Chao F, Liang GZ, Kong WF, et al. (2008) Study of dielectric property on BaTiO3/BADCy composite. Mater Chem Phys 108: 306-311.
    [37] Malmonge JA, Malmonge LF, Fuzari GC, et al. (2009) Piezo and dielectric properties of PHB-PZT composite. Polym Composite 30: 1333-1337.
    [38] Banerjee S, Cook-Chennault KA (2014) Influence of aluminium inclusions on dielectric properties of three-phase PZT-cement aluminium composites. Adv Cem Res 26: 63-76.
    [39] Banerjee S, Torres J, Cook-Chennault KA (2015) Piezoelectric and dielectric properties of PZT-cement-aluminium nano-composites. Ceram Int 41: 819-833.
    [40] Moffett MB, Robinson HC, Powers JM, et al. (2007) Single-crystal lead magnesium niobate-lead titanate (PMN/PT) as a broadband high power transduction material. J Acoust Soc Am 121: 2591-2599.
    [41] Mirjavadi SS, Forsat M, Barati MR, et al. (2019) Post-buckling analysis of piezo-magnetic nanobeams with geometrical imperfection and different piezoelectric contents. Microsyst Technol 25: 3477-3488.
    [42] Shankar G, Kumar SK, Mahato PK (2017) Vibration analysis and control of smart composite plates with delamination and under hygrothermal environment. Thin Wall Struct 116: 53-68.
    [43] Hadjiloizi DA, Kalamkarov AL, Georgiades AV (2017) Plane stress analysis of magnetoelectric composite and reinforced plates: Micromechanical modeling and application to laminated structures. ZAMM 97: 761-785.
    [44] Khan A, Kim HS, Youn BD (2017) Modeling and assessment of partially debonded piezoelectric sensor in smart composite laminates. Int J Mech Sci 131: 26-36.
    [45] Kumar PVS, Reddy DBC, Reddy KVK (2016) Transient analysis of smart composite laminate plates using higher-order theory. IJMET 7: 166-174.
    [46] Phung-Van P, De Lorenzis L, Thai CH, et al. (2014) Analysis of laminated composite plates integrated with piezoelectric sensors and actuators using higher-order shear deformation theory and isogeometric finite elements. Comp Mater Sci 96: 495-505.
    [47] Dumoulin C, Deraemaeker A (2018) A study on the performance of piezoelectric composite materials for designing embedded transducers for concrete assessment. Smart Mater Struct 27: 035008.
    [48] Gohari S, Sharifi S, Vrcelj Z (2016) A novel explicit solution for twisting control of smart laminated cantilever composite plates/beams using inclined piezoelectric actuators. Compos Struct 161: 471-504.
    [49] Swati RF, Elahi H, Wen LH, et al. (2018) Investigation of tensile and in-plane shear properties of carbon fibre-reinforced composites with and without piezoelectric patches for micro-crack propagation using extended finite element method. Microsyst Technol 15: 2361-2370.
    [50] Ye J, Cai H, Wang Y, et al. (2018) Effective mechanical properties of piezoelectric-piezomagnetic hybrid smart composites. J Intel Mat Syst Str 29: 1711-1723.
    [51] Rao MN, Tarun S, Schmidt R, et al. (2016) Finite element modeling and analysis of piezo-integrated composite structures under large applied electric fields. Smart Mater Struct 25: 055044.
    [52] Kulkarni P, Kanakaraddi RK (2015) Finite element modeling of piezoelectric patches for vibration analysis of structures. IRJET 2: 1207-1213.
    [53] Kishore MH, Singh BN, Pandit MK (2011) Non-linear static analysis of smart laminated composite plate. Aerosp Sci Technol 15: 224-235.
    [54] Beheshti-Aval SB, Lezgy-Nazargah M (2010) A finite element model for the composite beam with piezoelectric layers using a sinus model. J Mech 26: 249-258.
    [55] Sateesh VL, Upadhyay CS, Venkatesan C (2010) A study of the polarization-electric-field non-linear effect on the response of smart composite plates. Smart Mater Struct 19: 075012.
    [56] Lampani L, Sarasini F, Tirillò J, et al. (2018) Analysis of damage in composite laminates with embedded piezoelectric patches subjected to bending action. Compos Struct 202: 935-942.
    [57] Greminger M, Haghiashtiani G (2017) Multiscale modeling of PVDF matrix carbon fiber composites. Model Simul Mater Sci 25: 045007.
    [58] Ghasemi-Nejhad MN, Pourjalali S, Uyema M, et al. (2006) Finite element method for active vibration suppression of smart composite structures using piezoelectric materials. J Thermoplast Compos 19: 309-352.
    [59] Dutta G, Panda SK, Mahapatra TR, et al. (2016) Electro-magneto-elastic response of laminated composite plate: A finite element approach. Int J Appl Comput Math 3: 2573-2592.
    [60] Liu T, Pei JZ, Xu J, et al. (2019) Analysis of PZT/PVDF composites performance reinforced by aramid fibers. Mater Res Express 6: 066303.
    [61] Perez-Rosado A, Gupta SK, Bruck HA (2016) Mechanics of multifunctional wings with solar cells for robotic birds, In: Ralph C, Silberstein M, Thakre PR, et al., Mechanics of Composite and Multi-Functional Materials, Springer, Cham, 7: 1-10.
    [62] Narayana KJ, Burela RG (2018) A review of recent research on multifunctional composite materials and structures with their applications. Mater Today Proc 5: 5580-5590.
    [63] Thill CL, Etches J, Bond I, et al. (2008) Morphing skins. Aeronautical J 112: 117-139.
    [64] Mudupu V, Trabia MB, Yim W, et al. (2008) Design and validation of a fuzzy logic controller for a smart projectile fin with a piezoelectric macro-fibre composite bimorph actuator. Smart Mater Struct 17: 035034.
    [65] Tuss J, Lockyer A, Alt K, et al. (1996) Conformal load-bearing antenna structure. 37th Structure, Structural Dynamics and Materials Conference, 2: 836-843.
    [66] Lockyer AJ, Alt KH, Kinslow RW, et al. (1996) Development of a structurally integrated conformal load-bearing multifunction antenna: overview of the air force smart skin structures technology demonstration program, Smart Structures and Materials 1996: Smart Electronics and MEMS, 2722: 55-64.
    [67] Berden MJ, McCarville DA (2007) Structurally integrated X-band antenna large scale component wing test. SAMPE'07.
    [68] Lockyer AJ, Alt KH, Kudva JN, et al. (2001) Air vehicle integration issues and considerations for CLAS successful implementation, Smart Structures and Materials 2001: Industrial and Commercial Applications of Smart Structures Technologies, 4332: 48-59.
    [69] Yao L, Qiu Y (2009) Design and fabrication of microstrip antennas integrated in three-dimensional orthogonal woven composites. Compos Sci Technol 69: 1004-1008.
    [70] Yao L, Wang X, Xu F, et al. (2009) Fabrication and impact performance of three-dimensionally integrated microstrip antennas with microstrip and coaxial feeding. Smart Mater Struct 18: 095034.
    [71] Matsuzaki R, Melnykowycz M, Todoroki A (2009) Antenna/sensor multifunctional composites for the wireless detection of damage. Compos Sci Technol 69: 2507-2513.
    [72] Kumar S, Raj S, Jain S, et al. (2016) Multifunctional biodegradable polymer nano-composite incorporating graphene-silver hybrid for biomedical applications. Mater Design 108: 319-332.
    [73] Bai G, Tsang MK, Hao J (2016) Luminescent ions in advanced composite materials for multifunctional applications. Adv Funct Mater 26: 6330-6350.
    [74] Tandon B, Blaker JJ, Cartmell SH (2018) Piezoelectric materials as stimulatory biomedical materials and scaffolds for bone repair. Acta Biomater 73: 1-20.
    [75] Vaidya AS, Vaidya UK, Uddin N (2008) Impact response of three-dimensional multifunctional sandwich composite. Mater Sci EngA-Struct 472: 52-58.
    [76] Song G, Qiao PZ, Binienda WK, et al. (2002) Active vibration damping of composite beam using smart sensors and actuators. J Aerospace Eng 15: 97-103.
    [77] Sun BH, Huang D (2001) Vibration suppression of laminated composite beams with a piezoelectric damping layer. Compos Struct 53: 437-447.
    [78] Thierry O, De Smet O, Deü JF (2016) Vibration reduction of a woven composite fan blade by piezoelectric shunted devices. J Phys Conf Ser 744: 012164
    [79] Dong BQ, Liu YQ, Qin L, et al. (2016) In-situ structural health monitoring of a reinforced concrete frame embedded with cement-based piezoelectric smart composites. Res Nondestruct Eval 27: 216-229.
    [80] Zhang T, Zhang K, Liu W (2018) Exact impact response of multi-layered cement-based piezoelectric composite considering electrode effect. J Intel Mat Syst Str 30: 400-415.
    [81] Dao PB, Klepka A, Pieczonka L, et al. (2017) Impact damage detection in smart composites using non-linear acoustics cointegration analysis for removal of undesired load effect. Smart Mater Struct 26: 035012.
    [82] Bisheh HK, Wu N (2018) Analysis of wave propagation characteristics in piezoelectric cylindrical composite shells reinforced with carbon nanotubes. Int J Mech Sci 145: 200-220.
    [83] Bisheh HK, Wu N (2018) Wave propagation in smart laminated composite cylindrical shells reinforced with carbon nanotubes in hygrothermal environments. Composites Part B-Eng 162: 219-241.
    [84] Bisheh HK, Wu N (2019) On dispersion relations in smart laminated fibre-reinforced composite membranes considering different piezoelectric coupling effects. J Low Freq Noise V A 38: 487-509.
    [85] Bisheh HK, Wu N, Hui D (2019) Polarization effects on wave propagation characteristics of piezoelectric coupled laminated fibre-reinforced composite cylindrical shells. Int J Mech Sci 161: 105028
    [86] Bisheh HK, Wu N (2018) Wave propagation in piezoelectric cylindrical composite shells reinforced with angled and randomly oriented carbon nanotubes. Compos Part B-Eng 160: 10-30.
    [87] Bisheh HK, Rabezuk T, Wu N (2020) Effects of nanotube agglomeration on wave dynamics of carbon nanotube-reinforced piezo composite cylindrical shells. Compos Part B-Eng 187: 107739.
    [88] Bisheh HK, Wu N, Rabezuk T (2020) Free vibration analysis of smart laminated carbon nanotube-reinforced composite cylindrical shells with various boundary conditions in hygrothermal environments. Thin Wall Struct 149: 106500.
    [89] Bisheh HK, Civalek O (2020) Vibration of smart laminated carbon nanotube-reinforced composite cylindrical panels on elastic foundations in hygrothermal environments. Thin Wall Struct 155: 106945.

  • This article has been cited by:

    1. UO Uyor, API Popoola, OM Popoola, VS Aigbodion, Influence of graphene–carbon nanotubes and processing parameters on electrical and dielectric properties of polypropylene nanocomposites, 2021, 0021-9983, 002199832110067, 10.1177/00219983211006761
    2. Deepa Ahirwar, Amit Telang, Rajesh Purohit, Anurag Namdev, A short review on polyurethane polymer composite, 2022, 62, 22147853, 3804, 10.1016/j.matpr.2022.04.481
    3. Salah M.S. Al‐Mufti, S.J.A. Rizvi, 2023, 9781119829331, 137, 10.1002/9781119829553.ch7
    4. Md Zakir Hussain, Sabah Khan, Barnali Sharma, Pranjal Sarmah, Multiresponse optimization of fabrication variables of α-MnO2-epoxy nanocomposite through simulation-based Taguchi-grey relational analysis, 2024, 38, 1738-494X, 6799, 10.1007/s12206-024-1133-6
    5. Baraa Chasib Mezher AL-Kasar, Shahab Khameneh Asl, Hamed Asgharzadeh, Seyed Jamaleddin Peighambardoust, Enhancing soundproofing performance of polypropylene nanocomposites for implantable electrodes inside the body through graphene and nanoclay; thermomechanical analysis, 2024, 14, 2158-3226, 10.1063/5.0209738
  • Reader Comments
  • © 2020 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)
通讯作者: 陈斌, bchen63@163.com
  • 1. 

    沈阳化工大学材料科学与工程学院 沈阳 110142

  1. 本站搜索
  2. 百度学术搜索
  3. 万方数据库搜索
  4. CNKI搜索
AIMS Materials Science
1.4 3.6

Metrics

Article views(5143) PDF downloads(323) Cited by(5)

Preview PDF
Download XML
Export Citation
Article outline
Abstract
   Introduction
   Materials and methods
   Results and discussion
   Conclusions
Acknowledgements
Conflicts of interest
References

Figures and Tables

Figures(2)  /  Tables(5)

Other Articles By Authors

Related pages

Tools

Copyright © AIMS Press

/

DownLoad:  Full-Size Img  PowerPoint
Return
Return

Catalog