Citation: Katsumasa Satoh, Yasuhide Tsuji. A study on photonic crystal slab waveguide with absolute photonic band gap[J]. AIMS Materials Science, 2018, 5(1): 116-126. doi: 10.3934/matersci.2018.1.116
| [1] | Kah Hon Leong, Azrina Abd Aziz, Yee Li Kang, Sheau Wei Goh, Kulhar Vijay Singh, Lan Ching Sim, Pichiah Saravanan . Synergized mechanistic and solar photocatalysis features of N-TiO2 functionalised activated carbon. AIMS Materials Science, 2017, 4(3): 800-813. doi: 10.3934/matersci.2017.3.800 |
| [2] | HN Girish, P Madhusudan, CP Sajan, BV Suresh Kumar, K Byrappa . Supercritical hydrothermal synthesis of polycrystalline gadolinium aluminum perovskite materials (GdAlO3, GAP). AIMS Materials Science, 2017, 4(3): 540-550. doi: 10.3934/matersci.2017.3.540 |
| [3] | Mihaela Girtan, Laura Hrostea, Mihaela Boclinca, Beatrice Negulescu . Study of oxide/metal/oxide thin films for transparent electronics and solar cells applications by spectroscopic ellipsometry. AIMS Materials Science, 2017, 4(3): 594-613. doi: 10.3934/matersci.2017.3.594 |
| [4] | Jonathan P. Hayton, Andrew R.J. Marshall, Michael D. Thompson, Anthony Krier . Characterisation of Ga1-xInxSb quantum wells (x~0.3) grown on GaAs using AlGaSb interface misfit buffer. AIMS Materials Science, 2015, 2(2): 86-96. doi: 10.3934/matersci.2015.2.86 |
| [5] | Avner Neubauer, Shira Yochelis, Gur Mittelman, Ido Eisenberg, Yossi Paltiel . Simple down conversion nano-crystal coatings for enhancing Silicon-solar cells efficiency. AIMS Materials Science, 2016, 3(3): 1256-1265. doi: 10.3934/matersci.2016.3.1256 |
| [6] | K. Ravindranadh, K. Durga Venkata Prasad, M.C. Rao . Spectroscopic and luminescent properties of Co2+ doped tin oxide thin films by spray pyrolysis. AIMS Materials Science, 2016, 3(3): 796-807. doi: 10.3934/matersci.2016.3.796 |
| [7] | Haridas D. Dhaygude, Surendra K. Shinde, Ninad B. Velhal, G.M. Lohar, Vijay J. Fulari . Synthesis and characterization of ZnO thin film by low cost modified SILAR technique. AIMS Materials Science, 2016, 3(2): 349-356. doi: 10.3934/matersci.2016.2.349 |
| [8] | Lucangelo Dimesso, Michael Wussler, Thomas Mayer, Eric Mankel, Wolfram Jaegermann . Inorganic alkali lead iodide semiconducting APbI3 (A = Li, Na, K, Cs) and NH4PbI3 films prepared from solution: Structure, morphology, and electronic structure. AIMS Materials Science, 2016, 3(3): 737-755. doi: 10.3934/matersci.2016.3.737 |
| [9] | Alberto Debernardi . Ab initio calculation of band alignment of epitaxial La2O3 on Si(111) substrate. AIMS Materials Science, 2015, 2(3): 279-293. doi: 10.3934/matersci.2015.3.279 |
| [10] | Z. Aboub, B. Daoudi, A. Boukraa . Theoretical study of Ni doping SrTiO3 using a density functional theory. AIMS Materials Science, 2020, 7(6): 902-910. doi: 10.3934/matersci.2020.6.902 |
With the recent development of optical communication systems, in order to realize high-speed and large-capacity photonic network, compact and high-performance optical waveguide devices have been intensively developed. Under these circumstances, several kinds of photonic crystals (PhCs) have been proposed as an artificial material and the photonic devices based on PhCs have attracted a lot of attentions [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26]. PhCs are periodic nanoscale structures made of two or more kinds of dielectric materials and some of them prohibit light propagation with specific frequency into them. This frequency band is referred to as photonic band gap (PBG) and is utilized to realize ultra-compact photonic devices since radiation loss at sharp bends is able to be suppressed. In view of actual fabrication, two-dimensional slab type PhCs are most widely discussed. In slab type PhCs, the PBG usually exists only for one polarization state of two orthogonal polarization states. If an absolute PBG for both polarization states is realized, the applicability of PhCs is further extended. For that reason, several types of PhC structures to realize absolute PBGs have been reported [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16] and photonic devices utilizing an absolute PBG have been also reported [17,18,19,20,21,22]. However, in some of the PhCs proposed so far, the absolute PBGs have been realized in the higher frequency above light line. Therefore, in the actual application of those PhCs, the out-of-plane radiation loss may occur at waveguide discontinuities. Moreover, the most PhCs related to the absolute PBG has been studied in two-dimensional model. Although some PhCs with two-or three-dimensional structures have absolute PBGs below light line [11,12,13,14,15,16], these absolute PBGs do not exist between first and second photonic bands. In addition, these PhCs utilize anisotropic dielectric materials or three kinds of materials with higher refractive index to realize PhC slab with finite slab thickness. Considering to realize PhC devices on SOI platform, Si-based PhC seems to be preferable. In Ref. [9], it is demonstrated that the proposed Si-based honeycomb PhCs with finite slab thickness is able to realize an absolute PBG between first and second photonic bands. However, in this report, the approximated two-dimensional analysis is carried out and, in the actual three-dimensional model, the absolute PBG does not exist.
In this study, we propose novel Si-based PhCs with an absolute PBG and the structural parameters are optimized to expand a bandwidth of the absolute PBG. Through the numerical investigation in approximated two-dimensional model, it is shown that the optimized steering type PhC has the absolute PBG with a bandwidth of 164 nm at the center wavelength of 1.55 μm. Moreover, utilizing the designed PhC, we investigate the possibility of a compact photonic circuit which supports both polarization states. Finally, we analyze the dispersion property of the actual three-dimensional model of the proposed PhC and confirm the existence of an absolute PBG.
In this discussion, the slab type PhCs consist of Silicon (Si) sandwiched by silica (SiO2) is assumed and the slab thickness is set to be 240 nm. The refractive indices of Si, SiO2, and air are assumed to be nSi=3.4, nSiO2=1.45, and nair=1, respectively. For simplicity, by utilizing the effective index method (EIM) [27], the approximated two-dimensional models are discussed by using the finite element method (FEM) [28,29] developed in our group and the effective indices are, respectively, assumed to be 2.83 and 2.16 for TE and TM wave analysis.
First, we consider an air-ring type PhC [22] shown in Figure 1a and discuss optimal parameters to realize absolute PBG. This PhC is considered as a compound PhC of air hole type and rod type PhCs. It becomes a conventional air hole PhC when the rod radius r1=0. On the other hand, it becomes a rod type PhC when the air hole radius r2=a/√3. In general, air hole type PhCs have PBG for TE wave and rod type PhCs have PBG for TM wave. Thus, there seems to be a possibility to realize an absolute PBG by the optimal selection of the parameters. Figure 1b shows the dependence of the PBG band on r1 when r2 is set to be 0.48a. From this figure, we can see that the overlap of the PBGs for TE and TM waves is maximized at r1=0.29a. Figure 1c shows the dispersion properties of the air-ring type PhC with r1=0.29a and r2=0.48a. We can see that the absolute PBG exist in the normalized frequency range a/λ of 0.362∼0.371, in other words the mid-gap ratio (Δω/ω0) is 2.46% where Δω and ω0 are, respectively, the bandwidth and central the frequency of the absolute PBG. Although the PBG is realized below the light line, the PBG band is not enough wide compared with PhCs made of anisotropic dielectrics [13,14,15,16].
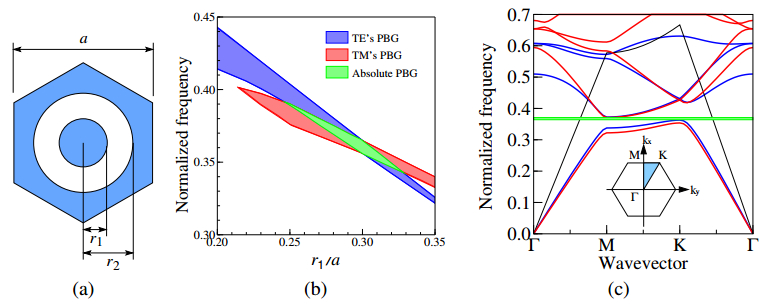 Figure 1. Air-ring type PhC. (a) Unit cell, (b) Dependence of the PBG band on r1 when r2, (c) Dispersion properties when r1=0.29a and r2=0.48a.
Figure 1. Air-ring type PhC. (a) Unit cell, (b) Dependence of the PBG band on r1 when r2, (c) Dispersion properties when r1=0.29a and r2=0.48a.Next, in order to improve the bandwidth of an absolute PBG, we consider the PhC as shown in Figure 2a. We refer this type of PhC to as a steering type PhC. The steering type PhC is considered to be a structure in which the position of the rod of the air-ring type PhC is shifted by a/√3 along y direction. Figure 2b shows the dependence of the PBG band on r1. From this figure, we can see that the overlap of the PBGs for TE and TM waves is maximized at r1=0.17a. Figure 2c shows the dispersion properties of the steering type PhC with r1=0.17a. We can see that the absolute PBG exist in the normalized frequency range a/λ of 0.421∼0.468, in other words the mid-gap ratio is 10.57%. This result corresponds the wavelength bandwidth of 164 nm at the center wavelength of 1.55 μm. This PBG exist below light line and its bandwidth is greatly expanded compared with that of air-ring type PhC.
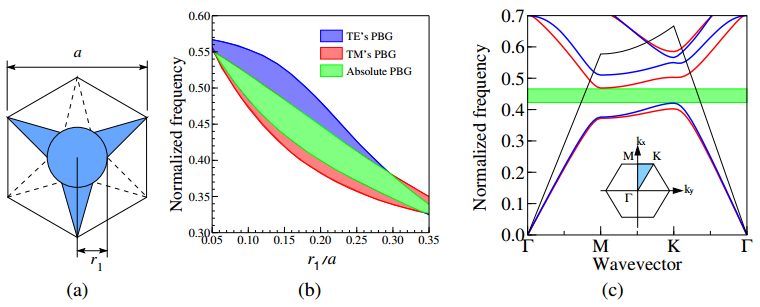 Figure 2. Steering type PhC. (a) Unit cell of steering type PhC, (b) Dependence of the PBG band on r1, (c) Dispersion properties when r1=0.17a.
Figure 2. Steering type PhC. (a) Unit cell of steering type PhC, (b) Dependence of the PBG band on r1, (c) Dispersion properties when r1=0.17a.In order to confirm the existence of absolute PBG, we calculate the transmission property of this PhC with finite periods when plane waves are incident along Γ-K and Γ-M directions, respectively. The actual computational model shown in Figures 3a and b are considered. Figure 3c shows their transmission and reflection properties for Γ-K direction incidence case and Figure 3d shows them for Γ-M direction incidence case. We can see that the transmission and reflection spectra are totally complementary since material absorption losses are ignored in this calculation.
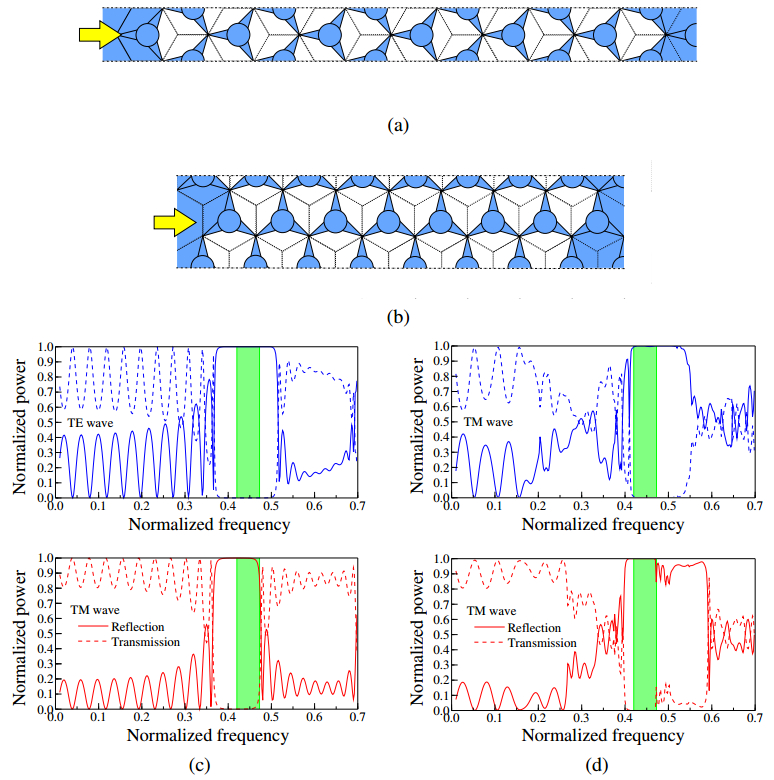 Figure 3. Transmission and reflection properties of the steering type PhC with r1=0.29a. (a) Computational model of Γ-K incidence case, (b) Computational model of Γ-M incidence case, (c) Transmission and reflection properties of Γ-K incidence case, (d) Transmission and reflection properties of Γ-M incidence case.
Figure 3. Transmission and reflection properties of the steering type PhC with r1=0.29a. (a) Computational model of Γ-K incidence case, (b) Computational model of Γ-M incidence case, (c) Transmission and reflection properties of Γ-K incidence case, (d) Transmission and reflection properties of Γ-M incidence case.In the previous section, we discussed the air-ring and the steering type PhCs. Next, we discuss PhC waveguides based on PhC with absolute PBG. In this section, we consider only the steering type PhC whose PBG band is wider than that of air-ring type PhC. In the following discussion, r1 is assumed to be 0.17a.
Here, we consider two types of PhC waveguides shown in Figure 4. The PhC waveguide in Figure 4a is designed by filling the unit cells by Si. The dispersion properties of this PhC waveguide are shown in Figure 5. From these results, it can be seen that the single mode operation is realized for TM mode. However, the higher order mode of TE mode is observed. Figure 6 shows the propagating fields in the straight PhC at a normalized frequency of a/λ=0.44. In this simulation, the PhC-based perfectly matched layer (PML) whose validity is confirmedin Ref. [30] is utilized as absorbing boundary conditions at the input and output end. We can see that, for both polarizations, the light is strongly confined in the core region owing to the absolute PBG. Next, we consider the 60 degree bend of this PhC waveguide. Figure 7 shows the structure of 60 degree bend and the propagating field through the bend. For TE mode, the excitation of the higher order mode is observed since this PhC waveguide is a multimode waveguide for TE mode. On the other hand, for TM mode, the higher order mode is not observed owing to the single mode operation although transmittance is fairly low. Thus, in order to improve the transmission property through waveguide bend, we modify the bending structure. Figure 8 shows the improved bend structure and the propagating fields. We can see that, for both modes, the transmission properties are greatly improved. However, for TE mode, higher order mode is still observed in the reflected wave.
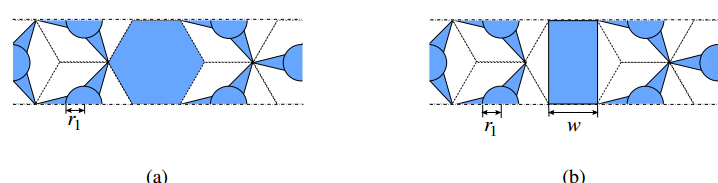 Figure 4. PhC waveguide based on the steering type PhC. (a) Type 1, (b) Type2.
Figure 4. PhC waveguide based on the steering type PhC. (a) Type 1, (b) Type2.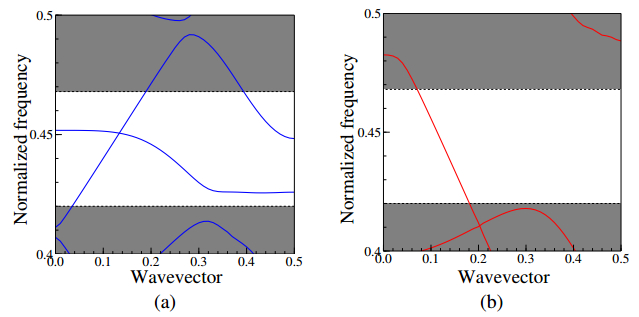 Figure 5. Dispersion properties of Type 1 PhC waveguide. (a) TE mode, (b) TM mode.
Figure 5. Dispersion properties of Type 1 PhC waveguide. (a) TE mode, (b) TM mode.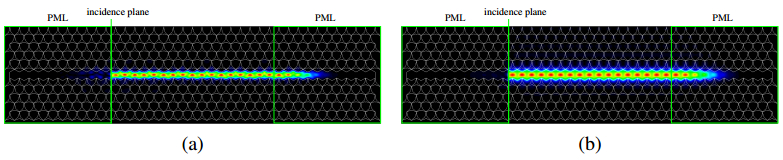 Figure 6. Propagating field through Type 1 PhC waveguide. (a) TE mode, (b) TM mode.
Figure 6. Propagating field through Type 1 PhC waveguide. (a) TE mode, (b) TM mode.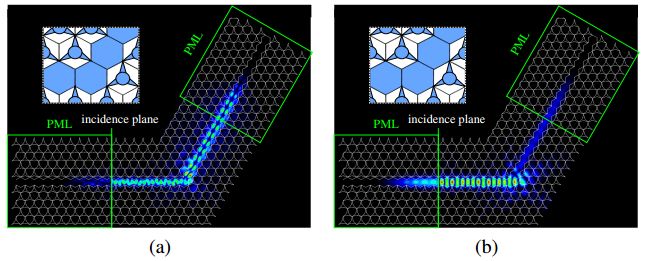 Figure 7. Propagating field through 60 degree bend of Type 1 PhC waveguide. (a) TE mode, (b) TM mode.
Figure 7. Propagating field through 60 degree bend of Type 1 PhC waveguide. (a) TE mode, (b) TM mode.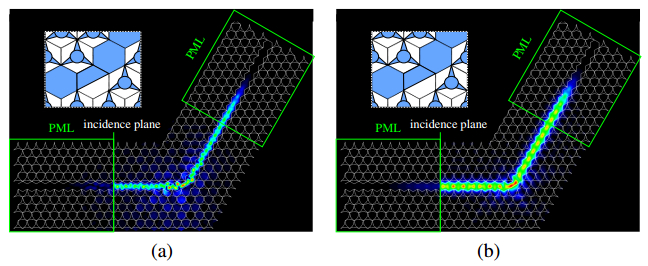 Figure 8. Propagating field through improved 60 degree bend of Type 1 PhC waveguide. (a) TE mode, (b) TM mode.
Figure 8. Propagating field through improved 60 degree bend of Type 1 PhC waveguide. (a) TE mode, (b) TM mode.Next, we consider the PhC waveguide shown in Figure 4b. Here, w is set to be w=0.58a. Figure 9 shows the dispersion property of this waveguide. In this PhC waveguide, the single mode operation bands exist for both TE and TM modes although these bands do not overlap. Though polarization independent operation is not achieved in this PhC waveguide, polarization dependent devices, such as polarization splitter, is able to be designed using this PhC waveguide [18,19]. Figure 10 shows the propagating fields in the straight PhC at a normalized frequency of a/λ=0.43. We can see that, for both polarizations, the light is strongly confined in the core region owing to the absolute PBG. Figure 11 shows the structure of 60 degree bend and the propagating field through the bend. We can see that the transmission properties are greatly improved compared with those of the previous examples.
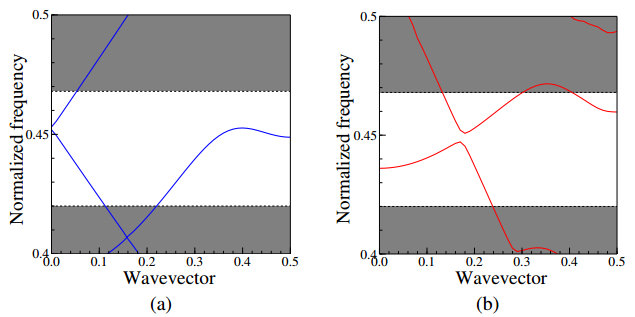 Figure 9. Dispersion properties of Type 2 PhC waveguide. (a) TE mode, (b) TM mode.
Figure 9. Dispersion properties of Type 2 PhC waveguide. (a) TE mode, (b) TM mode. Figure 10. Propagating field through Type 2 PhC waveguide. (a) TE mode, (b) TM mode.
Figure 10. Propagating field through Type 2 PhC waveguide. (a) TE mode, (b) TM mode.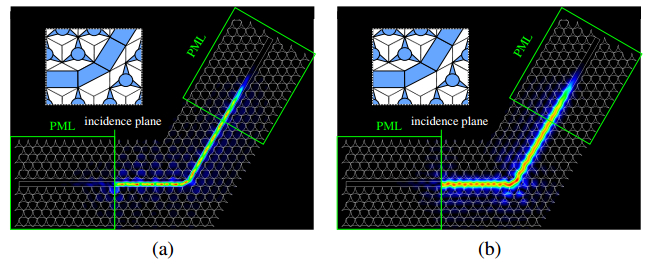 Figure 11. Propagating field through 60 degree bend of Type 2 PhC waveguide. (a) TE mode, (b) TM mode.
Figure 11. Propagating field through 60 degree bend of Type 2 PhC waveguide. (a) TE mode, (b) TM mode.Finally, we analyze an actual three-dimensional structure of the proposed PhC by using three-dimensional full vector FEM [28] developed in our group. Although, in the previous two-dimensional model, the slab thickness is assumed to be d=240 nm to use the effective index method, in this analysis, the slab thickness is defined by the normalized thickness and is assumed to be d/a=0.5. Figures 12a and b show the unit cell and the periodic slab of the proposed PhC and Figure 12c shows its dispersion property. We can see that the absolute PBG exist in this PhC although the bandwidth is narrowed compared with the two-dimensional model. This is due to that the parameters are not optimized in the three-dimensional model. By optimizing the structural parameters in an actual three-dimensional model, the bandwidth of an absolute PBG is considered to be expanded.
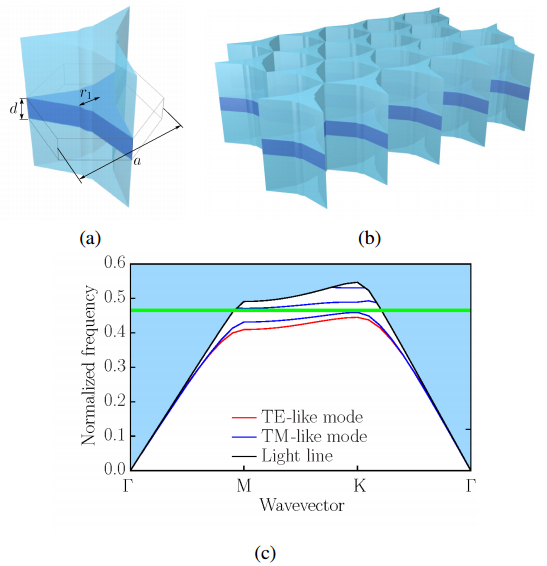 Figure 12. Actual three-dimensional steering type PhC slab. (a) unit cell, (b) periodic structure, (c) dispersion property.
Figure 12. Actual three-dimensional steering type PhC slab. (a) unit cell, (b) periodic structure, (c) dispersion property.We discussed novel photonic crystals which can realize absolute PBG. Furthermore, we designed the PhC waveguides based on the proposed PhCs and discussed the dispersion properties and the transmission properties through 60 degree bends. We are now studying the photonic devices utilizing absolute PBG, such as a polarization splitter, a polarization rotator, and an optical isolator. The design of photonic crystals with wider absolute PBG in an actual three-dimensional model is also now under consideration.
This work was supported by JSPS KAKENHI Grant Number 15K06009.
The authors declare that there is no conflict of interest regarding the publication of this manuscript.
| [1] |
Joannopoulos JD, Villeneuve PR, Fan S (1997) Photonic crystals: pitting a new twist on light. Nature 386: 143–149. doi: 10.1038/386143a0

|
| [2] |
Villeneuve PR, Piche M (1992) Photonic band gaps in two-dimensional square and hexagonal lattices. Phys Rev B 46: 4969–4972. doi: 10.1103/PhysRevB.46.4969

|
| [3] |
Anderson CM, Giapis KP (1996) Larger two-dimensional photonic band gaps. Phys Rev Lett 77: 2949–2951. doi: 10.1103/PhysRevLett.77.2949

|
| [4] | Kee CS, Kim JE, Park HY (1997) Absolute photonic bandgap in a two-dimensional square lattice of square dierectric rods in air. Phys Rev E 56: R6293. |
| [5] |
Anderson CM, Giapis KP (1997) Symmetry reduction in group 4 mm photonic crystals. Phys Rev B 56: 7313–7320. doi: 10.1103/PhysRevB.56.7313

|
| [6] |
Qiu M, He S (1999) Large complete bandgap in two-dimensional photonic crystals with elliptic air holes. Phys Rev B 60: 10610–10612. doi: 10.1103/PhysRevB.60.10610

|
| [7] |
Shen L, He S, Xian S (2002) Large absolute band gaps in two-dimensional photonic crystals formed by large dielectric pixels. Phys Rev B 66: 165315. doi: 10.1103/PhysRevB.66.165315

|
| [8] |
Trifonov T, Marsal LF, Rodriguez A, et al. (2004) E ects of symmetry reduction in twodimensional square and triangular lattices. Phys Rev B 69: 235112. doi: 10.1103/PhysRevB.69.235112

|
| [9] |
Wen F, David S, Checoury X, et al. (2008) Two-dimensional photonic crystals with large complete photonic band gaps in both TE and TM polarizations. Opt Express 16: 12278–12289. doi: 10.1364/OE.16.012278

|
| [10] |
Cerjan A, Fan S (2017) Complete photonic band gaps in supercell photonic crystals. Phys Rev A 96: 051802. doi: 10.1103/PhysRevA.96.051802

|
| [11] |
Kurt H, Citrin DS (2005) Annular photonic crystals. Opt Express 13: 10316–10326. doi: 10.1364/OPEX.13.010316

|
| [12] |
Kurt H, Hao R, Chen Y, et al. (2008) Design of annular photonic crystal slabs. Opt Lett 33: 1614–1616. doi: 10.1364/OL.33.001614

|
| [13] |
Shi P, Huang K, Kanng X, et al. (2010) Creation of large band gap with anisotropic annular photonic crystal slab structure. Opt Express 18: 5221–5228. doi: 10.1364/OE.18.005221

|
| [14] |
Razari B, Kalafi M (2006) Engineering absolute band gap in anisotropic hexagonal photonic crystals. Opt Commun 266: 159–163. doi: 10.1016/j.optcom.2006.04.035

|
| [15] |
Razari B, Khalkhali FT, Bala AS, et al. (2009) Absolute band gap properties in two-dimensional photonic crystals composed of air rings in anisotropic tellurium background. Opt Commun 282: 2861–2869. doi: 10.1016/j.optcom.2009.04.048

|
| [16] |
Khalkhali FT, Razari B, Kalafi M (2011) Enlargement of absolute photonic band gap in modified 2D anisotropic annular photonic crystals. Opt Commun 284: 3315–3322. doi: 10.1016/j.optcom.2011.03.006

|
| [17] |
Erol AE, Sӧzüer HS (2015) High transmission through a 90° bend in a polarization-independent single-mode photonic crystal waveguide. Opt Express 23: 32690–32695. doi: 10.1364/OE.23.032690

|
| [18] |
Tsuji Y, Morita Y, Hirayama K (2006) Photonic crystal waveguide based on 2-D photonic crystal with absolute photonic band gap. IEEE Photonic Tech L 18: 2410–2412. doi: 10.1109/LPT.2006.885295

|
| [19] |
Morita Y, Tsuji Y, Hirayama K (2008) Proposal for a compact resonant-coupling-type polarization splitter based on photonic crystal waveguide with absolute photonic bandgap. IEEE Photonic Tech L 20: 93–95. doi: 10.1109/LPT.2007.912558

|
| [20] |
Wu H, Citrin DS, Jiang L, et al. (2015) Polarization-Independent Single-ModeWaveguidingWith Honeycomb Photonic Crystals. IEEE Photonic Tech L 27: 840–843. doi: 10.1109/LPT.2015.2394463

|
| [21] |
Rani P, Kara Y, Sinha RK (2016) Design and analysis of polarization independent all-optical logic gates in silicon-on-insulator photonic crystal. Opt Commun 374: 148–155. doi: 10.1016/j.optcom.2016.04.037

|
| [22] |
Sӓynӓtjoki A, Mulot M, Ahopelto J, et al. (2007) Dispersion engineering of photonic crystal waveguides with ring-shaped holes. Opt Express 15: 8323–8328. doi: 10.1364/OE.15.008323

|
| [23] |
Hou J, Citrin DS, Wu H, et al. (2011) Enhanced bandgap in annular photonic-crystal silicon-oninsulator asymmetric slabs. Opt Lett 36: 2263–2265. doi: 10.1364/OL.36.002263

|
| [24] |
Wang F, Cheng YZ, Wang X, et al. (2018) Effective modulation of the photonic band gap based on Ge/ZnS one-dimensional photonic crystal at the infrared band. Opt Mater 75: 373–378. doi: 10.1016/j.optmat.2017.10.053

|
| [25] |
Wang X, Qi D, Wang F, et al. (2017) Design and fabrication of energy effcient film based on one-dimensional photonic band gap structures. J Alloy Compd 697: 1–4. doi: 10.1016/j.jallcom.2016.12.047

|
| [26] |
Qi D, Wang X, Cheng Y, et al. (2016) Design and characterization of one-dimensional photonic crystals based on ZnS/Ge for infrared-visible compatible stealth applications. Opt Mater 62: 52–56. doi: 10.1016/j.optmat.2016.09.024

|
| [27] | Okamoto K (2005) Fundamentals of optical waveguides, 2Eds, Academic Press. |
| [28] | Koshiba M (1992) Optical waveguide theory by the finite element method, Tokyo/Dordrecht: KTK Scientific Publishers/Kluwer Academic Publishers. |
| [29] |
Tsuji Y, Koshiba M (2002) Finite element method using port truncation by perfectly matched layer boundary conditions for optical waveguide discontinuity problems. J Lightwave Technol 20: 463–468. doi: 10.1109/50.988995

|
| [30] |
Koshiba M, Tsuji Y, Sasaki S (2001) High-performance absorbing boundary conditions for photonic crystal waveguide a simulations. IEEE Microw Wirel Co 11: 152–154. doi: 10.1109/7260.916327

|
| 1. | Jianxin Zhang, Jianhua Yuan, Wenbao Ai, Numerical optimization design for waveguide bends with low-loss and wide-bandwidth in two-dimensional photonic crystal slabs, 2019, 21, 2040-8978, 115103, 10.1088/2040-8986/ab4b6c |