Citation: Sabah Senouci, Mouhyddine Kadi-Hanifi, Azzeddine Abderrahmane Raho. Effect of a plastic deformation on the Guinier-Preston zones growth in Al-5at%Ag alloy[J]. AIMS Materials Science, 2017, 4(1): 16-26. doi: 10.3934/matersci.2017.1.16
| [1] | Faiza Lourdjane, Mouhyddine Kadi-Hanifi, Azzeddine Abderrahmane Raho . Precipitation of the metastable phases in a tin microalloyed Al-10at%Ag alloy. AIMS Materials Science, 2017, 4(1): 1-15. doi: 10.3934/matersci.2017.1.1 |
| [2] | Zoubir Chaieb, Ould Mohamed Ouarda, Azzeddine Abderrahmane Raho, Mouhyddine Kadi-Hanifi . Effect of Fe and Si impurities on the precipitation kinetics of the GPB zones in the Al-3wt%Cu-1wt%Mg alloy. AIMS Materials Science, 2016, 3(4): 1443-1455. doi: 10.3934/matersci.2016.4.1443 |
| [3] | Sabah Senouci, Azzeddine Abderrahmane Raho . Effect of the supersaturation on the precipitation kinetics of the Guinier-Preston zones in Al-rich Ag alloys. AIMS Materials Science, 2017, 4(1): 137-146. doi: 10.3934/matersci.2017.1.137 |
| [4] | Bobin Xing, Shaohua Yan, Wugui Jiang, Qing H. Qin . Deformation mechanism of kink-step distorted coherent twin boundaries in copper nanowire. AIMS Materials Science, 2017, 4(1): 102-117. doi: 10.3934/matersci.2017.1.102 |
| [5] | Hao Wang . On the annihilation of dislocation dipoles in metals. AIMS Materials Science, 2017, 4(6): 1231-1239. doi: 10.3934/matersci.2017.6.1231 |
| [6] | Na Ta, Lijun Zhang, Qin Li . Research on the oxidation sequence of Ni-Al-Pt alloy by combining experiments and thermodynamic calculations. AIMS Materials Science, 2024, 11(6): 1083-1095. doi: 10.3934/matersci.2024052 |
| [7] | Jian Qin, Zhan Zhang, X.-Grant Chen . Evolution of activation energy during hot deformation of Al–15% B4C composites containing Sc and Zr. AIMS Materials Science, 2019, 6(4): 484-497. doi: 10.3934/matersci.2019.4.484 |
| [8] | Nikolay A. Voronin . Specialties of deformation and damage of the topocomposite on a ductile substrate during instrumental indentation. AIMS Materials Science, 2020, 7(4): 453-467. doi: 10.3934/matersci.2020.4.453 |
| [9] | Songlin Zheng, Yong Ni, Linghui He . Concurrent interface shearing and dislocation core change on the glide dislocation-interface interactions: a phase field approach. AIMS Materials Science, 2015, 2(3): 260-278. doi: 10.3934/matersci.2015.3.260 |
| [10] | Pawan Kumar . Subgrain characterization of low carbon copper bearing steel under plane strain compression using electron backscattered diffraction. AIMS Materials Science, 2023, 10(6): 1121-1143. doi: 10.3934/matersci.2023060 |
Al-Ag supersaturated solid solution evolves towards the equilibrium state following the sequence [1,2,3,4]:
Supersaturated solid solution → Guinier-Preston (GP) zones → metastable γ' phase → equilibrium γ phase
The Guinier-Preston zones (GP), consisting of silver atom clusters, are coherent with the matrix. The metastable phase γ' (Ag2Al) is semi-coherent with the matrix and the equilibrium phase γ (Ag2Al), is incoherent with the matrix.
In Al-Ag alloys, two step of hardening are observed. The first one is due to the GPzones formation while the second one, more important, is due to the precipitation of the γ'metastable phase. The obtained degree of hardening depends on the volume fraction, the structure of the precipitates [5,6,7,8,9,10] and the nature of the interface between the metastable phases and the aluminum matrix [9,10,11]. It is well known that the formation of the GP zones in aluminium alloys is closely linked with the excess vacancies. A number of model of GP zones precipitation assisted by vacancies has been developed by several authors [5,12,13].
The GP zones formation is governed by a transport mechanism of solute atoms by solute atom-vacancy complexes. Generally, in aluminum alloys, the precipitation phenomena is controlled by the solute atoms diffusion and occurs through a nucleation, growth and coarsening mechanism.Knowing that the plastic deformation leads to a multiplication of dislocations in the alloys and the formation of vacancies [14], competitive phenomenon will occurs in a deformed alloy. The elastic field surrounding the dislocations reduce the critical size over that the precipitate particles grow and promote the diffusion of the solute atoms [7,14,15,16,17,18]. The dislocations, also, act as sinks for the vacancies and reduce the number of vacancies available for the diffusion. Our purpose is to study the effect of the plastic deformation on the GP zones precipitation kinetics in Al-Ag alloys using a technique based on microhardness measurements.
Al-Ag alloys were prepared by melting 99.99% and 99.99% pure aluminum and silver respectively, under argon protection. After a homogenization 15 days at 540 °C and an ice water quenching, the alloys are cut into platelets specimen which are mechanically polished, homogenized 6 hours at 540 °C and quenched into ice water. The Vickers microhardness measurements were carried out under a load of 100 g on specimen treated during different times at different aged temperatures (100, 150, 180 and 200 °C) and quenched into ice water. The specimens are treated at 100, 150, 180 and 200 °C. Another group of specimen are plastically deformed and then, treated at 100, 150, 180 and 200 °C. The plastic deformation consists in a rolling reduction of 5%. The Vickers hardnessmeasurements were made using a microhardness tester type SHIMADZU provided with a square pyramidal penetrator. The average value of ten readings was used foreach data point. The ageing temperatures 100, 150, 180 and 200 °C, are chosen below the temperature of the GP solvus in the Al rich Ag alloy.
The isothermal hardness curves, established at 100, 150, 180 and 200 °C show two steps of hardening in both the non deformed and the deformed alloys (Figures 1 and 2). The first one is due to the formation of the GP zones, while, the second one, more important, is attributed to the precipitation of the metastable γ' phase. The softening occurs at the coarsening of the γ' particles and the precipitation of the equilibrium phase γ [6,7,8,9,10,11]. The hardening observed is due to the interaction between the GP zones and the γ' particles with the moving dislocations. The intermediate plateau observed between the two steps hardening corresponds to the equilibrium state of the GP zones precipitation. At this stage, the maximum hardening due to the GP zones precipitation is obtained. The results show that this maximum hardening increases with the increasing of the volume fraction occupied by the GP zones at this stage maximum, fvmax = (x0 − xe)/(xpe − xe), where x0 is the alloy solute atom concentration, xe isthe matrix solute atom concentration at the metastable equilibrium state and xpe is the solute atom concentration in the GP zones at the metastable equilibrium state (Table 1). The softening is due to the coarsening of the particles of the γ'phase and the precipitation of the equilibrium γ phase.
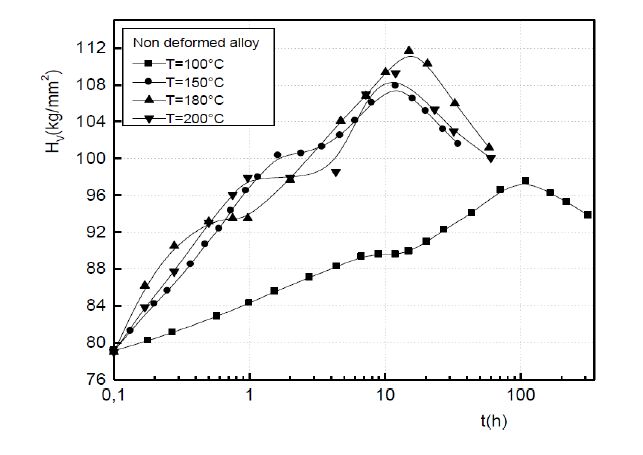 Figure 1. Isothermal hardness curves of the non deformed Al-Ag alloy.
Figure 1. Isothermal hardness curves of the non deformed Al-Ag alloy.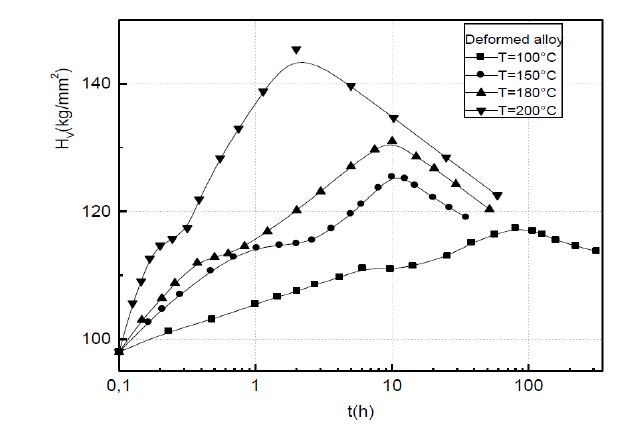 Figure 2. Isothermal hardness curves of the deformed Al-Ag alloy.
Figure 2. Isothermal hardness curves of the deformed Al-Ag alloy.| T (°C) | xe (at%) | xpe (at%) | Al-2.5at%Ag | Al-5at%Ag | Al-7at%Ag | Al-10at%Ag |
| 100 | 0.42 | 56.74 | 0.029 | 0.081 | 0.117 | 0.17 |
| 150 | 0.63 | 53.49 | 0.035 | 0.083 | 0.120 | 0.18 |
| 180 | 0.75 | 41.86 | 0.042 | 0.103 | 0.152 | 0.225 |
| 200 | 0.83 | 38.14 | 0.045 | 0.112 | 0.165 | 0.246 |
The hardness increase in the deformed alloy is due to the strain hardening. The establishment of the equilibrium state of the GP zones precipitation is faster in the deformed alloy and the precipitation of the γ' metastable phase occurs earlier in the deformed alloy.
The dislocations generated during the deformation will provide enough nucleation sites for the γ' metastable phase. In fact, γ' metastable phase precipitates prefer to nucleate and grow on dislocations which are increased in number density during the deformation. Therefore, the number density of γ' metastable phases in the deformed alloy is larger than that in the non deformed alloy. However, in the deformed alloy, which promotes the nucleation of the γ' metastable phase, there is not enough space for the formation of the GP zones. The dislocations generated from the deformation attract the solute atoms to form the γ' metastable phase, leading to the less concentration residing in matrix. Then the number density of the GP zones is decreased.
Precipitation transformation in Al-Ag alloys are considered as nucleation and growth type transformations. In such a case, the volume fraction of transformed solid solution, F, may be expressed by Johnson-Mehl [23] Avrami [24] and Kolmogorov [25] (JMAK) kinetics: F = 1 - exp[-(kt)n], where n and k are the growth parameters. The growth parameter n is a numerical temperature independent exponent. For the diffusional controlled growth n is in the range 0.5-2.5 [26,27]. The growth parameter k is a strongly temperature dependent constant whose value depend on both nucleation and growth rates includes nucleation and growth rates. The growth parameter k characterizes the precipitation kinetics and is expressed by an Arrhenius-type relationship with temperature as follows [28]: k = A exp[-(Q/RT)] where A is a constant, Q is the activation energy, R is the gas constant and T is the temperature.
During the precipitation of the GP zones, the transformed fraction, F, which represents the ratio between the volume occupied by the GP zones at a time t and their volume at the metastable equilibrium state, is given by the Merle relation [29]:
| ${{H}_{v}}\left( t \right)\text{ }=F\cdot {{H}_{v(metastable\text{ }equilibrium\text{ }state)}}+\text{ }(1-F)\cdot {{H}_{v}}\left( 0 \right)$ |
where Hv(0) is the as quenched hardness, Hv(t) isthe hardness of the alloy at the time t during the precipitation of the GP zones, and Hv(metastable equilibrium state)is the hardness of the alloy at the metastable equilibrium state of the GP zones precipitation.
In both the non deformed and the deformed alloys, the results show that the GP precipitation kinetics obeys to the JMAK law of the growth controlled by the diffusion of solute atoms: F = 1 - exp[-(kt)n] (Figures 3 and 4).
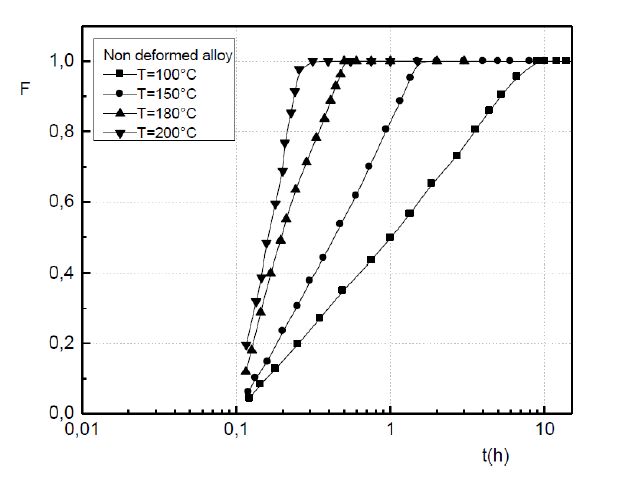 Figure 3. Transformed fraction during the GP zones precipitation in the non deformed Al-Ag alloy.
Figure 3. Transformed fraction during the GP zones precipitation in the non deformed Al-Ag alloy.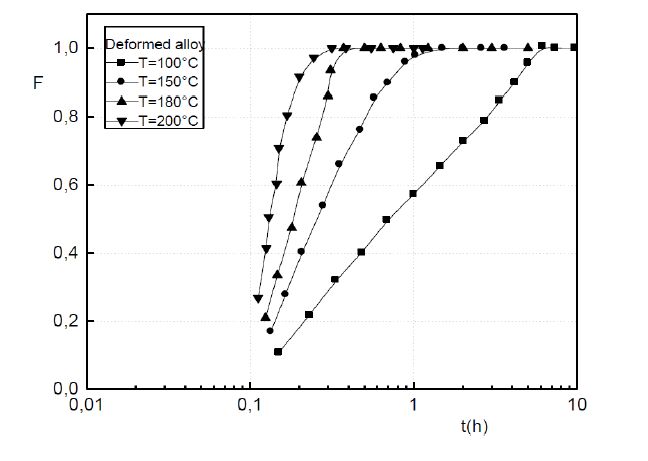 Figure 4. Transformed fraction during the GP zones precipitation in the deformed Al-Ag alloy.
Figure 4. Transformed fraction during the GP zones precipitation in the deformed Al-Ag alloy.The incubation times, which the determined values by extrapolation varies between 0.01 and 0.02 hours, compared with the necessary times to reach the metastable equilibrium state, are very short and are characteristics of rapid nucleation in the both all alloys, because of the high supersaturation of the quenched in vacancies (Figures 3 and 4).
The values of n, characteristics of heterogeneous at 100 °C and homogenous precipitation of the GP zones at higher temperatures [26,27] and the values of the parameter k, which characterize the reaction kinetics, are determined from the slopes of the LogLog(1/(1 − F)) curves (Figures 5 and 6) for both the non deformed and the deformed Al-Ag alloys (Table 2).
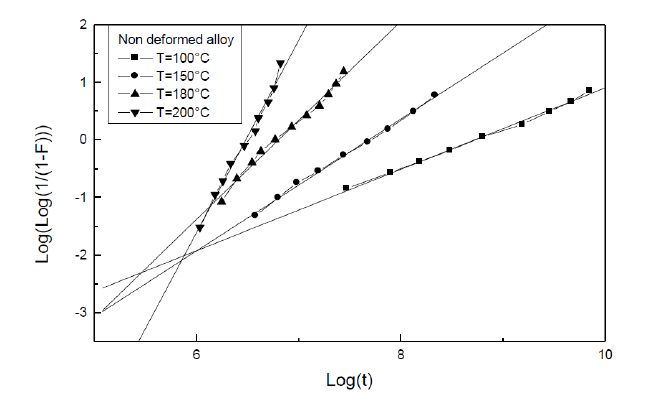 Figure 5. Determination of the growth parameters during the GP zones precipitation in the non deformed Al-Ag alloy.
Figure 5. Determination of the growth parameters during the GP zones precipitation in the non deformed Al-Ag alloy.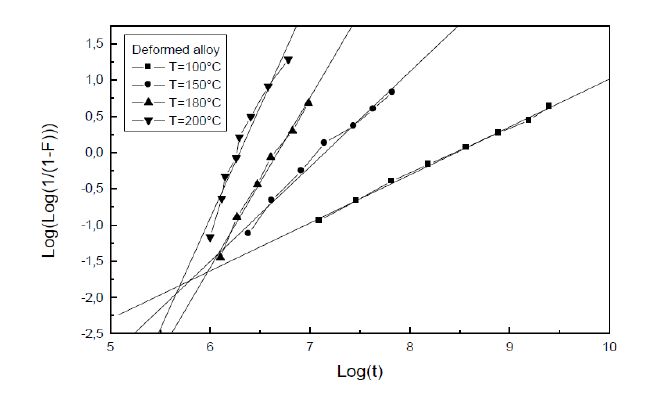 Figure 6. Determination of the growth parameters during the GP zones precipitation in the deformed Al-Ag alloy.
Figure 6. Determination of the growth parameters during the GP zones precipitation in the deformed Al-Ag alloy.| T (°C) | Non deformed alloy | Deformed alloy | ||
| n | k (10−4 s−1) | n | k (10−4 s−1) | |
| 100 | 0.7 | 1.48 | 0.7 | 2 |
| 150 | 1.3 | 4.4 | 1.3 | 7.5 |
| 180 | 2.3 | 10 | 2.3 | 11 |
| 200 | 3 | 14 | 3 | 16 |
The apparent activation energies during the GP zones growth in the non deformed and in the deformed alloys are determined using the Arrhenius-type relationship cited above: k = A·exp[-(Q/RT)]. The slopes of the variation curves Log(k) in a function of 1/T give an apparent activation energy Q, respectively, in the order of 30.1 kJ/mol and 28.1 kJ/mol, during the growth of the GP zones in the non deformed alloy and in the deformed alloy showing that the reaction of the GP zones growth is globally faster in the deformed alloy (Figure 7).
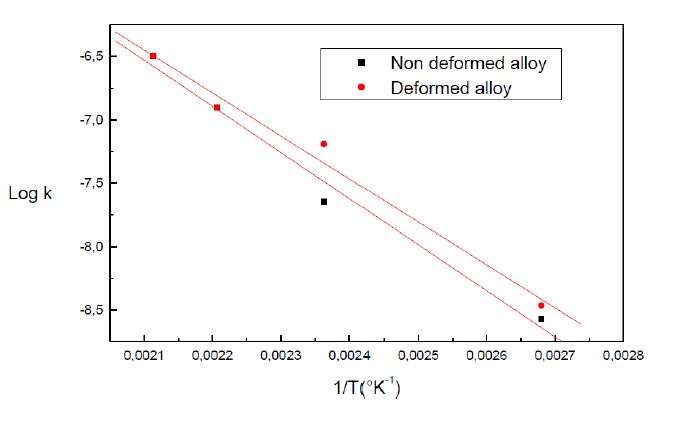 Figure 7. Activation energies determined from the k values.
Figure 7. Activation energies determined from the k values.The evolution of the apparent activation energy Q during the growth progress, is determined using the Arrhenius law which gives the necessary time to reach a certain transformed fraction at a given temperature T: t = A·exp(Q/RT), where A is a constant and R is the gas constant. During the GP zones growth, the apparent activation energy increases in the deformed alloy and remains almost constant in the non deformed alloy (Figures 8 and 9).
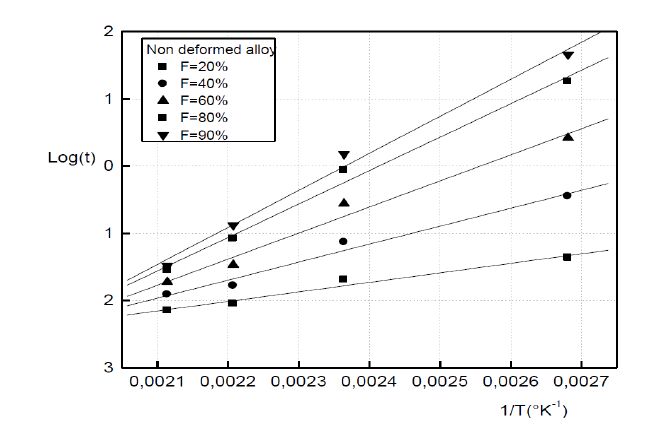 Figure 8. Determination of the apparent activation energy during the GP zones growth in the non deformed alloy.
Figure 8. Determination of the apparent activation energy during the GP zones growth in the non deformed alloy.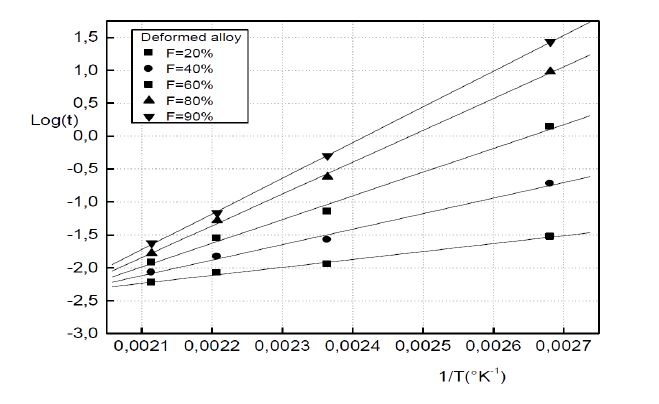 Figure 9. Determination of the apparent activation energy during the GP zones growth in the non deformed alloy.
Figure 9. Determination of the apparent activation energy during the GP zones growth in the non deformed alloy.The variation of the apparent activation energy during the GP formation showstwo stages (Figure 10).
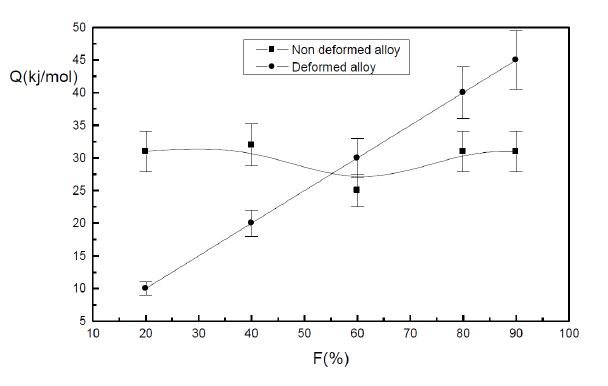 Figure 10. Apparent activation energy during the GPB zones growth in the non deformed alloy and in the deformed alloy.
Figure 10. Apparent activation energy during the GPB zones growth in the non deformed alloy and in the deformed alloy.During the first stage of the GP zones formation, the reaction is faster in the deformed alloy than that in the non deformed alloy because the preponderant effects of the dislocations introduced by plastic deformation are the reduction of the nucleus critical size and the promotion of the diffusion along the dislocations. During the second stage, a great number of the quenched in vacancies are eliminated at the sinks such dislocations and the preponderant effect of the dislocations introduced by plastic deformation is the reduction of the number of the free vacancies available to promote the diffusion of the solute atoms for the formation of the GP zonesand the reaction became slower in the deformed alloy than that in the non deformed alloy.
The results highligths the plastic deformation effect on the GP zones and on the γ' metastable phase precipitations in an Al-Ag alloy. In both the non deformed and the deformed alloys, the GP zones growth obeys to the JMAK law of the precipitation controlled by the diffusion. At 100, 150, 180 and 200 °C, the plastic deformation accelerates the establishment of the metastable equilibrium state of the GP zones precipitation and promotes precipitation of the γ' metastable phase and reduce the duration of the metastable equilibrium state of the GP zones precipitation. During the GP zones growth, in the non deformed alloy, the activation energy remains constant while it increases with the GP zones growth progress in the deformed alloy.
The authors declare that there is no conflict of interest regarding the publication of this manuscript.
| [1] |
Inoke K, Kaneko K, Weyland M, et al. (2006) Severe local strain and the plastic deformation of Guinier Preston zones in the Al-Ag system revealed by three-dimensional electron tomography. Acta Mater 54: 2957–2963. doi: 10.1016/j.actamat.2006.02.029

|
| [2] |
El-Khalek AMA (2008) Transformation characteristics of Al-Ag and Al-Ag-Ti alloys. J Alloy Compd 459: 281–285. doi: 10.1016/j.jallcom.2007.05.055

|
| [3] |
Dubey PA, Schönfeld B, Kostorz G (1991) Shape and internal structure of Guinier-Preston zones in Al-Ag. Acta Metall Mater 39: 1161–1170. doi: 10.1016/0956-7151(91)90204-E

|
| [4] | Schönfeld B, Malik A, Kostorz G, et al. (1997) Guinier-Preston zones in Al-rich Al-Cu and Al-Ag single crystals. Physica B 234: 983–985. |
| [5] |
Federighi T (1958) Quenched-in vacancies and rate of formation of zones in aluminum alloys. Acta Metall 6: 379–381. doi: 10.1016/0001-6160(58)90078-6

|
| [6] |
Guo Z, Sha W (2005) Quantification of precipitate fraction in Al-Si-Cu alloys. Mater Sci Eng A 392: 449–452. doi: 10.1016/j.msea.2004.09.020

|
| [7] |
Waterloo G, Hansen V, Gjønnes J, et al. (2001) Effect of predeformation and preaging at room temperature in Al-Zn-Mg-(Cu, Zr) alloys. Mater Sci Eng A 303: 226–233. doi: 10.1016/S0921-5093(00)01883-9

|
| [8] |
Wang G, Sun Q, Feng L, et al. (2007) Influence of Cu content on ageing behavior of AlSiMgCu cast alloys. Mater Design 28: 1001–1005. doi: 10.1016/j.matdes.2005.11.015

|
| [9] | Novelo-Peralta O, González G, Lara-Rodríguez GA (2007) Characterization of precipitation in Al-Mg-Cu alloys by X-ray diffraction peak broadening analysis. Mater Charact 59: 773–780. |
| [10] | Ahmadi S, Arabi H, Nouri S, et al. (2009) Mechanisms of precipitates formation in an Al-Cu-Li-Zr alloy using DSC technique and electrical resistance measurements. Iran J Mater Sci Eng 6: 15–20. |
| [11] | Anjabin N, Taheri K (2010) The effect of aging treatment on mechanical properties of AA6082 alloy: modelling experiment. Iran J Mater Sci Eng 7: 14–21. |
| [12] |
Federighi T, Thomas G (1962) The interaction between vacancies and zones and the kinetics of pre-precipitation in Al-rich alloys. Philos Mag 7: 127–131. doi: 10.1080/14786436208201864

|
| [13] |
Girifalco LA, Herman H (1965) A model for the growth of Guinier-Preston zones-the vacancy pump. Acta Metall 13: 583–590. doi: 10.1016/0001-6160(65)90120-3

|
| [14] |
Yassar RS, Field DP, Weiland H (2005) The effect of cold deformation on the kinetics of the β″ precipitates in an Al-Mg-Si alloy. Metall Mater Trans A 36: 2059–2065. doi: 10.1007/s11661-005-0326-6

|
| [15] | Martin JW (1968) Precipitation Hardening, New York: Pergamon Press. |
| [16] | Porter DA, Easterling KE, Sherif M (1992) Phase transformations in metals and alloys, 2rd Ed, Chapman & Hall. |
| [17] | Gubicza J, Schiller I, Chinh NQ, et al. (2007) The effect of severe plastic deformation on precipitation in supersaturated Al-Zn-Mg alloys. Mater Sci Eng A 460–461: 77–85. |
| [18] |
Tekmen C, Cocen U (2003) Role of cold work and SiC volume fraction on accelerated age hardening behavior of Al-Si-Mg/Si ccomposites. J Mater Sci Lett 22: 1247–1249. doi: 10.1023/A:1025497816387

|
| [19] |
Naudon A, Caisso J (1974) Etude de la lacune de miscibilité métastable et de la structure cristallographique des zones GP dans les alliages aluminum-argent. J Appl Crystallogr 7: 25–36. doi: 10.1107/S0021889874008648

|
| [20] |
Baur R, Gerold V (1962) The existence of a metastable miscibility gap in aluminium-silver alloys. Acta Metall 10: 637–645. doi: 10.1016/0001-6160(62)90053-6

|
| [21] | Hillert M (1962) Colloq. Int. CNRS Paris 118: 43. |
| [22] |
Osamura K, Nakamura T, Kobayashi A, et al. (1987) Chemical composition of GP zones in Al-Ag alloys. Scripta Metall 21: 255–258. doi: 10.1016/0036-9748(87)90208-0

|
| [23] | Johnson WA, Mehl RF (1939) Reaction kinetics in processes of nucleation and growth. Trans Amer Inst Mining (Metal) Engrs 135: 416–458. |
| [24] | Avrami M (1941) Kinetics of phase change. III. Granulation, Phase Change and Microstructure. J Chem Phys 9: 177–184. |
| [25] | Kolmogorov AN (1937) On the statistical theory of the crystallization of metals. Bull Acad Sci USSR, Math Ser 1: 355–359. |
| [26] | Doherty RD (1996) Diffusive phase transformations in the solid state, in Physical Metallurgy 4th edition, eds., Cahn RW, Hassen P, North Holland, Amsterdam, 2: 1364–1505. |
| [27] | Christian JW (1965) The theory of phase transformations in metals and alloys, New York: Pergamon Press. |
| [28] |
Esmaeili S, Lloyd DJ, Poole WJ (2003) A yield strength model for the Al-Mg-Si-Cu alloy AA6111. Acta Mater 51: 2243–2257. doi: 10.1016/S1359-6454(03)00028-4

|
| [29] | Merlin J, Merle P (1978) Analistic phenomena and structural state in aluminium silver alloys. Scripta Metall 12: 227–232. |
| T (°C) | xe (at%) | xpe (at%) | Al-2.5at%Ag | Al-5at%Ag | Al-7at%Ag | Al-10at%Ag |
| 100 | 0.42 | 56.74 | 0.029 | 0.081 | 0.117 | 0.17 |
| 150 | 0.63 | 53.49 | 0.035 | 0.083 | 0.120 | 0.18 |
| 180 | 0.75 | 41.86 | 0.042 | 0.103 | 0.152 | 0.225 |
| 200 | 0.83 | 38.14 | 0.045 | 0.112 | 0.165 | 0.246 |
| T (°C) | Non deformed alloy | Deformed alloy | ||
| n | k (10−4 s−1) | n | k (10−4 s−1) | |
| 100 | 0.7 | 1.48 | 0.7 | 2 |
| 150 | 1.3 | 4.4 | 1.3 | 7.5 |
| 180 | 2.3 | 10 | 2.3 | 11 |
| 200 | 3 | 14 | 3 | 16 |
| T (°C) | xe (at%) | xpe (at%) | Al-2.5at%Ag | Al-5at%Ag | Al-7at%Ag | Al-10at%Ag |
| 100 | 0.42 | 56.74 | 0.029 | 0.081 | 0.117 | 0.17 |
| 150 | 0.63 | 53.49 | 0.035 | 0.083 | 0.120 | 0.18 |
| 180 | 0.75 | 41.86 | 0.042 | 0.103 | 0.152 | 0.225 |
| 200 | 0.83 | 38.14 | 0.045 | 0.112 | 0.165 | 0.246 |
| T (°C) | Non deformed alloy | Deformed alloy | ||
| n | k (10−4 s−1) | n | k (10−4 s−1) | |
| 100 | 0.7 | 1.48 | 0.7 | 2 |
| 150 | 1.3 | 4.4 | 1.3 | 7.5 |
| 180 | 2.3 | 10 | 2.3 | 11 |
| 200 | 3 | 14 | 3 | 16 |