1. Introduction
The AlAg supersaturated solid solution is thermodynamically metastable. Consequently, there is a driving force for decomposition of the metastable phase at all temperatures below the equilibrium solvus temperature. The magnitude of this driving force increases with the increasing of the undercooling and with the increasing of the solute supersaturation. The specific identity of the metastable precipitate and the rate of the decomposition process are generally controlled by whether ageing is carried out below or above a critical temperature defined by the appropriate metastable solvus curve on the equilibrium phase diagram [1]. An Al-Ag supersaturated solid solution, aged at a temperature below the GP zones solvus, evolves towards the equilibrium state following the sequence [2,3,4,5]:
Supersaturated solid solution → Guinier-Preston (GP) zones → metastable γ'phase → equilibrium γ phase
The Guinier-Preston zones (GP), consisting of silver atom clusters, are coherent with the matrix. The metastable phase γ'(Ag2Al) is semi-coherent with the matrix and the equilibrium phase γ(Ag2Al), is incoherent with the matrix. It is well known that, while there is a higher driving force for precipitation of the equilibrium phase than the metastable GP zones, the GP zones initially form more rapidly because they are coherent and their coherency strain is very small. Thus there have a significantly lower energy barrier to nucleation [6]. The precipitation kinetics of the GP zones in a supersaturated solid solution depends on the level of its supersaturation which induces a driving force.
Our purpose is to study the effect of the supersaturation on the precipitation kinetics of the GP zones in the Al-rich Ag alloys using a method based on hardness measurements.
2. Materials and Methods
Alxat.%Ag alloys were prepared by melting 99.99% and 9.99% pure aluminum and silver respectively, under argon protection. After an homogenization during 15 days at 540 °C and an ice water quenching, the alloys are cut into platelets specimen which are mechanically polished, homogenized 6 hours at 540 °C and quenched into ice water. The Vickers microhardness measurements were carried out under a load of 100 g on specimen treated during different times at different aged temperatures (100, 150, 180 and 200 °C) and quenched into ice water. The Vickers hardness measurements were made using a microhardness tester type SHIMADZU provided with a square pyramidal penetrator. The average value of ten readings was used for each data point.The ageing temperatures 100, 150, 180 and 200 °C, are chosen below the temperature of the GP solvus in the Al rich Ag alloy phase diagram (figure 1).
3. Results and Discussion
3.1. Hardening evolution
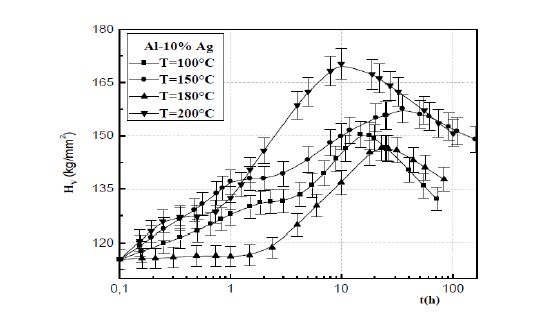
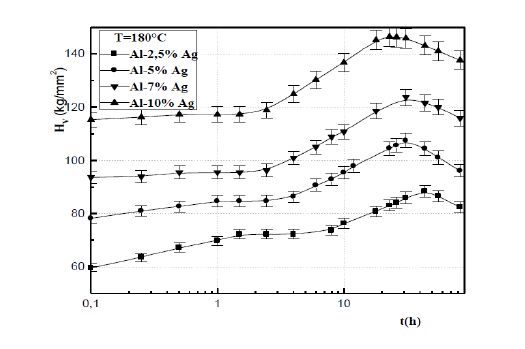
The isotherm curves of hardness, established at 100, 150, 180 and 200 °C show a first step of hardening due to the GP zones precipitation and a second step due to the precipitation of the metastable γ' phase (figures 2, 3). The obtained degree of hardening depends on the volume fraction, the structure of the precipitates and the nature of the interface between the metastable phases and the aluminum matrix [7,8,9,10,11,12]. The intermediate bearing corresponds to the metastable equilibrium state of the precipitation of the GP zones during which their volume fraction is maximum. At this stage, the maximum hardening due to the GP zones precipitation is obtained. The results show that this maximum hardening increases with the increasing of the volume fraction occupied by the GP zones at this stage maximum, fvmax= (x0-xe)/(xpe-xe), where x0 is the alloy solute atom concentration, xe, the matrix solute atom concentration at the metastable equilibrium state and xpe, the solute atom concentration in the GP zones at the metastable equilibrium state (Table 1) .The softening is due to the coarsening of the particles of the γ'phase and to the precipitation of the equilibrium γ phase.
Table 1. Volume fractions at the metastable equilibrium state of the precipitation of the GP zones, fvmax [1,13,14,15].
| T (°C) |
xe (at%) |
xpe (at%) |
Al2.5at.%Ag |
Al5at.%Ag |
Al7at.%Ag |
Al10at.%Ag
|
| 100 |
0.42 |
56.74 |
0.029 |
0.081 |
0.117 |
0.17
|
| 150 |
0.63 |
53.49 |
0.035 |
0.083 |
0.120 |
0.18
|
| 180 |
0.75 |
41.86 |
0.042 |
0.103 |
0.152 |
0.225
|
| 200 |
0.83 |
38.14 |
0.045 |
0.112 |
0.165 |
0.246
|
3.2. Precipitation kinetics of the GP zones
3.2.1. Growth regime
Precipitation transformation in AlAg alloys are considered as nucleation and growth type transformations. In such a case, the volume fraction of transformed solid solution, F, may be expressed by Johnson-Mehl [16] Avrami [17] and Kolmogorov [18] (JMAK) kinetics: F = 1 - exp - (kt)n, where n and k are the growth parameters. The growth parameter n is a numerical temperature independent exponent. For the diffusional controlled growth n is in the range 0.5-2.5 [19,20]. The growth parameter k is a strongly temperature dependent constant whose value depend on both nucleation and growth rates includes nucleation and growth rates. The growth parameter k characterizes the precipitation kinetics and is expressed by an Arrhenius-type relationship with temperature as follows [21]: k = A exp - (Q/RT) where A is a constant, Q, the activation energy, R, the gas constant and T, the temperature
During the precipitation of the GP zones, the transformed fraction, F, which represents the ratio between the volume occupied by the GP zones at a time t and their volume at the metastable equilibrium state, is given by the Merle relation [22]: Hv(t) = F. Hv(metastable equilibrium state)+ (1 − F). Hv(0) where Hv(0) is the as quenched hardness, Hv(t), the hardness of the alloy at the time t during the precipitation of the GP zones, and Hv(metastable equilibrium state), the hardness of the alloy at the metastable equilibrium state of the GP zones precipitation.
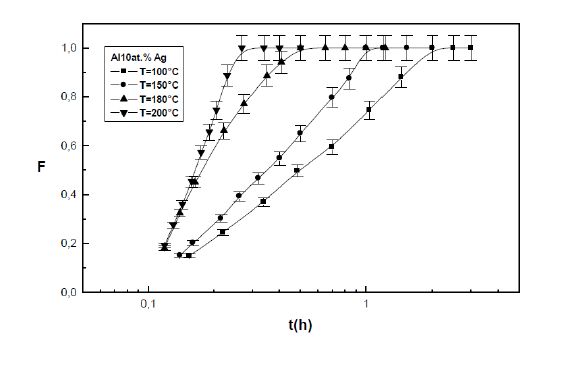
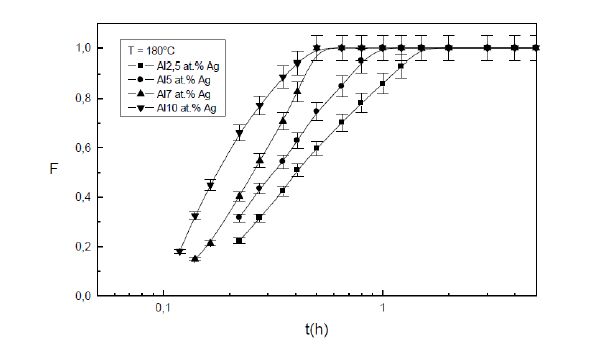
In all Alxat.%Ag alloys, the results show that the GP precipitation kinetics obeys to the JMAK law of the growth controlled by the diffusion of solute atoms: F = 1 - exp - (kt)n (figures 4, 5).
The incubation times, which the determined values by extrapolation varies between 0.01 and 0.02 hours, compared with the necessary times to reach the metastable equilibrium state, are very short and are characteristics of rapid nucleation in the both all alloys, because of the high supersaturation of the quenched in vacancies (figures 4, 5).
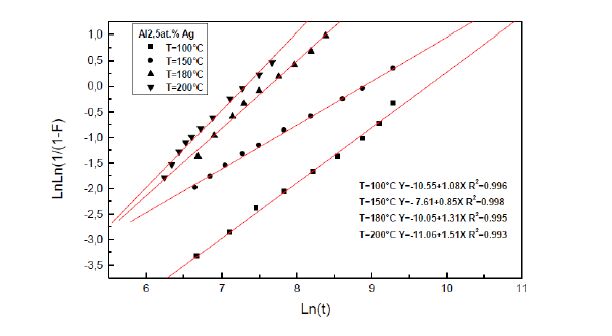
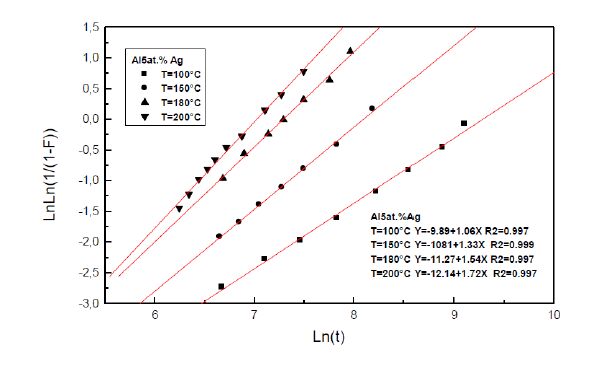
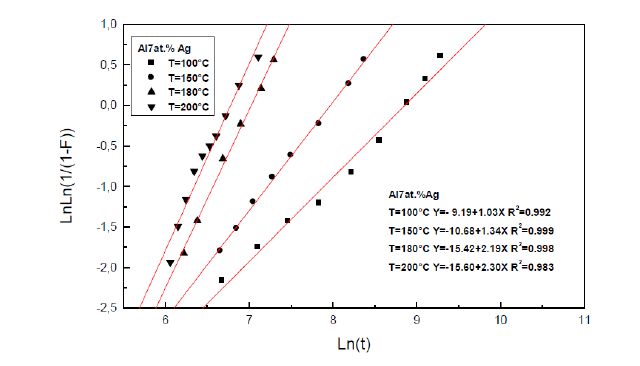
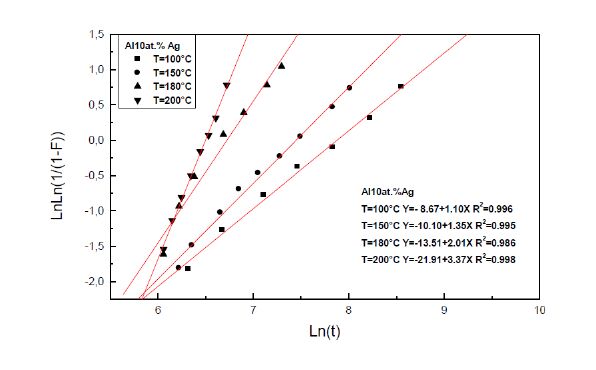
The curves of the variations of Ln(Ln(1/(1−F))) versus Ln(t) (figures 6, 7, 8, 9), show that the growth stage obeys to the JMAK (Johnson-Mehl-Avrami-Kolmogorov) law, F = 1 - exp(−kt)n, of the growth controlled by the solute atom diffusion, where n and k are the growth parameters (Tables 2 and 3).
Table 2. Values of the growth parameter n.
| T(°C) |
Al2,5at%Ag |
Al5at.%Ag |
Al7at.%Ag |
Al10at.%Ag
|
| 100 |
1 |
1 |
1 |
1.1
|
| 150 |
0.85 |
1.3 |
1.3 |
1.3
|
| 180 |
1.3 |
1.5 |
2.1 |
2
|
| 200 |
1.5 |
1.7 |
2.3 |
3.3
|
Table 3. Values of the growth parameter k in s−1.
| T(°C) |
Al2,5at%Ag |
Al5at.%Ag |
Al7at.%Ag |
Al10at.%Ag
|
| 100 |
5.7×10−5 |
8×10−5 |
1.3×10−4 |
3.7×10−4
|
| 150 |
1.29×10−4 |
2.95×10−4 |
3.45×10−4 |
5.63×10−4
|
| 180 |
4.65×10−4 |
6.63×10−4 |
8.75×10−4 |
12×10−4
|
| 200 |
6.5×10−4 |
8.65×10−4 |
11×10−4 |
15×10−4
|
3.2.2. Effect of the supersaturation
At a given temperature, the growth parameter k which represents the precipitation kinetics, increase with the increasing of the supersaturation x0−xe, where x0 is the alloy solute atom concentration and xe, the matrix solute atom concentration at the metastable equilibrium state.
3.2.3. Effect of the supersaturation and the undercooling
In the case of an Alxat.%Ag alloy, the transformation kinetics depends on two contributions . The first one is the driving force which increases with the undercooling which corresponds to a temperature decrease and the second one is the thermal activation which is linked with a temperature increase.
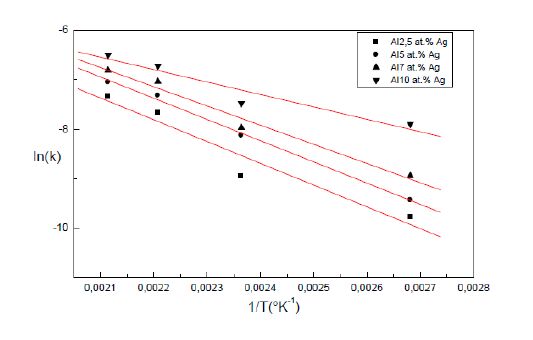
The apparent activation energy of the diffusion of the solute atoms, Q, is determined using the Arrhenius type law k = A exp(−Q/RT) where A is a constant, T, the temperature and R, the gas constant (figure 10). The apparent activation energy of the diffusion of the solute atoms, deduced from the slopes of the variation curves Ln(k) = f(1/T), and compared with the activation energy of the diffusion of the silver atoms in aluminium which is in the order of 117 kj/mol [23] show a rapid diffusion during the GP zones precipitation in all alloys (Table 4).
The results show that, the rise temperature decreases the supersaturation and accelerates the transformation. Consequently, in an Alxat.%Ag alloy, the contribution of the thermal activation is preponderant during the GP zones precipitation.
Table 4. Apparent activation energy of the diffusion of the solute atoms during the GP zones growth.
| Alloy |
Al2,5at%Ag |
Al5at.%Ag |
Al7at.%Ag |
Al10at.%at.Ag
|
| Activation energy (kj/mol) |
36.6 ± 9.1 |
35.6 ± 8.9 |
32.2 ± 8 |
20.9 ± 5.2
|
4. Conclusion
In the Alxat.%Ag alloys, the growth kinetics of the GP zones obeys to the JMAK law. The apparent activation energies, determined in Alxat.%Ag alloys are characteristics of a rapid transformation during the GP zones formation .
The precipitation kinetics of the GP zones in an Alxat.%Ag supersaturated solid solution isothermally aged, increases with the level of its supersaturation which induces a driving force. The precipitation kinetics of the GP zones in an Alxat.%Ag supersaturated solid solution, aged at different temperatures, depends on the contributions of the undercooling and that of the thermal activation which is preponderant.
Conflict of Interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: