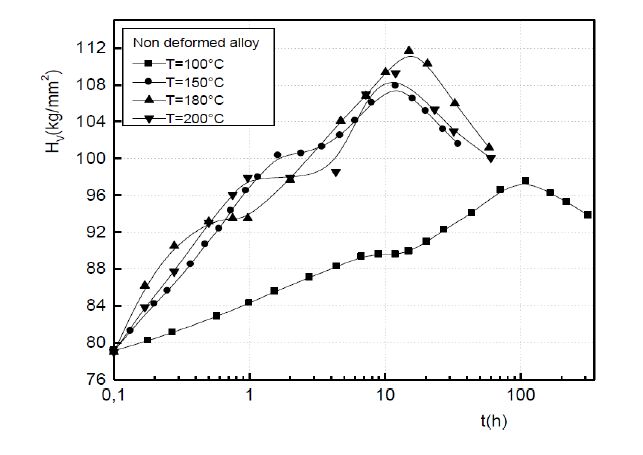
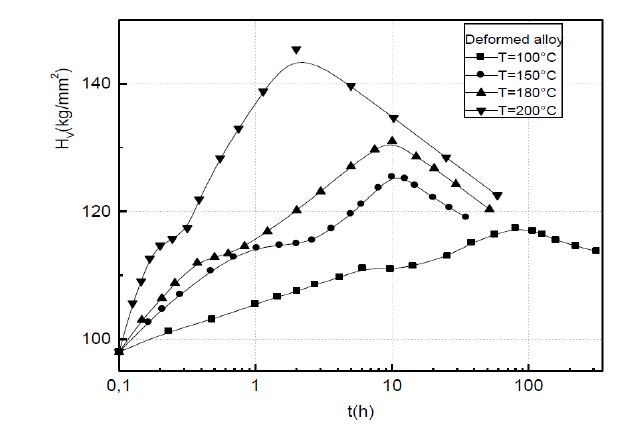
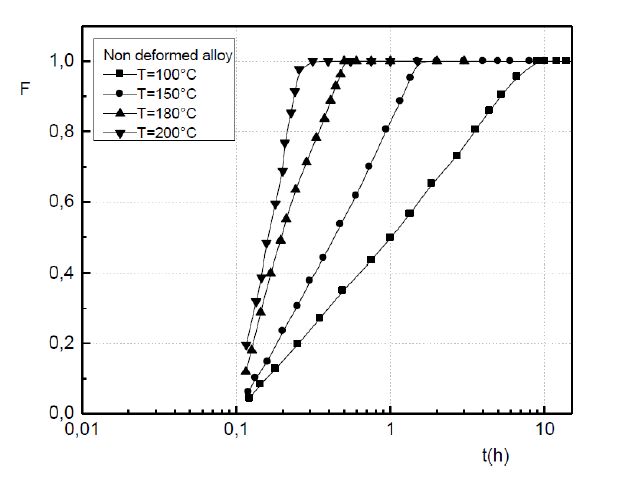
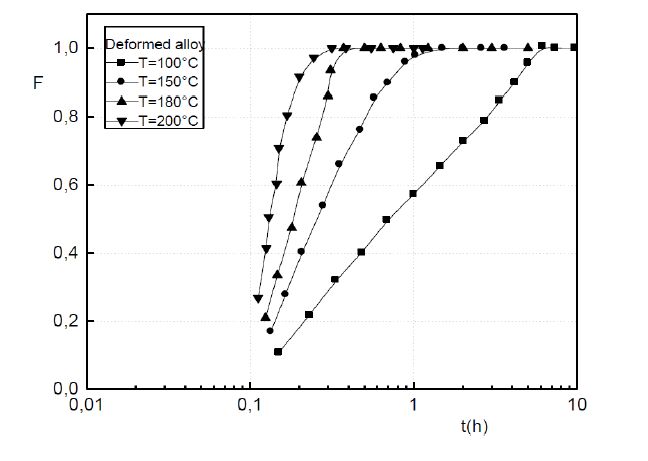
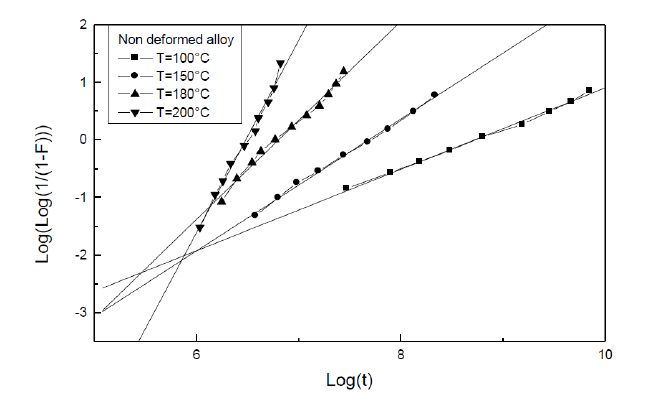
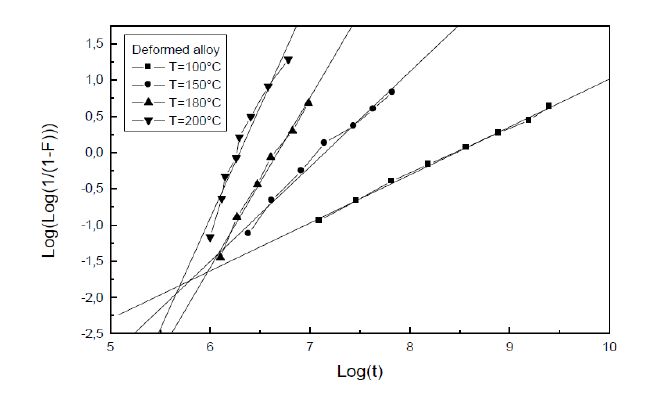
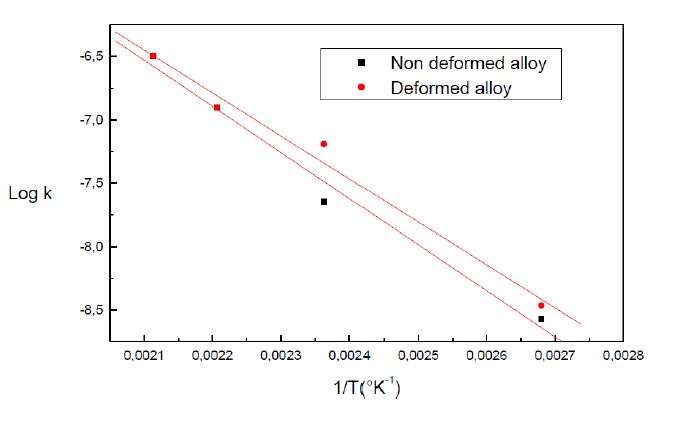
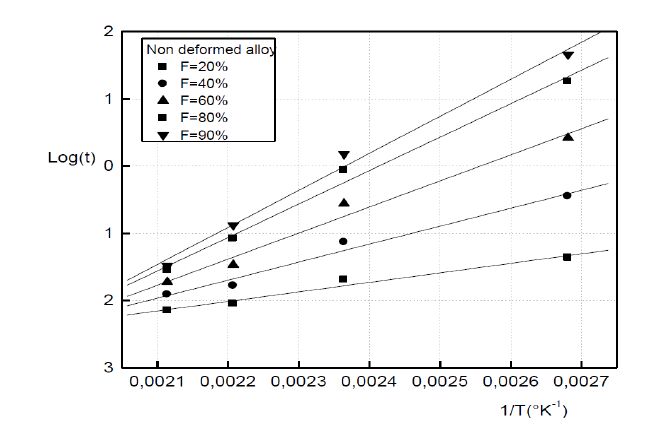
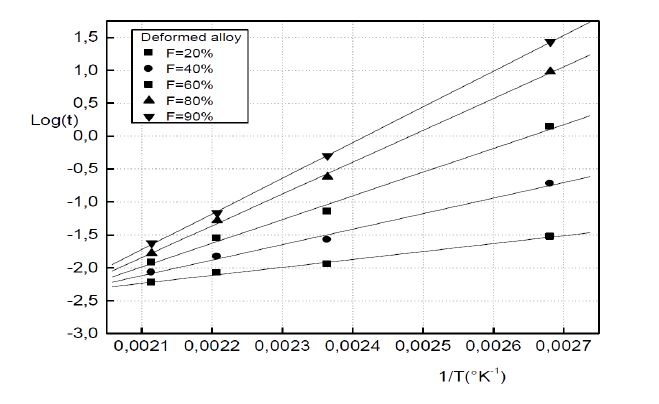
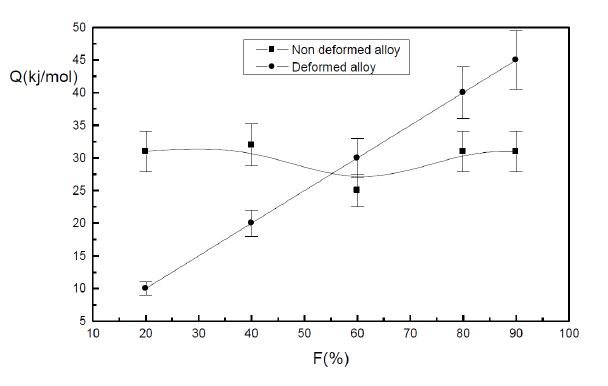
The formation of the Guinier-Preston zones in aluminium alloys is closely linked with the excess vacancies. A plastic deformation exerts an influence on the Guinier-Preston zones precipitation. As well as in the non deformed alloy and in the deformed alloy, the growth kinetics obeys to the JMAK law of the growth controlled by the solute atoms diffusion. However, during the GP zones growth, two stages are observed. During the first one, the plastic deformation slows down the Guinier-Preston zones formation and during the second stage, the plastic deformation accelerates their formation. The plastic deformation promotes the formation of the metastable γ’ phase.
1.
Introduction
In 1999, the concept of k-subdirect sums of square matrices was proposed by Fallat and Johnson [1], which is a generalization of the usual sum of matrices [2]. The subdirect sum of matrices plays an important role in many areas, such as matrix completion problems, global stiffness matrices in finite elements and overlapping subdomains in domain decomposition methods [1,2,3,4,5].
An important question for subdirect sums is whether the k-subdirect sum of two square matrices in one class of matrices lies in the same class. This question has attracted widespread attention in different classes of matrices and produced a variety of results. In 2005, Bru et al. gave sufficient conditions ensuring that the subdirect sum of two nonsingular M-matrices was also a nonsingular M-matrix [3]. Then the following year, they further came to the conclusion of the k-subdirect sum of S-SDD matrices is also an S-SDD matrix [2]. In [6], Chen and Wang succeeded in producing some sufficient conditions that the k-subdirect sum of SDD1 matrices is an SDD1 matrix. In [7], Li et al. gave some sufficient conditions such that the k-subdirect sum of doubly strictly diagonally dominant (DSDD) matrices is in the class of DSDD matrices. In addition, the k-subdirect sum of other classes of matrices were mentioned, such as Nekrasov matrices [8,9,10], quasi-Nekrasov (QN) matrices [11], SDD(p) matrices [12], weakly chained diagonally dominant matrices [13], Ostrowski-Brauer Sparse (OBS) matrices [14], {i0}-Nekrasov matrices [15], {p1,p2}-Nekrasov matrices [16], Dashnic-Zusmanovich (DZ) matrices [17], and B-matrices [18,19].
GSDD1 matrices as a new subclass of H-matrices was proposed by Dai et al. in 2023 [20]. In this paper, we focus on the subdirect sum of GSDD1 matrices, and some sufficient conditions such that the k-subdirect sum of GSDD1 matrices with SDD matrices belong to GSDD1 matrices are given. Numerical examples are presented to illustrate the corresponding results.
Now, some definitions are listed as follows.
Definition 1.1. ([2]) Let A and B be two square matrices of order n1 and n2, respectively, and k be an integer such that 1≤k≤min{n1,n2}, and let A and B be partitioned into 2×2 blocks as follows:
where A22 and B11 are square matrices of order k. Following [1], we call the square matrix of order n=n1+n2−k given by
the k-subdirect sum of A and B, denoted by C=A⊕kB. We can use the elements in A and B to represent any element in C. Before that, let us define the following set of indices:
Obviously, S1∪S2∪S3=N:={1,2,...,n}. Denoting C=A⊕kB=[cij], A=[aij] and B=[bij], then
Definition 1.2. ([20]) Given a matrix A=[aij]∈Cn×n, where Cn×n is the set of complex matrices. Let
It is easy to obtain that ¯NA is the complement of NA in N, i.e., ¯NA=N∖NA.
Definition 1.3. ([6]) A matrix A=[aij]∈Cn×n is called a strictly diagonally dominant (SDD) matrix if
Definition 1.4. ([20]) A matrix A=[aij]∈Cn×n is called a GSDD1 matrix if
where
Remark 1.1. From Definitions 1.3 and 1.4, it is easy to obtain that if a matrix A is an SDD matrix with ri(A)>0, then it is a GSDD1 matrix.
2.
Main results
First of all, a counterexample is given to show that the subdirect sum of two GSDD1 matrices may not necessarily be a GSDD1 matrix.
Example 2.1. Consider the following GSDD1 matrices A and B, where
and the 1-subdirect sum C=A⊕1B is
However, C is not a GSDD1 matrix because
Example 2.1 shows that the subdirect sum of GSDD1 matrices is not a GSDD1 matrix. Then, a meaningful discussion is concerned with: under what conditions will the subdirect sum of GSDD1 matrices is in the class of GSDD1 matrices?
In order to obtain the main results, several lemmas are introduced that will be used in the sequel.
Lemma 2.1. If matrix A=[aij]∈Cn×n is a GSDD1 matrix, then |ajj|−pjNA(A)>0 holds for all j∈NA.
Proof. According to the definition of GSDD1 matrices, we get
Since ri(A)−pi¯NA(A)>0,piNA(A), and pj¯NA(A) are all nonnegative, |ajj|−pjNA(A)>0 is obtained. □
Lemma 2.2. ([20]) If A=[aij]∈Cn×n is a GSDD1 matrix, then there is at least one entry aij≠0, i≠j, i∈¯NA, j∈N.
Lemma 2.3. ([20]) If A=[aij]∈Cn×n is a GSDD1 matrix with NA=∅, then A is an SDD matrix, and there is at least one entry aij≠0, i≠j, i∈¯NA, j∈¯NA.
Now, we consider the 1-subdirect sum of GSDD1 matrices.
Theorem 2.1. Let A=[aij] and B=[bij] be square matrices of order n1 and n2 partitioned as in (1.1), respectively. And let k=1, S1={1,2,…,n1−1}, S2={n1}, and S3={n1+1,n1+2,…,n1+n2−1}. We assume that A is a GSDD1 matrix, and B is an SDD matrix with ri(B)>0 for all i∈¯NB. If all diagonal entries of A22 and B11 are positive (or all negative), n1∈¯NA and
then the 1-subdirect sum C=A⊕1B is a GSDD1 matrix.
Proof. According to the 1-subdirect sum C=A⊕1B, we have
From n1∈¯NA, we know |an1,n1|>rn1(A). Because all diagonal entries of A22 and B11 are positive (or negative), we have
Since A is a GSDD1 matrix, B is an SDD matrix with ri(B)>0 for all i∈¯NB, C=A⊕1B, and according to Lemmas 2.2 and 2.3, we know that ri(C)≠0 for all i∈¯NC. Therefore, for any i∈¯NC,
For any j∈NC, we easily get j∈NC∩S1=NA∩S1⊂S1. For the three different selection ranges of i, that is, i∈¯NC∩S1=¯NA∩S1⊂S1, i∈¯NC∩S2={n1}, and i∈¯NC∩S3⊂S3, therefore, we divide the proof into three cases.
Case 1. For i∈¯NC∩S1=¯NA∩S1⊂S1, j∈NC, we have
Therefore, we obtain that
Case 2. For i∈¯NC∩S2={n1}, j∈NC,
We know that the results of the |cjj|, pjNC(C), and pj¯NC(C) are the same as (2.1), (2.2), and (2.3). Because B is an SDD matrix with ri(B)>0 for all i∈¯NB, we clearly get
Hence,
Case 3. For i∈¯NC∩S3⊂S3, j∈NC, in particular, we obtain that
So we easily come up with
From Cases 1–3, we have that for any i∈¯NC and j∈NC, the C matrix satisfies the definition of the GSDD1 matrix. The conclusion is as follows. □
Theorem 2.2. Let A=[aij] and B=[bij] be square matrices of order n1 and n2 partitioned as in (1.1), respectively. And let k, S1, S2, and S3 be as in Theorem 2.1. Likewise, we assume A is a GSDD1 matrix, and B is an SDD matrix with ri(B)>0 for all i∈¯NB. If all diagonal entries of A22 and B11 are positive (or all negative), n1∈NA, rn1(A)+r1(B)≥|an1,n1|+|b11| and
then C=A⊕1B is a GSDD1 matrix.
Proof. Since A is a GSDD1 matrix, B is an SDD matrix with ri(B)>0 for all i∈¯NB, n1∈NA, and rn1(A)+r1(B)≥|an1,n1|+|b11|, we get n1∈NC and then NC=NA.
For any i∈¯NC, by Lemmas 2.2 and 2.3, we have ri(C)≠0 and then
Since n1∈NC, i.e., i∈¯NC∩S2=∅, we prove it according to the two different selection ranges of i, namely i∈¯NC∩S1=¯NA∩S1⊂S1 and i∈¯NC∩S3⊂S3. For any j∈NC, that is, j∈NC∩S1=NA∩S1⊂S1 and j∈NC∩S2=NA∩S2={n1}. Therefore, we prove it from the following cases.
Case 1. For i∈¯NC∩S1=¯NA∩S1⊂S1, j∈NC∩S1=NA∩S1⊂S1, we obtain that
Therefore,
Case 2. For i∈¯NC∩S1=¯NA∩S1⊂S1, j∈NC∩S2=NA∩S2={n1}, we know that ri(C), piNC(C), and pi¯NC(C) have the same results as (2.4), (2.8), and (2.5). Moreover,
Hence, we obtain that
Case 3. For i∈¯NC∩S3⊂S3, j∈NC∩S1=NA∩S1⊂S1, we have
where l=i−n1+1. We have the same values of |cjj|, pjNC(C), and pj¯NC(C) as (2.6), (2.7), and (2.9). Therefore,
Case 4. For i∈¯NC∩S3⊂S3, j∈NC∩S2=NA∩S2={n1}, we get that the values of ri(C), piNC(C), and pi¯NC(C) are the same as (2.13), (2.15), and (2.14). Moreover, the results of |cjj|, pjNC(C), and pj¯NC(C) are the same as (2.10), (2.11), and (2.12). Hence, we obtain that
From Cases 1–4, we definitively get that C is a GSDD1 matrix. □
The following Example 2.2 shows that Theorem 2.1 may not necessarily hold when k≥2.
Example 2.2. Consider the following matrices:
where A is a GSDD1 matrix and B is an SDD matrix with ri(B)>0 for all i∈¯NB. It is easy to verify that A and B satisfy the conditions of Theorem 2.1 and A⊕1B is a GSDD1 matrix. However, C=A⊕2B is not a GSDD1 matrix. In fact,
By computation,
Therefore, C=A⊕2B is not a GSDD1 matrix.
The following Example 2.3 shows that Theorem 2.2 may not necessarily hold when k≥2.
Example 2.3. Consider the following matrices:
where A is a GSDD1 matrix and B is an SDD matrix with ri(B)>0 for all i∈¯NB. It is easy to verify that A and B satisfy the conditions of Theorem 2.2 and A⊕1B is a GSDD1 matrix. However, C=A⊕2B is not a GSDD1. In fact,
By computation, r3(C)−p3¯NC(C)=0, therefore, C=A⊕2B is not a GSDD1 matrix.
Those are sufficient conditions to ensure that the 1-subdirect sum of GSDD1 matrices with SDD matrices is a GSDD1 matrix. In fact, as the value of k increases, the situation becomes more complicated, so that the adequate conditions we give will also be more complicated.
Next, some sufficient conditions ensuring that the k-subdirect (k≥2) sum of GSDD1 matrices with SDD matrices is a GSDD1 matrix are given.
Theorem 2.3. Let A=[aij] and B=[bij] be square matrices of order n1 and n2 partitioned as in (1.1), respectively. And let 2≤k≤min{n1,n2}, S1, S2, and S3 be as in (1.2). We assume A is a GSDD1 matrix and B is an SDD matrix with ri(B)>0 for all i∈¯NB. If all diagonal entries of A22 and B11 are positive (or all negative), i∈¯NA for any i∈S2 and
where λi=ri(A)+ri−n1+k(B)+n1∑j=n1−k+1j≠i|aij+bi−n1+k,j−n1+k|−n1∑j=n1−k+1j≠i(|aij|+|bi−n1+k,j−n1+k|), then the k-subdirect sum C=A⊕kB is a GSDD1 matrix.
Proof. Since A is a GSDD1 matrix with i∈¯NA for any i∈S2, we get |aii|>ri(A). According to the k-subdirect sum C=A⊕kB, we have ri(C)=λi≤ri(A)+ri−n1+k(B). Because all diagonal entries of A22 and B11 are positive (or negative), we get |cii|=|aii|+|bi−n1+k,i−n1+k|. Therefore, we obtain that |cii|>ri(C), that is, for any i∈S2, i∈¯NC. Since A is a GSDD1 matrix, B is an SDD matrix with ri(B)>0 for all i∈¯NB, and C=A⊕kB, by Lemmas 2.2 and 2.3 we know that ri(C)≠0 for i∈¯NC∩S1∪S3=¯NA∩S1∪S3. For i∈S2, by sufficient conditions, we have λi≥ri(A)+pi−n1+k¯NB(B), which means that λi>0. Therefore, for any i∈¯NC, we obtain that
Moreover, for any j∈NC, we get j∈NC∩S1=NA∩S1⊂S1. For any i∈¯NC, similarly, we prove it from the following three cases, which are i∈¯NC∩S1=¯NA∩S1⊂S1, i∈¯NC∩S2=¯NA∩S2⊂S2, and i∈¯NC∩S3⊂S3.
Case 1. For i∈¯NC∩S1=¯NA∩S1⊂S1, j∈NC, we have
Therefore,
Case 2. For i∈¯NC∩S2=¯NA∩S2⊂S2, j∈NC, we obtain that
We know that |cjj|, pjNC(C), and pj¯NC(C) are the same as (2.16), (2.17), and (2.18). Therefore,
Case 3. For i∈¯NC∩S3⊂S3, j∈NC, specifically, we obtain that
Hence,
Therefore, we get that ri(C)−pi¯NC(C)>0 and (ri(C)−pi¯NC(C))(|cjj|−pjNC(C))>piNC(C)pj¯NC(C) for any i∈¯NC, j∈NC. □
Corollary 2.1. Let A=[aij] and B=[bij] be square matrices of order n1 and n2 partitioned as in (1.1), respectively. And let 2≤k≤min{n1,n2}, S1, S2, and S3 be as in (1.2). We assume A is a GSDD1 matrix and B is an SDD matrix with ri(B)>0 for all i∈¯NB. If all diagonal entries of A22 and B11 are positive (or all negative), i∈¯NA for any i∈S2 and
where λi is the same as λi of Theorem 2.3 and i∈S2, then the k-subdirect sum C=A⊕kB is a GSDD1 matrix.
Proof. For the inequality
multiplying both sides of this inequality by |aij| (i∈S1∪S2,j≠i) and summing for every j∈¯NA∖{i} (j∈S2), we have
Similarly, for i∈S2, we obtain that
By Theorem 2.3, we obtain that the k-subdirect sum C=A⊕kB is a GSDD1 matrix. □
Theorem 2.4. Let A=[aij] and B=[bij] be square matrices of order n1 and n2 partitioned as in (1.1), respectively. And let 2≤k≤min{n1,n2}, S1, S2, and S3 be as in (1.2). We assume A is a GSDD1 matrix and B is an SDD matrix with ri(B)>0 for all i∈¯NB. If all diagonal entries of A22 and B11 are positive (or all negative), i∈NA for any i∈S2, |aii|+|bi−n1+k,i−n1+k|≤λi and
where λi is the same as λi of Theorem 2.3, then the k-subdirect sum C=A⊕kB is a GSDD1 matrix.
Proof. Since A is a GSDD1 matrix with i∈NA for any i∈S2 and |aii|+|bi−n1+k,i−n1+k|≤λi, we have |aii|≤ri(A) and |cii|=|aii|+|bi−n1+k,i−n1+k|≤λi=ri(C), that is, for any i∈S2, we have i∈NC. Moreover, we know that i∈NC∩S1=NA∩S1⊂S1, which means that NC=NA. Combining Lemmas 2.2 and 2.3, we get that ri(C)≠0 for i∈¯NC∩S1∪S3=¯NA∩S1∪S3. Therefore, for any i∈¯NC, we obtain that
Since i∈¯NC∩S2=∅, we prove it from the following two aspects, which are i∈¯NC∩S1=¯NA∩S1⊂S1 and i∈¯NC∩S3⊂S3. For any j∈NC, that is, j∈NC∩S1=NA∩S1⊂S1 and j∈NC∩S2=NA∩S2⊂S2. Therefore, we prove it from the following cases.
Case 1. For i∈¯NC∩S1=¯NA∩S1⊂S1, j∈NC∩S1=NA∩S1⊂S1, we get
Therefore, we obtain that
Case 2. For i∈¯NC∩S1=¯NA∩S1⊂S1, j∈NC∩S2=NA∩S2⊂S2, we know that ri(C) and (2.19)} are equal, pi¯NC(C) and (2.20) are equal, and piNC(C) and (2.23) are equal. Moreover,
Hence,
Case 3. For i∈¯NC∩S3⊂S3, j∈NC∩S1=NA∩S1⊂S1, we obtain that
where l=i−n1+k. We know that |cjj|, pjNC(C), and pj¯NC(C) are the same as (2.21), (2.22), and (2.24). Therefore,
Case 4. For i∈¯NC∩S3⊂S3, j∈NC∩S2=NA∩S2⊂S2, we obtain that the values of ri(C), piNC(C), and pi¯NC(C) are equal to (2.28), (2.30), and (2.29). Moreover, the results of |cjj|, pjNC(C), and pj¯NC(C) are the same as (2.25), (2.26), and (2.27). Hence, we arrive at
In conclusion, for any i∈¯NC, j∈NC, we successfully derive that ri(C)−pi¯NC(C)>0 and} (ri(C)−pi¯NC(C))(|cjj|−pjNC(C))>piNC(C)pj¯NC(C). Therefore, C=A⊕kB is a GSDD1 matrix.
Example 2.4. Consider the following matrices:
where A is a GSDD1 matrix with i∈¯NA for all i∈S2, and B is an SDD matrix with ri(B)>0 for all i∈¯NB. By computation, we derive NA={1,3},¯NA={2,4,5,6}. Moreover,
we get that ∑j∈¯NA∖{i},j∈S2λj|ajj+bj−n1+k,j−n1+k||aij|≤∑j∈¯NA∖{i},j∈S2rj(A)|ajj||aij| is true for i∈S1∪S2.
we have that the second sufficient condition in Theorem 2.3 is true.
we get that the third sufficient condition in Theorem 2.3 is met. Therefore, by Theorem 2.3, C=A⊕3B is a GSDD1 matrix. In fact,
where NC={1,3},¯NC={2,4,5,6,7,8}. By computation,
It is not difficult to find that ri(C)−pi¯NC(C)>piNC(C) and |cjj|−pjNC(C)>pj¯NC(C) when i∈¯NC, j∈NC. So we deduce that ri(C)>pi¯NC(C) and (ri(C)−pi¯NC(C))(|cjj|−pjNC(C))>piNC(C)pj¯NC(C) are true when i∈¯NC, j∈NC. Thus, C=A⊕3B is a GSDD1 matrix.
Example 2.5. Consider the following matrices:
where A is a GSDD1 matrix and B is an SDD matrix with ri(B)>0 for all i∈¯NB. By computation, NA={1,4,5,6,7},S2={4,5,6,7},
Moreover,
Hence, the conditions in Theorem 2.4 are met. By Theorem 2.4, C=A⊕4B is a GSDD1 matrix. In fact,
By computation, NC={1,4,5,6,7}, ¯NC={2,3,8,9}. Moreover,
We see that ri(C)−pi¯NC(C)>piNC(C) and |cjj|−pjNC(C)>pj¯NC(C) when i∈¯NC, j∈NC. Therefore, we obtain that ri(C)>pi¯NC(C) and (ri(C)−pi¯NC(C))(|cjj|−pjNC(C))>piNC(C)pj¯NC(C) are true when i∈¯NC, j∈NC. Therefore, C=A⊕4B is a GSDD1 matrix.
Remark 2.1. Since the subdirect sum of matrices does not satisfy the commutative law, if we change "A is a GSDD1 matrix, and B is an SDD matrix" to "A is an SDD matrix, and B is a GSDD1 matrix", then we will obtain new sufficient conditions by using similar proofs in this paper.
3.
Conclusions
In this paper, some sufficient conditions are given to show that the subdirect sum of GSDD1 matrices with SDD matrices is in the class of GSDD1 matrices, and these conditions are only dependent on the elements of the given matrices. Furthermore, some numerical examples are also presented to illustrate the corresponding theoretical results.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
This work was partly supported by the National Natural Science Foundation of China (31600299), Natural Science Basic Research Program of Shaanxi, China (2020JM-622), and the Postgraduate Innovative Research Project of Baoji University of Arts and Sciences (YJSCX23YB33).
Conflict of interest
The authors declare there is no conflicts of interest.













 DownLoad:
DownLoad: