Citation: Mica Grujicic, S. Ramaswami, Jennifer S. Snipes. Use of the Materials Genome Initiative (MGI) approach in the design of improved-performance fiber-reinforced SiC/SiC ceramic-matrix composites (CMCs)[J]. AIMS Materials Science, 2016, 3(3): 989-1021. doi: 10.3934/matersci.2016.3.989
| [1] | Grujicic Mica, Galgalikar Rohan, Ramaswami S., Snipes Jennifer S. . Derivation, parameterization and validation of a creep deformation/rupture material constitutive model for SiC/SiC ceramic-matrix composites (CMCs). AIMS Materials Science, 2016, 3(2): 591-619. doi: 10.3934/matersci.2016.2.591 |
| [2] | Kiyotaka Obunai, Daisuke Mikami, Tadao Fukuta, Koichi Ozaki . Microstructure and mechanical properties of newly developed SiC-C/C composites under atmospheric conditions. AIMS Materials Science, 2018, 5(3): 494-507. doi: 10.3934/matersci.2018.3.494 |
| [3] | Reginald Umunakwe, Ifeoma Janefrances Umunakwe, Uzoma Samuel Nwigwe, Wilson Uzochukwu Eze, Akinlabi Oyetunji . Review on properties of hybrid aluminum–ceramics/fly ash composites. AIMS Materials Science, 2020, 7(6): 859-870. doi: 10.3934/matersci.2020.6.859 |
| [4] | Naofumi Nakazato, Akira Kohyama, Hirotatsu Kishimoto . Evaluation of strength anisotropy and fracture behavior of UD NITE-SiC/SiC composites with various fiber orientations. AIMS Materials Science, 2016, 3(4): 1382-1390. doi: 10.3934/matersci.2016.4.1382 |
| [5] | Araya Abera Betelie, Yonas Tsegaye Megera, Daniel Telahun Redda, Antony Sinclair . Experimental investigation of fracture toughness for treated sisal epoxy composite. AIMS Materials Science, 2018, 5(1): 93-104. doi: 10.3934/matersci.2018.1.93 |
| [6] | Daniela Šuryová, Igor Kostolný, Roman Koleňák . Fluxless ultrasonic soldering of SiC ceramics and Cu by Bi–Ag–Ti based solder. AIMS Materials Science, 2020, 7(1): 24-32. doi: 10.3934/matersci.2020.1.24 |
| [7] | Tomáš Meluš, Roman Koleňák, Jaromír Drápala, Paulína Babincová, Matej Pašák . Ultrasonic soldering of Al2O3 ceramics and Ni-SiC composite by use of Bi-based active solder. AIMS Materials Science, 2023, 10(2): 213-226. doi: 10.3934/matersci.2023012 |
| [8] | Carlos A. Sánchez, Yamile Cardona-Maya, Andrés D. Morales, Juan S. Rudas, Cesar A. Isaza . Development and evaluation of polyvinyl alcohol films reinforced with carbon nanotubes and alumina for manufacturing hybrid metal matrix composites by the sandwich technique. AIMS Materials Science, 2021, 8(2): 149-165. doi: 10.3934/matersci.2021011 |
| [9] | Elisa Padovano, Francesco Trevisan, Sara Biamino, Claudio Badini . Processing of hybrid laminates integrating ZrB2/SiC and SiC layers. AIMS Materials Science, 2020, 7(5): 552-564. doi: 10.3934/matersci.2020.5.552 |
| [10] | Mario Ceddia, Bartolomeo Trentadue . A review of carbon fiber-reinforced polymer composite used to solve stress shielding in total hip replacement. AIMS Materials Science, 2024, 11(3): 449-462. doi: 10.3934/matersci.2024023 |
High-temperature metallic materials such as nickel-, cobalt- or iron-based superalloys used in gas-turbine engines have been pushed to their thermal-stability limit since they are often made to operate at temperatures which are within 50 degrees of their melting point. To increase power density and energy efficiency of the gas-turbine engines, new materials are needed which can operate at temperatures as high as 1600 K (and as high as 1800 K, when these materials are protected with a so-called environmental barrier coating). The main candidate materials currently identified for use in the next generation of gas-turbine engines are (monolithic) ceramics and CMCs. Since these materials can withstand extremely high temperatures, their use in hot sections of gas-turbine engines can yield a number of benefits such as: (i) improvements in thrust and fuel efficiency; (ii) lower pollutant emissions; (iii) reduced cooling requirements; (iv) simplification of the engine-component design; and (v) reduced requirements for the strength/weight of the supporting structure. By DOE estimates [1], metal-with-ceramic substitutions in gas-turbine engine hot-section components would reduce the turbine fuel consumption by ca. 13% and reduce the emissions of NOx, CO and unburned hydrocarbons by ca. 75%.
Due to their relatively low fracture toughness, tensile strength and damage tolerance, monolithic ceramics are not currently being perceived as viable candidate materials for use in critical turbine-engine structural applications (e.g. turbine blades). On the other hand, CMCs, particularly fiber-reinforced CMCs, possess superior structural properties relative to their monolithic-ceramic counterparts, while retaining their high-temperature thermo-mechanical stability and structural integrity. This is the reason that the FR CMCs are being aggressively investigated and developed for use in advanced gas-turbine engine applications. The potential of the CMCs in revolutionizing the performance of the gas-turbine engines is shown schematically in Figure 1 [2,3,4,5,6,7]. In this figure, the x-axis represents the approximate period of dominance in usage of the particular class of high-temperature materials (and associated cooling technologies), while the y-axis denotes the temperature capability of the material class in question. It is seen that the temperature capability of CMCs lies above the fitting/extrapolation line for the temperature capabilities of the past and present gas-turbine engine materials.
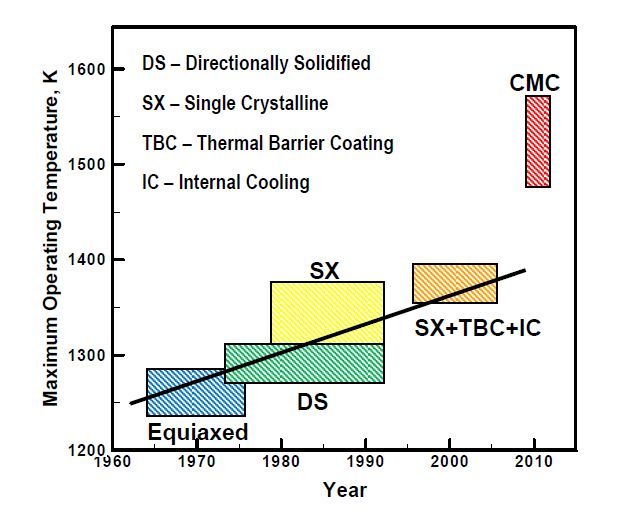 Figure 1. Temperature capability (i.e. maximum service temperature) of various gas-turbine engine materials as a function of the time period of their dominant usage
Figure 1. Temperature capability (i.e. maximum service temperature) of various gas-turbine engine materials as a function of the time period of their dominant usageFR-CMCs possess substantially higher levels of fracture toughness and effectively scale-invariant mechanical properties (allowing fabrication of structurally sound, high-reliability, large-sized engine components) relative to their monolithic counterparts. These advantages of the FR-CMCs are associated with the presence of weak matrix/fiber interfaces which promote fiber/matrix interfacial decohesion over fiber fracture, allowing the fibers residing in the crack wake to bridge crack interfaces and inhibit brittle response of the material. Typically, to prevent oxidation of the fibers by oxygen ingress through the matrix cracks, fibers are coated, and the coating chemistry is chosen in such a way that decohesion takes place along the weak matrix/coating interfaces. In addition, environmental barrier coatings (EBCs) are used to protect the entire CMC component from the aggressive gas-turbine engine environment. Thus the main microstructural constituents of the FR-CMCs materials and components are: (a) fibers/filaments; (b) fiber coatings; (c) matrix; and (d) EBCs.
Traditionally, new materials are not designed but rather discovered through trial-and-error, a time-consuming and costly approach. Once new materials are discovered, they are subjected to an even costlier and longer development and certification process. Within the materials-by-design methodology, a material-system-level approach is employed in order to design and fully develop new materials through the use of computer-aided engineering analyses, predictive tools and available material databases. The basic concept behind the materials-by-design methodology can be explained using a flow-block diagram like the one depicted in Figure 2. The design objective of the material in question will be the attainment of a superior combination of the specific material properties as dictated by the intended application of the material. In Figure 2, the first box, labeled "Processing", would contain the main processing steps used in the manufacture of the material in question. The third box, labeled "Properties", would identify the key properties of concern in the intended application(s) of the material in question. The second box, labeled "Microstructure", would list the main microstructural features which are influenced by the processes identified in the first box and affect quantitatively the properties and property tradeoffs identified in the third box. The last box, labeled "Performance", would list the key performance requirements for the component/structure to be made of the material being designed. Double-headed arrows are used in Figure 2 to indicate processing/microstructure, microstructure/property and property/performance relations. These relations for the class of FR SiC/SiC CMCs will be developed, parameterized and applied (to design a new grade of FR SiC/SiC CMCs) in the present work.
 Figure 2. Materials-by-design block diagram showing the interplay between processing, microstructure, properties and performance of a material being designed
Figure 2. Materials-by-design block diagram showing the interplay between processing, microstructure, properties and performance of a material being designedExamination of the flow-block diagram depicted in Figure 2 reveals that the material as a system can be viewed as a three-link (processing-microstructure, microstructure-property and property-performance) chain. Thus, the strength of this chain which quantifies the success of the materials-by-design approach is controlled by its weakest link. It should be noted that a flow-block diagram like the one depicted in Figure 2 is the result of deductive, cause-effect reasoning which quantitatively relates (from left to right) processing to microstructure, microstructure to properties and properties to performance. However, within the materials-by-design approach, the same block diagram is combined with inductive reasoning and utilized (from right to left). That is, once the performance requirements are identified in the "Performance" box, the necessary combination of the material properties is determined in the "Properties" box. This is then followed by identification of the required microstructural features in the "Microstructure" box, and lastly by identification of the required processing routes and the optimal process attributes in the "Processing" box.
It should be noted that the materials-by-design approach described above is an integral part of the so-called Materials Genome Initiative, which was launched in June 2011 by the White House Office of Science and Technology Policy [8,9] and is aimed at developing an infrastructure to accelerate advanced materials discovery and deployment in the United States. Within the biological sciences, a genome denotes the detailed information, encoded in DNA, which acts as a blueprint for building, "Running" and maintaining an organism. When used in a non-biological context, as in the present case, the word "genome" typically represents a basic structural block (e.g. a microstructural feature) used in the construction of a larger hierarchical multi-functional system.
Over the last several decades the US federal and state governments have made major investments in developing and establishing new experimental methods and techniques for designing, fabricating and characterizing advanced materials. One of the goals of the MGI is the improved leverage of these investments and speeding up the development of new materials through: (a) utilization of state-of-the-art computational modeling and simulation techniques in the materials design/development process; (b) development of readily accessible material databases; and (c) implementation of an integrated and dynamic approach to materials science and engineering. Advanced materials are crucial to addressing challenges associated with national security, clean energy and human welfare and, hence, accelerating the rate of their discovery and deployment will play a critical role in ensuring US global competitiveness in the 21st century.
Presently, it generally takes 10 to 20 years for a newly-discovered material to be employed commercially. This clearly demonstrates the fact that the development and certification of new materials proceeds much slower than the development of new products. The slow pace of material development/certification can be linked to the continued reliance on legacy knowledge and make-and-test empiricism. In other words, material development today relies heavily on the use of the materials processing and characterization experimental techniques. For some classes of engineering materials (e.g. FR SiC/SiC CMCs), whose computational material models have reached the required level of fidelity and whose material databases are comprehensive, these experimental techniques could be replaced with their virtual (in silico) counterparts. This approach, as suggested by the MGI and supported by the present work, is expected to reduce the time required to bring new and improved materials to market.
The main objective of the present work is to employ the materials-by-design methodology, overviewed in the previous subsection, in order to design a new class of FR SiC/SiC CMCs with an improved performance as related to the use of these materials in hot-section gas-turbine engine applications. Towards that end, the system-level MGI methodology is combined with multi-length scale, multi-disciplinary modeling and simulation approaches and the associated databases in order to develop a FR SiC/SiC CMC materials-by-design computational toolbox. It should be noted that the modeling and simulation approaches used have been developed and reported in the open literature by the present research team as well as by other researchers. Due to: (a) a large number of these approaches; (b) their highly diverse character; and (c) space limitations, they will not be overviewed in great detail in the present manuscript. Instead, for each of the computational modeling and simulation approaches used, the source references will be provided, as well as details regarding the associated input and output variables and a brief description of the modeling and simulation methodology used. The computational toolbox will help establish the functional relationships between: (a) the FR SiC/SiC CMC materials" processing parameters; (b) various microstructural and morphological characteristics of the FR SiC/SiC CMC constituents; (c) properties of the individual FR SiC/SiC CMC constituents; and (d) the properties and the performance of the FR SiC/SiC CMCs. The knowledge of these relationships is mandatory for the materials-by-design approach.
In this section, details are provided regarding the chemicalmakeup, microstructure and processing routes for the FR SiC/SiC CMCs, as well as for the associated materials-by-design methodology when applied to this class of high-temperature materials.
As established in Section 1.1, the four basic constituents of FR CMCs are: (a) fibers/filaments; (b) fiber coatings; (c) matrix; and (d) EBCs. In the remainder of this subsection, details are provided regarding the chemistry, microstructure and the basic processing route used in the fabrication of these constituents, with a particular emphasis being placed on the constituents associated with the FR SiC/SiC CMCs.
Since the experience gained over the last thirty years has clearly shown that the FR-CMCs based on large-diameter monofilament systems, fabricated by chemical vapor deposition (CVD), have severe shortcomings relative to manufacturing complex-shaped engine components as well as inferior through-the-thickness mechanical properties, the FR-CMCs investigated are reinforced with small-diameter, polymer-derived, multi-filament tows. Among the multi-filament fiber tows, the following two (SiC-based) classes have been identified as having the best combination of room-/high-temperature mechanical properties: (i) Nicalon, oxide-free Hi-Nicalon and oxide-free, crystalline Hi-Nicalon S from Nippon Carbon; (ii) Tyranno-LoxM, ZMI and oxide-free, crystalline Tyranno-SA; and (iii) oxide-free creep-resistant Sylramic, (coated with in-situ-grown BN) Sylramic-iBN and Super Sylramic-iBN from Dow Corning Corporation. All of these classes are fabricated from the corresponding polymeric-precursor (e.g. polycarbosilane, in the case of Nicalon fibers) filament tows. The latter are generally synthesized through a combination of chemical and physical processes, such as dechlorination, thermal decomposition, polymerization and melt-spinning. The spun-out polymeric fiber tow is subsequently air-cured, oxidized and pyrolyzed to form filament tows consisting of fine-grain polycrystalline SiC, unreacted Si and C, and other filament-class-dependent constituents (e.g. amorphous SiO2, in the case of Nicalon).
Since fiber coatings have to provide a number of functions, such as: protecting fibers during the formation of the SiC matrix, protecting fibers from oxygen ingression through the matrix cracks, and ensuring the presence of weak interfaces, fiber coatings (particularly in the case of the FR-CMCs in which SiC matrix is fabricated using so-called reactive melt infiltration, RMI, described below) are typically of a multi-layered (most often five-layered) character. The chemical makeup, microstructure and the functionality of the five layers, starting from the fiber surface, are as follows: (i) initial flash carbon, produced by thermal cracking of acetylene, which protects the fiber from chemical attack by the HCl by-product accompanying CVD processing of the BN second layer; (ii) BN layer, which acts as the main matrix/fiber debond layer and, thus, promotes high toughness and graceful failure of the FR-CMCs. Since BN possesses limited stability when exposed to molten silicon, additional coating layer(s) are required; (iii) flash carbon with a dual purpose of promoting nucleation and, thus, formation of a uniform-thickness Si3N4 fourth layer and of protecting the underlying BN layer from molten Si which has diffused through the interconnected pores of the Si3N4 by promoting the formation of SiC plugs within the Si3N4 layer; (iv) Si3N4 layer with a dual purpose of mechanical protection of the BN layer during the subsequent FR-CMC processing and chemical protection of the BN layer from direct exposure to molten silicon; and (v) flash carbon top layer which promotes good wetting of the coated fiber by both the C/SiC slurry and by the molten silicon.
In order to withstand aggressive service environments encountered in hot-sections of gas-turbine engines, FR-CMCs generally involve a SiC-based (e.g. SiC) matrix. A chemical composition of the matrix is selected in such a way that the following matrix-property objectives are met: (i) high thermal conductivity (to minimize the likelihood for hot-spot formation); (ii) low porosity/high structural integrity; (iii) low thermal expansion mismatch with the reinforcing fibers and their coating (to minimize the magnitude of in-service thermal stress); (iv) high maximum service temperature; (v) high creep-rupture resistance and microstructural stability at the maximum service temperature; and (vi) crack self-healing capability. SiC matrix (a typical choice) is generally produced using one of the following routes: (i) chemical vapor infiltration (CVI); (ii) room-temperature infiltration (or slurry casting) of C-/SiC-particulates into the fibrous preform, followed by ca. 1400 °C infiltration with molten silicon (the so-called reactive melt infiltration, RMI, route); and (iii) the so-called polymer infiltration pyrolysis (PIP) process, i.e. infiltration of the preform with SiC-yielding polymer precursor and subsequent high-temperature pyrolysis to form metal Si-free crystalline SiC.
When exposed to the oxidizing high-temperature gas-turbine engine environments, SiC/SiC FR CMCs tend to form SiO2 scale layer which acts as an effective oxidation barrier due to its very low permeability to oxygen [10]. However, under combustion environments within the engine, SiO2 reacts with water vapor, forming volatile hydroxides or oxyhydroxides, leading to significant material recession/loss. To remedy this problem, FR SiC/SiC CMC engine components are generally protected using multi-layer EBCs.
Since EBCs are the engine-component coating, they do not, to a first-order approximation, alter the bulk microstructure and properties of the FR-CMC material and, hence, are not investigated in the present work. However, as clearly demonstrated in our recent work [4], EBCs can significantly affect the durability, reliability and performance of various gas-turbine engine hot-section components.
As mentioned earlier, the main goal of the work presented here is to utilize the system-level Materials Genome Initiative (MGI) and the multi-length scale, multi-disciplinary modeling and simulation approaches and the associated databases in order to develop a suite of the computational tools which will be used to design the next generation FR SiC/SiC CMCs for use in gas-turbine engine hot-section components. These tools will help establish the functional relationships between: (a) the FR SiC/SiC CMC materials'processing parameters; (b) various microstructural and morphological characteristics of the FR SiC/SiC CMC constituents (i.e. fibers, fiber-coatings, and matrix; as mentioned earlier, CMC-component EBCs are not considered here); (c) properties of the individual FR SiC/SiC CMC constituents; and (d) the properties and the performance of the FR SiC/SiC CMCs. The knowledge of these relationships is mandatory for the materials-by-design approach.
The system approach to FR SiC/SiC CMC design used in the present work is schematically represented by the flow-block diagram in Figure 3, which reveals the complete structural hierarchy of the class of FR SiC/SiC CMCs under investigation. In this figure, the four aforementioned constituents are displayed along the left margin. Within the first column, labeled "Processing" the main processing routes are shown for each of the four FR SiC/SiC CMC constituents. The third column, labeled "Properties" identifies the key properties for each of the constituents in the FR SiC/SiC CMCs for use in the gas-turbine engine hot sections. The second column in the same figure, labeled "Microstructure" lists, for each constituent, the main microstructural sub-systems (genomes) which are influenced by the corresponding material-synthesis/processing parameters and affect quantitatively the level of, and the tradeoffs between, the material properties identified in the third column. The last column, labeled "Performance" lists the key performance requirements for the FR SiC/SiC CMC components that are used in the gas-turbine hot sections. Lines should be used in Figure 3 to indicate specific processing/microstructure, microstructure/property and property/performance functional relationships, which are derived and parameterized in the present work. However, this was not done in the current rendition of Figure 3, since the number of lines that would need to be drawn is too large and would hinder the clarity of the figure.
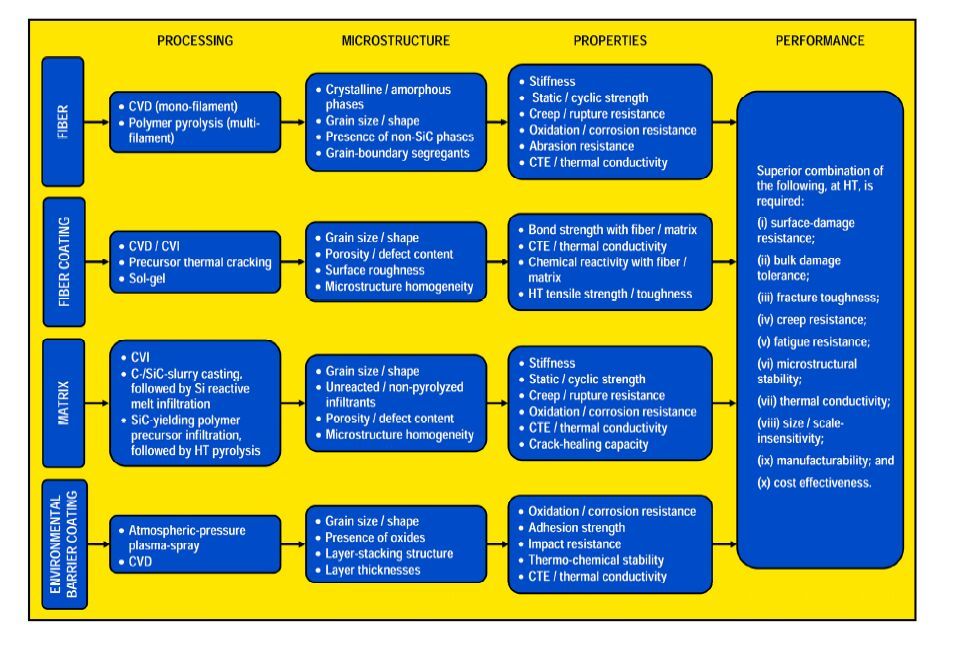 Figure 3. Materials-by-design block diagram for FR SiC/SiC CMCs
Figure 3. Materials-by-design block diagram for FR SiC/SiC CMCsIn this section, in accordance with the materials-by-design methodology depicted in Figure 3, for each of the FR SiC/SiC CMC constituents, the functional relationships between: (a) constituent-material synthesis parameters and the resulting material microstructure; and (b) material microstructure and the resulting thermo-mechanical and environment-resistant material properties are developed and parameterized. In addition, parameterized functional relationships are established between the constituent-material properties and the FR SiC/SiC CMC gas-turbine engine hot-section component performance, durability and reliability. It should be noted that in many cases, these functional relationships, due to their complexity, could not be given in closed-form. Rather, they are defined in terms of numerical models which relate the associated input and output variables.
As mentioned in Section 2.1, only polymer-derived multi-filament fiber-tows are considered in the present work. A detailed analysis of the public-domain literature dealing with the fabrication of this type of fibers, revealed that, for the polymeric-precursor of a given chemistry, the most critical step in the fiber fabrication process is conversion of the polymer-based fibers into their SiC-based counterparts. In the present work, two complementary approaches are used to model this fiber-processing step:
(a) Reactive molecular dynamics (RMD) simulations of the polymeric precursor oxidation/pyrolysis processes involving ab-initio quantum-mechanics based reactive force fields (RFFs). Once high-fidelity RFFs are derived, this approach is used to study the interaction and competition between various reactive processes (e.g. cleavage of the Si"H bonds, formation of H radicals, H gas formation through bonding of H radicals, formation of SiC bonds, etc.) accompanying SiC-fiber synthesis [11]. The RFFs derived in [12] were found to be, for the most part, of sufficient fidelity and, hence, were adopted in the present work. Minor deficiencies observed in these RFFs were rectified in the present work using quantum-chemical computations based on density functional theory [13,14]. The RMD computational procedure employed involves the following steps: (i) generation of an all-atom equilibrium model for the polymeric precursor in question; (ii) prolonged RMD simulations at specified temperatures and pressures to study thermal degradation and bond breaking and regeneration within the precursor; (iii) monitoring the rate of production of species (e.g. H radicals) as a function of time, and application of the classical Arrhenius-type functional relationship to assess the corresponding reference reaction rate constant and the activation energy; (iv) mimicking of the experimental conditions which involve purging of the furnace with a neutral gas to sweep the gaseous by-products out of the furnace, by dynamically removing such products from the RMD simulations; and (v) simultaneous monitoring of the progress of the SiC formation and the amorphous/crystalline nature of it, by determining, in real time, the associated radial distribution functions and the X-ray diffraction pattern of the as-pyrolyzed polymeric precursor. It should be noted that the RMD simulations described above mimic the fiber synthesis process, while making a number of simplifying assumptions like: (i) RMD simulations are carried out at temperatures higher than those expected during experimental runs because the affordable simulation timescale is on the order of nanoseconds, while conversion of the polymeric precursor to SiC typically takes minutes to hours. The use of higher temperatures within the RMD simulations is assumed to affect only the kinetics, but not the physics of the attendant chemical reaction; and (ii) the RMD computational domain is substantially smaller than the prototypical precursor subjected to the oxidation/pyrolysis heat treatment. Here, it is assumed that the overall rate of the oxidation/pyrolysis process is controlled by the rate of the attendant chemical reactions and not by the transport of the reaction products to the surface of the RMD computational domain, and their subsequent removal from the system. Examples of the RMD initial (SiH2CH2 hydridopolycarbosilane polymeric precursor) and final (fully pyrolyzed) atomistic configurations investigated in the present work are depicted in Figures 4(a)-(b), respectively.
 Figure 4. Examples of RMD simulation results showing: (a) initial hydridopolycarbosilane polymer precursor; and (b) fully pyrolyzed atomic configurations
Figure 4. Examples of RMD simulation results showing: (a) initial hydridopolycarbosilane polymer precursor; and (b) fully pyrolyzed atomic configurationsAs mentioned earlier, for each of the computational modeling/simulation analyses employed, details will be provided regarding the nature of the input and output parameters/variables, as well as a brief description of the modeling procedure and computational tool used. Input-chemical makeup of the polymeric precursor, ceramic-fiber synthesis parameters like temperature, time, furnace-purging schedule; Output-volume fraction and crystallinity of various phases present in the as-synthesized ceramic fiber; Methods/tools-RMD simulations using Discover, a general-purpose, molecular-statics and dynamics program [15]. Within the RFFs used, chemical bonding is not preassigned but, rather, is determined adaptively and dynamically during the simulation using the concepts of bond order and atomic valence; and
(b) The RMD computational methodology described in (a) does not yield detailed information regarding the average grain size or the grain-size distribution, the microstructural parameters which may significantly affect mechanical properties of the fibers. To overcome this shortcoming, semi-empirical models analyzing the competition between the SiC-crystallite nucleation and growth is employed. This model is an extension of the thermodynamics/kinetics model for the glass-devitrification process [16]. Within this model, experimental (e.g. small angle X-ray scattering (SAXS), X-ray diffraction (XRD), differential thermal analysis (DTA) and high resolution transmission electron microscopy (HRTEM)) post-processed results reported in the open literature [17,18], for the precursors pyrolyzed at different temperatures for different durations, are combined with the available thermodynamics and mobility data to determine the effect of various polymeric-precursor additives on the reference rates and the activation energies for the crystalline SiC (homogeneous and heterogeneous) nucleation, growth and coarsening processes. The results obtained (not shown for brevity) in this portion of the work revealed : (i) at lower temperatures a fine grain size is obtained since the nucleation process is dominant; (ii) at intermediate temperatures an intermediate grain size is obtained due to comparable rates of the nucleation and growth processes; (iii) at the highest temperatures, a coarse-grained microstructure is obtained due to the onset of the grain-coarsening process; and (iv) the effect of the non-Si/C atoms and the effect of C/Si atomic ratio deviating from 1 in the precursor on the kinetics of the grain-coarsening.
Input-empirically derived thermodynamic and atomic mobility data and the associated reference rate and activation energies for the crystalline SiC nucleation growth and coarsening; Output-temporal evolution of the ceramic-fiber average grain size and grain size distribution; Methods/tools-an in-house developed computer program.
In summary, by combining the two fiber-synthesis modeling schemes presented above, one can establish a direct link between the fiber-synthesis process parameters and the microstructure of the as-synthesized fibers. This, in turn, enables, once the optimal fiber microstructure is identified in a given application, determination of the optimum fiber-synthesis process parameters via the use of an optimization algorithm.
As mentioned earlier, the main fiber-coating synthesis techniques include CVD (for individual fibers) and CVI (for fiber tows or fiber-/fiber-tow-based FR-CMC preforms). Modeling of these two processes is carried out using the multi-length-scale, multi-disciplinary computational approach developed in our prior work for a number of coating systems and for single-walled carbon nanotubes [19,20,21,22,23,24,25,26]. Within this approach, the CVD/CVI processes are investigated simultaneously and interactively at four distinct length-scales (shown schematically in Figures 5(a)-(d)):
(a) At the chemical-reactor length scale, Figure 5(a), the process is studied by solving the appropriate reactive-gas, fluid-dynamics, heat-transfer boundary value problem. At this length scale, the FR-CMC preform is modeled using an effective medium approach. In other words, the filament and pore architectures within the preform, and their evolutions during the deposition process, are accounted for only implicitly through the use of the effective transport properties [27]. This is accomplished by representing the transient porous structure by a Bethe lattice (an infinite connected graph where each node is connected to z neighbors, where z is the coordination number) and by employing the percolation theory to account for utilized, unutilized, and filled pore space [28]. The total diffusion coefficient, which includes Knudsen and molecular contributions as well as the thermal conductivity, are determined using the effective medium theory, which relates the effective transport phenomena of a network of interconnected pores to the distribution of the transport properties and the pore inter-connectivity [29]. As far as the chemical reactivity is concerned, it is handled using a detailed analysis of the thermodynamics and kinetics of various gas and surface chemical reactions [30,31] and their competition and inter-relationships. For each of the gas and surface reaction species, the appropriate mass conservation equations are developed while utilizing the Arrhenius-type mass-action kinetics.
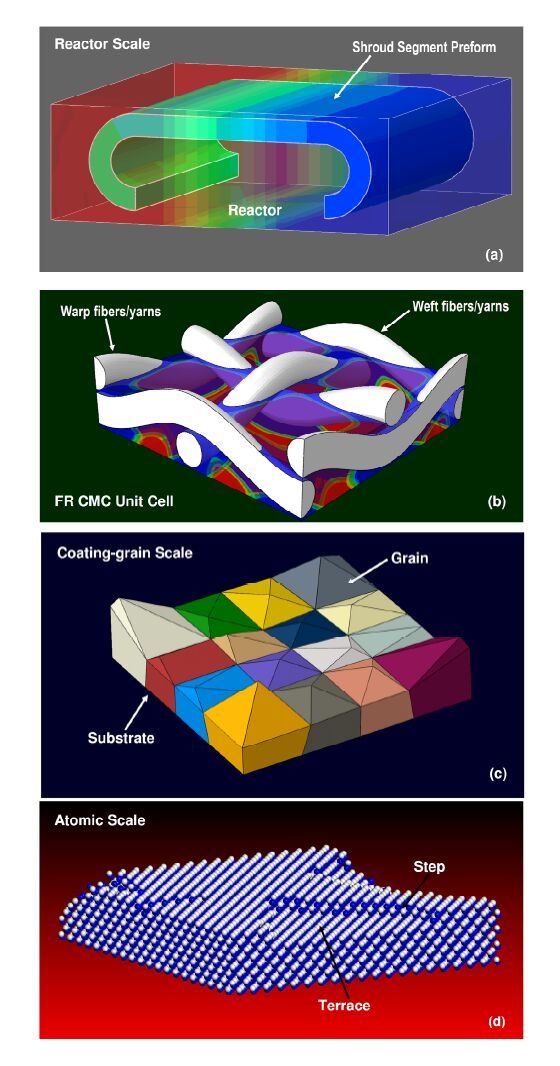 Figure 5. Multi-scale, multi-physics modeling of CVD/CVI fabrication of fiber/preform coating: (a) reactor scale; (b) FR CMC unit-cell scale; (c) coating-grain scale; and (d) atomic scale
Figure 5. Multi-scale, multi-physics modeling of CVD/CVI fabrication of fiber/preform coating: (a) reactor scale; (b) FR CMC unit-cell scale; (c) coating-grain scale; and (d) atomic scaleInput-pore connectivity, porosity distribution, operating pressure, gas inlet temperature, heater temperature and the preform size/geometry; Output-the temperature, pressure, gas velocity, species concentration and deposition rate fields; Methods/tools-computational analysis which: (i) includes the coupling between fluid flow and chemical kinetics; (ii) accounts for production/depletion of the species due to chemical reactions in the gas phase and at the substrate surface; (iii) considers the convective and diffusive transport of species within the gas phase and to the deposition surface; and (iv) incorporates the effect of the substrate local topology (e.g. the presence of steps and terraces) on the rate of the forward and reverse reactions are carried out using ChemKin [30] and Surface ChemKin [31] computer programs and databases.
(b) At the length scale of the FR-CMC preform unit cell, Figure 5(b), the architecture of the preform (e.g. cross-ply, plain-weave, etc.) is accounted for explicitly while the local temperature, pressure, gas velocity and species concentration fields are inherited from the reactor-length-scale analysis. Analyses at the two length scales are further inter-related in the following way: while the reactor-length-scale analysis enables the prediction of the local average coating deposition rate and the average residual porosity within a given computational cell (with a size comparable to that of the FR-CMC preform unit cell), the FR-CMC length scale analysis allows the deposition rates and residual porosities (and, thus, the potential defective regions) to be spatially resolved at the length scale of the preform-architecture unit cell. Consequently, the FR-CMC length scale CVI analysis is carried out for different regions of the preform for which the reactor-length-scale analysis has indicated potentially deficient coating (e.g. an insufficiently thick coating). As far as the governing equations for the FR-CMC length-scale analysis are concerned, they are effectively identical to their reactor-length-scale counterparts and include: (i) the mass, linear momentum and energy conservation equations for all the participating gas species; (ii) the mass conservation equations for all the participating surface species; (iii) Arrhenius-type gas kinetics; and (iv) coating-deposition rate functional relationships. The main difference in the two analyses is that the transport properties at the FR-CMC scale are of a local, rather than effective, character [5].
Input-the temperature, pressure, gas velocity, species concentration and deposition rate fields obtained in (a); Output-the temperature, pressure, gas velocity, species concentration and deposition rate fields at the length-scale of a FR-CMC unit cell; Methods/tools-same as in (a).
(c) The FR-CMC unit cell length-scale analysis enables a determination of the local fiber-coating thickness, but does not provide any information regarding the surface topology and bulk microstructure (including defects) or the as-deposited coating material. This deficiency is, at least partially, remedied using the atomic length-scale analysis, Figure 5(d), of the same deposition process. Due to restrictions associated with the maximum size of the computational crystal which can be handled using the available computational resources, typically only the CVD/CVI of the single-crystalline coating could be modeled, at the atomic length-scale. Furthermore, since the fiber coatings are generally of a polycrystalline nature and their surfaces are faceted with low growth-rate (e.g. {111}, {100}, etc.) crystallographic planes, only the coating deposition in the overall direction normal to such crystallographic planes was analyzed in the present work.
For each of these single-crystalline cases, the analysis is carried out under the following conditions:
(i) perfect rigid crystal lattice, i.e. atomic vibrations and potential local relaxations are neglected;
(ii) in the case of the stoichiometric compound-type coatings, the lattice is partitioned into the appropriate number of sub-lattices and each sub-lattice is assigned to the corresponding sub-species;
(iii) the rigid lattice, onto which the coating is deposited, is placed over the appropriate substrate. The CVD/CVI coating deposition process is simulated by enabling the interaction between hot, reactive gases, initially with the substrate (and subsequently with the as-deposited coating material). The concentrations of the gas-phase and surface species at the deposition surface are initially set to their values obtained in the FR-CMC unit cell length scale;
(iv) to prevent coating-edge effects, in-plane periodic boundary conditions are applied, while the deposition is enabled in the out-of-plane direction;
(v) to ensure consistency between the deposition rate predictions of the reactor, FR-CMC unit cell and the atomic-scale modeling schemes, the same surface reactions and their thermodynamics and kinetics data are used throughout;
(vi) since atomic-scale simulations are expected to yield reliable predictions regarding the evolution of the surface texture and the nature of the processes which can lead to formation of defects in the as-deposited material, in addition to considering the role of surface chemical reactions, the effect of surface diffusion also had to be taken into account. Surface diffusion for a given species is limited to its own sub-lattice and is not restricted to an atomically-flat crystallographic plane, but rather can involve jumps between surface planes of different altitude (terraces). Independent atomic-scale surface-diffusion calculations [19,20,21,22,23,24,25,26] are used to assess intrinsic diffusivity of each surface species and its temperature-dependence;
(vii) CVD/CVI processes, at the atomic length scale, are simulated in the present work using the adaptive time-step kinetic Monte Carlo method [32]. Within this method, the probability for the occurrence of a surface reaction at a particular surface site scales with the rate of this reaction relative to the rates of all other reactions which could take place at the same surface site; and
(viii) since the CVD/CVI process is, at least partly, of a stochastic character, it was found to result in the formation of various (point, line, surface and volume) crystalline defects within the as-deposited coating material. For example, entrapped gas species are often found to form point defects, while partial dislocations (line defects) are often found to encircle twinned domains (surface defects). Since these defects can greatly affect the quality and the mechanical properties of the as-deposited coatings, the ability of the atomic-scale modeling to predict the effect of various CVD/CVI process parameters on the extent and the degree of defect formation represents a great benefit of this modeling approach. However, it should be recognized that this approach is restricted to modeling the CVD/CVI process on a single crystallographic plane. On the other hand, fiber coatings are polycrystalline in nature and their surfaces are faceted.
Input-the temperature, pressure, gas velocity and species concentration fields at the length-scale of a FR CMC unit cell; Output-coating deposition rate and the rate of incorporation of various crystallographic defects of the as-deposited coating on low-index crystallographic plane; Methods/tools-the kinetics Monte Carlo algorithm is implemented in an in-house developed computer program; and
(d) One has to employ a coating-grain size modeling scheme to simulate the evolution of surface morphology, grain size distribution, evolution of the morphological and crystallographic texture, etc. in polycrystalline fiber coatings, since the atomic-scale simulations are limited to the CVD/CVI process modeling at the scale of a coating-material single crystallographic plane, and the reactor/FR-CMC modeling schemes did not even account for the crystalline nature of the coating material. In general, the grain-scale microstructure is expected to be controlled by growth competition and, to a lower extent, by twinning. Growth competition is governed by the relative growth rates (yielded by the atomic-scale model) of various facets of the coating surface, while twinning is controlled by the magnitude of the stacking-fault energy (was obtained, in the present work, using conventional molecular statics/dynamics calculations). Typically, the grain size CVD/CVI process modeling is carried out using the following steps:
(i) at the beginning of the simulation, the substrate is populated, at random, by a large number of sub-micron sized coating-material nuclei. The shape of each nucleus is obtained through random sectioning of the coating-material idiomorph (a single crystallite, growing without competition from other crystallites, the shape of which is controlled by the crystallographic planes associated with the lowest growth rates);
(ii) the nuclei are allowed to grow by prescribing, to each of their facets, the growth rates yielded by the atomic-scale analysis;
(iii) initially, the nuclei grow in isolation (becoming larger single-crystalline grains) but, after some time, they begin to impinge on each other, ultimately forming a continuous polycrystalline coating;
(iv) grain boundaries are formed when the adjacent crystals contact each other. While no migration of the grain boundaries is considered, they are allowed to extend as the contacting (columnar) grains continue to grow; and
(v) the growth competition between the various facets and grains controls the ultimate crystallographic and morphological character of the as-deposited fiber coating, its surface roughness and, due to the fact that the rate of defect generation is affected by the crystallographic-character of the growing surface facet, the extent and the degree of crystallographic defects.
Input-random population of sub-micron sized coating nuclei and facet growth rates and rates of incorporation of various crystalline defects, as yielded in (c); Output-temporal evolution of the coating grain-size, topological and crystallographic texture, surface topology and crystallographic-defect content; Methods/tools-the coating grain-microstructure evolution algorithm is implemented in an in-house-developed computer program.
In summary, by combining the four coating-deposition modeling schemes, one can establish a direct link between the CVD/CVI process parameters and the microstructure of the as-deposited coatings. This, in turn, enables, once the optimal coating microstructure is identified in a given application, determination of the optimum deposition process parameters via the use of an optimization algorithm. It should be also noted that the present approach can be extended to modeling an optimization of a functionally-graded coating. It is generally observed that the presence of sharp interfaces in multi-layer coatings results in some loss of the coating performance and durability, and that compositional and microstructural grading of the fiber coatings can help remedy this problem [33,34,35].
The functional relationships between the processing parameters and the matrix microstructure are developed in the present work for all three previously-mentioned processing routes for the FR-CMCs. The first of these matrix-processing routes involves the use of CVI, and is modeled using the same method as the one described in the context of the CVI-fabricated fiber coatings. As far as the processing route involving polymer infiltration and subsequent pyrolysis, is concerned, its first step is handled using the computer models developed for the slurry casting/RMI-process (described below), while its second step is handled using the computational approaches discussed above in the context of fiber synthesis from the polymeric precursors.
Both slurry casting and RMI can be characterized as porous-medium, liquid-infiltration processes. However, while the former is typically carried out at room temperature and is of a non-reactive nature, the latter is a high-temperature process and involves chemical reactions, phase transitions and the associated volumetric and latent-heat effects. Consequently, for the most part, an RMI process model can be employed in the simulation of slurry casting by excluding some of the chemical/physical processes and their governing equations. Taking this into account, the main emphasis in the present work is on developing a high-fidelity RMI process model which could be adapted to the slurry casting process. Towards that end, our recently developed multi-physics RMI process model [3] for FR SiC/SiC CMCs, a flowchart of which is depicted in Figure 6, was adopted and slightly modified. In Figure 6, each of the rounded rectangles denotes the specific single-physics analysis/module which has to be employed in the course of RMI modeling. In the same figure, arrows are used to denote one- or two-way coupling between different analyses. In what follows, brief descriptions are provided for each of the six single-physics computational analyses identified in Figure 6:
(a) Capillary- and gravity-driven unsaturated flow of the molten silicon into the FR SiC/SiC CMC preform (pre-infiltrated with a C/SiC particulate slurry and dried) is modeled using the Richard's equation [36], subjected to the appropriate pressure/velocity initial and boundary conditions and the auxiliary relations such as Darcy's law (which relates the pressure gradient and the fluid velocity), the van Genuchten functions (which describe pressure dependence of effective saturation, specific moisture capacity, storage coefficient and relative permeability) and the local permeability relations (bringing in the effect of local porosity, pore-connectivity, etc.). The solution of the governing equations, for a given period of infiltration, yields the associated fluid-velocity and fluid-volume-fraction fields;
(b) Chemical reactions between the silicon melt and carbon resulting in the formation of SiC are modeled by constructing and solving the appropriate SiC volume-fraction evolution equation subjected to the appropriate initial and boundary conditions along with the auxiliary thermodynamic and kinetic relations of the accompanying chemical reactions. Since the governing equation contains the molten Si velocity term, this module has to be interfaced with the infiltration module, to which it provides the current volume fraction of the as-reacted SiC (used by the infiltration module to compute the local porosity and saturation fluid volume fraction);
(c) Thermal-energy transfer and heat source/sink phenomena accompanying reactive-flow infiltration are modeled by solving the appropriate energy conservation equations subjected to the appropriate temperature gradient and thermal flux initial and boundary conditions and the auxiliary relations for the effective volumetric heat capacity, thermal conductivity and volumetric heat generation rate arising from the accompanying chemical reactions and phase transitions. The thermal-energy module provides the prior two modules with temperature, while it receives velocity, fluid volume fraction and SiC volume fraction from them;
(d) RMI is accompanied by a number of chemical and physical processes (e.g. formation of the solid SiC from liquid Si and solid C, solidification of unreacted molten silicon, cooling of SiC, etc.) which can result in (negative or positive) volumetric changes of the (reacted or unreacted) infiltrating material and the preform material. Since these volumetric changes can, and generally do, cause the development of thermal and residual stresses within the as-fabricated FR SiC/SiC CMC material/component, they must be accounted for by the RMI process model. Within the Volumetric-Change module of the RMI process model, detailed functional relationships are constructed and parameterized for all the chemical and physical processes contributing to the material-volume change during RMI. The present module requires the knowledge of SiC volume fraction, unreacted Si volume fraction and temperature, which are provided by the Chemical-Reaction and the Thermal-Energy-Balance modules. Furthermore, the present module provides information regarding the RMI-process-induced volumetric strains to the (next) Residual-Stress/Thermal-Distortion module;
(e) Since the processing-induced residual-stress fields can significantly affect the ability of FR SiC/SiC CMC materials and components to withstand applied loads, the RMI process model must be able to predict such stresses and their relationship to the RMI process parameters. In the present work, this is done by solving the appropriate thermo-mechanical equilibrium equation (subjected to the appropriate initial and boundary conditions) over the domain of interest and adopting the generalized Hooke's law with degradable elastic stiffnesses as the constitutive behavior for all the constituent materials. The output of this module is used as input to the portion of the FR SiC/SiC CMC model dealing with the microstructure/property relationships; and
(f) In addition to being able to predict the extent of silicon/carbon conversion into SiC, the RMI process model must also be able to predict the distribution of the FR-CMC matrix grain size, morphological and crystallographic textures and their fields, since these microstructural features can greatly affect the performance of the subject materials. This is accomplished in the present work by linking the cellular automaton method, refined in our prior work [37,38,39,40], with the Infiltration, Chemical-Reaction and Thermal-Energy modules. This enables analysis of the competition between the SiC formation via a chemical reaction and liquid-Si solidification, as well as the homogeneous vs. heterogeneous, nucleation vs. growth and grain- vs. grain-growth competition. An example of the matrix grain-microstructure results obtained is shown in Figure 7.
Input-preform architecture/geometry and RMI-process parameters; Output-microstructure, residual stresses and Si/SiC ratio; Methods/tools-the RMI-process modeling is implemented in an in-house developed computer program.
In summary, for the given matrix-fabrication process, the multi-physics process model enables establishment of a direct link between the process parameters and the microstructure and residual stresses in the as-fabricated matrix in FR SiC/SiC CMCs. This, in turn, enables, once the optimal matrix microstructure is identified in a given application, determination of the optimum matrix-fabrication process parameters via the use of an optimization algorithm.
For the fibers within FR-CMCs, the mechanical properties of key concern are:
(a) room- and high-temperature stiffness (influences fiber/matrix load-sharing and, thus, the onset and progression of matrix cracking);
(b) room- and high-temperature static strength (controls FR-CMC component abrasion, damage caused by foreign-object impact, thermal-shock damage resistance, and the ability of the fibers to toughen the matrix by bridging its cracks);
(c) resistance to creep and rupture (creep leads to a loss in critical dimensional tolerances and may cause material-property degradation); and
(d) thermo-mechanical fatigue strength (affects the component service life).
While fiber oxidation resistance is also important, if inadequate, it will be provided by the fiber coating. Other important properties include high thermal conductivity (to prevent formation of "hot-spots" it is attained through the selection of SiC-based fiber materials) and low thermal expansion coefficient mismatch with the coating and the matrix (to minimize the extent of thermal-stress development; it is attained through the proper selection of the FR-CMC constituent materials).
Room- and High-Temperature Stiffness: Fiber stiffness is controlled by the volume fractions, stiffnesses and crystallographic texture of its constituent phases, but is generally a weak function (and assumed here to be independent) of the constituent-phase(s) grain size. Room-temperature fiber stiffness was determined in the present work by applying a homogenization procedure [33] to the constituent-phase stiffnesses and constituent-phase volume fraction results yielded by the fiber-processing/microstructure computational models described in Section 3.1. As far as the high-temperature fiber stiffness is concerned, the following two observations reported in the open literature are taken into account: (i) short-term exposure to operating temperatures as high as 1400 K have relatively small effects (neglected in the present work) on fiber stiffness; and (ii) prolonged exposure of the fiber to high temperatures can result, particularly in the case of high-oxygen content fibers like Nicalon, in porosity formation, the phenomenon which degrades fiber stiffness. Functional relations developed in our recent work [6], which quantify: (a) temporal evolution of the porosity via the so-called Kolmogorov-Johnson-Mehl-Avrami relation [41]; and (b) the associated stiffness degradation via a homogenization procedure [33], are used in the present work.
Room- and High-Temperature Static Strength: Fiber strength is affected not only by the volume fractions and the nature of microstructural phases (the contribution of these is accounted for in the present work by using a homogenization procedure [33]) but also by the grain size and the grain-size distribution. The effect of the grain-size and its distribution on the fiber (room-temperature) static strength is accounted for using the Hall-Petch type functional relationship [42] and the procedure described in detail in Ref. [6]. As far as high-temperature fiber strength is concerned, it is determined by including the contribution of two high-temperature effects: (a) grain-coarsening-this effect is accounted for by first quantifying the kinetics of grain-coarsening using the Lifshitz-Slyozov functional relation [43] and then by quantifying the effect of the grain size on the material strength via the use of the Hall-Petch relation; and (b) porosity formation-this effect is accounted for by first quantifying the kinetics of porosity formation via the use of the Kolmogorov-Johnson-Mehl-Avrami relation [41] and then by employing a homogenization approach [33].
Creep and Rupture: Creep deformation in fibers is analyzed by accounting for the following experimental observations reported in the open literature: (a) in the case of SiC-based fibers, the tertiary stage of creep is generally not observed (i.e. rupture occurs in the secondary/steady-state stage of creep) [44]; (b) the time at which primary-to-secondary creep-stage transition takes place is very weakly sensitive (and assumed insensitive, in the present work) to the service temperature and stress. Consequently, only the time-dependent primary-creep relations of the form given in Refs. [7,45] are employed while the secondary-creep strain rate is assumed to be given by the primary creep rate evaluated at the primary-to-secondary creep-stage transition time.
The primary-creep equation used is a multiplicative decomposition of (a) a power function of stress; and (b) a standard Boltzmann-probability temperature-dependent term; and (c) a power function of time. Based on the work presented in Refs. [7,45], it is the creep-activation energy appearing the Boltzmann-probability term which is assumed to be an increasing function of the fiber-grain size (i.e. the larger is the grain size, the larger is the material's resistance to intergranular sliding and, thus, the smaller is the resulting creep rate). The primary creep-deformation and creep-rupture model parameterizations reported recently [7,45] are adopted in the present work.
Thermo-mechanical Fatigue Strength:In the current rendition of the FR SiC/SiC CMC material development, thermo-mechanical fatigue strength properties are not considered since, in the applications considered, these properties are found not to be component-life-limiting.
The key required properties of the coating include: (a) weak adhesion to the matrix (to promote matrix-crack deflection); (b) good adhesion to the fiber (to prevent fiber side-on exposure to the oxidizing/corrosive environment); (c) high chemical resistance to thermo-mechanical attack by molten Si (to ensure coating structural integrity and its fiber-protection role); and (d) high fracture toughness, i.e. a combination of low stiffness and high strength, to resist cracking (critical for the protection of the underlying fiber).
Characterization of the coating interfacial/surface properties listed in (a)-(c) is done in the present work using a series of all-atom molecular-level virtual tests related to coating/matrix as well as coating/fiber decohesion, and coating/molten-Si reactivity [46]. The required level of fracture toughness is obtained through grain-size refinement, defect-content reduction, and surface-roughness minimization (all quantified by the four-scale coating-deposition modelling scheme described in Section 3.1) and the toughness vs. microstructure functional relationships developed in our prior work [21].
The same mechanical and physical properties identified in the case of fibers are also of interest for the matrix. In addition, crack-healing capability of the matrix is also critical and will be attained by alloying the SiC-matrix with elements like B, which have a high affinity towards oxygen (and, thus, readily forms oxide on crack faces) and yield solid oxides with relatively large molar volumes.
Room- and High-Temperature Stiffness: The same procedure as that used in the case of the fiber and the coating will be employed to determine room- and high-temperature stiffness of the matrix. It should be noted that the employed material-by-design approach will be aimed at designing a matrix which is slightly more compliant than the fiber, since this will reduce stress within the matrix and delay the onset of cracking (and consequently, increase the matrix crack initiation stress for the CMC). This may be accomplished, for example, by leaving a small fraction of (more compliant) Si unreacted within the matrix.
Room- and High-Temperature Static Strength: Since the matrix and fiber fall into the same class of ceramic materials, matrix static strength and the creep resistance are modeled using the same type of property vs. microstructure functional relationships (with different parameterization) as those discussed above for the fibers. However, due to a difference in the processing route, the matrix microstructural parameters are provided by the RMI and polymer-pyrolysis process models described in Section 3.1.
Creep and Rupture: As mentioned above, the same creep-deformation and creep-rupture models as those used for the fibers are used for the CMC.
In Section 3.2, functional relationships were employed to establish connections between FR-CMC constituent microstructures and properties. These relationships are necessary but not sufficient for predicting the properties/performance of the FR-CMC materials and gas-turbine engine components. That is, the contributions of the constituent interactions to the FR-CMC material/component properties and performance must also be established and taken into account. This is achieved in the present work by employing a two-level homogenization procedure [5] for derivation of the FR SiC/SiC CMC material constitutive model. In this procedure, two distinct microstructural length-scales are identified within FR SiC/SiC CMCs: (a) fiber/tow length-scale, characterized by the following microstructural parameters: volume fraction of the fibers, thickness of the fiber coatings, decohesion properties of the coating/matrix interfaces, etc.; and (b) ply/lamina length-scale, characterized by the following microstructural parameters: 0°/90° cross-ply vs. plain-weave architectures, the extent of tow crimping in the case of the plain-weave plies, cohesive properties of the inter -ply boundaries, etc.
At the fiber/tow length-scale, the procedure involves the following steps:
(i) assignment of the appropriate mechanical material models, including parameterization, for the CMC constituents. These models include linear elastic response the formulation of which is consistent with the extent of isotropy in the constituents in question. For example, fibers are treated as being transversely isotropic with the unique direction aligned with the fiber axis, while the coating and matrix are treated as being elastically isotropic. As far as the constituent strength is concerned, it is assumed to be a stochastic quantity, and to be given by a two-parameter Weibull distribution. Also, a traction vs. separation mechanical constitutive model is used to address potential matrix/coating decohesion;
(ii) Next, a representative volume element is constructed and subjected to a set of virtual mechanical tests. The results of these mechanical tests are used to formulate and homogenize a CMC material model at the fiber/tow length-scale; and
(iii) By varying the aforementioned microstructural parameters for the fiber/tow length-scale, constructing the representative volume element and carrying out the same type of virtual mechanical tests, and employing a least-squares curve-fitting procedure, homogenized-material model parameters are changed from being constant to being functions of the microstructural parameters at the fiber/tow length-scale.
At the ply/lamina length-scale, the procedure involves the following steps:
(i) assignment of the appropriate mechanical material model for the CMC plies/laminae. In this case, the homogenized material model yielded by the fiber/tow length-scale is assigned to both laminae. However, material axes of the model have to be rotated differently for the two laminae in order to account for potential differences in their orientation and potential crimping. Also, a traction vs. separation material constitutive law has to be defined to address interaction and potential decohesion between contacting laminae;
(ii) Next, a representative volume element is constructed and subjected to a set of virtual mechanical tests. The results of these mechanical tests are used to formulate and homogenize a CMC material model at the ply/lamina length-scale; and
(iii) By varying the aforementioned microstructural parameters for the ply/lamina length-scale, constructing the representative volume element and carrying out the same type of virtual mechanical tests, and employing a least-squares curve-fitting procedure, homogenized-material model parameters are changed from being constant to being functions of the microstructural parameters at the ply/lamina length-scale.
After the second level of homogenization, the CMC becomes a fully homogeneous material but the parameters in its constitutive model (referred to as turbine-engine component-level material model) are functions of the fiber/tow and ply/lamina length-scale microstructural parameters. The three microstructural length-scales associated with the two-level homogenization procedure are shown schematically in Figure 8. The turbine-engine component-level material model is subsequently: (i) integrated into a user-material subroutine and linked with a finite element solver; and (ii) interfaced with an optimization algorithm [47].
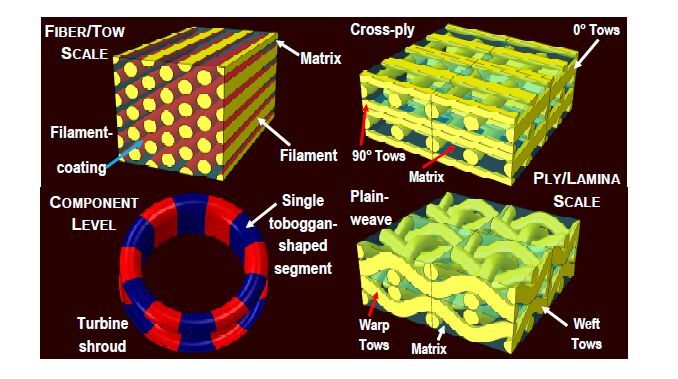 Figure 8. Schematics of the three length scales covered by the multi-length scale FR-CMC material constitutive model [5]
Figure 8. Schematics of the three length scales covered by the multi-length scale FR-CMC material constitutive model [5]In this way, FR SiC/SiC CMCs with a specific combination of properties can be designed by identifying the required values of the fiber/tow and ply/lamina microstructural parameters. Then, using the functional relationships overviewed in Section 3.1, the associated FR SiC/SiC CMC constituent process parameters are identified, completing the task of the material-by-design approach.
As indicated in the last column of Figure 3, the key FR-CMC material/component performance metrics include:
(a) the ability to withstand harsh thermo-mechanical and chemical environments within the gas-turbine engine without experiencing performance-limiting surface damage. This ability is imparted to the FR-CMC by the EBC (not considered in the present work);
(b) the ability to successfully tolerate bulk material/coating/fiber damage caused by excessive in-service loads, foreign object impact, etc. This FR-CMC performance requirement is met in two ways: (i) by delaying the onset of first matrix cracking; and (ii) by providing the matrix with the crack-healing capability. Within (i), matrix/coating interfaces of the proper adhesion strength will be designed (details presented in (c)) in order to promote ductile response of the FR-CMC, while within (ii) the matrix will be properly alloyed by species with high oxygen affinity and a large solid-oxide molar volume. It should be noted that the changes in the matrix chemical composition will not only affect its crack-healing capability but may also affect (typically negatively) other FR-CMC properties (e.g. microstructural stability through the accompanying changes in the relative thermodynamic stability of various constituent phases [48]). Additional details regarding the property trade-offs and the ways in which they are addressed are given below;
(c) high fracture toughness, a property which, provided matrix/coating interfaces of the proper adhesion strength are present, is derived through proper combination of high first matrix cracking stress (affected not only by the matrix strength, but also by the fiber/matrix elastic-stiffness mismatch), high FR-CMC ultimate strength (controlled by the fiber strength, but also affected by the matrix strength through the rate of the matrix-to-fiber load transfer) and large strain-to-failure (controlled by the competition between stress increase, due to the need to fracture fibers of higher intrinsic strength, and the load-carrying cross-sectional area reduction, due to the decreasing number of unbroken fibers; effectively the ultimate strength and the strain-to-failure are directly correlated). It should be noted that fracture toughness is generally maximized at an optimum level of the matrix/coating interfacial adhesion strength. That is, interfaces which are too weak promote matrix-to-fiber load transfer and, thus, premature fiber failure. On the other hand, interfaces which are too strong promote brittle trans-fiber extension of the matrix cracks, rather than crack deflection;
(d) high creep resistance of the FR-CMC, which is not necessarily associated with the microstructural conditions of the fiber and the matrix, which yield maximum creep resistance to these constituents. That is, the fiber/matrix creep-strain mismatch can increase the creep rate of the less creep-prone constituent and, thus, the effective creep rate of the FR-CMC. Consequently, to maximize the FR-CMC creep resistance, the aforementioned optimization procedure is employed;
(e) superior low-cycle (due to high-amplitude stress oscillations like the ones accompanying engine shut-down/start-up and operation under partial load) and superior high-cycle (due to low-amplitude stress oscillations like those encountered under normal operating conditions) fatigue resistance. As mentioned earlier, detailed analysis of low-/high-cycle fatigue strength of the FR-CMCs is beyond the scope of the present work. Nevertheless, it should be noted that while, in homogeneous materials, fatigue-resistance is controlled by surface cracking, in heterogeneous materials, like FR-CMCs, fatigue-crack initiation could be a bulk/sub-surface phenomenon. That is, elastic heterogeneities of the constituents can produce high local stress concentrations and bulk-material cracking. Thus, to minimize sub-surface cracking under cyclic loading conditions, preference will be given to the FR SiC/SiC CMC constituents with comparable elastic properties; and
(f) high microstructural stability/aging resistance. Due to their exposure to high temperature (as well as to the oxidizing and corroding conditions and in-service stresses), FR-CMCs tend to age, i.e. undergo (generally undesirable) microstructural and property changes, while in service. Consequently, while it is important to design FR-CMCs which, in their as-fabricated state, meet the performance objectives for a given high-temperature application, it is equally important that such FR-CMCs possess high microstructural stability, which ensures that the properties are retained over the expected service life of the component. High-temperature material microstructure evolution/metastability is manifested in many ways, e.g. grain growth/coarsening, metastable-phase decomposition/transformation, formation of the new phases at the constituent FR-CMC interfaces, etc. Modeling of the FR SiC/SiC CMC microstructural stability is a formidable task and is beyond the scope of the present work. However, this problem is being addressed in our ongoing work in which a microstructure-evolution tool is being developed by combining ThermoCalc> (a multi-component material-thermodynamics program [49]), DICTRA> (a multi-component reaction-kinetics and diffusional phase transformation program [50]) and TC-PRISMA> (a software package which treats concurrent nucleation, growth/dissolution and coarsening under arbitrary thermal history conditions in multi-component and multi-phase systems [51]) with a microstructure/property inter-relationship module.
Functional relationships developed and parameterized in Section 3 enable prediction of the FR SiC/SiC CMC properties and performance as a function of the CMC-constituents' processing parameters. Since parameterization of these functional relationships for the CMC-constituents is carried out using a least-squares-based curve-fitting procedure, the relationships can be considered as valid. However, one must still establish that the materials-by-design methodology developed in Section 3 will yield reliable predictions for the material properties of the FR SiC/SiC CMC as a whole. This type of validation is carried out in this section by comparing the experimental data with their corresponding computational counterparts for one case of the FR SiC/SiC CMC (reported in [10] and described below).
· Fiber: 32 vol. %; fiber diameter = 12mm; fiber type-low-oxygen Hi-Nicalon; polymeric precursor-polycarbosilane, −[−SiCH3H−CHH−]−; processing route-oxidation temperature/time = 473 K/10 min, pyrolysis temperature/time = 1273 K/15 min; fiber preform architecture-cross-ply.
· Coating: Layers and thicknesses starting from fiber-BN/0.3 mm, C/0.05 mm, Si3N4/0.4 mm, C/0.05 mm; CVD precursors-boron trichloride (BCl3) + ammonia (NH3) for BN, methane (CH4) for C, dichlorosilane (SiH2Cl2) + ammonia (NH3) for Si3N4; CVD reactor/process conditions-pressure = 0.013 atm, temperature = 1000 K, flow rates (in sccm): 20 for BCl3, 60 for NH3, 150 for H2 in the case of BN, and 20 for SiH2Cl2, 60 for NH3, 150 for H2 in the case of Si3N4.
· Matrix: chemical makeup-boron-alloyed SiC with B/Si atomic ratio of 0.15, for crack-healing; processing route-Si/C slurry infiltration followed by drying and molten Si reactive infiltration, molten Si temperature = 1673 K, infiltration pressure = 1 atm.
Two sets of experimental results reported in [10] are used for validation of the present FR SiC/SiC CMC materials-by-design approach: (a) in-plane tensile test results, at different temperatures, in the direction of one of the two mutually-orthogonal fiber families; and (b) in-plane uniaxial-stress creep-deformation test results at different temperature/stress combinations, also in the direction of one of the two mutually-orthogonal fiber families.
A schematic of a prototypical in-plane stress-strain curve is depicted in Figure 9. This figure reveals the presence of four distinct regions (labeled Ⅰ-Ⅳ), each associated with the characteristic mechanical response of the loaded material. The four regions of the stress-strain curve can be explained as follows:
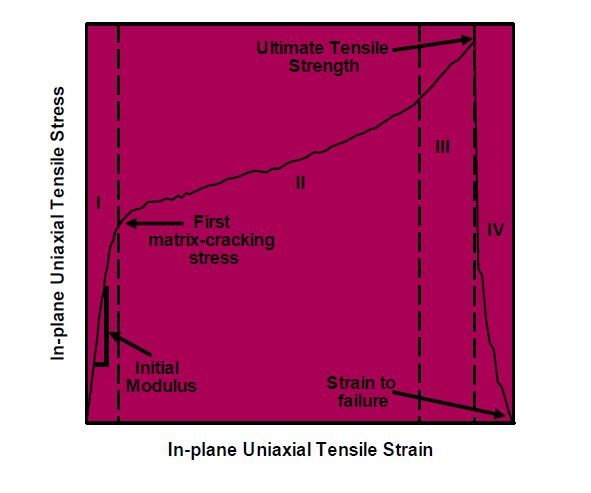 Figure 9. A schematic of an in-plane uniaxial-tension stress-strain curve, depicting the room-temperature mechanical behavior of FR CMCs
Figure 9. A schematic of an in-plane uniaxial-tension stress-strain curve, depicting the room-temperature mechanical behavior of FR CMCs(i) Region I is characterized by the linear elastic response of the (virgin) composite material. The slope of the stress-strain curve in this region is defined as the initial Young's modulus of the material. This region extends up to the stress level commonly referred to either as first matrix-cracking stress or proportional-limit stress, and does not induce any noticeable damage into the material;
(ii) In region Ⅱ, the material deformation involves an inelastic component resulting from the continuing matrix cracking. Concomitantly, fibers bridging the matrix cracks are shear-debonded from the matrix. These damage processes are accompanied by a reduction in the material stiffness and a gradual increase in the material strength (as flaws of progressively lower potency have to be activated to produce additional matrix cracks);
(iii) In region Ⅲ, continuation of the matrix cracking would require the activation of very weak flaws while the extent of load transfer from the fibers to the fractured-matrix fragments is severely decreased. Consequently, matrix-crack density begins to saturate while the material response to the applied loading begins to include fiber cracking. These microstructural-evolution processes are accompanied by further material-stiffness degradation and by "strain hardening" (the rate of which is higher than that in region Ⅱ); and
(iv) As the loading proceeds, progressively more fibers are broken and although the remaining unbroken fibers are stronger, the number of unbroken fibers decreases (causing the stress within these fibers to increase). Consequently, as loading continues, the material passes, at the stress level commonly referred to as the ultimate tensile strength, through the state of critical stability (corresponding to a critical fraction of the broken fibers). Beyond this point the increase in the average unbroken fiber strength is exceeded by an increase in the average stress experienced by these fibers (Region Ⅳ). As a result, the material begins to fail. Since at this point some of the fibers may still be bonded to the matrix, their sliding and the final pullout is associated with an additional strain and, consequently, the material fails gradually rather than abruptly with the final fracture occurring at a strain commonly referred to as strain to failure.
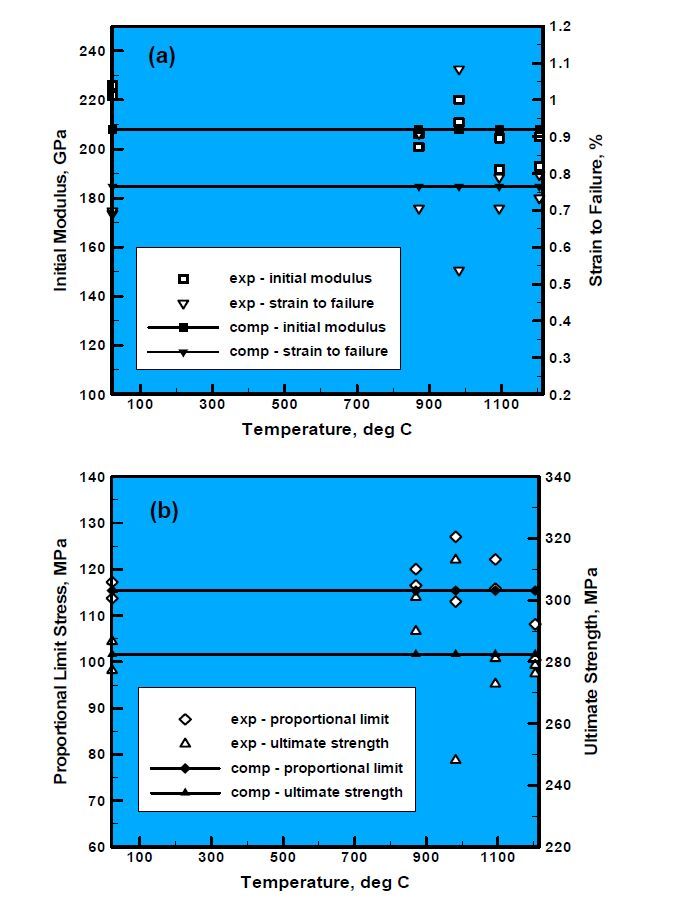 Figure 10. Experimental ("exp" [10] and present computational ("comp" in-plane tensile test results showing the effect of test temperature on: (a) the initial Young's modulus and the strain to failure; and (b) the proportionality limit and ultimate (tensile) strength
Figure 10. Experimental ("exp" [10] and present computational ("comp" in-plane tensile test results showing the effect of test temperature on: (a) the initial Young's modulus and the strain to failure; and (b) the proportionality limit and ultimate (tensile) strengthExperimental results [10] for the four parameters characterizing the stress-strain curve are shown as discrete white-filled symbols in Figures 10(a)-(b). It is seen that the experimental results were generated at five temperatures and that at the four lowest temperatures, two specimens were tested, and at the highest temperature, three specimens were tested. The corresponding computational results yielded by the present FR SiC/SiC CMC materials-by-design approach are also given in Figures 10(a)-(b), but they are shown with line-connected black-filled symbols. Examination of the results displayed in Figures 10(a)-(b) reveals: (a) a relatively weak experimentally-measured temperature dependence of the four parameters characterizing the CMC stress-strain curve. It should be noted that the effect of temperature shown in these figures is associated with short-duration high-temperature exposure and does not include microstructural changes resulting from prolonged high-temperature exposure. As far as the computational results displayed in Figures 10(a)-(b) are concerned, they are temperature-invariant in accordance with the assumptions/approximations made in the current rendition of the FR SiC/SiC CMC materials-by-design methodology; and (b) a reasonable agreement between the experimental and computational results, considering the fact that the mechanical properties have been treated as being temperature-independent within the computational model.
Experimentally measured creep strain results as reported in [10], as a function of the exposure temperature, applied stress and exposure time are shown in the next to the last column of Table 1. The corresponding computational results for the creep strain obtained in the present work are depicted in the last column of this table. A comparison of the corresponding measured and calculated creep strains shown in Table 1, reveals a generally good agreement, over a relatively large range of exposure temperature applied stress and exposure time.
| Specimen ID | Test Temperature (°C) | Stress (MPa) | Exposure Time (h) | Creep Strain, measured (%) | Creep Strain, calculated (%) |
| 68-HN-11-10 | 1093 | 110 | 1000 | 0.17 | 0.174 |
| 68-HN-11-7 | 1093 | 125 | 91.1 | 0.21 | 0.205 |
| 68-HN-11-9 | 1093 | 125 | 140.6 | 0.20 | 0.204 |
| 68-HN-11-6 | 1093 | 150 | 0.021 | 0.24 | 0.251 |
| 68-HN-11-5 | 1093 | 165 | 0.040 | 0.44 | 0.452 |
| 68-HN-11-13 | 1204 | 110 | 1000 | 0.59 | 0.610 |
| 68-HN-11-11 | 1204 | 110 | 250 | 0.39 | 0.376 |
| 68-HN-11-8 | 1204 | 120 | 183.1 | 0.51 | 0.516 |
| 68-HN-11-3 | 1204 | 125 | 113.8 | 0.46 | 0.473 |
| 68-HN-11-12 | 1204 | 140 | 0.740 | 0.53 | 0.534 |
| 68-HN-11-4 | 1204 | 140 | 1.210 | 0.21 | 0.204 |
| 68-HN-11-2 | 1204 | 150 | 0.0006 | 0.16 | 0.158 |
Based on the findings reported in the previous subsection, it appears that the present FR SiC/SiC CMC materials-by-design methodology makes reliable predictions regarding the effect of the CMC-constituent processing parameters on the CMC material properties and performance, at least with respect to the low-rate (quasi-static) loading and high-temperature creep deformation.
In this section, the materials-by-design methodology developed, parameterized and validated in the previous sections of this manuscript, is used to identify changes in the FR SiC/SiC CMC-constituent process parameters which can enhance the properties and the performance of this material as a whole. The specific material properties targeted in the present case include: (a) three (first matrix-cracking stress, ultimate tensile strength, and strain to failure) of the four parameters characterizing the in-plane tensile test response of this class of materials. An increase in these three parameters gives rise to an increase in the material fracture toughness. It was found in our prior work [4] that an increase in fracture toughness substantially increases the ability of the CMCs to withstand impact by foreign objects ingested and accelerated by the gas turbine engine; and (b) the creep strain experienced by the CMC, subjected to a given combination of the exposure temperature, applied stress and exposure time. Excessive creep deformation, as demonstrated in our prior work [7,45] can compromise critical clearances within the gas-turbine engine hot section and give rise to initially, functional, and ultimately, structural failure of the CMC components.
To demonstrate the utility of the present materials-by-design approach, the following property/performance targets are defined and used as components of the vector-type objective function in the FR SiC/SiC CMC-constituent processing-parameter optimization procedure: (a) for each of the three tensile-test parameters identified above, the new target value should be maximum and at least 10% higher than the corresponding computational values depicted in Figures 10(a)-(b); and (b) the creep-strain data should be minimized but not higher than 90% of the corresponding computed values shown in the last column of Table 1.
To simplify the optimization procedure, a majority of the FR SiC/SiC CMC constituent processing and microstructural parameters as specified in Section 4, subsection entitled "FR SiC/SiC CMC under Investigation, " are kept unchanged. The only parameters from this subsection which were allowed to change and thus become design variables in the FR SiC/SiC CMC-constituent processing-parameter optimization procedure, include: (a) fiber volume fraction; (b) pyrolysis temperature for the fiber; (c) CVD temperature for Si3N4 coating; (d) CVD pressure for Si3N4 coating; and (e) molten Si temperature for the matrix.
Among the five design variables, the following two are assigned an upper bound: (a) fiber volume percent = 37, since at larger values of the fiber volume percent, problems may arise during the CMC-lamination process; and (b) CVD pressure = 0.008 atm, since at higher pressures, undesirable formation of Si3N4 within the gas phase or "sooting" takes place. No other upper or lower bounds or other constraints are applied to the five design variables.
The FR SiC/SiC CMC-constituent processing-parameter optimization procedure yielded the following optimal values of the design variables: (a) fiber volume percent = 36.1; (b) pyrolysis temperature for the fiber = 1315 K; (c) CVD temperature for Si3N4 coating = 985 K; (d) CVD pressure for Si3N4 coating = 0.025 atm; and (e) molten Si temperature for the matrix = 1695 K. The ratio of the first three components of the objective function to their counterparts depicted in Figures 10(a)-(b) are found to be as follows: (a) first matrix-cracking stress-1.11; (b) tensile strength-1.27; and (c) strain at failure-1.13. Since these ratios exceed the minimum target value of 1.1, the optimization procedure is successful relative to these three parameters characterizing the in-plane quasi-static response of the FR SiC/SiC CMC. As far as the remaining components of the objective function, i.e. the 12 components of the creep strain, are concerned, the ratio of their values yielded by the optimization procedure and the values listed in the last column of Table 1, is found to be no greater than 0.89. Since the objective of the present materials-by-design approach was to reduce creep strains by at least 10% relative to their computational counterparts given in the last column of Table 1, the present FR SiC/SiC CMC optimization procedure is found to be also successful with respect to meeting the more-stringent creep-resistance requirement.
The results reported in this subsection clearly demonstrate that the newly-developed materials-by-design methodology can be used to design FR SiC/SiC CMC with improved mechanical properties and performance. In addition, a detailed analysis of the results yielded by the optimization procedure can be used to gain a deeper insight into the complex processing/microstructure/property/performance inter-relationship in FR SiC/SiC CMCs. For example, a higher pyrolyzing temperature for the SiC-fiber precursor has been identified as being beneficial. Such a temperature gives rise to a coarser grain size and, hence, to a lower strength of the fiber. However, this strength-reducing effect is more than compensated by the strength-increasing effect, also brought about by the same increase in the fiber-pyrolyzing temperature, associated with a larger fraction of the amorphous SiC being converted into the crystalline SiC. At the same time, coarser grain size and a lower volume fraction of the amorphous phase in the fiber reduce the creep rate within the fiber, the fiber creep rate over the matrix creep rate ratio and, finally, the creep rate of the CMC. Similar explanations can be provided for optimal values of the remaining four design variables.
Based on the results obtained in the present work, the following main summary remarks and conclusions can be drawn:
1. The present work deals with a non-traditional approach to the development of new materials, the so-called materials-by-design approach. Within this approach, a material is treated as a complex hierarchical system, and its design and optimization is carried out by employing computer-aided engineering analyses, predictive tools and available material databases.
2. The materials-by-design methodology developed in the present work focuses on fiber-reinforced (FR) SiC/SiC ceramic matrix composites (CMCs), the type of materials which are currently being used in stationary components, and are considered for use in rotating components, of the hot sections of gas-turbine engines. Towards that end, a number of mathematical functions and numerical models are developed which relate CMC constituents' (fibers, fiber coating and matrix) microstructure and their properties to the properties and performance of the CMC as a whole.
3. The newly-developed materials-by-design approach is validated by comparing experimentally measured and computationally predicted CMC in-plane tensile and creep-deformation properties.
4. In the last portion of the present work, the newly-developed materials-by-design approach with an optimization procedure in order to determine the chemical makeup and processing routes for the CMC constituents so that the resulting in-plane tensile and creep-deformation properties of the resulting CMCs are increased to a preset target value.
The material presented in this paper is based on work supported by the National Aeronautics and Space Administration (NASA) research contract entitled "Development of Next-Generation Ceramic-Matrix Composites via the Materials-by-Design Approach, " Contract Number NNX15AL49H.
The authors declare that there is no conflict of interest regarding the publication of this manuscript.
| [1] | Office of Science (2014) Basic Energy Sciences, Core Research Activities, Department of Energy. Available from: http://science.energy.gov/~/media/bes/pdf/brochures/bes-cras/2014-feb/BES_CRAs_FEB2014.pdf (accessed June 17, 2016). |
| [2] | Luthra K (2014) Melt infiltrated SiC/SiC ceramic composites for industrial gas turbines and aircraft engines. GE Global Research Technical Report 2014GRC125. |
| [3] | Grujicic M, Galgalikar R, Ramaswami S, et al. (2015) Multi-physics modeling and simulations of reactive melt infiltration process used in fabrication of ceramic-matrix composites (CMCs). Multidiscip Mod Mater Struct 11: 43–74. |
| [4] | Grujicic M, Snipes JS, Yavari R, et al. (2015) Computational investigation of foreign object damage sustained by environmental barrier coatings (EBCs) and SiC/SiC ceramic-matrix composites (CMCs). Multidiscip Mod Mater Struct 11: 238–272. |
| [5] | Grujicic M, Snipes JS, Galgalikar R, et al. Multi-length-scale derivation of the room-temperature material constitutive model for SiC/SiC ceramic-matrix composites (CMCs). J Mater: Des Appl [in press], doi: 10.1177/1464420715600002. |
| [6] |
Grujicic M, Galgalikar R, Snipes JS, et al. (2016) Multi-length-scale material model for SiC/SiC ceramic-matrix composites (CMCs): inclusion of in-service environmental effects. J Mater Eng Perform 25: 199–219. doi: 10.1007/s11665-015-1850-1

|
| [7] |
Grujicic M, Galgalikar R, Snipes JS, et al. (2016) Material constitutive models for creep and rupture of SiC/SiC ceramic-matrix composites (CMCs) under multi-axial loading conditions. J Mater Eng Perform 25: 1697–1708. doi: 10.1007/s11665-016-2036-1

|
| [8] | Corman GS and Luthra KL (2006) Melt Infiltrated Ceramic Composites (HIPERCOMP®) For Gas Turbine Engine Applications, Continuous Fiber Ceramic Composites Program Phase II Final Report, Niskayuna, NY: GE Global Research, Technical Report DOE/CE/41000-2. |
| [9] |
Grujicic M, Yavari R, Snipes JS, et al. (2014) All-atom molecular-level computational analyses of polyurea/fused-silica interfacial decohesion caused by impinging tensile stress-waves. Int J Struct Integr 5: 339–367. doi: 10.1108/IJSI-01-2014-0001

|
| [10] | OSTP (2011) Materials genome initiative for global competitiveness. Washington, DC: Office of Science and Technology Policy. Available from: https://www.whitehouse.gov/sites/default/files/ microsites/ostp/materials_genome_initiative-final.pdf (accessed June 21, 2016). |
| [11] | Drosback M (2013) The Materials Genome Initiative and Materials Innovation Infrastructure (presentation). Washington, DC: Office of Science and Technology Policy. Available from: https://hubzero.org/resources/1167/download/Cyberinfrastructure_for_the_Materials_Genome_Initiative.pdf (accessed June 17, 2016). |
| [12] | Naserifar S, Liu L (2013) Toward a process-based molecular model of SiC membranes. Part 1. Development of a reactive force field. J Phys Chem C 117: 3308–3319. |
| [13] |
Grujicic M, Cao G, Singh R (2003) The effect of topological defects and oxygen adsorbates on the electronic transport properties of single-walled carbon nanotubes. Appl Surf Sci 211: 166–183. doi: 10.1016/S0169-4332(03)00224-1

|
| [14] |
Grujicic M, Cao G, Rao AM, et al. (2003) UV-light enhanced oxidation of carbon nanotubes through adsorption of polar molecules. Appl Surf Sci 214: 289–303. doi: 10.1016/S0169-4332(03)00361-1

|
| [15] | Accelrys Software Inc. (2011) Discover Datasheet. Accelrys Software Inc.. Available from: http://accelrys.com/products/datasheets/discover.pdf (accessed June 21, 2016). |
| [16] | Grujicic M, Megusar J, Erturk T (1986) Elastic moduli, yield stress and ductility of fully-crystallized Co84Nb10B6 metallic glass. Int J Rapid Solidif 2: 165–173. |
| [17] | Roewer G, Herzog U, Trommer K, et al. (2002) Silicon Carbide—A Survey of synthetic approaches, properties and applications, In: Jansen M, Ed., High Performance Non-Oxide Ceramics I, Berlin: Springer-Verlag, 59–135. |
| [18] | Monthioux M, Delverdier O (1996) Thermal behavior of (organosilicon) polymer-derived ceramics. V: Main facts and trends. J Eur Ceram Soc 16: 721–737. |
| [19] |
Grujicic M, Cao G, Gersten B (2002) An atomic-scale analysis of catalytically-assisted chemical vapor deposition of carbon nanotubes. Mater Sci Eng B 94: 247–259. doi: 10.1016/S0921-5107(02)00095-8

|
| [20] |
Grujicic M, Cao G, Gersten B (2002) Optimization of the chemical vapor deposition process for carbon nanotubes fabrication. Appl Surf Sci 191: 223–239. doi: 10.1016/S0169-4332(02)00210-6

|
| [21] |
Grujicic M, Cao G, Gersten B (2003) Reactor length-scale modeling of chemical vapor deposition of carbon nanotubes. J Mater Sci 38: 1819–1830. doi: 10.1023/A:1023252432202

|
| [22] |
Grujicic M, Lai SG (1999) Kinetic Monte Carlo modeling of chemical vapor deposition of (111) oriented diamond film. J Mater Sci 34: 7–20. doi: 10.1023/A:1004488818266

|
| [23] |
Grujicic M, Lai SG (2000) Multi length-scale modeling of CVD of diamond: Part I: A combined reactor scale/atomic-scale analysis. J Mater Sci 35: 5359–5369. doi: 10.1023/A:1004851029978

|
| [24] |
Grujicic M, Lai SG (2000) Multi length-scale modeling of CVD of diamond: Part II: A combined atomic-scale/grain-scale analysis. J Mater Sci 35: 5371–5381. doi: 10.1023/A:1004803114048

|
| [25] |
Grujicic M, Lai SG (2000) Grain-scale modeling of microstructure evolution in CVD-grown polycrystalline diamond films. J Mater Synth Proces 8: 73–85. doi: 10.1023/A:1026517919085

|
| [26] |
Grujicic M, Lai SG (2001) Multi length-scale modeling of CVD of titanium nitride coatings. J Mater Sci 36: 2937–2953. doi: 10.1023/A:1017958621586

|
| [27] | Gupte SM, Tsamopoulos JA (1990), An effective medium approach for modeling chemical vapor infiltration of porous ceramic materials. J Electrochem Soc 137: 1626–1638. |
| [28] |
Grujicic M, Cao G, Roy WN (2004) A computational analysis of the percolation threshold and the electrical conductivity of carbon nanotubes reinforced polymeric materials. J Mater Sci 39: 4441–4449. doi: 10.1023/B:JMSC.0000034136.11779.96

|
| [29] | Battaile CC, Srolovitz DJ, Butler JE (1991) Morphologies of diamond films from atomic-scale simulations of chemical vapor deposition. Diam Relat Mater 6: 1198–1206. |
| [30] | Kee RJ, Rupley FM, Miller JA (1989) Chemkin-II: A Fortran chemical kinetics package for the analysis of gas-phase chemical kinetics, Sandia National Laboratories Technical Report SAND89-8009. |
| [31] | Surface Chemkin III User Manual, Sandia National Laboratories, San Diego, CA, 1996. |
| [32] |
Battaile CC, Srolovitz DJ, Butler JE (1997) A kinetic Monte Carlo method for the atomic-scale simulation of chemical vapor deposition: application to diamond. J Appl Phys 82: 6293–6300. doi: 10.1063/1.366532

|
| [33] |
Grujicic M, Zhang Y (1998) Determination of effective elastic properties of functionally graded materials using Voronoi cell finite element method. Mater Sci Eng A 251: 64–76. doi: 10.1016/S0921-5093(98)00647-9

|
| [34] |
Grujicic M, Zhao H (1998) Optimization of 316 stainless steel/alumina functionally graded material for reduction of damage induced by thermal residual stresses. Mater Sci Eng A 252: 117–132. doi: 10.1016/S0921-5093(98)00618-2

|
| [35] |
Huang J, Fadel GM, Blouin VY et al. (2002) Bi-objective optimization design of functionally gradient materials. Mater Des 23: 657–666. doi: 10.1016/S0261-3069(02)00048-1

|
| [36] |
Richards LA (1931) Capillary conduction of liquids through porous mediums. Physics 1: 318–333. doi: 10.1063/1.1745010

|
| [37] |
Grujicic M, Cao G, Figliola RS (2001) Computer simulations of the evolution of solidification microstructure in the LENSTM rapid fabrication process. Appl Surf Sci 183: 43–57. doi: 10.1016/S0169-4332(01)00553-0

|
| [38] |
Miller RS, Cao G, Grujicic M (2001) Monte Carlo simulation of three-dimensional non-isothermal grain-microstructure evolution: application to LENS™ rapid fabrication. J Mater Synth Proces 9: 329–345. doi: 10.1023/A:1016304606563

|
| [39] |
Grujicic M, Cao G, Miller RS (2002) Computer modeling of the evolution of dendrite microstructure in binary alloys during non-isothermal solidification. J Mater Synth Proces 10: 191–203. doi: 10.1023/A:1023022214920

|
| [40] |
Grujicic M, Galgalikar R, Snipes JS, et al. (2013) Multi-physics modeling of the fabrication and dynamic performance of all-metal auxetic-hexagonal sandwich-structures. Mater Des 51: 113–130. doi: 10.1016/j.matdes.2013.04.004

|
| [41] |
Kruger P (1993) On the relation between non-isothermal and isothermal Kolmogorov-Johnson-Mehl-Avrami crystallization kinetics. J Phys Chem Solids 54: 1549–1555. doi: 10.1016/0022-3697(93)90349-V

|
| [42] |
Gore M, Grujicic M, Olson GB (1989) Thermally activated grain boundary motion through a dispersion of particles. Acta Metall 37: 2849–2854. doi: 10.1016/0001-6160(89)90320-9

|
| [43] |
Lifshitz IM, Slyozov VV (1961) The kinetics of precipitation from supersaturated solid solutions. J Phys Chem Solids 19: 35–50. doi: 10.1016/0022-3697(61)90054-3

|
| [44] | Grujicic M, Galgalikar R, Snipes JS, et al. Creep-behavior-based material selection for a clamping spring of ceramic-matrix composite inner-shroud in utility and industrial gas-turbine engines. J Mater: Des Appl [in press], doi: 10.1177/1464420715627658. |
| [45] |
Grujicic M, Galgalikar R, Ramaswami S, et al. (2016) Derivation, parameterization and validation of a creep deformation/rupture material constitutive model for SiC/SiC ceramic-matrix composites (CMCs). AIMS Mater Sci 3: 591–619. doi: 10.3934/matersci.2016.2.591

|
| [46] |
Grujicic M, Arokiaraj S (1993) Chemical compatibility between zirconia dispersion and gamma titanium aluminide matrix. Calphad 17: 133–140. doi: 10.1016/0364-5916(93)90013-2

|
| [47] |
Grujicic M, Arakere G, Bell WC, et al. (2010) Reliability-based design optimization for durability of ground-vehicle suspension-system components. J Mater Eng Perform 19: 301–313. doi: 10.1007/s11665-009-9482-y

|
| [48] |
Singhal SC (1976) Thermodynamic analysis of high-temperature stability of silicon nitride and silicon carbide. Ceramurgia Int 2: 123–130. doi: 10.1016/0390-5519(76)90022-3

|
| [49] |
Sundman B, Jansson B, Anderson JO (1985) The Thermo-Calc databank system. Calphad 9: 153–190. doi: 10.1016/0364-5916(85)90021-5

|
| [50] |
Borgenstam A, Engström A, Höglund L, et al. (2000) DICTRA, a tool for simulation of diffusional transformations in alloys. J Phase Equilib 21: 269–280. doi: 10.1361/105497100770340057

|
| [51] | TC-Prisma brochure (2013) Thermo-Calc Software. Available from: http://www.thermocalc.com/media/6026/tc-prisma-flyer-20130627.pdf (accessed June 21, 2016). |
| 1. | Jingyu Zhang, Shurong Ding, Mesoscale simulation research on the homogenized elasto-plastic behavior of FeCrAl alloys, 2020, 22, 23524928, 100718, 10.1016/j.mtcomm.2019.100718 |
| Specimen ID | Test Temperature (°C) | Stress (MPa) | Exposure Time (h) | Creep Strain, measured (%) | Creep Strain, calculated (%) |
| 68-HN-11-10 | 1093 | 110 | 1000 | 0.17 | 0.174 |
| 68-HN-11-7 | 1093 | 125 | 91.1 | 0.21 | 0.205 |
| 68-HN-11-9 | 1093 | 125 | 140.6 | 0.20 | 0.204 |
| 68-HN-11-6 | 1093 | 150 | 0.021 | 0.24 | 0.251 |
| 68-HN-11-5 | 1093 | 165 | 0.040 | 0.44 | 0.452 |
| 68-HN-11-13 | 1204 | 110 | 1000 | 0.59 | 0.610 |
| 68-HN-11-11 | 1204 | 110 | 250 | 0.39 | 0.376 |
| 68-HN-11-8 | 1204 | 120 | 183.1 | 0.51 | 0.516 |
| 68-HN-11-3 | 1204 | 125 | 113.8 | 0.46 | 0.473 |
| 68-HN-11-12 | 1204 | 140 | 0.740 | 0.53 | 0.534 |
| 68-HN-11-4 | 1204 | 140 | 1.210 | 0.21 | 0.204 |
| 68-HN-11-2 | 1204 | 150 | 0.0006 | 0.16 | 0.158 |
| Specimen ID | Test Temperature (°C) | Stress (MPa) | Exposure Time (h) | Creep Strain, measured (%) | Creep Strain, calculated (%) |
| 68-HN-11-10 | 1093 | 110 | 1000 | 0.17 | 0.174 |
| 68-HN-11-7 | 1093 | 125 | 91.1 | 0.21 | 0.205 |
| 68-HN-11-9 | 1093 | 125 | 140.6 | 0.20 | 0.204 |
| 68-HN-11-6 | 1093 | 150 | 0.021 | 0.24 | 0.251 |
| 68-HN-11-5 | 1093 | 165 | 0.040 | 0.44 | 0.452 |
| 68-HN-11-13 | 1204 | 110 | 1000 | 0.59 | 0.610 |
| 68-HN-11-11 | 1204 | 110 | 250 | 0.39 | 0.376 |
| 68-HN-11-8 | 1204 | 120 | 183.1 | 0.51 | 0.516 |
| 68-HN-11-3 | 1204 | 125 | 113.8 | 0.46 | 0.473 |
| 68-HN-11-12 | 1204 | 140 | 0.740 | 0.53 | 0.534 |
| 68-HN-11-4 | 1204 | 140 | 1.210 | 0.21 | 0.204 |
| 68-HN-11-2 | 1204 | 150 | 0.0006 | 0.16 | 0.158 |