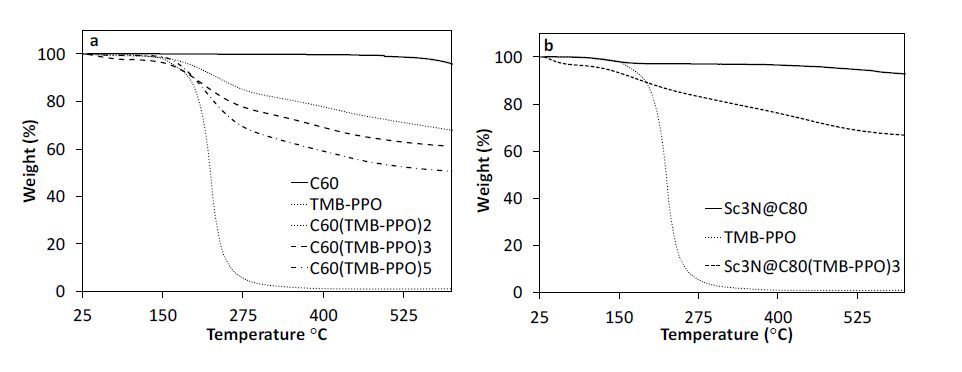
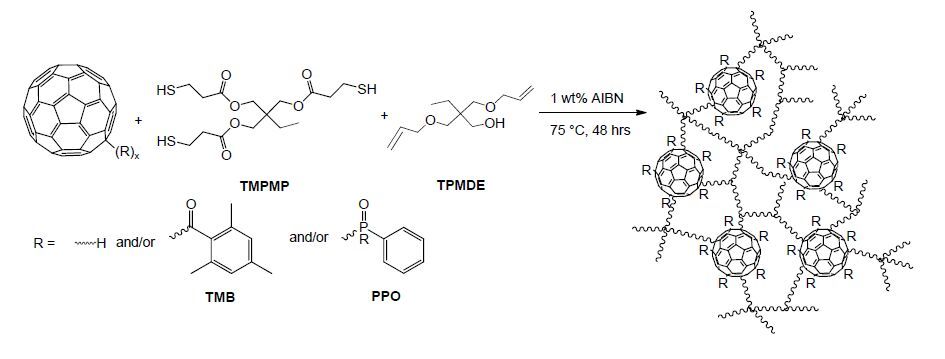
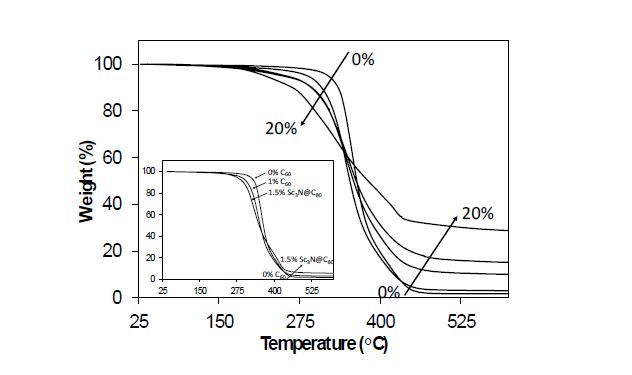
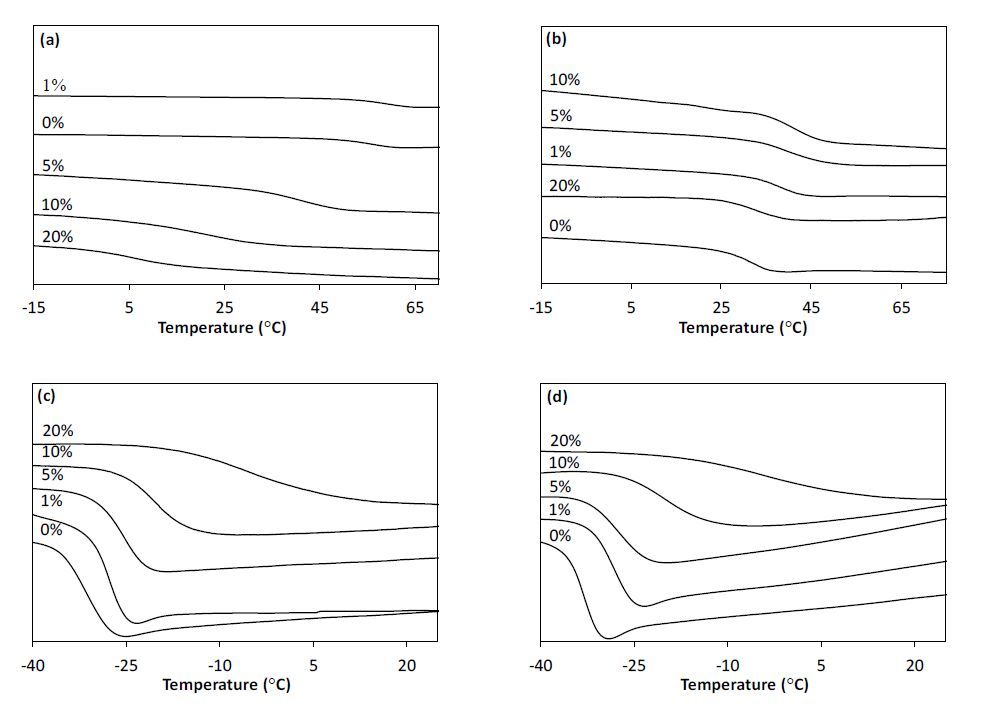
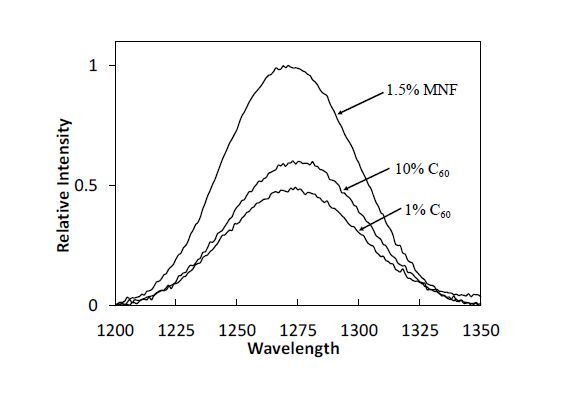
Numerous functionalization methods have been employed to increase the solubility, and therefore, the processability of fullerenes in composite structures, and of these radical addition reactions continue to be an important methodology. C60 and Sc3N@C80 derivatives were prepared via radical addition of the photodecomposition products from the commercial photoinitiator TMB-PPO, yielding C60(TMB-PPO)5 and Sc3N@C80(TMB-PPO)3 as preferred soluble derivatives obtained in high yields. Characterization of the mixture of isomers using standard techniques suggests an overall 1PPO:6TMB ratio of addends, reflecting the increased reactivity of the carbon radical. Although, a higher percentage of PPO is observed in the Sc3N@C80(TMB-PPO)3 population, perhaps due to reverse electronic requirements of the substrate. Visually dispersed thiol-ene nanocomposites with low extractables were prepared using two monomer compositions (PETMP:TTT and TMPMP:TMPDE) with increasing fullerene derivative loading to probe network structure-property relationships. Thermal stability of the derivatives and the resulting networks decreased with increased functionality and at high fullerene loadings, respectively. TMPMP:TMPDE composite networks show well-dispersed derivatives via TEM imaging, and increasing Tg’s with fullerene loading, as expected for the incorporation of a more rigid network component. PETMP:TTT composites show phase separation in TEM, which is supported by the observed Tg’s. Singlet oxygen generation of the derivatives decreases with increased functionality; however, this is compensated for by the tremendous increase in solubility in organic solvents and miscibility with monomers. Most importantly, singlet oxygen generation from the composites increased with fullerene derivative loading, with good photostability of the networks.
1.
Introduction
Spatial patterns are widespread in ecological and chemical systems, such as salt marshes [1,2,3], predator-prey systems [4,5,6], the Brusselator model [7,8,9], Sel'kov model [10,11], Lengyel-Epstein system [12,13] and Degn-Harrison system [14,15]. It was proposed that spatial patterns may unveil underlying mechanisms that drive ecological resilience, and may serve as signals for environmental changes in many ecological systems (see [16,17,18]). It is assumed that self-organization theory is of great significance in helping us to understand spatial patterns, which was first proposed by Alan Turing in his seminal work [19]. Mathematically, asymptotic dynamics, which corresponds to persistent patterns, has been intensively studied, and the underlying mechanism was proposed as scale-dependent alternation between facilitation and inhibitory interactions, also called scale-dependent feedback [20]. There are many interesting persistent patterns which have been discovered, such as stable fairy circles and ring type patterns ([21,22,23,24,25,26]). There also is an increasing recognition that dynamics on ecological time scales, called transient patterns, may be of some significance. The impermanence of transient patterns means that an ecological system in a transient state may change abruptly, even without any underlying change in environmental conditions, while the possibility of transient patterns implies that an ecological system may remain far from its asymptotic patterns for some period of time [27]. In a recent study conducted by Zhao et al. [28], transient fairy circles of S. alterniflora were observed in salt marsh pioneer zones in the Yangtze estuary north branch in eastern China coasts. The authors proposed that hydrogen sulfide (H2S) may serve as a feedback regulator to drive such transient fairy circles, and proposed the following mathematical model to demonstrate the sulfide feedback mechanism:
The plant biomass concentration at the location x and time t is denoted by P(x,t), where x is a point on the plane. Assume the plant population growth follows the Verhulst-Pearl logistic pattern with the intrinsic growth rate r and the carrying capacity K. The sulfide concentration is denoted by S(x,t). Organic matters including plant biomass in intertidal salt marshes can produce hydrogen sulfide (H2S). Assume the plant population produces hydrogen sulfide proportionally with the effective production rate ϵ. Hydrogen sulfide is toxic to plants and can lead plants to die off. It was assumed that the loss of plants is to increase with an increase of the sulfide concentration and plant biomass, represented by cPS. As field studies about salt marsh plant species S. mariqueter and S. alterniflora show that plant lateral expansion through vegetative growth can be described by random walk, the diffusion process without drifts was employed to model plant dispersal with diffusion coefficient DP. DS is the planar dispersion rate of the sulfide concentration. In addition, plants produce dissolved organic carbon which promote bioactivities of sulfate-reducing bacteria which, in turn, promote sulfide enrichment. This effect is represented by the term ksP(x,t)+ks. The parameter d is the maximum escape rate of sulfide through the mud-air interface. The parameter ξ is dimensionless, which controls the time scale between the plant biomass and sulfide concentration. For a more detailed description of the model (1.1), we refer the reader to [28,29,30]. The conclusion of the study [28] is that transient fairy circle patterns in intertidal salt marshes can both infer the underlying ecological mechanisms and provide a measure of ecosystem resilience.
In this study, we would like to investigate how the self-correcting mechanism of the plant population influence transient patterns of fairy circles in salt marshes. For a single population growth, Hutchinson considered that for K−PK formally describing a self-regulatory mechanism, the only formal conditions that must be imposed on the biologically possible mechanism is that they operate so rapidly that the lag, τ, is negligible between t when any given value of P is reached, and the establishment of the appropriately corrected value of the effective reproductive rate rK−PK [31]. Now, we would like to consider the "negligible time lag" for the plant population. It should be noticed that the time lag may not be negligible since different populations may have different growth properties. Particularly, for plant populations within constricted environments, the self-correcting adjustment with time lag may be necessary for understanding the underlying ecological mechanisms. Thus, the time delay will be incorporated in the self-regulatory mechanism. That is, the logistic growth term rP(x,t)(1−P(x,t)K) for the plant population will be replaced by rP(x,t)(1−P(x,t−τ)K). Thus, we will have a delayed plant-sulfide feedback model as follows:
For simplicity, we introduce the following non-dimensional variables
Dropping the hats of ˆt and ˆτ, we get the system with Neumann boundary conditions and initial conditions as follows
where ν is the outward unit normal vector on ∂Ω.
The aim of this article is to conduct a detailed analysis about the effect of the time delay on the dynamics of the system (1.3). Our analysis shows that there is a critical value of the time delay. When the time delay is greater than the critical value, the system will have temporal periodic solutions. Since there are no analytical methods to study transient patterns yet, we will use numerical simulations to study transient patterns. We show that there are transient fairy circles for any time delay. However, there are different types of fairy circles and rings occurring in this system.
The rest of this paper is organized as follows. In Section 2, we mainly study the stability of the positive steady state of the system (1.3) by discussing the distribution of the eigenvalues, and give the sufficient conditions for the occurrence of Hopf bifurcations induced by the time delay. In Section 3, by using the center manifold theory and normal form theory for partial differential equations, we analyze the properties of Hopf bifurcations, and obtain the formulas determining the direction of Hopf bifurcation and stability of bifurcating periodic solutions. In Section 4, we conduct numerical studies to demonstrate transient patterns, and give some simulations to illustrate our theoretical results. The paper is closed with a brief discussion.
2.
Stability and Hopf bifurcation
Clearly, the system (1.3) has two nonnegative constant steady states: E0=(0,0) and E∗=(u∗,v∗), where
We claim that 0<u∗<k. In fact,
Notice that a,b,k>0, and we can obtain that E∗=(u∗,v∗) is the unique positive steady state of the system (1.3).
Let Ω⊂R2 be a bounded domain with smooth boundary ∂Ω, and denote
In the phase space C=C([−τ,0],X), we can rewrite the system (1.3) as
where D=diag(d1,d2), Ut(⋅)=U(t+⋅), and F:C→X is defined by
By calculation, we have the linearization of system (2.1) at E∗, which can be written as
where L:C→X is given by
and
Let
be all the eigenvalues of the operator −Δ on Ω with the Neumann boundary conditions. Using the techniques in [32], we obtain that the characteristic equation of the system (2.2) can be expressed as
where I2 is the 2×2 identity matrix and Qn=μndiag(d1,d2). That is, each eigenvalue λ should satisfy the equation as follows
where
When τ=0, the characteristic equation (2.4) becomes
We give the following conclusion about the stability of the positive steady state E∗ as τ=0.
Theorem 2.1. When τ=0, all of the roots of the Eq (2.4) have negative real parts. That is, the positive steady state E∗ of the system (1.3) without delay is locally asymptotically stable.
Proof. If Tn+B>0,Dn+Mn>0 for all n∈N0, then all roots of the Eq (2.5) have negative real parts. By calculation, we have that 0<u∗<k and v∗>0. Recall that k>0,a>0, and b>0, we can get
for any n∈N. So, we complete the proof.
In the following, we will study the effect of delay on the stability of E∗. Recall that Dn+Mn>0 for any n∈N0, we can see that 0 is not the root of (2.4). Now, we will check whether there exist the critical values of τ such that (2.4) has a pair of simple purely imaginary eigenvalues for some n∈N0. Let ±iω(ω>0) be the solutions of the (n+1)-th Eq (2.4), then we get
Separating the real and imaginary parts, and we obtain that ω and τ should satisfy
It yields
where
Denote Z=ω2, and then (2.7) becomes
(2.9) has two roots:
From the proof of Theorem 2.1, we get Dn+Mn>0 for any n∈N. So, the sign of D2n−M2n is the same to that of
To study the existence of positive roots of (2.9), we only need to discuss the sign of Dn−Mn, T2n−B2−2Dn, and (T2n−B2)(T2n−B2−4Dn)+4M2n. It is not difficult to get the following Lemma.
Lemma 2.2. For the Eq (2.9), the following conclusions hold.
1) If T2n−B2−2Dn>0 and Dn−Mn>0 or (T2n−B2)(T2n−B2−4Dn)+4M2n<0 for any n∈N0, then the Eq (2.9) has no positive root.
2) If there exists some n∈N0 such that Dn−Mn<0, then the Eq (2.9) has a positive root Z+n.
3) If there exists some n∈N0 such that T2n−B2−2Dn<0, Dn−Mn>0, and (T2n−B2)(T2n−B2−4Dn)+4M2n≥0, then the Eq (2.9) has two positive roots Z±n.
Next, we discuss some sufficient conditions for Lemma 2.2 to hold. Using the first equation of (2.8), we have
It is easy to see that T20−B2−2D0>0 when
holds. Similarly, we can get from (2.10) that D0−M0>0 provided that
To illustrate the existence of positive roots of the Eq (2.9), we mainly study three cases as follows.
Case Ⅰ: b>b_. If b>b_, we can obtain that D0−M0<0. It is easy to see that Dn−Mn→∞ as n→∞. So there must exist a N∈N such that Dn−Mn<0 for n<N and Dn−Mn≥0 for n≥N. From Lemma 2.2, we know that the Eq (2.9) has positive roots Z+n for n<N.
Case Ⅱ: u∗(1+u∗)d2kd1<b<min{b_,¯b}. If b<b_, then D20−M20>0. Furthermore, we can obtain from (2.10) that D2n−M2n>0 for any n∈N0 when b>u∗(1+u∗)d2kd1. Notice that T20−B2−2D20<0 when b<¯b, and then from (2.8), we know that there exists some N1∈N such that T2n−B2−2D2n<0 for n<N1, and T2n−B2−2D2n≥0 for n≥N1. Through calculation, we can obtain
where
Notice that limn→∞(T2n−B2)(T2n−B2−4Dn)+4M2n=∞, and we can find a N2∈N such that (T2n−B2)(T2n−B2−4Dn)+4M2n≥0 for n≥N2. Therefore, when N2<N1 and u∗(1+u∗)d2kd1<b<min{b_,¯b} are satisfied, the Eq (2.9) has two positive roots Z±n for N2≤n<N1. Otherwise, the Eq (2.9) does not have a positive root for any n∈N0.
Case Ⅲ: max{¯b,u∗d2(1+u∗)kd1}<b<b_. We have from Case Ⅰ and Case Ⅱ that D2n−M2n>0 and T2n−B2−2D2n>0 for any n∈N0 when max{¯b,u∗d2(1+u∗)kd1}<b<b_. Therefore, the Eq (2.9) has no positive root as max{¯b,u∗d2(1+u∗)kd1}<b<b_.
Combining Lemma 2.2 with the above analysis, we have the following result.
Corollary 2.3. Denote D1={n∈N0|T2n−B2−2D2n<0}, D2={n∈N0|(T2n−B2)(T2n−B2−4Dn)+4M2n≥0}, ω±n=√Z±n.
1) If b>b_, then there exists some N∈N0 such that the Eq (2.7) has a positive root ω+n for n<N.
2) If u∗(1+u∗)d2kd1<b<min{b_,¯b} and D1⋂D2≠∅, then the Eq (2.7) has two positive roots ω±n for n∈D1⋂D2.
3)If max{¯b,u∗(1+u∗)d2kd1}<b<b_, or u∗(1+u∗)d2kd1<b<min{b_,¯b} and D1⋂D2=∅, then the Eq (2.7) has no positive roots for any n∈N0.
For simplicity, we define the following set
It is easy to see that Eq (2.7) has a pair of positive roots ω±n for n∈Γ⊂N0. Then the Eq (2.4) has a pair of purely imaginary roots ±iω±n when τ takes the critical values τ±n,j, which can be determined from (2.6), given by
for j∈N0. Let λ(τ)=α(τ)+iω(τ) be the root of (2.4) satisfying Reλ(τ±n,j)=0 and Imλ(τ±n,j)=ω±n.
Lemma 2.4. Assume that the condition 2 or 3 of Lemma 2.2 holds, then
1) Reλ′(τ±n,j)=0, when (T2n−B2)(T2n−B2−4Dn)+4M2n=0.
2) Reλ′(τ+n,j)>0, Reλ′(τ−n,j)<0, when (T2n−B2)(T2n−B2−4Dn)+4M2n>0.
Proof. Differentiating the two sides of the Eq (2.4) with respect to τ, we have
Thus,
Following the techniques in Cooke and Grossman [33], and using the Eqs (2.4) and (2.6), we obtain that
Note that
and we can complete the proof.
Combining Theorem 2.1 and Lemma 2.4, we have that τ+n,0<τ−n,0 holds true for n∈Γ. Then, we define the smallest critical value such that the stability of E∗ will change, which can be given by
Combined the above analysis with Corollary 2.4 in Ruan & Wei [34], we know that all of the roots of (2.4) have negative real parts when τ∈[0,τ∗), and the (n+1)-th equation of (2.4) has a pair of simply purely imaginary roots when τ=τ±n,j. Moreover, we see that (2.4) has at least one pair of conjugate complex roots with positive real parts when τ>τ∗. Based on the above discussion, we can obtain the following conclusion about the stability of E∗.
Theorem 2.5. For τ∗ defined in (2.15), the following statements about system (1.3) hold true.
1) If T2n−B2−2Dn>0 and Dn−Mn>0 or (T2n−B2)(T2n−B2−4Dn)+4M2n<0 hold for any n∈N0, then the positive steady state E∗ is locally asymptotically stable for any τ≥0.
2) If Dn−Mn<0 holds for some n∈N0, then
(a) the positive steady state E∗ is locally asymptotically stable for τ∈[0,τ∗), and unstable for τ>τ∗.
(b) the system (1.3) undergoes a Hopf bifurcation at E∗ when τ=τ+n,j for j∈N0.
3) If T2n−B2−2Dn<0, Dn−Mn>0, and (T2n−B2)(T2n−B2−4Dn)+4M2n>0 hold for some n∈N0, then the positive steady state E∗ is locally asymptotically stable for τ∈[0,τ∗). Moreover, the system (1.3) undergoes a Hopf bifurcation at E∗ when τ=τ±n,j for j∈N0, where τ±n,j is defined in (2.14).
Remark 2.6. From Lemma 2.4 and Theorem 2.5, we have that
provided that T2n−B2−2Dn<0, Dn−Mn>0, and (T2n−B2)(T2n−B2−4Dn)+4M2n>0 are satisfied. In this case, the stability switch may exist.
3.
Stability and direction of the Hopf bifurcations
In this section, we study the stability and direction of the Hopf bifurcations by applying the center manifold theorem and the normal formal theory of partial functional differential equations [32,35]. First, the system (1.3) can be represented as an abstract ODE system. Second, on the center manifold of the ODE system corresponding to E∗, the normal form or Taylor expansion of the ODE system will be computed. Then, using the techniques in [36], the coefficients of the first 4 terms of the normal form will reveal all the properties of the periodical solutions. These analytical results will also be used in numerical studies.
In this section, we choose Ω=[0,lπ]×[0,lπ]. To write the system (1.3) as an ODE system, we define a function space
where u1(⋅,t)=u(⋅,τt)−u∗,u2(⋅,t)=v(⋅,τt)−v∗, and U(t)=(u1(⋅,t),u2(⋅,t))T. Then the system (1.3) can be written as
in the function space C=C([−1,0],X), where D=diag(d1,d2), L(τ)(⋅):C→X and f:C×RC→X are given, respectively, by
with
f1(φ,τ)=a1φ1(0)φ2(0)+a2φ1(0)φ1(−1),
f2(φ,τ)=a3φ21(0)+a4φ1(0)φ2(0)+a5φ31(0)+a6φ21(0)φ2(0)+O(4),
for φ=(φ1,φ2)T∈C,
where
Let τ=τ∗+μ, and then (3.1) can be rewritten as
where
for φ∈C.
From the analysis in Section 2, we know that system (3.2) undergoes Hopf bifurcation at the equilibrium (0,0) when μ=0 (i.e., τ=τ∗). We assume that when μn0=j20+k20l2, (2.4) has roots ±iω∗ as τ=τ∗. Moreover, we also have that ±iω∗τ∗ are simply purely imaginary eigenvalues of the linearized system of (3.2) at the origin:
as μ=0 and all other eigenvalues of (3.3) at μ=0 have negative real parts.
The eigenvalues of τDΔ on X are −τd1j2+k2l2 and −τd2j2+k2l2,j,k∈N0, with corresponding eigenfunctions β1j,k(x)=(γj,k(x),0)T and β2j,k(x)=(0,γj,k(x))T, where x=(x1,x2), γj,k(x)=cosjx1lcoskx2l√∫lπ0cos2jx1ldx1∫lπ0cos2kx2ldx2.
We define a space as Mj,k=span{⟨φ,βij,k⟩βij,k:φ∈C,i=1,2},j,k∈N0, and the inner product ⟨⋅,⋅⟩ is defined by
Then, on Mj,k, the Eq (3.3) is equivalent to the ODE on R2:
Now, we compute the normal form in the center manifold. There are several steps. We first compute eigenvectors of the infinitesimal generator of the semigroup defined by the linearized system at τ=τ∗. From the Riesz representation theorem, there exists a bounded variation function ηj,k(μ,θ) for θ∈[−1,0], such that
for φ∈C([−1,0],R2). In fact, we can choose
Let A denote the infinitesimal generator of the semigroup defined by (3.4) with μ=0,j=j0,k=k0 and A∗ denote the formal adjoint of A under the bilinear form
for ϕ∈C([−1,0],R2) and ψ∈C([0,1],R2T). Then, we know that ±iω∗τ∗ are simply purely imaginary eigenvalues of A, and they are also eigenvalues of A∗. By direct computations, we get q(θ)=q(0)eiω∗τ∗θ=(1,q1)Teiω∗τ∗θ(θ∈[−1,0]) is eigenvector of A corresponding to iω∗τ∗, where
Similarly, we have q∗(s)=e−iω∗τ∗s(1,q2)(s∈[0,1]) is eigenvector of A∗ corresponding to iω∗τ∗, where
Let Φ=(Φ1,Φ2)=(Req,Imq) and Ψ∗=(Ψ∗1,Ψ∗2)T=(Req∗,Imq∗)T. Denote
where
Let Ψ=(Ψ1,Ψ2)T=(Ψ∗,Φ)−1j0,k0Ψ∗, (Ψ,Φ)j0,k0=I2, and I2 is a 2×2 identity matrix.
We now write the reduced equation on the center manifold. The center subspace of linear equation (3.3) with μ=0 is given by PCNC, where
with βj0,k0=(β1j0,k0,β2j0,k0) and c⋅βj0,k0=c1β1j0,k0+c2β2j0,k0 for c=(c1,c2)T∈C. Let PSC denote the stable subspace of linear equation (3.3) with μ=0, and then C=PCNC⨁PSC.
Using the decomposition C=PCNC⨁PSC and following [32], the flow of (3.2) with μ=0 in the center manifold is given by the following formulae:
with h(0,0,0)=0 and Dh(0,0,0)=0.
Let us write the reduced equation in complex form. Set z=y1−iy2 and Ψ(0)=(Ψ1(0),Ψ2(0))T, and then q=Φ1+iΦ2 and Φ(y1(t),y2(t))T⋅βj0,k0=(qz+¯q¯z)⋅βj0,k0/2. Thus, (3.7) can be written as
where
From (3.8) and (3.9), we obtain that z satisfies
where
Now, let us compute g(z,¯z). Set
Let (ψ1,ψ2)=Ψ1(0)−iΨ2(0). From (3.7), (3.9) and (3.10), we can get the following quantities:
and
To obtain g21, we need to compute w11 and w20. The calculation of w11 and w20 is somewhat tedious. Let AU denote the generator of the semigroup generated by the linear system (3.3) with μ=0. From (3.9) and (3.10), we have
where
Let
Furthermore, by comparing the coefficients, we obtain that
By using the chain rule,
and we obtain, from (3.11) and (3.12), that
As 2iω∗τ∗ and 0 are not characteristic values of (3.3), (3.14) has unique solutions w20 and w11 in PSC, given by
Using the definition of AU, we get, from the first equation (3.13) and (3.14), that for θ∈[−1,0],
Therefore
where E is a 2-dimensional vector in X. According to the definition of βij,k(i=1,2) and q(θ)(θ∈[−1,0]), we have
From (3.14), we get that
Representing E and fz2 by series:
We get from (3.16) that
So, Ej,k could be calculated by
where
with
Similarly, we get
where
with
Then, the coefficient g21 is completely determined.
Let λ(τ)=α(τ)+iω(τ) denote the eigenvalues of (3.3). Thus we can compute the following quantities:
According to the Hopf bifurcation theory (see [36]), we write our derivation as a theorem which is well-known.
Theorem 3.1. The quantity μ2 determines the direction of the Hopf bifurcation (forward if μ2>0, backward if μ2<0). The quantity β2 determines the stability of the bifurcating periodic solutions (stable if β2<0, unstable if β2>0). The quantity T2 determines the period of the bifurcating periodic solutions (the period increases if T2>0, decreases if T2<0).
4.
Numerical studies
In this section, we perform two sets of numerical studies. According to theoretical derivations in the previous sections, we choose parameter values to produce numerical simulations. We observe several different shapes of transient fairy circles, and stable temporal periodic solutions.
Example 4.1. We choose x=(x1,x2)∈Ω=[0,2π]×[0,2π],d1=1,d2=3,a=0.1,b=0.4,k=1. This set of parameters satisfies Case Ⅰ of Section 2. Through calculation, we get E∗(0.7016,0.2984), and only for
(2.4) has pure roots ±iω+n,n=0,1,2, where
and the corresponding bifurcation values τ+k,j are
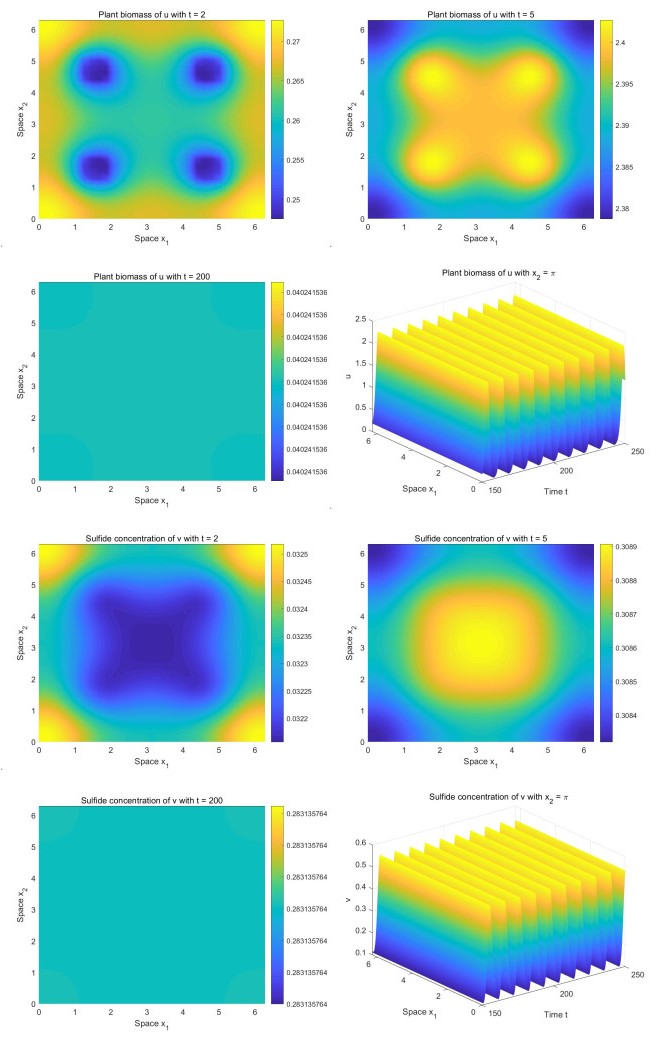
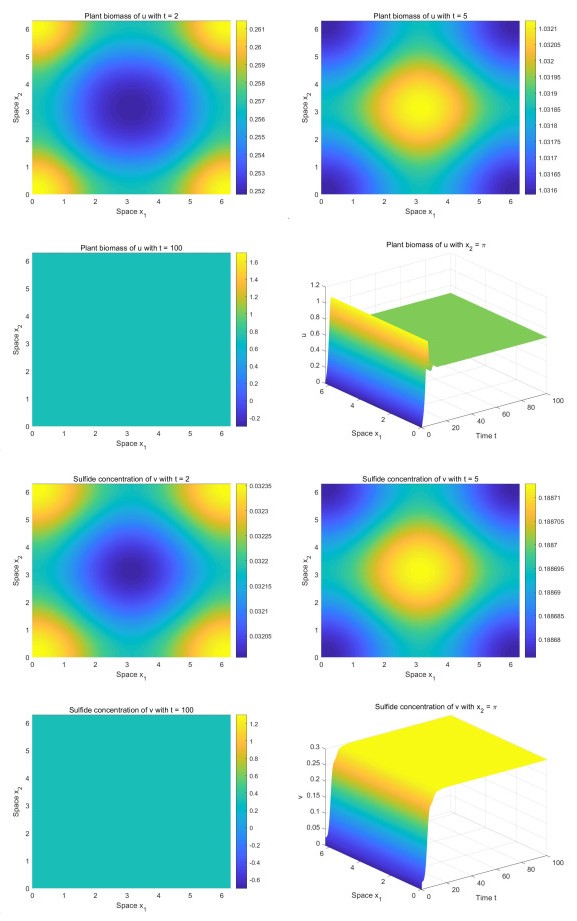
respectively. When τ<τ∗=1.9885, the positive equilibrium E∗(0.7016,0.2984) of (1.3) is asymptotically stable (see Figure 1). Before the system reaches this stable equilibrium solution, there are transient fairy circles. The plant population and sulfide concentration have similar-shaped fairy circles.
By the formulas derived in the previous section, we get c1(0)≈−0.5506+1.3320i. Because Rec1(0)<0, we know that when τ>τ∗=1.9885, there exist orbitally stable periodic solutions (see Figure 2). We observe that there are transient fairy circles before the system tends to stable periodic solutions. However, the shapes of the fairy circles for the plant population and sulfide concentration are different. In the numerical simulations for Figures 1 and 2, the initial conditions are
for t∈[−τ,0].
Example 4.2. We choose x=(x1,x2)∈Ω=[0,2π]×[0,2π],d1=0.5,d2=0.1,a=0.2,b=0.2,k=1. This set of parameters satisfies Case Ⅱ of Section 2. Through calculation, we get E∗(0.4142,0.5858), and only for
(2.4) has pure roots ±iω±n,n=0,1,2, where
and the corresponding bifurcation values τ+k,j are
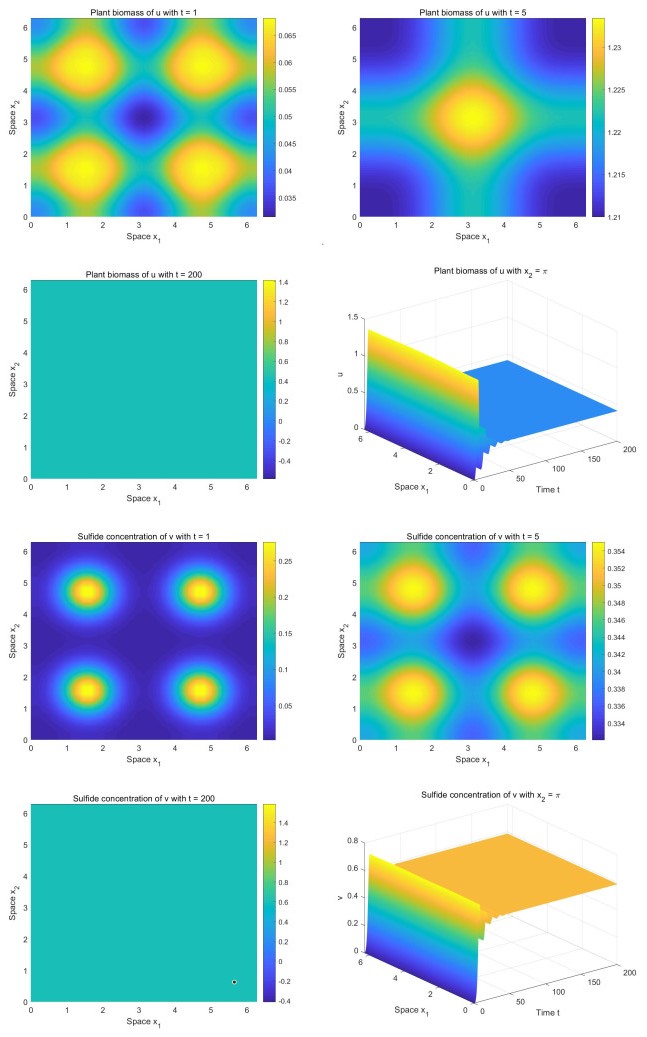
respectively. When τ<τ∗=2.8577, the positive equilibrium E∗(0.7016,0.2984) of (1.3) is asymptotically stable (see Figure 3). We observe that there are transient fairy circles before the system reaches the stable equilibrium point. The shapes of the fairy circles for the plant population and sulfide concentration are different.
By the formulas derived in the previous section, we get c1(0)≈−1.3262+1.2114i. Because Rec1(0)<0, we know that when τ>τ∗=2.8577, there exist orbitally stable periodic solutions (see Figure 4). We observe that there are transient fairy circles. The shapes of the fairy circles for the plant population and that for the sulfide concentration are the same as that in the equilibrium point case, respectively, although the shapes of the fairy circles for the plant population and sulfide concentration are different. In the numerical simulations for Figures 3 and 4, the initial conditions are
for t∈[−τ,0].
5.
Discussion
Transient spatial patterns in ecosystems have gained more attention in recent research. Several mathematical models were proposed to understand fairy circles and rings observed in salt marshes. One conclusion drawn from this research was that transient fairy circle patterns can infer the underlying ecological mechanisms and provide a measure of resilience of salt marsh ecosystems. The underlying mechanism proposed was plant-sulfide feedbacks instead of scale-dependent feedbacks. It is assumed that any population of a species in a location has a self-regulatory mechanism, and the time of mechanism action has some time lag. In this research, we consider how the time delay in the self-regulatory mechanism influences fairy circle formations in plant-sulfide feedbacks. Based on a mathematical model [28], we proposed a delay plant-sulfide feedback system. We performed a detailed investigation of the plant-sulfide feedback system subject to Neumann boundary conditions, and identified the parameter ranges of stability of the positive equilibrium and the existence of Hopf bifurcation. There is a critical value of the time delay. When the time delay is smaller than the critical value, the system will approach the spatial homogeneous equilibrium state asymptotically. At the critical value, Hopf bifurcations occur. When the time delay is greater than the critical value, the system will have temporal periodic solutions. Since we do not have any method to analyze transient patterns yet, we numerically demonstrated that there always are transient fairy circles for any time delay. We also found that there are different shapes of fairy circles or rings. This confirms that transient fairy circle patterns in intertidal salt marshes can infer the underlying ecological mechanisms and provide a measure for ecosystem resilience.
In [28], simulations were conducted with several points as initial values, and several circles progressed to one circle and to a uniform distribution. It is easy to see that the number and shape of fairy circles may depend on initial values. In our numerical study, we observed several different patterns of transient fairy circles. The number and shape of these fairy circles seem also to depend on initial distributions. This may be reasonable in reality since a natural species population usually starts with various situations and then progresses to its asymptotical patterns.
It is conventional that a natural population will obey the self-regulatory mechanism which is different from the scale-dependent feedback mechanism. The scale-dependent feedback mechanism assumes that scale-dependent feedbacks between localized facilitation and large-scale inhibition induce spatial self-organization. The self-regulatory mechanism assumes that the population growth rate is limited by its total population. The former may be considered as a special case of the latter. However, when mathematical models are constructed for those mechanisms, different terms should be taken in the equations. This is the reason we incorporate the self-regulatory mechanism with time delay to the plant-sulfide feedback mechanism.
In [28], two additional models, the nutrient depletion model and scale-dependent model, were also proposed to explain transient fairy circle patterns. We may consider to study time delayed versions of those models in order to compare how different mechanisms with natural time delay influence transient spatial patterns in the future.
In general, it is difficult to characterize transient patterns in dynamical systems. One direction to attempt may be time-transformation. Given that we want to know the dynamics of a system during a finite period of time, we make a time-transformation that changes this finite period of time to infinity, and then study the transformed system. However, it is required that the time period is given. It seems that we need to develop new analytical tools for transient patterns. This is an interesting mathematical question in dynamical systems for the future.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgment
This research is supported by the National Natural Science Foundation of China (Nos.11901172, 12271144) and Fundamental Research Fund for Heilongjiang Provincial Colleges and Universities (Nos. 2021-KYYWF-0017, 2022-KYYWF-1043).
Conflict of interest
The authors declare that there is no conflict of interest.









 DownLoad:
DownLoad: