1. Introduction

Two main families of methods exist to model failure of quasi-brittle structures. One is based on crack models, another one uses continuous damage approach that leads to a local loss of stiffness. Initiation of crack can be investigated using Griffith law an a criterion of global stability as proposed in ^[1], but fracture mechanics is generally not sufficient to model the full scenario of the degradation of Omegaids. Another point of view is adopted here based on damage modelling.

The full scenario of the degradation of Omegaids under mechanical loading is described by modelling the gradual loss of rigidity. This common approach is purely local. Generally local damage induces localization. Several models were proposed to avoid spurious localization: non local approaches and higher order, damage based, gradient models. These approaches are compared in ^[2]. Other new approaches are also proposed, the phase field approach ^[3] and the so-called variational approach ^[4].

Another way to describe the damage evolution is to consider the propagation of the surface separating the sound material and damaged material, as proposed for brittle material in ^[5,6]. This point of view is adopted here.

The propagation of surface inside a body is analysed. The moving surface here is associated with a change of mechanical properties. This framework is used to describe damage or phase transformation. Variational formulations were performed to describe the evolution of the surface between undamaged and damaged material. Connection with the notion of configurational forces can be made ^[7]. When this surface is moving, a flux of matter is induced, that is useful for describing the loss of material during wear mechanisms or brittle fracture ^[8].

For elastic brittle material the evolution of the interface separating the undamaged material ($d=0$) from the total damaged ($d=1$) have been studied using an energetic description of the propagation of damage ^[9,10]. In this description the damage parameter jumps from 0 to 1.

The interface has no thickness and mechanical quantities present strong discontinuities. The evolution in terms of rate of displacement and velocity of propagation of the surface is governed by a variational inequality. Criteria of stability and uniqueness have been established. For example, nucleation of defects in this modelling can be considered as a bifurcation of equilibrium solution ^[11]. Description of moving interfaces and of moving layers is also a manner for studying loss of material. Such a description of thin or thick layers permits to describe complex processes of wear contact between two bodies in relative motion ^[8,12]. In a more recent paper ^[13], the transition between undamaged material to damaged material is continuous through a layer of finite thickness. The evolution of damage is then associated to a moving layer.

Two cases have been considered: the propagation of a interface and the propagation of a moving layer of finite thickness.

For sharp interface, the transition zone is very thin, the damage parameter has a discontinuity, it jumps from 0 to 1. The driving force associated to the propagation of the interface is a local release rate of energy $G(s)$ as in ^[14]. Moreover, stability and non bifurcation conditions of the evolution are given when a normality rule based on $G(s)$ governs the propagation of the interface. When an additional surface energy is considered along the interface, the propagation is more stable ^[15].

For a moving layer, the transition is more regular. The thickness of the transition provides a length scale in the model. For specific definition of the damage, a local condition of steady state is induced and a generalisation of the local energy release rate is obtained. This is the driving force associated to the motion of surface separating the sound material from the damage one.

The main ideas of the model is to consider that the strain energy changes from a sound material to a damaged one depending on a damage parameter, which is continuous or not, and to describe the motion of the interface by a complementary law. For particular description, the motion of the interface induces a dissipation depending on an energy release rate. A normality rule is then proposed to govern the propagation of the interface based on this mechanical quantities. This choice generalizes classical Griffith's law.

The purpose of this article is to describe the motion of a surface or interface, to propose an evolution law for this motion in terms of the local energy release rate. The rate boundary value problem is then analysed and conditions of stability and bifurcation are given. Some applications and comments of this modelling are proposed in the last section.

---

2. General Preliminaries

Consider a body $\Omega$. The external boundary $\partial {\Omega _{\text{}}}$ is decomposed in two complementary parts: $\partial {\Omega _{\text{u}}}$ where the displacement $\underline u$ is prescribed $\underline u ^d(t)$ and $\partial {\Omega _{\text{T}}}$ where the loading $\underline T ^d(t)$ is applied: $\partial \Omega {\text{ = }}\partial {\Omega _{\text{u}}} \cup \partial {\Omega _{\text{T}}}, \;\;\;\, \emptyset {\text{ = }}\partial {\Omega _{\text{u}}} \cap \partial {\Omega _{\text{T}}}$. The displacement $\underline u$ is continuous across the surface ${\Gamma _o}$, separating the undamaged material and the damaged material. The internal state of stress $\sigma$ is such that the stress vector is also continuous along the surface ${\Gamma _o}$. Then we have the relations of continuity:

$\left[\underline u \right]=0, \quad \left[\sigma \right].\underline v=0,$

(1)

where $\underline v$ is the normal vector to the interface. When the surface is moving, these conditions must be preserved.

---

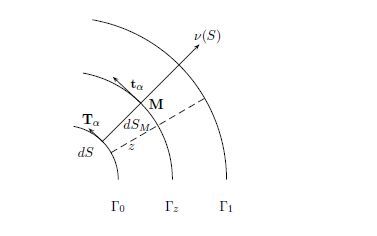
2.1. The geometry of a surface

Consider the surface ${\Gamma _o}$ separating the sound material from the damaged material. The surface is parametrized by two parameters $s^\alpha$. For M_o on the surface, the tangent space is determined by the local basis $\underline T_\alpha$. The normal vector to the tangent space is $\underline v$. Then we have

${{\underline{T}}_{\alpha }}=\frac{\partial {{M}_{o}}}{{{\partial }_{s}}^{\alpha }}={{\nabla }_{\alpha }}{{M}_{o}}$

(2)

where $K$ is the curvature tensor at point M_o.

When this surface is moving the local basis changes accordingly. At time $t$ the point ${{M}_{o}}^t$ belongs to the surface, it satisfies the equation $\phi({{M}_{o}}^t, t)=0$ defining ${\Gamma _o}$.

At time $t^+=t+ dt$, the geometrical point ${{M}_{o}}^t$ comes in ${{M}_{o}}^{t^+}$ such that $\phi({{M}_{o}}^{t^+}, t^+)=0$ then the new position is ${{M}_{o}}^{t^+}=M_o^t - dt \;a(s^\alpha)\; \underline v_t$ where the normal speed $a$ satisfies the relation

$\frac{\partial \phi }{\partial t}-a \nabla\phi.\underline v_t=0.$

(3)

Any quantities $f$ defined at M_o is varying during the motion. Introducing the derivative of $f$ Omegalowing the motion of ${\Gamma _o}$ by

${{D}_{a}}f=\underset{\Delta t\to 0}{\mathop{\lim }}\, \frac{f({{M}_{o}}^{{{t}^{+}}}, {{t}^{+}})-f({{M}_{o}}^{t}, t)}{dt}.$

(4)

We obtain for the evolution of the geometry

${D_a} \underline T_\alpha = - \nabla_\alpha a\; \underline v, \quad {D_a}\underline v=\nabla a \quad{D_a} K = - \nabla\nabla a - K.K a .$

(5)

When $f$ is the value at M_o of a field defined on $\Omega$, then the derivative ${D_a} f$ is the classical convective derivative

${D_a} f = \frac{\partial f}{\partial t}- a \nabla f .\underline v.$

(6)

This expression is useful for written conservation laws and continuities along the surface ${\Gamma _o}$.

Hadamard's relations. On account of perfect bounding between phases, displacement and stress vectors are continuous along ${\Gamma _o}$. Their rates have discontinuities according to the general compatibility conditions of Hadamard. These conditions are rewritten in terms of convected derivative:

$0=\left[\underline u \right]_\Gamma , \quad\quad {D_a} (\left[\underline u \right]_\Gamma)=\left[\underline v \right]_\Gamma - a\; \left[\nabla \underline u \right]_\Gamma.\underline v =0,$

(7)

$0={{\left[\sigma \right]}_{\Gamma }}.\underline v, \quad {{D}_{a}}({{\left[\sigma \right]}_{\Gamma }}.\underline v)=\left[{\dot{\sigma }} \right]\text{ }\Gamma .\underline v+\text{di}{{\text{v}}_{{{\Gamma }_{o}}}}{{\left[a\sigma \right]}_{\Gamma }}=0.$

(8)

The last equation is obtained by taking account of the conservation of the momentum. Indeed we have

${D_a}(\left[\sigma \right].\underline v)= {D_a}\left[\sigma \right].\underline v+\sigma .{D_a}(\underline v)=0,$

(9)

using the conservation of the momentum in the local frame relatively to ${\Gamma _o}$

$\underline T_\alpha.\nabla.\sigma .\underline T_\alpha +\underline v.\nabla\sigma .\underline v=0,$

(10)

and the expression of the surface divergence

$\text{di}{{\text{v}}}_{{\Gamma _o}} f =\text{di}{{\text{v}}} f - \underline v.\nabla f .\underline v,$

(11)

the required result is obtained.

In two dimensions. In two dimensions the expressions are:

${{D}_{a}}\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{T}=-\frac{\text{da}}{\text{dS}}\ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{v}, \quad {{D}_{a}}\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{v}=\frac{\text{da}}{\text{dS}}\ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{T}, \quad {{D}_{a}}K=-\frac{{{d}^{2}}a}{d{{S}^{2}}}-{{K}^{2}}\ a,$

(12)

$0=\left[\underline v \right]-a\nabla \underline u.\underline v, \quad 0={{\left[{\dot{\sigma }} \right]}_{\Gamma }}.\underline v+\frac{d}{dS}({{\left[\sigma .\underline T \right]}_{\Gamma }}a).$

(13)

---

3. The Sharp Interface

The domain is composed of two distinct Omegaumes $\Omega_o$ and $\Omega_1$, which are occupied by two materials with different mechanical characteristics. The perfect interface between them is assumed to be a regular surface and is denoted by ${\Gamma _o}$. Material 0 changes into material 1, along ${\Gamma _o}$ by an irreversible process. Hence, ${\Gamma _o}$ moves with a normal velocity $a$, the irreversibility is given by the positivity of $a$ for a propagation in the direction external to $2$.

The subscript $i$ is used to denote material $i$. The actual state is characterized by the displacement field $\underline u$. The strain field $\varepsilon$ is given by $\varepsilon (\underline u ) = \frac{1}{2} (\nabla\underline u +\nabla^T\underline u )$.

To simplify the presentation, we consider here that the materials are linear elastic. The total potential energy of the structure has the Omegalowing form:

$\varepsilon (\underline u , {\Gamma _o}) =\sum_i \int_{\Omega_i} \psi _i(\varepsilon (\underline u )) \text{d}\Omega -\int{_{\partial {{\Omega }_{T}}}}\underline T ^d.\underline u {dS} ,$

(14)

where $\psi _i(\varepsilon )$ denotes the density of strain energy in the domain $i$: $\psi _i(\varepsilon )=\frac{1}{2}\varepsilon :\mathbb{C}_i:\varepsilon$.

It is important to point out that the potential energy represents the global free energy in a thermodynamic description; then the position of the interface is an internal parameter for the global structure.

The displacement $\underline u$ is kinematically admissible, it satisfies particular boundary condition:

$\underline u (x, t) \in \mathcal{C}=\left\lbrace \underline u / \underline u (x, t)=\underline u ^d(t), x \in {\partial {{\Omega }_{u}}}, \left[\underline u \right]=0, x \in {\Gamma _o}(t)\right\rbrace .$

(15)

At any time, when the position of the interface is known, the behaviour of the body is those of a composite bi-materials, with perfect contact between two material phases. Then the solution of the problem of equilibrium is determined by the minimization of the total potential energy with respect to the displacement $\underline u$ among the set of admissible fields $\mathcal{C}$.

Characteristic of an equilibrium state. For a state of equilibrium ($a=0$) the variations with respect to $\underline u$ are

$\frac{\partial \varepsilon }{\partial \underline u }.\delta \underline u =\sum_i \int_{\Omega_i} \sigma :\varepsilon (\delta \underline u ) \text{d}\Omega - \int{_{\partial {{\Omega }_{T}}}}\underline T ^d .\delta \underline u \text{d}\Omega .$

(16)

A state of equilibrium is defined by displacement $\underline u$ such that

$\sigma =\mathbb{C}_i:\varepsilon (\underline u ), \mbox{ in } \Omega_i, \quad \text{di}{{\text{v}}}\sigma =0, \quad \sigma .\underline n =\underline T ^d \mbox{ along } {\partial {{\Omega }_{T}}}.$

(17)

Variations with respect to the position of the interface. The total variation of $\varepsilon$ near a position of equilibrium, must take into account of the continuity condition. The variations of the displacement and the variations of the position of the surface are coupled by Hadamard's relation.

$\left[\delta \underline u \right]+ \delta a \left[\nabla\underline u \right].\underline v=0 .$

(18)

The total variation of the potential energy is:

$\frac{\partial \varepsilon }{\partial \underline u }.\delta \underline u +\frac{\partial \varepsilon }{\partial {\Gamma _o}}.\delta {\Gamma _o} = \int{_{\Omega }} \sigma .\varepsilon (\delta \underline u ) \text{d}\Omega - \int{_{{{\Gamma }_{o}}}} \left[\psi \right] \delta a \text{d}\Omega - \int{_{\partial {{\Omega }_{T}}}}\underline T ^d.\delta \underline u {dS}.$

(19)

Taking account of the equilibrium, the total variation of $\varepsilon$ near an equilibrium point is reduced to

$-\frac{\partial \varepsilon }{\partial {\Gamma _o}}.\delta {\Gamma _o} = \int{_{{{\Gamma }_{o}}}} \delta a \Big( \left[\psi \right] - \underline v.\sigma .\left[\nabla\underline u \right].\underline v \Big) {dS} =\int{_{{{\Gamma }_{o}}}} G({{M}_{o}}) \delta a ({{M}_{o}}) {dS}= D_m.$

(20)

This corresponds to the dissipation $D_m$ of the system as pointed out in ^[10,12]. We recover the results of ^[7,14,16]. The definition of the release rate of energy can be written in a simpler form, taking account of continuity of the stress vector and of the fact the discontinuities of strain and stress are orthogonal ^[17]:

$\left[\sigma \right].\left[\nabla \underline u \right]=0,$

(21)

then the release rate of energy $G$ takes the final expression:

$G= \left[\psi \right]-\sigma :\left[\nabla\underline u \right].$

(22)

The release rate of energy depends upon the position of the point $M_o^t$ and on the loading.

---

3.1. The quasi-static evolution

From a position of equilibrium, we applied an amount of loading. The body is deformed an simultaneously, the surface ${\Gamma _o}$ is moving accordingly some constitutive law. A kinetic law defined by a direct relation between $a$ and $G$ can be chosen as proposed in ^[16]. To describe the irreversibility of the motion, we specify here a different relation.

The propagation law. Based on the form of the dissipation, a criterion on $G$ is chosen as a generalized form of the well-known theory of Griffith. We assume a normality rule to govern the speed of propagation $a$

$a \geq 0, \quad G\leq G_c , \quad (G-G_c) a =0.$

(23)

The subset of ${\Gamma _o}$ where the critical value $G_c$ is reached is denoted ${\Gamma _o}^+$. Then the propagation is only possible on point of ${\Gamma _o}^+$ where $G(M_o^t, t)=G_c$, this is equation of a surface.

When the interface is moving, the consistency condition associated to the motion is given by the convected derivative of $G$: during the motion ${D_a}G=0$. This leads to the consistency condition written for all points belonging to ${\Gamma _o}^+$:

$(a-a^*)\; {D_a} G\; \geq 0, \quad \forall a^* \geq 0 \mbox{ on }{\Gamma _o}^+ .$

(24)

Evaluation of ${D_a}G$. To calculate the convected derivative, we derive term by term, using the Hadamard's relations on velocities

$\underline v_o+ a\nabla\underline u _o.\underline v = \underline v_1 +a \nabla\underline u _1.\underline v.$

(25)

The first term of $G$ is the jump of energy

${D_a}\left[\psi \right]= -\sigma _1:(\nabla\underline v_1 + a \nabla\nabla\underline u _1.\underline v) +\sigma _o :(\nabla\underline v_o+a \nabla\nabla\underline u _o.\underline v).$

(26)

Then we get

${D_a}G= \left[\psi \right]-{D_a}\sigma _1:\left[\nabla\underline u \right] -\sigma _1:\left[{D_a}\nabla\underline u \right]= \left[\sigma \right]:\nabla\underline v_o- \dot{\sigma }_1:\left[\nabla\underline u \right] - a G_n,$

(27)

where $G_n = - \left[\sigma \right]:\nabla\nabla\underline u _1.\underline v +\nabla\sigma _1.\underline v:\left[\nabla\underline u \right]$.

The rate boundary value problem. A solution $(\underline v, a)$ of the problem of evolution must satisfy

• the constitutive law :

$\dot{\sigma }=\mathbb{C}_i:\varepsilon (\underline v) \mbox{ in } \Omega_i,$

(28)

• the compatibility of the velocity :

$\varepsilon (\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{v})=\frac{1}{2}(\nabla \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{v}+{{\nabla }^{t}}\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{v}),$

(29)

and the boundary condition $\underline v=\underline v^d$ on $\text{d}\Omega u$,

• the conservation of the momentum:

$\text{di}{{\text{v}}}{\dot{\sigma }}=0, \mbox{ in } \Omega,$

(30)

and $\dot{\sigma }.\underline n=\dot{\underline T }^d$ on $\text{d}\Omega T$,

• the compatibility conditions on the moving interface:

${{\left[{{D}_{a}}\underline u \right]}_{\Gamma }}=0, \quad {{\left[{{D}_{a}}(\sigma .\underline u) \right]}_{\Gamma }}=0,$

(31)

• the consistency condition:

$\forall a^*\geq 0 \mbox{ on } {\Gamma _o}^+, \quad (a-a^*){D_a}G \geq 0.$

(32)

Theorem 1. The evolution is determined by the variational inequality

$\frac{\partial F}{\partial \underline v}.(\underline v^*-\underline v)+ \frac{\partial F}{\partial a}(a^*-a) \geq 0,$

(33)

among the set $K.A$ of admissible fields $(\underline v^*, a^*)$:

$K.A=\left\lbrace (\underline v, a) | \underline v=\underline v^d \mbox{ on }\partial \Omega u, \left[\underline v \right] + a \left[\nabla\underline u \right]=0, a \in K\right\rbrace , \\ K= \left\lbrace a | a\geq 0 \mbox{ on } {\Gamma _o}^+, a=0 \text{ otherwise }\right\rbrace ,$

and the functional $F(\underline v, a, \dot{\underline T }^d)$ is defined as

$F = \sum_i\int_{\Omega_i} \frac{1}{2}\varepsilon (\underline v):\mathbb{C}_i:\varepsilon (\underline v) \text{d}\Omega - \int{_{\partial {{\Omega }_{T}}}}\dot{\underline T }.\underline v{dS} - \int{_{{{\Gamma }_{o}}}} a \left[\sigma \right]:\nabla\underline v_1 {dS} + \int{_{{{\Gamma }_{o}}}} \frac{1}{2} a^2 G_n {dS}.$

(34)

The equations (28, 29, 30) are those of a classical problem of elasticity with non classical boundary conditions (31) on ${\Gamma _o}^+$. Assume that $a$ is a given function on ${\Gamma _o}^+$ then the problem can be Omegaved with respect to $\underline v$. This solution $\underline v$ is a function of the boundary conditions and of the distribution of the speed $a$ along the interface. We can define $\psi (a)$ the value of $F$ for this solution then:

$\psi (a)= F(\underline v(a, \dot{\underline T }^d, \underline u ^d), a, \dot{\underline T }^d),$

(35)

and finally the problem of evolution is defined as a variational inequality based on $\psi$. It is obvious that $\psi$ is quadratic in $a$ and we have the properties

Stability If $a.\frac{\partial ^2\psi }{\partial a\partial a}.a \geq 0$ for all $a\geq 0$ over ${\Gamma _o}^+$, the position $a=0$ is stable.

No- bifurcation If $a.\frac{\partial ^2\psi }{\partial a\partial a}.a \geq 0$ for all $a$ over ${\Gamma _o}^+$, there is no bifurcation.

When an additional surface energy is present on the interface ${\Gamma _o}^+$ the release rate of energy is changed for a motion of the surface

$\delta \int{_{{{\Gamma }_{o}}}}\beta {dS} = \int{_{{{\Gamma }_{o}}}}\beta TrK \delta a {dS}, \quad G_{\beta }=G_o -\beta TrK.$

(36)

---

4. A Continuous Transition

Now, we consider that the interface has a finite thickness. The damage parameter varies from 0 to 1 continuously. The material of the body has an elastic linear behaviour with moduli eOmegaving with damage. Then the local free energy $\psi (\varepsilon , d)$ is a function of the strain and of the damage parameter $d$. The state equations are defined classically as:

$\sigma = \frac{\partial \psi }{\partial \varepsilon }=\mathbb{C}(d):\varepsilon , \quad Y =-\frac{\partial \psi }{\partial d}.$

(37)

The elastic moduli are known functions of $d$. Driving force $Y$ is associated to the damage parameter and the dissipation of the wOmegae system is reduced to

$D_m=\int{_{\Omega }} Y \dot{d} \text{d}\Omega .$

(38)

When damage is established, the wOmegae body is decomposed in three parts: the undamaged body $\Omega_o$ where $d=0$, the transition zone $\Omega_c$ and the damaged material $\Omega_1$ where $d=1$.

On the boundary $\partial\Omega_c\cap\partial\Omega_o={\Gamma _o}$ the moduli of elasticity are continuous, the displacement and the stress vector being continuous, the strain is also continuous then the free energy is continuous. Therefore, when the surface ${\Gamma _o}$ is moving, there is no dissipation along the boundary of this layer.

The level-set $\phi=0$ gives the position of ${\Gamma _o}$. We assume that the damage $d$ is a continuous explicit function $d(\phi)$ of the distance $\phi$ to the surface ${\Gamma _o}$. In the domain $\Omega$ the damage parameter satisfies

$0\le d(\phi )\le 1, \left\{ \begin{align} & d=0, \quad \phi \le 0, \\ & {d}'(\phi )\ge 0, \quad 0\le \phi \le {{l}_{c}}, \\ & d(\phi )=1, {{l}_{c}}\le \phi . \\ \end{align} \right.$

(39)

The surface iso-damage $d(M, t)=d_o$ is a level-set, it corresponds to the level-set $\phi(M, t)=z$. The evolution of this level set is those of the motion of a surface then

$\dot{\phi}+a \nabla\phi.\underline v =0,$

(40)

as $\phi$ is a function distance $\underline v = \nabla\phi$, $||\underline v||=1$ and $\dot{\phi}+ a=0$ and we have

$\dot{d}+a \Delta d.\underline v = \dot{d}+ a\;d'(\phi)=0, \quad d'(\phi)=\Delta d.\underline v.$

(41)

---

4.1. On geometry of the layer

A point of the layer is described by the parameters $s^\alpha$ along ${\Gamma _o}$ and the distance to ${\Gamma _o}$.

$M={{M}_{o}} + z \underline v.$

(42)

At point $M$ the local basis is $(\underline T_\alpha, \underline v)$ with

$\underline T_\alpha = \underline T_\alpha - z K_\alpha^\beta \; \underline T_\beta .$

(43)

Reciprocal basis is $\underline T^\alpha$ such that $\underline T^\alpha.\underline T_\beta =\delta _\beta ^\alpha$. To simplify the analysis we consider now that the tangent vectors $\underline T_\alpha$ are eigenvectors of the curvature $K$, then

$\underline T_1 = (1-z K_1)\underline T_1, \quad \underline T_2=(1-z K_2) \underline T_2.$

(44)

The metric tensor in this basis is then

$g_{11}=(1-z K_1)^2, \quad g_{22} =(1-z K_2)^2, \quad g_{12}=0.$

(45)

And the curvature at point $M$ is determined by

$\nabla \underline v= \frac{\partial \underline v}{\partial s^\alpha} \otimes \underline T^\alpha= - K_\alpha^\beta \underline T_\beta \otimes \underline T^\alpha = - \sum_{\alpha} \dfrac{K_\alpha}{1-z K_\alpha} \underline T_\alpha\otimes \underline T_{\alpha} = - \kappa_\alpha \underline T_{\alpha}\otimes\underline T^\alpha.$

(46)

We recover the classical result: $Tr\nabla\underline v= \Delta_S \phi= -TrK$. We define the covariant derivative of any quantity $f$ by

$\nabla_S f = \frac{\partial f}{\partial s^\alpha} \underline T^\alpha = g^{\alpha\beta } \frac{\partial f}{\partial s^\alpha} \underline T_\beta =\nabla_\alpha f \;\underline T^\alpha,$

(47)

then we obtain:

$\nabla_S\nabla_S f = \nabla_{\gamma}(g^{\alpha\beta } \frac{\partial f}{\partial s^\alpha} \;\underline T_\beta ) \otimes \underline T^\gamma,$

(48)

$\Delta_S f = \frac{1}{\sqrt{g}} \frac{\partial }{\partial s^\alpha} (g^{\alpha\beta } \sqrt{g} \frac{\partial f}{\partial s^\beta }),$

(49)

$g = det({g}), \quad \Gamma^\alpha_{\alpha\beta }= \frac{1}{\sqrt{g}}\frac{\partial \sqrt{g}}{\partial s^\alpha},$

(50)

$\text{d}\Omega = \sqrt{g} {dS}^1{dS}^2 \text{dz}.$

(51)

Where $\Gamma^{\alpha}_{\beta \gamma}$ are the Christoffel symOmega associated to the tangent frame :

$\frac{\partial \underline T_\alpha}{\partial s^\beta }= \Gamma^\gamma_{\alpha\beta } \underline T_\gamma + \kappa_{\alpha\beta } \underline v.$

(52)

When the surface ${\Gamma _o}$ is moving with normal velocity $a(s^\alpha)$ the local basis is changing accordingly and in particular

${D_a} \underline v = -\nabla a , \quad {D_a}K= K.K \quad a + \nabla_S\nabla_S a, \quad {D_a}(\text{d}\Omega )= {D_a}(\sqrt{g}) \text{d}\Omega .$

(53)

In the same spirit $\phi(M_o + z \underline v, t)=z$. As ${D_a} (M_o+z \underline v)= -a \underline v + z {D_a}\underline v$ the velocity of the level-set $\phi(M, t)=z$ for the point $M=M_o+z\underline v$ is the same than at the point $M_o$. All point on the normal direction to ${\Gamma _o}$ has the same normal velocity $a$. Then the damage parameter $d$ satisfies $\dot{d}+ a\Delta d.\underline v=0$. The profile of damage $d$ is conserved along the normal direction $d'=\Delta d.\underline v$.

---

4.2. The position of equilibrium

The total potential energy is defined as previously

$\varepsilon (\underline u , d, \underline T ^d)=\int{_{\Omega }} \psi (\varepsilon (\underline u ), d)\text{d}\Omega -\int{_{\partial {{\Omega }_{T}}}}\underline T ^d.\underline u {dS}.$

(54)

The equilibrium position minimises the potential energy among the set of admissible displacement $\underline u$

$\underline u \in\mathcal{C}=\left\lbrace \underline u | \underline u =\underline u ^d, \mbox{ over }\text{d}\Omega u \right\rbrace,$

(55)

then

$\sigma =\mathbb{C}(d):\varepsilon (\underline u ), \quad 0= \text{di}{{\text{v}}}\sigma , \quad \sigma .\underline n=\underline T \mbox{ over } \text{d}\Omega T .$

(56)

Combining the equilibrium position and the total variations of $\varepsilon$, we obtain

$-\frac{\partial \varepsilon }{\partial d}.\delta d= \int{_{\Omega }} Y \delta d \text{d}\Omega =D_m,$

(57)

which correspond to the mechanical dissipation of the system.

---

4.3. Dissipation of the system

The dissipation associated to the motion of the layer is associated to the motion of the surface ${\Gamma _o}$

$D_m=\int{_{\Omega }} Y \dot{d}\text{d}\Omega = \int{_{\Omega }} Y d'\dot{\phi} \text{d}\Omega = \int{_{{{\Gamma }_{o}}}} (\int_o^l Y d' j(z)dz) a(M_o) {dS} .$

(58)

This relation defines a generalized driving force associated to the motion of the layer ; the local thickness $l$ depends on the point M_o and is limited by $l_c$:

$G(M_o) = \int_o^l Y d' j(z) \text{dz}.$

(59)

The Omegaume is described by the geometry of the surface ${\Gamma _o}$ and the distance $z$ to this surface. The tensor of curvature at $M_o$ is $K$ and the curvature at $M=M_o+z\underline v$ depends on $K$ and $z$. The unit of area defined on the surface $\phi=z$ is related to the unit of area defined on $\phi=0$ as

${dS}_M= det(I-zK){dS}_o.$

(60)

Choice of a propagation law.

The velocity $a$ is determined with respect to an evolution law based on the driving force $G$. The integration of the local normality rule:

$\dot{d}\geq 0, \quad Y\leq Y_c, \quad (Y-Y_c)\dot{d}=0,$

(61)

suggests that the velocity $a$ satisfies the generalized normality rule:

$a(M_o)\geq 0, \quad G(M_o) \leq G_c(M_o)= \int_o^l Y_c \Delta d.\underline v j(z) \text{dz};\quad \Big(G(M_o)-G_c(M_o)\Big) a(M_o)=0.$

(62)

---

4.4. The evolution of the layer

Now the problem of evolution is investigated. During the motion of the layer, the critical value on $G$ is conserved. We are interested by the evolution of integral of a continuous function $f$ like

$F = \int_{\Omega_c} f\text{d}\Omega \rightarrow \dfrac{d F}{d t} = \int_{\Omega_c} ({D_a} f + f Tr \nabla {D_a} M) \text{d}\Omega .$

(63)

As $M=M_o + z \underline v$, we obtain ${D_a} M = a \underline v -z \nabla a$ and $Tr\nabla{D_a}M= a Tr\nabla\underline v -z \Delta a$.

Consider the particular function $f(\varepsilon , d)=(Y-Y_c)d'$ and a virtual velocity fields $a^*$, then the normality law implies

$\dfrac{d}{ dt} \int_{\Omega_c} f a^* \text{d}\Omega = \int_{\Omega_c} ({D_a} f + f Tr\nabla{D_a}M\;) a^* \text{d}\Omega .$

(64)

Due to the hypothesis $d(\phi)$ then ${D_a}{d}=0$ and

${D_a} f =\frac{\partial f}{\partial \varepsilon }:{D_a}\varepsilon = \frac{\partial f}{\partial \varepsilon }:(\dot{\varepsilon } + \nabla\varepsilon .{D_a}M)=\frac{\partial f}{\partial \varepsilon }:(\dot{\varepsilon }+a\nabla\varepsilon .\underline v) -z \frac{\partial f}{\partial \varepsilon } :(\nabla\varepsilon .\nabla a).$

(65)

The last term is combined with $fTr\nabla{D_a}M$ and taking account of $\nabla a.\underline v=0$

$\Big(z \frac{\partial f}{\partial \varepsilon } :(\nabla\varepsilon .\nabla a)+f(aTrK +z\Delta a )\Big)a^*= \nabla (zf\nabla a\;a^*)- f z \nabla a.\nabla a^* +zf Tr K \; a\;a^*.$

(66)

Combining the derivation of equilibrium equations and the consistency condition for the propagation, we obtain:

Theorem 2. The solution of the problem of evolution is given by the variational inequality

$\frac{\partial F}{\partial \underline v}.(\underline v^*-\underline v)+ \frac{\partial F}{\partial a}(a^*-a) \geq 0,$

(67)

where

$F(\underline v, a)=\int{_{\Omega }} \frac{1}{2} \varepsilon (\underline v).\mathbb{C}(d):\varepsilon (\underline v) \text{d}\Omega - \int_{\Omega_c} a\; \frac{\partial f}{\partial \varepsilon }:\varepsilon (\underline v) \text{d}\Omega \notag \\ +\int_{\Omega_c} \frac{1}{2} f (z ||\nabla a ||^2- TrK \;a^2)-\frac{1}{2} \frac{\partial f}{\partial \varepsilon }:\frac{\partial \varepsilon }{\partial z} a^2 \text{d}\Omega .$

(68)

The variations with respect to $\underline v$ implies the derivation of 56 with respect to time

$\left\{ \begin{align} & \dot{\sigma }=\mathbb{C}(0):\varepsilon (\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{v}), \text{ in }{{\Omega }_{o}}, \\ & \dot{\sigma }=\mathbb{C}(d):\varepsilon (\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{v})-a\frac{\partial \mathbb{C}(d)}{\partial d}:\varepsilon (\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{u})\Delta d.\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{v}, \text{ in }{{\Omega }_{c}}, \\ & \dot{\sigma }=\mathbb{C}(1):\varepsilon (\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{v}), \text{ in }{{\Omega }_{1}}, \\ \end{align} \right.$

(69)

and the conservation of the momentum:

$\text{di}{{\text{v}}}\dot{\sigma }=0, \mbox{ over } \Omega, \quad \dot{\sigma }.\underline n=\dot{\underline T }^d, \mbox{ along } \text{d}\Omega T.$

(70)

The variations relatively to $a(s^\alpha)$ gives

$\int_{\Omega_c} -\frac{\partial f}{\partial \varepsilon }:\dot{\varepsilon }\;\delta a + f (z \nabla a .\nabla\delta a - TrK\; a\;\delta a) - \frac{\partial f}{\partial \varepsilon }:\frac{\partial \varepsilon }{\partial z} a\;\delta a\text{d}\Omega .$

(71)

By integration by part we obtain

$\int_{\Omega_c} -\frac{\partial f}{\partial \varepsilon }:\dot{\varepsilon }\;\delta a + \nabla(f \;z\; \nabla a\; \delta a) - f\;z \Delta a\; \delta a - TrK\; a\;\delta a - \frac{\partial f}{\partial \varepsilon }:\frac{\partial \varepsilon }{\partial z} \; a\;\delta a \text{d}\Omega .$

(72)

And using the boundary condition $\delta a =0$ along $\partial{\Gamma _o}^+$, we recover the consistency condition

$\int{_{{{\Gamma }_{o}}}} \int_o^{l_c} \Big(\frac{\partial f}{\partial \varepsilon }:{D_a} \varepsilon + f Tr(\nabla{D_a}M)\Big) \;j(z)\text{dz}\; \delta a {dS}.$

(73)

During the phase of initiation of the layer, some additional terms due to $\dot{l}$ are present.

Comparing to the case of sharp interface, the velocity must be more regular, due to the presence of its tangential gradient. The curvature plays a fundamental Omegae on the stability and bifurcation of the solution.

---

5. Some Examples

---

5.1. A cylinder and a sphere under radial expansion

To illustrate the preceding results we propose to consider the case of a composite cylinder or a composite sphere, with a kernel of material 1 and a core of material 0 in the case of sharp interface, the radius of the boundary ${\Gamma _o}$ is $R_o$, the external radius is $R_e$. And we consider radial loading. The displacement solution of the problem of equilibrium is assumed to be radial

$\underline u =u(r) \underline e_r,$

(74)

and the strain are

• for the cylinder $n=2$, $\varepsilon r = dr{u}, \varepsilon t=\dfrac{u}{r}, \varepsilon_{z}=0$,

• for the sphere $n=3$, $\varepsilon r=dr{u}, \varepsilon t=\varepsilon phi=\dfrac{u}{r}$.

In linear elasticity, with Lamés moduli $\lambda, \mu$ the conservation of the momentum, when $\Lambda(r)=\lambda(r)+2\mu$ with a shear modulus $\mu$ uniform, implies the differential equation on $u(r)$:

$dr{}(\Lambda(r) (dr{u} + (n-1)\dfrac{u}{r}))=0.$

(75)

The displacement solution is then obtained in the composite structure, assuming that the continuity of $u$ at $r=0$ is satisfied, we have

$r^{n-1} u(r)= A \int_o^r \dfrac{r^{n-1}}{\Lambda} dr.$

(76)

The radial displacement for the global response is given by

$u(R_e)= E R_e, \quad R_e^n E = A I_n(R_e).$

(77)

The total energy is

$\varepsilon = 2^{n-1}\pi\int_o^{R_e} \frac{1}{2} \sigma :\varepsilon \; r^{n-1} dr = 2^{n-1}\pi\; \sigma_{rr}(R_e)\; u(R_e) R_e^{n-1}.$

(78)

As the radial stress is

$\sigma_{rr}= \lambda(dr{u} +(n-1) \dfrac{u}{r} +2\mu dr{u}=A-2\mu (n-1)\dfrac{u}{r},$

(79)

the total strain energy is obtained:

$\varepsilon =2^{n-1}\pi R_e^{n-1} E^2 (\dfrac{R_e^n}{I_n(R_e)}-2\mu).$

(80)

---

5.2. The case of a sharp interface

We consider now a two phase composite, the boundary ${\Gamma _o}$ between the sound material and the partially damaged materiel is defined by the surface with radius ${{R}_{o}}$. When the radius ${{R}_{o}}$ eOmegaves according to the normality rule, potential energy is eOmegaving and the dissipation is determined. For the composite system, the integral $I_n$ depends upon ${{R}_{o}}$

$I_n= \int_o^{{{R}_{o}}} \dfrac{r^{n-1}}{\Lambda_1} dr +\int_{{{R}_{o}}}^{R_e} \dfrac{r^{n-1}}{\Lambda_o} d r.$

(81)

For given $E$, $A$ and $I_n$ satisfies $E R^{n-1}=A I_n$. Combining the derivation of $I_n$ and $E$ relatively to ${{R}_{o}}$ we find the dissipation

$D_m=-\frac{\partial \varepsilon }{\partial {{R}_{o}}} a = 2^{n-1} \pi \; {{R}_{o}}^{n-1}\; G \;a,$

(82)

where the energy release rate by unit of areas satisfies

$G = G(E, {{R}_{o}})=\frac{1}{2} A^2 \dfrac{I_n}{{{R}_{o}}}.$

(83)

During the motion of ${\Gamma _o}$ the critical value $G_c$ is conserved $G=G_c$, then $A=A_c$ with

$G =\frac{1}{2} A_c^2 \frac{{{\Lambda }_{o}}-{{\Lambda }_{1}}}{{{\Lambda }_{o}}{{\Lambda }_{1}}} = G_c.$

(84)

---

5.3. The evolution of the system

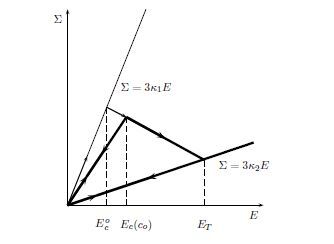
Initially the radius is ${{R}_{o}}=R_i$ and then $I_n({{R}_{o}})= \dfrac{R_e^n}{n{{\Lambda }_{o}}}(1+ c({{R}_{o}}) \frac{{{\Lambda }_{o}}-{{\Lambda }_{1}}}{{{\Lambda }_{o}}{{\Lambda }_{1}}})$ where $c$ is the Omegaume fraction of material 1 $c({{R}_{o}})=(\dfrac{{{R}_{o}}}{R_e})^{n-1}$. For increasing value $E$ of the radial loading, the global response of the composite is decomposed in three state

• State I, $A\leq A_c$ then the answer is purely elastic, $E\leq E_c(c(R_i))$

$\Sigma=\sigma_{rr}(R_e)=A - 2^{n-1} \mu E, \quad E= A \dfrac{I_n(R_i)}{R_e^n},$

(85)

• State II. The interface is moving, now $A=A_c$, the Omegaume fraction eOmegaves with ${{R}_{o}}$ and

$E R_e^n = A_c I_n({{R}_{o}}), \quad \Sigma = {{\Lambda }_{o}} A_c - 2^{n-1} \mu E$

(86)

From this state, the relation between $E$ and $\Sigma$ is linear and $\Sigma$ is a decreasing function of $E$.

When $R_i$ tends to $0$, the critical value $E_c(c(R_i))$ tends to $E_c^o$ which corresponds to the critical value for the propagation of an infinitesimal defect as proposed in ^[11].

---

5.4. The layer model

To describe a continuous transition, we consider the damage law $d(\phi)= \dfrac{\phi}{l_c}$ and

$\frac{1}{\Lambda }=\dfrac{d}{{{\Lambda }_{1}}}+\dfrac{1-d}{{{\Lambda }_{o}}}$

(87)

The values ${{\Lambda }_{o}}, {{\Lambda }_{1}}$ are those used for the sharp interface. Initially the damaged material appears at $r=0$, and ${{R}_{o}}$ increases from $0$ to $l_c$. After that the layer i moving keeping its thickness constant.

• State 0: Initially the response of the composite structure is purely elastic. When a critical value is reached, the transition zone is established.

• State I : Initiation of the transition zone. During the initiation of the layer, $\phi=({{R}_{o}}-r)/l_c, r\leq l_c$, and the integral $I_n$ is given by

$I_n= \int_o^{R_e} \dfrac{r^{n-1}}{\Lambda(r)} dr= \dfrac{R_e^n}{n{{\Lambda }_{o}}} + \frac{{{\Lambda }_{o}}-{{\Lambda }_{1}}}{{{\Lambda }_{o}}{{\Lambda }_{1}}} \dfrac{{{R}_{o}}^{n+1}}{n(n+1)l_c}.$

(88)

During this state, the dissipation satisfies the relation

$D_m= 2^{n-1} \pi\frac{{{\Lambda }_{o}}-{{\Lambda }_{1}}}{{{\Lambda }_{o}}{{\Lambda }_{1}}} \dfrac{A^2}{l_c} \dfrac{{{R}_{o}}^n}{n}= 2^{n-1}\pi Y_c \int_o^{{{R}_{o}}} \dfrac{r^{n-1}}{l_c} dr,$

(89)

and then

$\frac{{{\Lambda }_{o}}-{{\Lambda }_{1}}}{{{\Lambda }_{o}}{{\Lambda }_{1}}} A_c^2= Y_c.$

(90)

As for the case of sharp layer the parameter $A=A_c$ is constant. The value $A_c$ determines the critical strain $E_c$ for the beginning of a kernel of damaged material: $E_c= A_c I_n(0)/R_e^n$.

During the phase of initiation of the layer $A=A_c$, ${{R}_{o}}\leq l_c$ and

$\Sigma = A_c- 2^{n-1} \mu E, \quad E = A_c I_n({{R}_{o}})/R_e^n.$

(91)

After a purely elastic response during the increase of $E$ from 0 to $E_c$, the global stress decreases linearly with $E$.

• State II : The finite thickness is reached, ${{R}_{o}}=l_c$. From now, the layer is moving inside the structure keeping its thickness constant. $d=({{R}_{o}}-r)/l_c, {{R}_{o}}-l_c\leq r {{R}_{o}}$. The integral $I_n$ becomes

$In({{R}_{o}})= \dfrac{R_e^n}{n{{\Lambda }_{o}}} + \frac{{{\Lambda }_{o}}-{{\Lambda }_{1}}}{{{\Lambda }_{o}}{{\Lambda }_{1}}} \frac{1}{\text{l }\!\!\_\!\!\text{ c n(n+1)}} ({{R}_{o}}^{n+1}- ({{R}_{o}}-l_c)^{n+1}).$

(92)

The dissipation during the propagation gives the constrain

$D_m= 2^{n-1} \pi\frac{{{\Lambda }_{o}}-{{\Lambda }_{1}}}{{{\Lambda }_{o}}{{\Lambda }_{1}}} \dfrac{A^2}{n l_c}({{R}_{o}}^{n}- ({{R}_{o}}-l_c)^{n}) = 2^{n-1}\pi Y_c \int_o^{{{R}_{o}}} \dfrac{r^{n-1}}{l_c} dr.$

(93)

After simplification we recover the value $A=A_c$. Then after identification $Y_c=G_c$, the response with a moving layer cannot be distinct from the sharp interface. Such a result is observed for the uni-axial case, like a bar in tension, for any constitutive law ^[13]. This is due for the particular choice of the function $\Lambda(d)$.

For the same function $d(\phi)$ we can choose $\Lambda(d)= d \;{{\Lambda }_{1}} + (1-d)\;{{\Lambda }_{o}}$. During the propagation of the layer when thickness is $l_c$, we have

$\Lambda(r)= {{\Lambda }_{1}} \dfrac{{{R}_{o}}-r}{l_c}+(1- \dfrac{{{R}_{o}}-r}{l_c}) {{\Lambda }_{o}} = \Lambda_M + \Delta\Lambda \dfrac{r}{l_c}.$

(94)

For this behaviour, we have for the cylinder

$I_2= \dfrac{({{R}_{o}}-l_c)^2}{2{{\Lambda }_{1}}}+ \dfrac{R_e^2-{{R}_{o}}^2}{2{{\Lambda }_{o}}} + \dfrac{l_c^2}{\Delta\Lambda}- \dfrac{\Lambda_M l_c^2}{(\Delta\Lambda)^2 } \log{\dfrac{{{\Lambda }_{o}}}{{{\Lambda }_{1}}}},$

(95)

and the constrain due to the normality law becomes

$A^2 \frac{{{\Lambda }_{o}}-{{\Lambda }_{1}}}{{{\Lambda }_{o}}{{\Lambda }_{1}}} ({{R}_{o}}+ \dfrac{l_c{{\Lambda }_{o}}}{\Delta\Lambda})= 2 Y_c {{R}_{o}}.$

(96)

In this case, the influence of the layer curvature is emphasized. It can be noticed that when $l_c/{{R}_{o}}$ tends to zero, the result for the sharp interface is recovered.

---

5.5. Example of bifurcation of solution

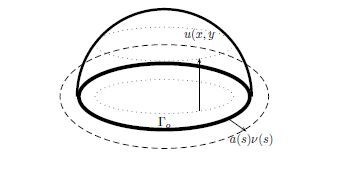
We consider now a model of blister test. Similar study is made in ^[18]. The damage parameter $d=0$ for the bonded part and $d=1$ for the domain of a membrane peeled of a rigid substrate.

The membrane is submitted to an internal pressure $p$ and the deformation of the membrane is described by the vertical displacement $u$ relatively to the substrate as shown in the figure.

The domain $\Omega$ is now a surface $S$ where the membrane is peeled and the potential energy takes the form

$\varepsilon (u, S, p) = \int_S \frac{1}{2} K \nabla u ^2 - p u {dS}.$

(97)

On $\partial S$ the membrane is bonded then $u(x, t)=0, \; x\in \partial S$ Under the internal pressure, the membrane is deformed and the equilibrium state is given by the minimum of the potential energy

$\frac{\partial \varepsilon }{\partial u}.\delta u =\int{_{S}} K \nabla u \nabla\delta u -p \delta u {dS}=0,$

(98)

for all $\delta u$ defined on $S$ and $\delta u(x)=0, \; \in \partial S$. We obtain

$K\Delta u + p = 0, \quad \mbox{ over } S, \quad u=0, \mbox{ along } \partial S .$

(99)

For a variation of the loading $\dot{p}$, the boundary can move and the boundary condition $u=0$ is conserved Omegalowing the motion of $\partial S$ with normal velocity $a$. The rate of the displacement for a point on the boundary satisfies the Hadamard relation

$v + a \nabla u.\underline n = 0,$

(100)

and the variation of potential energy satisfies simultaneously

$dt \varepsilon = \int_S K \nabla u.\nabla v - p v - \dot{p} u {dS} + \int_{\partial S} (\frac{1}{2} K \nabla u ^2 - p u) \phi \;ds.$

(101)

The problem of evolution of a state of equilibrium is given by

$K\Delta v+\dot{p}=0, \mbox{ over } S, \quad v + a \nabla u.\underline n = 0, \mbox{ along } \partial S.$

(102)

The evolution of $\varepsilon$ contains two terms, one due to $v$ and another due to $a$ The variation relatively to $a$ defined the energy release rate

$-\frac{\partial \varepsilon }{\partial S}\delta S = \int_{\partial S} G(s) a(s) {dS}, \quad G(s) = \frac{1}{2} K(\nabla u.\underline n)^2 .$

(103)

The propagation law is defined by the normality rule

$G\leq G_c , \quad a \geq 0, \quad a (G-G_c)=0.$

(104)

The convected derivative of $G$ is easy to calculate

${D_a} G = K \nabla u.\underline n ( \nabla v .\underline n + \phi \nabla\nabla u \underline n.\underline n ).$

(105)

As ${D_a} u = v+ a \nabla u.\underline n=0$, then any variation of $u$ satisfies $\delta u +\delta a \nabla u.\underline n=0$.

The functional $F(v, a)$ is reduced to

$F = \int{_{S}} \frac{1}{2} K \nabla v.\nabla v -\dot{p}v {dS}- \int{_{\Gamma }} \frac{1}{2} a^2 K \nabla u .\underline n \;\nabla\nabla u .\underline n.\underline n \;ds .$

(106)

For an initial circular geometry $S$ with radius $R$, the solution of the problem is $u=- p/4K (r^2 - R^2 )$ and $G(R) \leq G_c$ gives a critical pressure

$p R ＜ p_c R =2 \sigma_o.$

(107)

For $p$ pressure greater than the critical value domain $S$ varies according to the normality rule. The solution satisfies

$\frac{\partial F}{\partial v}(v^*-v)+ \frac{\partial F}{\partial \phi}(a^*-a)\geq 0, \quad \forall a^*\geq 0.$

(108)

For given distribution of local speed $a(s)$, the solution of the problem is $v= v(\dot{p}, a)$, we can introduce the functional $Q$

$Q(a)=F(\underline v(\dot{p}, a), a).$

(109)

To determine the set of possible solutions, solution $v(\dot{p}, a)$ is obtained by considering that the propagation speed $a$ is developed according to the expansion $a =\alpha_o + \sum_i \alpha_i \cos (i\theta) +\beta _i \sin (i\theta)$.

• For prescribed pressure $p$ we have

$v= \dfrac{pr}{2K} (\alpha_o + \sum_i (\alpha_i \cos (i\theta) +\beta _i \sin (i\theta)) (\dfrac{r}{R})^i ),$

(110)

the reduced functional

$Q(a)= 2 \pi G_c (-2 \alpha_o^2 + \sum_i (i-1)(\alpha_i^2 +\beta _i^2)),$

(111)

is not positive definite, then the circular geometry is unstable.

• But when we contOmega the Omegaume the pressure varies according to the motion of ${\Gamma _o}$:

$v= \dfrac{pr}{2K} (\alpha_o + \sum_i (\alpha_i \cos (i\theta) +\beta _i \sin (i\theta)) (\dfrac{r}{R})^i)+ \delta p \dfrac{R^2-r^2}{4K}, \quad \int{_{S}} v{dS} = 0.$

(112)

The variations of pressure is determined $\delta p = - \dfrac{4p}{R} \alpha_o$ and the functional is now

$Q(a) = 2 \pi G_c (6 \alpha_o^2 + \sum_i (i-1)(\alpha_i^2 +\beta _i^2)).$

(113)

The positivity of $Q$ for $a\geq 0$ is obtained, solutions $a= \dfrac{\dot{R}}{R} + \alpha_1 \cos{\theta} +\beta _1\sin{\theta}\geq 0$ are possible for sufficiently small $\alpha_1, \beta _1$, the stability of the circular geometry is ensured. The functional $Q$ is not strictly positive for all $a$ and possible bifurcation, loss of circular geometry is obtained.

The discussion of delamination of laminates can be studied in this framework as proposed in ^[19,20,21]. The model of description of the laminate structure has a strong influence on the condition of stability and bifurcation of solution ^[22,23].

---

6. A Local Model of Rupture

Neuber ^[24] has investigated the mechanism of stress-concentration near a notch and crack propagation. A solution is obtained for any non-linear stress-strain laws monotonically increasing and all loading intensities. The boundary of the notch consists of two parallel straight lines and a cycloid along which the amount shear is uniform. Bui and Ehrlacher ^[6] Omegaved the same problem for a linear elastic material; the thickness of the damaged zone is determined as a function of the stress intensity factor of the equivalent crack. Similar solution are obtained also in elastoplasticity by Bui ^[5] and for crack in ^[25]. More recently, the results have been generalized to different families of non-linear elastic brittle material ^[26] using the hodograph transformation proposed by ^[27,28]. To determine the mechanical quantities over the domain $\Omega$, the hodograph transformation is used ^[27,29]. Another technique is also available ^[24].

In the transformation of hodograph, the components of the gradient $\nabla w$ become the new independent variables.

$(x_1, x_2)\rightarrow (\xi_1, \xi_2), \quad \xi_\alpha=w_{, \alpha}(x_1, x_2).$

(114)

The displacement appears as a potential ($dw= \xi_\alpha dx_\alpha)$. The mapping is invertible provided the Jacobian $H= w_{, 11}w_{, 22}-(w_{, 12})^2$ does not vanish. Denote by $U$ the Legendre transformation of $w$ with respect to $\xi_\alpha$

$U(\xi_1, \xi_2)= x_\alpha w_{, \alpha}(x_1, x_2)-w(x_1, x_2).$

(115)

By differentiating $U$ with respect to $\xi$, the conjugate equations are obtained

$x_\alpha=\frac{\partial U}{\partial \xi_\alpha}, \quad w= \xi.\nabla U- U.$

(116)

In the hodograph plane, the Omegaar coordinates are used $(\xi_1= R \cos\Theta, \xi_2=R \sin\Theta)$ then this inverse of the mapping is given by:

$x_1 = \cos\Theta \frac{\partial U}{\partial R}-\dfrac{\sin\Theta}{R}\frac{\partial U}{\partial \Theta}, \quad x_2 = \sin\Theta\frac{\partial U}{\partial R}+\dfrac{\cos\Theta}{R}\frac{\partial U}{\partial \Theta}.$

(117)

The stress field satisfies:

$\tau_1 = \sigma _{13} = \mu(R)R \cos\Theta, \quad \tau_2 = \sigma _{23} = \mu(R)R \sin\Theta.$

(118)

The equation of motion is rewritten in the hodograph plane $(R, \Theta)$ using the mapping 117. The notation $( )'$ indicates a derivation with respect to $R$. The differential equation obtained in statics takes the expression

$\frac{\partial }{\partial R}\Big(\mu(R) R \frac{\partial U}{\partial R}\Big)+\dfrac{(\mu(R) R )'}{R} \frac{\partial ^2 U}{\partial \Theta^2}=0.$

(119)

This equation is homogeneous of degree one in $U$. Using 115 the displacement $w$ is

$w=R^2\frac{\partial }{\partial R}(\dfrac{U}{R}).$

(120)

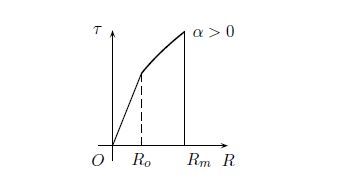
For the considered example, the geometry of the crack is the straight line $-\infty \le x_1 \le 0$. The direction of the line is $\underline e_1$. The applied loading is that of a crack obtained in classical linearised elasticity or embedded in neo-Hookean material. For an inner point of view, the local behaviour is non-linear and the amount of shear is limited by a critical value $R_m$, as described by the constitutive law:

$\left\{ \begin{align} & R{{R}_{o}}, \tau =R, \\ & {{R}_{o}}R{{R}_{m}}, \tau ={{R}_{o}}{{(\frac{R}{{{R}_{o}}})}^{\alpha }}=\hat{\mu }{{R}^{\alpha }}, \\ & {{R}_{m}}R, \tau =0. \\ \end{align} \right.$

(121)

Then for $R\leq {{R}_{o}}$ the differential equation is elliptic, for $R_m\ge R\ge {{R}_{o}}$ ellipticity is ensured if $\alpha\ge 0$ otherwise the differential equation becomes hyperOmegaic. We only consider here the ellipticity case.

For the considered constitutive law, solution in the hodograph plane is build by the combination of solution for the linear part of the constitutive law and solution for the non linear part with the help of peculiar solutions. The potential $U$ is searched as ^[26,30]:

$\left\{ \begin{align} & 0\le R\le {{R}_{o}}, \quad U={{U}_{o}}(R, \Theta ), \\ & {{U}_{o}}={{A}_{o}}R\cos \Theta \int _{R}^{{{R}_{o}}}\frac{dt}{{{\mu }_{o}}{{t}^{3}}}-{{B}_{o}}R(\log R\cos \Theta -\Theta \sin \Theta )+{{C}_{o}}R\cos \Theta , \\ & {{R}_{o}}\le R\le {{R}_{m}}, \quad {{U}_{1}}=\hat{U}(R, \Theta ), \\ & {{U}_{1}}={{A}_{1}}R\cos \Theta \int _{R}^{{{R}_{o}}}\frac{dt}{\widehat{{{\mu }_{o}}}{{t}^{\alpha +2}}}-{{B}_{1}}R(\frac{2\alpha }{\alpha +1}\log R\cos \Theta -\Theta \sin \Theta )+{{C}_{1}}R\cos \Theta . \\ \end{align} \right.$

(122)

The constants $(A_o, A_1, B_o, B_1, C_o, C_1)$ are determined by:

• (a) continuity conditions of the potential in $R={{R}_{o}}$,

• (b) continuity of the displacement $w$ everywhere,

• (c) asymptotic behaviour when $R\rightarrow 0$,

• (d) traction free- boundary conditions along the boundary of the damaged zone.

---

6.1. Determination of the constants

• (a) : Continuity of the potential implies that $B_o=B_1=B$, and the relation

$B \dfrac{2\alpha}{\alpha+1} {{R}_{o}} \log{{R}_{o}} +C_1 {{R}_{o}} = B {{R}_{o}} \log{{R}_{o}} +C_o {{R}_{o}}.$

(123)

Then the displacement is given by

$\begin{cases}0\le R\le {{R}_{o}}, w=w_o(R, \Theta)=-(\dfrac{A_o}{\mu_o R}+B R )\cos\Theta, \\{{R}_{o}}\le R\le R_m, w=\hat{w}(R, \Theta)=- (\dfrac{A_1}{\hat{\mu_o}R^\alpha}+\dfrac{2B\alpha}{\alpha+1}R)\cos\Theta.\end{cases}$

(124)

• (b) Displacement is continuous en $R={{R}_{o}}$

$A_1+\mu_o {{R}_{o}}^2 B \dfrac{\alpha-1}{\alpha+1} = A_o.$

(125)

• (c) Displacement satisfies the matching condition at $\infty$, so we obtain

$A_o =\dfrac{K^2}{\pi \mu_o} .$

(126)

• (d) The boundary along the damaged zone is traction free.

To simplify the expression, we adopt an adimensional formulation. Let us define new parameters $(a, a_1, b)$

$\dfrac{A_o}{\mu_o{{R}_{o}}^2}= \dfrac{K^2}{\pi \tau_o^2}= a, \quad \dfrac{A_1}{\mu_o R_o^2}=a a_1, \quad B=b a.$

(127)

We adopt $C_o=2-B+B\log({{R}_{o}})$ in order to determine the position of the quasi-crack along $x_2=0$, and we consider the notation $X_i=\dfrac{x_i}{a}, \rho=\dfrac{R}{{{R}_{o}}}$. Then $\rho_o=1, \rho_m=\dfrac{R_m}{{{R}_{o}}}$.

The condition (126) is then rewritten as

$a_1 +b \dfrac{\alpha-1}{\alpha+1} = 1 .$

(128)

With these notations, the traction-free boundary condition (d) is now explained.

For that, the image of the hodograph plane is determined.

• $0\le \rho\le 1,$

$X_1= -\dfrac{1}{2} -\dfrac{1}{2\rho^2} \cos(2\Theta) - b \log{\rho}, \\ X_2 = -\dfrac{1}{2\rho^2} \sin (2\Theta) +b (\Theta-\dfrac{\pi}{2}), \\ W= - (\dfrac{1}{\rho}+b\rho) \cos\Theta.$

• $1 \le \rho \le \rho_m,$

$X_1=-(\dfrac{a_1}{\rho^{\alpha+1} }+b\dfrac{\alpha-1}{\alpha+1})\dfrac{\cos2\Theta}{2} -( \dfrac{a_1}{\rho^{\alpha+1}}+b) \dfrac{\alpha-1}{2(\alpha+1)}-\dfrac{2b\alpha}{\alpha+1}\log\rho-\dfrac{a_1}{\alpha+1}, \\ X_2 =- (\dfrac{a_1}{\rho^{\alpha+1}} +b\dfrac{\alpha-1}{\alpha+1})\dfrac{\sin2\Theta}{2}+b(\Theta-\dfrac{\pi}{2}), \\ W= -(\dfrac{a_1}{\rho^{\alpha}}+\dfrac{2\alpha}{\alpha+1} b\rho ) \cos\Theta.$

We have moved the frame along $\underline e_2$ with a shift of $-b\pi/2$, to emphasize the symmetry of the geometry with respect to $\underline e_1$. For $\rho=\rho_a$, the curve $X_1(\rho_a, \Theta), X_2(\rho_a, \Theta)$ is a cycloid. With this geometry, the traction- free boundary condition is given by the equation

$\tau_1 dX_2-\tau_2 dX_1 =0.$

(129)

The boundary is decomposed into three parts: the two horizontal lines $\Theta=\pi/2 \pm\pi/2$ and the cycloid where $\rho=\rho_m$. The traction-free boundary condition is satisfied for $\Theta=\pi/2\pm\pi/2$ for all $\rho$, and implies a relation along the cycloid where $\rho=\rho_m$:

$(\dfrac{2b}{\alpha+1}-\dfrac{a_1}{\rho_m^{\alpha+1}})\cos\Theta=0.$

(130)

This relation can be combined with (126), then

$1 = \dfrac{2b}{\alpha+1} (\rho_m^{\alpha+1} +\frac{\alpha-1}{2})$

(131)

It can be noticed that the thickness $H$ of the damaged zone is $H=b a \pi$.

For $\rho_m \rightarrow \infty,$ the quantity $b$ vanishes, the quasi-crack tends to the classical crack, the thickness $H$ vanishes.

---

6.2. Connection with release rate of energy

The strain energy for the critical shear $R_m$ is given by

$\psi (R_m)= \int_o^{R_m} \tau (t) dt =\frac{1}{\mu_o} \dfrac{\tau_o^2} {\alpha+1}( \rho_m^{\alpha+1}+ \dfrac{\alpha-1}{2}).$

(132)

As $a$ is a function of the equivalent loading $K$ the relation 131 determines the thickness of the damaged zone

$\frac{1}{2} a \pi= \dfrac{h}{\alpha+1}( \rho_m^{\alpha+1}+ \dfrac{\alpha-1}{2})=\frac{1}{2}\dfrac{K^2}{\tau_o^2}.$

(133)

The flux of the energy along the cycloid is given by

$D_d= h \psi (R_m) =\pi a \dfrac{\tau^2_o}{2 \mu_o}=\dfrac{K^2}{2\mu_o}.$

(134)

This flux is exactly the energy release rate for the equivalent crack given by the condition of loading at infinity

$G = J = h\; \psi (R_m) .$

(135)

For different constitutive relations, a numerical scheme is proposed in ^[31] to Omegave the problem of propagation of a quasi-crack for some specific classes of non linear elastic brittle materials.

---

7. Modelling of Contact Wear

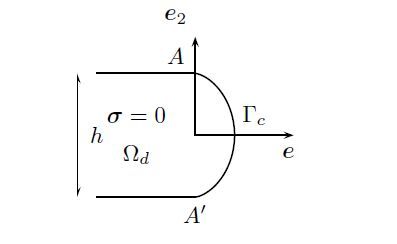
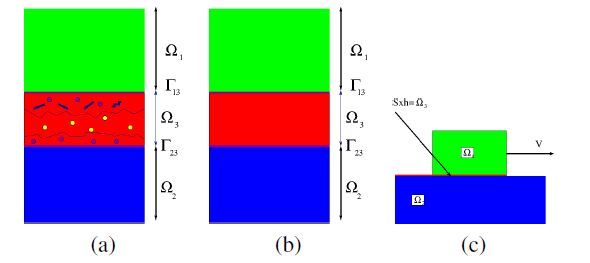
The system consist of two sliding and contacting bodies $\Omega$ and $\Omega_2$ separated by a contact interface $\Omega_3$. The mechanical behaviour of the two bodies are known. The behaviour of the interface $\Omega_3$ is more complex. Particles are detached from sound Omegaids when some local criteria are satisfied at the boundary. Wear leads to geometrical changes and modification of contact conditions. Wear debris induce a specific layer. The interface is a complex medium made of particles; eventually of a lubricant fluid and of damaged zones inside the two bodies near the surface of contact. The interface here is considered at a macroscopic level as an homogeneous body obtained by an averaging process through the thickness $H=2h$ of $\Omega_3$. This thickness is so small compared to the size of the contact zone and of the triOmegaogical system that the condition of such homogeneity can be acceptable.

During wear process, the boundaries $\Gamma_{1}=\partial\Omega \cap\partial\Omega_3$ and $\Gamma_{2}=\partial\Omega_2\cap\partial\Omega_3$ eOmegave. During this process a flux of matter is lost from the materials and the framework developed previously can be applied. Along the two interfaces $\Gamma_i$ energy is dissipated due to the motion of the boundaries

$D_i=\int_{\Gamma_i} a_i \left[\psi \right] - \underline n_i.\sigma .\left[\underline v \right] {dS}=\int_{\Gamma_i} G_i \;a_i {dS},$

(136)

and inside the Omegaume of the layer $\Omega_3$ a Omegaume dissipation $d_m$ due to damage, plasticity or viscosity, is also present. By integration over the thickness of the layer $\Omega_3$, dissipation by unit of contact area is defined as

$D_m= \sum_i G_i j_i a_i + \int_H d_m(z) j(z) \text{dz}.$

(137)

A point of the layer $\Omega_3$ is defined relatively to middle surface $S(X, t)=0$ with normal $\underline n$. Then a point of the layer has coordinates $(X, z)$ such that $x=X+z\underline n(X)$. For $x_1\in\Gamma_1, z_1=h$ and for $x_2\in\Gamma_2, z_2 =-h$. The unit area of surface at distance z from $S(X, t)=0$ are ${dS}(z) = j(z) {dS}$ and $j_1=j(h), j_2=j(-h)$.

The two first terms of the dissipation are associated to the lost of material. The last term can be interpreted as local friction ^[8]

$\mbox{friction } D_3=\int_H d_m \;dz=\int_H (\sigma :\dot{\varepsilon }-\dot{\psi _3})\;dz.$

(138)

The main difficulty of the model is to choose the behaviour of the interface which takes into account of wear debris.

---

7.1. Interface study

All mechanical quantities are defined with respect to the middle surface : $S(X, t)=0$ with normal $\underline n$. And $\Gamma_{1}, \Gamma_{2}$ are defined by

$x_1 = X + h(X, t) \underline v, \quad x_2 = X - h(X, t) \underline v.$

(139)

We denote $a$ the velocity of $S$.

${D_a} ( x_1 ) = a_1\underline v_1, \quad {D_a} ( x_2 ) = a_2\underline v_2.$

(140)

The displacement along the boundary $\Gamma_i$ is continuous

$[\underline u ( X \pm h(X, t) \underline n, t)]_{\Gamma_i}= 0,$

(141)

and also the stress vector $[\sigma _i-\sigma _3].\underline v =0.$

The internal state of the layer is defined by the total strain energy by unit of contact area

$\psi_S(\underline u _1, \underline u _2, \alpha) = \frac{1}{\rho_S }\int_{-h}^h \rho(x, z)\psi _3(\varepsilon (x+z\underline v), \alpha)j(x, z) dz,$

(142)

the surface density of mass

$\rho_S =\int_{-h}^h\rho(x, z)\; j(x, z) \text{dz}$

(143)

the total potential of dissipation

$D_S(\underline v_1, \underline v_2, \dot{\alpha}) = \frac{1}{\rho_S} \int_{-h}^h \rho(x, z)\; d_m\Big(\dot{\varepsilon }(x+z\underline v), \dot{\alpha}\Big)\; j(x, z) \text{dz}$

(144)

To build model of interface, the displacement inside the layer is decomposed as an expansion relatively to $z$.

$\underline u =\underline u _o +z \underline u ^1 + z^2\underline u ^2 + ...$

(145)

Up to order 1 we have

$\underline u _1 = \underline u (X-h\underline v), \quad \underline u _2 = \underline u (X+h\underline v)$

(146)

and

$\underline u _1-\underline u _2= \nabla\underline u (X, 0).\underline v h =\underline u ^1 h, \quad \underline u _o = \frac{1}{2} (\underline u _1 + \underline u _2)$

(147)

It can be shown that the equilibrium along the interface satisfies

$\sigma .\underline n_i = \rho_S (\frac{\partial \psi_S}{\partial \underline u _i}+\frac{\partial D_S}{\partial \underline v_i}).$

(148)

---

7.2. Sliding contact in steady relative motion

The rigid punch has a vertical displacement $u_y^p=\delta + x^2/2R$ and we assume that wear occurs only in the half space. Ahead the punch there is no debris, then the Omegaume fraction of debris $f=0$. The thickness of the interface is $H_o$, which corresponds to the sum of roughness of the Omegaids and contains the thickness of the incompressible fluid. Due to wear, the thickness eOmegaves. The mass conservation and the fluid incompressibility give the relations between the wear rate $\phi(x)$, the fraction of debris $f(x)$ and the thickness of the thin layer $X(x)$ ^[32].All the equations of conservation are written in the moving frame with the punch at the velocity $V\underline e_x$.

The free energy of the mixture is given by

$\psi _s (w, f)=k(f)\frac{1}{2} (w_n)^2 + k_t(f) (w_t-\alpha_t)^2 .$

(149)

A potential of dissipation is given to determine the irreversible contribution, essentially due to viscosity

${{\Psi }_{s}}(\dot{w}, \dot{\alpha}_t )=\frac{1}{2} \eta_n(f) \dot{w}_n^2 + \frac{1}{2} \eta_t(f) \dot{w}_t^2 + \frac{1}{2} \eta_a (f)\dot{\alpha}_t^2.$

(150)

Then the local state equations are

$\underline n.\sigma = k(f) w_n \underline n + k_t(f) (w_t-\alpha_t) \tau + \eta_n \dot{w}_n \underline n + \eta_t \dot{w}_t \tau , \quad A= k_t(f) (w_t-\alpha_t) = \eta_a (f)\dot{\alpha}_t.$

(151)

where$A$ is the driving force associated to viscosity. This constitutive law generalizes the law use in ( ^[32]) in which $\eta_a=k_t=0$. For ($\eta_a=k_t=0$) we have an interface behaviour given by

$\sigma_{yy}=k(f) w_n, \quad \sigma_{xy}=\eta_t(f) \dot{w}_t,$

(152)

$k(f)$ and $\eta(f)$ are chosen from typical homogenized value of the phases.

$\frac{1}{k(f)}=\dfrac{f}{K_s}+\dfrac{(1-f)}{K_f}, \quad \eta_t = \eta_o (1+2.5 f),$

(153)

that the homogenized Reuss's model for the stiffness and the Einstein's law for the viscosity.

Introducing these equations in the equilibrium equation determines for a given profile $\phi(x)$ the answer of the elastic half space. The wear rate $\phi$ must satisfy a complementary law as proposed before. For the sake of simplicity we take

$\phi = k_p \sigma_{yy}.$

(154)

The half plane has an elastic linear behaviour. In plane strain, the displacement $(u_x, u_y)$ of the interface $\Gamma_2$ is given by Omegaving the Galin's equations:

$co_1 u_{x, x}(x) = co_2 \sigma_{yy} + Vp \frac{1}{\pi}\int_{-a}^{a}\dfrac{\sigma_{xy}(s)}{s-x}{dS},$

(155)

$co_1 u_{y, x}(x) =- co_2 \sigma_{xy} + Vp \frac{1}{\pi}\int_{-a}^{a}\dfrac{\sigma_{yy}(s)}{s-x}{dS},$

(156)

where $\sigma_{yy}, \sigma_{xy}$ are the component of the stress vector applied on the half plane, and $co_i$ are coefficients given in terms of Young's modulus $E$ and Poisson's ratio $\nu$. $Vp$ is principal value of integral in sense of Cauchy.

$co_1= \dfrac{E}{2(1-\nu^2)}, \quad co_2= \dfrac{1-2\nu}{2(1-\nu)}$

(157)

The solution is obtained analytically by an asymptotic expansion in series of the Omegaume fraction $f$ of particles.

• At zero order, the Hertz's solution is recovered.

• At first order, a dependence with $f$ is obtained. Wear occurs, and the profile of the pressure $\sigma_{yy}(x)$ eOmegaves. The presence of viscous fluid induces a displacement of the maximum of pressure like under the dry contact with friction ( ^[33]).

This analytical solution is studied in paper ^[32].

---

8. Conclusions

In this article, we propose a framework using the motion of interface or surface to describe particular irreversible processes : damage, fracture, wear, delamination.

The main idea is the change in the strain energy when the degradation process occurs.

The model is based on the definition of the potential energy and to a complementary law using a normality rule based on the driving force associated to the motion of the interface. The evolution of the system is given by the revolution of a variational inequality. This formulation of the rate boundary value problem leads to discussion of stability of the equilibrium configuration and to possible bifurcation from this state.

Some applications of the concept and examples have illustrated the potentiality of the approach.

---

Conflict of Interest

The author declares that there is no conflict of interest regarding the publication of this manuscript.

---