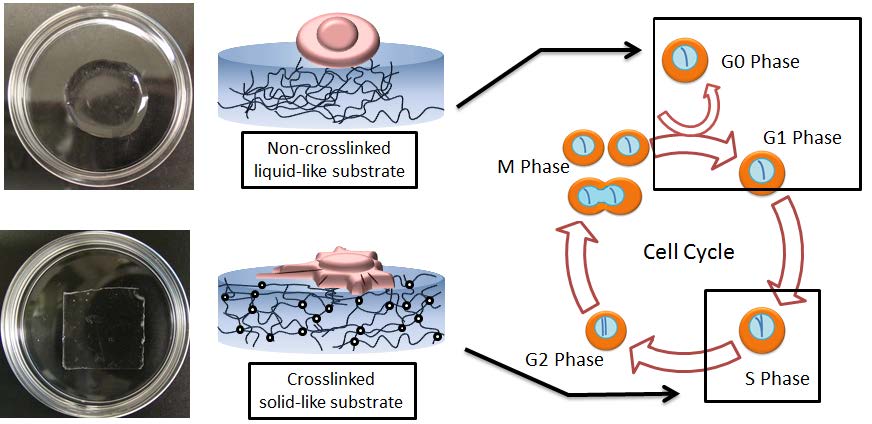
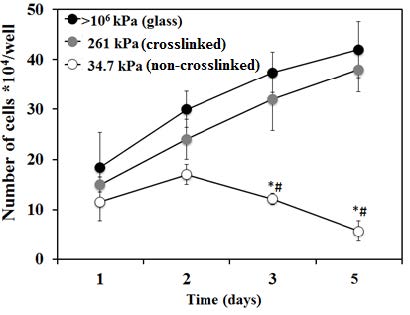
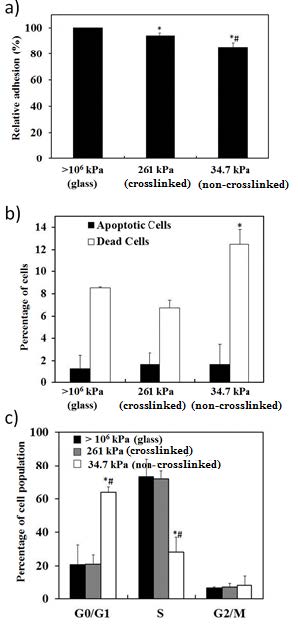
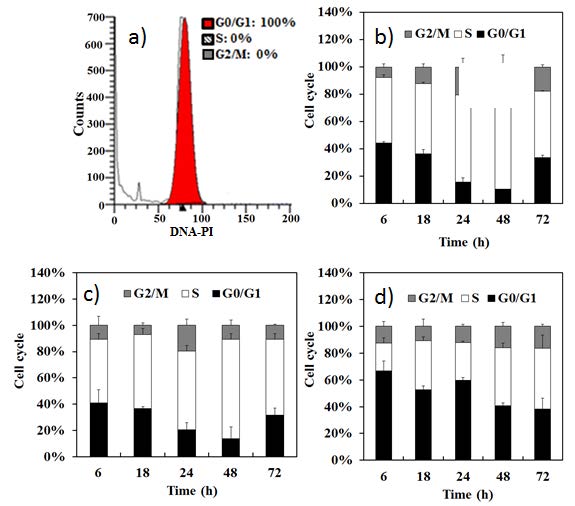
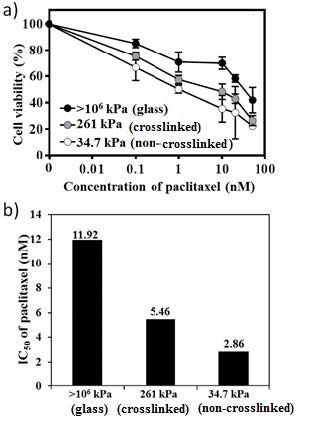
Although various polymeric substrates with different stiffness have been applied for the regulation of cells’ fate, little attention has been given to the effects of substrates’ fluidity. Here, we implement for the first time biodegradable polymer with fluidic property for cancer therapy by investigating cell adhesion, proliferation, apoptosis/death, cycles of cancer cells as well as the anticancer drug efficacy. To achieve this, we prepared crosslinked and non-crosslinked copolymers of ɛ-caprolactone-co-D, L-lactide (P(CL-co-DLLA)). The tensile test showed the crosslinked P(CL-co-DLLA) substrate has the stiffness of 261 kPa while the loss modulus G’’ of the non-crosslinked substrate is always higher than the storage modulus G’ (G’’/G’=3.06), indicating a quasi-liquid state. Human lung epithelial adenocarcinoma cells on crosslinked substrate showed well- spread actin stress fibers and visible focal adhesion with an increased S phase (decreased G0/G1 phase). The cells on non-crosslinked substrate, on the other hand, showed rounded morphology without visible focal adhesion and an accumulated G0/G1 phase (decreased S phase). These results suggest that the behavior of cancer cells not only depends on stiffness but also the fluidity of P(CL-co-DLLA) substrate. In addition, the effects of substrate’s fluidity on anti-cancer drug efficacy were also investigated. The IC50 values of paclitaxel for cancer cells on crosslinked and non-crosslinked substrates are 5.46 and 2.86 nM, respectively. These results clearly indicate that the fluidity of polymeric materials should be considered as one of the crucial factors to study cellular functions and molecular mechanism of cancer progression.
1.
Introduction
In this paper, we shall present a incisive analysis of a finite difference method for solving the following supergeneralized viscous Burgers' equation in the domain $ [0, L] \times [0, T] $:
here $ L $ and $ T $ are positive constants, $ \Psi(x) $ that satisfies $ \Psi(0) = \Psi(L) = 0 $ is smooth on $ [0, L] $, $ p \geq 1 $ and $ q \geq 0 $ are two positive integers, and positive constant $ \nu $ denotes the dynamic viscosity coefficient.
In the last few decades, Burgers' equation for the case of supergeneralized viscous Burgers' equation with $ p = 1 $ and $ q = 0 $ has attracted much attention from researchers. It is caused by numerous effective applications of Burgers' equation to many fields of science and engineering like shock wave theory, cosmology, gas dynamics, quantum field and traffic flow, see e.g., [2,3,4,5,6]. The supergeneralized viscous Burgers' equation is a typical evolution equation, and recently a series of numerical methods have been developed to solve it, e.g., finite difference method [7,8,9,10,11], finite volume method [12,13,14], ADI method [15,16,17,18], collocation method [19,20], two-grid method [21,22] and extrapolation method [23]. Meanwhile, as the other simplified form of supergeneralized viscous Burgers' equation with $ p \geq 1 $ and $ q = 0 $, the generalized Burgers' equation also plays an important role in applied mathematics and engineering, see e.g., [24,25,26,27]. Recently, Wang et al. [28] established two conservative fourth-order compact schemes for Burgers' equation. Zhang et al. [29,30] derived various efficient difference schemes for Burgers' type equations. Gao et al. [31] proposed a bounded high-order upwind scheme in the normalized-variable formulation for the modified Burgers' equations. Guo et al. [32] proposed a BDF3 finite difference scheme for the generalized viscous Burgers' equation. Hu et al. [33] considered an implicit difference scheme to study the local conservation properties for Burgers' equation. Pany et al. [34] investigated an $ H^1 $-Galerkin mixed finite element method to approximate the solution of the Burgers' equation. In addition, Jiwari et al. [35] studied a numerical scheme which is a composition of forward finite difference, quasilinearization process and uniform Haar wavelets for solving Burgers' equation. Wang et al. [36] used the weak Galerkin finite element method to study a class of time fractional generalized Burgers' equation. Wang et al. [37,38,39] presented an implicit robust difference method to solve the modified Burgers equation on graded meshes. Zhang et al. [40] provided a fourth-order compact difference scheme for time-fractional Burgers' equation. Zhang et al. [41] considered a conservative decoupled difference scheme for the rotation-two-component Camassa-Holm system. Sun et al. [42] obtained nonlinear discrete scheme for generalized Burgers' equation with the help of meshless method. Zhang et al. [1] constructed various difference schemes for generalized Burgers' equation only with one positive parameter $ p\geq 1 $.
The previous works are mainly concerned with the simple case of the parameter $ p = 1 $ for problem (1.1)–(1.3). Our scheme can extended the results in the previous work [1] with a positive integer $ p\geq 1 $. In this paper, the main contributions are as follows:
● We construct the discretization of the nonlinear term by a second-order operator in supergeneralized viscous Burgers' equation and provide complete theoretical analysis on the proposed scheme, including conservation, existence, uniqueness and convergence.
● We prove $ L_2 $-norm and $ L_{\infty} $-norm convergence in pointwise sense by the cut-off function method, which doesn't have any step ratio restrictions. The $ L_2 $-norm and $ L_{\infty} $-norm convergence are proved with separate and different ways, which is different from previous work in [1].
The rest of the paper is arranged as follows. We introduce some useful notations for discretization and construct our proposed scheme in Section 2. In Section 3, we present certain conclusions about conservative invariants and boundedness of the suggested numerical scheme, and we provide the proof of unique solvability and convergence. The numerical test in Section 4 is given to demonstrate the reliability of our analysis. A brief conclusion is followed in Section 5.
2.
Derivation of the three-level difference scheme
Firstly, for any integer $ s $, we denote set $ N_{s} = \{i| 1\leq i\leq s, i\in Z\} $ and $ N_{s}^0 = \{i| 0\leq i\leq s, i\in Z\} $. For two positive integers $ \tilde{m} $ and $ \tilde{n} $, define the spatial step $ h = \frac{L}{\tilde{m}} $, and the temporal step $ \tau = \frac{T}{\tilde{n}} $. Denote$ \, x_i = ih, \, i\in N_{\tilde{m}}^0;\ t_k = k\tau, \, k\in N_{\tilde{n}}^0 $. We introduce the mesh $ \tilde{\omega}_{LT} = \tilde{\omega}_L\times \tilde{\omega}_T, $ where $ \tilde{\omega}_L = \{x_i\, |\, i\in N_{\tilde{m}}^0\} $, and $ \tilde{\omega}_T = \{t_k\, |\, k\in N_{\tilde{n}}^0\} $. Denote $ x_{i+\frac12} = \frac12(x_i+x_{i+1}), i\in N_{\tilde{m}-1}^0 $ and $ t_{k+\frac12} = \frac{1}{2}(t_k+t_{k+1}), k\in N_{\tilde{n}-1}^0 $.
Let $ \mathcal{J}_h = \{j\, |\, j = (j_0, j_1, \cdots, j_{\tilde{m}})\} $ and $ {\mathop{\mathcal{J}}\limits^\circ}_h = \{j\, |\, j\in \mathcal{J}_h, j_0 = j_{\tilde{m}} = 0\} $ be the spaces of grid functions on $ \tilde{\omega}_L $. For $ d, j\in \mathcal{J}_h $, introducing the following notations:
Lemma 2.1. [28] Let $ j\in \mathcal{J}_h $ and $ r\in {\mathop{\mathcal{J}}\limits^\circ}_h, $ then
Lemma 2.2. [28] Set $ j\in {\mathop{\mathcal{J}}\limits^\circ}_h $, then
Lemma 2.3. Suppose that $ U = (U_0, U_1, \ldots, U_{\tilde{m}}) $, $ u = (u_0, u_1, \ldots, u_{\tilde{m}})\in \mathcal{J}_h $ and $ g(u) $ is a second-order smooth function. Denote $ e = (e_0, e_1, \ldots, e_{\tilde{m}}) $ and $ e_i = U_i-u_i $, $ i\in N_{\tilde{m}}^0 $. Then there are $ \rho\in (0, 1) $ and $ \zeta_i\in(y_i, r_i) $ such that
where
Proof. Using the mean value theorem, one has
Again, applying the mean value theorem, we have
The proof is finished.
In order to construct a three-level conservative numerical scheme for supergeneralized viscous Burgers' equation (1.1)–(1.3), we first turn problem (1.1) into an equivalent form as follows:
where $ C_q^m $ is the binomial coefficient, $ 0\leq m\leq q $.
We denote $ U^k_i = u(x_i, t_k) $, and let $ u_i^k $ denote the nodal approximation to the exact solution computed at the mesh point $ (x_i, t_k) $.
Considering (2.2) at the point $ (x_i, t_k) $, $ i\in N_{\tilde{m}-1} $, $ k\in N_{\tilde{n}-1} $, one gets
By Taylor expansion, one gets
where $ c_1 $ is a positive constant.
We consider (1.1) at the point $ (x_i, t_0) $, $ i\in N_{\tilde{m}-1} $, noticing (1.2), and one gets
Denote
Considering (2.2) at the point $ (x_i, t_{\frac{1}{2}}) $, $ i\in N_{\tilde{m}-1} $, one gets
and
Noticing (1.2) and (1.3), we get
Omitting the small terms $ P_i^k $ in (2.3) and $ P_i^0 $ in (2.7), and replacing $ U_i^k $ by $ u_i^k $, and $ {W_{(m)}}_i^k $ by $ {w_{(m)}}_i^k $, $ i\in N_{\tilde{m}-1} $, $ k\in N_{\tilde{n}-1} $, respectively. Thus, we can obtain the three-level difference approximation for (1.1)–(1.3) as follows
Noticing that substituting (2.12) into (2.10), the three-level difference scheme only contains one variable $ u^k_i $.
3.
The numerical analysis of three-level difference scheme
We now begin to consider the energy conservation and boundedness of solution of the three-level numerical scheme (2.10)–(2.14).
Theorem 3.1. Suppose that $ \{u^k_i, {w_{(m)}}_i^k\, |\, i\in N_{\tilde{m}}^0, k\in N_{\tilde{n}}^0\} $ is the solution of (2.10)–(2.14), we get
where
Proof. 1) Taking the inner product of (2.11) with $ u^{\frac12} $, one obtains
Since $ u^{\frac12}\in {\mathop{\mathcal{J}}\limits^\circ}_h $, by Lemmas 2.1 and 2.2, one gets
Thus,
Namely,
2) Taking the inner product of (2.10) with $ u^{\bar{k}} $, one gets
Since $ u^{\bar{k}}\in {\mathop{\mathcal{J}}\limits^\circ}_h $, by Lemmas 2.1 and 2.2, we have
Thus,
Above equality can be rewritten as
Thus,
Corollary 3.2. Let $ \{u^k_i, {w_{(m)}}_i^k\, |\, i\in N_{\tilde{m}}^0, k\in N_{\tilde{n}}^0\} $ represent the solution of (2.10)–(2.14). Then one has
Proof. According to Theorem 3.1,
Thus,
Corollary 3.3. Let $ \{u^k_i, {w_{(m)}}_i^k\, |\, i\in N_{\tilde{m}}^0, k\in N_{\tilde{n}}^0\} $ represent the solution of (2.10)–(2.14). Then the computed solution $ u^k_i $ can satisfy
Proof. From (3.4) and (3.5) in Theorem 3.1, we can get Corollary 3.3 directly. □
Furthermore, we will carry out the proof of existence and uniqueness of the solution of (2.10)–(2.14).
Theorem 3.4. The solution of (2.10)–(2.14) exists and it is unique.
Proof. According to (2.13) and (2.14), $ u^0 $ has been determined uniquely. From (2.11) and (2.14), establishing a linear system with respect to $ u^1 $, and considering the corresponding homogeneous system
Taking the inner product of (3.6) with $ u^1 $, one has
By Lemmas 2.1 and 2.2, one gets
Therefore,
It is easy to obtain
It implies that (2.11) and (2.14) determine $ u^1 $ uniquely.
Assume that $ u^k $ and $ u^{k-1} $ have been known. By (2.10), (2.12) and (2.14), we get the following linear homogeneous system of equations with respect to $ u^{k+1} $:
Taking the inner product of (3.8) with $ u^{k+1} $, one has
By Lemmas 2.1 and 2.2, one gets
Therefore,
It is easy to obtain
Consequently, it implies that $ u^{k+1} $ solved by (2.10), (2.12) and (2.14) is unique.
Based on mathematical induction, (2.10)–(2.14) is uniquely solvable, and this completes the proof. □
In order to establish the convergence of (2.10)–(2.14), we will introduce the cut-off function method next.
Denote
Define a group of second-order smooth functions
where $ 0\leq m\leq q $.
Denote
Based on the cut-off function method, we construct a new difference scheme as follows:
For the above difference scheme, it is conservative.
Theorem 3.5. Suppose that $ \{u^k_i, {w_{(m)}}_i^k\, |\, i\in N_{\tilde{m}}^0, k\in N_{\tilde{n}}^0\} $ represents the solution of (3.11)–(3.15), we get
where
Proof. The proof of (3.16) and (3.17) is similar to the proof of Theorem 3.1. □
Now we prove the $ L_2 $-norm and $ L_{\infty} $-norm convergence of (3.11)–(3.15).
Theorem 3.6. Assume that $ \{u^k_i, {w_{(m)}}_i^k\, |\, i\in N_{\tilde{m}}^0, k\in N_{\tilde{n}}^0\} $ is the solution of (3.11)–(3.15) and $ \{U^k_i, {W_{(m)}}_i^k\, |\, i\in N_{\tilde{m}}^0, k\in N_{\tilde{n}}^0\} $ is the solution of (1.1)–(1.3), there exists a positive constant $ c_{2} $ such that
Proof. Define
Since (3.10), we get
Subtracting (3.11)–(3.15) from (2.3), (2.7) and (2.9) follows
When $ k = 0 $, from (3.22) and (3.23), we get
Taking the inner product of (3.19) with $ e^{\frac12} $, one gets
By Lemmas 2.1 and 2.2, we obtain
Substituting (3.26)–(3.28) into (3.25), we have
Thus,
When $ \frac{\tau}{2}\leq \frac{1}{3} $, noticing (2.8), one gets
or
By (3.10) and Lagrange mean value theorem, one gets
Taking the inner product of (3.20) with $ e^{\bar{k}} $, one gets
Using Lemma 2.2, one obtains
Substituting (3.33) and (3.34) into (3.32), above equality (3.32) becomes
where $ a_0 = \max_{0\leq m\leq q} C^m_q $.
Noticing that
Thus, by Lemma 2.1, we have
Noticing (3.30), (3.31) and (3.10), we have
Substituting (3.37) into (3.35), (3.35) yields
Combining (2.4), above equality (3.38) becomes
where $ c_{3} = \frac{a_0(1+q)\tilde{c}_1\hat{c}_1}{2(p+2)} + \frac{a_0^2(1+q)^2M^2\hat{c}_1^2}{4(p+2)^2\nu} $ and $ c_{4} = \frac{a_0(1+q)\tilde{c}_1\hat{c}_1}{4(p+2)} +\frac{1}{4} $ are two positive constants.
Rearranging (3.39) to yield
For $ k\in N_{\tilde{n}-1} $, when $ 4c_{4}\tau\leq \frac{1}{3} $, (3.40) yields
Therefore,
According to Gronwall's inequality, we obtain
Noticing (3.24) and (3.29), one gets
where $ c_{2} = e^{6(c_{3}+2c_{4})T}\cdot[Lc^2_1 +\frac{Lc^2_1}{2(c_{3}+2c_{4})}]^{\frac{1}{2}} $.
Namely,
Theorem 3.7. Assume that $ \{u^k_i, {w_{(m)}}_i^k\, |\, i\in N_{\tilde{m}}^0, k\in N_{\tilde{n}}^0\} $ is the solution of (3.11)–(3.15) and $ \{U^k_i, {W_{(m)}}_i^k\, |\, i\in N_{\tilde{m}}^0, k\in N_{\tilde{n}}^0\} $ is the solution of (1.1)–(1.3), there exists positive constants $ c_7 $ and $ c_8 $ such that
Proof. We will use the mathematical induction to prove the result. When $ k = 0 $, from (3.22) and (3.23), we get
Therefore, the conclusion is valid for $ k = 0 $.
1) Taking the inner product of (3.19) with $ \delta_te^{\frac12} $, one gets
Noticing that
then (3.46) becomes
Using Lemmas 2.1 and 2.2, we have
From (2.8), we get
When $ \tau\leq2\nu $, one gets
or
2) Taking the inner product of (3.20) with $ \Delta_te^k $, one gets
Suppose (3.43) and (3.44) hold for $ 0\leq k\leq s $ $ (1\leq s\leq \tilde{n}-1) $.
From (3.10) and Lemma 2.2, one gets
When $ c_7(\tau^2 + h^2)\leq 1 $, one gets
Using Lemma 2.2, above equality (3.50) becomes
Noticing that
By Lagrange mean value theorem and the Lemma 2.3, we have
Thus, combining (3.54) and (3.55) yields
Using Lemma 2.2, combining (3.51), (3.52) and (3.56), it is easy to get
where $ c_{9} = (L\hat{c}_1\tilde{c}_1 +\frac{1}{2}L\hat{c}_1\tilde{c}_1 +\frac{1}{2\sqrt{6}}L^2\hat{c}_2\tilde{c}_1^2) $ and $ c_{10} = 2\hat{c}_0+\frac{1}{2}\sqrt{L}\hat{c}_1(\sqrt{L}\tilde{c}_1+1) $.
Thus, (3.53) becomes
where $ a_0 = \max_{0\leq m\leq q}C^m_q $.
Noticing (2.4), (3.58) becomes
where $ c_5 = \frac{a_0^2(q+1)^2c_{9}^2}{(p+2)^2} $ and $ c_6 = \frac{a_0^2(q+1)^2c_{10}^2}{(p+2)^2} $ are two positive constants.
For $ 1\leq k\leq s $, rearranging (3.59) to yield
When $ \frac{2c_6\tau}{\nu}\leq \frac{1}{3} $, (3.60) yields
Therefore,
According to Gronwall's inequality, (3.61) yields
Noticing (3.45) and (3.49), one gets
where $ c_7 = e^{\frac{3c_5+3c_6}{\nu}T}\cdot[Lc^2_1 +\frac{Lc^2_1}{2(c_5+c_6)}]^{\frac{1}{2}} $.
Namely,
Consequently, (3.43) holds for $ k = s+1 $.
From Lemma 2.2, it is easy to get
Corollary 3.8. Let $ \{u^k_i, {w_{(m)}}_i^k\, |\, i\in N_{\tilde{m}}^0, k\in N_{\tilde{n}}^0\} $ be the solution of (3.11)–(3.15). When $ c_7(\tau^2+h^2)\leq 1 $, there exists two constants $ c_{11} $ and $ c_{12} $ such that
Proof. When $ c_7(\tau^2+h^2)\leq 1 $, one has
By Lemma 2.2, we get $ \|u^k\|_\infty \leq \frac{\sqrt{L}}{2} c_{10} \equiv c_{12} $.
This means the solution of (3.11)–(3.15) is bounded. □
In the end, for the proposed scheme (2.10)–(2.14), we can obtain the following convergence.
Corollary 3.9. Let $ \{u^k_i, {w_{(m)}}_i^k\, |\, i\in N_{\tilde{m}}^0, k\in N_{\tilde{n}}^0\} $ be the solution of (2.10)–(2.14) and $ \{U^k_i, {W_{(m)}}_i^k\, |\, i\in N_{\tilde{m}}^0, k\in N_{\tilde{n}}^0\} $ be the solution of (1.1)–(1.3). When $ c_8(\tau^2+h^2)\leq 1 $, one has
where $ c_{13} $ is a constant.
Proof. Let $ \{\hat{u}^k_i\, |\, i\in N_{\tilde{m}}^0, k\in N_{\tilde{n}}^0\} $ be the solution of (3.11)–(3.15). When $ c_8(\tau^2+h^2)\leq 1 $, one has
Thus, $ g_m(\hat{u}_i^k) = (\hat{u}_i^k)^{p+m} $.
This means the difference scheme (2.10)–(2.14) is equivalent to (3.11)–(3.15). According to Theorems 3.6 and 3.7, we finish the proof of Corollary 3.9. □
4.
Numerical test
A numerical example is given to verify theoretical conclusions of the three-level difference scheme for supergeneralized viscous Burgers' equation.
Example 4.1. We consider (1.1)–(1.3) with $ T = L = 1 $, $ \nu = 1 $, $ \Psi(x) = \sin(\pi x) $, and $ p $, $ q $ take some different integer values, respectively.
To describe the numerical errors in $ L_{\infty} $-norm for the computed solution and corresponding convergence orders, we denote
and
where $ h $ and $ \tau $ are sufficiently small.
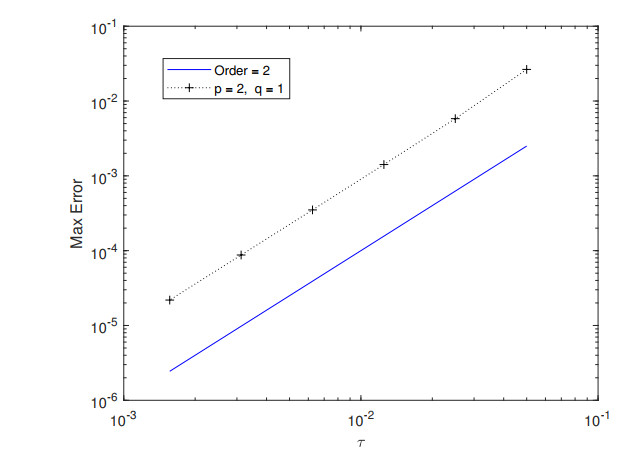
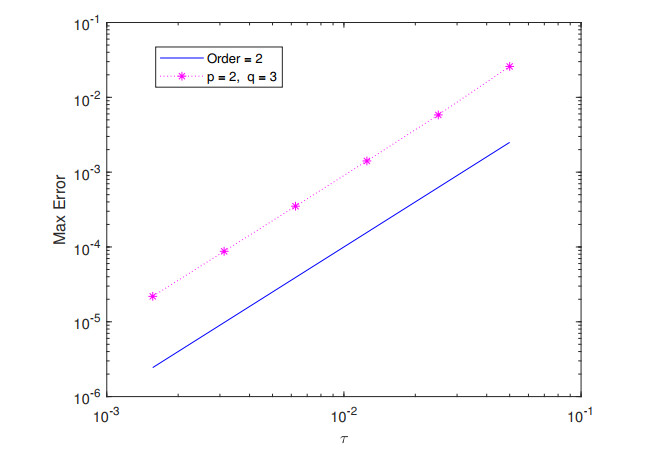
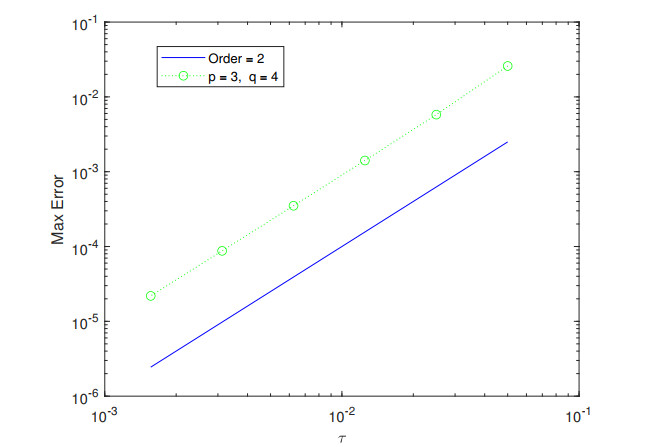
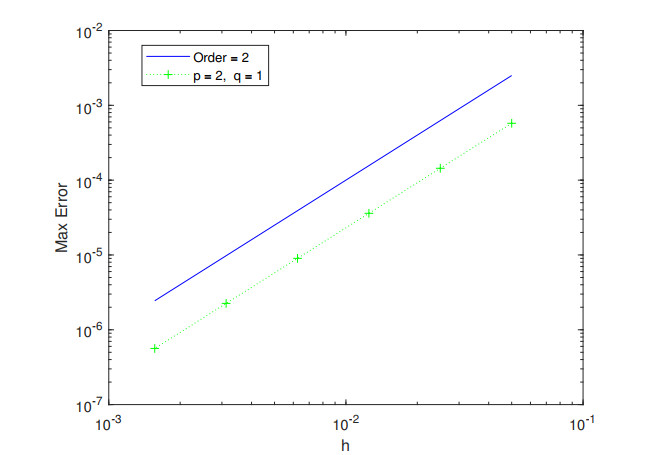
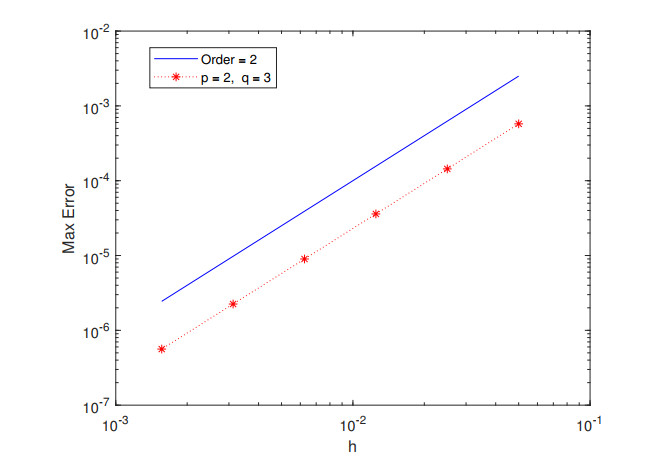
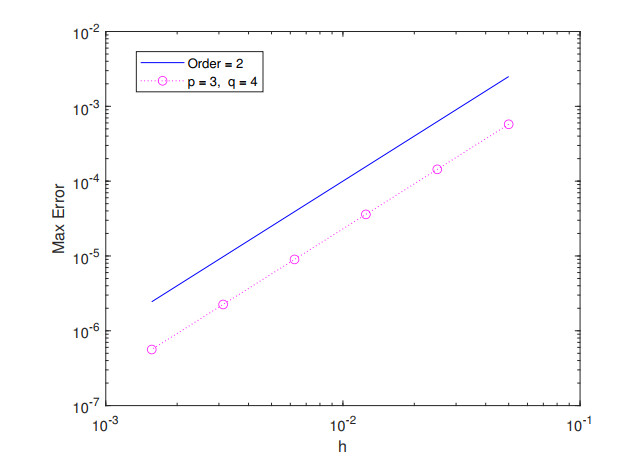
Table 1 lists the temporal convergence orders with $ h = \frac{1}{64} $. We compute the spatial convergence orders with $ \tau = \frac{1}{64} $ in Table 2. Table 3 presents the temporal and spatial errors and convergence orders with $ \tau = h $. The corresponding error and convergence orders are presented in Figures 1–6. The results demonstrate (2.10)–(2.14) is convergent with the convergence order of two both in space and in time.
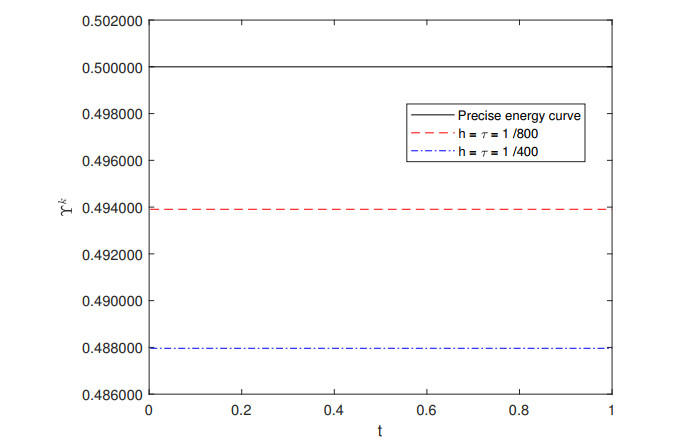
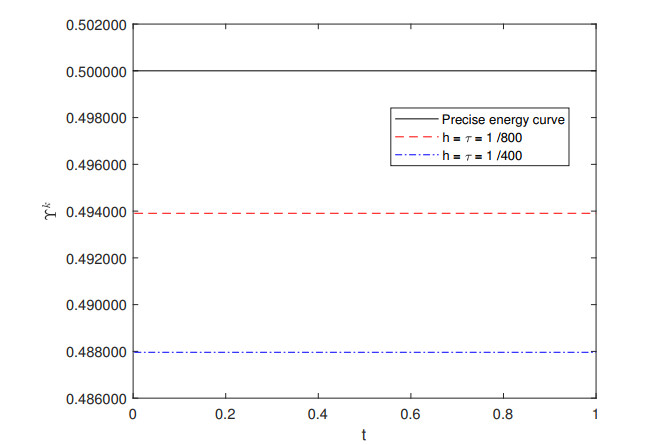
In Figures 7–9, we compute $ \Upsilon^k $ in Theorem 3.1 to verify the conservativity of the difference scheme (2.10)–(2.14). The results demonstrate that difference scheme (2.10)–(2.14) is conservative.
5.
Conclusions
In this paper, a three-level linearized conservative scheme approximating supergeneralized viscous Burgers' equation is studied. We construct the discretization of the nonlinear term by a second-order operator in supergeneralized viscous Burgers' equation and prove the three-level scheme is uniquely solvable based on the mathematical induction. At last, the $ L_2 $-norm and $ L_{\infty} $-norm convergence are proved with separate and different ways.
Use of AI tools declaration
The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.
Conflicts of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad: