Associations of CYP1A1 gene polymorphisms and risk of breast cancer in Indian women: a meta-analysis

1.   Introduction

In recent years, the study of fractional derivatives has been an important topic. It has been used to model many phenomena in numerous fields such as science and engineering. There are many interpretations for fractional derivatives, such as the definition of Caputo ^[1], the definition of Riemann-Liouville ^[2], the definition of Grunwald-Letnikov ^[3], and most recently, Conformable ^[4], Atangana-Baleanu ^[5], Wallström ^[6], Jumarie ^[7], Klimek ^[8] and others.

In practice, where quantitative results are needed for given real-world problems, numerically approximate solutions can often be demonstrably better, more reliable, more detailed, efficient and cost-effective than analytical ones for certain fractional structures. A number of studies ^{[9,10,11,12,13,14]} were therefore involved in developing approaches for providing estimated solutions. One of these approaches is the Hilbert space kernel reproduction (RKHS) method used for the first time by S. Zaremba for the harmonic and biharmonic functions at the beginning of the 20th century to find solutions for boundary value problems (BVPs).

The RKHS precede the Dirac delta function in many ways, among which we mention providing an important structure for random distribution of multi-round data and, providing accurate approximation of multi-dimensional general functions and the possibility to pick any point in the integration interval.

The RKHS algorithm has been successfully applied to various fields of numerical analysis, computational mathematics, probability and statistics ^[15,16], biology ^[17], quantum mechanics and wave mechanics ^[18]. Therefore wide range of research works have been directed to its applications in various stochastic categories ^[19], and defined problems involving operator equations ^[20], partial differential equations ^[21,22], integrative equations ^[23,24], and differential integration equations ^{[24,25,26,27,28,29]}. In addition, many studies have focused in recent years on the use of the RKHS method as a framework for seeking approximate numerical solutions to different problems ^{[30,31,32,33,34,35,36,37,38,39]}.

Moreover, the numerical solution of the different groups of BVP can be found in ^[40,41,42]. The two-point BVPs has a strong interest in applied mathematics, this kind of problems arise directly from mathematical models or by turning partial differential equations into ordinary differential equations. As this type of problems does not have an exact solution, many special techniques have been used to solve it, including the shooting method ^[43,44], the collocation method ^[45,46], the finite difference method ^[47,48], and the quasilinearization method ^[49,50]. The continuous genetic algorithm approach was used to solve these schemes in ^[51,52,53].

The present paper is structured as follows: in Section 2, we set out some basic concepts and results from fractional calculus theory. In Section 3, the iterative form of the reproducing kernel algorithm is used to build and measure the solution of the fractional differential method with temporal two points. In Section 4 and 5, the convergence and error estimator are discussed to provide a number of numerical results to demonstrate the efficiency and accuracy of the reproducing kernel Hilbert space method. At last in section 6, a conclusion of the results is made.

2.   Preliminaries

In applied mathematics and mathematical analysis, there are several definitions of fractional derivatives, Riemann-Liouville and Caputo are the most popular of all ^[54]. In this section, we list some of these definitions in addition to reproducing kernel spaces on finite domain $ [t_0, t_f] $.

Definition 2.1. ^[55] Let $ n \in \mathbb{R}^+ $. The operator $ \mathscr{J}^{n}_{t_0} $ defined on $ L_1[t_0, t_f] $ by

for $ t_0\leq x\leq t_f $, is called the Riemann-Liouville fractional integral operator of order $ n $. For $ n = 0 $, we set $ \mathscr{J}^{0}_{t_0}: = I $, the identity operator.

Definition 2.2. ^[55] Let $ n\in \mathbb{R}^+ $ and $ m = \left[n \right] $. The operator $ \mathcal{D}^{n}_{t_0} $ defined by

is called the Riemann-Liouville fractional differential operator of order $ n $. For $ n = 0 $, we set $ \mathcal{D}^{0}_{t_0}: = I $, the identity operator.

Definition 2.3. ^[55] Let $ \alpha \in \mathbb{R}^+ $ and $ n-1 < \alpha < n $. The operator $ \mathcal{D}^{\alpha}_{*t_0} $ defined by

for $ t_0\leq x\leq t_f $, is called the Caputo differential operator of order $ \alpha $.

Definition 2.4. ^[35] Let $ \mathcal{M} $ be nonempty set, the function $ \mathcal{K} :\mathcal{M}\times \mathcal{M}\longrightarrow \mathbb{C} $ is a reproducing kernel of the Hilbert space $ \mathcal{H} $ if the following conditions are met:

(1) $ \mathcal{K}(., t)\in \mathcal{M}, \forall t \in \mathcal{M} $,

(2) the reproducing property: $ \forall t\in \mathcal{M}, \forall z\in \mathcal{H}: \langle z(.), \mathcal{K}(., t) \rangle = z(t). $

The second condition means that the value of $ z $ at the point $ t $ is reproduced by the inner product of $ z $ with $ \mathcal{K} $.

Note: The reproducing kernel is unique, symmetric and positive definite.

Definition 2.5. $ L^2[t_0, t_f] = \left\{ \vartheta\; |\int_{t_0}^{t_f}\vartheta^2(t)\; dt < \infty \right\} $.

Definition 2.6. The space $ \mathcal{W}^{1}_{2}[t_0, t_f] $ is defined as:

The inner product and its norm are given by:

Definition 2.7. The space $ \mathcal{W}^{2}_{2}[t_0, t_f] $ is defined by:

$ \mathcal{W}^{2}_{2}[t_0, t_f] = \left\{ \vartheta|\vartheta, \vartheta'\;{ are \;absolutely\; continuous \;real \;value \;functions, }\vartheta''\in L^{2}[t_0, t_f], \vartheta(t_0) = 0 \right\} $.

The inner product and its norm are given by:

Definition 2.8. $ \mathcal{W}^{3}_{2}[t_0, t_f]\! = \!\left\{ \vartheta|\vartheta, \vartheta', \vartheta''\;{are\; absolutely\; continuous, }\vartheta^{(3)}\!\in L^{2}[t_0, t_f], \vartheta(t_0)\! = \!0, \vartheta(t_f)\! = \!0 \right\} $.

The inner product and its norm in $ \mathcal{W}^{3}_{2}[t_0, t_f] $ are given by:

Remark 2.1. The Hilbert space $ \mathcal{W}_{2}^{m}[t_0, t_f] $ is called a reproducing kernel if for any fixed $ t \in [t_0, t_f] $, $ \exists \mathcal{K}_{t}(s)\in \mathcal{W}_{2}^{m}[t_0, t_f] $ such that $ \langle \vartheta(s), \mathcal{K}_{t}(s) \rangle_{\mathcal{W}_{2}^{m}} = \vartheta(t) $ for any $ \vartheta(s) \in \mathcal{W}_{2}^{m}[t_0, t_f] $ and $ s \in [t_0, t_f] $.

Remark 2.2.

(1) In ^[56], $ \mathcal{W}^{1}_{2} $ is RKHS and its reproducing kernel is:

(2) In ^[57], $ \mathcal{W}^{2}_{2} $ is RKHS and its reproducing kernel is:

3.   Reproducing kernel Hilbert space method (RKHSM)

In this section, we develop an iterative method for constructing and calculating fractional differential equations with a temporal two-point solution. In order to emphasize the idea, we start by considering the general form of the BVP:

Subject to BC's:

where:

$ \delta $, $ \beta $ $ \in \mathbb{R} $, and $ \mathcal{D}^{\alpha} $ denotes the Caputo fractional derivative of order $ \alpha $ and

We use the RKHS method to obtain a solution of BVPs (3.1) and (3.2) based on the following methodology:

● To attain a problem with homogenous BC's, we first assume that: $ Y(t_0) = \gamma $, ($ \gamma $ arbitrary) and

We get:

Subject to:

● Then, we construct the reproducing kernel space $ \mathcal{W}_{2}^{2}[t_0, t_f] $ in which each function satisfies the homogeneous boundary conditions of (3.5) using the space $ \mathcal{W}_{2}^{1}[t_0, t_f] $.

Take $ \mathcal{K}_t(\tau) $ and $ \mathcal{R}_t(\tau) $ to be the reproducing kernel functions of the spaces $ \mathcal{W}_{2}^{2}[t_0, t_f] $ and $ \mathcal{W}_{2}^{1}[t_0, t_f] $ respectively.

● Next, we define the invertible bounded linear operator $ L:\mathcal{W}_{2}^{2}[t_0, t_f]\longrightarrow \mathcal{W}_{2}^{1}[t_0, t_f] $ such that:

The BVPs (3.4), (3.5) can therefore be transformed to the following form:

Where $ \mathcal{U}(t) $ and $ \mathcal{V}(t) $ are in $ \mathcal{W} _{2}^{2}[t_0, t_f] $ and $ \mathcal{F}, \mathcal{G}\in \mathcal{W} _{2}^{1}[t_0, t_f] $.

Applying Riemann-Liouville fractional integral operator $ \mathscr{J}^{\alpha}_{t_0} $ to both sides using $ \mathcal{U}(t_{0}) = 0 $ and $ \mathcal{V}(t_{0}) = 0 $, we get:

Thus, we can notice that: $ L \mathcal{U}(t) = \mathcal{U}(t), $ and so the BVPs are transformed to the equivalent form:

● When choosing a countable dense set $ \left\{ t _{i} \right\}_{i = 1}^{\infty } $ from $ [t_0, t_f] $ for the reproducing kernel of the space $ \mathcal{W} _2^{2}[t_0, t_f] $, we define a complete system on $ \mathcal{W} _2^{2}[t_0, t_f] $ as: $ \Psi_i(t) = L^*\Phi_i(t) $ where $ \Phi_{i}(t) = \mathcal{R}_{t _{i}}(\tau) $, and $ L^* $ is the adjoint operator of $ L $.

Lemma 3.1. $ \Psi_{i}(t) $ can be written on the following form:

Proof. It is clear that:

● The orthonormal function system $ \{\overline{\Psi}_i^\eta(t)\}_{i = 1}^\infty $, $ \eta = 1, 2 $ of the space $ \mathcal{W}_2^{2}[t_0, t_f] $ can be derived from Gram-Schmidt orthogonalization process of $ \{\Psi_i^\eta(t)\}_{i = 1}^\infty $ as follows:

where $ \mathcal{B}^{\eta}_{ik} $ are positive orthogonalization coefficients such that:

$ \mathcal{C}^\eta_{ik} $ given by: $ \langle \Psi_{i}^\eta, \Psi_{k}^\eta\rangle_{\mathcal{W}_{2}^{2}} $.

Theorem 3.1. If the operator $ L $ is invertible i.e: $ L^{-1} $ exist, and if $ \left\{ t _{i} \right\}_{i = 1}^{\infty } $ is dense on $ [t_0, t_f] $, then $ \left\{ \Psi_{i}^\eta \right\}_{i = 1}^{\infty } $, $ \eta = 1, 2 $ is the complete function system of the space $ \mathcal{W}_2^{2}[t_0, t_f] $.

Proof. For each fixed $ \mathcal{U}(t), \; \mathcal{V}(t) \in \mathcal{W}_2^{2}[t_0, t_f] $, let $ \langle \mathcal{U}(t), \Psi_{i}^1(t) \rangle = 0, \; \text{and }\; \langle \mathcal{V}(t), \Psi_{i}^2(t) \rangle = 0, \; \; i = 1, 2, ... $ that is:

since $ \{t _{i}\}_{i = 1}^\infty $ is dense on $ [t_0, t_f] $ then $ L\mathcal{U}(t) = 0 $, and $ L \mathcal{V}(t) = 0 $ it follows that $ \mathcal{U}(t) = 0, \; \mathcal{V}(t) = 0 $ since $ L^{-1} $ exist and $ \mathcal{U}(t), \; \mathcal{V}(t) $ are continuous.

Theorem 3.2. For each $ \mathcal{U}(t), \; \mathcal{V}(t)\in \mathcal{W}_2^{2}[t_0, t_f] $ the series

are convergent in the sense of the norm of $ \mathcal{W}_2^{2}[t_0, t_f] $. In contrast if $ \left\{ t_{i} \right\}_{i = 1}^{\infty } $ is dense subset on $ [t_0, t_f] $ then the solutions of (3.8) given by:

Proof. Let $ \mathcal{U}(t), \; \mathcal{V}(t)\in \mathcal{W}_2^{2}[t_0, t_f] $ be the solutions of (3.8), since $ \mathcal{U}(t), \; \mathcal{V}(t)\in \mathcal{W}_2^{2}[t_0, t_f] $, and $ \sum_{i = 1}^{\infty }\langle \mathcal{U}(t), \overline{\Psi}^1_{i}(t) \rangle_{\mathcal{W}_2^{2}[t_0, t_f]}\overline{\Psi}^1_{i}(t) $ and $ \sum_{i = 1}^{\infty }\langle \mathcal{V}(t), \overline{\Psi}^2_{i}(t) \rangle_{\mathcal{W}_2^{2}[t_0, t_f]}\overline{\Psi}^2_{i}(t) $ represent the Fourier series expansion about normal orthogonal system $ \{\overline{\Psi}^\eta_{i}(t)\}_{i = 1}^{\infty} $, $ \eta = 1, 2 $, and $ \mathcal{W}_2^{2}[t_0, t_f] $ is Hilbert space, then the series $ \sum_{i = 1}^{\infty }\langle \mathcal{U}(t), \overline{\Psi}^1_{i}(t) \rangle_{\mathcal{W}_2^{2}[t_0, t_f]}\overline{\Psi}^1_{i}(t), \; \sum_{i = 1}^{\infty }\langle \mathcal{V}(t), \overline{\Psi}^2_{i}(t) \rangle_{\mathcal{W}_2^{2}[t_0, t_f]}\overline{\Psi}^2_{i}(t) $ are convergent in the sense of $ \left\|. \right\|_{\mathcal{W}_2^{2}[t_0, t_f]} $. In contrast, according to the orthogonal basis $ \{\overline{\Psi}^\eta_{i}(t)\}_{i = 1}^\infty $, we have:

The same for finding $ \mathcal{V}(t) $:

The theorem is proved.

Since $ \mathcal{W}_{2}^{2} $ is Hilbert space we get:

$ \sum_{i = 1}^{\infty }\sum_{k = 1}^{i}\mathcal{B}^1_{ik}\langle L\mathcal{U}(t), \Phi^1_{k}(t) \rangle_{\mathcal{W}_{2}^{1}}\overline{\Psi}^1_{i}(t) < \infty $ and $ \sum_{i = 1}^{\infty }\sum_{k = 1}^{i}\mathcal{B}^2_{ik}\langle L\mathcal{V}(t), \Phi^2_{k}(t) \rangle_{\mathcal{W}_{2}^{1}}\overline{\Psi}^2_{i}(t) < \infty $.

Hence:

are convergent in the sense of $ \left\|. \right\|_{\mathcal{W}_{2}^{2}} $ and (3.11) represents the numerical solution of (3.8).

Remark 3.1.

(1) If the system (3.7) is linear, then the exact solutions can be found directly from (3.10).

(2) If the system (3.7) is non linear, then the exact and numerical solutions can be obtained by:

where:

We use the known quantities $ \lambda_{i}^{\eta }, \; \eta = 1, 2 $ to approximate the unknowns $ \mathcal{A}_{i}^{\eta}, \; \eta = 1, 2 $ as follows: we put $ t_{1} = t_{0} $ and set $ \mathcal{U}_{0}(t_{1}) = \mathcal{U}(t_{1}), \; \mathcal{V}_{0}(t_{1}) = \mathcal{V}(t_{1}) $ then $ \mathcal{U}_{0}(t_{1}) = \mathcal{V}_{0}(t_{1}) = 0 $ from the conditions of (3.8), and define the n-term approximation to $ \mathcal{U}(t), \; \mathcal{V}(t) $ by:

where the coefficient $ \lambda_{i}^{\eta }\; \; (\eta = 1, 2, \; \; i = 1, 2, ..., n $), are presented as follows:

and so:

We can guarantee that the approximations $ \mathcal{U}_n(t), \; \mathcal{V}_n(t) $ satisfies the conditions enjoined by (3.7) through the iterative process of (3.16).

4.   Error estimation and convergence

In this section, we present some convergence theories to emphasize that the approximate solution we got is close to the exact solution. Indeed, this finding is very powerful and efficient to RKHS theory and its applications.

Lemma 4.1. $ \left\| \mathcal{U}_n(t) \right\|_{n = 1}^{\infty } $, and $ \left\| \mathcal{V}_n(t) \right\|_{n = 1}^{\infty } $ are monotone increasing in the sense of the norm of $ \left\|. \right\|^{2}_{{{\mathcal{W} _{2}^{2}}}} $.

Proof. Since $ \left\| \overline{\Psi}^\eta _{i}(t) \right\|_{i = 1}^{\infty }, \; \eta = 1, 2 $ are the complete orthonormal systems in the space $ {{\mathcal{W} _{2}^{2}}}[t_0, t_f] $ then we have:

Thus $ \left\| \mathcal{U}_n(t) \right\|_{{{\mathcal{W} _{2}^{2}}}}, \; \left\| \mathcal{V}_n(t) \right\|_{{{\mathcal{W} _{2}^{2}}}} $ are monotone increasing.

Lemma 4.2. As $ n\to \infty $, the approximate solutions $ \mathcal{U}_{n}(t), \; \mathcal{V}_{n}(t) $ and its derivatives $ \mathcal{U'}_{n}(t), \; \mathcal{V'}_{n}(t) $ are uniformly convergent to the exact solutions $ \mathcal{U}(t), \; \mathcal{V}(t) $ and its derivatives $ \mathcal{U'}(t), \; \mathcal{V'}(t) $ respectively.

Proof. For any $ t \in [t_0, t_f] $:

and

if $ \left\| \mathcal{U}_{n}(t)-\mathcal{U}(t) \right\|_{\mathcal{W} _{2}^{2}}\longrightarrow 0, \; \left\| \mathcal{V}_{n}(t)-\mathcal{V}(t) \right\|_{\mathcal{W} _{2}^{2}}\longrightarrow 0 $ as $ n\to \infty $, then the approximate solutions $ \mathcal{U}^{(i)}_{n}(t), \; \mathcal{V}^{(i)}_{n}(t) $ are uniformly converges to the exact solutions $ \mathcal{U}^{(i)}(t), \; \mathcal{V}^{(i)}(t)\; \; \\i = 1, 2 $ respectively.

Theorem 4.1. If

and $ \mathrm{F}(t, \mathcal{U}(t), \mathcal{V}(t)), \; \mathrm{G}(t, \mathcal{U}(t), \mathcal{V}(t)) $ are continuous in $ [t_0, t_f] $, then:

Proof. For the first part, we will prove that:

it is easy to see that:

$ \left\{

$$\begin{array}{cl} \left| \mathcal{U}_{n-1}(t_{n})-\mathcal{U}(t) \right| = & \left|\mathcal{U}_{n-1}(t_{n})-\mathcal{U}_{n-1}(t)+\mathcal{U}_{n-1}(t)- \mathcal{U}(t) \right| \le \left| \mathcal{U}_{n-1}(t_{n})-\mathcal{U}_{n-1}(t) \right|+\left|\mathcal{U}_{n-1}(t)-\mathcal{U}(t) \right|, \\ \left| \mathcal{V}_{n-1}(t_{n})-\mathcal{V}(t) \right| = & \left|\mathcal{V}_{n-1}(t_{n})-\mathcal{V}_{n-1}(t)+\mathcal{V}_{n-1}(t)- \mathcal{V}(t) \right|\le\left| \mathcal{V}_{n-1}(t_{n})-\mathcal{V}_{n-1}(t) \right|+\left|\mathcal{V}_{n-1}(t)-\mathcal{V}(t) \right|, \end{array}$$ \right. $

by reproducing property of $ \mathcal{K}_{t}(\tau) $ we have:

and

thus

$ \left\{

$$\begin{array}{cl} \left|\mathcal{U}_{n-1}(t_{n})-\mathcal{U}_{n-1}(t)\right| = & \left|\langle \mathcal{U}_{n-1}(\tau), \mathcal{K}_{t_{n}}(\tau)-\mathcal{K}_{t}(\tau) \rangle_{\mathcal{W}_{2}^{2}} \right| \le \left\| \mathcal{U}_{n-1}(\tau) \right\|_{\mathcal{W}_{2}^{2}}\left\| \mathcal{K}_{t_{n}}(\tau)-\mathcal{K}_{t}(\tau) \right\|_{\mathcal{W}_{2}^{2}}, \\ \left|\mathcal{V}_{n-1}(t_{n})-\mathcal{V}_{n-1}(t)\right| = & \left|\langle \mathcal{V}_{n-1}(\tau), \mathcal{K}_{t_{n}}(\tau)-\mathcal{K}_{t}(\tau) \rangle_{\mathcal{W}_{2}^{2}} \right| \le \left\| \mathcal{V}_{n-1}(\tau) \right\|_{\mathcal{W}_{2}^{2}}\left\| \mathcal{K}_{t_{n}}(\tau)-\mathcal{K}_{t}(\tau) \right\|_{\mathcal{W}_{2}^{2}}, \end{array}$$ \right. $

and from the symmetric property of $ \mathcal{K}_{t}(\tau) $ we get:

hence: $ \left| \mathcal{U}_{n-1}(t_{n})-\mathcal{U}_{n-1}(t) \right|\longrightarrow 0 $ as $ t_{n}\to t $.

By lemma (4.2)

thus:

Therefore

in the sense of the $ \left\|. \right\|_{\mathcal{W}_{2}^{2}} $ as $ t_n\longrightarrow t $ and $ n \longrightarrow \infty $ for any $ t \in [t_0, t_f] $.

Moreover, since $ \mathrm{F} $ and $ \mathrm{G} $ are continuous, we obtain:

Theorem 4.2. Suppose that $ \left\| \mathcal{U}_{n} \right\|_{\mathcal{W}_{2}^{2}} $ and $ \left\| \mathcal{V}_{n} \right\|_{\mathcal{W}_{2}^{2}} $ are bounded in Eq (3.14), if $ \left\{ t_{i} \right\}_{i = 1}^{\infty } $ is dense on $ [t_0, t_f] $, then the approximate solutions $ \mathcal{U}_{n}(t) $, $ \mathcal{V}_{n}(t) $ in Eq (3.14) convergent to the exact solutions $ \mathcal{U}(t), \; \mathcal{V}(t) $ of Eq (3.7) in the space $ {\mathcal{W}_{2}^{2}}[t_0, t_f] $ and $ \mathcal{U}(t), \; \mathcal{V}(t) $ given by (3.12).

Proof. We first start by proving the convergence of $ \mathcal{U}_{n}(t) $ and $ \mathcal{V}_{n}(t) $ from Eq (3.14) we conclude that:

by orthogonality of $ \left\{ \overline{\Psi}^\eta _{i}(t) \right\}_{i = 1}^{\infty }, \; (\eta) = 1, 2 $ we get:

$ \left\| \mathcal{U}_{n}(t) \right\|_{\mathcal{W}_{2}^{2}}, \; \left\| \mathcal{V}_{n}(t) \right\|_{\mathcal{W}_{2}^{2}} $ are monotone increasing by Lemma (2). From the assymption that $ \left\| \mathcal{U}_{n}(t) \right\|_{\mathcal{W}_{2}^{2}}, \; \left\| \mathcal{V}_{n}(t) \right\|_{\mathcal{W}_{2}^{2}} $ are bounded, $ \left\| \mathcal{U}_{n}(t) \right\|_{\mathcal{W}_{2}^{2}}, \; \left\| \mathcal{V}_{n}(t) \right\|_{\mathcal{W}_{2}^{2}} $ are convergent as $ n \to \infty $, then $ \exists \; c, \; d $ constants such that

if $ m > n $ using

further that

so:

since $ \mathcal{W}_{2}^{2}[t_0, t_f] $ is complete, $ \exists \; \mathcal{U}(t), \; \mathcal{V}(t) $ in $ \mathcal{W}_{2}^{2}[t_0, t_f] $ such that

in the sense of the norm of $ \mathcal{W}_{2}^{2}[t_0, t_f] $.

Now, we prove that $ \mathcal{U}(t), \; \mathcal{V}(t) $ are solutions of Eq (3.7). Since $ \left\{ t_{i} \right\}_{i = 1}^{\infty } $ is dense on $ [t_0, t_f], \; \forall\; t \in [t_0, t_f], \; \exists $ subsequence $ \left\{ t_{n_j} \right\} $ such that $ t_{n_j}\underset{j\to \infty }{\longrightarrow }t $. From lemma (3) and (4) in ^[25] we have:

let $ j $ goes to $ \infty $, by theorem (4.1) and the continuity of $ \mathrm{F} $ and $ \mathrm{G} $ we have:

that is $ \mathcal{U}(t), \; \mathcal{V}(t) $ are solutions of Eq (3.7).

Theorem 4.3. Let $ \xi_{n} = \left| \mathcal{U}_n(t)-\mathcal{U}(t) \right| $, $ \xi^{'}_{n} = \left| \mathcal{V}_{n}(t)-\mathcal{V}(t) \right| $, where: $ \mathcal{U}_{n}(t), \; \mathcal{V}_{n}(t), \; \mathcal{U}(t), \; \mathcal{V}(t) $ denote the approximate and the exact solutions respectively, then the sequences of numbers $ \left\{ \xi _{n} \right\}, \; \left\{ \xi^{'} _{n} \right\} $ are decreasing in the sense of the norm $ \left\|. \right\|_{{\mathcal{W}_{2}^{2}}} $ and $ \xi _{n}\underset{n\to \infty }{\longrightarrow }0, \; \xi^{'} _{n}\underset{n\to \infty }{\longrightarrow }0 $.

Proof. From the extension form of $ \mathcal{U}(t), \; \mathcal{V}(t) $ and $ \mathcal{U}_n(t), \; \mathcal{V}_{n}(t) $ in Eqs (3.12), (3.14) and (3.15) we can write:

and

Clearly: $ \left\| \xi _{n} \right\|^{\infty}_{n = 1}, \; \left\| \xi^{'} _{n} \right\|^{\infty}_{n = 1} $ are decreasing in a sense of $ \left\|. \right\|_{{{\mathcal{W}_{2}^{2}}}} $ from theorem (3.2) the series $ \sum_{i = 1}^{\infty }\lambda_{i}^{1}\overline{\Psi}^1_{i}(t), \; \sum_{i = 1}^{\infty }\lambda_{i}^{2}\overline{\Psi}^2_{i}(t) $ are convergent, thus $ \left\| \xi _{n} \right\|_{{{\mathcal{W}_{2}^{2}}}}\longrightarrow 0, \; \left\| \xi^{'} _{n} \right\|_{{{\mathcal{W}_{2}^{2}}}}\longrightarrow 0 $ as $ n\longrightarrow \infty $.

Theorem 4.4. The approximate solutions $ \mathcal{U}_n(t), \; \mathcal{V}_n(t) $ of (3.7) converge to its exact solutions $ \mathcal{U}(t), \; \mathcal{V}(t) $ with not less than the second order convergence. That is: $ \left| \mathcal{U}_n-\mathcal{U} \right| \le Mk^{2} $ and $ \left| \mathcal{V}_n-\mathcal{V} \right| \le Nk^{2} $, where $ k = \frac{t_f-t_0}{n} $.

Proof. See ^[36].

5.   Numerical examples and algorithm

Numerical examples are conducted in order to verify the accuracy of this method. Computations are performed using Mathematica 11.0.

Algorithm 1: Use the following stages to approximate the solutions of BVPs (3.4) and (3.5) based on RKHS method.

● Stage A: Fixed $ t \in [t_0, t_f] $ and set $ \tau \in [t_0, t_f] $

for $ i = 1, ..., n $ do the following stages:

- stage 1: set $ t_i = t_0+\frac{(t_f-t_0)i}{n} $;

- stage 2: if $ \tau \leq t $ let

else let

- stage 3: For $ \eta = 1, 2 $;

set

Output the orthogonal functions system $ \Psi_i^\eta(t) $.

● Stage B: Obtain the orthogonalization coefficients $ \mathcal{B}^{\eta}_{ij} $ as follows:

For $ \; \; \eta = 1, 2 $;

For $ \; \; i = 1, ..., n $;

For $ \; \; j = 1, ..., i\; \; $ set $ \; \; \mathcal{C}_{ik}^{\eta} = \langle \Psi_{i}^\eta, \Psi_{j}^\eta\rangle_{\mathcal{W}_{2}^{2}} $ and $ \mathcal{B} _{11} = \frac{1}{Sqrt (\mathcal{C}_{11}^{\eta})} $.

Output $ \mathcal{C}_{ij}^{\eta} $ and $ \mathcal{B} _{11} $.

● Stage C: For $ \; \; \eta = 1, 2 $;

For $ i = 1, ..., n $, set $ \mathcal{B}^\eta _{ii} = (\left\| \Psi_{i}^\eta \right\|^{2}_{\mathcal{W}^{2}_{2}}-\sum_{k = 1}^{i-1}(\mathcal{C}_{ik}^\eta)^{2})^{\frac{-1}{2}} $;

else if $ j\neq i\; \; \; \; \; \; $ set $ \mathcal{B}^{\eta}_{ij} = -(\sum_{k = 1}^{i-1}\mathcal{C}^{\eta}_{ik}\mathcal{B}^{\eta}_{kj}).(\left\| \Psi_{i}^{\eta} \right\|^{2}_{\mathcal{W}^{2}_{2}}-\sum_{k = 1}^{i-1}(\mathcal{C}^{\eta}_{ik})^{2})^\frac{-1}{2} $.

Output the orthogonalization coefficients $ \mathcal{B}^{\eta}_{ij} $.

● Stage D: For $ \; \; \eta = 1, 2 $;

For $ \; \; i = 1, ..., n\; \; $ set $ \; \; \overline{\Psi}_i^\eta(t) = \sum_{k = 1}^{i}\mathcal{B}^{\eta}_{ik}\Psi_{i}^{\eta}(t) $.

Output the orthonormal functions system $ \overline{\Psi}_i^\eta(t). $

Stage E: Set $ \; \; t_1 = 0\; \; $ and choose $ \mathcal{U}_0(t_1) = 0, \; \; \mathcal{V}_0(t_1) = 0 $;

For $ \; \; \eta = 1, 2 $;

For $ \; \; i = 1\; \; $ set

For $ \; \; i = 2, 3, ..., n\; \; $ set

set

Outcome the numerical solutions $ \mathcal{U}_n(t), \; \mathcal{V}_n(t) $.

Then we implement the above algorithm using numerical simulations. We arrange the resulting data in tables and graphs for examples discussed on $ [t_0, t_f] $ as follows:

Example 5.1. Consider the following system:

subject to:

with exact solution when $ \alpha = 1 $ is:

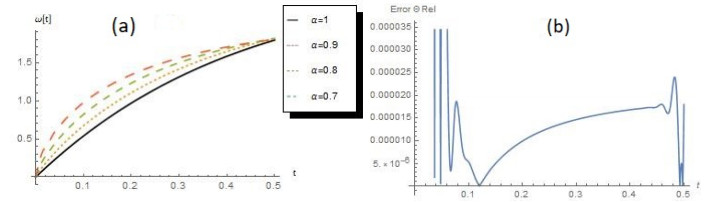
After the initial conditions have been homogenised and algorithm 1 used, apply $ t_i = \frac{0.5i}{n} $, $ \overline{i = 1, n}\; $ and $ n = 40 $, the tables 1 and 2 describe the exact solutions of $ \omega(t) $ and $ \Theta(t) $ and approximate solutions for different values of $ \alpha $.

Graphs of the approximate solutions of $ \omega(t) $ are plotted in Figure 1 (a), for different values of $ \alpha $. It is obvious from Figure 1 (a) that the approximate solutions are in reasonable alignment with the exact solution when $ \alpha = 1 $ and the solutions are continuously based on a fractional derivative. The graph in Figure 1 (b) represent the absolute errors of $ \theta(t) $.

Example 5.2. Consider the following system:

with conditions:

when $ \alpha = 1 $ the exact solution is:

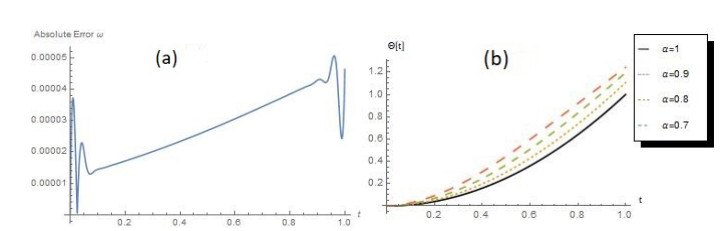
After homogenizing the initial conditions and using algorithm 1, apply $ t_i = \frac{i}{n} $, $ \overline{i = 1, n}\; $ and $ n = 35 $, the tables 3 and 4 describe the exact solutions of $ \omega(t) $ and $ \Theta(t) $ and approximate solutions for different values of $ \alpha $.

Graphs of the approximate solutions of $ \theta(t) $ are plotted in Figure 2 (b) for different values of $ \alpha $. The graph in Figure 2 (a) represent the absolute errors of $ \omega(t) $.

Example 5.3. Consider the following fractional system:

subject to:

with exact solution:

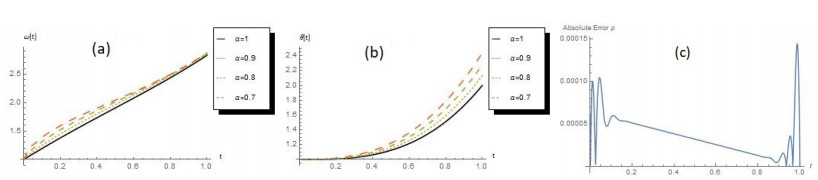
After the initial conditions have been homogenised and algorithm 1 used, apply $ t_i = \frac{i}{n} $, $ \overline{i = 1, n}\; $ and $ n = 30 $, the tables 5-7 describe the exact solutions of $ \omega(t) $, $ \Theta(t) $ and $ \rho $ and approximate solutions for different values of $ \alpha $.

Graphs of the approximate solutions of $ \omega(t) $ and $ \theta(t) $ are plotted in Figure 3 (a), Figure 3 (b) for different values of $ \alpha $. The graph in Figure 3 (c) represent the absolute errors of $ \rho(t) $.

Now, we consider the following tables where the RKHS method has been applied in order to give numerical approximations with other values of n, and then compare it with finite difference and collocation methods.

6.   Conclusions

In this article, we effectively utilize the RKHSM to develop an approximate solution of differential fractional equations with temporal two-point BVP. The results of examples demonstrate reliability and consistency of the method. In the future, we recommend further research on the RKHS method, as solving the temporal two-point boundary value problems with the conformable and the Atangana-Baleanu derivatives. We expect to achieve better results and good approximations for the solutions.

Conflict of interest

The authors state that they have no conflict of interest. All authors have worked in an equal sense to find these results.