Chaotic dynamics analysis and control of fractional-order ESER systems using a high-precision Caputo derivative approach

XiongFei Chi; Ting Wang; ZhiYuan Li; XiongFei Chi; Ting Wang; ZhiYuan Li

doi:10.3934/era.2025161

Electronic Research Archive

2025, Volume 33, Issue 6: 3613-3637. doi: 10.3934/era.2025161

Previous Article Next Article

Research article

Chaotic dynamics analysis and control of fractional-order ESER systems using a high-precision Caputo derivative approach

1.
Department of Mechanical and Electrical Engineering, Ordos Vocational College, Ordos 017010, China
2.
College of Date Science and Application, Inner Mongolia University of Technology, Hohhot 010080, China

Received: 02 May 2025 Revised: 30 May 2025 Accepted: 06 June 2025 Published: 11 June 2025

This paper investigates the chaotic dynamics and control of a fractional-order energy-saving and emission-reduction (ESER) system using a high-precision method. By constructing a four-dimensional fractional-order system, the complex interactions between new energy, carbon emissions, economic growth, and carbon trading volume are studied. A novel high-precision numerical method, based on generating functions, is introduced to analyze the dynamic behaviors of the system at various fractional derivatives and parameters. Numerical simulations find all kinds of dynamic behaviors, including stable, rapid divergence, and chaotic attractors. In this study, we design feedback and adaptive control strategies to achieve chaos synchronization and system stability. The results highlight the effectiveness of the proposed control methods in stabilizing the system and synchronizing drive-response systems, underscoring the pivotal role of fractional-order derivatives in regulating system dynamics.

Keywords:

Citation: XiongFei Chi, Ting Wang, ZhiYuan Li. Chaotic dynamics analysis and control of fractional-order ESER systems using a high-precision Caputo derivative approach[J]. Electronic Research Archive, 2025, 33(6): 3613-3637. doi: 10.3934/era.2025161

Related Papers:

[1]	Shanshan Yang, Ning Li . Chaotic behavior of a new fractional-order financial system and its predefined-time sliding mode control based on the RBF neural network. Electronic Research Archive, 2025, 33(5): 2762-2799. doi: 10.3934/era.2025122
[2]	Li Tian, Ziqiang Wang, Junying Cao . A high-order numerical scheme for right Caputo fractional differential equations with uniform accuracy. Electronic Research Archive, 2022, 30(10): 3825-3854. doi: 10.3934/era.2022195
[3]	S. Suganya, V. Parthiban, R Kavikumar, Oh-Min Kwon . Transmission dynamics and stability of fractional order derivative model for COVID-19 epidemic with optimal control analysis. Electronic Research Archive, 2025, 33(4): 2172-2194. doi: 10.3934/era.2025095
[4]	Janarthanan Ramadoss, Asma Alharbi, Karthikeyan Rajagopal, Salah Boulaaras . A fractional-order discrete memristor neuron model: Nodal and network dynamics. Electronic Research Archive, 2022, 30(11): 3977-3992. doi: 10.3934/era.2022202
[5]	Bin Zhen, Wenwen Liu, Lijun Pei . An analytic estimation for the largest Lyapunov exponent of the Rössler chaotic system based on the synchronization method. Electronic Research Archive, 2024, 32(4): 2642-2664. doi: 10.3934/era.2024120
[6]	Leiting Wang, Yang Jin, Wangxiang Li, Chenyang Tang . Analysis of the nonlinear dynamic behavior of longitudinal systems in heavy-haul trains. Electronic Research Archive, 2025, 33(2): 582-599. doi: 10.3934/era.2025027
[7]	Mengting Sui, Yanfei Du . Bifurcations, stability switches and chaos in a diffusive predator-prey model with fear response delay. Electronic Research Archive, 2023, 31(9): 5124-5150. doi: 10.3934/era.2023262
[8]	Ning Li, Yuequn Gao . Modified fractional order social media addiction modeling and sliding mode control considering a professionally operating population. Electronic Research Archive, 2024, 32(6): 4043-4073. doi: 10.3934/era.2024182
[9]	Caiwen Chen, Tianxiu Lu, Ping Gao . Chaotic performance and circuitry implement of piecewise logistic-like mapping. Electronic Research Archive, 2025, 33(1): 102-120. doi: 10.3934/era.2025006
[10]	Qun Dai, Zeheng Wang . SIRV fractional epidemic model of influenza with vaccine game theory and stability analysis. Electronic Research Archive, 2024, 32(12): 6792-6821. doi: 10.3934/era.2024318

Abstract

1. Introduction

In recent years, fractional-order chaotic systems and patterns have emerged as a research hotspot in nonlinear science. Yu et al. ^[1,2,3] developed 4D/5D memristive neural networks exhibiting multi-stability and infinite attractors and a memristor characteristic equation that goes beyond the traditional cubic polynomial. Lai et al. ^[4,5,6] created hidden multiscroll systems and 2D hyperchaotic maps for secure communication. Feng et al. ^[7,8,9] pioneered hyperchaos-based image encryption using fractional-order Lorenz systems and pixel fusion, and so on ^[10,11]. Han et al. ^[12] analyzed the reaction-diffusion model under the fractional derivative of Riesz and revealed the pattern formation mechanism induced by non-local effects. Che et al. ^[13] proposed a numerical algorithm with superlinear convergence accuracy for the spatial fractional Gray-Scott model, and Wang et al. ^[14] studied the Hasting-Powell ecological model defined by Grünwald-Letnikov. Zhang et al. ^[15] constructed a fractional-order dynamic model of the plankton ecosystem. These studies have promoted the theoretical and applied development of fractional-order chaotic systems. However, there are relatively few studies on fractional-order chaotic systems in energy-economy-environment coupled systems. In ^[16], Fang et al. proposed the following three-dimensional ESER dynamic system:

$\begin{equation} \begin{cases} \dot{x} = a_1 x\left(\frac{y}{M} - 1\right) - a_2 y + a_3 z \\ \dot{y} = -b_1 x + b_2 y\left(1 - \frac{y}{C}\right) + b_3 z\left(1 - \frac{z}{E}\right) \\ \dot{z} = c_1 x\left(\frac{x}{N} - 1\right) - c_2 y - c_3 z \end{cases} \end{equation}$

(1.1)

In ^[16], the dynamic behavior of this system was analyzed using Lyapunov exponents and bifurcation diagrams. Additionally, the Silnikov theorem was applied to prove the existence of Smale horseshoes and chaos. Furthermore, an artificial neural network was employed to calibrate the model based on statistical data from China. In ^[17], studied an ESER system with two delays was studied.

In ^[18], Fang et al. constructed the following nonlinear coupled four-dimensional ESER system (1.2), which considers the complex relationships between new energy, carbon emissions, economic growth, and carbon trading:

$\begin{equation} \begin{cases} \dot{x} = a_1 x(y - M) + a_2 z + a_3 u\left(\frac{u}{N} - 1\right), \\ \dot{y} = -b_1 x + b_2 y\left(1 - \frac{y}{C}\right) + b_3 z\left(1 - \frac{z}{E}\right) - b_4 u, \\ \dot{z} = c_1 x\left(\frac{x}{F} - 1\right) - c_2 y - c_3 z - c_4 u, \\ \dot{u} = d_1 u\left(\frac{y}{P} - 1\right) - d_2 x + d_3 z. \end{cases} \end{equation}$

(1.2)

The dynamic behavior of this system was analyzed through numerical simulations, particularly using the maximum Lyapunov exponent to determine whether the system exhibits chaotic behavior, i.e., sensitivity to initial conditions. Additionally, the paper employed a BP neural network to identify model parameters to ensure that the system accurately reflects real-world scenarios. The four-dimensional ESER system expands upon the three-dimensional model by incorporating the dimension of carbon trading volume $u$ , thereby providing a more comprehensive description of the interactions between new energy $x$ , carbon emissions $y$ , economic growth $z$ , and carbon trading volume $u$ .

In actual economic, environmental, and energy systems, the current state is often significantly influenced by past states. For example, the cumulative effect of carbon emissions, the long-term trend of economic growth, and the continuous investment in new energy development all exhibit pronounced memory characteristics. Fang et al. ^[19] developed an ESER system with carbon tax constraints for the Yangtze River Delta urban agglomeration, providing a quantitative analysis tool for the regional carbon tax policy pilot. In ^[20], the authors explored the dynamical behavior of a three-dimensional fractional-order ESER system. The stability analysis of the equilibrium points for the fractional-order system was conducted. The system was discretized, and stability conditions were derived. Additionally, numerical simulations were performed to examine the asymptotically stable attractors and chaotic dynamics. Considering the memory effect inherent in Caputo fractional derivatives, we introduce Caputo fractional derivatives into system (1.2) to construct the four-dimensional fractional-order ESER system:

$\begin{equation} \begin{cases} D^{\alpha_1} x = a_1 x(y - M) + a_2 z + a_3 u\left(\frac{u}{N} - 1\right), \\ D^{\alpha_2} y = -b_1 x + b_2 y\left(1 - \frac{y}{C}\right) + b_3 z\left(1 - \frac{z}{E}\right) - b_4 u, \\ D^{\alpha_3} z = c_1 x\left(\frac{x}{F} - 1\right) - c_2 y - c_3 z - c_4 u, \\ D^{\alpha_4} u = d_1 u\left(\frac{y}{P} - 1\right) - d_2 x + d_3 z, \end{cases} \end{equation}$

(1.3)

where the explanations of all terms are shown in Table 1.

Table 1. Explanation of parameters and terms.

Term	Explanation
$a_1x(y-M)$	Impact of carbon emissions on new energy. $y < M$ : Low emissions reduce pressure for new energy.
$a_2z$	Positive influence of economic growth on new energy.
$-b_1x$	Reduction effect of new energy on carbon emissions.
$b_2y(1-y/C)$	Self-limiting growth of emissions. $y < C$ : Rapid emission growth. $y > C$ : Growth slows.
$b_3z(1-z/E)$	Economic impact on emissions. $z < E$ : Industrial-driven growth increases emissions.
$c_1x(x/F-1)$	New energy investment impact: $x < F$ : Early investment drags on economy.
$-c_2y$	Negative impact of emissions on economic growth.
$-c_3z$	Net effect of new energy investment on economy.
$a_3u(u/N-1)$	Carbon trading impact on new energy. $u < N$ : Immature market has little effect.
$-b_4u$	Emission reduction from carbon trading.
$-c_4u$	Net economic impact of carbon trading.
$d_1u(y/P-1)$	Supply-demand balance. $y > P$ : High emissions increase trading volume.
$-d_2x$	New energy substitution effect on carbon trading.
$d_3z$	Economic input driving trading volume.
$\alpha_1/\alpha_2/\alpha_3/\alpha_4$	Memory effect index of new energy/carbon emissions/economic growth/carbon trading.

| Show Table

DownLoad: CSV

Definition 1.1. The Caputo fractional derivative of order $\alpha > 0$ for a function $f(t)$ is defined as:

$D^\alpha_t f(t) = \frac{1}{\Gamma(n - \alpha)} \int_0^t \frac{f^{(n)}(\tau)}{(t - \tau)^{\alpha - n + 1}} \, d\tau,$

$n = \lceil \alpha \rceil$ is the smallest integer greater than or equal to $\alpha$ ), $f^{(n)}$ is the $n$ -th derivative of $f$ , and $\Gamma$ is the Gamma function.

In this paper, the complex dynamic behavior of the fractional-order system (1.2) is studied by combining theoretical analysis and numerical simulation. The main contributions of this paper are as follows:

● A novel high-precision numerical method based on generating functions is proposed.

● Numerical simulations reveal previously unknown chaotic attractors, demonstrating the nonlinear interactions among new energy $x$ , carbon emissions $y$ , economic growth $z$ , and carbon trading volume $u$ .

● A robust adaptive control strategy is designed to achieve chaos synchronization and stabilize the system around equilibrium points.

2. Stability analysis

The equilibrium point refers to the situation where the state variables of the system no longer change over time, that is, $D^{\alpha_1} x, D^{\alpha_1} y, D^{\alpha_1} z, D^{\alpha_1} u = 0$ . Therefore, we need to solve the following system of equations:

$\begin{equation} \begin{cases} f1 = a_1 x(y - M) + a_2 z + a_3 u\left(\frac{u}{N} - 1\right) = 0, \\ f2 = -b_1 x + b_2 y\left(1 - \frac{y}{C}\right) + b_3 z\left(1 - \frac{z}{E}\right) - b_4 u = 0, \\ f3 = c_1 x\left(\frac{x}{F} - 1\right) - c_2 y - c_3 z - c_4 u = 0, \\ f4 = d_1 u\left(\frac{y}{P} - 1\right) - d_2 x + d_3 z = 0, \end{cases} \end{equation}$

(2.1)

By solving Eq (2.1), we can find the equilibrium point $(x^*, y^*, z^*, u^*)$ . The equations may have multiple solutions, and each solution represents an equilibrium point. For simplicity, we assume that the system has nontrivial equilibrium point $(x^*, y^*, z^*, u^*)$ . Its Jacobian matrix $J$ at the equilibrium point $(x^*, y^*, z^*, u^*)$ is:

$J = \begin{bmatrix} \dfrac{\partial f_1}{\partial x} & \dfrac{\partial f_1}{\partial y} & \dfrac{\partial f_1}{\partial z} & \dfrac{\partial f_1}{\partial u} \\[10pt] \dfrac{\partial f_2}{\partial x} & \dfrac{\partial f_2}{\partial y} & \dfrac{\partial f_2}{\partial z} & \dfrac{\partial f_2}{\partial u} \\[10pt] \dfrac{\partial f_3}{\partial x} & \dfrac{\partial f_3}{\partial y} & \dfrac{\partial f_3}{\partial z} & \dfrac{\partial f_3}{\partial u} \\[10pt] \dfrac{\partial f_4}{\partial x} & \dfrac{\partial f_4}{\partial y} & \dfrac{\partial f_4}{\partial z} & \dfrac{\partial f_4}{\partial u} \end{bmatrix} = \begin{bmatrix} a_1 (y^* - M) & a_1 x^* & a_2 & a_3 \left(\dfrac{2u^*}{N} - 1\right) \\[10pt] -b_1 & b_2 \left(1 - \dfrac{2y^*}{C}\right) & b_3 \left(1 - \dfrac{2z^*}{E}\right) & -b_4 \\[10pt] c_1 \left(\dfrac{2x^*}{F} - 1\right) & -c_2 & -c_3 & -c_4 \\[10pt] -d_2 & d_1 \dfrac{u^*}{P} & d_3 & d_1 \left(\dfrac{y^*}{P} - 1\right) \end{bmatrix}.$

In order to analyze the stability of the equilibrium point $(x^*, y^*, z^*, u^*)$ , we need to find the eigenvalues of the Jacobian matrix at the equilibrium point. The eigenvalue $\lambda$ satisfies the characteristic equation:

$\begin{vmatrix} a_1 (y^* - M)-\lambda^{\alpha_1} & a_1 x^* & a_2 & a_3 \left(\dfrac{2u^*}{N} - 1\right) \\[10pt] -b_1 & b_2 \left(1 - \dfrac{2y^*}{C}\right)-\lambda^{\alpha_2} & b_3 \left(1 - \dfrac{2z^*}{E}\right) & -b_4 \\[10pt] c_1 \left(\dfrac{2x^*}{F} - 1\right) & -c_2 & -c_3-\lambda^{\alpha_3} & -c_4 \\[10pt] -d_2 & d_1 \dfrac{u^*}{P} & d_3 & d_1 \left(\dfrac{y^*}{P} - 1\right)-\lambda^{\alpha_4} \end{vmatrix} = 0.$

Solving the characteristic equation, we can obtain the eigenvalue $\lambda$ . The stability condition of the system is that the phase angle of the eigenvalue must satisfy the following condition for all roots:

$\left| \arg(\lambda) \right| > \frac{\pi}{2} \cdot \max(\alpha_i), i = 1, 2, 3, 4.$

For $\alpha_i = 1, i = 1, 2, 3, 4$ , if the real parts of all eigenvalues are less than zero, then the equilibrium point is stable. If the real part of at least one eigenvalue is greater than zero, then the equilibrium point is unstable.

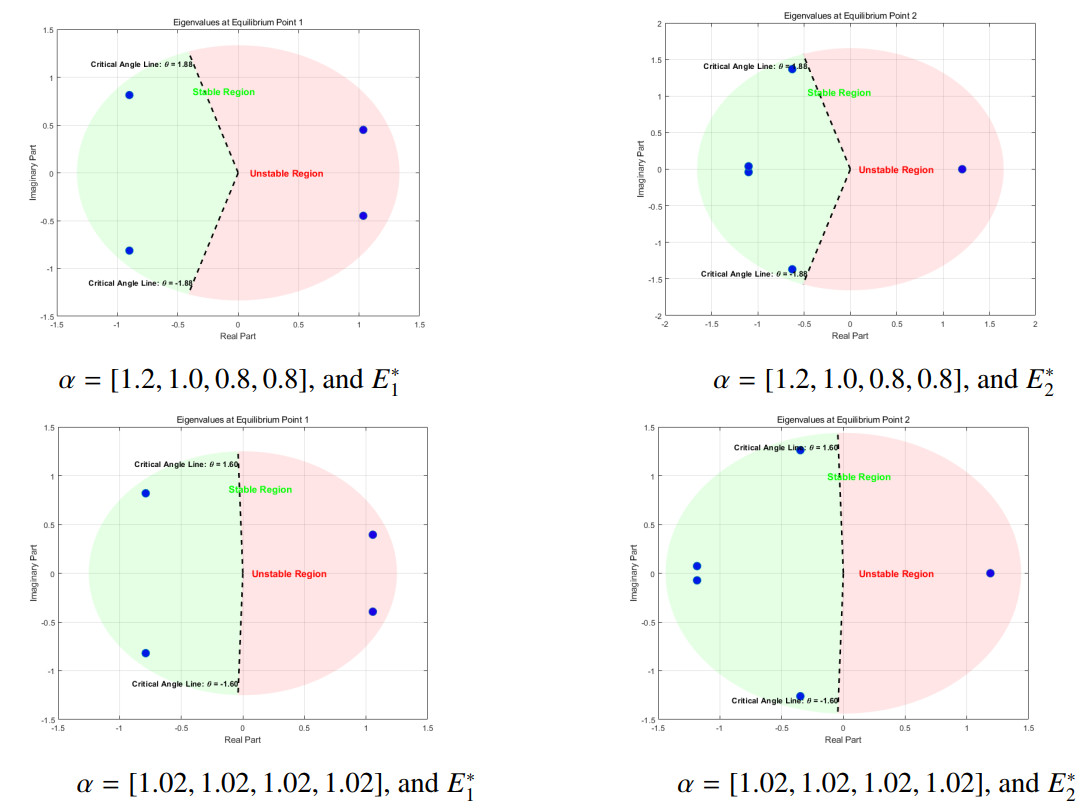
We set parameters in . Stability analysis of the equilibrium points at different fractional derivative $\alpha$ are shown in the Tables 3 and 4 and Figure 1.

Table 2. Parameters of the system for Tables 3 and 4 and Figures 1 and 7 and 8.

$a_1$	$a_2$	$a_3$	$b_1$	$b_2$	$b_3$	$b_4$	$c_1$	$c_2$	$c_3$
0.3927	0.2037	0.8952	0.0139	0.1229	0.7954	0.3133	0.3110	0.9192	0.0035
$c_4$	$d_1$	$d_2$	$d_3$	$M$	$C$	$E$	$N$	$F$	$P$
0.7012	0.4818	0.1125	0.1277	2.955	1.2576	3.7085	0.5871	0.1417	0.9222

| Show Table

DownLoad: CSV

Table 3. Stability analysis of equilibrium points at

$\alpha_i = 1,$

$E^*_1(1.153, 2.746, 0.658, 0.04797)$ , and

$E^*_2(0.9377, 1.019, 0.4294, 0.998)$ .

Equilibrium Points	Jacobian Matrix	Eigenvalues	Phase Angle
$E^*_1$	$\begin{pmatrix} -0.0820 & 0.4529 & 0.2037 & -0.7489 \\ -0.0139 & -0.4138 & 0.5131 & -0.3133 \\ 4.7511 & -0.9192 & -0.0035 & -0.7012 \\ -0.1125 & 0.0251 & 0.1277 & 0.9529 \end{pmatrix}$	$\begin{aligned} -0.8276 \pm 0.7839i \\ 1.054 \pm 0.403i \end{aligned}$	$\begin{aligned} \pm 2.383 \\ \pm 0.3651 \end{aligned}$
$E^*_2$	$\begin{pmatrix} -0.7601 & 0.3683 & 0.2037 & 2.1483 \\ -0.0139 & -0.0763 & 0.6112 & -0.3133 \\ 3.8052 & -0.9192 & -0.0035 & -0.7012 \\ -0.1125 & 0.5214 & 0.1277 & 0.0508 \end{pmatrix}$	$\begin{aligned} 1.195 \\ -0.3965 \pm 1.255i \\ -1.191 \end{aligned}$	$\begin{aligned} 0 \\ \pm 1.877 \\ 3.142 \end{aligned}$

| Show Table

DownLoad: CSV

Table 4. Stability analysis of equilibrium points at different fractional derivative

$\alpha$ .

$\alpha$	Equilibrium Point	Eigenvalue	Phase Angle	Stability
$\alpha =[1.02, 1.02, 1.02, 1.02]$	$E_1^*$	$-0.7881 \pm 0.8196i$	$\pm2.3366$
		$1.0547 \pm 0.3945i$	$\pm0.3579$	Unstable
	$E_2^*$	$-1.1848 \pm 0.0731i$	$\pm3.0800$
		$-0.3482 \pm 1.2614i$	$\pm1.8401$	Unstable
		$1.1907$	$0.0000$
$\alpha =[1.2, 1.0, 0.8, 0.8]$	$E_1^*$	$1.0348 \pm 0.4493i$	$\pm0.4096$
		$-0.8999 \pm 0.8135i$	$\pm2.4066$	Unstable
	$E_2^*$	$-1.0991 \pm 0.0397i$	$\pm3.1055$
		$-0.6273 \pm 1.3681i$	$\pm2.0007$	Unstable
		$1.2079$	$0.0000$

| Show Table

DownLoad: CSV

Figure 1. Stability analysis of equilibrium points at different fractional derivative

$\alpha = [1,1,1,1]$ .

DownLoad: Full-Size Img PowerPoint

3. Brief description of the methodology

How to solve fractional differential equations efficiently and accurately remains a challenge. This paper aims to construct a four-dimensional fractional-order ESER system by introducing Caputo fractional-order derivatives and propose a high-precision numerical method to analyze the dynamic behavior of the system. For the numerical solutions of fractional differential equations, there are already some numerical methods, such as, the spectral method for fractional KdV equation solutions ^[21], spectral method for KdV-mKdV ^[22], reproducing kernel method for integral equations ^[23], a piecewise reproducing kernel method for space-time PDEs ^[24], the spectral method for KdV-Burgers ^[25], high-precision numerical method for predator-prey pattern dynamics ^[26], spectral method for fractional vegetation-water modeling ^[27], high-precision numerical method for chaotic financial system analysis ^[28], and so on ^{[29,30,31,32]}. The commonly used approximation formats for Caputo fractional derivative are L1 formula ( $0 < \alpha < 1$ ) ^[33,34,35], L1–2 formula ^[33,34,35], High-order approximation ( $n-1 < \alpha < n$ ) ^[33], Adams-Bashforth-Moulton predictor-corrector method ^[35], matrix approach ^[33]. A comparison of the numerical scheme is shown in Table 5.

Table 5. Comparison of numerical schemes.

Method	Accuracy	Computational Cost
L1 formula ( $0 < \alpha < 1$ ) ^[33,34,35]	$\mathcal{O}(\tau^{2-\alpha})$	$\mathcal{O}(N^2)$
L1-2 formula ^[33,34,35]	$\mathcal{O}(\tau^{3-\alpha})$	$\mathcal{O}(N^2)$
High-order approximation ^[33,34,35]	$\mathcal{O}(\tau^p)$ ( $p \geq 3$ )	$\mathcal{O}(N^2)$
Predictor-corrector ^[35]	$\mathcal{O}(\tau^{1+\alpha})$	$\mathcal{O}(N^2)$
Matrix approach ^[33]	$\mathcal{O}(\tau^{2-\alpha})$	$\mathcal{O}(N^2)$

| Show Table

DownLoad: CSV

To obtain higher calculation accuracy, Podlubny ^[33] and Xue ^[36,37] considered replacing the binomial expansion with a polynomial expansion in the calculation formula of Grünwald-Letnikov fractional derivatives. Podlubny ^[33] presented the generating function for calculating the accuracy $o(h^P)$ (where $p\leq 6$ ), and higher-order generating functions also exist. Xue ^[36,37] explored the construction method of generating functions and presented the high-precision numerical calculation method of the fractional-order Grünwald-Letnikov derivative and Caputo derivative.

The difference scheme of order one $o(h)$ of the first-order derivative can be expressed as:

$y_k' = \lim\limits_{h \to 0} \frac{y(t) - y(t - h)}{h} \approx \frac{y_k - y_{k-1}}{h}.$

The difference scheme of order two $o(h^2)$ of the first-order derivative can be expressed as:

$y_k' \approx \frac{1}{h} \left( \frac{3}{2}y_k - 2y_{k-1} + \frac{1}{2}y_{k-2} \right).$

Similarly, the difference scheme of order three $o(h^3)$ of the first-order derivative can be expressed as:

$y_k' \approx \frac{1}{h} \left( \frac{11}{6}y_k - 3y_{k-1} + \frac{3}{2}y_{k-2} - \frac{1}{3}y_{k-3} \right).$

So, Podlubny ^[33] presented the following generating functions.

Definition 3.1. $\omega$ -order polynomial generating function is defined as:

$g_\omega(z) = \sum\limits_{k = 1}^{\omega} \frac{1}{k}(1 - z)^k.$

where $\omega$ is a positive integer. $\omega = 1, 2, 3, 4, 5, 6$ -order generating functions are shown in Table 6.

Table 6. Low-order generating function.

$\omega$	$g_\omega(z)$	$\omega$	$g_\omega(z)$
1	$1 - z$	4	$25 - 4z + 3z^2 - \frac{4}{3}z^3 + \frac{1}{4}z^4$
2	$\frac{3}{2} - 2z + \frac{1}{2}z^2$	5	$137 - 5z + 5z^2 - \frac{10}{3}z^3 + \frac{5}{4}z^4 - \frac{1}{5}z^5$
3	$\frac{11}{6} - 3z + \frac{3}{2}z^2 - \frac{1}{3}z^3$	6	$147 - 6z + \frac{15}{2}z^2 - \frac{20}{3}z^3 + \frac{15}{4}z^4 - \frac{6}{5}z^5 + \frac{1}{6}z^6$

| Show Table

DownLoad: CSV

If $\omega = 4$ , then the difference scheme expression of order $o(h^4)$ of the first-order derivative is

$y_k' = \frac{1}{h} \left( \frac{25}{12} y_k - 4y_{k-1} + 3y_{k-2} - \frac{4}{3} y_{k-3} + \frac{1}{4} y_{k-4} \right).$

In order to obtain the generating function of polynomials of any order, Xue ^[36,37] introduced the following theorem.

Theorem 3.2. The $\omega$ -order generating function $g_\omega(z)$ can be expressed as the following polynomial:

$g_\omega(z) = \sum\limits_{k = 0}^{\omega} g_k z^k,$

where the coefficients $g_k$ can be computed directly from the following equation:

$\begin{pmatrix} 1 & 1 & 1 & \cdots & 1 \\ 1 & 2 & 3 & \cdots & \omega+1 \\ 1 & 2^2 & 3^2 & \cdots & (\omega+1)^2 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & 2^\omega & 3^\omega & \cdots & (\omega+1)^\omega \end{pmatrix}\begin{pmatrix} g_0 \\ g_1 \\ g_2 \\ \vdots \\ g_\omega \end{pmatrix} = - \begin{pmatrix} 0 \\ 1 \\ 2 \\ \vdots \\ \omega \end{pmatrix}.$

Definition 3.3. A $\omega$ -order polynomial generating function with fractional-order $\alpha$ is defined as references ^[33,36,37]:

$\begin{align} \begin{array}{l} g_\omega^{\alpha}(z) = (g_0 + g_1z + \cdots + g_\omega z^\omega)^{\alpha}, \end{array} \end{align}$

(3.1)

Podlubny ^[33] introduced a method based on the fast Fourier transform. Assume the Taylor series expansion coefficients of the generating function $g_\omega^{\alpha}(z)$ are $\Upsilon^{(\alpha, \omega)} = [\Upsilon^{(\alpha, \omega)}_0, \Upsilon^{(\alpha, \omega)}_1, \Upsilon^{(\alpha, \omega)}_2, \cdots]$ . The Taylor series expansion can be written as:

$g_\omega^{\alpha}(z) = \sum\limits_{k = 0}^{\infty} \Upsilon^{(\alpha, \omega)}_k z^k.$

Theorem 3.4. Taylor series expansion of the generating function $g_\omega^{\alpha}(z)$ can be expressed as ^[33]:

$\begin{align} \begin{array}{l} g_\omega^{\alpha}(z) = \sum\nolimits_{k = 0}^{\infty}\Upsilon^{(\alpha, \omega)}_kz^k. \end{array} \end{align}$

(3.2)

Here, for $k = 0$ , $\Upsilon^{(\alpha, \omega)}_0 = g_0^{\alpha}$ , and for $k > 0$ , the subsequent coefficients $\Upsilon^{(\alpha, \omega)}_k$ can be computed recursively as:

$\begin{align} \begin{array}{l} \Upsilon^{(\alpha, \omega)}_k = -\frac{1}{g_0}\sum\nolimits_{i = 1}^{p}g_i\left(1-i\frac{1+\alpha}{k}\right)\Upsilon^{(\alpha, \omega)}_{k-i}, \quad \Upsilon^{(\alpha, \omega)}_k = 0, \mathit{\text{if}}\; k < 0 . \end{array} \end{align}$

(3.3)

Corollary 3.5. If the generating function and its Taylor series expansion are still represented by Eqs (3.1) and (3.2), then the Taylor series coefficients $w_k$ can be computed recursively as:

$\Upsilon^{(\alpha, \omega)}_k = \frac{1}{g_0} \sum\limits_{i = 1}^{p} g_i \left( 1 - i \frac{1 + \alpha}{k} \right) \Upsilon^{(\alpha, \omega)}_{k-i}, \quad \mathit{\text{if}}\; k = \omega, \omega+1, \omega+2, \cdots.$

For $m = 1, 2, \cdots, \omega-1$ , the initial coefficients are computed as:

$\Upsilon^{(\alpha, \omega)}_m = \frac{1}{g_0} \sum\limits_{i = 1}^{m-1} g_i \left( 1 - i \frac{1 + \alpha}{m} \right) \Upsilon^{(\alpha, \omega)}_{m-i},$

with $\Upsilon^{(\alpha, \omega)}_0 = g_0^\alpha$ .

Definition 3.6. The Grünwald-Letnikov definition of the $\alpha$ -order derivative of a function $f(t)$ is defined as:

${}^{GL}D_{t}^{\alpha} f(t) = \lim\limits_{h \rightarrow 0} \frac{1}{h^{\alpha}} \sum\limits_{k = 0}^{\left\lfloor\left(t-t_{0}\right) / h\right\rfloor}(-1)^{k}\binom{\alpha}{k} f(t-k h)$

where the binomial coefficient can be expressed as

$(-1)^{k}\binom{\alpha}{k} = \frac{(-1)^{k} \Gamma(\alpha+1)}{\Gamma(k+1) \Gamma(\alpha-k+1)}$

and $\lfloor \cdot \rfloor$ denotes the floor function, which takes the greatest integer less than or equal to the argument.

The binomial coefficient $(-1)^{k}\binom{\alpha}{k}$ is replaced by $\Upsilon^{(\alpha, \omega)}_k$ ^[33], and a high-precision algorithm can be defined.

Definition 3.7. The high-precision Grünwald-Letnikov definition of the $\alpha$ -order derivative of a function $f(t)$ is given by

${}^{GL}D_{t}^{\alpha} f(t) = \lim\limits_{h \rightarrow 0} \frac{1}{h^{\alpha}} \sum\limits_{k = 0}^{\left\lfloor\left(t-t_{0}\right) / h\right\rfloor}\Upsilon^{(\alpha, \omega)}_k f(t-k h)$

where $\Upsilon^{(\alpha, \omega)} = [\Upsilon^{(\alpha, \omega)}_0, \Upsilon^{(\alpha, \omega)}_1, \Upsilon^{(\alpha, \omega)}_2, \cdots]$ are the Taylor series expansion coefficients of the generating function $g_\omega^{\alpha}(z)$ .

Theorem 3.8. The high-precision Grünwald-Letnikov fractional calculus can be approximated by ^[36,37]:

${}^{GL}\mathcal{D}_t^{\alpha} f(t) \approx \frac{1}{h^\alpha} \sum\limits_{k = 0}^{[(t-t_0)/h]}\Upsilon^{(\alpha, \omega)}_k f(t-kh).$

Here, the vector $\Upsilon^{(\alpha, \omega)}$ consists of the coefficients of the Taylor series expansion of the generating function. The coefficient vector $\Upsilon^{(\alpha, \omega)} = [\Upsilon^{(\alpha, \omega)}_0, \Upsilon^{(\alpha, \omega)}_1, \Upsilon^{(\alpha, \omega)}_2, \cdots]$ can be computed. The accuracy of this algorithm is $o(h^p)$ .

If a first-order generating function is chosen, the coefficient vector $\Upsilon^{(\alpha, \omega)}$ can be computed recursively as:

$\Upsilon^{(\alpha, \omega)}_0 = 1, \quad \Upsilon_k = \left( 1 - \frac{\alpha + 1}{k} \right)\Upsilon^{(\alpha, \omega)}_{k-1}.$

Because of,

$\frac{1}{h^{\alpha}} \sum\limits_{j = 0}^{m} \Upsilon^{(\alpha, \omega)}_j f(t_{k-j}) = \frac{1}{h^{\alpha}} \left[ f(t_k) + \sum\limits_{j = 1}^{m} \Upsilon^{(\alpha, \omega)}_j z(t_{k-j}) \right],$

where $m = [t_k/h] + 1$ . The Caputo fractional derivative and the Grünwald-Letnikov fractional derivative are closely related. For a function $f(t)$ that is $n$ -times continuously differentiable on $[0, t]$ , where $n-1 < \alpha < n$ , the relation is:

$D^{\alpha}_{t} f(t) = {}^{GL}D^{\alpha}_{t} f(t) - \sum\limits_{k = 0}^{n-1} \frac{t^{k-\alpha}}{\Gamma(k-\alpha+1)} f^{(k)}(0),$

If $f(t)$ and its first $n-1$ derivatives vanish at $t = 0$ , then:

$D^{\alpha}_{t} f(t) = {}^{GL}D^{\alpha}_{t} f(t).$

Using Theorem 3, for the system (1.2) with non-zero initial conditions $x(0) = [x(0), x_2(0), z(0), u(0)]^T$ , and defining a set of zero-initial condition state variables $\tilde{x}(t) = x(t) - x(0)$ , $\tilde{y}(t) = y(t) - y(0)$ , $\tilde{z}(t) = z(t) - x(0)$ , and $\tilde{u}(t) = u(t) - u(0)$ , $\omega$ -order accuracy numerical scheme can be rewritten as:

$\begin{eqnarray} \left\{ \begin{array}{l} x\left( t_k \right) = h^{\alpha _1}\left( a_1 x\left( t_{k-1} \right)(y\left( t_{k} \right) - M) + a_2 z\left( t_{k} \right) + a_3 u\left( t_{k} \right)\left(\frac{u\left( t_{k} \right)}{N} - 1\right)\right) +x\left( 0 \right) - \psi_1, \\ y\left( t_k \right) = h^{\alpha _2}\left( -b_1 x\left( t_{k} \right) + b_2 y\left( t_{k-1} \right)\left(1 - \frac{y\left( t_{k-1} \right)}{C}\right) + b_3 z\left( t_{k} \right)\left(1 - \frac{z\left( t_{k} \right)}{E}\right) - b_4 u\left( t_{k} \right) \right) +y\left( 0 \right) - \psi_2, \\ z\left( t_k \right) = h^{\alpha _3}\left( c_1 x\left( t_{k} \right)\left(\frac{x\left( t_{k} \right)}{F} - 1\right) - c_2 y\left( t_{k} \right) - c_3 z\left( t_{k-1} \right) - c_4 u\left( t_{k-1} \right)\right) +z\left( 0 \right) - \psi_3.\\ z\left( t_k \right) = h^{\alpha _4}\left( d_1 u\left( t_{k-1} \right)\left(\frac{y\left( t_{k} \right)}{P} - 1\right) - d_2 x\left( t_{k} \right) + d_3 z\left( t_{k} \right)\right) +u\left( 0 \right) - \psi_4.\\ \end{array} \right. \end{eqnarray}$

(3.4)

where

$\psi_1 = \sum\limits_{j = 1}^{m}\Upsilon^{(\alpha_1, \omega)}_jx(t_{k-j}), \; \; \; \; \psi_2 = \sum\limits_{j = 1}^{m}\Upsilon^{(\alpha_2, \omega)}_jy(t_{k-j}), \; \; \; \; \psi_3 = \sum\limits_{j = 1}^{m}\Upsilon^{(\alpha_3, \omega)}_jz_i(t_{k-j}), \; \; \; \; \psi_4 = \sum\limits_{j = 1}^{m}\Upsilon^{(\alpha_4, \omega)}_jz_i(t_{k-j}).$

If the number of simulation points is large, the short-memory effect can be utilized to approximate the summation terms. Assuming only the most recent $L_0$ samples are retained, the summation can be approximated as:

$\begin{eqnarray} \left\{ \begin{array}{l} \psi_1 = \sum\nolimits_{j = 1}^{m}\Upsilon^{(\alpha_1, \omega)}_jx(t_{k-j}) \approx \sum\nolimits_{j = 1}^{\min(L_0, k)}\Upsilon^{(\alpha_1, \omega)}_jx(t_{k-j}), \\ \psi_2 = \sum\nolimits_{j = 1}^{m}\Upsilon^{(\alpha_2, \omega)}_jy(t_{k-j}) \approx \sum\nolimits_{j = 1}^{\min(L_0, k)}\Upsilon^{(\alpha_2, \omega)}_jy(t_{k-j}), \\ \psi_3 = \sum\nolimits_{j = 1}^{m}\Upsilon^{(\alpha_3, \omega)}_jz(t_{k-j}) \approx \sum\nolimits_{j = 1}^{\min(L_0, k)}\Upsilon^{(\alpha_3, \omega)}_jz(t_{k-j}), \\ \psi_4 = \sum\nolimits_{j = 1}^{m}\Upsilon^{(\alpha_4, \omega)}_ju(t_{k-j}) \approx \sum\nolimits_{j = 1}^{\min(L_0, k)}\Upsilon^{(\alpha_4, \omega)}_ju(t_{k-j}). \end{array} \right. \end{eqnarray}$

(3.5)

Algorithm 1 is shown in the following:

Algorithm 1
1: Input: Function $f$ , fractional order $\alpha$ , initial value $x_0$ , step size $h$ , end time $t_n$ , maximum history length $L_0$ (optional) If $nargin = 5$ $L_0 \gets 10^{20}$ EndIf
2: $n \gets \text{length}(x_0)$ ; $m \gets \text{round}(t_n / h) + 1$ ; $t \gets 0$ ; $g \gets \text{genfunc}(1)$ ; $x_0 \gets x_0(:)$ ; $ha \gets h.^{\alpha}$ ; $z \gets \text{zeros}(n, m)$ ; $x_1 \gets x_0$ ;
3: For $i = 1$ to $n$ $\Upsilon(i, :) \gets \text{get_vecw}(\alpha(i), \min(m, L_0 + 1), g)$ EndFor
4: For $k = 2$ to $m$ $t_k \gets (k - 1) \cdot h$ ; $L \gets \min(k - 1, L_0)$ ;
For $i = 1$ to $n$ $x_1(i) \gets f(t_k, x_1, i) \cdot ha(i) - \Upsilon(i, 2:L + 1) \cdot z(i, k - 1:-1:k - L)' + x_0(i)$
EndFor $t \gets [t, t_k]$ ; $z(:, k) \gets x_1 - x_0$ ;
5: EndFor $x \gets (z + \text{repmat}(x_0, [1, m]))'$
6: Output: $x$ , $t$

Table 7. Parameters of the system at the initial condition [0.2, 0.1, 0.2, 0.01], and

$\alpha = [1,1,1,1]$ .

$a_1$	$a_2$	$a_3$	$b_1$	$b_2$	$b_3$	$b_4$	$c_1$	$c_2$	$c_3$
0.3927	0.2037	0.8952	0.0139	0.1229	0.7954	0.3133	0.3110	0.9192	0.035
$c_4$	$d_1$	$d_2$	$d_3$	$M$	$C$	$E$	$N$	$F$	$P$
0.7012	0.8818	0.2125	0.1277	0.5	0.5	4	4	4	4

| Show Table

DownLoad: CSV

4. Numerical simulation

To validate the effectiveness and accuracy of the proposed method, we conducted numerical simulations and compared its performance with two well-established numerical methods: the Runge-Kutta method (ode45 solver) and the Adams-Bashforth-Moulton method. Stability analysis at equilibrium points with the given parameters is shown in Table 8.

Table 8. Stability analysis of positive equilibrium points

$E^*_1(11.15, 4.312,$

$1.564, 1.506)$ and

$E^*_2(11.59, 4.833,$

$2.564, 1.62)$ .

$(x^, y^, z^, u^)$	Jacobian Matrix	Eigenvalue	Stability
$E^*_1$	$\begin{pmatrix} 1.4972 & 4.3805 & 0.2037 & -0.221 \\ -0.0139 & -1.9971 & 0.1733 & -0.3133 \\ 1.4236 & -0.9192 & -0.035 & -0.7012 \\ -0.2125 & 0.33205 & 0.1277 & 0.068881 \end{pmatrix}$	$\begin{aligned} \lambda_1 & = 1.825 \\ \lambda_2 & = -1.399 \\ \lambda_3 & = -0.8913 \\ \lambda_4 & = -5.938\times10^{-17} \end{aligned}$	Unstable
$E^*_2$	$\begin{pmatrix} 1.7017 & 4.55 & 0.2037 & -0.17001 \\ -0.0139 & -2.2531 & -0.22439 & -0.3133 \\ 1.4907 & -0.9192 & -0.035 & -0.7012 \\ -0.2125 & 0.35717 & 0.1277 & 0.18368 \end{pmatrix}$	$\begin{aligned} \lambda_1 & = -2.383 \\ \lambda_2 & = 1.673 \\ \lambda_3 & = -1.777\times10^{-16} \\ \lambda_4 & = 0.3067 \end{aligned}$	Unstable

| Show Table

DownLoad: CSV

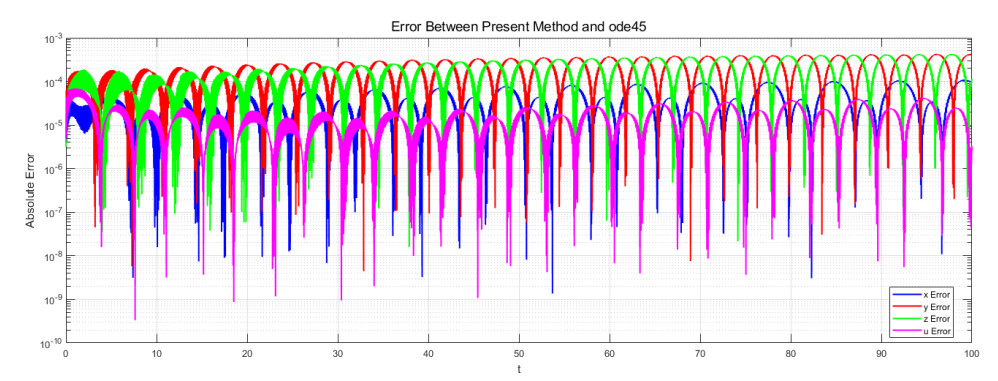
We utilize the parameters from and set the step size for the present method to $h = 0.005$ , while the step size for the ode45 solver is set to $h = 0.000001$ . The simulation time is $t = 500$ , and the initial condition is $x_0 = [0.1, 0.1, 0.1, 0.1]$ . The fractional orders are set to $\alpha = [1,1,1,1]$ . Figures 2–5 demonstrate the excellent agreement between the present method and the ode45 solver. Specifically, Figure 2 shows that the calculation results of the present method are highly consistent with those obtained using the ode45 solver, thereby verifying the accuracy of the present method. The small error value indicates that the present method can maintain high accuracy even at a significantly larger step size compared to the ode45 solver.

Figure 2. Absolute error of the present method with ode45.

DownLoad: Full-Size Img PowerPoint

Figure 3. Comparing time series plots of the present method with ode45.

DownLoad: Full-Size Img PowerPoint

Figure 4. Comparing 2D phase diagrams of the present method with ode45.

DownLoad: Full-Size Img PowerPoint

Figure 5. Comparing 3D phase diagrams of the present method with ode45.

DownLoad: Full-Size Img PowerPoint

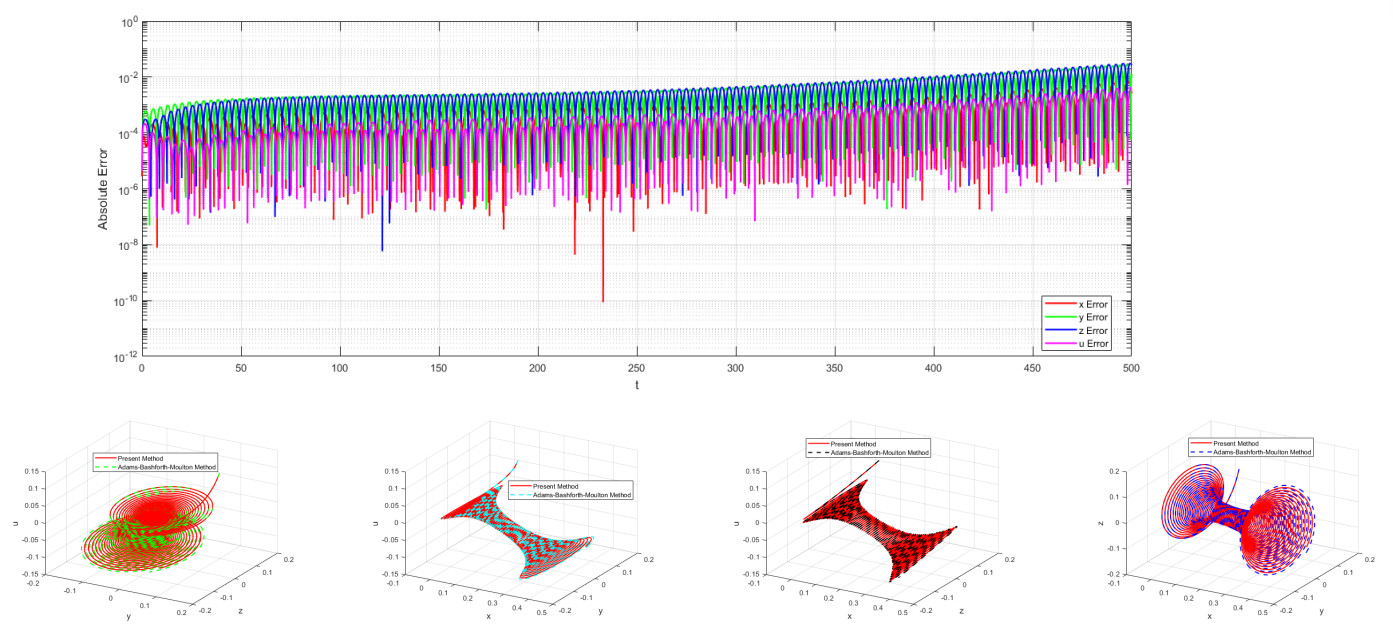
We again use the parameters from , and compared the present method with the Adams-Bashforth-Moulton method. The step size for both methods is set to $h = 0.01$ . The simulation time is $t = 500$ , the initial condition is $\mathbf{x}_0 = [0.1, 0.1, 0.1, 0.1]$ , and the fractional orders are $\alpha = [1,1,1,1]$ . Figure 6 demonstrates the excellent agreement between the present method and the Adams-Bashforth-Moulton method. Collectively, Figures 2–6 serve to validate the accuracy of the present method and highlight its effectiveness by comparing it with traditional methods (ode45 and Adams-Bashforth-Moulton). The phase diagram trajectories shown in Figures 3–6 for all three methods overlap almost completely, indicating that the present method can accurately capture the chaotic attractor.

Figure 6. Comparing 3D phase diagrams of the present method with the Adams-Bashforth-Moulton method.

DownLoad: Full-Size Img PowerPoint

Figures 2–6 demonstrates the superiority of the present method in simulating fractional-order ESER systems through error analysis and phase diagram comparison. High accuracy can be maintained at larger step sizes, and the calculation efficiency is higher. This is consistent with the results of traditional methods, and is suitable for simulating complex dynamic behaviors.

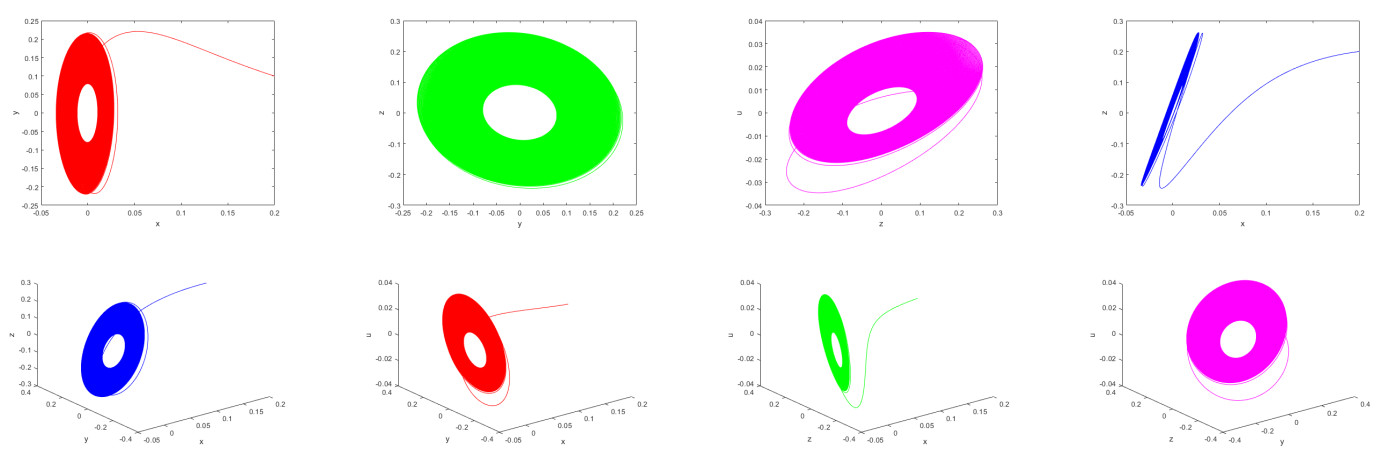
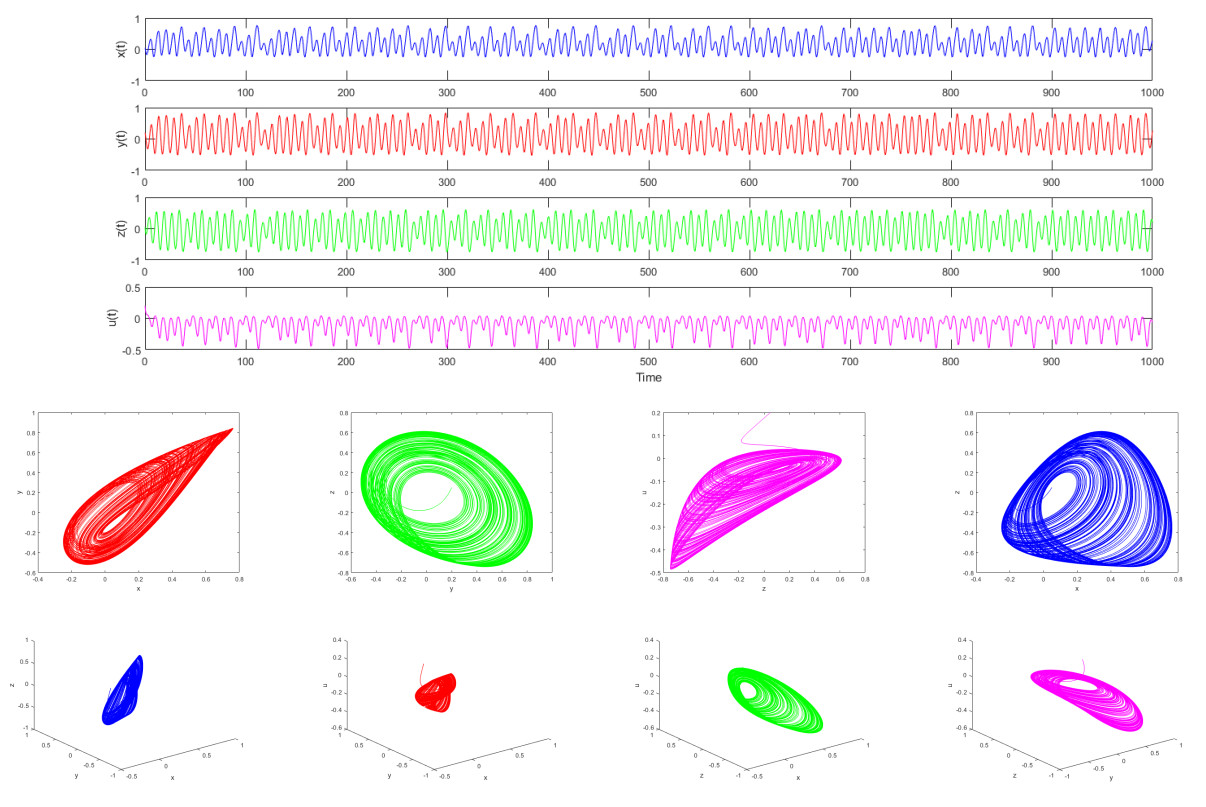
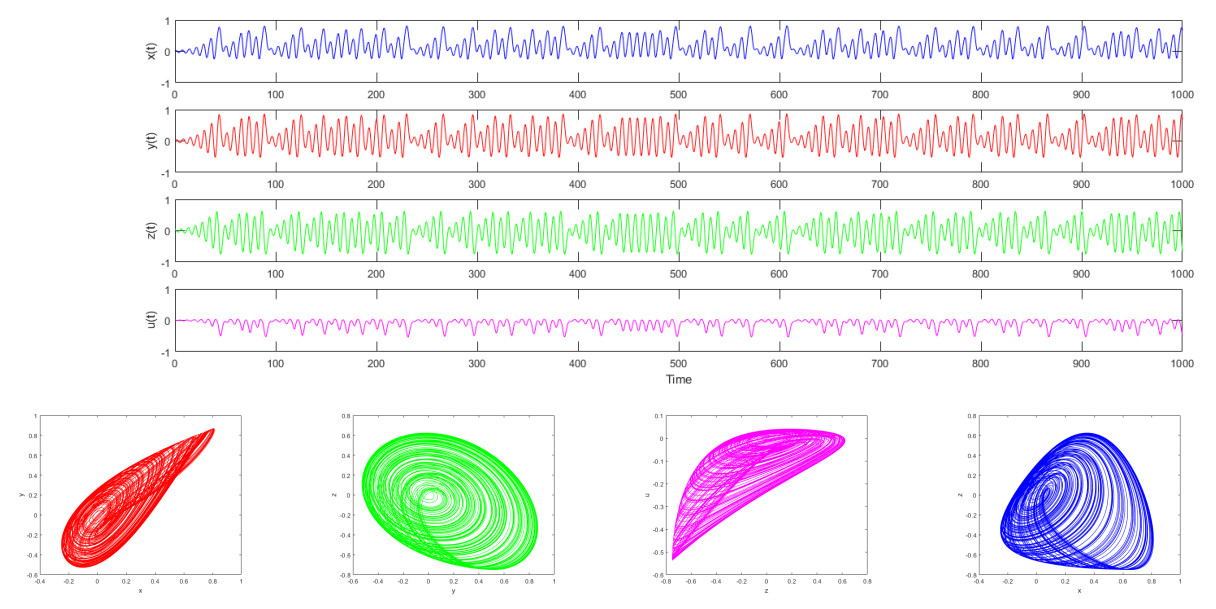
Second, we investigate the dynamic behavior of the system variables, including new energy, carbon emissions, economic growth, and carbon trading volume, at different fractional derivative orders and parameter settings. We set the step size $h = 0.01$ , the simulation time is $t = 1000$ , and the initial condition is $[0.05, 0.2, 0.05, 0.2]$ . The dynamic behavior is illustrated by time series plots and phase diagrams in Figures 7 and 8, with the parameters listed in Table 2. The time series exhibit irregular oscillations, while the phase diagrams reveal the presence of strange attractors, confirming the existence of chaotic behavior in the system. Figures 7 and 8 collectively demonstrate the dynamic behavior of the fractional-order ESER system at varying parameters and fractional-order derivatives, highlighting the complex interactions between new energy, carbon emissions, economic growth, and carbon trading volume.

Figure 7. Time series plots for the system at

$alpha = [1.02, 1.02, 1.02, 1.02]$ .

DownLoad: Full-Size Img PowerPoint

Figure 8. Time series plots and phase diagrams for the system with parameters in Table 2.

DownLoad: Full-Size Img PowerPoint

We set the parameters in Table 9.

Table 9. Parameters of the system for Figures 10–12.

$a_1$	$a_2$	$a_3$	$b_1$	$b_2$	$b_3$	$b_4$	$c_1$	$c_2$	$c_3$	$c_4$	$d_1$	$d_2$	$d_3$	$M$	$C$	$E$	$N$	$F$	$P$
1	1	1	0.02	0.1	1	1	0.1	1	0.01	1	1	0.4459	0.1277	1	1	4	1	1	2

| Show Table

DownLoad: CSV

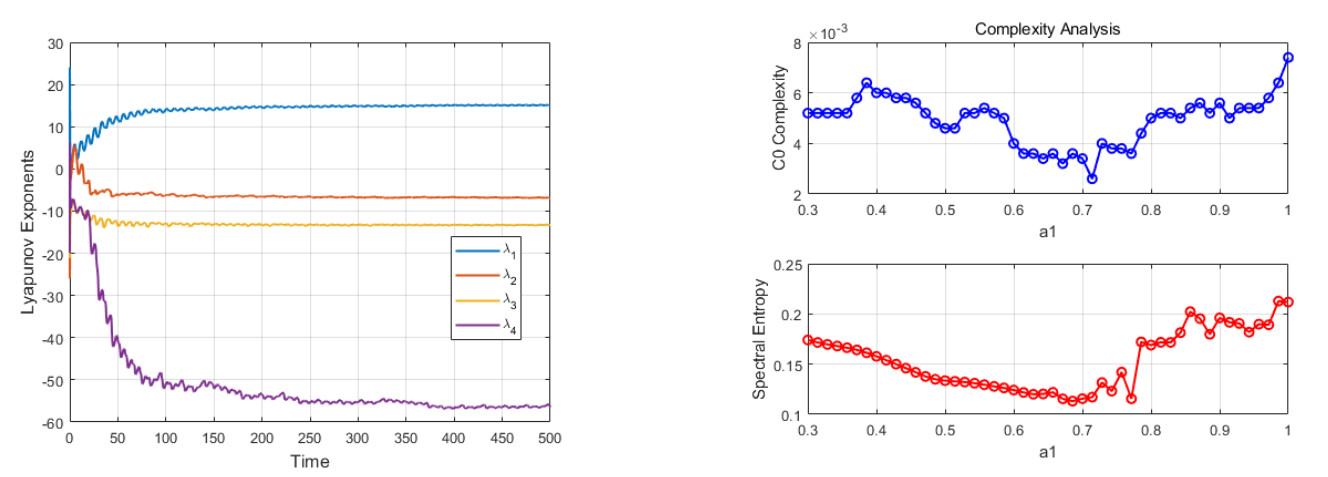
Lyapunov exponents, $C_0$ complexity, and spectral entropy complexity for the system for the parameters (), are $\alpha = [1,1,1,1]$ are shown in Figure 9.

Figure 9. Lyapunov exponents,

$C_0$ complexity and spectral entropy complexity for the system at parameters(Table 9),

$\alpha = [1,1,1,1]$ .

DownLoad: Full-Size Img PowerPoint

provides a quantitative analysis of the dynamic characteristics of the fractional-order ESER system using three key metrics: the Lyapunov exponent, $C_0$ complexity, and spectral entropy complexity. reveals that the maximum Lyapunov exponent (MLE) is positive, indicating a strong sensitivity to initial conditions, which is a hallmark of chaotic behavior. Additionally, the high values of $C_0$ complexity reflect the highly unpredictable nature of the system's state evolution. The significant spectral entropy complexity further confirms the presence of chaos by demonstrating a broadband distribution of system energy in the frequency domain. The consistency among these three metrics not only verifies the chaotic nature of the system under the given parameters and fractional orders ( $\alpha = [1,1,1,1]$ ), but also corroborates the qualitative observations of aperiodic oscillations and strange attractors seen in and . Moreover, they highlight the pivotal role of the fractional-order derivative $\alpha$ as a bifurcation parameter in the system's dynamics. Specifically, when $\alpha = 1$ . Moreover, they highlight the pivotal role of the fractional-order derivative $\alpha$ as a bifurcation parameter in the system's dynamics. Specifically, when $\alpha = 1$ , the system exhibits chaos, whereas it tends to stabilize when $\alpha = 0.95$ . This underscores the fine-tuning capability of fractional calculus in regulating the system's dynamic behavior.

The stability analysis of the positive equilibrium point $(x^*, y^*, z^*, u^*) = (7.38, 2.904, 4.68, 1.063)$ is presented in Table 10. The Jacobian matrix and its eigenvalues are computed to assess the system's behavior near this equilibrium point.

Table 10. Positive equilibrium point, Jacobian matrix, eigenvalues, and phase angles.

Positive Equilibrium Point: $x^* = 7.38$ , $y^* = 2.904$ , $z^* = 4.68$ , $u^* = 1.063$
Jacobian Matrix: $\begin{pmatrix} 1.9035 & 7.3797 & 1 & 1.1253 \\ -0.02 & -0.4807 & -1.3401 & -1 \\ 1.3759 & -1 & -0.01 & -1 \\ -0.4459 & 0.53133 & 0.1277 & 0.45176 \end{pmatrix}$
Eigenvalues and Phase Angles at $\alpha_i = 1$ , $i = 1, 2, 3, 4$ :
$\begin{aligned} \lambda_1 & = 1.912 + 1.462i, & \text{Phase Angle} & = 0.6528, \\ \lambda_2 & = 1.912 - 1.462i, & \text{Phase Angle} & = -0.6528, \\ \lambda_3 & = -1.959, & \text{Phase Angle} & = \pi, \\ \lambda_4 & = -1.772 \times 10^{-16} & \text{Phase Angle} & = -\pi \end{aligned}$

| Show Table

DownLoad: CSV

The eigenvalues $\lambda_{1, 2} = 1.912 \pm 1.462i$ have positive real parts ( $\text{Re}(\lambda) > 0$ ), indicating that the equilibrium point is unstable when $\alpha_i = 1$ for $i = 1, 2, 3, 4$ . This instability is a key characteristic of the system's behavior under these conditions.

To further investigate the impact of fractional-order parameters on stability, we set $\alpha_i = \alpha$ for $i = 1, 2, 3, 4$ and treat $\alpha$ as a bifurcation parameter. A bifurcation occurs at $\frac{\alpha \pi}{2} = 0.6528$ . Specifically, for $\frac{\alpha \pi}{2} > 0.6528$ , the system remains unstable. For $\frac{\alpha \pi}{2} < 0.6528$ , the system remains stable.

In a more general scenario, we define $\beta = \max\{\alpha_i\}$ and $\beta = \min\{\alpha_i\}$ to analyze the stability: if $\frac{\beta \pi}{2} < 0.6528$ (where $\beta = \max\{\alpha_i\}$ ), the system remains stable, and this stability persists. $\frac{\beta \pi}{2} > 0.6528$ (where $\beta = \max\{\alpha_i\}$ ), the system may be stable or unstable, requiring further analysis. $\frac{\beta \pi}{2} > 0.6528$ (where $\beta = \min\{\alpha_i\}$ ), the system remains unstable, and this instability persists. $\frac{\beta \pi}{2} < 0.6528$ (where $\beta = \min\{\alpha_i\}$ ), the system may be stable or unstable, requiring further analysis. These results highlight the critical role of the fractional-order parameter $\alpha$ in determining the system's stability. The eigenvalues $\lambda_{1, 2} = 1.912 \pm 1.462i$ with $\text{Re}(\lambda) > 0$ confirm the instability for $\alpha_i = 1$ . When $\alpha_i = \alpha$ and $\alpha$ serves as a bifurcation parameter, a bifurcation occurs at $\frac{\alpha \pi}{2} = 0.6528$ . The system remains unstable for $\frac{\alpha \pi}{2} > 0.6528$ and stable for $\frac{\alpha \pi}{2} < 0.6528$ .

In general, let $\beta = \max\{\alpha_i\}$ . For $\frac{\beta \pi}{2} < 0.6528$ , the system remains stable, and this stability persists. For $\frac{\beta \pi}{2} > 0.6528$ , the system may be stable or unstable, requiring further judgment. Let $\beta = \min\{\alpha_i\}$ . For $\frac{\beta \pi}{2} > 0.6528$ , the system remains unstable, and this instability persists. For $\frac{\beta \pi}{2} < 0.6528$ , the system may be stable or unstable, requiring further judgment.

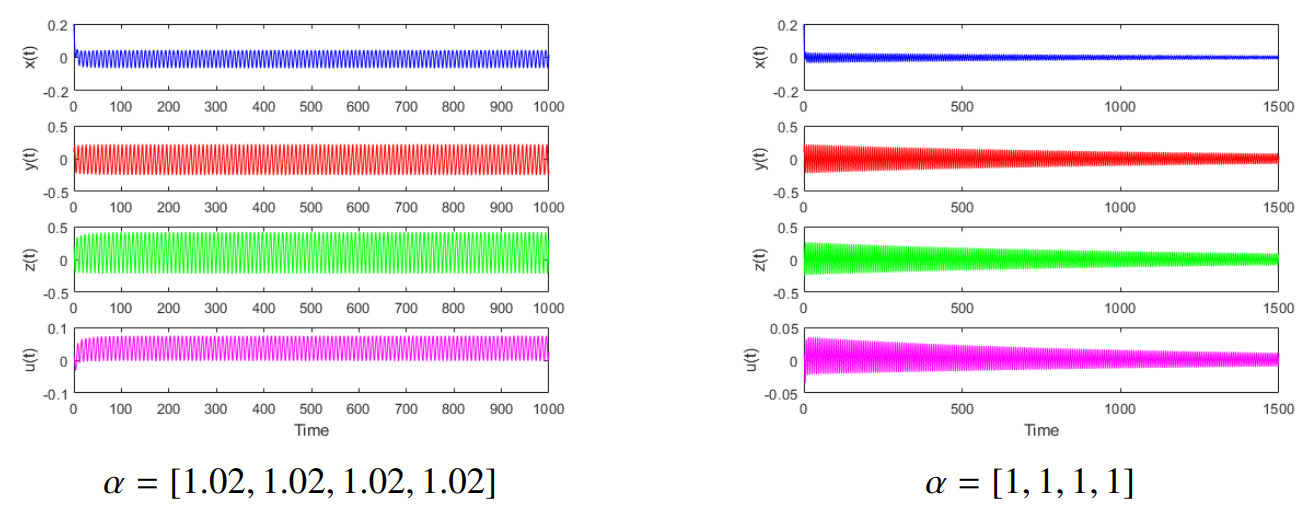
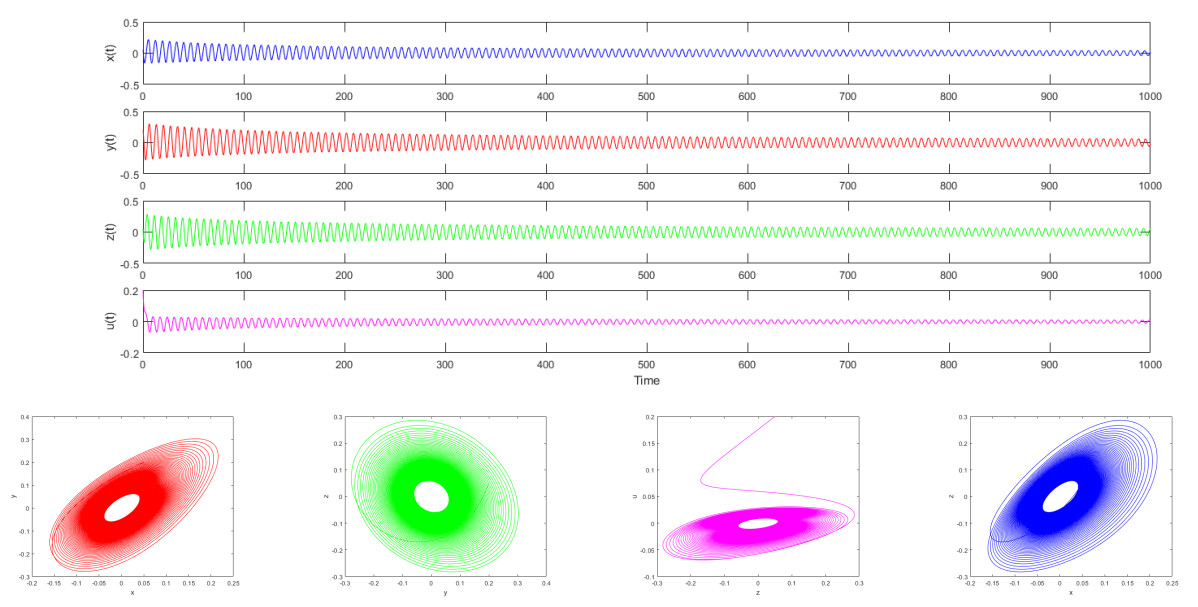
Set the step size is $h = 0.01$ , to time $t = 1000$ , the initial condition is $[0.05, 0.2, 0.05, 0.2]$ , and different fractional derivative $\alpha = [\alpha_1, \alpha_2, \alpha_3, \alpha_4]$ . The numerical simulation results are shown in Figures 10–12.

Figure 10. Time series plots and phase diagrams for the system at

$\alpha = [1,1,1,1]$ .

DownLoad: Full-Size Img PowerPoint

Figure 11. Time series plots and phase diagrams for the system at

$\alpha = [0.95, 0.95, 0.95, 0.95]$ .

DownLoad: Full-Size Img PowerPoint

Figure 12. Time series plots and phase diagrams for the system at

$\alpha = [1.002, 1.002, 1.002, 1.002]$ .

DownLoad: Full-Size Img PowerPoint

– illustrate the dynamic behavior of the fractional-order ESER system under varying fractional-order derivative parameters ( $\alpha$ ), revealing the transition of the system from stability to chaos through time series and phase diagrams. The following provides a detailed analysis.

Figure 10 demonstrates that the system is in a typical chaotic state. The time series exhibits irregular oscillations, and the phase diagram reveals complex strange attractor structures, indicating extreme sensitivity to initial conditions. This chaotic behavior is corroborated by the quantitative indicators in Figure 9 (such as positive Lyapunov exponents), reflecting the inherent instability of the system under integer-order derivatives.

shows significantly different characteristics. The amplitude of the time series gradually decays to zero over time, and the phase diagram trajectory converges to a fixed point. This indicates that when the fractional-order derivative $\alpha$ is slightly lower than the integer order, the system's memory effect is enhanced, and its dissipative characteristics dominate, ultimately stabilizing the system at the equilibrium point. This transition highlights the critical role of $\alpha$ as a bifurcation parameter.

displays an even more extreme divergent behavior. The time series diverges exponentially, and the phase diagram trajectory moves infinitely far from the equilibrium point. This instability suggests that when $\alpha$ is slightly higher than the integer order, the system's accumulation effect exceeds a critical threshold, causing the state variables to become uncontrollable. Collectively, these three sets of comparative experiments demonstrate that a small change in the fractional derivative $\alpha$ (± 0.05) can fundamentally alter the qualitative behavior of the system.

Next, we design a chaos synchronization control method for the fractional-order chaotic system (1.2). The drive-response system synchronization is achieved through linear feedback control. The drive system is (1.2). The response system has identical structure, but the includes control inputs:

$\begin{eqnarray} \left\{ \begin{array}{l} D^{\alpha_1}\hat{x} = a_1\hat{x}(\hat{y} - M) + a_2\hat{z} + a_3\hat{u}(\hat{u}/N - 1) + U_1, \\ D^{\alpha_2}\hat{y} = -b_1\hat{x} + b_2\hat{y}(1 - \hat{y}/C) + b_3\hat{z}(1 - \hat{z}/E) - b_4\hat{u} + U_2, \\ D^{\alpha_3}\hat{z} = c_1\hat{x}(\hat{x}/F - 1) - c_2\hat{y} - c_3\hat{z} - c_4\hat{u} + U_3, \\ D^{\alpha_4}\hat{u} = d_1\hat{u}(\hat{y}/P - 1) - d_2\hat{x} + d_3\hat{z} + U_4.\\ \end{array} \right. \end{eqnarray}$

(4.1)

Define the error vector $\mathbf{e} = [e_1, e_2, e_3, e_4]^\top$ , where $e_1 = \hat{x} - x, e_2 = \hat{y} - y, e_3 = \hat{z} - z,$ and $e_4 = \hat{u} - u.$ The linear feedback control law is designed as

$\begin{equation*} U_i = -K_ie_i, \quad i = 1, 2, 3, 4 \end{equation*}$

In the program implementation, a uniform gain $K = 10$ is used:

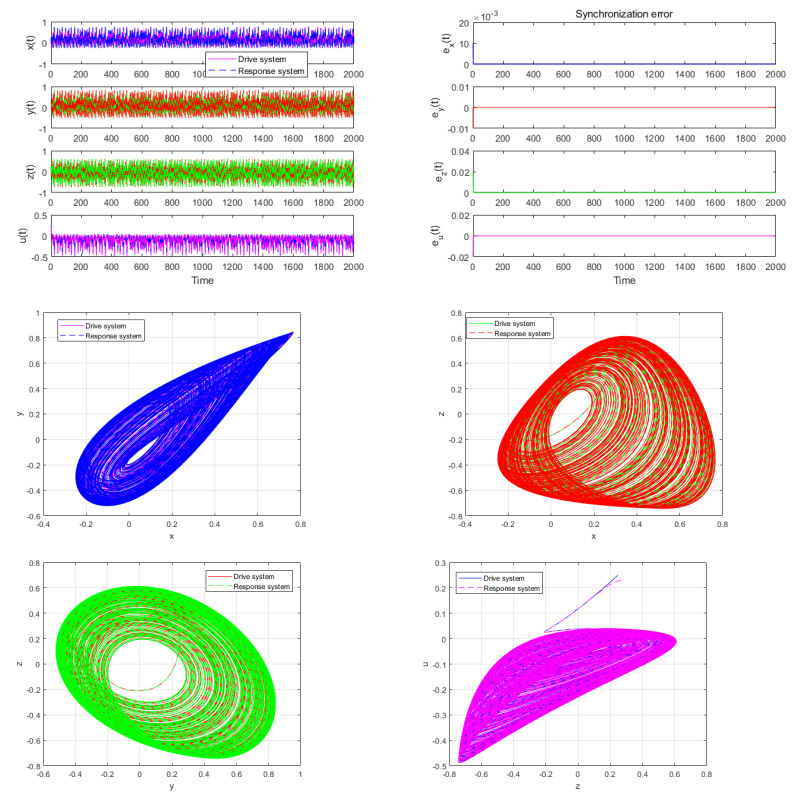
$\begin{equation*} \mathbf{U} = -K\mathbf{e} \end{equation*}$

The initial conditions of the drive system is $[0.25, 0.25, 0.25, 0.25]$ . The initial conditions of the response system is $[0.26, 0.24, 0.27, 0.23]$ . The parameters are in Table 9. The numerical simulation results are shown in the Figures 13 and 14.

Figure 13. Simulation results of time series plots and 2D phase diagram synchronization.

DownLoad: Full-Size Img PowerPoint

Figure 14. Simulation results of 3D phase diagram synchronization.

DownLoad: Full-Size Img PowerPoint

illustrates the synchronization of the fractional-order ESER system using linear feedback control, showing both time series plots and 2D phase diagrams. The time series plots clearly reflect the dynamic changes of the drive and response systems during the synchronization process. Before synchronization, the state variables (such as new energy $x$ , carbon emissions $y$ , economic growth $z$ , and carbon trading volume $u$ ) exhibit different fluctuation patterns. After synchronization, the curves of the response system gradually overlap with those of the drive system, indicating that the response system can accurately track the dynamic behavior of the drive system. The 2D phase diagrams further verify the synchronization effect by comparing the trajectories of the drive and response systems in the phase space. The overlapping trajectories after synchronization demonstrate that the two systems have consistent evolution patterns in the phase space, thereby proving the effectiveness of the feedback control strategy.

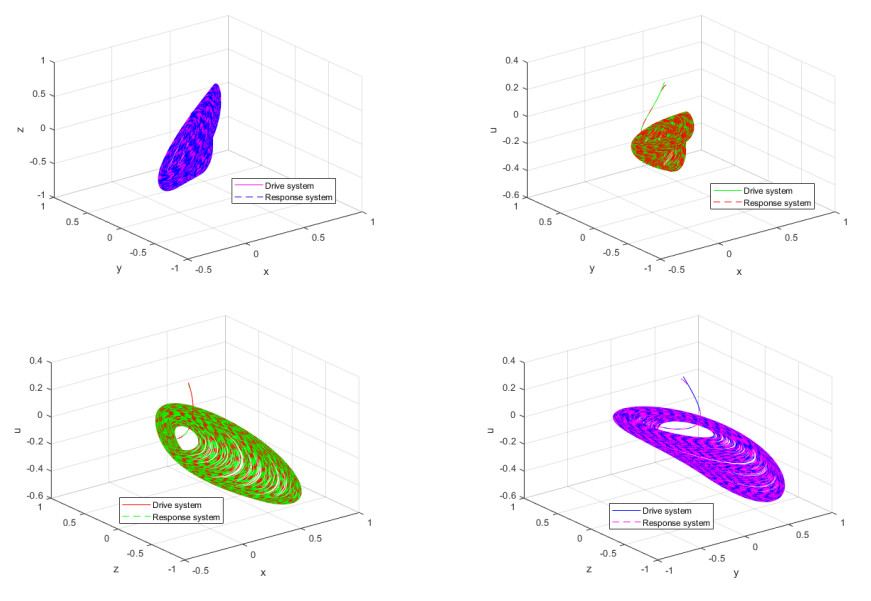
presents the synchronization of the fractional-order ESER system using 3D phase diagrams. The 3D phase diagrams provide a more comprehensive view of the system's complex dynamic characteristics, especially in the context of multi-variable interactions. The figure shows the trajectories of the drive and response systems in a three-dimensional space (e.g., the $x-y-z$ space). Before synchronization, the trajectories of the two systems are distinctly different. However, as synchronization control is implemented, the trajectory of the response system gradually overlaps with that of the drive system. This overlap not only indicates synchronization in the time series but also shows that the movement patterns of the two systems in the 3D phase space become consistent. This further validates the effectiveness of the control strategy and highlights the dynamic characteristics of the fractional-order system in high-dimensional space.

Next, we design the adaptive control method for the fractional-order chaotic system (1.2). The system state to the desired stable equilibrium point $(0, 0, 0, 0)$ . The control equation is described by the following fractional-order differential equations:

$\begin{eqnarray} \left\{ \begin{array}{l} D^{\alpha_1}x = a_1x(y-M) + a_2z + a_3u\left(\frac{u}{N}-1\right)- k_x(t)(x-x_d) \\ D^{\alpha_2}y = -b_1x + b_2y\left(1-\frac{y}{C}\right) + b_3z\left(1-\frac{z}{E}\right) - b_4u- k_y(t)(y-y_d) \\ D^{\alpha_3}z = c_1x\left(\frac{x}{F}-1\right) - c_2y - c_3z - c_4u- k_z(t)(z-z_d) \\ D^{\alpha_4}u = d_1u\left(\frac{y}{P}-1\right) - d_2x + d_3z- k_u(t)(u-u_d) \end{array} \right. \end{eqnarray}$

(4.2)

The adaptive law is

$\begin{eqnarray} \left\{ \begin{array}{l} \dot{k}_x = \gamma_x (x-x_d)^2 \\ \dot{k}_y = \gamma_y (y-y_d)^2 \\ \dot{k}_z = \gamma_z (z-z_d)^2 \\ \dot{k}_u = \gamma_u (u-u_d)^2 \end{array} \right. \end{eqnarray}$

(4.3)

A Lyapunov function is designed to prove stability:

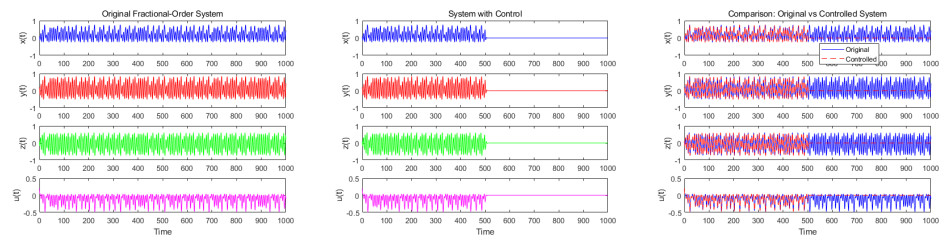
$\begin{eqnarray*} \begin{array}{ll} V & = \frac{1}{2}(x-x_d)^2 + \frac{1}{2}(y-y_d)^2 + \frac{1}{2}(z-z_d)^2 + \frac{1}{2}(u-u_d)^2 + \frac{1}{2\gamma_x}(k_x-k_x^*)^2 \\& +\frac{1}{2\gamma_y}(k_y-k_y^*)^2 + \frac{1}{2\gamma_z}(k_z-k_z^*)^2 + \frac{1}{2\gamma_u}(k_u-k_u^*)^2 \end{array} \end{eqnarray*}$

$k_x^*, k_y^*, k_z^*, k_u^*$ is the ideal gain value. By calculating its fractional derivative and applying the adaptive law, it can be proved that the system is stable. This adaptive control method can effectively stabilize the chaotic system to the desired equilibrium point without the need to accurately know the system parameters and has strong robustness. We set $k_x, k_y, k_z, k_u = [0.1, 0.1, 0.1, 0.1]$ , $(x_d, y_d, z_d, u_d) = (0, 0, 0, 0)$ , $[k_x^*, k_y^*, k_z^*, k_u^*] = [0,0,0,0]$ , and start control time is $500$ . The parameters are in Table 9. The numerical simulation results with adaptive control are shown in Figure 15.

Figure 15. Simulation results of time series plots with adaptive control.

DownLoad: Full-Size Img PowerPoint

shows the time series plots of the fractional-order ESER system under adaptive control, demonstrating how the system stabilizes to the desired equilibrium point from its initial state. The figure clearly reflects the chaotic or unstable state of the system before the control is applied (e.g., before $t = 500$ ). The state variables fluctuate significantly and irregularly. However, once the adaptive control strategy is implemented, the fluctuations of the state variables gradually decrease, and the system eventually stabilizes near the desired equilibrium point (e.g., $(x_d, y_d, z_d, u_d) = (0, 0, 0, 0)$ ). This indicates that the adaptive control strategy can effectively regulate the system's dynamic behavior and achieve rapid convergence to the target equilibrium point. Even with uncertain system parameters, the adaptive control maintains a good control effect, demonstrating its strong robustness and adaptability. Stabilize the chaotic system to the target equilibrium point, the system stabilizes quickly after control is started at $t = 500$ , verifying the robustness of the adaptive law.

5. Conclusions

This paper comprehensively explores the chaotic dynamics and control of a fractional-order energy-saving, and emission-reduction (ESER) system using a high-precision method. By constructing a four-dimensional fractional-order system, we successfully model the complex interactions among new energy, carbon emissions, economic growth, and carbon trading volume. A novel high-precision numerical method based on generating functions has been proposed to analyze the dynamic behaviors of the system in various fractional derivatives and parameters. The present method demonstrates accuracy and efficiency, particularly in simulating complex dynamic phenomena such as stable state, rapid divergence, and chaotic attractors. Numerical simulations reveal that the system's behavior is highly sensitive to changes in fractional-order parameters, with small variations leading to significant alterations in qualitative behavior. Furthermore, this research has designed and implemented linear feedback and adaptive control strategies to achieve chaos synchronization and system stability. In conclusion, the present numerical method and control strategies offer robust tools for analyzing and controlling complex fractional-order chaotic systems. Future research may further investigate the impacts of time delays, stochastic disturbances, and the application of these methods to more complex ESER systems or fractional pattern dynamic equations.

Use of AI tools declaration

The authors declare we have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This paper is supported by Scientific Research Project of Higher Education Institutions of the Department of Education of Inner Mongolia Autonomous Region (NJZY22237). Ordos Vocational College's "Action Plan for Improving the Quality and Excellence of Vocational Education (2020-2023)" (EZTZ20210303). Doctoral research start-up fund of Inner Mongolia University of Technology (DC2400003130) and the Natural Science Foundation of Inner Mongolia (2024LHMS06025).

Conflicts of interest

The authors declare that there are no conflicts of interest regarding the publication of this article.

References

[1]	F. Yu, S. Zhang, D. Su, Y. Wu, Y. M. Gracia, H. Yin, Dynamic analysis and implementation of FPGA for a new 4D fractional-order memristive Hopfield neural network, Fractal Fractional, 9 (2025), 115. https://doi.org/10.3390/fractalfract9020115 doi: 10.3390/fractalfract9020115
[2]	F. Yu, W. Zhang, X. Xiao, W. Yao, S. Cai, J. Zhang, et al., Dynamic analysis and field-programmable gate array implementation of a 5D fractional-order memristive hyperchaotic system with multiple coexisting attractors, Fractal Fractional, 8 (2024), 271. https://doi.org/10.3390/fractalfract8050271 doi: 10.3390/fractalfract8050271
[3]	F. Yu, X. Kong, W. Yao, J. Zhang, S. Cai, H. Lin, et al., Dynamics analysis, synchronization and FPGA implementation of multiscroll Hopfield neural networks with non-polynomial memristor, Chaos Solitons Fractals, 179 (2024), 114440. https://doi.org/10.1016/j.chaos.2023.114440 doi: 10.1016/j.chaos.2023.114440
[4]	Q. Lai, Y. Liu, L. Fortuna, Dynamical analysis and fixed-time synchronization for secure communication of hidden multiscroll memristive chaotic system, IEEE Trans. Circuits Syst. I, 71(10) (2024), 4665–4675. https://doi.org/10.1109/TCSI.2024.3434551
[5]	Q. Lai, Z. J. Chen, Dynamical analysis and finite-time synchronization of grid-scroll memristive chaotic system without equilibrium, Chaos Solitons Fractals, 176 (2023), 114118. https://doi.org/10.1016/j.chaos.2023.114118 doi: 10.1016/j.chaos.2023.114118
[6]	Q. Lai, L. Yang, G. Chen, Two-dimensional discrete memristive oscillatory hyperchaotic maps with diverse dynamics, IEEE Trans. Ind. Electron., 72 (2025), 969–979. https://doi.org/10.1109/TIE.2024.3417974 doi: 10.1109/TIE.2024.3417974
[7]	W. Feng, J. Yang, X. Zhao, Z. Qin, J. Zhang, Z. Zhu, et al., A novel multi-channel image encryption algorithm leveraging pixel reorganization and hyperchaotic maps, Mathematics, 12 (2024), 3917. https://doi.org/10.3390/math12243917 doi: 10.3390/math12243917
[8]	W. Feng, Q. W. Wang, H. Liu, Y. Ren, J. H. Zhang, S. B. Zhang, et al., Exploiting newly designed fractional-order 3D Lorenz chaotic system and 2D discrete polynomial hyper-chaotic map for high-performance multi-image encryption, Fractal Fractional, 7 (2023), 887. https://doi.org/10.3390/fractalfract7120887 doi: 10.3390/fractalfract7120887
[9]	W. Feng, J. Zhang, Y. Chen, Z. T. Qin, Y. S. Zhang, M. Ahmad, et al., Exploiting robust quadratic polynomial hyperchaotic map and pixel fusion strategy for efficient image encryption, Expert Syst. Appl., 246 (2024), 123190. https://doi.org/10.1016/j.eswa.2024.123190 doi: 10.1016/j.eswa.2024.123190
[10]	K. Qian, Y. Xiao, Y. J. Wei, D. Liu, Q. W. Wang, W. Feng, A robust memristor-enhanced polynomial hyper-chaotic map and its multi-channel image encryption application, Micromachines, 14 (2023), 2090. https://doi.org/10.3390/mi14112090 doi: 10.3390/mi14112090
[11]	C. H. Wang, D. W. Luo, Q. L. Deng, G. Yang, Dynamics analysis and FPGA implementation of discrete memristive cellular neural network with heterogeneous activation functions, Chaos Solitons Fractals, 187 (2024), 115471. https://doi.org/10.1016/j.chaos.2024.115471 doi: 10.1016/j.chaos.2024.115471
[12]	H. Che, Y. L. Wang, Z. Y. Li, Novel patterns in a class of fractional reaction-diffusion models with the Riesz fractional derivative, Math. Comput. Simul., 202 (2022), 149–163. https://doi.org/10.1016/j.matcom.2022.05.037 doi: 10.1016/j.matcom.2022.05.037
[13]	C. Han, Y. L. Wang, Z. Y. Li, A high-precision numerical approach to solving space fractional Gray-Scott model, Appl. Math. Lett., 125 (2022), 107759. https://doi.org/10.1016/j.aml.2021.107759 doi: 10.1016/j.aml.2021.107759
[14]	X. H. Wang, H. L. Zhang, Y. L. Wang, Z. Y. Li, Dynamic properties and numerical simulations of the fractional Hastings-Powell model with the Grünwald-Letnikov fractional derivative, Int. J. Bifurcation Chaos, Forthcoming, 2025.
[15]	S. Zhang, H. L. Zhang, Y. L. Wang, Z. Y. Li, Dynamic properties and numerical simulations of a fractional phytoplankton-zooplankton ecological model, Networks Heterog. Media, 20 (2025), 648–669. https://doi.org/10.3934/nhm.2025028 doi: 10.3934/nhm.2025028
[16]	G. C. Fang, L. X. Tian, M. Sun, M. Fu, Analysis and application of a novel three-dimensional energy-saving and emission-reduction dynamic evolution system Energy, 40 (2012), 291–299. https://doi.org/10.1016/j.energy.2012.01.072
[17]	J. Wang, Y. L. Wang, Study on the stability and entropy complexity of an energy-saving and emission-reduction model with two delays, Entropy, 18 (2016), 371. https://doi.org/10.3390/e18100371 doi: 10.3390/e18100371
[18]	G. Fang, L. Lu, L. Tian, Y. He, H. Yin, Research on the influence mechanism of carbon trading on new energy-a case study of ESER system for China, Phys. A, 545 (2020), 123572. https://doi.org/10.1016/j.physa.2019.123572 doi: 10.1016/j.physa.2019.123572
[19]	G. Fang, L. Tian, M. Fu, M. Sun, R. Du, M. Liu, Investigating carbon tax pilot in YRD urban agglomerations-analysis of a novel ESER system with carbon tax constraints and its application, Appl. Energy, 194 (2017), 635–647. https://doi.org/10.1016/j.apenergy.2016.09.022 doi: 10.1016/j.apenergy.2016.09.022
[20]	Z. J. Chen, W. J. Liu, Dynamical behavior of fractional-order energy-saving and emission-reduction system and its discretization, Nat. Resour. Model., 32 (2019), e12203. https://doi.org/10.1111/nrm.12203 doi: 10.1111/nrm.12203
[21]	Z. Y. Li, M. C. Wang, Y. L. Wang, Numerical solutions of variable-coefficient fractional-in-space KdV equation with the Caputo fractional derivative, Fractal Fractional, 6 (2022), 207. https://doi.org/10.3390/fractalfract6040207 doi: 10.3390/fractalfract6040207
[22]	H. Che, Y. L. Wang, Z. Y. Li, Numerical solutions of space fractional variable-coefficient KdV-modified KdV equation by Fourier spectral method, Fractals, 29 (2021), 2150246. https://doi.org/10.1142/S0218348X21502467 doi: 10.1142/S0218348X21502467
[23]	Z. Y. Li, M. C. Wang, Y. L. Wang, Solving a class of variable order nonlinear fractional integral differential equations by using reproducing kernel function, AIMS Math., 7 (2022), 12935–12951. https://doi.org/10.3934/math.2022716 doi: 10.3934/math.2022716
[24]	Y. L. Wang, L. Jia, H. L. Zhang, Numerical solution for a class of space-time fractional equation by the piecewise reproducing kernel method, Int. J. Comput. Math., 96 (2019), 2100–2111. https://doi.org/10.1080/00207160.2018.1544367 doi: 10.1080/00207160.2018.1544367
[25]	J. Ning, Y. L. Wang, Fourier spectral method for solving fractional-in-space variable coefficient KdV-Burgers equation, Indian J. Phys., 98 (2024), 1727–1744. https://doi.org/10.1007/s12648-023-02934-2 doi: 10.1007/s12648-023-02934-2
[26]	X. L. Gao, H. L. Zhang, X. Y. Li, Research on pattern dynamics of a class of predator-prey model with interval biological coefficients for capture, AIMS Math., 9 (2024), 18506–18527. https://doi.org/10.3934/math.2024901 doi: 10.3934/math.2024901
[27]	X. L. Gao, H. L. Zhang, Y. L. Wang, Z. Y. Li, Research on pattern dynamics behavior of a fractional vegetation-water model in arid flat environment, Fractal Fractional, 8 (2024), 264. https://doi.org/10.3390/fractalfract8050264 doi: 10.3390/fractalfract8050264
[28]	X. L. Gao, Z. Y. Li, Y. L. Wang, Chaotic dynamic behavior of a fractional-order financial system with constant inelastic demand, Int. J. Bifurcation Chaos, 34 (2024), 2450111. https://doi.org/10.1142/S0218127424501116 doi: 10.1142/S0218127424501116
[29]	C. P. Li, Z. Wang, The local discontinuous Galerkin finite element methods for Caputo-type partial differential equations: Numerical analysis, Appl. Numer. Math., 140 (2019), 1–22. https://doi.org/10.1016/j.apnum.2019.01.007 doi: 10.1016/j.apnum.2019.01.007
[30]	C. P. Li, Z. Wang, The local discontinuous Galerkin finite element methods for Caputo-type partial differential equations: Mathematical analysis, Appl. Numer. Math., 150 (2020), 587–606. https://doi.org/10.1016/j.apnum.2019.11.007 doi: 10.1016/j.apnum.2019.11.007
[31]	C. P. Li, Z. Wang, Non-uniform L1/discontinuous Galerkin approximation for the time-fractional convection equation with weak regular solution, Math. Comput. Simul., 182 (2021), 838–857. https://doi.org/10.1016/j.matcom.2020.12.007 doi: 10.1016/j.matcom.2020.12.007
[32]	C. P. Li, Z. Wang, Numerical methods for the time fractional convection-diffusion-reaction equation, Numer. Funct. Anal. Optim., 42 (2021), 1115–1153. https://doi.org/10.1080/01630563.2021.1936019 doi: 10.1080/01630563.2021.1936019
[33]	I. Podlubny, Fractional Differential Equations, Academic Press, San Diego, 1999. https://doi.org/10.1016/B978-0-12-558840-9.X5000-4
[34]	V. Daftardar-Gejji, Fractional Calculus and Fractional Differential Equations, Springer Singapore, 2019. https://doi.org/10.1007/978-981-13-9227-6
[35]	I. Petráš, Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation, Springer, Heidelberg, 2011. https://doi.org/10.1007/978-3-642-18101-6
[36]	D. Y. Xue, Fractional Calculus and Fractional-Order Control, Science Press, 2018. https://doi.org/10.1007/978-981-10-6064-2
[37]	D. Y. Xue, L. Bai, Numerical algorithms for Caputo fractional-order differential equations, Int. J. Control, 90 (2016), 1201–1211. https://doi.org/10.1080/00207179.2016.1158419 doi: 10.1080/00207179.2016.1158419

Reader Comments

Your name:*

Email:*
© 2025 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

Electronic Research Archive

1.1 1.7

Metrics

Article views(158) PDF downloads(21) Cited by(0)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

Figures and Tables

Figures(15) / Tables(10)

Electronic Research Archive

Chaotic dynamics analysis and control of fractional-order ESER systems using a high-precision Caputo derivative approach

Related Papers:

Abstract

1. Introduction

2. Stability analysis

3. Brief description of the methodology

4. Numerical simulation

5. Conclusions

Use of AI tools declaration

Acknowledgments

Conflicts of interest

References

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Catalog

Abstract

1. Introduction

2. Stability analysis

3. Brief description of the methodology

4. Numerical simulation

5. Conclusions

Use of AI tools declaration

Acknowledgments

Conflicts of interest

References

Electronic Research Archive

Chaotic dynamics analysis and control of fractional-order ESER systems using a high-precision Caputo derivative approach

Related Papers:

Abstract

1. Introduction

2. Stability analysis

3. Brief description of the methodology

4. Numerical simulation

5. Conclusions

Use of AI tools declaration

Acknowledgments

Conflicts of interest

References

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog

Abstract

1. Introduction

2. Stability analysis

3. Brief description of the methodology

4. Numerical simulation

5. Conclusions

Use of AI tools declaration

Acknowledgments

Conflicts of interest

References