An intelligent optimization method for accelerating physical quantity reconstruction in computational fluid dynamics

1.   Introduction

Solving hyperbolic partial differential equations, like the time-dependent Euler equations for compressible flow, demands numerical schemes that can precisely capture shock wave discontinuities and effectively resolve small-scale flow features^[1,2]. These schemes have two seemingly contradictory requirements. First, they must provide sufficient numerical dissipation around the shock waves to avoid spurious oscillations. Second, they need to minimize numerical dissipation in smooth regions to preserve flow field integrity. Reconciling these competing demands poses a significant ongoing challenge in crafting numerical schemes for computational fluid dynamics.

The key aim of shock-capturing techniques is to swiftly resolve shock waves while preventing unphysical oscillations and preserving high accuracy in smooth flow areas^[3]. A major breakthrough in this domain was Harten's ^[4] development of high-resolution methods that attain second-order accuracy near shockwaves without causing spurious oscillations. Following this, in 1997, Harten et al. ^[5] introduced essentially non-oscillatory (ENO) schemes, a type of high-resolution method. These schemes dodge interpolation at discontinuities by assessing solution smoothness across multiple stencils and computing the flux using the smoothest one. These schemes exhibit nonlinear characteristics (even for linear partial differential equations) because the interpolation coefficients depend on the solution itself. Later, in 1996, Jiang and Shu^[6] improved these ideas to the WENO-JS method, which re-evaluated the smoothness of multiple stencils. Many studies have made progress based on the original WENO-JS scheme by adjusting the smoothness indicators^[7,8,9], modifying the nonlinear weights^[10,11,12], and using WENO-JS as part of a hybrid scheme^[13,14].

Since the initial ENO scheme was introduced, a common argument is that designing shock-capturing methods depends on human intuition. This is especially true for the nonlinear parts of the scheme, like smoothness indicators and weighting functions. Even though these methods have been widely studied, there is no proof that they are optimal. Researchers have tried to create the best spatial discretization methods by reducing wave propagation errors ^[15,16,17] and errors in certain frequency ranges ^[18,19]. Some of these methods have been combined with shockwave capture schemes ^[20,21]. Thus, the design optimization problem still needs to rely on human intuition to balance competing goals rather than impartially learning the best scheme through data-driven methods.

In recent years, machine learning has become pervasive in data analysis^[22,23] and is being increasingly utilized to enhance (or redesign) Numer. Methods Partial Differ. Equations^[24,25,26]. Several studies have concentrated on boosting the WENO method's performance via neural networks. Most existing investigations optimize the nonlinear weight settings of the WENO method using neural networks to improve its numerical performance and stability. For example, Bezgin et al.^[27] (2022) proposed the use of deep learning to perturb the smoothness indicator of the WENO-JS scheme, thereby reducing numerical diffusion and shock overshoot. Liu ^[28] (2020) and Nogueira et al.^[29] (2024) determined nonlinear weights in the WENO scheme by constructing artificial neural networks, ensuring high-order convergence and non-oscillatory characteristics.

Moreover, some studies have focused on using neural networks to improve the shock-capturing performance of the WENO method as a whole in complex flow scenarios. For example, Stevens and Colonius^[30] (2020) further enhanced the generalization ability and stability of the WENO method under different conditions by directly fitting or combining prior knowledge. Takagi et al.^[31] (2022) attempted to minimize the residual of the solution using neural networks to obtain a nonlinear finite volume coefficient solution scheme that was closer to the optimal one. This method not only improves the accuracy and stability of the WENO scheme but also expands its applicability in practical engineering applications.

This study aimed to approximate the WENO-JS reconstruction technique using machine learning methods. Using high-quality data generated by the WENO-JS method, we trained a neural network model to learn nonlinear mapping relationships during the reconstruction process. This approach avoids perturbing the smoothness indicator or weights, thereby ensuring the original high-order accuracy and is especially able to maintain a high accuracy similar to that of the classic WENO method in smooth regions. Our method exhibits significant advantages in adapting to different reconstruction formats while maintaining a high degree of consistency in time efficiency. Specifically, by training a neural network to learn the reconstruction process of reconstruction formats, our method can seamlessly adapt to various high-order reconstruction formats, such as WENO-Z and WENO-M, without the need to design a specific network structure or adjust the calculation process for each format. This versatility not only simplifies the implementation process but also enhances the flexibility and scalability of the algorithm in practical applications.

The remainder of this paper is organized as follows. In Section 2, we review the classic WENO-JS format. Further, we introduce the WENO-NN method, describe the training process, and discuss some performance improvement methods and research findings of the WENO-NN format in detail. In Section 3, we introduce the application of several one-dimensional, two-dimensional, and three-dimensional model problems, including Euler equations, two-dimensional Riemann problems, and three-dimensional Riemann problems. Finally, we provide a summary and future outlook.

2.   Materials and methods

2.1.   WENO5-JS reconstruction under finite volume

In this subsection, we provide a concise review of the classical fifth-order weighted essentially non-oscillatory scheme (WENO5-JS)^[6] used for hyperbolic conservation laws in a finite-volume framework. We consider the one-dimensional scalar hyperbolic conservation laws given in Eq (2.1), without losing the essence of the general case.

We divide the spatial domain into finite-volume cells of uniform size. Let ${x_i}$ represent the central position of the $i$-th cell and let ${x_{i + 1/2}}$ and ${x_{i - 1/2}}$ represent the left and right boundary surfaces of this cell, respectively. Based on this division, the semi-discrete finite volume form of the equation can be expressed as Eq (2.2).

where we assume that the computational grid is evenly spaced and is denoted by $\Delta x = {x_{i + 1/2}} - {x_{i - 1/2}}$. The cell average value of the piecewise smooth function $u(x, t)$ on the grid ${I_i} = \left[ {{x_{i - {1/2}}}, {x_{i + {1/2}}}} \right]$ is

Integrating Eq (2.1) over ${I_i}$ yields

and the flux $f\left({u\left({{x_{i + {1/2}}}, t} \right)} \right)$ in Eq (2.4) can be approximated by the numerical flux ${\hat f_{i + 1/2}}$. We obtain the following conservative semi-discrete format:

where ${\hat f_{i + 1/2}}$ can be represented by any monotone numerical flux, such as the Lax-Friedrichs flux as follows:

where $\lambda = \mathop {\max }\limits_u \left| {f'(u)} \right|$. The numerical flux ${\hat f_{i + 1/2}} = \hat f\left({{u_{i - {1/2}}}, {u_{i + {1/2}}}} \right)$, where $u_{i + {1/2}}^ \pm$ can be obtained by WENO reconstruction. The specific implementation process is as follows:

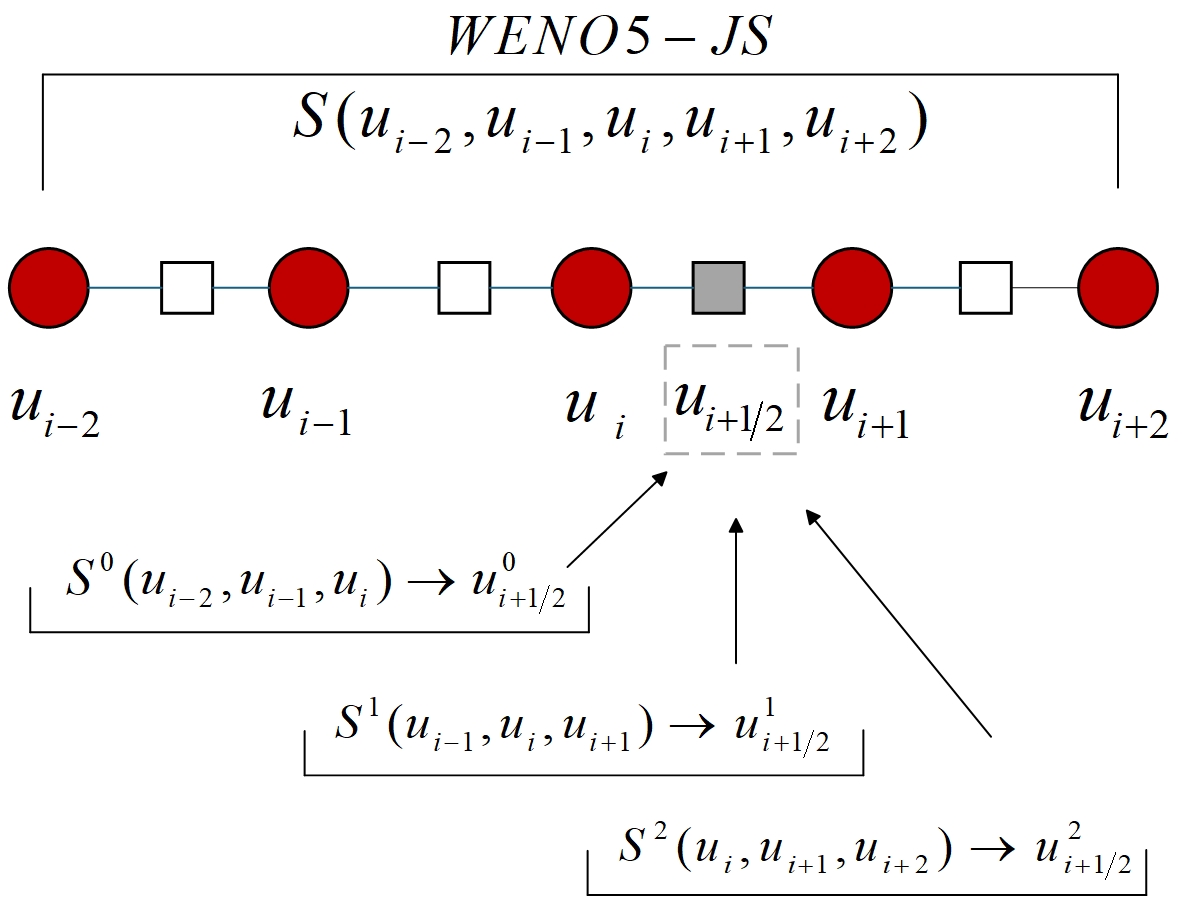
In this section, taking the fifth-order finite-volume WENO5-JS scheme^[6] as an example, we elaborate on the high-precision spatial discretization process. The unknown cell surface value ${u_{i \pm 1/2}}$ must be reconstructed from the known cell average value ${u_i}$. Hereinafter, for convenience, we introduce only the calculation of ${u_{i \pm 1/2}}$. As shown in Figure 1, to reconstruct the polynomial, we choose the following three small stencils in Eq (2.7).

The average cell value of ${I_i}$ is briefly recorded as ${\bar u_j} = u\left({{x_j}, t} \right).$ Let ${p_1}(x), {p_2}(x)$, and ${p_3}(x)$ be the reconstructed quadratic polynomials on the three stencils, which must satisfy the following conditions:

where these candidate templates, the polynomials of any convex combination, theoretically have only third-order accuracy. To achieve higher numerical accuracy in the smooth region of the solution, we choose a large template $S = \left\{ {{I_{i - 2}}, {I_{i - 1}}, {I_i}, {I_{i + 1}}, {I_{i + 2}}} \right\}$ that contains all the candidate template meshes. When constructing a fourth-order polynomial reconstruction on a large template, the following specific conditions must be satisfied:

This polynomial Eq (2.8) must satisfy certain conditions at the boundary of ${I_i}$ as follows:

where ${\gamma _k}$ denotes a linear weight. As the linear weight must satisfy the relationship in Eq (2.9), the linear weight is related to the topological structure of the computational grid and cannot assume an arbitrary value. Through calculations, a set of linear weights for these polynomials at ${I_i}$ can be obtained as:

Jiang and Shu^[6] used the following smoothness indicator to represent the degree of smoothness of the reconstruction polynomial in the target cell ${I_i}$:

For a uniform grid, the calculation results for the three smoothness indicators are as follows.

In Harten's method^[4], the authors finally select the template with the smallest overall change and the smoothest one under the norm by recursively evaluating the overall change in the candidate templates under the norm. Shu and Osher^[32] pre-computed the measurement coefficients by measuring the total variation of the norm; therefore, a recursive template search process is eliminated. Liu et al.^[33] first proposed the WENO scheme in the related literature. This scheme uses nonlinear weights to combine multiple candidate templates linearly. In other words, WENO approximates the flux at the cell boundary using a weighted summation of the candidate extensions ($r = 3$).

where $\varepsilon$ is an extremely small positive number, and we usually take ${10^{ - 6}}$ to avoid a situation where the denominator is zero. The convex combination of the reconstruction polynomials formed by nonlinear weights constructed using this method can achieve fifth-order numerical accuracy in a smooth region of the solution.

2.2.   WENO-NN reconstruction process based on neural networks

2.2.1.   Basics of neural networks

Neural networks are a category of parameterizable nonlinear composite functions capable of mapping any input $x$ to an output $y = f(x, \theta)$, with $\theta$ representing free and trainable parameters. Deep neural networks (DNNs) are composed of numerous hidden layers of units (or neurons) sandwiched between the input and output layers. To map $x$ to $y$, successive elementary nonlinear transformations are executed. The numerical values present in each layer are referred to as hidden-state activations. In a multilayer perceptron (MLP), neurons in neighboring layers exhibit dense connections. The activation vector ${a^l}$ in layer $l$ is derived from the activations of the preceding layer ${a^{l - 1}}$ through the application of an affine linear transformation first, succeeded by an element-wise nonlinearity $\sigma \left(\cdot \right)$. Similar to ${a^{l - 1}}$, the activation of the $i$-th neuron is computed as

where $W_{i, j}^{l - 1}$ denotes the weight matrices of layer $(l - 1)$, $b_i^{l - 1}$ stands for the bias vector, and ${N^{l - 1}}$ indicates the neuron count in layer $(l - 1)$. The discrepancy between the network's predicted output $y$ and the actual target $\hat y$ is assessed via a suitable loss function $L(y, \hat y)$. The process of neural network training entails finding a set of parameters $\theta$ that can approximately reduce the chosen loss function to a minimum. Typically, this minimization of the loss function is achieved through minibatch gradient descent or the widely used Adam optimization algorithm.

2.2.2.   WENO-NN

The traditional WENO reconstruction method calculates the reconstructed values of the left and right interfaces using five adjacent grid points combined with nonlinear weights. Their specific forms are expressed as follows:

${\omega _1}, {\omega _2}, {\omega _3}, {\omega _4}, {\omega _5}$ and $\omega _1^ *, \omega _2^ *, \omega _3^ *, \omega _4^ *, \omega _5^ *$ are nonlinear weights based on the smoothness of the local solution. ${u_1}, {u_2}, {u_3}, {u_4}, {u_5}$ and $u_1^ *, u_2^ *, u_3^ *, u_4^ *, u_5^ *$ are the function values on the left and right sides of the reconstruction point, respectively. The WENO method ensures high-order accuracy in smooth regions through the adaptive adjustment of these weights, and effectively suppresses numerical oscillations when discontinuities exist.

Similarly, the WENO reconstruction can be summarized as

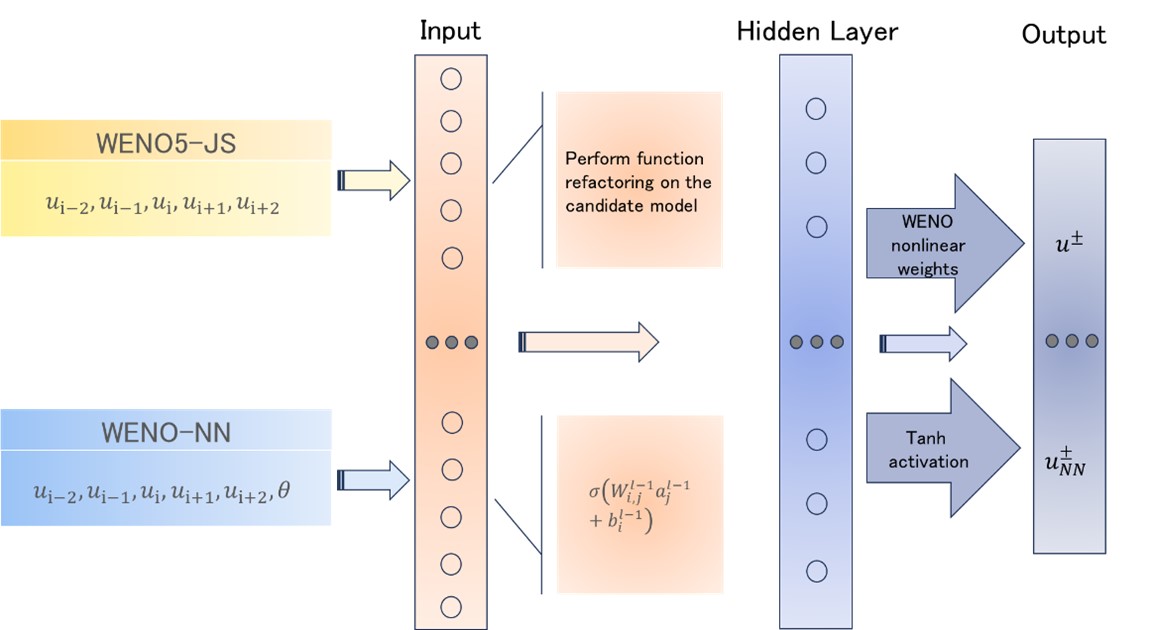
where for any $k$, ${\omega _k} = 1$, $0 \le {\omega _k} \le 1$. Therefore, any function $f:{R^5} \to R$ subject to the aforementioned restrictions can be regarded as a fifth-order WENO-type weighting function. Based on this, any artificial neural network with appropriate input and output spaces can be used for parameterized WENO weighted functions. Figure 2 shows the new WENO-NN format constructed by us referring to the traditional WENO format. The specific form is as follows:

In order to explore more comprehensively the learning ability of the neural network model regarding the reconstruction capability of the WENO scheme, we propose two neural network frameworks in this paper for further illustration. The first one is based on a purely data-driven neural network framework. Specifically, we used the WENO5-JS scheme to compute the left and right fluxes ${u^ \pm }$ based on the function values at five neighboring grid points, which were used as the dataset for neural network training. In this process, the inputs of the neural network are set to the function values at the five neighboring grid points, and the outputs of the neural network are the left and right flux values $u_{NN}^ \pm$ predicted by the neural network. Accordingly, the loss function $L_d$ used in this part is shown below:

The second approach is a neural network framework based on physical information. In this architecture, we introduced the WENO5-JS reconstruction process into the neural network and optimized it with relevant physical information. Specifically, we improved the loss function so that it not only contained the loss with respect to the true reconstructed value, but also incorporated physical information, thus enhancing the physical consistency of the model. Its loss function is:

where $\beta_P$ represents the physical reconstruction weight, and $\beta_W$ represents the regularization weight. The total $Loss$ consists of three separate components: the cell-face reconstruction loss ${L_d}$, the physical reconstruction loss ${L_P}$, and the regularization loss ${L_2}$ applied to the neural network weights $W$. ${u_1}, {u_2} \ldots {u_5}$ and ${v_1}, {v_2} \ldots {v_5}$ are the values of the five adjacency functions of the candidate templates for the left and right interface cells of the desired reconstruction value.

In the subsequent sections of this paper, we focused on purely data-driven neural network architectures. Although architectures that incorporated physical information had shown certain advantages, the framework of a purely data-driven architecture provided more possibilities for further optimization of the model. At the same time, this architecture could be integrated into other data formats more smoothly. This had expanded a broader application prospect and development space for research and practice in related fields.

To gain a more comprehensive understanding of the performance of the traditional WENO5-JS scheme and the neural-network-based WENO-NN method in practical applications, we conducted a detailed comparative analysis across multiple dimensions. Table 1 presents the comparison of these two methods on several key performance indicators, including accuracy, computational efficiency, adaptability, and resource consumption. These comparisons provide a clearer evaluation of the advantages and disadvantages of each method and their applicability in different scenarios.

2.3.   Construction of the training set and differences in different scales

2.3.1.   Training dataset

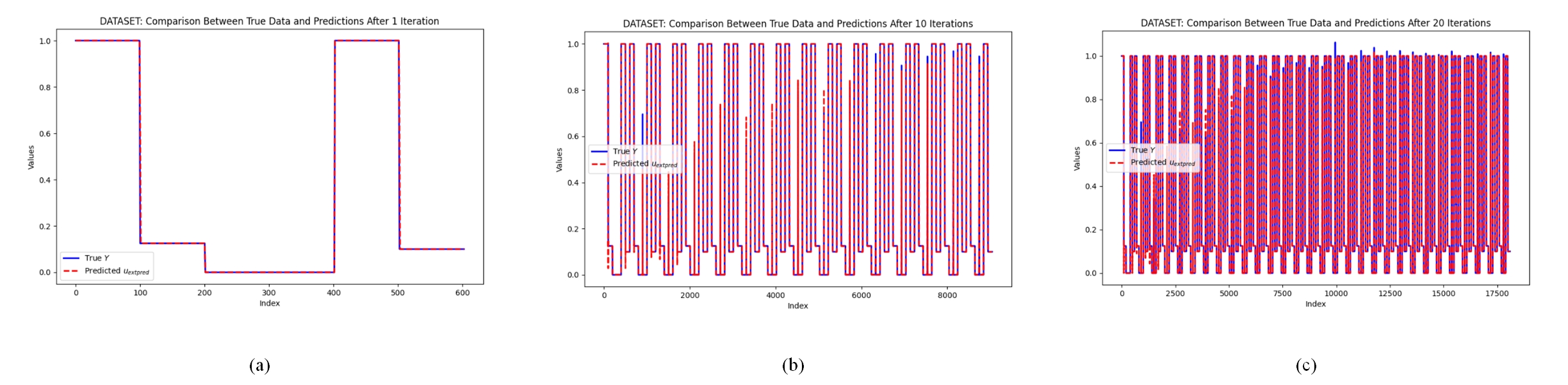
The training dataset is obtained by collecting the dynamically evolving reconstructed values of one-dimensional surge tubes in the WENO5-JS scheme. The time discretization is performed using the third-order Ronger-Kuta method combined with an adaptive time-step strategy with a CFL of 0.5 for iterative training, with a total number of 211 iteration steps. As shown in the figure, we intercept the data at the time points of 1, 10, and 20 iterations, as shown in Figure 3 corresponding to 600, 9000, and 18,000 data points, which account for 1%, 5%, and 10% of the total sampled data, respectively. The purpose of this paper is to investigate whether a very small amount of data, and what critical data volume threshold can be reached, can allow the model to have some WENO5-JS reconstruction capability.

From the Figure 3, it can be seen that the neural network prediction value has a certain fit to the target data as a whole, but there are deviations in some areas because the network structure is relatively simple, making it difficult to fully capture the complex local features and details in the data. Meanwhile, it is precisely this concise network structure that reduces the overlearning of the training data in the presence of noise. As seen from Table 2, with the gradual increase of the collected data volume, the error value decreases gradually from 1.70E-2 to 3.94E-3, which indicates that with the increase of the data volume, the neural network has richer samples for learning the features and laws, the fitting accuracy of the true solution improves continuously, and the error decreases continuously.

To compare the accuracy of our model and traditional methods, we introduced ${L_2}$ and ${L_\infty }$ as the measurement indicators. ${L_2}$ was used to measure the overall deviation between the predicted and true values and is defined as the square root of the sum of the squares of the prediction errors. This error measure reflected the mean-square error of the model for the entire dataset. A smaller ${L_2}$ indicates higher overall prediction accuracy of the model. The mathematical formula is as follows:

where ${y_i}$ represents the true value, ${\hat y_i}$ is the predicted value of the model, and $N$ is the total number of data points.

${L_\infty }$ (also known as the maximum error) was used to measure the most extreme error values in the model prediction process. It reflects the maximum deviation between the predicted and true values and can effectively evaluate the performance of the model in the worst case. A smaller ${L_\infty }$ indicates better robustness of the model in extreme cases. The mathematical formula is as follows:

2.3.2.   Differences in the scales of different training sets

Next, by using a one-dimensional shock tube (Sod) example, we evaluated the performance differences across datasets of different scales, focusing on the neural network's ability to capture shock wave characteristics and the corresponding ${L_2}$ error. Our goal was to optimize the training of the WENO-NN model (as shown in Table 3) by analyzing the performance of different datasets to achieve higher accuracy and improved generalization performance.

It can be clearly observed from Figures 4 and 5 that the fitting effect of the WENO-NN (small) model is poor. This is because the amount of data is insufficient for the neural network to fully learn the nonlinear weight assignment process. The WENO-NN (medium) and WENO-NN (large) models have shown significant improvements in prediction performance. They can not only accurately reconstruct the interface values, but also effectively capture the shock wave features, and exhibit a high degree of compatibility with the WENO5-JS format under different mesh conditions. From the scaling diagrams, it can be seen that although WENO-NN has some oscillations at the discontinuities, its ability to fit the discontinuities in some local regions is better than that of WENO5-JS. This is because the physical quantities at the discontinuities of the flow field change drastically. This situation poses a challenge to the extrapolation and generalization ability of the model. To address this phenomenon, the oscillation problem can be mitigated by supplementing high-quality local data samples to strengthen the model's learning.

This study further analyzes four reconstruction methods: On the one hand, it evaluates the model's learning effect on the flow field characteristics of the WENO5-JS scheme by comparing the result errors of these four numerical schemes with those of the WENO5-JS scheme. On the other hand, it verifies the model's approximation to the true solution by comparing the errors of each format with the true solution.

From the data in Tables 4 and 5, it can be seen that with the encryption of the number of grids, the errors of all the formats are gradually reduced, and gradually approach the true solution; meanwhile, the increase of the amount of training data also further strengthens the fitting ability of the model. This fully indicates that both encrypting the number of grids and expanding the size of the training set can provide strong support for improving the model fitting effect. Importantly, we can see that both WENO (medium) and WENO (large) are very close to the WENO5-JS format under different grid conditions, and the error is always kept at a very small level. This remarkable result shows that the WENO-NN model is able to learn the WENO5-JS format even with a small amount of data.

2.4.   Exploration of out-of-distribution generalization ability and long-term stability

In this context, this section focuses on the out-of-distribution generalization ability of the constructed models. Specifically, we comprehensively and systematically evaluated the model's performance on data outside the predicted dataset. Our aim was to precisely define the boundaries and potential of its generalization ability.

At the same time, model stability is crucial for assessing generalization ability. It is one of the most important indicators of a model's strength. Especially in long-term prediction tasks or complex dynamic system simulations, a model's long-term stable running ability is particularly critical.

2.4.1.   Generalization test and inspection of fitting ability effect

In this paper, we configured data-driven models with different scales of reconstructed values, namely the Model-S model and Model-L model. The following are the Riemann initial conditions required to generate the training set:

Initial conditions for the Model-S model:

Initial conditions for the Model-L model:

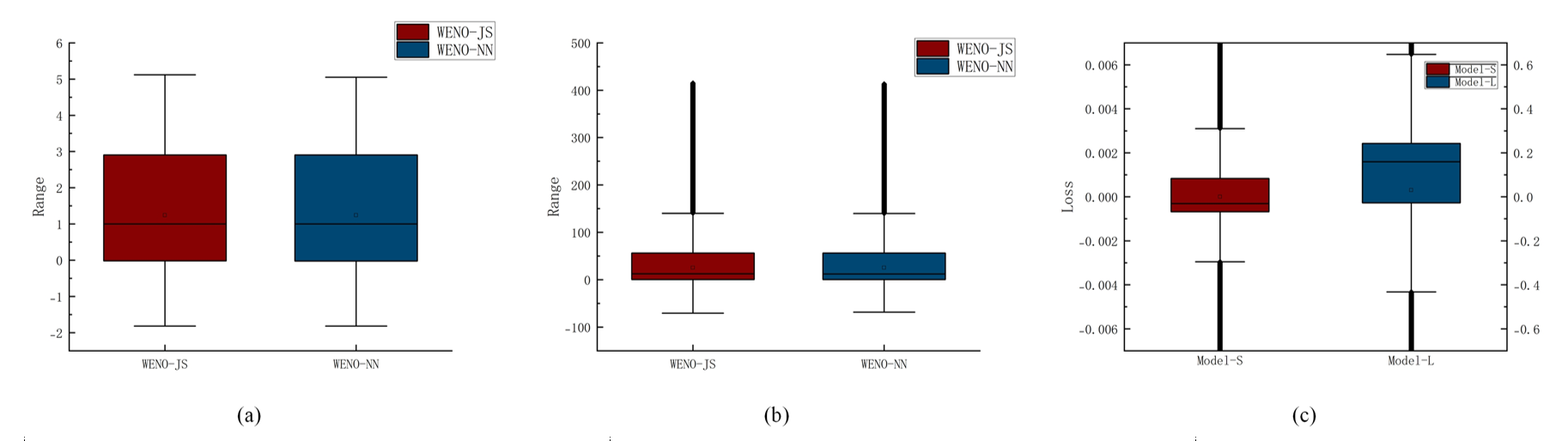
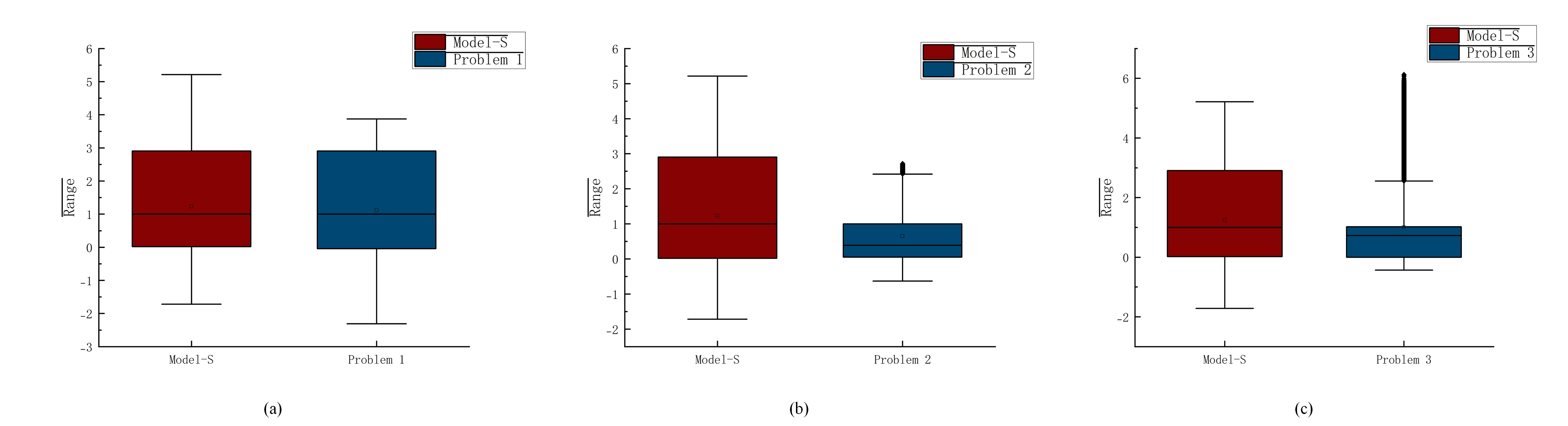
In this study, we constructed two training sets with different data ranges. These training sets were generated by simulating the WENO5-JS scheme under two different initial conditions, respectively. We set the simulation parameters as follows: The end time is $0.25\;$s, the CFL is 0.75, and the grid size is $200\times200$. The whole numerical simulation process contained 163 time steps, and we selected the data corresponding to the first 25 time steps as the training set for this study, which accounted for about 10% of the total data volume. As was seen in Figure 6(a), (b), the data range for the Model-S model training set was $[-1.83, 5.12]$. In contrast, the data range for the Model-L model training set was $[-70.35,417.64]$, which was approximately a hundred times that of the Model-S training set.

By fitting the reconstructed values through a neural network, we obtained the fitting loss errors for both models. The distribution of the loss errors is shown in Figure 6(c), with a fitting loss error of 2.74E-3 for the Model-S model and 4.39E-3 for the Model-L model. In addition, the data generation time and model training time are detailed in Table 6.

In the subsequent part of this study, we applied the two constructed models to experimentally simulate test sets of different sizes in order to comprehensively evaluate the fitting ability of the neural network. Specifically, the test sets Eval Set A, Eval Set B, and Eval Set C were constructed based on the WENO5-JS scheme, and were numerically simulated using the initial conditions of the Model-S model, the initial conditions of the 1.5-fold Model-S model, and the initial conditions of the 2-fold Model-S model, respectively. In all simulation experiments, the CFL was fixed at 0.75 and the grid step size was set to $200\times200$.

By analyzing the performance of these two models on different test sets, this study aims to examine two key capabilities of WENO-NN: first, to assess the Model-S model's ability to deal with out-of-distribution generalization beyond the range of its training data distribution; and second, to examine the Model-L model's adaptability in simulating data much smaller than its training scale. Through these experiments, we expect to validate the effectiveness and robustness of WENO-NN in coping with prediction tasks of different scales and complexity.

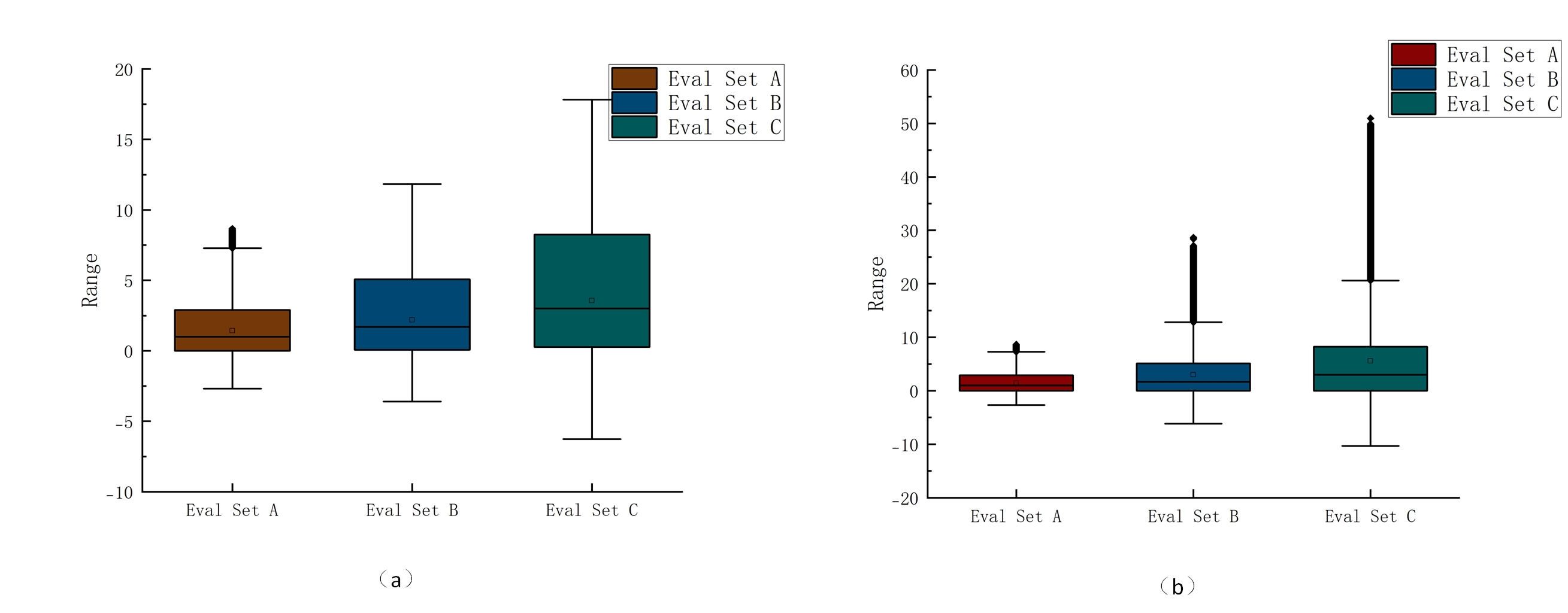
To start with, we explored the out-of-distribution generalization ability of the Model-S model. We conducted numerical simulations based on the WENO5-JS scheme under specific initial conditions, with simulation parameters set to as-of times of $1\;$s, $0.05\;$s, and $0.025\;$s, with a CFL of 0.75, and generated the corresponding test sets using an adaptive time step. The Model-S model was trained on a training set with a data range of $[-1.83, 5.12]$. In contrast, the ranges of the test sets Eval Set A, Eval Set B, and Eval Set C extend to $[-2.81, 10.67]$, $[-4.25, 12.62]$, and $[-7.04, 23.97]$, respectively, as shown in Figure 7(a), and thus the Model-S model faces the problem of out-of-distribution generalization when predicting on these test sets.

As can be seen from Table 7, the Model-S model does not show divergence when predicting the Eval Set A test set, indicating that the model has a certain degree of out-of-distribution generalization ability. However, in the neural network simulations for the Eval Set B and Eval Set C test sets, divergence occurs at $0.05\;$s and $0.025\;$s, respectively, revealing that the model still faces some challenges in fitting data far beyond the range of the training set. Nonetheless, it is clear from the data information presented in Table 7 that the model constructed based on a purely data-driven approach still shows some fitting potential and capability when dealing with data outside the training set.

Next, we aim to explore the model's fitting ability when simulating data of a scale smaller than its own. We also performed numerical simulations based on the WENO5-JS scheme under specific initial conditions, with the simulation parameters set to an as-of-time of $1\;$s, a CFL of 0.75, and an adaptive time-step to generate the corresponding test sets. The Model-S model was trained on a training set with a data range of $[-70.35,417.64]$, as shown in Figure 7(b), the ranges of the test sets Eval Set A, Eval Set B, and Eval Set C are $[-2.81, 10.67]$, $[-6.39, 33.41]$, and $[-17.49, 72.59]$, respectively, and the ranges of the test sets are significantly reduced in comparison with the ranges of the training sets, which are about one order of magnitude of the ranges of the training sets.

As can be seen from Table 7, the Model-L model reaches a state of convergence during the simulation of all three test sets, and its fitting accuracy exhibits a similar level as that of the Model-S model. This phenomenon strongly confirms that the Model-L model still has an effective fitting capability when dealing with data much smaller than its own size, providing solid supporting evidence for the application of the model in diverse data scenarios.

2.4.2.   Long-term simulation and stability analysis

To comprehensively evaluate the performance of our model, this study designed and carried out a long-term scale simulation experiment process. Stability is a core metric in pure data-driven neural networks, especially crucial when dealing with large-scale data. During long-term simulations, ensuring that the model does not suffer from problems such as data drift and overfitting is a prerequisite for achieving reliable predictions. The dimensional Riemann problem is essentially a difficult problem involving complex physical processes that require long-term evolution. Therefore, the stability performance of the model on a long-term scale has become an important criterion for evaluating its effectiveness and applicability.

The simulation initial conditions are set as:

The long-time simulations were carried out on a $200\times200$ grid with the CFL set to 0.75 and simulation durations of $1\;$s, $3\;$s, $5\;$s, and $10\;$s. By numerically simulating the Riemann problem under these initial conditions, we aimed to systematically explore the strengths and limitations of the models. To this end, we used three different models to simulate and comparatively analyze the Riemann problem under the same initial conditions in order to assess the performance and applicability of each model in long-time scales.

Here, we introduced a physics-informed neural network architecture, the Model-PINN model. It employed a specific $(5, 3, 1)$ neural network layer structure and applied Tanh as the activation function. Its training process was based on the Model-S model training set. The aim is to deeply investigate the difference in accuracy performance between physics-informed neural networks and traditional pure data-driven approaches.

According to Table 8, although the training set of the Model-L model has expanded significantly compared to that of the Model-S model, the Model-L model still shows good adaptability and simulation ability when simulating a small test set. Its simulation error values are in a similar range to those of the Model-S model. The Model-PINN model shows relatively excellent prediction ability at any set cutoff time. Meanwhile, it is worth noting that with the increase of time, the $L_\infty$ error hardly changes. The maximum degree to which the model's prediction deviates from the true value remains stable to a certain extent. This indicates that the errors caused by shock waves and strong discontinuities remain stable during the time evolution, and the maximum deviation does not deteriorate due to the strong discontinuity in the critical region. However, the $L_2$ error increases to a certain extent, which means that the overall error accumulates over time. This may be due to the gradual superposition of small error sources or insufficient capture of the overall behavior of the dynamic system.

As seen from Figure 8, the WENO-NN model is stable during long-time evolution. It can maintain its performance across different time scales. This strongly supports its application in solving complex two-dimensional Riemannian problems and other related fields.

2.5.   Algorithm optimization of WENO-NN

In this study, using a two-dimensional shock tube (2D Sod) example, we first compared the reconstruction times of two acceleration methods and analyzed the advantages of the WENO-NN method in terms of computational efficiency compared to the WENO5-JS method from the perspective of time complexity. Moreover, we systematically evaluated the impacts of different methods for constructing training sets and model architectures on the ability of the neural network to simulate WENO reconstruction. The experimental results showed that the WENO-NN method performs better than the WENO5-JS method in terms of both reconstruction time and computational complexity.

2.5.1.   Analysis of time complexity

To verify the computational efficiency advantages of WENO-NN over the traditional WENO scheme, we conducted evaluations through the following experiments, accompanied by a theoretical analysis of time complexity:

We conducted a simulation test on the specific running speeds of the two methods by using a two-dimensional shock tube example. The test conditions were as follows: the CFL was set to 0.6, the time step was fixed at $0.001\;$s, 100,200, and 1000 steps were performed, and the number of meshes was $200\; \times\; 200$. During the test, all models were run in the same hardware environment, i.e., a system equipped with an Intel(R) Core(TM) i7-14650HX 2.20 GHz processor and 32.0 GB of memory, with CPU acceleration provided in the PyCharm development environment. Note that, aside from the differences in the reconstruction process, all other components of the two algorithms were completely identical, ensuring the comparability and fairness of the comparison in terms of computational speeds. Here, we calculated the total time that only included the reconstruction process of the methods.

The experimental results are presented in Table 9, which compares the reconstruction times of the two methods. In preliminary tests using the NumPy acceleration library, we found that the running times of the two schemes were comparable. To eliminate potential acceleration bias caused by third-party numerical libraries, we replaced NumPy arrays with Python lists for the input data structure and performed the following experimental procedures.

This can be observed from the data comparison shown in Table 9 that WENO-NN exhibits a significant acceleration advantage over WENO5-JS. Specifically, in the computing scenarios of 100,200, and 1000 steps, the reconstruction time of the WENO-NN method was shortened by approximately three to four times compared to that of the WENO5-JS method. Next, we conducted a theoretical analysis of the two methods from the perspective of time complexity to further validate the acceleration effect of the WENO-NN method and its advantages in numerical computation.

To further verify the validity of our algorithm's acceleration at the theoretical level, we conducted a detailed theoretical analysis of its time complexity. Specifically, the time complexity is $O\left(N \right)^2$, where $N^2$ is equivalent to $nx \times ny$, and $nx$ and $ny$ represent the number of subdivision points in the $x$- and $y$-directions, respectively.

This study evaluates algorithmic performance by quantifying the complexity of basic arithmetic operations. Using standardized computations with a fixed time step $\Delta t$, we compare the WENO5-JS and WENO-NN methods through single-step operation counting. The WENO5-JS method quantifies arithmetic operations in traditional approaches, while the WENO-NN method quantifies matrix operations during network forward propagation.

Here, we use the Four-Model architecture as an example for detailed analysis. The WENO5-JS model calculates values based on established formulas. The calculation process involves reconstruction in the $x$- and $y$-directions, as well as the left and right interface units. Since the calculation principle is straightforward, we only need to compute the reconstruction time for one interface unit and multiply it by four to obtain the result; thus, we will not elaborate further here.

Regarding the Four-Model WENO-NN, it consists of four structurally identical models, each reconstructing the left and right interface units in the $x$- and $y$-directions. The number of operations for the specific algorithm can be precisely calculated based on the network structure $(5, 3, 1)$ that we adopt. For example, the total number of addition operations is $(5\times3 + 3)\times4$. Here, $5\times3$ represents the addition operations from the input layer to the hidden layer of a single model, while 3 represents the addition operations from the hidden layer to the output layer. For multiplication operations, the total number is $(6\times3 + 3)\times4$. Here, $6\times3$ represents the multiplication operations from the input layer to the hidden layer of a single model, including the multiplication of weights and input values, as well as the activation function and output values.

Similarly, for other similar models, since the total data volume remains constant, the number of operations during the forward-propagation process is also fixed. Thus, the final total number of operations is the same.

As shown in Table 10, the specific steps of the WENO5-JS algorithm involve a large number of addition, multiplication, and division operations in each iteration. Notably, the addition and division operations account for a relatively larger number of computational steps, indicating that their computational complexity is high and there are more constant factors. By contrast, through the structural optimization of the neural network, the WENO-NN method significantly reduced the number of addition operations to just 72 steps each, while also eliminating the division operation. This improvement significantly reduces the constant factors in the calculations, making the algorithm more efficient in practical operations.

2.5.2.   Discussion on the differences in the number and structure of the models

In the task of two-dimensional flow field reconstruction, this study discusses three different neural network model architectures: the Two-Model architecture, Four-Model architecture, and Sixteen-Model architecture. Each architecture has its own design characteristics with different advantages and limitations, and is suitable for different application scenarios and task complexities.

Two-Model architecture: This architecture contains two independent neural network models, as shown in Figure 9(a), which are used to predict the left and right interface characteristics in the $x$- and $y$-directions. The advantage of this architecture is that the number of models is small, which results in faster training and inference speeds, making it particularly suitable for simple two-dimensional flow field reconstruction tasks. Nevertheless, because each model focuses only on a single direction and lacks the ability to integrate cross-directional features, it may not fully capture the complex characteristics of the flow-field, thereby limiting the reconstruction accuracy.

Four-Model architecture: This architecture is further refined in each direction, and four independent neural network models are constructed, as shown in Figure 9(b), which are respectively responsible for the feature reconstruction of the left interface in the $x$-direction, right interface in the $x$-direction, left interface in the $y$-direction, and right interface in the $y$-direction. Compared with the Two-Model architecture, the Four-Model architecture can capture the flow characteristics in different directions more finely by dividing specific directions and interfaces, thereby improving the reconstruction accuracy. The Four-Model architecture can customize the model structure according to specific problem scenarios and fuse specific information in the $x$- and $y$-directions, thereby enhancing the learning ability of the model for features in different directions. An increase in the number of models also results in a corresponding increase in training costs, which may become a limiting factor when computing resources are limited.

Sixteen-Model Architecture: As shown in Figure 10, this architecture makes a more detailed division in terms of direction and characteristic quantities. Sixteen independent neural network models are constructed to predict multiple characteristic quantities such as the density and velocity of the left and right interfaces in the $x$- and $y$-directions, respectively. The advantage of this architecture is that each model focuses on a specific direction and feature quantity, allowing it to capture complex features in the flow field to a greater extent, thereby significantly improving the reconstruction accuracy. This architecture can incorporate more specific information, such as feature quantities (e.g., density and velocity), which enhances its ability to capture detailed flow field characteristics. However, this comes with a certain increase in the number of models and training costs, resulting in a corresponding increase in computational resource requirements for the inference process. This may make the architecture less practical for resource-constrained systems.

In summary, the three architectures have unique applications. The Two-Model architecture is more suitable for simple tasks, whereas the Four- and Sixteen-Model architectures are gradually becoming more suitable for flow-field reconstruction scenarios with higher precision requirements and greater complexity. The choice of a specific architecture should comprehensively consider the complexity of the task, precision requirements, and available computing resources to achieve the best balance between performance and efficiency.

We conducted simulation tests on the specific running speeds of the three methods using a two-dimensional shock tube example. The configurations of the models used in the experiment were as follows: The Two-Model architecture used 10% of the vortex surface dataset for training. The Four-Model architecture used 10% of the rarefaction wave dataset in the $x$-direction and 10% of the vortex surface dataset in the $y$-direction for training. The Sixteen-Model-A architecture used 10% of the corresponding characteristic quantity datasets for different feature quantities during training. The Sixteen-Model-B architecture was trained with the dataset from the more complex two-dimensional Riemann problem. The results presented in Table 11 show that different combinations of models have varying impacts on the results. Among them, the Sixteen-Model-B architecture demonstrates superior prediction accuracy for the velocity characteristic quantity compared to the other models. This result indicates that, by optimizing the model training, the accuracy of predicting the reconstructed values can be effectively enhanced, leading to more precise reconstruction of various characteristic quantities.

To further explore the impact of different training sets on the training results, we analyzed the Sixteen-Model-A and Sixteen-Model-B models. As shown in the table, using a dataset of complex flow fields for training can improve the accuracy of the models more effectively. This further indicates that when training the corresponding models for complex problems, more abundant flow-field data can be incorporated. For specific characteristic quantities, we can incorporate the corresponding physical properties to build our models, making them more consistent with the real physical background.

The results presented in Table 11 show that with an increase in the number of models, the computing time does not change significantly. This indicates that increasing the complexity of the models does not significantly affect computing efficiency. This provides a valuable reference for the balance between model complexity and computing time in practical applications.

2.6.   Training details

In this study, the neural network architecture mainly consisted of an input layer, a hidden layer, and an output layer. The hidden layer contained three nodes and tanh was used as the activation function. The network structure used in all the experiments adopted the configuration listed in Table 12.

This network architecture has several significant advantages, and the network structure can effectively learn the process of WENO reconstruction. WENO reconstruction involves the nonlinear weighted addition of three reconstructed values and can effectively simulate this nonlinear process through an appropriate hierarchical structure and activation function. In addition, because the network structure is designed with a relatively shallow layer configuration, it has low computational complexity, reduces redundant calculations between neurons, and can achieve a certain degree of computational acceleration, thereby reducing the computational time and improving the work efficiency. The design of a shallow network structure also helps alleviate the common problems of vanishing or exploding gradients in deep networks. When the number of layers in a deep learning model increases, the gradient often disappears gradually, leading to difficulties in model training.

In this study, the $xavier\_init$ method was used for network initialization to create weights that follow a truncated normal distribution by setting the standard deviation to ensure the stability of the network's gradients. The specific formula is as follows:

This initialization method aims to keep the input variance of each layer relatively stable during forward propagation, thereby improving the convergence speed and training performance. The optimization uses the L-BFGS-B algorithm in the Scipy Optimizer Interface and sets multiple hyperparameters. These values are listed in Table 13 in detail.

The input data are normalized using $H = 2.0*{\left({X - lb} \right) /\left({ub - lb} \right) - 1.0}$ to the range of $[- 1, 1]$ to accelerate the network training process and reduce the training difficulties caused by differences in feature value ranges.

Unless otherwise specified, all the training processes were performed under the same settings. To enable a parallel comparison between WENO5-JS and WENO-NN, all settings remained the same except for the difference in the WENO reconstruction methods. This included the LF flux format and time-step advancement scheme, all of which were implemented using the same code. All experiments were conducted on a system with an Intel(R) Core(TM) i7-14650HX 2.20 GHz processor and 32.0 GB memory, within the PyCharm development environment and utilizing CPU acceleration. Notably, WENO-NN employed TensorFlow 1.1.5 for CPU acceleration.

To optimize the computational workflow and ensure reasoning efficiency, the trained weight parameters of the WENO-NN model have been persistently stored as independent files through TensorFlow's built-in serialization interface. During actual numerical simulations, the model directly loads pre-trained parameters for forward inference calculations, a process fully implemented using TensorFlow's native computational graph operators. It should be specifically noted that although TensorFlow's underlying computations have compatibility interfaces with NumPy, no explicit NumPy vectorization acceleration strategies were employed during model invocation. All operations were strictly executed through TensorFlow 1.1.5's static graph mechanism, ensuring backend consistency with WENO5-JS comparative experiments.

2.7.   Differences and connections with related WENO-NN works

In order to comprehensively demonstrate the advantages and limitations of the WENO-NN (Ours) model, this study selects a comparative benchmark. The comparative benchmark is the open-source model improved by Lin et al. based on the article by Stevens et al. ^[30]. The detailed implementation of this model can be viewed in the code repository at https://github.com/yungtlin/WENO-NN. Subsequently, we conduct a systematic comparative analysis from three key dimensions, which are accuracy, time complexity, and adaptability.

2.7.1.   Comparison of fitting accuracy

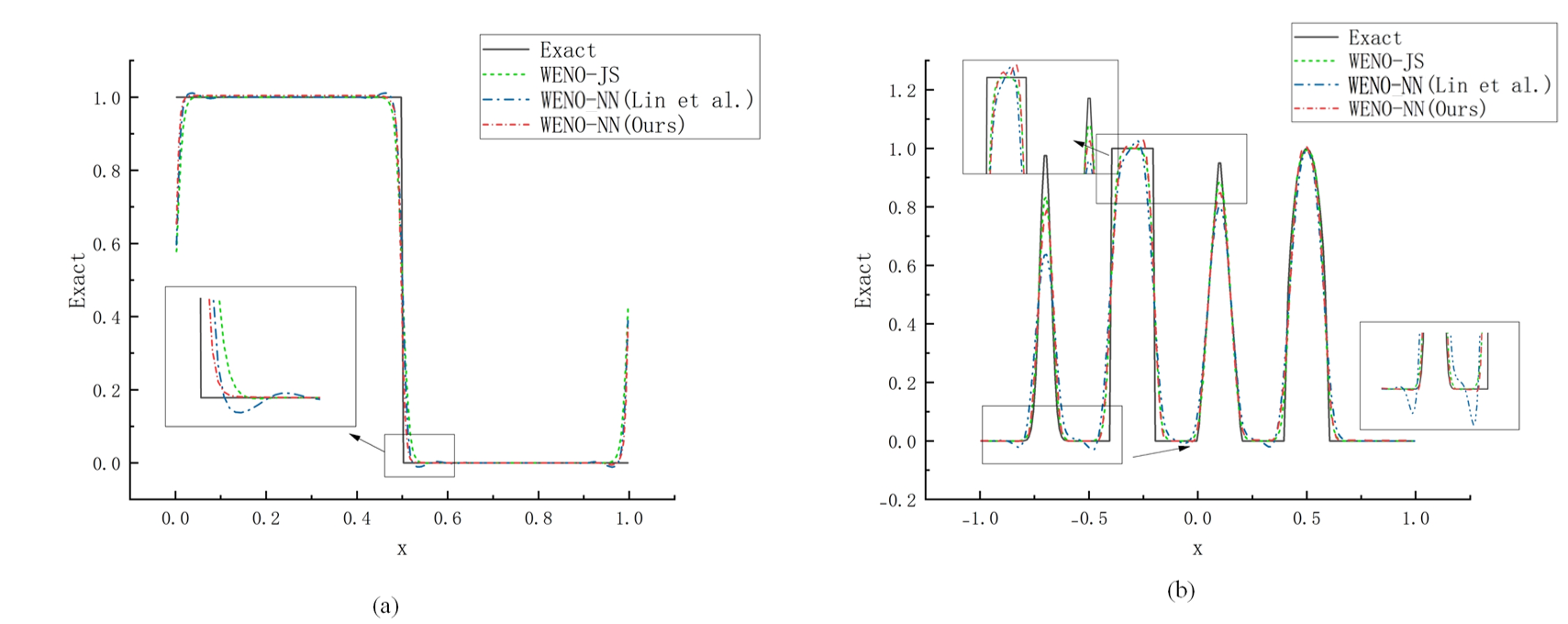
We tested the WENO-NN model on the linear advection equation. For this purpose, we considered two types of functions: a square-wave function and a piece-wise function composed of a Gaussian, a square, a triangle, and a semi-ellipse (GSTE). The computational domains were set as $[0, 1]$ and $[-1, 1]$, with periodic boundary conditions applied. The resolution was fixed at $N = 200$. Under these settings, the initial conditions were evolved up to $t = 10.0\;$s.

It can be seen from Figure 11 that the WENO-NN (Ours) model proposed in this paper is able to capture the excitation positions more accurately in the square wave test problem. In the GSTE solution test problem, the WENO-NN (Lin et al.) model shows a certain degree of oscillation during the fitting process and is significantly less effective than the WENO-NN (Ours) model proposed in this paper in multiple excitation wave locations. In addition, as can be seen from the results of Tables 14 and 15, our method is roughly the same as the WENO-NN (Lin et al.) model in terms of accuracy, and the overall effect is slightly better than the comparison method. The comprehensive experimental results show that the WENO-NN (Ours) model proposed in this paper demonstrates strong effectiveness and advantages in dealing with complex surge problems. Compared with the existing methods, our method not only has similar fitting ability, but also shows more excellent results in the treatment of excitations, demonstrating its stronger robustness.

In the experimental process, regarding the statistics of the specific time, due to the significant difference in the code structure used by both parties and the different depth frames invoked, it made it difficult for us to make a precise side-by-side comparison between the two in terms of the specific time. In view of this, we explored the issue from the perspective of time complexity, aiming to analyze the differences between our proposed method and the other one in terms of computational efficiency.

2.7.2.   Analysis of time complexity

The WENO-NN (Lin et al.) model simulates the numerical effects of the WENO5-JS scheme by training the coefficients in the WENO5-JS scheme. In contrast, the WENO-NN (Ours) model proposed in this paper is iteratively updated by directly predicting the left-right interface reconstruction values corresponding to the five points contained in each set of alternate templates, followed by flux reconstruction. Different from the way the WENO-NN (Lin et al.) model tries to improve the performance of the WENO5-JS scheme by optimizing the coefficients, the method in this paper simplifies the computational process and reduces the computational complexity. Next, we performed a time complexity analysis to further evaluate the computational efficiency of different models.

As seen from Table 16, the WENO-NN (Ours) model proposed in this paper has an obvious time-complexity advantage over the WENO-NN (Lin et al.) model, with significantly improved computational efficiency. Analyzing the algorithmic process of the WENO-NN (Lin et al.) model in detail (Table 17), its computational complexity has two parts. First, there is the complexity inherent in the WENO5-JS scheme itself. This is closely related to the WENO5-JS scheme's characteristics and computational process. Second, the introduction of the neural network for coefficient optimization adds complexity from the neural network's framework. Therefore, the comparison shows the WENO-NN outperforms the WENO-NN (Lin et al.) model in optimizing computational efficiency. It has lower complexity and a significant boost in computational efficiency.

Meanwhile, in terms of computational efficiency, this study focused on recent relevant work in related fields and selected some targeted research results. Guided by the idea of standardization, we standardized the respectively proposed WENO-NN models^[27,28]. Then we calculated their relevant time shares to highlight each model's advantages and limitations.

Table 18 shows that, within the scope of existing related research, the WENO-NN (Ours) model proposed in this paper has certain computational-efficiency advantages. Specifically, after accurate measurement and comparative analysis, its time-efficiency ratio is 1:0.3. This means that for the same amount of computational tasks, the WENO-NN (Ours) model takes less time than other similar methods. The WENO-NN (Ours) model improves efficiency without sacrificing computational accuracy, maintaining its fitting ability.

2.7.3.   Adaptability

To start the analysis from the training results' perspective, we found that the WENO-NN (Lin et al.) model had certain limitations. A large portion of the model's training results did not meet the desired performance criteria, and some were violently oscillating. Also, some models could not be applied to different spatial steps. This might have been because the time step's change affected the input coefficients, thus interfering with the models' fitting effect.

Accordingly, the model constructed in this study has certain properties and advantages. Most of the datasets we train on cover data samples with various types of excitations. This endows the model with a certain degree of adaptability and responsiveness in the face of many complex real-world situations. The model is based on purely data-driven modeling. This gives it a unique advantage in flexibility when dealing with different numerical formats and diverse flow-field problems. Compared with models relying on the embedding of specific physical information, this model does not need to add additional complicated physical information. Thus, it avoids problems caused by improper adaptation of physical information and effectively reduces the additional computational overhead during the computation process. As a result, the computation speed has been improved to a certain extent.

3.   Results and discussion

In this study, the Euler equation was solved using the WENO5-JS scheme, and the overall Lax-Friedrichs^[34] flux splitting program method was adopted. This section presents the results obtained using the WENO-NN method and compares them with those obtained using the WENO5-JS method. Next, we solve the Euler equation unless otherwise specified. We used the explicit third-order Runge-Kutta scheme^[35] for time integration.

To further compare the performance of the algorithms, all calculations are numerically simulated using the method of adaptive time steps within a specific cut-off time. In addition, to unify the comparison of reconstruction times, we stipulated a fixed step length of $0.001\;$s and 100 iterations as the standard to calculate the reconstruction efficiency.

3.1.   Shock tube problem

Within this subsection, we analyze the performance of our scheme when utilized for several shock tube problems^[32,36,37]. Specifically, we display outcomes for both the Sod and Shu-Osher problems. For these cases, Neumann boundary conditions were employed at the extremities of the computational domain.

3.1.1.   Sod problem

This problem^[36] is defined in the domain $[0, 1]$ and the initial conditions are as follows:

where $\left({{\rho _L}, {u_L}, {p_L}} \right) = \left({1, 0, 1} \right), {\rm{ }}\left({{\rho _R}, {u_R}, {p_R}} \right) = \left({0.125, 0, 0.1} \right).$

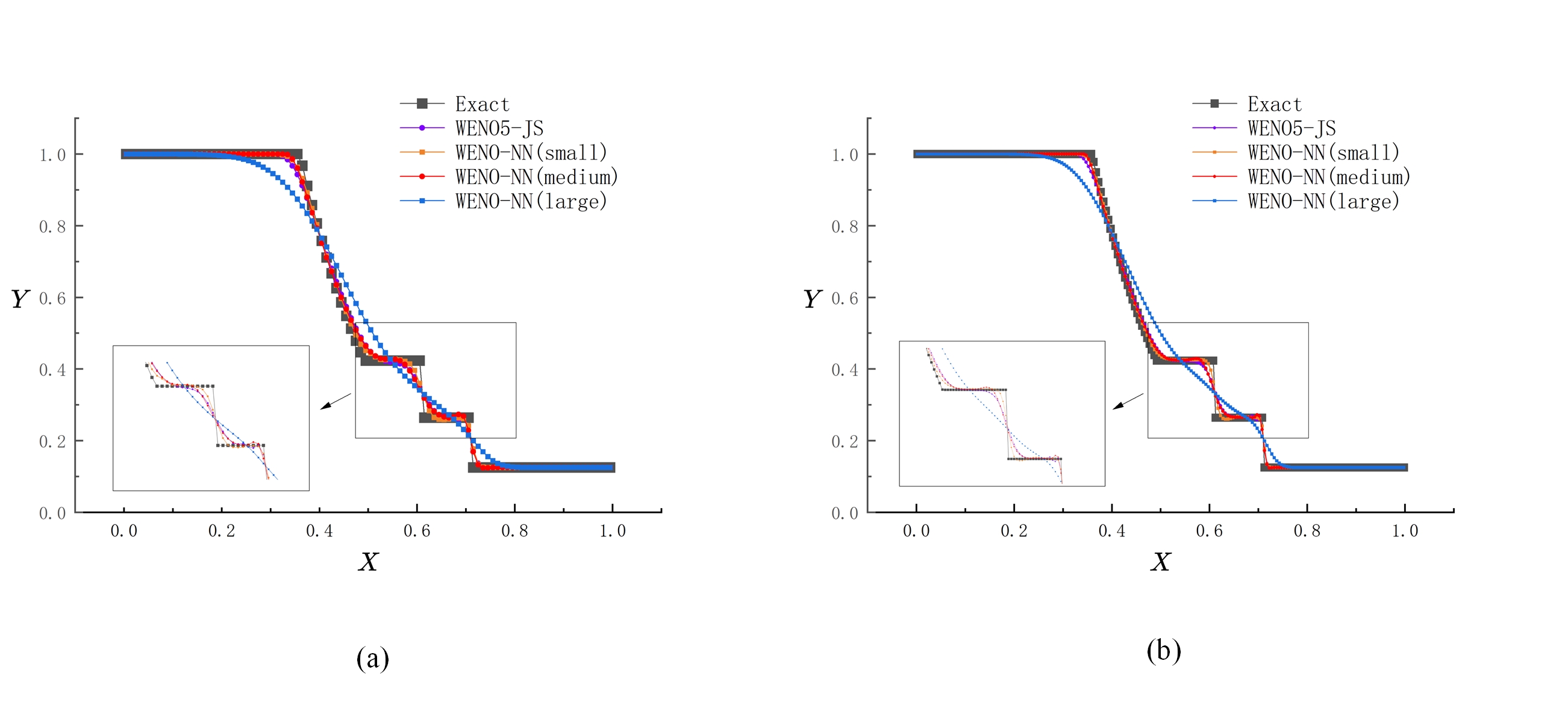
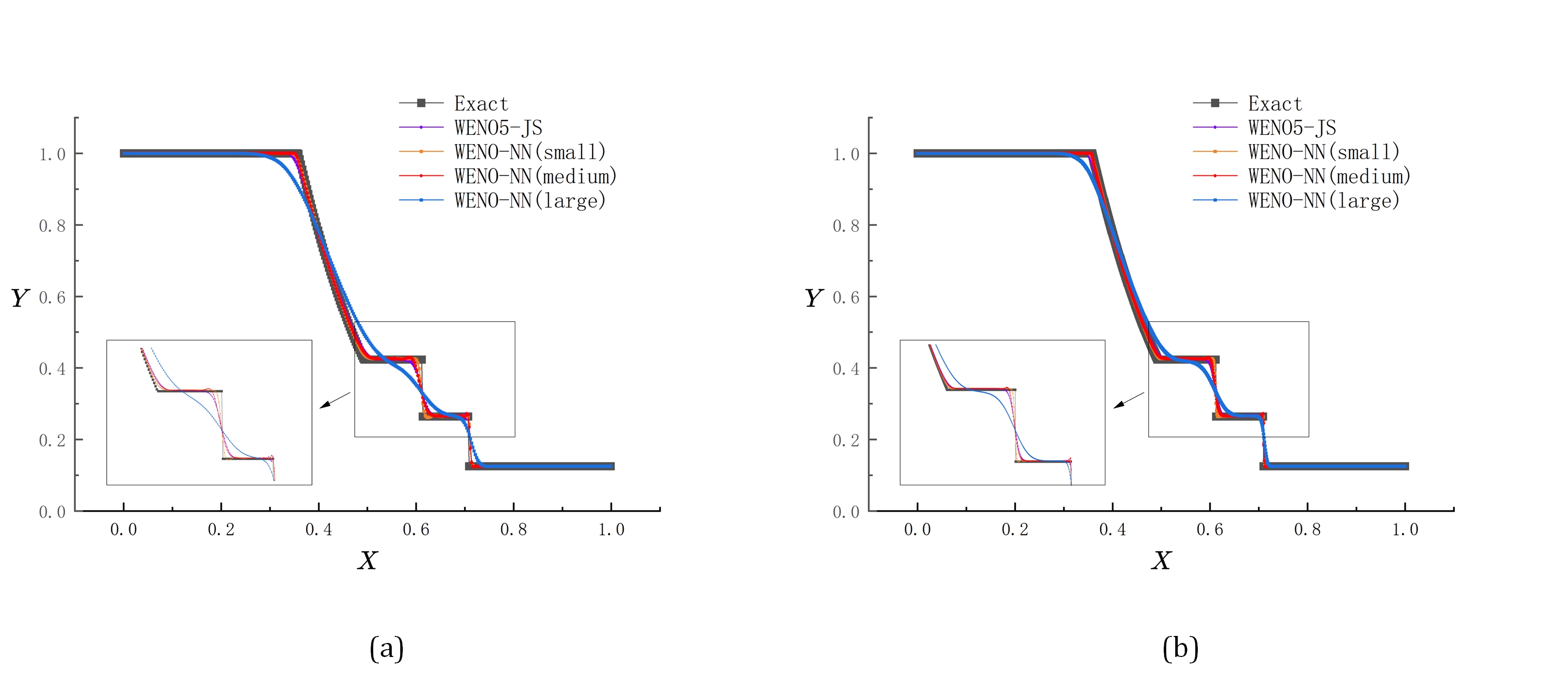
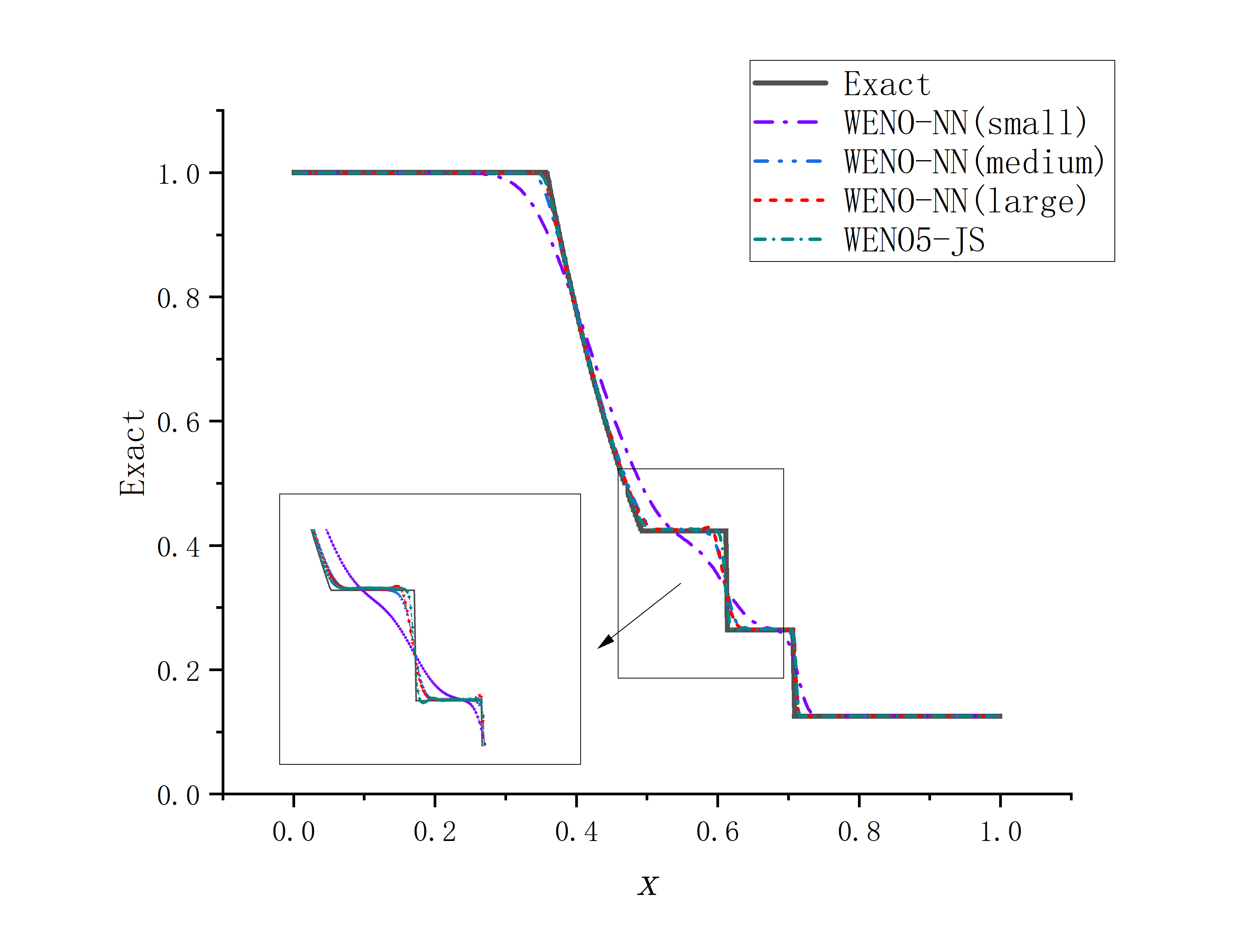
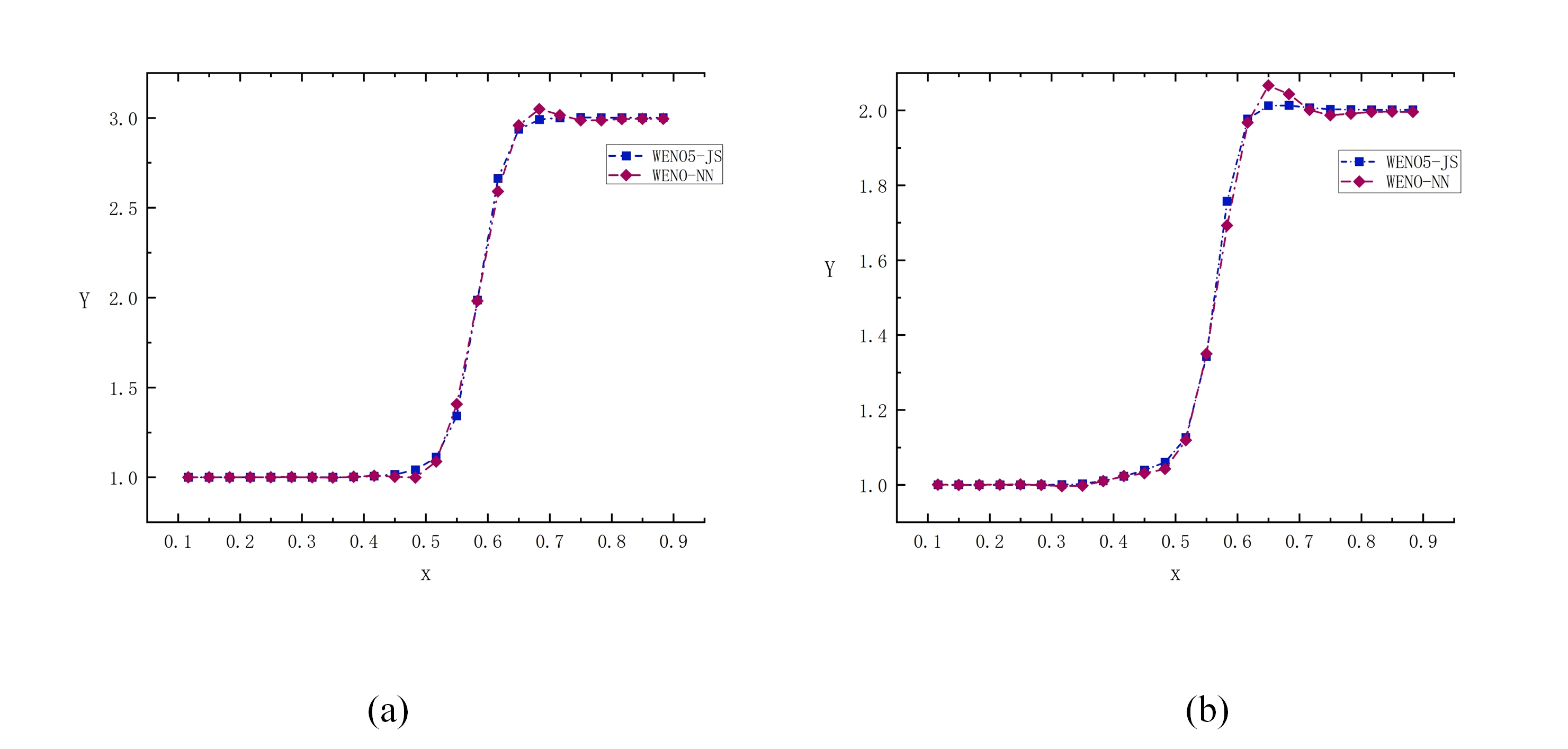
The simulation was run until the final time $t = 0.14\;$s when the CFL was 0.5. Figure 12 shows the results obtained by WENO-NN with different data volume scales. In the Sod shock tube simulation involving sharp characteristic changes, the model trained with different dataset sizes significantly impacted the accuracy of the numerical solution. We trained three models using the datasets in Table 19. It can be observed that the WENO-NN method optimized by neural networks trained with different datasets can significantly improve the quality of the solution as the training set size increases, approaching the WENO numerical solution.

Simultaneously, we observed that, as listed in Table 20, the WENO-NN scheme can also capture contact discontinuities, and both schemes capture the right-moving shock wave. In contrast, WENO-NN (small) exhibits a certain deviation, whereas WENO-NN (large) captures shock waves well and approximates the WENO numerical solution. This comparison reflects the effectiveness of different numerical methods for handling complex fluid dynamics problems. In particular, when a high-precision simulation of sharp features, such as shock waves, is required, mesh refinement and optimization of numerical methods are particularly crucial.

3.1.2.   Shu-Osher problem

The last one-dimensional test case^[32] is the interaction between a Mach 3 shock wave and an upstream sinusoidal density wave—the Shu-Osher problem^[32]. It assesses if the neural network can separate scales in flows with diverse scales. The simulation ran until $t = 1.8\;$s, with the computational domain being $x \in [- 5, 5]$. Inflow and outflow boundary conditions were set at $x = - 5$ and $x = 5$, respectively. The CFL was 0.5. The model was trained based on the dataset provided in Table 19. The initial conditions were defined as follows:

where ${\rm{ }}\left({{\rho _L}, {u_L}, {p_L}} \right) = \left({3.857143, 2.629369, 10.33333} \right), {\rm{ }}\left({{\rho _R}, {u_R}, {p_R}} \right) = \left({1 + \sin (5x), 0, 1} \right).$

In this framework, our neural network adopted the architecture presented in $[5, 20, 20, 3, 1]$. Because the Shu-Osher problem^[32] involves complex flow characteristics on a wide scale, a deep network was selected to learn its wide-scale changes, which can better capture the detailed features in scale separation. This network structure allows the model to extract and process input information at multiple levels, thereby enhancing the expression ability of different-scale features and ultimately making the solution more accurate, particularly in complex scenarios involving the interaction between shock waves and density waves.

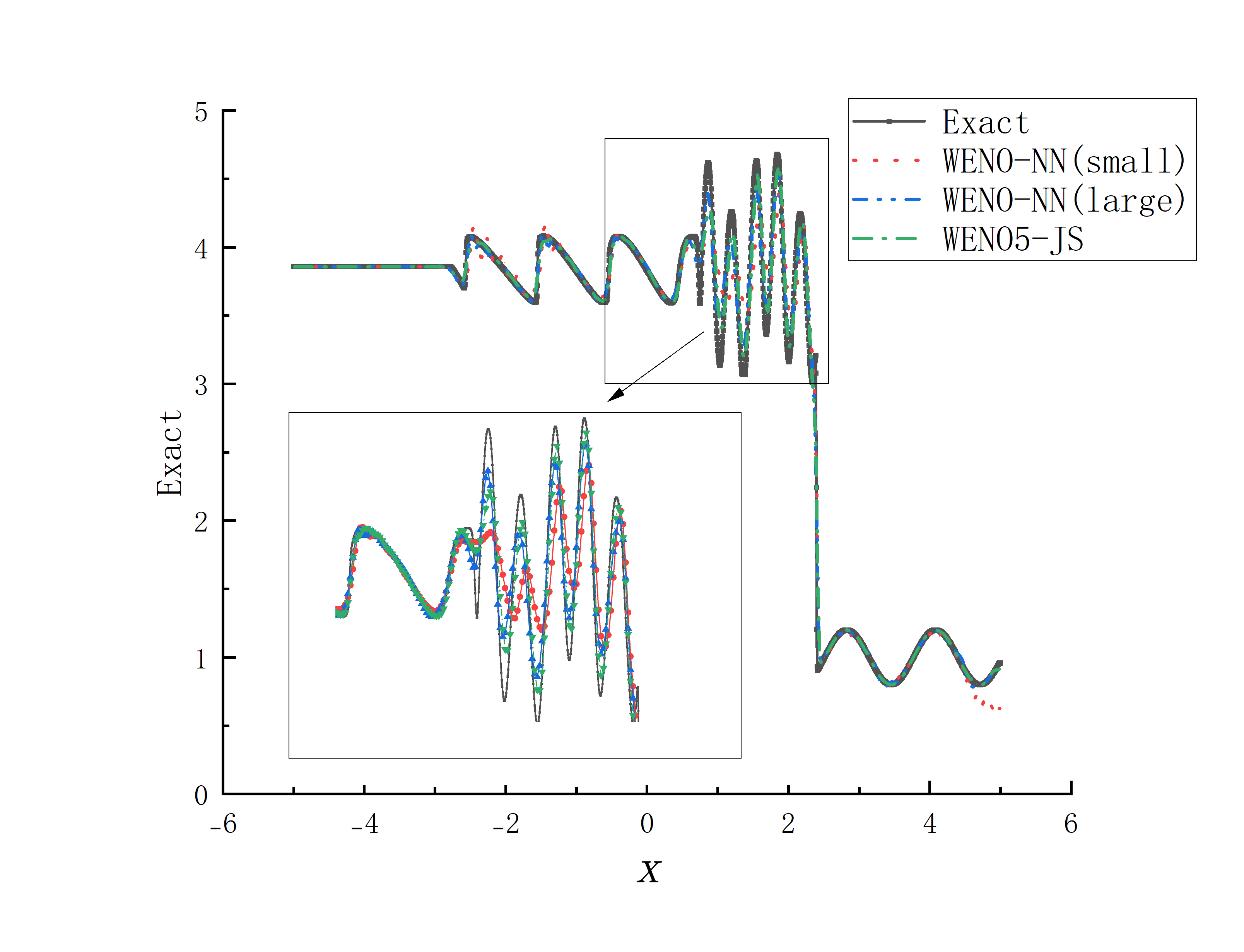
The comparison in Figure 13 shows that although all methods can generally capture the main fluctuation characteristics of the exact solution, there are differences in details. In particular, in capturing the peaks and troughs, the WENO-NN method using a larger dataset is closer to the exact solution. This indicates that grid refinement and method optimization can significantly improve the quality of the solution.

Therefore, numerical methods must consider physical oscillations in the flow. Finally, as noted in Table 21, the amount of data used still has a certain impact on the Shu-Osher problem. At the same time, it is fully proved that using neural networks to learn the reconstruction of WENO is feasible across a wide scale range and can effectively detect the shocks present in the solution.

3.2.   Two-dimensional Riemann problem

Next, we extended the use of neural networks to multi-dimensional applications. In the finite volume framework of this study, the same neural network was used in each direction. For two-dimensional Riemann problems, owing to more complex changes in the internal flow field and the existence of multi-scale flow characteristics and interactions, modeling the flow is challenging. The neural network framework adopts a structure of $[5, 3, 1]$, which reduces the number of model parameters, effectively prevents overfitting, accelerates calculations, and ensures fast and reliable predictions in complex flow scenarios. For detailed configurations, please refer to Table 22. The following three examples were predicted by the neural network trained based on this dataset, demonstrating the application of neural networks in complex two-dimensional Riemann problems.

In this study, three different configurations of two-dimensional Riemann problems are considered. These problems are set in a square region divided into four parts, each with distinct values for the basic variables. The selected cases are as follows.

3.2.1.   Interaction of planar contact discontinuities of vortex sheets

Four planar contact discontinuities separate the adjacent states. This separation leads to complex flow phenomena. The evolution of contact discontinuities promotes the formation of a vortex surface. The vortex surface is an area where fluid rotates like a rotating "sheet". In this problem, it is a clockwise rotating vortex. The configuration of this phenomenon is as follows.

The initial conditions were as follows:

The boundary conditions are set as follows:

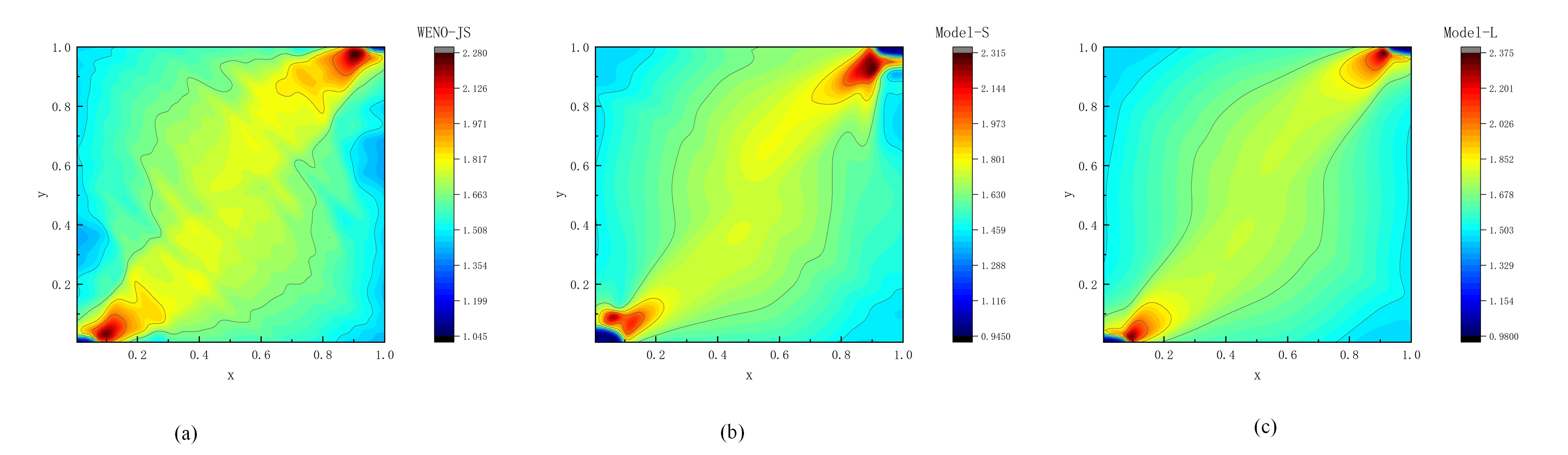
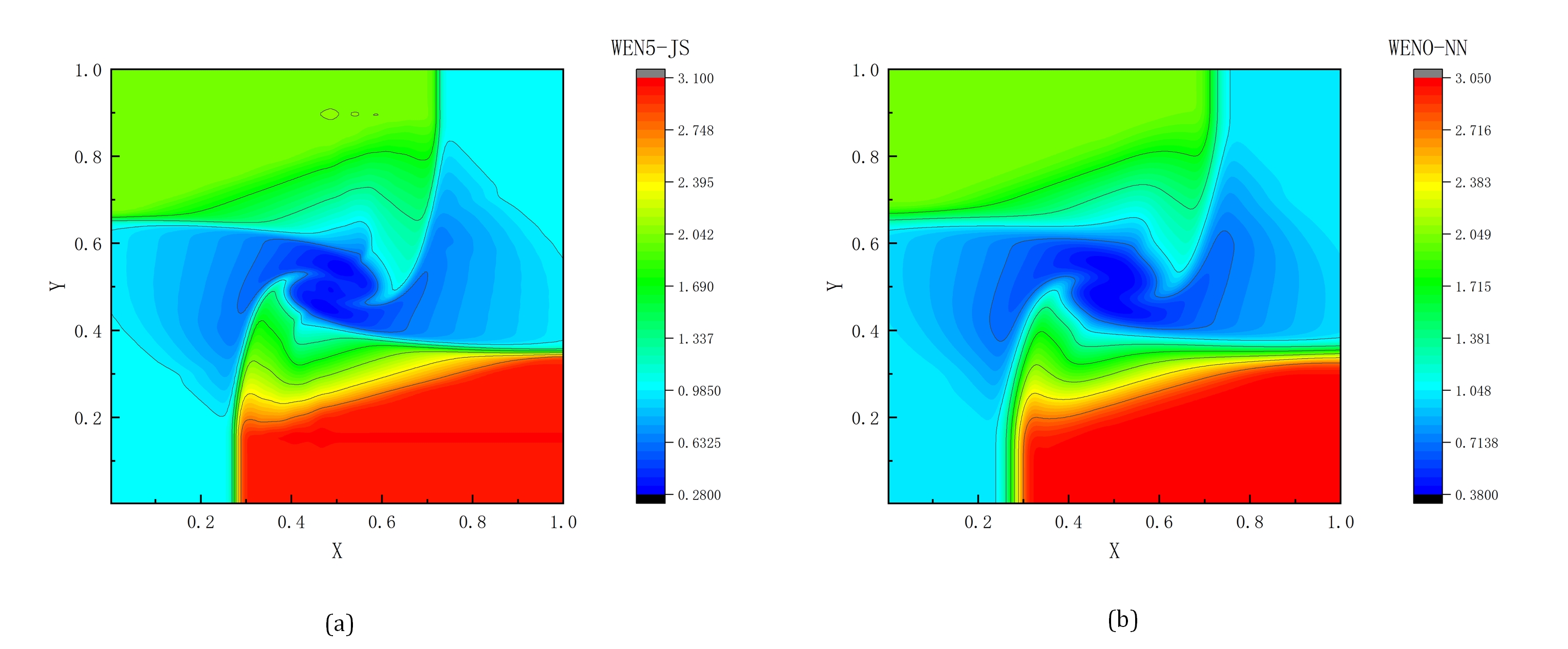
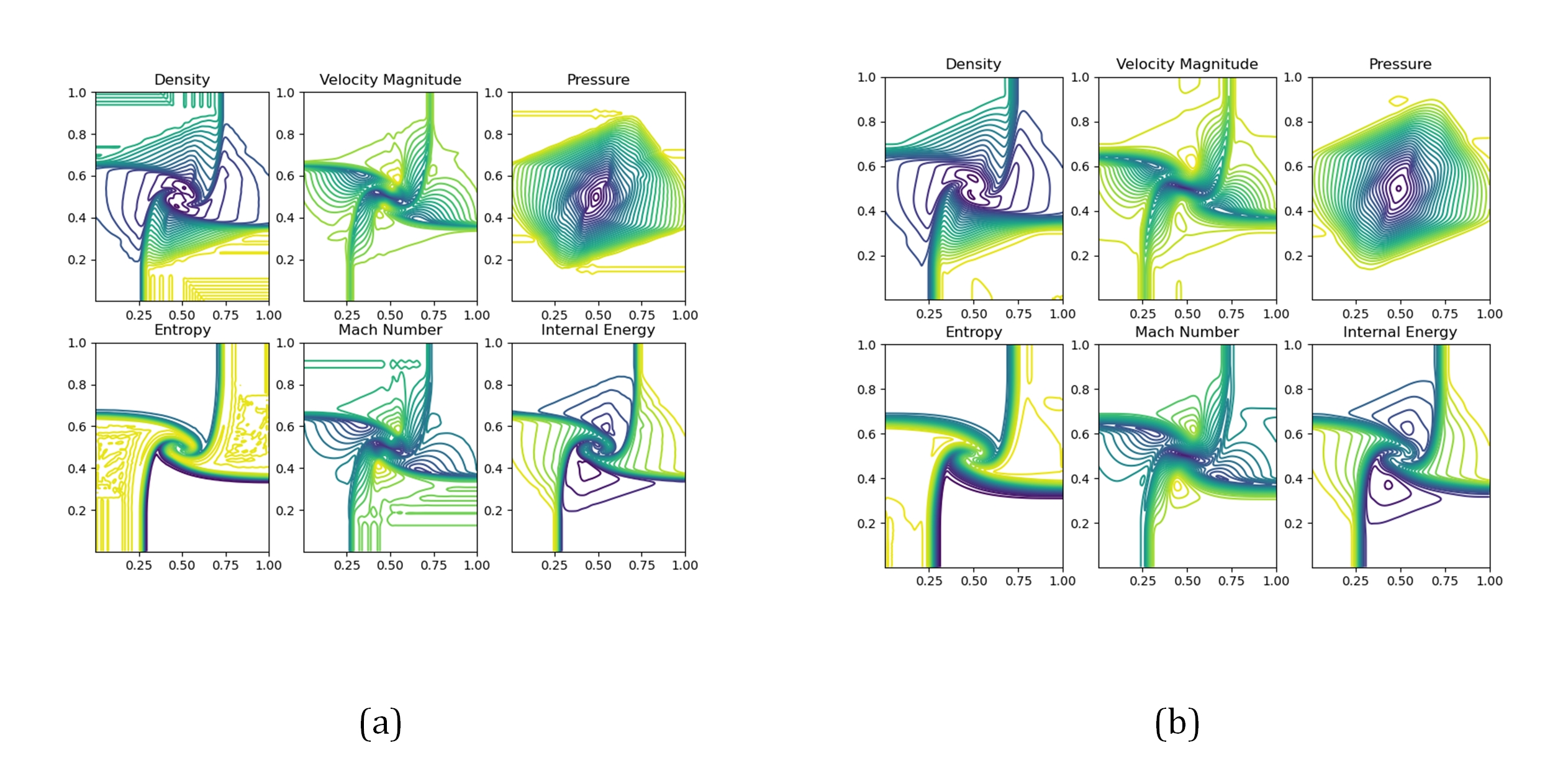
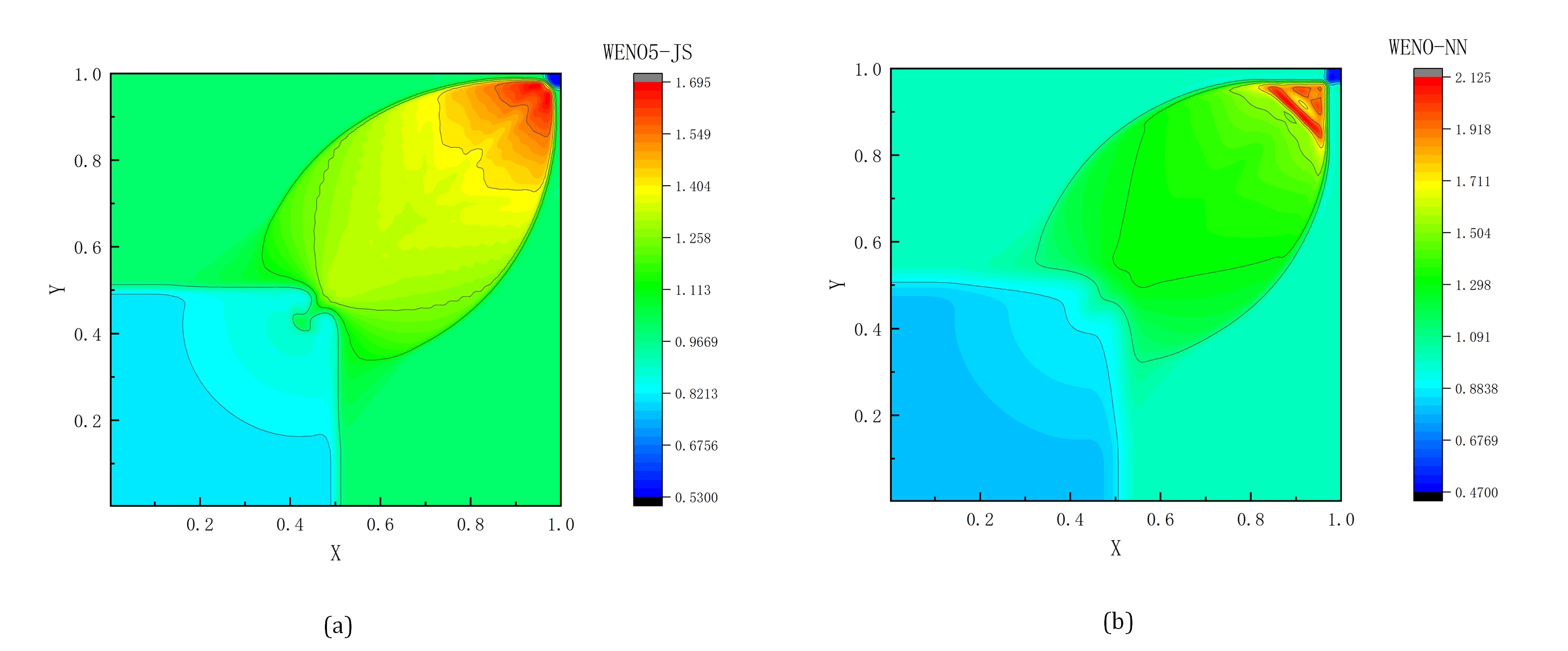
The simulation was run on a $200 \times 200$ grid with the CFL set to 0.6 and continued until time $t = 0.3\;$s. As shown in Figure 14(a), this example is a two-dimensional Riemann problem. The Model-S model trained with data in the range of $[-1.83, 5.12]$ predicts that the range of the reconstructed values is $[-2.31, 3.88]$. In this configuration^[38], four planar contact discontinuities divide the adjacent states. For specific model details, see Table 22. Figure 15 shows that the contact discontinuities' evolution creates complex wave patterns. The solution forms a clockwise-rotating vortex. Slip lines spiral around the center and enter a low-density region at the domain's core. When the pressure is set to a specific value (initially constant at 1 in all regions), the system's evolution should generate small-scale structures.

According to the numerical results in Table 23, there are certain differences in errors between the WENO-NN scheme and WENO5-JS scheme. Specifically, the relatively smaller $L_2$ error indicates that WENO-NN demonstrates good overall prediction accuracy in approximating WENO5-JS solutions. However, the larger ${L_\infty }$ error suggests that WENO-NN may fail to precisely capture local extreme variations in regions with strong discontinuities, leading to significant local error increases.

Figure 16 shows that the WENO-NN scheme can successfully detect the appearance of small-scale structures along slip lines. Its overall trends are highly consistent with those of WENO5-JS. Even though the density trend graphs match, there are still some disparities in the results. This divergence does not stem from fundamental model flaws. Instead, it likely arises from potential limitations in the generalization ability of WENO-NN. When the model extrapolates beyond its training data range, it may experience a loss of accuracy, which contributes to the generation of overall errors.

3.2.2.   Interaction of rarefaction waves and contact waves

The interaction between rarefaction waves and contact waves is a complex fluid–mechanical phenomenon. In this interaction, rarefaction waves gradually reduce physical quantities such as the density, pressure, and velocity of the fluid. A contact wave is an interface wave between different fluid states, where physical quantities may undergo sudden changes. The configuration of this phenomenon is as follows:

The initial conditions were as follows:

The boundary conditions were set as follows:

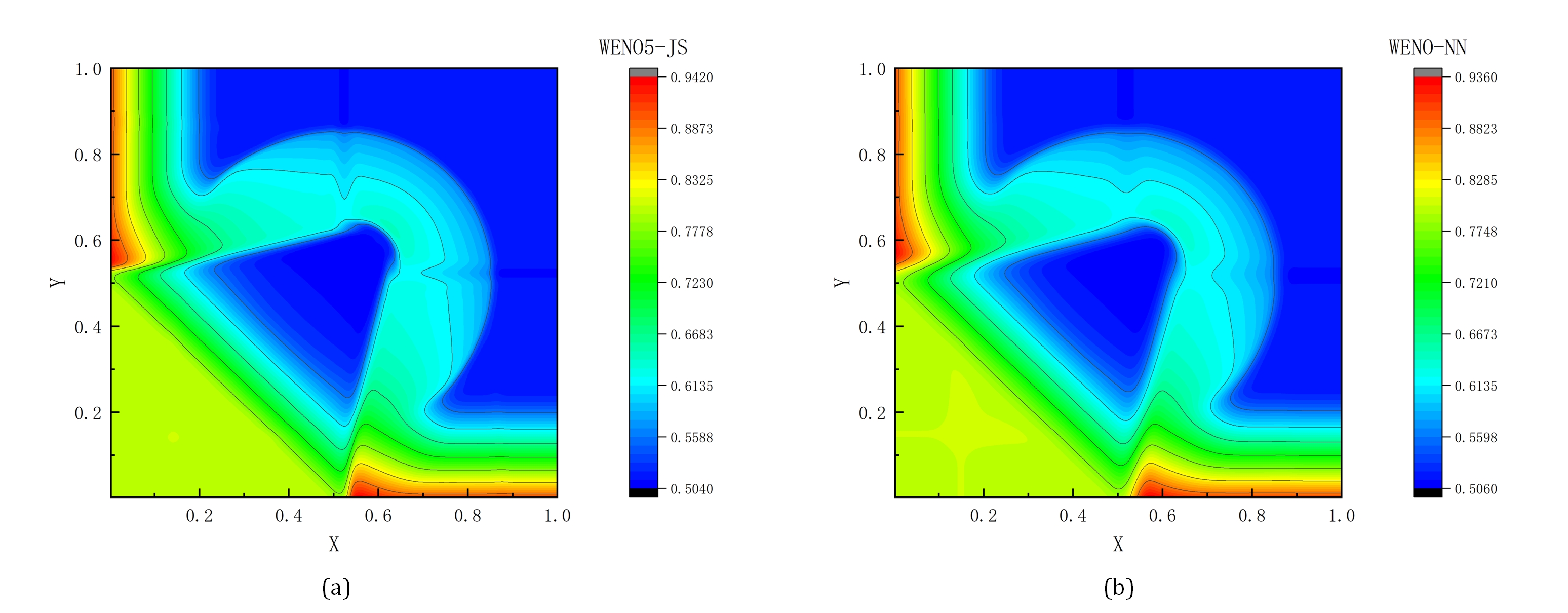
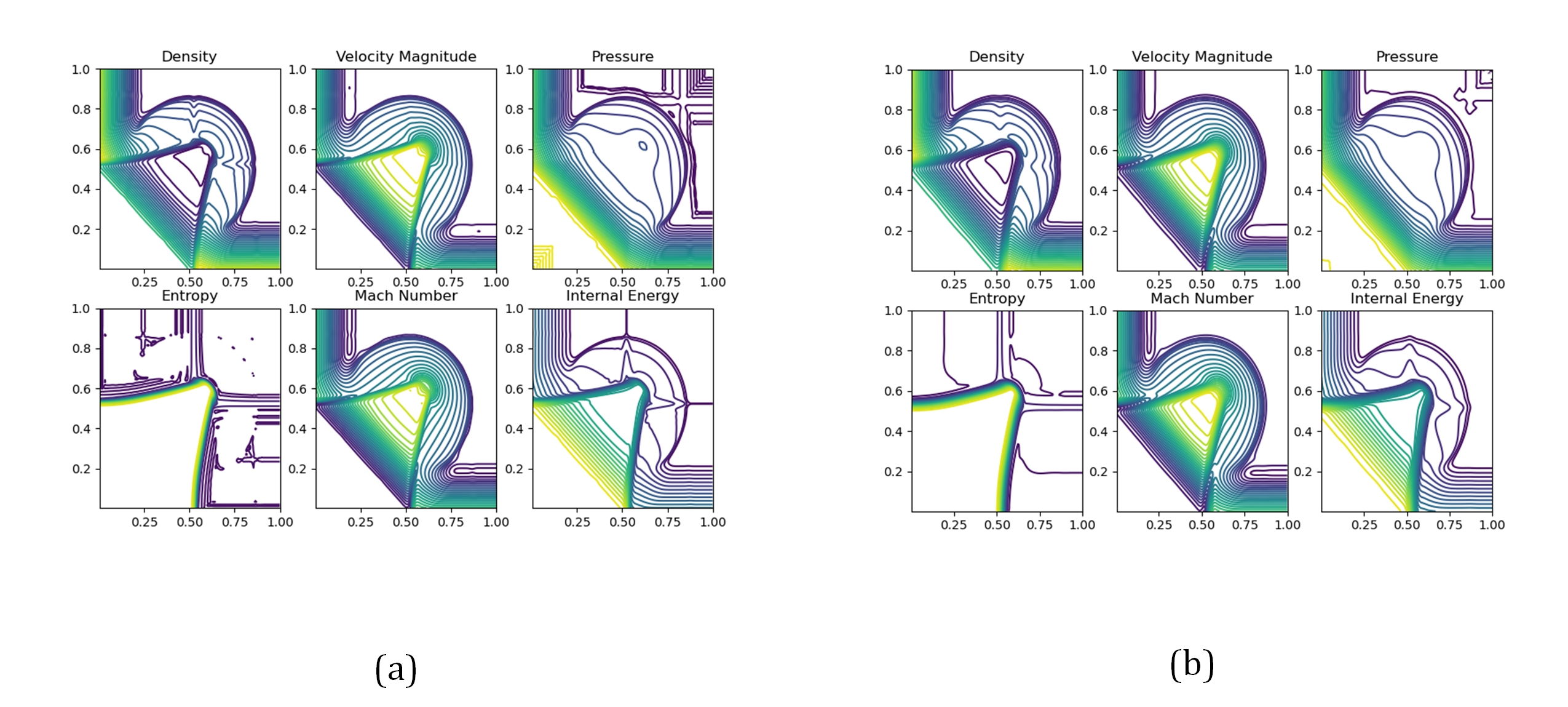
In this setting^[39], the square area is divided into four quadrants, each containing different initial conditions. The simulation was performed on a $200 \times 200$ grid with the CFL set to 0.75 and continued until time $t = 0.25\;$s. For detailed model configurations, refer to Table 22. As shown in Figure 14(b), this example is a two-dimensional Riemann problem. The Model-S model trained with data in the range of $[-1.83, 5.12]$ predicts that the range of the reconstructed values is $[-0.63, 2.72]$. Figure 17's right panel clearly depicts circular shock waves at the boundary of the supersonic region within the rarefaction wave. These high-resolution results are in strong agreement with those reported in literature ^[39].

The results for multiple physical quantities, such as density, are plotted in Figure 18, which show that the WENO-NN scheme effectively captures the relative symmetry of shock lines and the multi-scale wave structures generated by shock wave interactions. According to the error analysis in Table 24, WENO-NN shows smaller $L_2$ errors compared to WENO5-JS. This indicates its capacity to accurately approximate WENO5-JS solutions throughout the computational domain. Nevertheless, the relatively larger $L_{\infty}$ errors imply potential precision discrepancies in local areas, especially near strong discontinuities or complex flow structures.

It is important to note that for this particular case, the prediction scope lies entirely within the model's training data range. As a result, it exhibits the smallest errors among the three examples. This validates that within its training domain, WENO-NN can achieve high accuracy and stability, effectively capturing the main flow characteristics. The scheme demonstrates good numerical performance and high resolution. However, there is still room for improvement in local complex regions. This observed phenomenon offers valuable insights. By expanding the scope and scale of the training data, we may enhance the fitting accuracy. This, in turn, could effectively improve the model's generalization ability for a wider range of operating conditions.

3.2.3.   Interaction of shock waves and contact discontinuities

When a shock wave interacts with a contact discontinuity, complex fluid mechanics phenomena occur, including the shock wave affecting the position and shape of the contact discontinuity, which changes the propagation speed and intensity of the shock wave. During this process, physical quantities such as the density, pressure, and velocity of the fluid undergo complex changes. The configuration of this phenomenon is as follows:

The initial conditions were as follows:

The boundary conditions were set as follows:

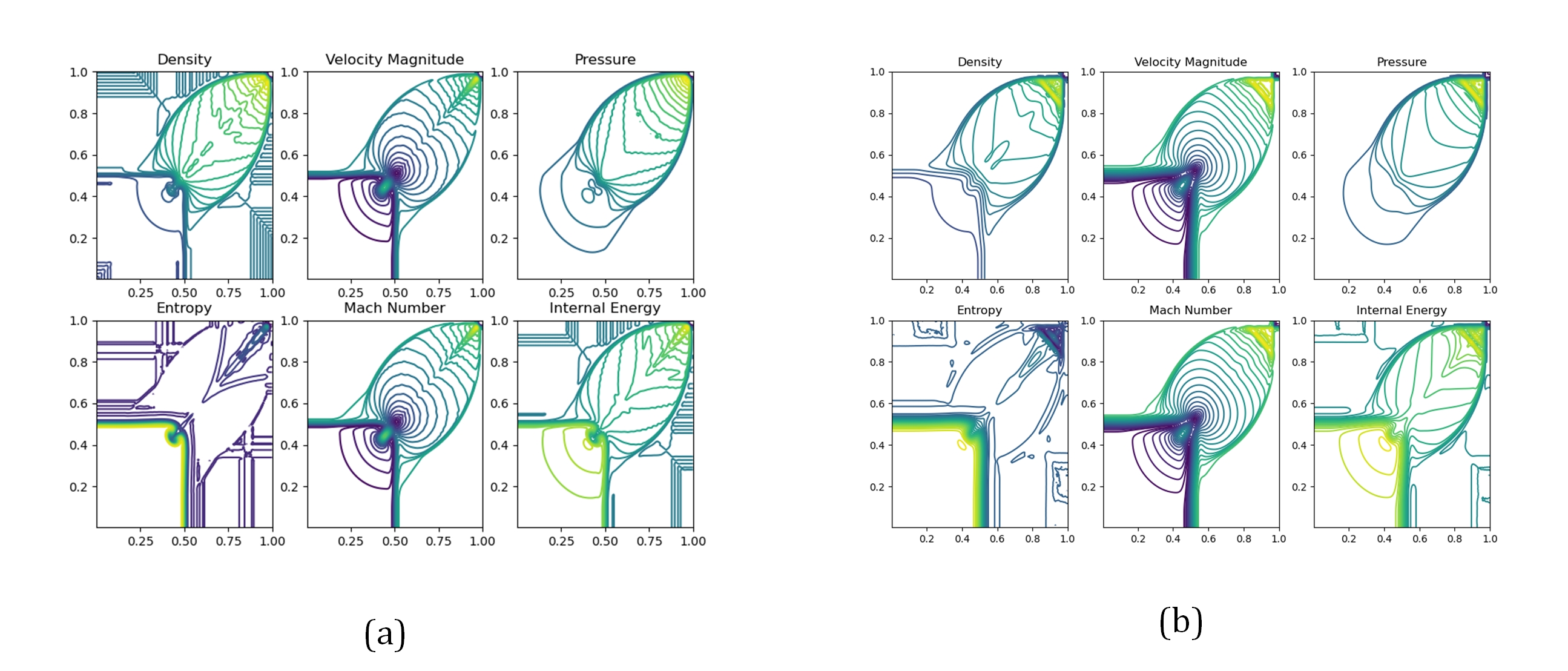
In this setting^[40], the square area is divided into four quadrants, each containing different initial conditions. The simulation was performed on a $200 \times 200$ grid with the CFL set to 0.75 and continued until time $t = 0.25\;$s. For detailed model configurations, refer to Table 22. As shown in Figure 14(c), this example is a two-dimensional Riemann problem. The Model-S model trained with data in the range of $[-1.83, 5.12]$ predicts that the range of the reconstructed values is $[-0.65, 6.77]$. As shown in Figure 19, the flow field features (in the right figure) are relatively smooth. In particular, when shock waves and rarefaction waves interact, the streamline and isoline are evenly distributed, indicating the continuity of the numerical solution and a good capture of details. The figure on the left shows more detailed features, including the complex interaction between the shock waves and small-scale instabilities near the main slip line, such as the Kelvin–Helmholtz instability, which indicates more advanced dynamic processes in the flow field.

The results for multiple physical quantities, such as density, are plotted in Figure 20, which show that the WENO-NN scheme effectively captures the relative symmetry of shock lines and the multi-scale wave structures generated by shock wave interactions. When handling complex flow fields with high-speed nonlinear waves, WENO5-JS provides significantly more details about flow field dynamics, particularly in describing shock interactions and identifying flow instabilities. Nonetheless, WENO-NN demonstrates comparable capabilities in solution smoothness and numerical stability, making it suitable for scenarios requiring high precision.

We conduct an error analysis, as shown in Table 25. WENO-NN has smaller ${L_2}$ errors. This indicates that it can globally approximate WENO5-JS solutions quite well. Nevertheless, it has larger ${L_\infty }$ errors. This suggests that there are precision challenges in local areas, especially near strong discontinuities. This difference might be related to the generalization limits of WENO-NN. WENO-NN can maintain high accuracy within its training ranges. But when it comes to processing complex flow features that are beyond the training scope, its performance decreases.

3.3.   Three-dimensional Riemann problem

Based on the verification of existing two-dimensional examples, we further explore the applicability of the WENO-NN method in three-dimensional complex flow scenarios. Three-dimensional flow simulations pose more stringent requirements for algorithm efficiency due to their higher computational complexity (for example, the number of grids increases cubically). It is worth noting that in this study, we did not retrain the model for three-dimensional problems. Instead, we directly adopted the network architecture of the two-dimensional model (i.e., the $[5, 3, 1]$ network structure in Table 22). This approach not only maintains the universality of the model but also significantly reduces the three-dimensional computational cost. We selected a three-dimensional example extended from the two-dimensional vortex-surface contact discontinuity problem. Its initial conditions are constructed by adding a velocity component in the $z$-direction.

The initial conditions were as follows:

The boundary conditions are set as follows:

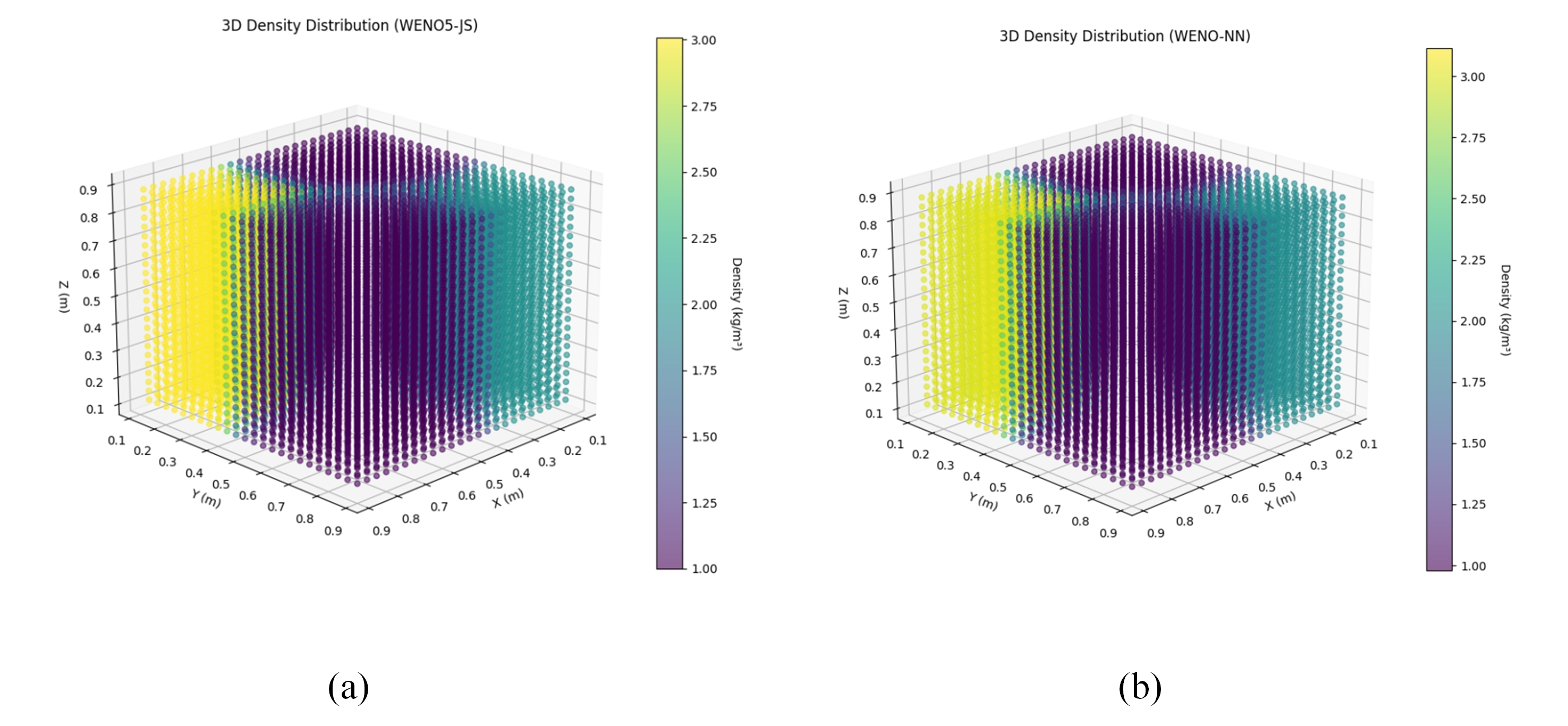
The simulation was carried out on a [$30\!\times30\!\times30$] grid with the CFL set to 0.75. To facilitate the statistics of the reconstruction time, we used a fixed step size of $0.001\;$s for the calculation. The simulation ran for 100 steps in total, and the cut-off time of the simulation was $0.1\;$s. This extended example retains the core physical characteristics of the two-dimensional problem (such as the evolution of the vortex surface and the interaction of contact waves), while introducing the flow coupling effect in three-dimensional space. As shown in Figure 21, the three-dimensional evolution process of the contact discontinuity forms a complex wave system structure. The solution field exhibits a spatial vortex structure, in which the slip surfaces are spirally distributed around the vortex core and extend to the extremely low-density region in the core area of the computational domain. Under the condition of three-dimensional flow where the initial pressure is a constant value of 1 throughout the entire field, the evolution of the system will trigger the formation of multi-scale flow structures.

Figure 22 shows the distribution of two-dimensional contour lines cut at the fixed $z$-axis coordinate $z = 0.55$ within the given three-dimensional computational domain. It includes the visualization results of physical quantities such as density and velocity. With this slice visualization, it can be clearly observed that the WENO-NN format is able to successfully detect three-dimensional small-scale structures distributed along the slip plane, and the spatial distribution trend highly matches that of the WENO5-JS format. Figure 23 shows the characteristics of the density change along a single axis after fixing the two axes. As can be seen from the figure, both methods are able to capture the location and propagation direction of the discontinuity, but there is a slight shift of contours in local areas (e.g., high-density gradient areas). This divergence does not stem from an intrinsic flaw in the model, rather, it may be due to limitations in the generalization ability of WENO-NN under three-dimensional flow conditions. When the model infers complex flow patterns beyond the distribution of the three-dimensional training data, there may be a situation of data extrapolation, which in turn leads to the accumulation of multiscale errors.

According to the numerical results in Table 26, there are error differences between the WENO-NN scheme and the WENO5-JS scheme. The relatively small $L_2$ error indicates that WENO-NN has good overall prediction accuracy in approximating the WENO5-JS solution, while the large ${L_\infty }$ error reflects that WENO-NN has difficulty in accurately capturing the local extreme value changes in the strong intermittent region, which results in a significant increase in the local error. In addition, Table 26 shows that the time efficiency of WENO-NN is also improved by a factor of three in the three-dimensional problem. It is noteworthy that the reconstruction time of the [$30\; \!\times30\; \!\times30$] grid is close to that of the $200\times200$ grid, which fully reflects that the computational cost of the three-dimensional problem is much higher than that of the two-dimensional problem.

Based on this, the time efficiency is further analyzed: Table 27 shows the computational complexity of the three-dimensional problem under different grid numbers. As the number of grids increases from [$10\; \!\times\!\; 10\; \!\times\!\; 10$] to [$100\; \!\times\!\; 100\; \!\times\!\; 100$], the computation time increases from $41\;$s to 37,529 s, which is an increase of about 915 times. It can be seen that the computational complexity increases exponentially when the number of grids is expanded by 10 times, which also highlights the urgency of improving the efficiency of the computation.

Overall, our results from the neural network learning of WENO5-JS reconstruction based on WENO-NN revealed the same detailed information regarding the formation of various waves. Comparisons with the classical WENO5-JS scheme demonstrate that WENO-NN can also capture the details of each interaction. On this basis, WENO-NN exhibits a significant improvement in computational efficiency. While accelerating the running speed and reducing the computational cost, it can maintain the approximation effect on the target features. This indicates that numerical reconstruction using neural networks not only maintains accuracy but also significantly improves computational efficiency, providing strong support for efficiently handling complex flow problems.

4.   Conclusions

This study successfully improved the computational efficiency significantly while maintaining the accuracy of WENO5-JS reconstruction results by introducing a machine learning-based WENO-NN neural network method. The analysis of various wave interactions showed that WENO-NN can capture the same detailed information as the classic WENO5-JS and exhibits good universality in one-dimensional, two-dimensional, and three-dimensional test cases. This achievement provides an efficient new method for handling complex flow problems^[41,42,43] and overcomes the limitations of traditional WENO formats in terms of computational efficiency.

Overall, we used the WENO-NN neural network to learn the reconstruction results of WENO5-JS and revealed the same detailed information regarding the formation of various waves. Compared with the classic WENO5-JS scheme, WENO-NN can also accurately capture the details of each interaction. Based on this, WENO-NN showed significant advantages in terms of computational efficiency. Experiments showed that it achieves an acceleration of approximately three times the reconstruction time. This shows that using neural networks for numerical reconstruction not only maintains accuracy but also remarkably improves computational efficiency and provides strong support for efficiently dealing with complex flow problems.

Future research could be expanded in the following ways. First, instead of being limited to the WENO5-JS numerical scheme, various complex numerical schemes that are time-consuming in terms of computation should be attempted to test whether our framework can maintain excellent computational efficiency under different circumstances. Next, the network architecture should be optimized and improved. The current network was relatively shallow. Adjusting the network structure is expected to further enhance the training and reconstruction of the learning abilities of the network. For the training set, the possibilities of constructing a universal and highly generalized dataset should be explored to improve the applicability and stability of the model. For the proposed multi-model architecture, the configuration of the neural network can be customized and combined with physical information to further enhance the interpretability and physical consistency of the model. Exploring this combination with other numerical methods or machine-learning techniques is expected to lead to the development of more powerful numerical simulation tools. The introduction of super-resolution reconstruction technology^[44] will improve the spatial accuracy of low-resolution data. Combined with multi-source data fusion^[45], this will enhance the prediction accuracy of the model in complex flow scenarios. This method can be extended to more complex flow problems, such as multiphase flows and combustion, to verify its effectiveness in different fields. In practical engineering applications, it is important to further reduce the acquisition cost of high-fidelity data and improve the practicability of the method. In conclusion, WENO-NN introduces novel ideas and methods for research in fluid mechanics and related fields, demonstrating significant potential for future development and applications.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported in part by the Tianshan Talents Training Program of Xinjiang province, China (NO. 2022TSYCTD0019), the Natural Science Foundation of Xinjiang province, China (No. 2022D01D32), and the Foundation of the National Key Laboratory of Computation Physics (No. 6142A05230203). Additionally, we sincerely thank the reviewers and editors for their valuable suggestions and comments, which significantly improved the quality of this manuscript.

Conflict of interest

The authors declare there are no conflicts of interest.