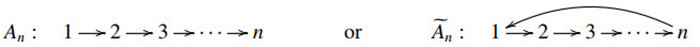1.
Introduction
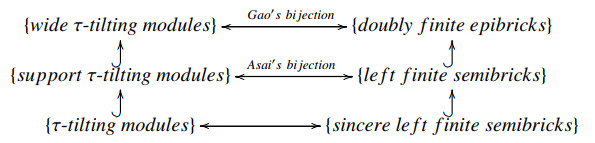
In 2014, Adachi, Iyama and Reiten[1] introduced the concept of support τ-tilting modules, and showed that there exists a bijection between support τ-tilting modules and functorially finite torsion classes. Recently, Enomoto[2] studied image-cokernel-extension-closed (ICE-closed) subcategories that contain torsion classes and wide subcategories. Moreover, it is shown that a subcategory is ICE-closed if and only if it is a sincere torsion class for some wide subcategory (see, [2, Corollary 2.5, Proposition 4.2]). Note that every functorially finite wide subcategory is equivalent to a module category. Enomoto and Sakai introduced the concept of wide τ-tilting modules that are τ-tilting modules over some functorially finite wide subcategory. Moreover, a bijection was established between wide τ-tilting modules and doubly functorially finite ICE-closed subcategories, which extended Adachi et al.'s bijection. Note that τ-tilting modules are exactly sincere support τ-tilting modules. Adachi et al. also showed that there is a bijection between τ-tilting modules and sincere functorially finite torsion classes.
Bricks and semibricks are considered, and they have long been studied in [3,4]. Asai proved that a bijection exists between support τ-tilting modules and left finite semibricks (see [5, Theorem 2.3]). Gao[6] also showed that Asai's bijiection can be restricted to a sincere case. Moreover, considering the dual definition of Enomoto about monobricks, Gao[7] introduced the concept of epibricks and then established a bijection between wide τ-tilting modules and doubly finite epibricks.
The aim of this paper is to show that Enomoto and Sakai's bijection and Gao's bijection can be restricted to support sets. In particular, it will be proved that there are bijections between sincere wide τ-tilting modules, sincere ICE-closed subcategories, and sincere epibricks. Then we show that its number is related to the little Schr¨oder number for Nakayama algebras.
All algebras will be basic, finite dimensional K-algebras over an algebraically closed field K. Let A:=KQ/I be an algebra, modA be the category of finitely generated right A-modules and τ be the Auslander-Reiten translation of A. We also denote the number of pairwise nonisomorphic indecomposable summands of M by |M|, and the Loewy length of M by l(M). We use Si, Pi, and Ii to denote the indecomposable simple, projective, and injective modules of an algebra corresponding to the vertex i, respectively. For any i,j∈{1,2,⋯,n}, we denote by [i,j]={i,i+1,⋯,j} if i⩽j; otherwise, [i,j]=∅. Let ei be the primitive idempotent element of an algebra corresponding to the vertex i. We write e[i,j]:=ei+ei+1+⋯+ej.
2.
Some bijections
We recall some notions and results about support τ-tilting modules, wide τ-tilting modules, and some subcategories.
Let A be an algebra. An A-module M is called τ-tilting if HomA(M,τM)=0 and |M|=|A|. M is support τ-tilting if it is a τ-tilting A/AeA-module for some idempotent e of A. The set of all support τ-tilting A-modules (respectively, τ-tilting A-modules) will be denoted by sτ−tiltA (respectively, sτ−tiltA). Enomoto showed that every functorially finite wide subcategory W is equivalent to a module category (i.e., W is equivalent to modΓ for some algebra Γ), and then he introduced the concept of wide τ-tilting modules as follows.
Definition 2.1. ([2, Definition 4.11])
(1) Let W be a functorially finite wide subcategory of modA and M∈W. Fix an equivalent F:W≃modΓ. M is called τW-tilting if F(M) is a τ-tilting Γ-module.
(2) An A-module M is wide τ-tilting if M is τW-tilting for some functorially finite wide subcategory W of modA. The set of all wide τ-tilting A-modules will be denoted by wτ−tiltA.
An A-module E is called a brick if HomA(E,E) is a K-division algebra. A set E of isomorphism classes of bricks in modA is said to be a epibrick if every morphism between elements of E is zero or a surjection in modA. We denote by ebrickA the set of epibricks in modA. A subcategory C of modA is right Schur if it is closed under extensions and, for every simple object M in C, every morphism X→M with X∈C is zero or a surjection in modA. Here, M is a simple object in C if there no exists any short exact sequence with M as the middle term. The set of right Schur subcategories of modA will denoted by schurRA. The following proposition follows from the dual of [8, Theorem 2.11].
Proposition 2.2. Let A be an algebra. Then, there is a bijection:
where Filt(E) stands for the minimal extension-closed subcategory that contains E for E∈ebrickA and Sim(C) stands for the set of all simple objects of the right Schur subcategory C.
A subcategory C of modA is called ICE-closed if it is closed under images, cokernels, and extensions. Both torsion classes and wide subcategories are ICE-closed, and ICE-closed subcategories are right Schur. Moreover, it is shown that C is ICE-closed if and only if there is a wide subcategory W such that C is a torsion class over W. Enomoto called C is doubly functorially finite if C is a functorially finite torsion class over some functorially finite wide subcategory W. The set of all doubly functorially finite ICE-closed subcategories of modA will be denoted by df−iceA.Let E be an epibrick in modA. We say E is doubly finite if Filt(E) is a doubly functorially finite ICE-closed subcategory. The set of all doubly finite epibricks in modA will be denoted by df−ebrickA. The following result extends Adachi et al.'s bijection and Asai's bijection.
Theorem 2.3. ([2, Theorem 4.13] and [7, Theorem 2.6]) Let A be an algebra. Then, there are bijections:
where cok(M) denotes the subcategory of modΛ consisting of cokernels of morphisms in addM, and P(C) denotes the maximal Ext-projective object of C.
3.
Main results
For M∈modA, let SuppM:={i|HomA(Pi,M)≠0}, which is called the support of M. In addition, a set E consists of some modules is called sincere if SuppE=SuppA={1,2,3,⋯,n} where SuppE:=⋃M∈ESuppM is called the support of E. It is clear that SuppE=∅ if and only if E={0}. The set of sincere wide τ-tilting modules (respectively, sincere right Schur subcategories, sincere doubly functorially finite ICE-closed subcategories, sincere ICE-closed subcategories, sincere doubly finite epibricks, and sincere epibricks) in modA will be denoted by swτ−tiltA (respectively, sschurRA, sdf−iceA, siceA, sdf−ebrickA, and sebrickA).
Theorem 3.1. Let A be a finite dimensional algebra. Then, those bijections in Proposition 2.2 and Theorem 2.3 can be restricted to the support sets. In particular, there are bijections:
and
Proof. We only need to prove that four mappings preserve support sets. First, for an exact sequence 0→L→M→N→0 in modA, it is clear SuppM=SuppL∪SuppN since Hom(Pi,−) is exact. Note that modA has finite length, we claim Filt(−) preserve support sets (i.e., SuppFiltE=SuppE). Second, SuppN⊂SuppM for any epimorphism from M to N. This implies that SuppcokM⊂SuppM. Thus SuppcokM=SuppM since M∈cokM. Similarly, SuppP(C)=SuppC since every functorially finite subcategory has enough Ext-projective objects. Finally, SuppSimC=SuppFiltSimC=SuppC. □
Remark 3.2. (1) Adachi et al.'s bijection can be restricted to the support sets since Fac(−) preserve support sets.
(2) Enomoto showed that there exists a bijection between rigid modules and ICE-closed subcategories with enough Ext-projective objects [9, Theorem 2.3] for hereditary algebras. This bijection also can be restricted to the support sets.
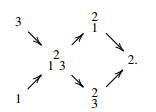
Example 3.3. Let Q be the quiver: 1←2→3 and A=KQ. The Auslander-Reiten quiver of modA is as follows:
For a full subcategory C of modA, we use ∙ or ∘ instead of each indecomposable module in the Auslander-Reiten quiver, and ∙ means that the module belongs to C and ∘ means not. For example, 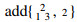 will be denoted by
will be denoted by  . Now, we list wτ−tiltA, df−iceA, and df−ebrickA in table 1 (sincere cases) and 2 (non-sincere cases).
. Now, we list wτ−tiltA, df−iceA, and df−ebrickA in table 1 (sincere cases) and 2 (non-sincere cases).
#wτ−tiltA=22 and #swτ−tiltA=11 (in Table 1), but #ebrickA=26 and #sebrickA=15. In fact, there are four sincere epibricks 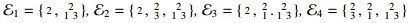 corresponding to four sincere right Schur subcategories
corresponding to four sincere right Schur subcategories  are not ICE-closed.
are not ICE-closed.
An algebra is Nakayama if its quiver is
see [10, V.3.2]. [8, Theorem 6.1] stated that all left Schur subcategories are IKE-closed (i.e., closed under extensions, kernels and images) for Nakayama algebras. Further, we have all right Schur subcategories are ICE-closed. Hence, all ebricks are doubly finite for Nakayama algebras. Therefore, we have
Theorem 3.4. There are bijections for a Nakayama algebra A :
Ler Λrn:=KAn/radr and ~Λrn:=K˜An/radr. Enomoto showed that
which is the n-th large Schr¨oder number. Next, the number of sincere wide τ-tilting modules will be obtained by calculating the number of sincere epibricks over Λrn and ~Λrn. Further, we show that
which is the n-th little Schr¨oder number, and
Proposition 3.5. Let A be a Nakayama algebra whose quiver is An and LS0=1. Then,
Proof. Let Ei,j be the brick of A with topEi,j=Si and socEi,j=Sj. Let E∈sebrickA. Because E is a sincere epibrick, it satisfies exactly one of the following conditions (ⅰ): En−i+1,n belongs to E (i∈{1,2,...l(In)}). Define Wi as the subset of sebrickA consisting of the epibricks satisfying the condition (ⅰ). Then, sebrickA=l(In)⋃i=1Wi. Hence #sebrickA=l(In)∑i=1#Wi.
For i=1,2,3,,⋯,l(In), there exists a bijection
given by E↦({E∈E∣SuppE⊂[n−i+1,n−1]},{E∈E∣SuppE∩[n−i+1,n]=∅}). The inverse is given by (E1,E2)↦E1∪E2∪En−i+1,n. Theorem 3.4 and A/⟨1−e[n−i+1,n−1]⟩≅KAi−1 imply
□
Let san,r:=#swτ−tiltΛrn, and we have the following recurrence relation.
Corollary 3.6.
The number an:=#wτ−tiltKAn=LSn. Consider the generating function F(x)=∞∑n=0anxn with a0=1. Thus it is known that the following holds for the large Schr¨oder number
Let san:=#swτ−tiltKAn and its generating function be f(x)=∞∑n=0sanxn with sa0=1. Then, san,n=san. Proposition 3.1 implies the recurrence relation
Thus,
which implies f(x)=11−xF(X)=1+x−√x2−6x+14x=12F(x)+12. This coincides with the generating function of little Schr¨oder number and implies san=12an,n≥1, (sa0=12a0+12=1).
Now, let sbn,r:=#swτ−tilt~Λrn. Note that M∈mod~Λrn is a brick if and only if l(M)⩽n, we get sbn,r=sbn,n when r⩾n. Hence, we only need to calculate sbn,r for r⩽n.
Lemma 3.7.
Proof. Let E∈sebrick~Λrn. Because E is a sincere epibrick, it satisfies exactly one of the following conditions (ⅰ): max{l(S)|S∈E,n∈SuppS}=i, (i∈{1,2,...r}).
Define Vi as the subset of sebrick~Λrn satisfying the condition (ⅰ). Then, sebrick~Λrn=r⋃i=1Vi. Hence sbn,r=r∑i=1#Vi.
First, there exists a bijection V1↦sebrick~Λrn/⟨en⟩ given by V1∋E↦E∖{En,n}. Because ~Λrn/⟨en⟩≅Λrn−1, we have #V1=san−1,r.
Second, let i∈{2,3,4,⋯,r}. Eu,v is a brick if the pair (u,v) satisfying n∈[[u,v]] and #[[u,v]]=i, where
Now, let Vu,v⊆Vi consists of sincere epibricks E with Eu,v∈E.
For E∈Vu,v, any brick E∈E different from Eu,v satisfies SuppE∈[[u,v]]∖{v} or SuppE∩[[u,v]]=∅. Moreover, Eu,v is the unique brick E∈E satisfying n∈SuppE and #SuppE=i.
Hence, we have a decomposition which is a disjoint union:
For any pair (u,v) satisfying n∈[[u,v]] and #[[u,v]]=i, there exists a bijection
given by
with inverse given by (E1,E2)↦E1∪E2∪{Eu,v}, where
Since there are isomorphisms of algebras,
we have #Vu,v=LSi−1⋅san−i,r. There exist exactly i pair (u,v) such that n∈[[u,v]] and #[[u,v]]=i, so we get #Vi=i⋅LSi−1⋅san−i,r. Finally, Theorem 3.4 implies
□
In particular, sbn,n=n∑i=1i⋅LSi−1⋅san−i,n=n∑i=1i⋅ai−1⋅san−i. Considering the generating function g(x)=∞∑n=1sbn,nxn, we obtain the following equality:
which implies sbn,n=n−1∑i=0(n−1i)(n+ii+1) [11, A002002].
Note that sbn,r is a linear combination of some san−i,r(i=1,2,⋯,r), we get the some recurrence relation on sbn,r with san,r.
Corollary 3.8.
Proof. It follows from the equations:
□
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
This paper is partially supported by National Natural Science Foundation of China (No.12301041).
Conflict of interest
The authors declare there is no conflicts of interest.











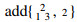 will be denoted by
will be denoted by  . Now, we list
. Now, we list  DownLoad:
DownLoad:

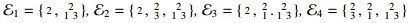 corresponding to four sincere right Schur subcategories
corresponding to four sincere right Schur subcategories  are not ICE-closed.
are not ICE-closed.