Analysis of a reaction-diffusion AIDS model with media coverage and population heterogeneity

1.   Introduction

Recently, neural networks (NNs) has received considerable attention from various fields of engineering and science, including secure communication, brain science and pattern recognition. As we know, Cohen-Grossberg NNs is a well-known network model, many famous networks like Hopfield NNs and Cellular NNs can be regarded as its special case. Since it was first proposed in 1983 ^[1], Cohen-Grossberg NNs has received increasing attention from different areas, such as neurobiology, pattern recognition and parallel computation. To better understand the application of Cohen-Grossberg NNs, the dynamical behavior of this network need to be further studied ^[2,3,4,5].

The second-order term in NNs is called inertial term. Physically, it represents the inductance in a neural circuit system ^[6,7]. It is known that, the inertial NNs have strong backgrounds from both biology and engineering ^[8,9]. The inertial term can arouse more complicated dynamical behavior to the systems, like chaos and bifurcations. Recently, the dynamical behavior of inertial NNs has become a hot topic both in theory and applications.

To cope with the effect caused by inertial (second-order) term, most of the previous literature use the variable translation to reduce the second-order system to first-order system. However, this approach may increase the system's dimension and add the complexity of analysis process. Due to this great shortage, it is necessary to propose a non-reduced order method to deal with the second-order system directly and some results have come out recently ^{[10,11,12,13]}. In ^[10], the asymptotic stabilization of inertial memristive NNs with mixed time delays is explored by non-reduced order method. In ^[12], by proposing a direct analysis method, the asymptotic stabilization of Cohen-Grossberg inertial NNs is investigated. In ^[13], a novel criteria is derived for global stabilization of delayed inertial MNNs, both feedback control and adaptive control are considered. However, these investigations only focus on the asymptotic stabilization, the corresponding results on finite-time or fixed-time stabilization have not been reported yet.

Memristor is considered as the fourth fundamental circuit element, which can memorize the passed amount of electronics ^[14,15]. Due to the function of memory, the memristor can be used to emulate the neural synapses with better performance than normal resistors ^{[16,17,18,19,20]}. Thus, by introducing the memristor into NNs, the memristive NNs (MNNs) is formulated. Recently, the research of dynamical behavior of MNNs has attracted various attention ^{[21,22,23,24,25,26]}. As we concern, the combination of inertial term and memristive connections can widen the application scope of our model.

In recent decades, a great many literatures have been published on asymptotic and exponential stabilization ^{[24,25,26,27,28]}. However, the convergence time of asymptotic stability tend to infinity, owing to the limited life span of engineering machines, the asymptotic stability is invalid for some applications. Hence, to overcome this shortage, the issue of finite-time stability is introduced, in which the system state is required to converge to zero in finite time. Also, the finite-time control shows strong robustness and fast convergence rate ^{[29,30,31,32,33,34]}. However, the settling time of finite-time control is dependent on initial information of system, which may be difficult to obtain some times. To overcome such shortage, the concept of fixed-time control is proposed later ^[36], in which the settling time can be computed without the knowledge of initial condition. Hence, fixed-time control shows great advantage among various areas ^{[37,38,39,40,41,42]}. As we considered, there are still no results on finite-time (fixed-time) stabilization of inertial Cohen-Grossberg NNs by non-reduced order approach. Thus, our research is novel and has a good application prospect.

Owing to the finite switching rate of amplifier, time delay is an unavoidable phenomenon in signal transmission and information processing. Due to the parallel pathways in NNs, there exists another type of time delay named distributed time delay. It is known that, mixed time delays can cause oscillation and instability to systems ^[25,26,31]. Thus, the stabilization of NNs with mixed time delays is a meaningful topic and deserves further discussion.

The main contribution of this work is as follows.

1) Different from the reduced-order method in ^[37,38], this paper uses a non-reduced order method to cope with the second-order Cohen-Grossberg neural networks. Novel criteria on finite-time (fixed-time) stabilization of inertial Cohen-Grossberg NNs are derived.

2) Two types of time delays are considered in this work: the time-varying delays and mixed time delays. To cope with such time delays, different types of feedback controllers and Lyapunov functionals are designed to solve the problem. Moreover, the memristive connections are taken into the network model, which gives a better application prospect.

3) The non-reduced order approach has been used to solve the asymptotic stabilization of inertial NNs in many previous literature. However, the finite-time or fixed-time stabilization problem has not been investigated by this approach yet. In this work, we extend the asymptotic stabilization to fixed-time stabilization by designing novel control schemes.

The contents of our work is as follows. In part 2, the preliminaries are introduced. The main results are given in part 3. Simulations are given to demonstrate our theorem in part 4. At last, the conclusion is achieved in part 5.

Notations. In this work, $\mathbb{R}$ denotes the real field. For any vector $\chi = (\chi_{1}, \cdots, \chi_{n})^{T}\in \mathbb{R}^{n}$, it is noted that $|\chi| = (|\chi_{1}|, \cdots, |\chi_{n}|)^{T}$. The vector norm is defined as $\|\chi\|_{1} = \sum\limits_{q = 1}^{n}|\chi_{q}|$. $sgn(\cdot)$ denotes the sign function. $C^{(1)}([-\tau, 0], \mathbb{R}^{n})$ denotes the family of continuous functions from $[-\tau, 0]$ to $\mathbb{R}^{n}$.

2.   Preliminaries

The model of inertial memristive Cohen-Grossberg NNs is as follows:

where $i = 1, \cdots, n$; $x_{i}(t)\in \mathbb{R}$ is the state value of $i$th neuron. $f_{j}(x_{j}(\cdot)), g_{j}(x_{j}(\cdot))\in\mathbb{R}$ denote the activation function satisfying that $f_{j}(0) = g_{j}(0) = 0$. $c_{i}(x_{i}(t))$ is the amplification function. $k_{i}(x_{i}(t))$ is the behaved function of the $i$th node satisfying $k_{i}(0) = 0$. $a_{ij}(x_{i}(t))$ and $b_{ij}(x_{i}(t))$ represent the memristor connection weights. $u_{i}(t)$ is the control input to achieve the stabilization goal. The time delay $\tau(t)$ satisfy $\dot{\tau}(t)\leq\rho < 1$ and $0\leq\tau(t) < \tau$, $\rho$, $\tau$ are positive numbers. The initial condition of system (2.1) is taken as $x_{i}(s) = \phi_{i}(s), -\tau\leq s\leq0$. According to the Kirchhoff's current law, the memristive connections are defined as:

where the switching jump $T_{i} > 0$, $\hat{a}_{ij}, \check{a}_{ij}, \hat{b}_{ij}, \check{b}_{ij}$ are known constants.

Remark 1. From the characteristic of memristors, the connection weights $a_{ij}(x_{i}(t)), b_{ij}(x_{i}(t))$ are state-dependent switched according to the state $x_{i}(t)$. Obviously, the righthand of Eq (2.1) is discontinuous. Hence, the solution is in the sense of Filippov.

Definition 1. (^[24]) Suppose $E\subseteq R^{n}$, then $x\mapsto F(x)$ is called a set-valued map from $E\mapsto R^{n}$, if for each point $x\in E$, there exists a nonempty set $F(x)\subseteq R^{n}$. A set-valued map F with nonempty values is said to be upper semicontinuous at $x_{0}\in E$, if for any open set N containing $F(x_{0})$, there exists a neighbourhood M of $x_{0}$ such that $F(M)\subseteq N$. The map $F(x)$ is said to have a closed image if for each $x\in E$, $F(x)$ is closed.

Definition 2. (^[24]) For the system $dx/dt = f(t, x)$, $x\in R^{n}$, with discontinuous right-hand sides, a set-valued map is defined as

where $\overline{co}[E]$ is the closure of the convex hull of set E, $B(x, \delta) = \{y:\|y-x\|\leq \delta\}$, and $\mu(N)$ is the Lebesgue measure of set N. A solution in Filippov's sense of the Cauchy problem for this system with initial condition $x(0) = x_{0}$ is an absolutely continuous function $x(t)$, $t\in [0, T]$, which satisfies the differential inclusion

Definition 3. ^[29] If there exists positive constant $T^{*}$ that depends (or not depend) on initial condition of system (2.1), such that

Then, the system (2.1) is said to achieve finite-time (or fixed-time) stabilization under control input $u_{i}(t)$.

Lemma 1. ^[29] Assume that the function $V(t)$ is continuous and nonnegative, if there is positive constant $q_{1}$ such that

for some $0 < \alpha < 1$. Then, $V(t) = 0$ for all $t\geq T_{0}$, and the settling time is

Lemma 2. ^[36] Assume that function $V(t)$ is continuous and nonnegative, if there are positive constants $q_{1}$ and $q_{2}$ such that

for some $0 < \alpha < 1, \beta > 1$. Then, $V(t) = 0$ for all $t\geq T_{\max}$, and the settling time is

Lemma 3. For constants $x_{1}, \cdots, x_{n}\geq0, 0 < p < 1, q > 1$, the following conditions hold.

3.   Main results

Assumption 1. Suppose there exists positive constants $l_{i}, h_{i}$ such that for any $x, y\in \mathbb{R}$

Assumption 2. Suppose there exists constants $0 < \underline{c}_{i}\leq\bar{c}_{i}$ and $0 < \underline{k}_{i}\leq\bar{k}_{i}$ such that for any $x\in \mathbb{R}$,

Remark 2. For convenience of discussion, we denote that: $\tilde{b}_{ij} = \max\{|\hat{b}_{ij}|, |\check{b}_{ij}|\}, \tilde{a}_{ij} = \max\{|\hat{a}_{ij}|, |\check{a}_{ij}|\}$.

To achieve the finite-time(or fixed-time) stabilization of system (2.1), the following feedback controller is designed.

where $\alpha, \beta, \xi_{i}, \eta_{i}, k_{1i}, k_{2i}, k_{3i}, k_{4i}, k_{5i}, k_{6i}$ are positive constants.

Theorem 1. Under Assumption 1 and 2, if the following conditions hold:

Then,

(1) When $0 < \alpha < 1$ and $0 < \beta < 1$, the system (2.1) can reach finite-time stabilization under controller (3.1), the settling time $T_{1}$ is

where $\tilde{q}_{1} = \min_{i\in\{1, \cdots, n\}}\{k_{1i}, k_{3i}, k_{5i}\}, \tilde{q}_{2} = \min_{i\in\{1, \cdots, n\}}\{k_{2i}, k_{4i}, k_{6i}\}$.

(2) When $0 < \alpha < 1$ and $\beta > 1$, the system (2.1) can reach fixed-time stabilization under controller (3.1), the settling time $T_{2}$ is estimated as

where $\tilde{q}_{1} = \min_{i\in\{1, \cdots, n\}}\{k_{1i}, k_{3i}, k_{5i}\}, \tilde{q}^{'}_{2} = (2n+n^{2})^{1-\beta}\min_{i\in\{1, \cdots, n\}}\{k_{2i}, k_{4i}, k_{6i}\}$.

Proof. Constructing the Lyapunov functional

Calculating the derivative along trajectory (2.1), we have

Then, it follows that

After calculation, we have

Thus, it can be derived that

When $0 < \alpha < 1, 0 < \beta < 1$, According to Lemma 3, we have

Then, we have

where $\tilde{q}_{1} = \min_{i\in\{1, \cdots, n\}}\{k_{1i}, k_{3i}, k_{5i}\}, \tilde{q}_{2} = \min_{i\in\{1, \cdots, n\}}\{k_{2i}, k_{4i}, k_{6i}\}$. It can be achieved that $V(t) = 0, t\geq T_{1}, T_{1} = \min\{\frac{V^{1-\alpha}\;(0)}{\tilde{q}_{1}(1-\alpha)}, \frac{V^{1-\beta}\;(0)}{\tilde{q}_{2}(1-\beta)}\}$. Hence, system (2.1) is finite-time stabilized with settling time $T_{1}$.

When $0 < \alpha < 1, \beta > 1$, according to Lemma 3, we have

Then, we have

where $\tilde{q}_{1} = \min_{i\in\{1, \cdots, n\}}\{k_{1i}, k_{3i}, k_{5i}\}, \tilde{q}^{'}_{2} = (2n+n^{2})^{1-\beta}\min_{i\in\{1, \cdots, n\}}\{k_{2i}, k_{4i}, k_{6i}\}$. Hence, we have $V(t) = 0, t\geq T_{2}, T_{2} = \frac{1}{\tilde{q}_{1}(1-\alpha)}+\frac{1}{\tilde{q}^{'}_{2}(\beta-1)}$. Thus, the fixed-time stabilization of system (2.1) can be obtained under feedback controller (3.1). The proof is finished.

Remark 3. The finite-time or fixed-time stabilization of second-order system has been investigated by reduced-order method in some previous papers ^{[32,33,34,37,38]}. For example, in ^[32,33,34], the finite-time synchronization of delayed inertial neural networks is investigated by integral inequality method and maximum value approach. However, the above results are achieved by reduced order method, there are still no results on finite-time (fixed-time) stabilization by non-reduced order method yet. Thus, the research gap is filled in this work.

Next, we consider the inertial memristive Cohen-Grossberg NNs with mixed time delays:

the memristive weights are defined as:

where the switching jump $T_{i} > 0$, $\hat{a}_{ij}, \check{a}_{ij}, \hat{b}_{ij}, \check{b}_{ij}, \hat{d}_{ij}, \check{d}_{ij}$ are known constants. The initial condition of system (3.15) is taken as $x_{i}(s) = \phi_{i}(s), -\tau\leq s\leq0$.

Assumption 3. Suppose there exists positive constants $\sigma, \bar{\sigma}$ such that

To achieve our control goal, the following feedback controller is proposed:

where $\tilde{a}_{ij} = \max\{|\hat{a}_{ij}|, |\check{a}_{ij}|\}, \tilde{b}_{ij} = \max\{|\hat{b}_{ij}|, |\check{b}_{ij}|\}, \tilde{d}_{ij} = \max\{|\hat{d}_{ij}|, |\check{d}_{ij}|\}$.

Theorem 2. Under Assumption 1, 2 and 3, if the following conditions hold:

Then,

(1) When $0 < \alpha < 1$ and $0 < \beta < 1$, the system (2.1) can reach finite-time stabilization under controller (3.17), the settling time $T_{1}$ is estimated as

where $\tilde{q}_{1} = \min_{i\in\{1, \cdots, n\}}\{k_{1i}, k_{3i}, k_{5i}, k_{7i}\}, \tilde{q}_{2} = \min_{i\in\{1, \cdots, n\}}\{k_{2i}, k_{4i}, k_{6i}, k_{8i}\}$.

(2) When $0 < \alpha < 1$ and $\beta > 1$, the system (2.1) can reach fixed-time stabilization under controller (3.17), the settling time $T_{2}$ is estimated as

where $\tilde{q}_{1} = \min_{i\in\{1, \cdots, n\}}\{k_{1i}, k_{3i}, k_{5i}, k_{7i}\}, \tilde{q}^{'}_{2} = (2n+2n^{2})^{1-\beta}\min_{i\in\{1, \cdots, n\}}\{k_{2i}, k_{4i}, k_{6i}, k_{8i}\}$.

Proof. Constructing the Lyapunov functional

Computing the derivative along trajectories (3.15), we have

It is obvious that

Then, we have

Case 1: When $0 < \alpha < 1$ and $0 < \beta < 1$,

where $\tilde{q}_{1} = \min_{i\in\{1, \cdots, n\}}\{k_{1i}, k_{3i}, k_{5i}, k_{7i}\}, \tilde{q}_{2} = \min_{i\in\{1, \cdots, n\}}\{k_{2i}, k_{4i}, k_{6i}, k_{8i}\}$.

Case 2: When $0 < \alpha < 1$ and $\beta > 1$,

where $\tilde{q}_{1} = \min_{i\in\{1, \cdots, n\}}\{k_{1i}, k_{3i}, k_{5i}, k_{7i}\}, \tilde{q}^{'}_{2} = (2n+2n^{2})^{1-\beta}\min_{i\in\{1, \cdots, n\}}\{k_{2i}, k_{4i}, k_{6i}, k_{8i}\}$. Following the same discussion in Theorem 1, the conclusion can be derived.

Remark 4. In this work, two types of time delays are considered. It is known that, mixed time delays may cause oscillation and instability of NNs. This may arouse more complex dynamical behavior in this network model. Moreover, the memristive connections is taken into our network, which gives a better application prospect. Compared with the previous literature ^[12], the model is more general and the results can be applied to wider application.

4.   Numerical examples

To verify the validity of the theoretical results, some simulations are provided in this part. First, we give the numerical example of Theorem 1.

Example 1. Consider the inertial memristive Cohen-Grossberg neural networks with 2 neurons as below

where $d_{1} = d_{2} = 0.5$, $f_{1}(v) = f_{2}(v) = v$, $g_{1}(v) = g_{2}(v) = \tanh(v)$, $c_{1}(v) = 0.8+\frac{0.4}{v^{2}+1}$, $c_{2}(v) = 1.2-\frac{0.3}{v^{2}+1}$, $k_{1}(v) = 1.5v$, $k_{2}(v) = 2v$, $\tau(t) = 0.5+0.5sin(t)$. The memristive connections are as below:

It is not difficult to check that $\underline{c}_{1} = 0.8, \overline{c}_{1} = 1.2, \underline{c}_{2} = 0.9, \overline{c}_{2} = 1.2$. $\underline{k}_{1} = 1.5, \overline{k}_{1} = 1.5, \underline{k}_{2} = 2, \overline{k}_{2} = 2$, $l_{1} = l_{2} = 1, h_{1} = h_{2} = 1$. Thus, the conditions in Assumption 1 and 2 are satisfied. Choose the feedback control gains as $\xi_{1} = 6, \xi_{2} = 6, \eta_{i} = 1, k_{1i} = k_{2i} = k_{3i} = k_{4i} = k_{5i} = k_{6i} = 1$. Thus, the condition in Theorem 1 is satisfied.

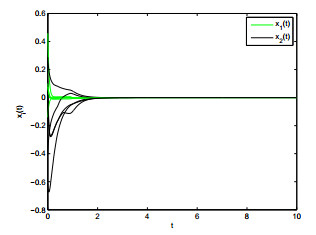
Case 1: Let $\alpha = 0.5$, $\beta = 0.5$. By case 1 of Theorem 1, the system (4.1) can reach finite-time stabilization under control. The settling time is estimated as:

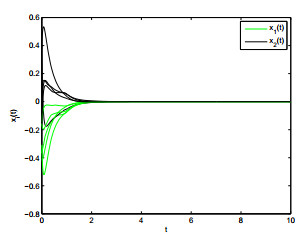
where $\tilde{q}_{1} = \min_{i\in\{1, \cdots, n\}}\{k_{1i}, k_{3i}, k_{5i}\} = 1, \tilde{q}_{2} = \min_{i\in\{1, \cdots, n\}}\{k_{2i}, k_{4i}, k_{6i}\} = 1$. Choose 5 random initial values in interval $[-0.8, 0.8]$, the state trajectories of system (4.1) is plotted in Figure 1. It is obvious that the state trajectories converge to origin point in a finite time.

Case 2: Let $\alpha = 0.5$, $\beta = 1.5$. By case 2 of Theorem 1, the system (4.1) can reach fixed-time stabilization under control. The settling time is estimated as:

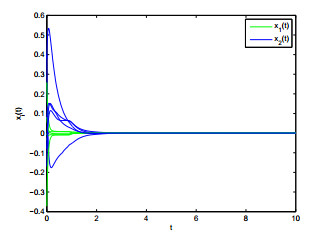
where $\tilde{q}_{1} = \min_{i\in\{1, \cdots, n\}}\{k_{1i}, k_{3i}, k_{5i}\} = 1, \tilde{q}^{'}_{2} = (2n+n^{2})^{1-\beta}\min_{i\in\{1, \cdots, n\}}\{k_{2i}, k_{4i}, k_{6i}\} = 0.35$. Choose 5 random initial values in interval $[-0.8, 0.8]$, the state trajectories of system (4.1) is plotted in Figure 2. Therefore, the validity of Theorem 1 is demonstrated.

Secondly, we consider the case of Theorem 2.

Example 2. Consider the inertial memristive Cohen-Grossberg NNs with mixed time delays as below

where $d_{1} = d_{2} = 0.5$, $f_{1}(v) = f_{2}(v) = v$, $g_{1}(v) = g_{2}(v) = \tanh(v)$, $c_{1}(v) = 0.8+\frac{0.4}{v^{2}+1}$, $c_{2}(v) = 1.2-\frac{0.3}{v^{2}+1}$, $k_{1}(v) = 1.5v$, $k_{2}(v) = 2v$, $\tau(t) = 0.3+0.4sin(t)$, $\sigma(t) = 0.6+0.4\cos(t)$, thus $\tau = 0.7, \dot{\tau}(t)\leq\rho = 0.4\leq1, \bar{\sigma} = 1, \sigma = 0.4$. The memristive connections are as below:

Choose the feedback control gains as $\xi_{1} = \xi_{2} = 8.8, \eta_{i} = 1, k_{1i} = k_{2i} = k_{3i} = k_{4i} = k_{5i} = k_{6i} = k_{7i} = k_{8i} = 1$. Thus, the conditions in Theorem 2 are satisfied.

Case 1: Let $\alpha = 0.5$, $\beta = 0.5$. By case 1 of Theorem 2, the system (4.6) can reach finite-time stabilization. The settling time is estimated as:

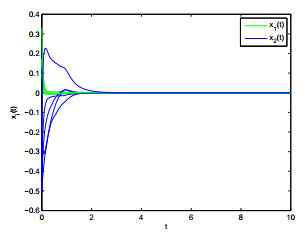
where $\tilde{q}_{1} = \min_{i\in\{1, \cdots, n\}}\{k_{1i}, k_{3i}, k_{5i}, k_{7i}\} = 1, \tilde{q}_{2} = \min_{i\in\{1, \cdots, n\}}\{k_{2i}, k_{4i}, k_{6i}, k_{8i}\} = 1$. Choose 5 random initial values in interval $[-0.6, 0.6]$, the state trajectories of system (4.6) is plotted in Figure 3.

Case 2: Let $\alpha = 0.5$, $\beta = 1.5$. By case 2 of Theorem 2, the system (4.6) can reach fixed-time stabilization. The settling time is estimated as:

$\tilde{q}_{1} = \min_{i\in\{1, \cdots, n\}}\{k_{1i}, k_{3i}, k_{5i}, k_{7i}\} = 1, \tilde{q}^{'}_{2} = (2n+2n^{2})^{1-\beta}\min_{i\in\{1, \cdots, n\}}\{k_{2i}, k_{4i}, k_{6i}, k_{8i}\} = 0.29$. Choose 5 random initial values in interval $[-0.6, 0.6]$, the state trajectories of system (4.6) is plotted in Figure 4. Thus, the validity of Theorem 2 is demonstrated.

5.   Conclusion

By designing novel control scheme and constructing Lyapunov functional, this work proposed a non-reduced order method to deal with the finite-time (fixed-time) stabilization problem of second-order memristive Cohen-Grossberg neural networks. Compared with the traditional reduced-order approach, the method adopted in this paper can simplify the analysis process and solve the control problem of second-order system directly. Two kinds of time delays: time-varying delays and mixed time delays are taken into consideration. Then, two criteria are derived to ensure the finite-time (fixed-time) stabilization of inertial Cohen-Grossberg NNs. Lastly, simulations are presented to verify the validity of our results.

In our future study, we will try to extend our results to complex-valued and quaternion-valued field.

Acknowledgments

This research was supported by National Natural Science Foundations of China (No. 11861060).

Conflict of interest

The authors declare that they have no competing interests.