Modeling the co-infection of HTLV-2 and HIV-1 in vivo

1.   Introduction

MDS is a common disorder of the hematologic system that often manifests as a hematopoietic stem cell disorder with somatic cell mutations, bone marrow cell dysplasia and ineffective hematopoiesis, in which dysregulation of hematopoietic cells and immune function is the primary etiology of the disease, and the greatest risk factor for the development of MDS is advanced age, with the median age of MDS onset being approximately 70 years [1]. In the process of aging, the immune and hematopoietic systems will gradually become dysfunctional and their functions will decline, and the inherent disorders of innate immune and inflammatory pathways will cause hematopoietic cell senescence [2]. Senescence is a cellular process characterized by stable growth arrest and functional deterioration that is associated with many chronic and age-related diseases. It has been found that both cellular senescence and tumorigenesis are the result of accumulated cellular damage [3]. Cellular senescence can prevent both tumor cell proliferation and promote tumor growth. There is growing evidence that cellular senescence is associated with the pathogenesis and development of hematologic malignancies, and MDS pathophysiology involves multiple factors, the most important of them is aging, because somatic mutations in hematopoietic cells that contribute to clonal proliferation are often acquired throughout human aging. [4]. In addition, as the immune system declines with age, senescence becomes increasingly prominent in the immune microenvironment; therefore, a series of therapeutic strategies targeting cellular senescence have been gradually developed, including induction of cellular senescence [5] and elimination of senescent cells [6]. In this paper, we use bioinformatics and machine learning methods to mine ARGs, elucidate the role of cellular senescence in tumorigenesis and potential clinical applications, reveal the relationship between the immune microenvironment and senescence in MDS, and develop ideas for the design of rational therapeutic strategies for MDS.

2.   Materials and methods

2.1.   Data collection and preprocessing

GSE4619, GSE2779 and GSE19429 datasets were obtained from the Gene Expression Omnibus database (https://www.ncbi.nlm.nih.gov/geo/). The GSE2779 and GSE19429 datasets were combined using the R package “inSilicoMerging” [7]. The GSE2779 and GSE19429 datasets were combined, and the batch effect using the ComBat technique was removed using the R package “sva” [8] for the training and testing cohorts. As an external validation dataset, the GSE4619 dataset was used. Table S1 lists 307 ARGs derived from the Human Senescence Genome Repository (https://genomics.senescence.info/genes/index.html). In GSE180298, 10 scRNA-seq data were acquired from 4 MDS samples.

2.2.   Identification of differentially expressed ARGs (DE-ARG)

The intersection of MDS genes and 307 ARGs was obtained using the R package “limma” [9], and the differentially expressed genes were filtered out using the standard expression of |log2-fold change (FC)| > 0.4 and p-value <0.05 to obtain 11 DE-ARGs. The volcano map and heat map were made using the R packages “ggplot11” and “pheatmap”, respectively, for visualizing DE-ARGs. To reveal clusters of samples with the first two components, principal component analysis (PCA) was used on DE-ARG, utilizing the R package “factoextra” (https://cloud.r-project.org/package=factoextra/). Following that, a protein-protein interaction (PPI) network was built, and gene interactions between DE-ARGs were evaluated by STRING (https://cn.string-db.org/) [10] with a confidence score of greater than 0.4.

2.3.   Functional enrichment of differentially expressed ARGs (DE-ARG)

Using the Metascape (https://metascape.org/gp/index.html) website, the “clusterProfiler” [11] and “enrichplot” [12] were utilized. R packages were used to perform functional and pathway enrichment analysis of DE-ARG, including gene ontology (GO) terminology, Kyoto Encyclopedia of Genes and Genomes (KEGG) pathway analysis and disease ontology (DO) analysis.

2.4.   Identify hub ARG by integrating 3 machine learning algorithms

The logistic regression, support vector machine recursive feature elimination (SVM-RFE) and random forest (RF) techniques were used to identify collectors using the R packages “glmnet” [13], “e1071” [14] and “randomForest” [15] to filter ARGs. To find the optimal tuning parameter for LASSO, 10 cross-validations were performed (λ). SVM is a widely used monitoring machine learning algorithm for classification and regression analysis. To avoid overfitting, the RFE algorithm is used to filter the training cohort for the best genes in the training cohort. As a result, SVM-RFE is utilized to find the set of genes with the greatest discriminative strength. RF analysis is an appropriate approach since there are no constraints on changeable conditions and it has higher accuracy, sensitivity and specificity. To identify hub ARGs, univariate logistic regression was also used. Finally, seven genes that overlapped between the three machine learning algorithms were identified as hub ARGs.

2.5.   Artificial neural network model construction and validation based on MDS-related hub ARG

The key component of deep learning associated with artificial intelligence is ANN. ANN models are built using the R package “neural network” and the training queue [16]. The training data goes through processing before being fed into the ANN model, which includes seven input layers, five hidden layers and two output layers. The R package “Caret” [17] is used to perform 5-fold cross-validation on the ANN model to reduce overfitting and improve the model. Furthermore, subject job characteristics and decision curve analysis (DCA) were employed to confirm the ANN model's accuracy and clinical importance. Following that, the classification models (classifiers) based on hub-ARGs were validated in the same way on both the internal training set and the external validation dataset.

2.6.   Correlation analysis of hub-ARGs with immune features

Cell type identification (CIBERSORT) was determined for 1000 iterations using the “iobr” R [18] package to estimate relative subsets of RNA transcripts for assessing the proportion of assumed immune cells in MDS tissue. To ensure the trustworthiness of the deconvolution technique, samples with CIBERSORT p-values of 0.05 were chosen for further study. Following that, Spearman correlation coefficients for the fraction of potential immune cells between central ARGs were obtained.

2.7.   Identification of senescent expression isoforms and functional enrichment analysis

Based on the expression patterns of 307 ARGs, the unsupervised clustering technique was utilized to identify distinct senescence expression isoforms. A total of 1000 iterations were done to control the robustness of clustering, with each iteration having 80% of the samples. The preceding procedure was carried out using the R package “ConsensuClusterPlus” [19]. To determine the ideal number of clusters, cumulative distribution function (CDF) curves of consensus scores were employed. Genetic distribution of subtypes is assessed by PCA. The Wilcox test was used to examine the expression of the critical ARG between two aging-associated subgroups. The gene set variation analysis (GSVA) [20] method was used to study pathway differences in each subtype, and the single sample gene enrichment analysis “ssGSEA” [21] technique was utilized to evaluate immune function differences between the two subtype houses.

2.8.   Identification of senescence phenotype-associated gene modules

To find genes in modules linked with the aging phenotype, the R package “WGCNA” was utilized [22]. The association between genes characterizing the module and the aging phenotype correlation pattern was displayed using the R package “ggplot2” [23], after determining the power 9 of the gene dendrogram and the minimum size (genome) of 30. The genes in the key module were classified as senescence phenotype-related genes because they had the highest correlation coefficient and the most significant p-value. Metascape also performed functional enrichment analysis on the most relevant genes in the modules to identify GO and KEGG pathways.

2.9.   Single-cell sequencing data processing

To keep cellular data of great quality, we utilized the R package “harmony” to remove batch effects between samples [24]. Using the “Seurat” R package [25], the scRNA-seq data were normalized using the “NormalizeData” function. The normalized scRNA-seq data were then turned into Seurat objects, with the “FindVariableFeatures” algorithm identifying the first 2000 highly variable genes. Then, we used the “RunPCA” function of the “Seurat” R package to perform principal component analysis (PCA) on the top 2000 genes to minimize the dimensionality of the scRNA-seq data. We identified important PCs using JackStraw analysis and chose relevant PCs for cell clustering analysis based on the proportion of variance. Cells were shown using the UAMP approach after the integrated data was clustered using the “FindNeighbors” and “FindClusters” functions. The “scran” R package's “FindAllMarkers” and “FindMarkers” functions were used to perform Wilcoxon tests between pairs of cell clusters to find genes that were specifically expressed in each cluster. We utilized the R package “SingleR” [26] and an annotation of cell types from a prior study [27]. Using a multi-genomic enrichment approach, the “irGSEA” R package (https://github.com/chuiqin/irGSEA/) can score individual cells and generate a multi-genomic enrichment score matrix. The Wilcoxon test is subsequently applied to each gene set to compute the set of genes with differential expression in the enrichment score matrix. The “tricycle” R software, which scores each cell according to the expression of G2/M and S-phase marker genes, is a recent approach for calculating the cell cycle [28].

3.   Results

3.1.   Preprocessing and analysis of variance of GEO expression data

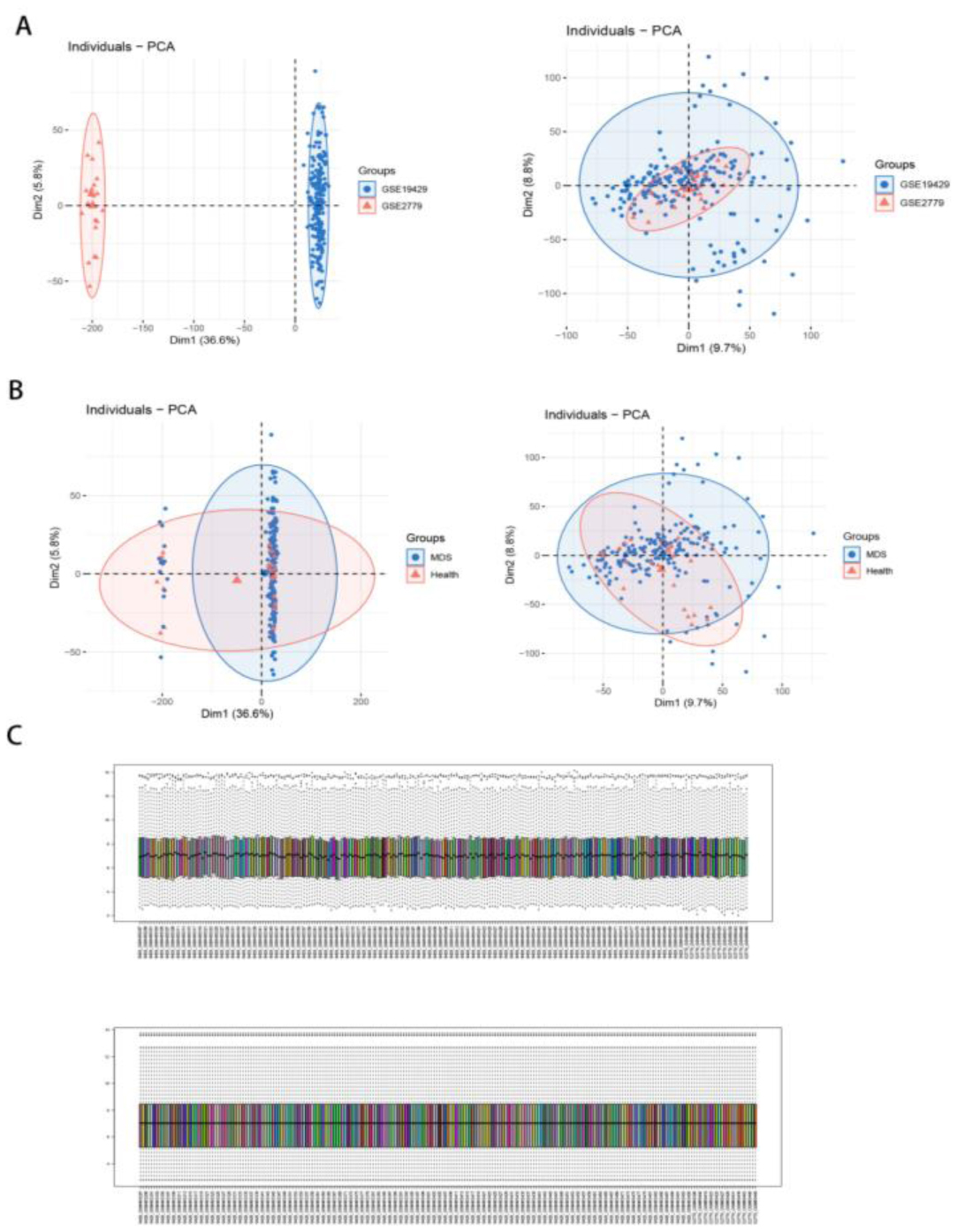
First, we used quantile normalization to standardize the gene expression data from GSE19429 and GSE2779 before merging the datasets with the R package ‘sva’ to avoid batch effects. Figure 1A depicts the principal component analysis of the two datasets before and after treatment. As depicted in the figure, the two datasets were initially separated without any intersection. Then, the intersection of the two datasets can be used as a batch for further analysis. The results of principal component analysis for the healthy and endometriosis groups in the dataset are shown in Figure 1B. Figure 1C depicts a box plot of the two datasets after normalization, with different colors representing different samples and columns representing gene expression values in the samples. Finally, using the pooled dataset, we ran illness differential gene analysis and took the intersection with the aging genes.

Figure 1.  Preprocessing and analysis of variance of GEO expression data. (A,B) Principal component analysis of MDS data types and clinical characteristics before and after de-batching. (C) Box plots of the raw data normalized between samples.

DownLoad: Full-Size Img PowerPoint

3.2.   Differential analysis of aging related genes in the GEO matrix

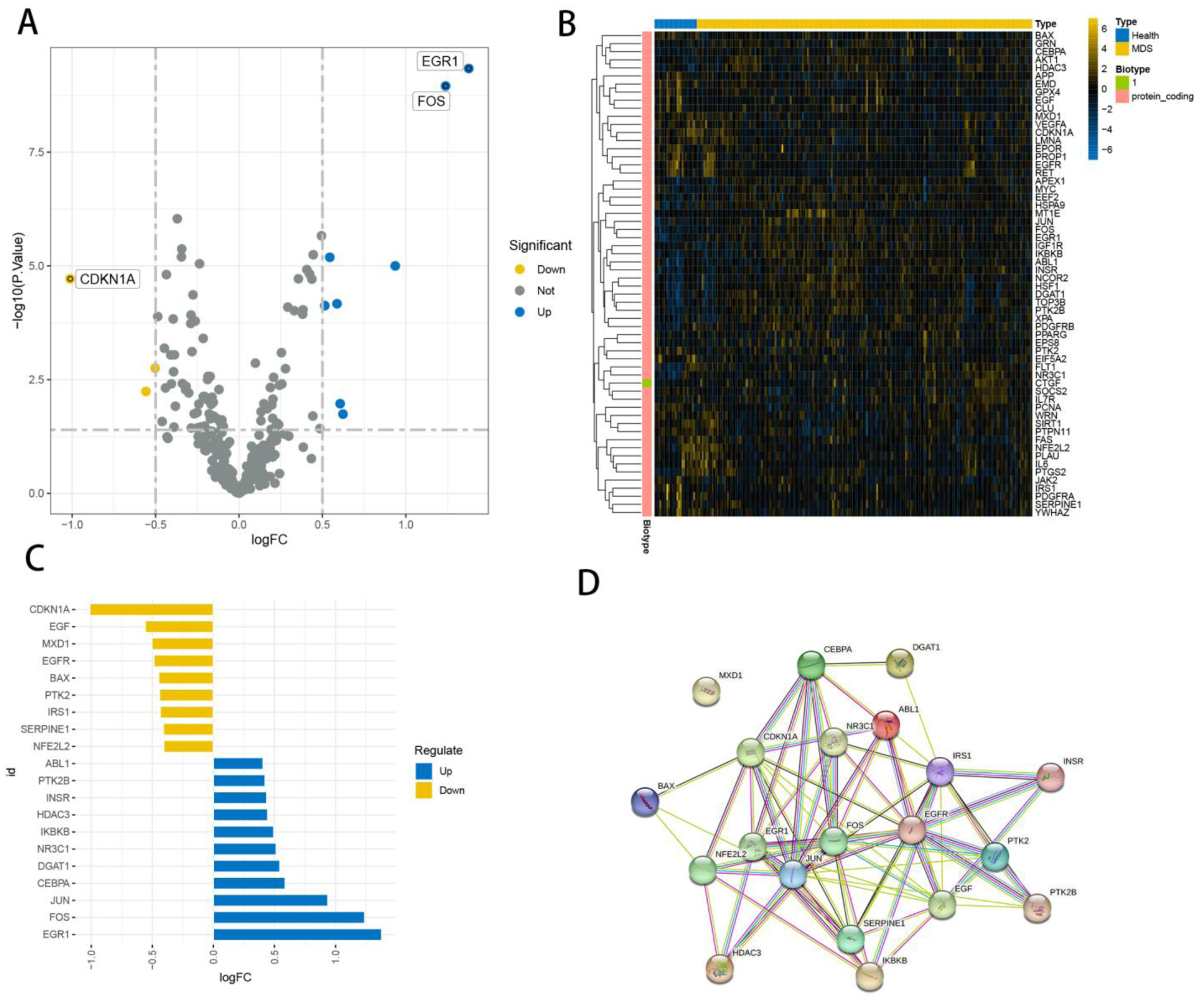
The intersection of the two data sets, as illustrated in the picture, can be used as a batch of data for further analysis. Using the criteria of P-adjustment 0.05 and log₂|fold-change(FC)| > 0.5, a total of 20 genes were identified as DEGs. The volcano and deviation plots reveal 9 down-regulated genes and 11 up-regulated genes, with CDKN1A, EGR1 and FDS showing the greatest differences (Figure 2A,C). Figure 2B depicts a heat map of the top 50 DEG genes. Finally, we searched the STRING database for Protein-Protein Interaction Networks (PPI, Protein-Protein Interaction Networks), which are networks of proteins that interact with one another to participate in biological signaling, gene expression regulation, energy and material metabolism and cell cycle progression (Figure 2D). The PPI is composed of proteins that interact with one another to engage in several life processes such as biological signaling, gene expression regulation, energy and material metabolism and cell cycle regulation, and it may have significant implications for sickness.

Figure 2.  Differential analysis of aging related genes in the GEO matrix. (A) Volcano diagram of DE-ARGs, (B) heat map, (C) deviation map and (D) PPI network diagram of DE-ARGs.

DownLoad: Full-Size Img PowerPoint

3.3.   GO, KEGG and DO enrichment analysis of aging genes

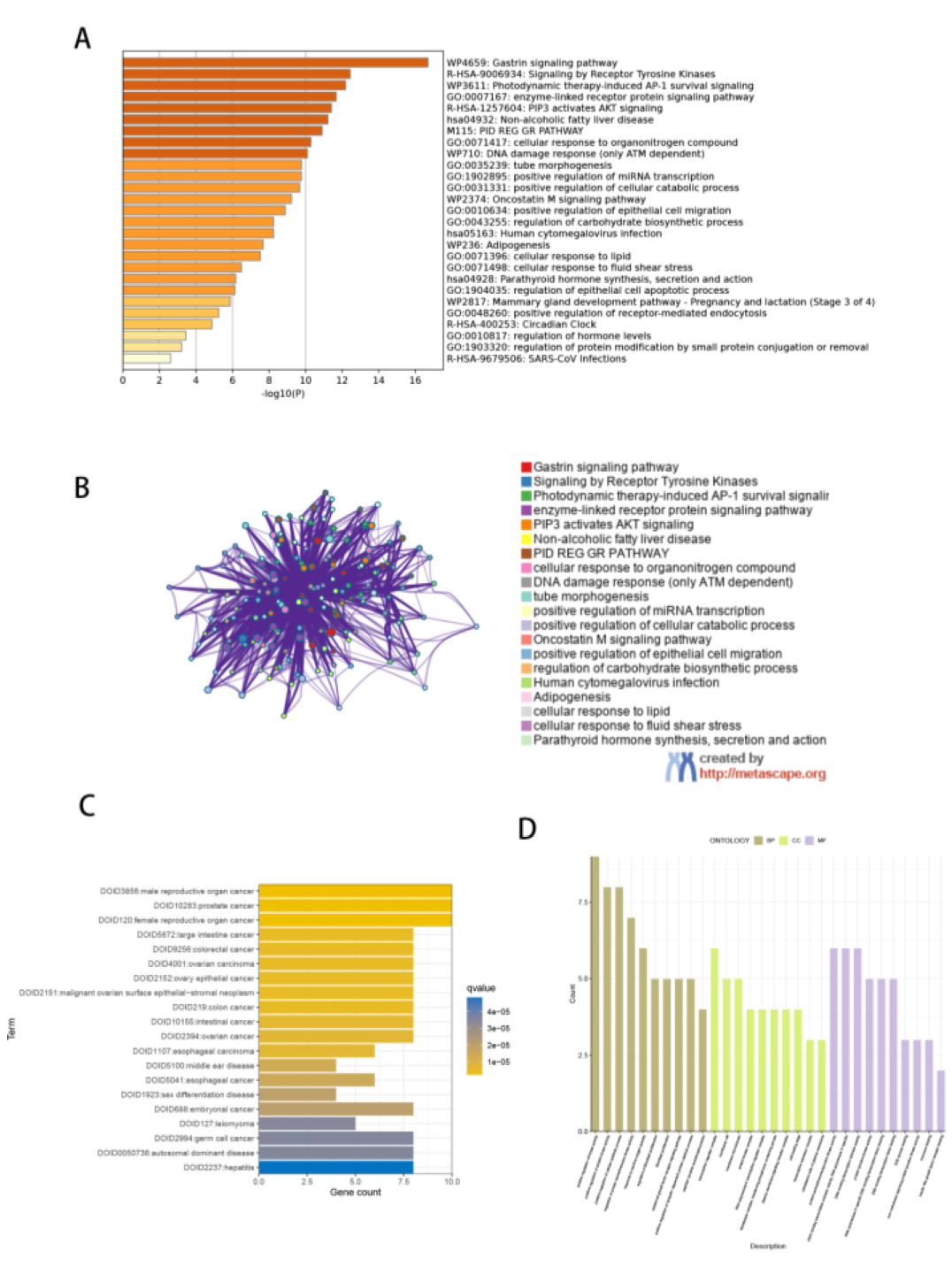
We performed a combined analysis of multiple enrichment methods such as KEGG and GO through the metascape library to gain insight into the role of the 20 differentially expressed genes and discovered functional enrichment in aging genes, hormone level regulation and positive regulation of receptor-mediated endocytosis and other pathways and pathways (Figure 3A,B). We used p-value 0.01 and q-value 0.05 as thresholds to identify items that were considerably enhanced. To further investigate the biological activities of the differential genes, we used GO functional analysis and DO disease analysis. DO study revealed sex differentiation illness and numerous tumor connections (Figure 3C). The response to fibroblast proliferation and the signaling pathway of the epidermal growth factor receptor were examples of biological processes (BP). The transcription repressor complex and the cytoplasmic side of the plasma membrane are examples of cellular components (CC). DNA-binding transcription factor binding and other molecular functions (MF) include DNA-binding transcription activator activity in Figure 3D. In conclusion, distinct genes have a big effect on the cell, and variable genes significantly affect the pathways and activities involved in cellular signal reception and may likely play a substantial part in disease causes.

Figure 3.  GO, KEGG and DO enrichment analysis of aging genes. (A) Histogram and (B) network diagram of DE-ARGs enrichment were obtained by metascrape database analysis. (C) GO and (D) DO analyses revealed the enriched biological functions of differentially expressed gene profiles.

DownLoad: Full-Size Img PowerPoint

3.4.   Three machine learning algorithms for screening signature genes

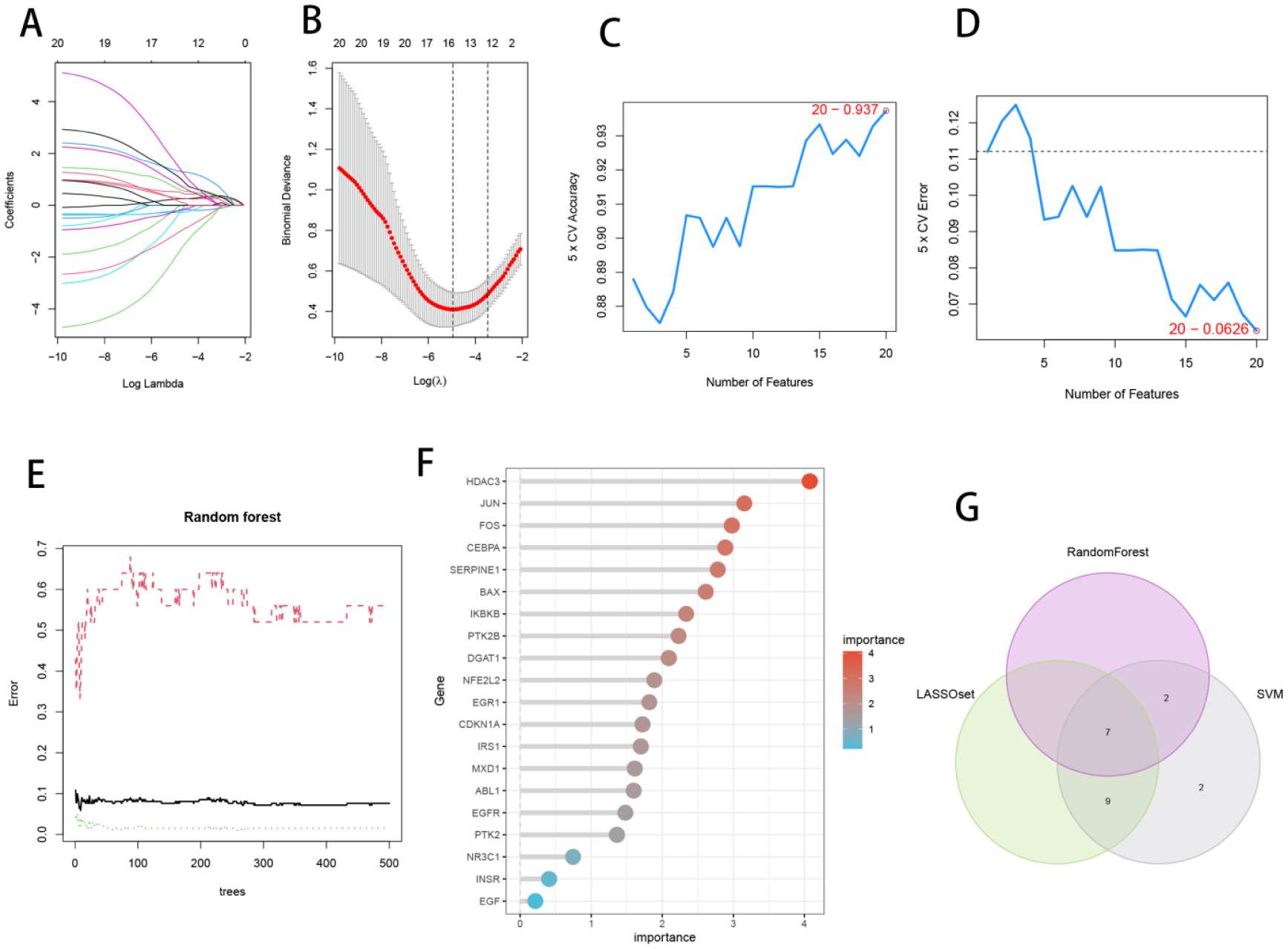
To identify feature genes among differentially expressed genes linked with critical MDS development and aging processes, the LASSO, random forest and SVM-RFE algorithms were used. After cross-validation, we utilized the LASSO algorithm's minimum criterion for creating the LASSO classifier to identify 16 feature genes (Figure 4A,B). The error in SVM-RFE was lowest when the number of features was 20 (Figure 4C,D), hence 20 relevant feature genes were obtained. The top 9 genes with relevance larger than 0.2 were chosen from the classification tree findings using RandomForest feature selection (Figure 4E,F). Seven feature genes shared by the LASSO, RandomForest and SVM-RFE algorithms were eventually identified using crossover, including FOS, IKBKB, HDAC3, JUN, PTK2B, CEBPA and BAX, and their associations were illustrated by VENN plots (Figure 4G).

Figure 4.  Three machine learning algorithms for screening signature genes. (A) Tenfold cross-validation of tuning parameter selection in the LASSO model. Each curve corresponds to one gene. (B) Lasso coefficient curves. The genes are ranked according to their relative importance. The solid vertical line indicates the partial likelihood deviation SE. The dashed line is drawn at the best λ. (C,D) Biomarker signature gene expression validation by support vector machine recursive feature elimination method (SVM-RFE). (E) Relationship between the number of trees and error rate in random forests. (F) Gene importance ranking. (G) Venn diagram of candidate genes common to LASSO, random forest and SVM-RFE algorithms.

DownLoad: Full-Size Img PowerPoint

3.5.   Development and validation of the 3-ARG-based ANN model and Nomogram

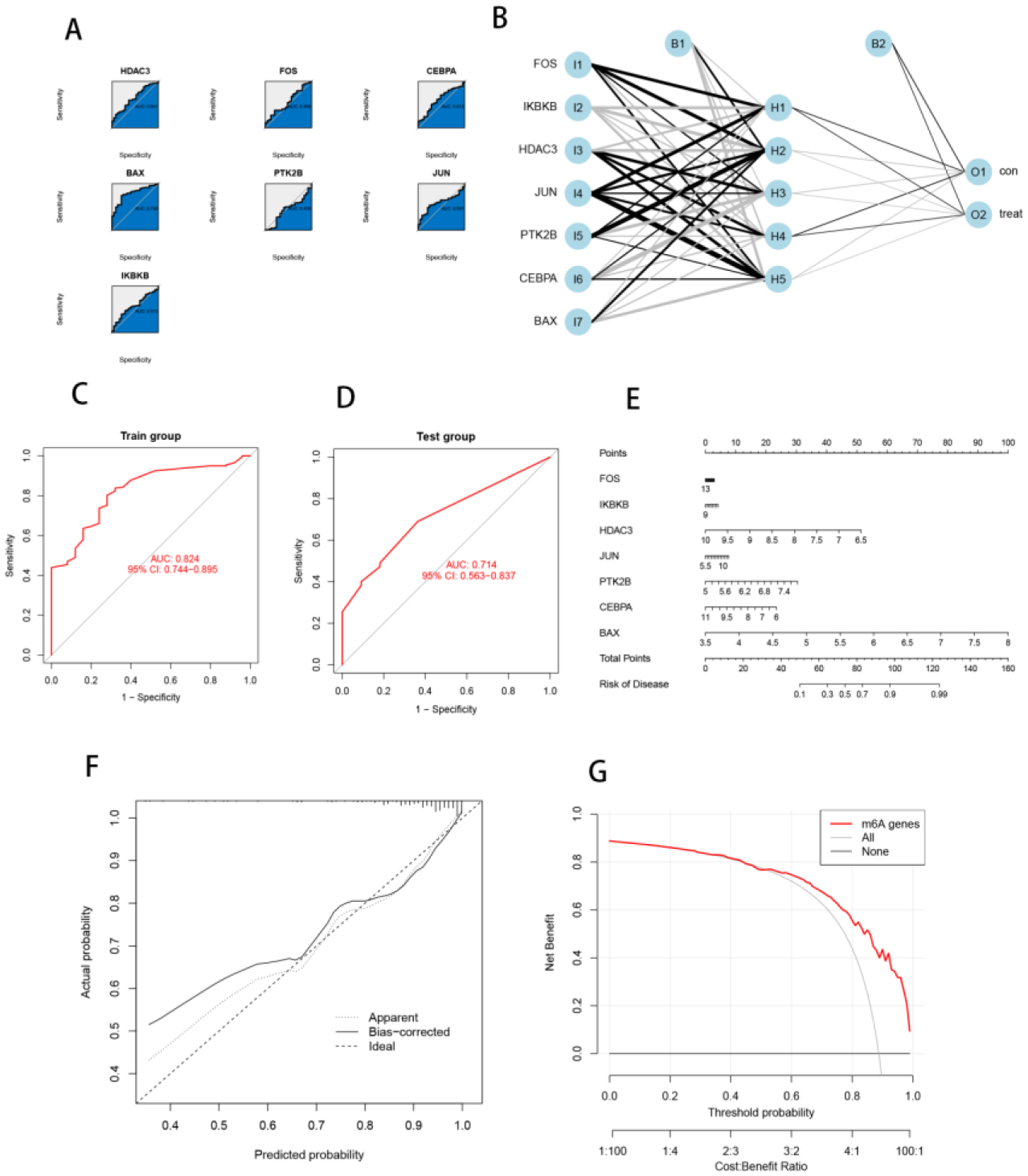
When we used these 7 feature genes separately for MDS prediction, we observed that the ROC values were not sufficient (Figure 5A). Finally, we chose 7 critical ARGs to build an ANN model with hidden layer number 5 for clinical MDS diagnosis prediction (Figure 5B). ROC curves confirmed the prediction model's satisfactory reliability and accuracy, with AUC values more than 0.70 obtained in both the training (AUC = 0.842) and validation cohorts (AUC = 0.714) (Figure 5C,D). We also displayed the Nomogram (Figure 5E) to help with the clinical use of the three ARG biomarkers in this investigation. To predict the likelihood of disease in EM patients, the Nomogram plot was used to construct patient scores based on the expression data of three biomarkers. Furthermore, both DCA curves and calibration curves demonstrated greater net benefit and accuracy in diagnosing EM patients using Nomogram (Figure 5F,G).

Figure 5.  Development and validation of the 3-ARG-based ANN model and Nomogram. (A) Roc curves of 7-ARGs for disease prediction. (B) Artificial neural network plot. (C) Internal training group ROC curves. (D) External validation group ROC curves. € Nomogram graph constructed using candidate genes. (F) Calibration curve of nomogram graph and (G) DCA curve.

DownLoad: Full-Size Img PowerPoint

3.6.   Detection of immunological features in MDS and normal samples

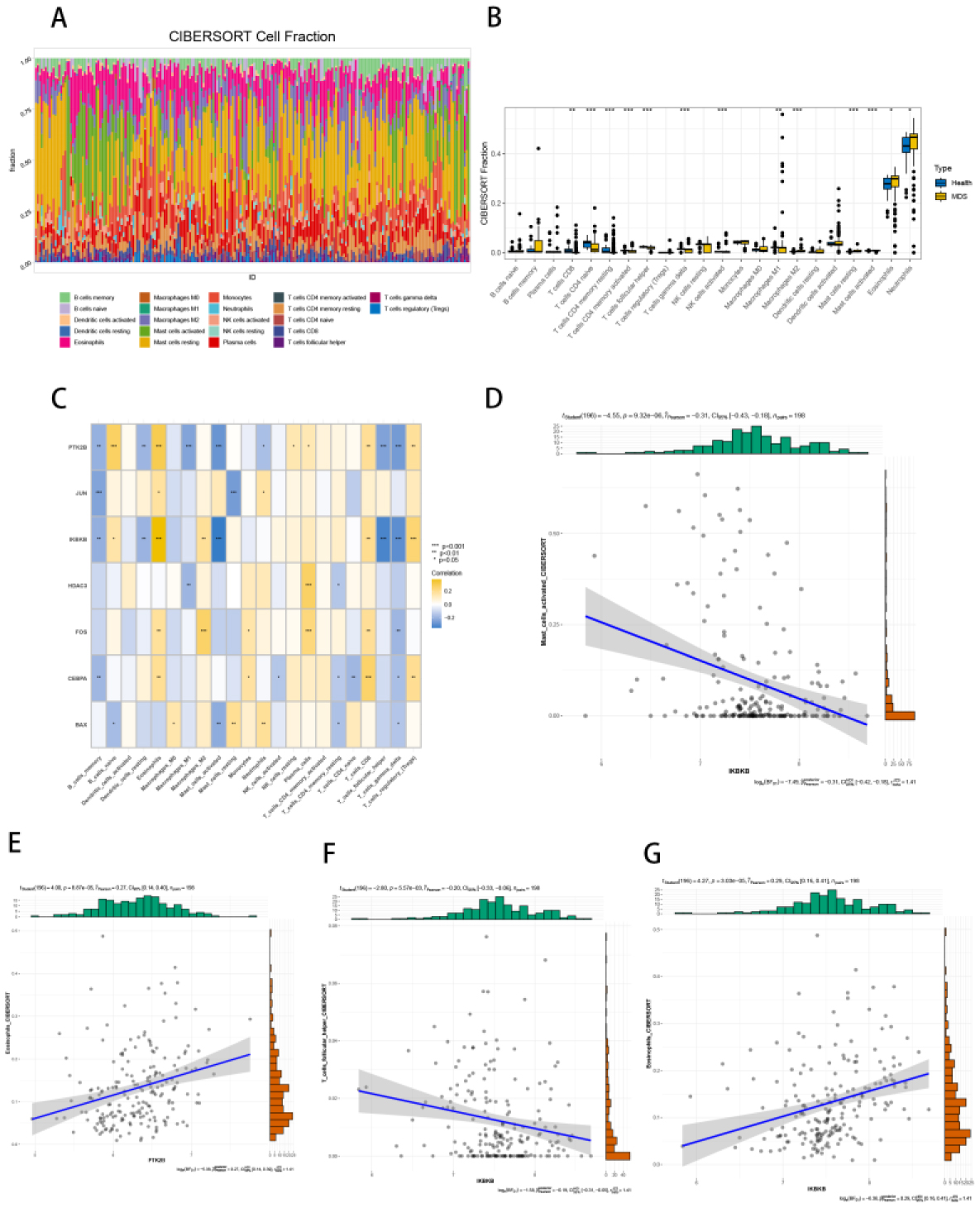
Immune cells play an important part in the disease's development and final regression, and an excess of immune cells in an aberrant immunological milieu is thought to have a role in the pathogenesis of MDS. The CIBERSORT algorithm in “IOBR” was used to compute the fraction of 22 immune cell infiltrates in MDS tissues. A stacked plot (Figure 6A) with a sum of all immune cell proportions of 1 was used to fully show the distribution of immune infiltrates in MDS tissue, and a significant increase in immune cells, such as mast cell resting phase and neutrophils, and a significant decrease in immune cells such as T-cell CD8 and T-cell CD4 naive phase, were observed in patients (Figure 6B). Furthermore, the “Spermanent” approach was used to investigate the connection between 7 ARG and immune cells (Figure 6C), and scatter plots were created between genes with strong correlation and immune cells (Figure 6D–G).

Figure 6.  Detection of immunological features in MDS and normal samples. (A) Immune infiltration stacking map. (B) Comparison of immune cell content between MDS patients and control samples. (C) Correlation of 7-ARGs with immune cells. (D) Scatter plot of the correlation between IKBKB and Mast_cells_activated. (E) Scatter plot of the correlation between PTK2B and Eosinophils. (F) Correlation scatterplot of IKBKB and T_cells_follicular_helper. (G) Correlation scatterplot of IKBKB and Eosinophils.

DownLoad: Full-Size Img PowerPoint

3.7.   Two aging expression isoforms were identified based on the aging gene

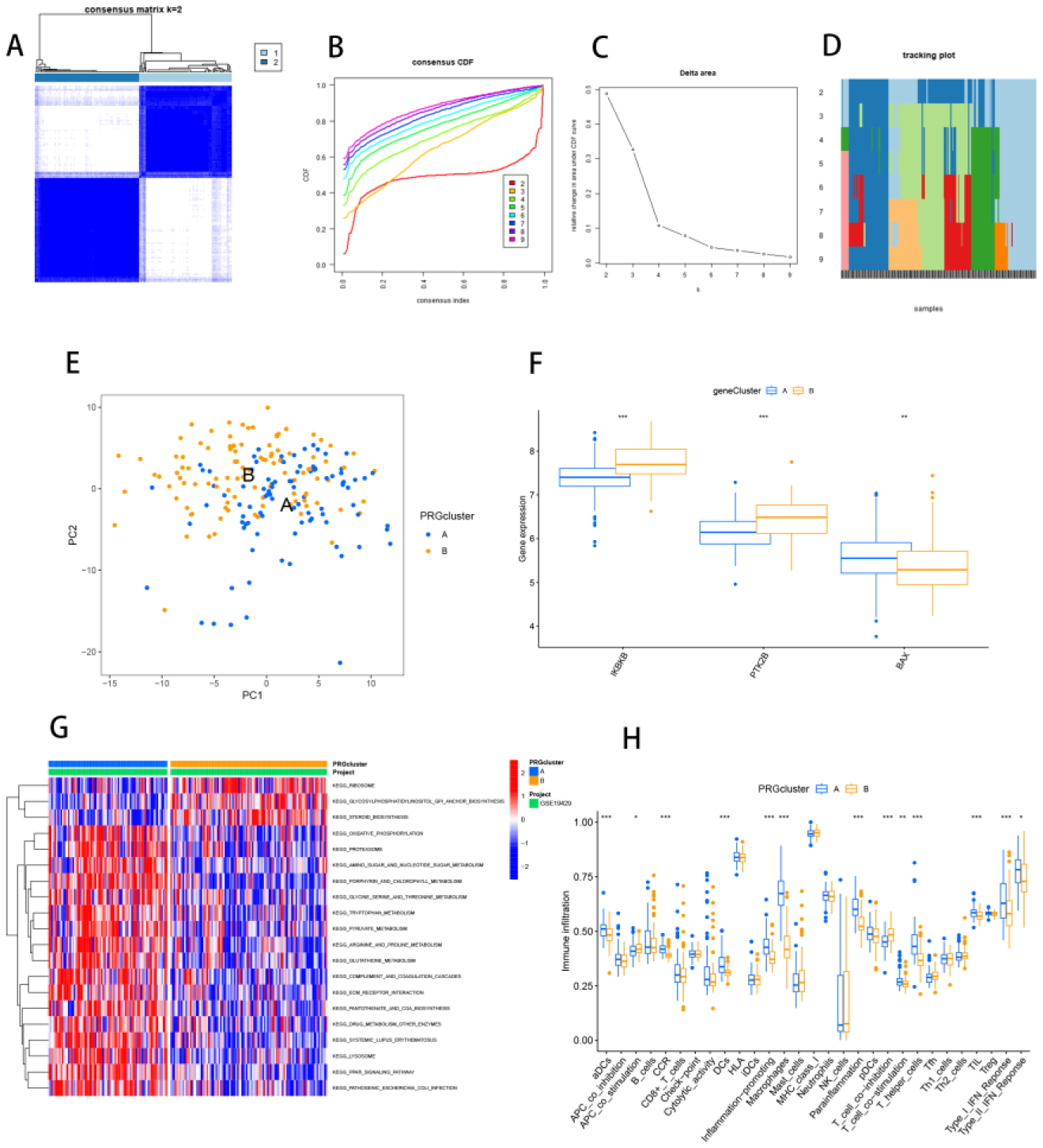
To investigate the relationship between marker genes and the prognosis of patients with different subtypes of MDS, a consensus clustering analysis based on expression levels of aging genes was performed using the “ConsensionClusterPlus” R package. When k = 2, the color-coded heat map of the consensus matrix showed high intra-group correlation and low inter-group correlation (Figure 7A), and the CDF curve, Delta area and tracking plot plots could strongly suggest that cluster (Figure 7B–D). The PCA method revealed considerable differences between the two categories. Patients in clusters A and B differ greatly from one another (Figure 7E). There were considerable metabolic variations in gene expression across clusters A and B (Figure 7F). Pathway analysis and immune infiltration analysis of the clusters revealed that enrichment in cluster A resulted in more pathways and higher immune infiltration (Figure 7G,H).

Figure 7.  Two aging expression isoforms were identified based on the aging gene. (A) Clustering plot of MDS patient samples. (B) CDF curve. (C) Delta area. (D) Tracking plot. (E) PCA plot of two subgroups. (F) Box line plot of the difference in expression of hub ARGs in two clusters. (G) Heat map of the difference in GSEA in two clusters. (H) Box line plot of the difference in immunity in two clusters.

DownLoad: Full-Size Img PowerPoint

3.8.   WGCNA identifies MDS high relevance modules and analyzes related functions

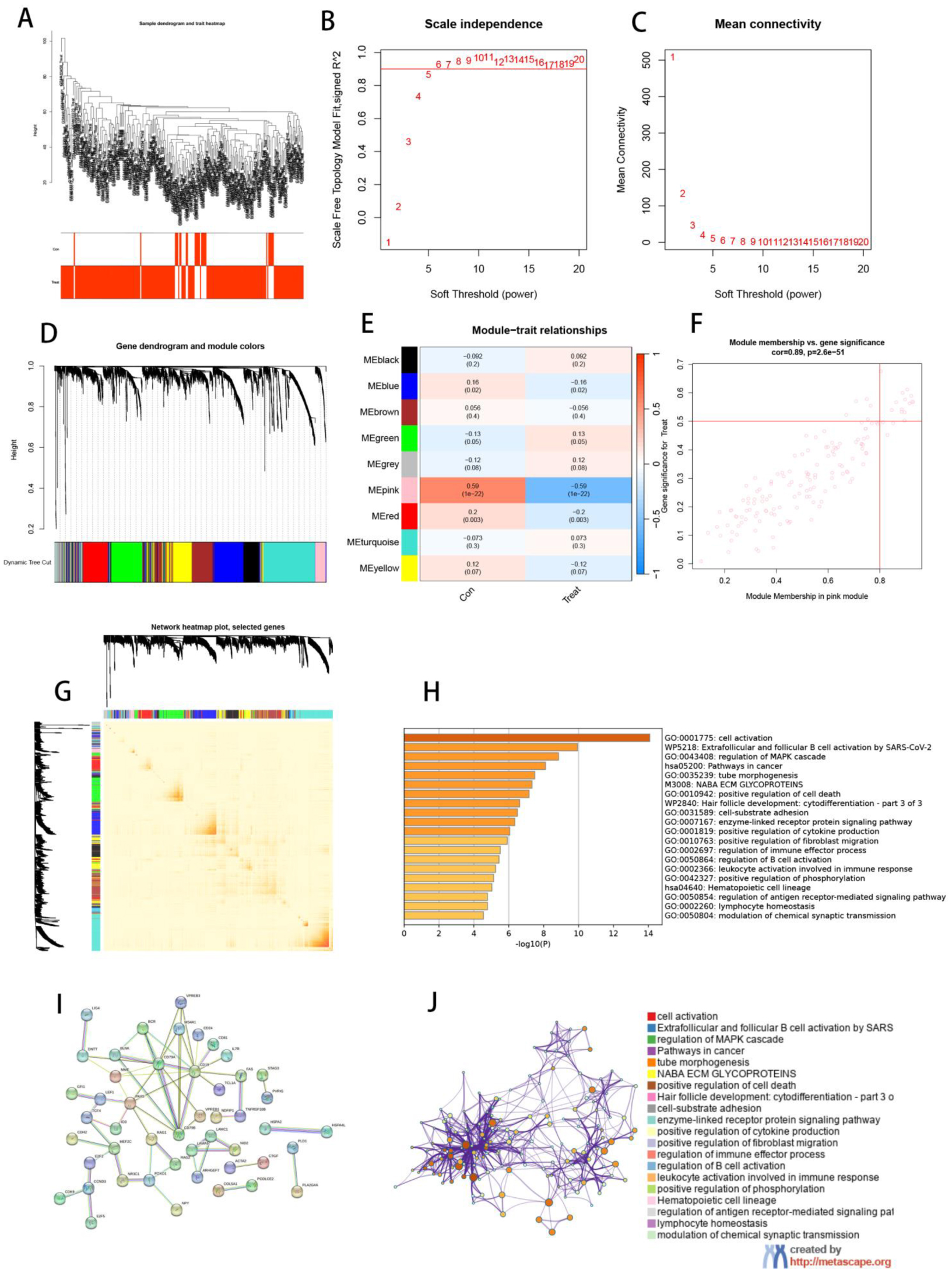
We selected and examined modules that are highly linked with MDS using the WGCNA analysis approach. We initially clustered the samples based on their clinical attributes and then processed the queue using the correlation coefficient method to generate a sample clustering tree (Figure 8A). The samples were then filtered using hierarchical clustering to obtain a soft threshold, which resulted in a high average connectedness (Figure 8B,C). We next created a gene co-expression network using dynamic cutting (Figure 8D) and combined highly comparable modules to create 9 modules (Figure 8E). The pink module was the most significant and highly associated, thus we chose 148 of the most interconnected module genes and generated a scatter plot of the gene correlations inside the module (cor = 0.89, P = 2.6e−51) (Figure 8F). We evaluated the combined results to show the relative independence of gene expression within these modules and found no significant differences between the modules (Figure 8G). To better understand the roles of the 106 hub genes, we first used the Metascape database to perform KEGG and GO enrichment analysis, which revealed considerable enrichment in numerous immune-related pathways and functions linked to cell activation and lymphocyte homeostasis (Figure 8H,J). Finally, we performed PPI analysis on the genes in the pink module using the STRING database and discovered that proteins like CD19, CD79A and CD79B interacted with a range of other proteins (Figure 8I).

Figure 8.  WGCNA identifies MDS high relevance modules and analyzes related functions. (A) Clustering dendrogram. (B,C) Network topology analysis for various soft threshold powers. (D) Clustered dendrograms of genes based on topological overlap, and assigned module colors. (E) Module-trait heat map. (F) Scatter plot of gene importance within pink modules. (G) TOM heat map. (H) Histogram. (I) PPI network plot of genes within the pink module. (J) Network diagram of Metascrape's enrichment analysis of genes within pink modules.

DownLoad: Full-Size Img PowerPoint

3.9.   MDS single cell analysis

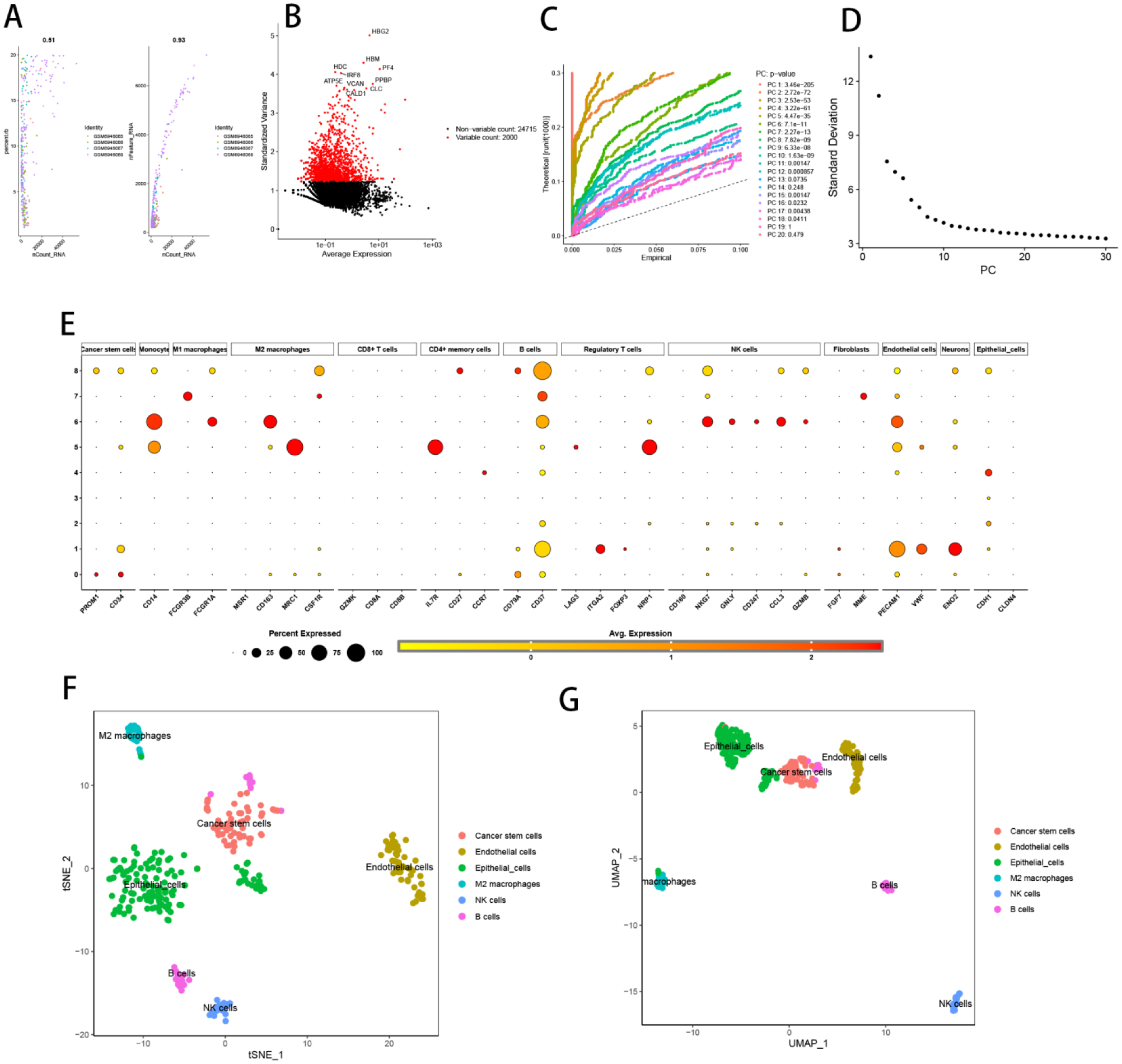
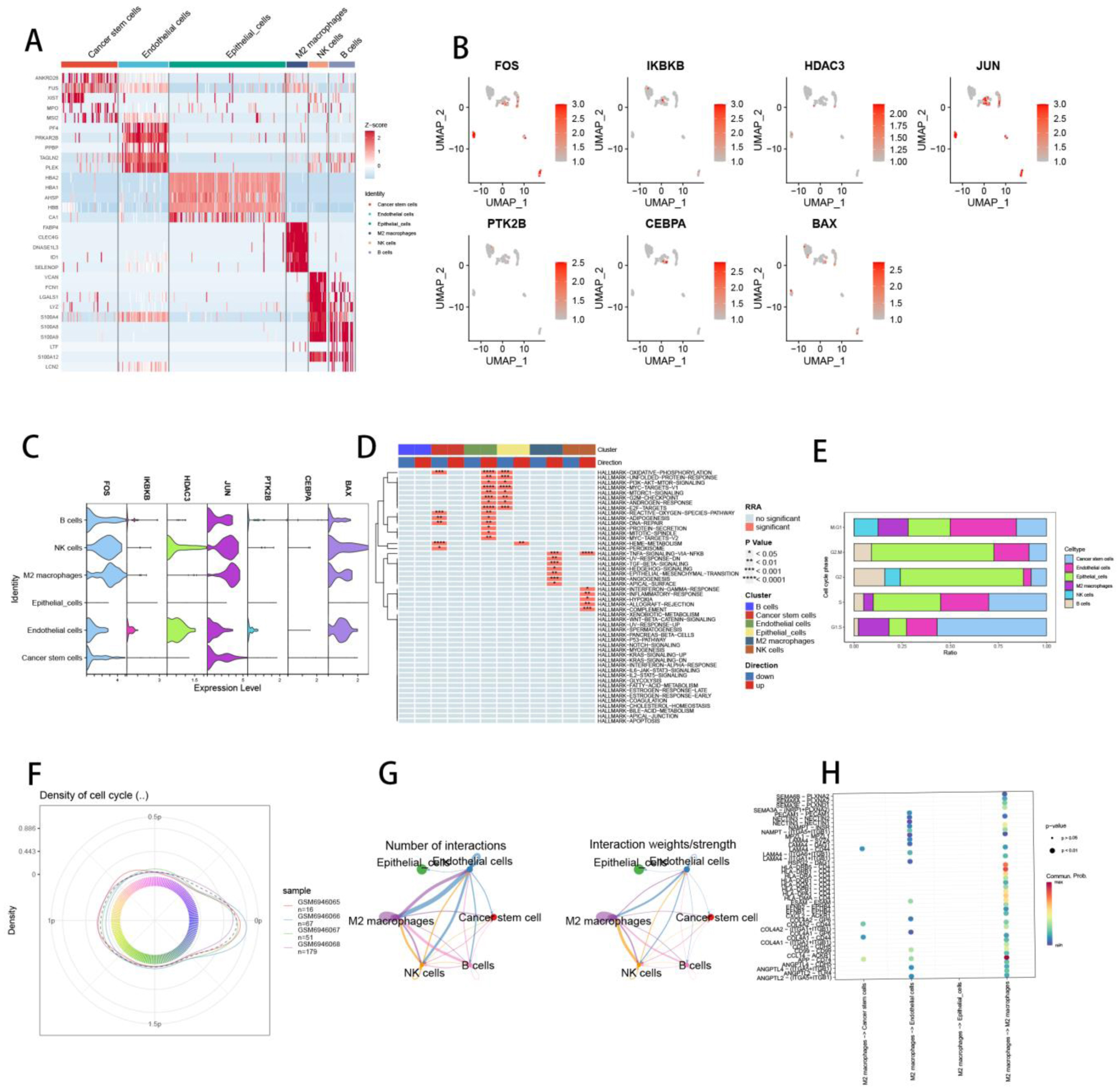
We increased the correlation of single-cell samples after quality control of single-cell data (Figure 9A,B). The data was then subjected to Principal Component Analysis (PCA) to minimize its dimensionality. Using the Jackstraw plot and the Elbow plot (Figures 9C,D), the number of selected major components was computed. The clustered cells were then displayed using the dimensional reduction methods t-distributed stochastic neighbor embedding (tSNE) and Uniform Manifold Approximation and Projection (UMAP). We manually searched for correlations between marker genes in each cluster and cell subtypes and chose the subtypes with the strongest correlation to annotate the clustering results (Figure 9E). This method resulted in the identification of six distinct cell types, as illustrated by the annotated tSNE and UMAP plots in Figures 9F,G.

Heatmap analysis of cell subtypes was undertaken to validate the manually annotated cell clustering results (Figure 10A), which revealed that the correlation within cell subtypes was quite high, while the disparities between subtypes were rather substantial. In addition, we investigated the expression of seven model genes (FOS, IKBKB, HDAC3, JUN, PTK2B, CEBPA, BAX) in each cell type, as well as the relationship between these seven essential genes and six cell subtypes (Figure 10B,C). According to the findings of irGSEA, epithelial cells in MDS patients were primarily positively connected with tumor-related pathways such as oxidation-phosphorylation and non-folded protein response (EMT) (Figure 10D). In terms of cell cycle, epithelial cells primarily aggregated during the G2 phase (Figure 10E) and the cell cycle density maps for the four samples are given in Figure 10F. Finally, in MDS patients, we used CellChat to assess putative signaling pathways and interactions across distinct cell subtypes. The closest communication was observed to be between epithelial cells and M2 macrophages (Figure 10G), and M2 macrophages were most influenced by the HLA signal (Figure 10H).

Figure 9.  Single cell analysis. (A) Correlation of data in the four cohorts before and after quality control. (B) The top 2000 genes that were highly expressed after quality control, with the top ten genes annotated. (C) Jackstrawplot. (D) ElbowPlot. (E) Identification of cell subpopulations based on known marker genes. (F) tSNE and (G) UMAP plots after manual annotation of immune cell subpopulations.

DownLoad: Full-Size Img PowerPoint

Figure 10.  Single cell analysis. (A) Heat map showing the relative expression of the 6 cell clusters. Red represents highly expressed genes and blue represents lowly expressed genes. (B) Distribution of 7-ARGs in cell subpopulations and (C) correlation violin plot. (D) GSVA plots showing the terms of the enrichment pathway for each identified cell subpopulation. (E,F) Proportion of the number of each cell subpopulation in different cycles of cell development. (G) Diagram of cellular communication networks. (H) Cellular signals from different cell types to M2 macrophages. The vertical axis shows the interactions between receptors and ligands in selected cell types, with different colors representing the intensity.

DownLoad: Full-Size Img PowerPoint

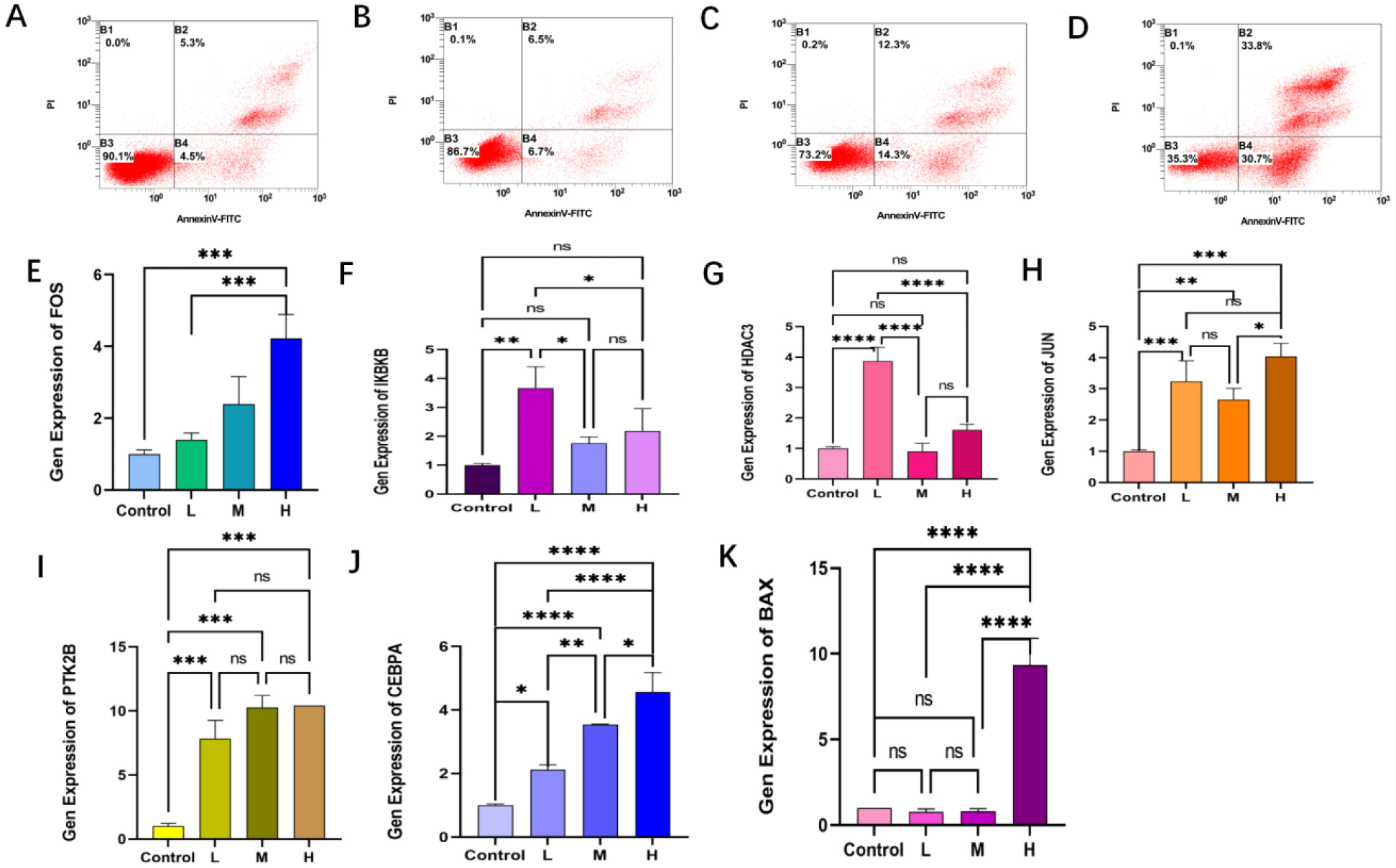
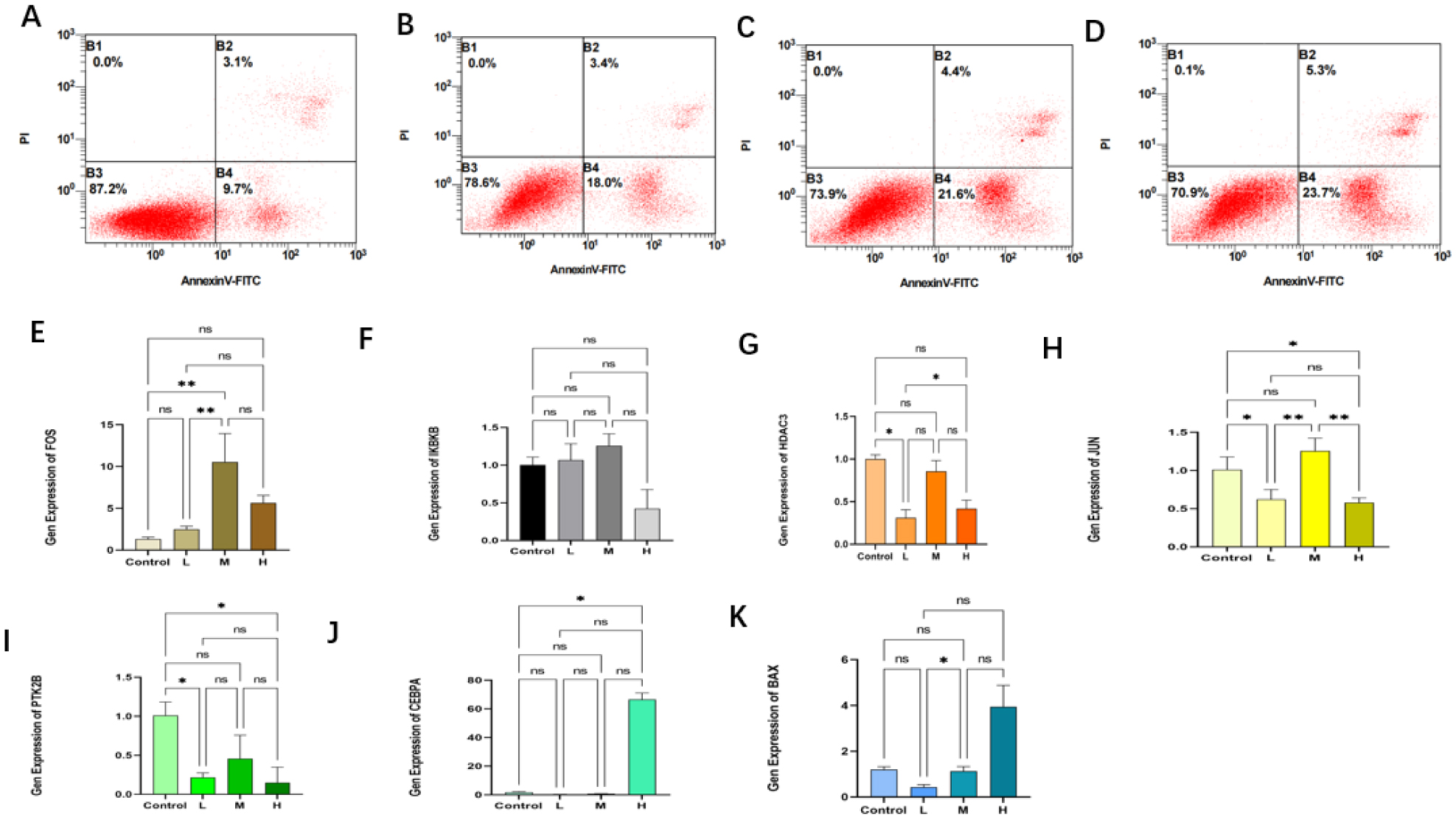
3.10.   Flow cytometry and RT-PCR techniques to validate the results

In order to verify the correlation between the genes, we screened and performed MDS using bioinformatics techniques, machine learning methods, etc. We also examined the apoptosis of SKM-1 and K562 cell lines in different subgroups by flow cytometry, and we intervened in the two cell lines using different concentrations of cycloheximide, which consists of indocyanine and As2S2, with the low-cycloheximide group plus 20 umol/L. We used different concentrations of cyanidazole to intervene the two cell lines, cyanidazole consists of As2S2 and As2S2, low cyanidazole group with 20 umol/L As2S2 + 40 umol/L indole, medium cyanidazole group with 40 umol/L As2S2 + 40 umol/L indole and high cyanidazole group with 40 umol/L As2S2 + 60 umol/L indole. Apoptosis of SKM-1 cell line (Figure 11A–D) and K562 cell line (Figure 12A–D) were seen. In Figures 11 and 12, A is the blank group, which was cultured from the original cell line without drug interference, B is the Qinghuangsan low dose group with 20 umol/L As2S2 + 40 umol/L indigohematoxylin for drug intervention, C is the Qinghuangsan low dose group with 40 umol/L As2S2 + 40 umol/L indigo red for pharmacological intervention and D is the low dose group of Qinghuangsan with 40 umol/L As2S2 + 60 umol/L for pharmacological intervention. The apoptosis rate of the cells showed an increasing trend with the increase in the dosage of Qinghuangsan. In addition, we verified the expression of 7 pivotal genes in different subgroups of MDS by RT-PCR (Figure 11E–K and Figure 12E–K), in which the * symbols represent statistically significant (*P ≤ 0.05, **P ≤ 0.01, ***P ≤ 0.001, ****P ≤ 0.0001 and ns represents no statistical significance (P > 0.05)), which can be seen by the different subgroups of each gene in the apoptosis of the K562 cell line (Figure 12A–D, where A is the blank group, B is the low-dose group of Qinghuang powder, C is the low-dose group of Qinghuang powder and D is the low-dose group of Qinghuang powder). It can be seen that by different subgroups of each gene in the MDS cell line SKM-1 are statistically significant, K562 the vast majority of them are statistically significant. This indicates that the seven hub genes we screened are expressed in MDS, so it can be verified that the senescent genes we screened play a key role in the diagnosis and treatment of MDS.

Figure 11.  Flow cytometry and RT-PCR techniques to validate the results. (A–D) are the apoptosis of SKM-1 cell line after cyanidin intervention detected by flow cytometry, and it can be seen that the percentage of apoptosis gradually increased with the addition of the intervention drug. (E–K) are the mRNA expression of Seven hub ARGs (FOS,IKBKB,HDAC3,JUN,PTK2B,CEBPA,BAX), each core gene showed different expression trends in low, medium and high groups compared with the control group.

DownLoad: Full-Size Img PowerPoint

Figure 12.  Flow cytometry and RT-PCR techniques to validate the results. (A–D) are the apoptosis of K562 cell line after cyanidin intervention detected by flow cytometry, and it can be seen that the percentage of apoptosis gradually increased with the addition of the intervention drug. (E–K) are the mRNA expression of Seven hub ARGs (FOS, IKBKB, HDAC3, JUN, PTK2B, CEBPA, BAX), each core gene showed different expression trends in low, medium and high groups compared with the control group.

DownLoad: Full-Size Img PowerPoint

4.   Discussion

There is growing evidence that the refractory nature, complexity and prolonged course of MDS, a disease of hematopoietic stem cells, is closely related to aging, which leads not only to DNA damage, telomere erosion or abnormal activation of oncogenes, but also to dysregulation of the immune system. In aging and multiple chronic diseases, senescent cells can accumulate in dysfunctional tissues and can impede innate and adaptive immune responses [29]. Thus, there is an urgent need for potential biomarkers that can be used for early diagnosis and therapeutic targets. Aging is thought to have a significant influence on the modulation of the MDS immunological microenvironment. In this study, we used gene sets from public databases and bioinformatics analysis to characterize the role of aging in the pathogenesis of MDS.

First, we selected three datasets about MDS from the GEO database, two of which were used as internal training sets and one as external validation set, suggesting differences in the results of principal component analysis between healthy and diseased groups. Then, screening for ARG differentially expressed genes associated with MDS, a total of 20 DE-ARGs were screened, showing the correlation between MDS and ARG, with the largest differences being CDKN1A, EGR1 and FOS. Cdkn1a (cell cycle protein-dependent kinase inhibitor 1A) is a marker of senescence and cellular senescence, and the Cdkn1a transcriptome variant 2 is preferentially induced with age [30]. CDK1N1A polymorphism may play an important role in age-related cancer risk [31]. Early growth response factor 1 (EGR1) is a transcription factor that performs a key function in tumor cell proliferation, angiogenesis, invasion and immune response [32],[33]. FOS is a transcription factor that is a granulocyte apoptosis and inflammatory mediator production a key regulator of granulocyte apoptosis and inflammatory mediator production, and impaired FOS mRNA stability has been shown to affect translational arrest in granulocytes from MDS patients [34]. Subsequently, 20 DE-ARGs were analyzed for GO, KEGG and DO aging gene enrichment to explore their biological functions, and revealed that DE-ARGs have important roles on gene expression, cell proliferation, epidermal growth factor and cell cycle regulation.

Next, we took three machine learning algorithms to identify seven identification hub ARGs (FOS, IKBKB, HDAC3, JUN, PTK2B, CEBPA and BAX), built a classifier and built an ANN model and Nomogram model based on the seven ARGs. The ANN model can accurately distinguish MDS high-risk patients from healthy individuals The DCA curve and ROX curve were used to determine the reliability of the model. IKBKB can release and activate NF-κB, which regulates cell survival and apoptosis [35] and is involved in cell proliferation, differentiation and other functions [36],[37]. HDAC3 is HDAC3 is a dichotomous transcriptional activator and repressor that is essential for the innate immune system [38], and HDAC3 is an epigenetic drug target that is currently being labeled as a potential therapeutic strategy against various cancers [39]. JUN (c-Jun) is an oncoprotein involved in many cellular activities such as proliferation, apoptosis, survival, tumorigenesis and histomorphogenesis [40],[41]. PTK2B is present in many age-related diseases and can influence various aging disorders by influencing the functioning of a particular group of genes [42], such as Alzheimer's disease. ceBPA is a transcription factor that is closely associated with myelopoiesis by controlling the proliferation and differentiation of myeloid progenitor cells [43], and dysfunction of CEBPA in patients with acute myeloid leukemia (AML) has been identified to be related [44]. BAX regulates cell death through its permeabilization of the mitochondrial outer membrane, and BAX dysregulation is particularly prone to abnormal cell death and senescence [45],[46]. It is easy to see by the functions of the above genes that the setters screened using machine learning are closely related to cell proliferation, growth and senescence, and validate the excellence of the classifiers established by the ANN model, laying the foundation for future studies of molecular mechanisms.

We all know that the immune system is the first line of defense against diseases. In this paper, in order to detect the role of immunity in MDS, the CIBERSORT algorithm was used to calculate the proportion of 22 types of immune cell infiltration in MDS tissues, and the results showed that the proportion of resting mast cells, neutrophils and other immune cells increased significantly, and the proportion of T cells CD8, T cells CD4 naive and other immune cells decreased significantly. The correlation between 7 ARG and immune cells was explored by the “Spermanent” method. JUN, as an oncoprotein, has a close relationship with immune cells and induces cancer, and its mechanism of carcinogenesis with the immune system needs to be studied. To further investigate the immune characteristics of MDS, we identified two senescence expression isoforms based on DE-ARG, indicating that senescence has an enforced effect on the immune microenvironment of MDS. The PCA algorithm showed significant differences between the two isoforms. Patients in cluster A and cluster B were significantly different when compared with each other, and there were also significant metabolic differences in gene expression in clusters A and B. Pathway analysis and immune infiltration analysis of the clusters revealed more enriched pathways and a higher degree of immune infiltration in cluster A. Each subtype had a different immune profile, which confirmed the reliability of our immunophenotypic classification of DE-ARG. This immunophenotypic classification strategy can expand the molecular study mechanisms and clinical therapeutic approaches to subtype MDS at the molecular or immune level rather than only at the clinical phenotype level. Thus, aging, expression and subtyping of MDS can replace or combine with existing clinical subtyping of MDS to improve the diagnosis and treatment of MDS.

We identified MDS highly correlated modules by WGCNA, analyzed the related functions and found that the most significant and highest correlated modules were pink modules. A total of 148 module genes with high connectivity in pink modules were screened, and these 148 module genes were enriched by metascape library with KEGG and GO, etc. We found that multiple immune-related pathways and functions were significantly enriched. Finally, the pink modular genes were put into the STRING database for PPI analysis, and it was found that CD19, CD79A, CD79B and other proteins have related interactions with various other proteins, and it was found that CD19, CD79A and CD79B are closely related to cell growth and apoptosis [47]–[49], especially to tumor cell death, and can be combined with other therapies to produce antitumor effects. We also used single-cell analysis to visualize clustered cells by descending and clustering subgroups and to find the most relevant cell subgroups, identifying six different cell subgroups (Cancer stem cells, Epithelial cells, NK cells, B cells, M2 macrophages, Endotheial cells). irGSEA results showed that Epithelial cells in MDS patients are mainly positively associated with tumor-related pathways such as oxidative-phosphorylation and unfolded protein response (MDST). In the cell cycle, Epithelial cells are predominantly clustered in the G2 phase. Finally, in MDS patients, we utilized CellChat to assess putative signaling pathways and interactions between distinct cell subpopulations. The closest intercellular communication is between Epithelial cells and M2 macrophages, which are mainly influenced by HLA (human leukocyte antigen) signaling.The discovery of HLA has caused the availability of hematopoietic cell transplantation as a therapeutic tool for hematological diseases to greatly increase.Significant advances in HLA in this field have revealed that the perfect match of alleles, antigens, and loci provides a more optimized solution for the treatment of diseases[50], and nowadays, the clinical relevance of donor-specific antibodies (DSAs) against anti-HLA antigens in organ transplantation (SOT) is widely recognized [51]–[53]. Changes in M2 macrophages are strongly associated with HLA expression in them, such as in hematologic diseases [48], colorectal cancer [54] and periodontitis [55].

According to the literature, this strategy regarding the construction of a classifier according to Hub-ARGs to distinguish MDS patients from healthy human controls was first proposed and systematically investigated the association link aging and the MDS immune microenvironment, which provides new ideas for immunotherapeutic approaches to MDS. Considering the increasing aging in contemporary society, the studies on aging genes in this paper are beneficial not only for middle-aged and elderly MDS patients, but also for healthy aging with preventive and corrective possibilities, and such studies have far-reaching implications.The aging subtypes and cellular subpopulations we have differentiated based on DE-ARGs and single-cell analysis need to be explored for their clinical applicability and provide new references for clinical treatment.

5.   Conclusion

In this study, we constructed a “classifier” of MDS based on seven pivotal ARGs (FOS, IKBKB, HDAC3, JUN, PTK2B, CEBPA and BAX). In addition, two distinct senescence-associated subtypes were identified, enriched for functional biological functions and differences in the immune microenvironment, contributing to immune infiltration, immune cells and HLA genes. These findings reveal potential regulatory mechanisms of aging in the immune microenvironment of MDS and stimulate more effective therapeutic approaches.

Use of AI tools declaration

The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.