Nanocrystalline SEM image restoration based on fractional-order TV and nuclear norm

1.   Introduction

In materials science, nanomaterials have been widely used in the fields of catalysis, biomedicine, fine chemical industry, and defense technology for their good chemical and thermal stability. However, due to the factors such as imaging equipment and human operation, the nanocrystalline images obtained by SEM are inevitably contaminated by Poisson noise, which brings serious obstacles to the further study of the properties, morphology, and microstructure of nanomaterials. Therefore, it is very important to choose a reasonable image restoration method to obtain high quality nanocrystalline SEM image quickly.

To remove Poisson noise, one of the most classical models is based on the TV regularization and Kullback-Leibler (KL) divergence fidelity ^[1,2]. This model classifies images into a bounded variation function space, which can effectively preserve edge details of the images while denoising. Unfortunately, the introduction of the TV regularization term results in obvious staircase artifacts in smooth regions of the images.

In view of this defect, a series of improved regularization models have been proposed recently. For example, there exist the higher-order derivative-based higher-order TV (HOTV) model ^[3,4], total generalized variation model ^[5,6], nonconvex HOTV with overlapping group sparsity ^[7] (NOGS for short), and so on. This kind of strategy can significantly reduce the staircase artifacts in smooth regions. However, because these schemes are established based on high-order derivatives, it is inevitable to produce some edge blurring when they are used in image restoration. The other improved model is the variationa model based on fractional-order TV (FOTV, ^[8,9,10]), which contains the fractional-order derivatives, can be seen as a compromise between TV and higher-order TV. Therefore, when used in image restoration, it can achieve the ability of maintaining edge details while alleviating the staircase effect. Besides, there exist other improved methods for noise reduction, such as the sparse and nonlocal regularization approach ^[11] and the spectral unmixing method ^[12] in the case of hyperspectral images. However, when the intensity of noise is large, some of the above methods cannot effectively remove noise or lose important detail features, which have some application limitations.

Note that the intensity of noise can influence the singular values of an image, and penalizing the singular values helps to improve the quality of image restoration. Nuclear norm (the sum of all singular values of a matrix), which is the best convex approximation of the rank function, can characterize the sparsity of data. Thus, nuclear norm minimization has been applied to the problems such as data recovery and feature extraction, and has achieved good reconstruction results. In the meanwhile, according to ^[13], it follows that the hybrid regularizers technique is beneficial for achieving accurate image reconstruction. Based on this, the authors in ^[14] proposed the TV and nuclear norm-based method for image restoration, and the work ^[15] investigates a new variational model that contains the higher-order TV and nuclear norm constraints. Compared to the single regularizer models, these hybrid regularizers models have achieved certain improvements in image quality. However, due to the inclusion of TV and higher-order TV frameworks, the phenomenon of the staircase effect and blurred edges is inevitable.

Based on the above analysis, this paper will add the nuclear norm constraint to the fractional-order TV regularization, and propose a hybrid of the fractional-order TV and nuclear norm regularizers model for image restoration. The constructed new model takes into account the sparsity of data and combines the advantage of the fractional-order derivative penalty. Therefore, when applied for Poissonian image restoration, it can not only overcome the staircase effect in smooth regions, but also maintain small edge features in the images, thereby achieving high-precision image restoration.

The main innovations of this article can be generalized as follows. First of all, by integrating the advantages of fractional-order TV and nuclear norm constraints, this paper proposes a novel model for Poissonian image restoration. Second, to quickly deal with the established optimization model, an improved alternating direction method of multipliers is proposed by combining the variable separation technique and singular value thresholding algorithm. Finally, compared with several existing numerical methods, the provided numerical experiments demonstrate the superiority of our new method in visual quality and quantitative evaluation.

2.   Proposed model

Following the works ^[1,2], the image restoration model based on the TV regularization and KL divergence fidelity can be represented as

where $\|\nabla u\|_1$ denotes the TV regularization, and $\lambda > 0$ is a weighting parameter, which is used to balance the regularization term and the data fidelity term. In addition, $K$ stands for a linear blurring operator, and $u, f$ are the original clean image and the observed degraded image, respectively.

As an improvement of model (1), a related variational model is established by replacing TV with fractional-order TV as the regularization term, namely,

where $\alpha > 0$, and $\nabla^\alpha$ represents the Grünwald-Letnikov fractional-order gradient operator. For the convenience of numerical calculations, some definitions and properties of fractional-order operators are presented below. For more details, please refer to ^[16,17]. Consequently, the discrete fractional-order gradient can be written as

Here, $D_1^{\alpha} u, D_2^{\alpha} u$ denote the discrete gradients along the $x, y$ axes respectively, and their calculation formulas are given by

Note that the symbol $S$ represents the number of adjacent pixels, $\mathcal{C}_s^{\alpha} = \Gamma(\alpha+1)/(\Gamma(s+1)\Gamma(\alpha+1-s))$, and $\Gamma$ denotes the classical Gamma function. Based on these preliminaries, the discrete fractional-order TV can be represented as

As far as the relationship between fractional-order gradient and divergence is concerned, we derive that $(\nabla^{\alpha})^T = \overline{(-1)^{\alpha}}{\rm div}^{\alpha}$, with $(\nabla^{\alpha})^{T}$ being the adjoint operator of $\nabla^{\alpha}$. Specifically, the fractional-order divergence is determined by the following expression:

Meanwhile, considering that the nuclear norm can serve as a loose approximation of the rank constraint, it can effectively characterize the sparsity of data. Based on the above discussions, to improve the quality of image reconstruction, this paper adds the nuclear norm constraint to the fractional-order TV regularization and proposes a Poisson denoising model that contains a hybrid of fractional-order TV and nuclear norm regularizers. Formally speaking, the established mathematical model is

where $\beta > 0$ denotes a weighting parameter, and the nuclear norm is defined as $\|u\|_* = \sum_i\sigma_i(u)$, with $\sigma_i(u)$ being the $i$-th singular value of the matrix $u$.

3.   Optimization algorithm

To solve the optimization problem (3), we use the variable separation method and introduce three auxiliary variables $d, v$, and $z$, such that $d = \nabla^\alpha u, v = u$, and $z = Ku$. So, the aforementioned model can be equivalently transformed into

As for the above constrained optimization problem, we first establish its corresponding augmented Lagrangian equation as

where $\gamma_1, \gamma_2, \gamma_3 > 0$ are three penalty parameters, and $\eta_1, \eta_2, \eta_3$ denote the Lagrange multipliers.

Generally speaking, obtaining the optimal solution of the convex optimization problem (4) amounts to finding a saddle point $(u^*, d^*, v^*, z^*; \eta_1^*, \eta_2^*, \eta_3^*)$ such that

To solve the saddle point problem (6), using the augmented Lagrangian method ^[18] leads to the following iterative algorithm:

which is implemented by maximizing $\eta_1, \eta_2$, and $\eta_3$ via the gradient ascent method, namely, the update formulas for the above mentioned Lagrange multipliers are

Note that it is a challenging task to obtain the solutions of four variables in (7) simultaneously. Using the idea of alternating minimization, the above algorithm can be decomposed into four subproblems with respect to the variables $u, d, v$, and $z$. This leads to the following iterative framework:

In what follows, our purpose is to solve each subproblem in detail one by one. First, regarding the subproblem of $u$, its first-order optimization condition can be written as

Under the assumption of the periodic boundary condition, the operators $(\nabla^\alpha)^T\nabla^\alpha$ and $K^TK$ are both block circulant. Therefore, by using fast Fourier transform (FFT) and its inverse transform, the solution to the $u$-subproblem is characterized by

where $F, F^{-1}$ represent the FFT and its inverse transform, respectively, $*$ denotes complex conjugation, and $\odot$ is componentwise multiplication.

Second, using the generalized soft thresholding formula, the solution to the $d$-subproblem can be obtained as

where shrink means the shrinkage operator, and ${\rm shrink}(t, \tau) = {\rm sgn}(t).\ast\max(\|t\|_2-\tau, 0)$, with ${\rm sgn}$ being the signum function.

For the $v$-subproblem, it is very difficult to solve directly due to its inclusion of nuclear norm. Here, we use the singular value thresholding (SVT) algorithm to solve it. Referring to ^[19], given an $n_1\times n_2$ matrix $X$, the singular value decomposition (SVD) of this matrix is

Therefore, for a fixed parameter $\delta > 0$, the SVT operator satisfies the following equation:

More specifically, the formula is ${\rm SVT}(X, \delta) = U{\rm diag}(\max\{\sigma_i-\delta, 0\})V^{T}$. Applying this formula, the solution to the $v$-subproblem is

Finally, for the $z$-subproblem, by combining the first-order optimization condition and the root finding formula, it can be concluded that

In summary, the solving processes of the joint subproblems lead to a modified alternating direction method of multipliers (ADMM), which is summarized as follows.

It is noteworthy that in the developed algorithm, the calculation of $u$-subproblem includes FFT and inverse FFT operations. Therefore, the complexity of computing the $u$-subproblem is $O(n_1n_2{\rm log}(n_1n_2))$ for an $n_1\times n_2$ image. Moreover, from the calculations of the $d, z$ subproblems, it yields that their computation costs are both linear with $n_1n_2$. As far as the subproblem with respect to $v$ is concerned, its calculation contains the SVD operation ^[20], which is most time-consuming. This means that the computational complexity of the $v$-subproblem arrives at $O(\min(n_1^2n_2, n_1n_2^2))$.

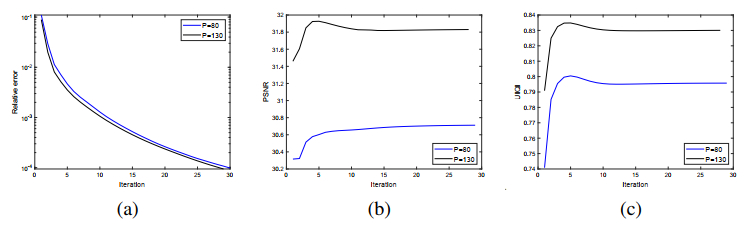
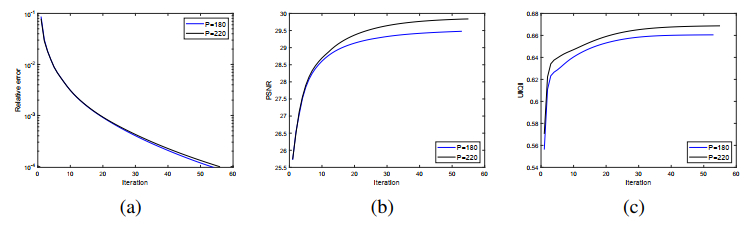
In what follows, we briefly discuss the convergence of the designed algorithm. The resulting optimization problem is convex and four variables can be divided into two blocks $\{u\}$ and $\{d, v, z\}$. For a given $u$, the updates of auxiliary variables $d, v, z$ are independent of each other. Based on this observation, our algorithm framework can be regarded as an application of the original ADMM ^[21]. Therefore, the sequence $\{u^k, d^k, v^k, z^k\}$ obtained by Algorithm 1 is convergent. Moreover, as a visual display, Figures 4 and 7 show the numerical convergence of our proposed algorithm.

4.   Numerical experiments

In this section, our main purpose is to provide several numerical experiments to validate the effectiveness of the developed scheme. To demonstrate its superiority, the newly proposed method will be compared with the TV, FOTV, HOTV, and NOGS models. All experiments are conducted on Matlab R2023b software under Windows 10 system, with 32 GB RAM and an Intel(R) Core(TM) i9-10900 CPU at 2.81 GHz. It is noteworthy that in the simulation experiments, the addition of Poisson noise is achieved using the Matlab library function Poissrnd.

Throughout the numerical experiments, all algorithms are terminated when the relative error is less than $10^{-4}$. Several parameters used in the proposed algorithm are fixed as follows: $\alpha = 1.8, \beta = 0.1, \gamma_1 = 0.2, \gamma_2 = 0.2, \gamma_3 = 0.2$. Meanwhile, two commonly adopted peak signal-to-noise ratio (PSNR), and universal image quality index (UIQI, ^[22]) criteria are adopted to evaluate the quality of image reconstruction. The calculation formula for PSNR is

where $u$ and $\tilde{u}$ are the clean original image and the restored image respectively, $n_1n_2$ represents the size of an image, and $P$ denotes the maximum peak value. In general, the higher the values of PSNR and UIQI, the better the quality of the restored image.

First, let us verify the Poisson denoising ability of our newly proposed model. In the experiment, the original images (Figure 1(a), (b)) are two SEM grayscale images both sized by $620\times620$ pixels. Figures 2(a1), (a2) and 3(a1), (a2) show the degraded images contaminated by Poisson noise with $P = 80,130$, respectively. Subsequently, by using the TV, FOTV, HOTV, NOGS methods and our proposed scheme, the recovered visual results are detailed in Figures 2 and 3. As shown in Figure 4, it illustrates the numerical convergence of our designed algorithm on the image of Figure 1(a) by characterizing the changing trends of relative error, PSNR, and UIQI versus the number of iterations separately. In addition, the quantitative comparison results of different methods are listed in Table 1, where the best and the second-best results of restoration quality are highlighted in bold and underlined, respectively. It should be noted that corresponding to different noise intensities, our restoration results on two images are achieved by setting the parameter $\lambda\in\{8, 10\}$ and $\{6.5, 8.5\}$.

The second experiment is used to evaluate the denoising and deblurring ability of the proposed model. In this case, two test nanocrystal SEM images have dimensions of $1000\times1000$ and $800\times800$ pixels, which are separately listed in Figure 1(c), (d). The degraded images obtained by adding motion blur with "$len = 13$" and "$theta = 60$", and polluted by Poisson noise with the intensity of $P = 180,220$, are exhibited in Figures 5(a1), (a2) and 6(a1), (a2). For these four degraded images, the restoration results and quality comparisons obtained using five different strategies are listed in Figures 5 and 6 and Table 2. Note that the recovered images by our scheme are obtained when the parameter $\lambda$ is set to 33 and 43. Moreover, by taking Figure 1(c) as an example, Figure 7 also indicates the numerical convergence behaviors of the proposed new method.

From Figures 2, 3, 5, and 6, it can be observed that the TV-based scheme produces obvious staircase artifacts in smooth regions of the images, such as Figure 2(b1), (b2). Although the FOTV, HOTV, and NOGS models have alleviated the staircase effect to a certain extent, they have also resulted in residual noise or blurred edges, so the restoration results are not very satisfactory. Our hybrid regularization technique overcomes the above shortcomings, and the restored results not only achieve smooth transitions in smooth regions, but also maintain the detailed features of the image, such as Figure 6(f1), (f2). The main reasons of such phenomenon are that the test image has a low rank and the sparsity induced by the nuclear norm regularization is helpful in solving the ill-conditioned inverse problem such as image deblurring. In addition, observed from Tables 1 and 2, it follows that the restoration results of the proposed scheme have higher PSNR and UIQI values, which further prove the superior performance of our novel method for image restoration.

Finally, we select a real nanocrystalline SEM image to further validate the effectiveness of our designed method. The tested image, which has the size of $500\times500$, contains low intensity Poisson noise. The restoration results obtained using five different methods are presented in Figure 8. After careful observation and comparison, it can be seen that our new approach can effectively remove noise while better preserving fine details of the image, thereby possessing the unparalleled superiority and application value.

5.   Conclusions

With the aim of removing Poisson noise in nanocrystalline SEM images effectively, this paper proposed a novel image restoration model based on the fractional-order TV and nuclear norm constraints. More precisely, fractional-order TV was used to overcome the staircase artifacts and maintain edge details, while nuclear norm constraint helped with feature extraction and improved the accuracy of image restoration. Methodologically, this paper combined the variable separation method and singular value thresholding algorithm to design an improved alternating direction method of multipliers. Finally, numerical experiments on simulated and real data illustrated the superiority of the newly developed method both visually and quantitatively. As a future prospect, motivated by the patch-based low rank approximation ^[23], our next work will focus on researching the low rank constraint models for image restoration, which helps to reduce the computational cost and improve the quality of image reconstruction.

Use of AI tools declaration

The author declares she has not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by Research Project of Guangxi Minzu University (2023KJQD10) and Scientific Research Fund of Hunan Provincial Education Department (22A0339, 22C0263).

Conflict of interest

The author declares there is no conflicts of interest.