1. Introduction
The physical phenomena of real world can effectively be modeled by making use of the theory of derivatives and integrals of fractional order. In this sense, the nonlinear fractional order evolution equations (NLFEEs) have recently become a burning topic to the researchers for searching their exact traveling wave solutions to depict the physical phenomena due to the nonlinear mechanisms arisen in various fields. The use of nonlinear equations is extensive as the nonlinearity exists everywhere in the world. NLFEEs have been attracted great interest due to their frequent appearance in many applications such as in biology, physics, chemistry, electromagnetic, polymeric materials, neutron point kinetic model, control and vibration, image and signal processing, system identifications, the finance, acoustics and fluid dynamics [1,2,3]. Many researchers have offered different approaches to construct analytic and numerical solutions to NLFEEs as well as NLEEs and put them forward for searching traveling wave solutions, such as the exponential decay law [4], the Ibragimov's nonlocal conservation method [5], the reproducing kernel method [6], the Jacobi elliptic function method [7], the (G′/G)-expansion method and its various modifications [8,9,10,11,12], the Exp-function method [13,14], the sub-equation method [15,16], the first integral method [17,18], the functional variable method [19], the modified trial equation method [20,21], the simplest equation method [22], the Lie group analysis method [23], the fractional characteristic method [24], the auxiliary equation method [25,26], the finite element method [27], the differential transform method [28], the Adomian decomposition method [29,30], the variational iteration method [31], the finite difference method [32], the various homotopy perturbation method [33,34,35,36,37] and the He's variational principle [38] etc. But no method is uniquely appreciable to investigate the exact solutions to all kind of NLFEEs. That is why; it is very much needed to introduce new method. In this study, we implemented recently established effectual and reliable productive method, called the fractional generalized (DαξG/G)-expansion method to construct closed form analytic wave solutions to some NLFEEs in the sense of conformable fractional derivative [39]. The results obtained throughout the article have been compared with those existing in the literature and shown that the achieved solutions are new and much more general. We have finally concluded that the solutions might bring up their importance through the contribution and be recorded in the literature.
2. Preliminaries and methodology
2.1. Conformable fractional derivative
A new and simple definition of derivative for fractional order introduced by Khalil et al. [39] is called conformable fractional derivative. This definition is analogous to the ordinary derivative
where ψ(x):[0,∞]→R and x>0. According to this classical definition, d(xn)dx=nxn−1. According to this perception, Khalil has introduced α order fractional derivative of ψas
|
Tαψ(x)=limε→0ψ(x+εx1−α)−ψ(x)ε , 0<α⩽1.
|
If the function ψ is α-differentiable in (0,r) for r>0 and limx→0+Tαψ(x) exists, then the conformable derivative at x=0 is defined as Tαψ(0)=limx→0+Tαψ(x). The conformable integral of ψ is
|
Irαψ(x)=∫xrψ(t)t1−αdt, r⩾0, 0<α⩽1.
|
This integral represents usual Riemann improper integral.
The conformable fractional derivative satisfies the following useful properties [39]:
If the functions u(x) and v(x) are α-differentiable at any pointx>0, for α∈(0,1], then
(a) Tα(au+bv)=aTα(u)+bTα(v) ∀a,b∈R.
(b) Tα(xn)=nxn−α ∀n∈R.
(c) Tα(c)=0, where c is any constant.
(d) Tα(uv)=uTα(v)+vTα(u).
(e) Tα(u/v)=vTα(u)−uTα(v)v2.
(f) if u is differentiable, then Tα(u)(x)=x1−αdudx(x).
Many researchers used this new derivative of fractional order in physical applications due to its convenience, simplicity and usefulness [40,41,42].
2.2. The fractional generalized (DαξG/G)-expansion method
Consider a nonlinear partial differential equation of fractional order in the independent variables t,x1,x2,...,xn as
|
F(u,Dαtu,Dαx1u,Dαx2u,...,Dαxnu,D2αtu,D2αx1u,D2αx2u,...,D2αxnu,...)=0,
|
(2.2.1)
|
where F is a polynomial in u(t,x1,x2,...,xn) and it's various conformable fractional derivatives. The main steps of the fractional generalized (DαξG/G)-expansion method referred as follows:
Step 1: Use the wave transformation
|
ξ=ξ(t,x1,x2,...,xn),ui=ui(t,x1,x2,...,xn)=Ui(ξ)
|
(2.2.2)
|
to reduce Eq. (2.2.1) to the following ordinary differential equation of fractional order with respect to the variable ξ:
|
P(U,DαξU,D2αξU,...)=0,
|
(2.2.3)
|
Take anti-derivative of Eq. (2.2.3), if possible, one or more times and the integral constant can be set to zero as soliton solutions are sought.
Step 2: Assume that Eq. (2.2.3) has solution in the form
|
u(ξ)=n∑i=0ai(d+DαξG/G)i+n∑i=1bi(d+DαξG/G)−i,
|
(2.2.4)
|
where ai(i=0,1,2,...,n), bi(i=1,2,3,...,n) and d are arbitrary constants with at least one of an and bn is nonzero and G=G(ξ) satisfies the auxiliary equation
|
AGD2αξG−BGDαξG−EG2−C(DαξG)2=0,
|
(2.2.5)
|
where 0<α⩽1 and DαξG(ξ)stands for the conformable fractional derivative G(ξ) of order α with respect to ξ; A,B,C and E are real parameters.
Making use of the transformation G(ξ)=H(η), η=ξα/α, Eq. (2.2.5) turns into the equation
|
AHH″−BHH′−EH2−C(H′)2=0,
|
(2.2.6)
|
whose solutions are well-known. Utilizing the solutions in Ref. [10] of Eq. (2.2.6) together with the transformation DαξG(ξ)=DαξH(η)=H′(η)Dαξη=H′(η), which can be derived by using conformable fractional derivative, we can easily obtain the following solutions to Eq. (2.2.5):
Family 1: When B≠0, ψ=A−C and Ω=B2+4Eψ>0,
|
(DαξG/G)=B2ψ+√Ω2ψC1sinh(√Ωξα2Aα)+C2cosh(√Ωξα2Aα)C1cosh(√Ωξα2Aα)+C2sinh(√Ωξα2Aα)
|
(2.2.7)
|
Family 2: When B≠0, ψ=A−C and Ω=B2+4Eψ<0,
|
(DαξG/G)=B2ψ+√−Ω2ψ−C1sin(√−Ωξα2Aα)+C2cos(√−Ωξα2Aα)C1cos(√−Ωξα2Aα)+C2sin(√−Ωξα2Aα)
|
(2.2.8)
|
Family 3: When B≠0, ψ=A−C and Ω=B2+4Eψ=0,
|
(DαξG/G)=B2ψ+αC2C1α+C2ξα
|
(2.2.9)
|
Family 4: When B=0, ψ=A−C and Δ=ψE>0,
|
(DαξG/G)=√ΔψC1sinh(√ΔξαAα)+C2cosh(√ΔξαAα)C1cosh(√ΔξαAα)+C2sinh(√ΔξαAα)
|
(2.2.10)
|
Family 5: When B=0, ψ=A−C and Δ=ψE<0,
|
(DαξG/G)=√−Δψ−C1sin(√−ΔξαAα)+C2cos(√−ΔξαAα)C1cos(√−ΔξαAα)+C2sin(√−ΔξαAα)
|
(2.2.11)
|
Step 3: Take the homogeneous balance between the highest order linear and nonlinear terms appearing in Eq. (2.2.3) to determine the positive constant n.
Step 4: Using the value of n obtained in step 3, Eq. (2.2.3) along with Eqs. (2.2.4), (2.2.5) makes available polynomials in (d+DαξG/G)n (n=0,1,2,...) and (d+DαξG/G)−n (n=1,2,3,...). Equalize each coefficient of these polynomials to zero yield a system of algebraic equations for ai(i=0,1,2,...), bi(i=1,2,3,...) and d. Solve this system by Maple to obtain the values of ai(i=0,1,2,...), bi(i=1,2,3,...) and d.
Step 5: Eq. (2.2.4) together with Eqs. (2.2.7)–(2.2.11) and the values appeared in step 4 provides traveling wave solutions of the nonlinear evolution equation (2.2.1) in closed form.
3. Formulation of the solutions
In this section, the closed form traveling wave solutions to the suggested equations are examined.
3.1. The space time fractional (2+1)-dimensional dispersive long wave equations
Consider the space time fractional (2+1)-dimensional dispersive long wave equations
|
∂2αu∂yα∂tα+∂2αv∂x2α+∂α(u(∂αu/∂xα))∂yα=0∂αv∂tα+∂αu∂xα+∂α(uv)∂xα+∂3αu∂x2α∂yα=0},
|
(3.1.1)
|
where 0<α⩽1; the notation ∂αu∂xα denotes the α-order partial derivative of u with respect to x and the other notations are so. This system of equations was first obtained by Boiti et al. [43] as compatibility condition for a weak Lax pair.
The composite transformation
|
u(t,x,y)=U(ξ),v(t,x,y)=V(ξ),ξ=k1/αx+l1/αy+w1/αt,
|
(3.1.2)
|
where k, l and w are constants, with the aid of chain rule
|
DαxU=∂αU∂xα=∂αU∂ξα.∂ξα∂xα=∂αU∂ξα.(∂ξ∂x)α=kDαξU,
|
forces Eq. (3.1.1) to take the form
|
lwD2αξU+k2D2αξV+kl(UD2αξU+(DαξU)2)=0wDαξV+kDαξU+kDαξ(UV)+k2lD3αξU=0}
|
(3.1.3)
|
The positive constant n under the homogeneous balance from Eq. (3.1.3) reduces Eq. (2.2.4) into the form
|
U(ξ)=a0+a1φ+b1φ−1V(ξ)=c0+c1φ+c2φ2+d1φ−1+d2φ−2},
|
(3.1.4)
|
where φ=(d+DαξG/G). Eq. (3.1.3) with the aid of Eq. (3.1.4) and Eq. (2.2.5) produces a polynomial in φ. Setting each coefficient of this polynomial to zero gives a set of algebraic equations for the constants in Eq. (3.1.4). Solving these equations by the computational software Maple present the following results:
|
Set−1:a0=±1Ak3/2{k3(2dψ+B)∓Aw√k},a1=∓2Ak3/2ψ,b1=∓2k3/2A(d2ψ+Bd−E),c1=2k2lψA2(2dψ+B),c2=−2A2k2lψ2,d1=2k2lA2(2dψ+B)(d2ψ+Bd−E),c0=−1,d2=−2k2lA2(d2ψ+Bd−E)2
|
(3.1.5)
|
|
Set−2:a0=±1Ak3/2{k3(2dψ+B)∓Aw√k},a1=0,b1=∓2k3/2A(d2ψ+Bd−E),c1=0,c0=−1A2{2k2lψ(d2ψ+Bd−E)+A2},d1=2k2lA2{(2d2ψ+3Bd−2E)dψ+B2d−BE},c2=0,d2=−2k2lA2{d2ψ(d2ψ+2Bd−2E)+E2+B2d2−2BdE}
|
(3.1.6)
|
|
Set−3:a0=±1Ak3/2{k3(2dψ+B)∓Aw√k},a1=∓2Ak3/2ψ,b1=0,c1=2k2lψA2(2dψ+B),c0=−1A2{k2lψ(2d2ψ+2Bd−2E)+A2},c2=−2A2k2lψ2,d1=0,d2=0
|
(3.1.7)
|
Putting Eqs. (3.1.5)–(3.1.6) into Eq. (3.1.4) yields
|
U1(ξ)=±1Ak3/2{k3(2dψ+B)∓Aw√k}∓2Ak3/2ψ(d+DαξG/G)∓2k3/2A(d2ψ+Bd−E)(d+DαξG/G)−1
|
(3.1.8)
|
|
V1(ξ)=−1+2k2lψA2(2dψ+B)(d+DαξG/G)−2A2k2lψ2(d+DαξG/G)2+2k2lA2(2dψ+B)(d2ψ+Bd−E)(d+DαξG/G)−1−2k2lA2(d2ψ+Bd−E)2(d+DαξG/G)−2
|
(3.1.9)
|
|
U2(ξ)=±1Ak3/2{k3(2dψ+B)∓Aw√k}∓2k3/2A(d2ψ+Bd−E)(d+DαξG/G)
|
(3.1.10)
|
|
V2(ξ)=−1A2{2k2lψ(d2ψ+Bd−E)+A2}+2k2lA2{(2d2ψ+3Bd−2E)dψ+B2d−BE}(d+DαξG/G)−1−2k2lA2{d2ψ(d2ψ+2Bd−2E)+E2+B2d2−2BdE}(d+DαξG/G)−2
|
(3.1.11)
|
|
U3(ξ)=±1Ak3/2{k3(2dψ+B)∓Aw√k}∓2Ak3/2ψ(d+DαξG/G)
|
(3.1.12)
|
|
V3(ξ)=−1A2{k2lψ(2d2ψ+2Bd−2E)+A2}+2k2lψA2(2dψ+B)(d+DαξG/G)−2A2k2lψ2(d+DαξG/G)2
|
(3.1.13)
|
where ξ=k1/αx+l1/αy+w1/αt.
Eqs. (3.1.8), (3.1.9) together with Eqs. (2.2.7)–(2.2.11) make available the following three types solutions in terms hyperbolic function, trigonometric function and rational function as:
When B≠0, ψ=A−C and Ω=B2+4Eψ>0,
|
U11(ξ)=±1Ak3/2{k3(2dψ+B)∓Aw√k}∓2Ak3/2ψ{d+B2ψ+√Ω2ψC1sinhΦ+C2coshΦC1coshΦ+C2sinhΦ}∓2k3/2A(d2ψ+Bd−E){d+B2ψ+√Ω2ψC1sinhΦ+C2coshΦC1coshΦ+C2sinhΦ}−1
|
(3.1.14)
|
|
V11(ξ)=−1+2k2lψA2(2dψ+B){d+B2ψ+√Ω2ψC1sinhΦ+C2coshΦC1coshΦ+C2sinhΦ}−2A2k2lψ2{d+B2ψ+√Ω2ψC1sinhΦ+C2coshΦC1coshΦ+C2sinhΦ}2+2k2lA2(2dψ+B)(d2ψ+Bd−E)×{d+B2ψ+√Ω2ψC1sinhΦ+C2coshΦC1coshΦ+C2sinhΦ}−1−2k2lA2(d2ψ+Bd−E)2{d+B2ψ+√Ω2ψC1sinhΦ+C2coshΦC1coshΦ+C2sinhΦ}−2
|
(3.1.15)
|
where Φ=√Ωξα2Aα.
Since C1 and C2 are arbitrary constants, ifC1≠0 and C2=0, then Eqs. (3.1.14), (3.1.15) become
|
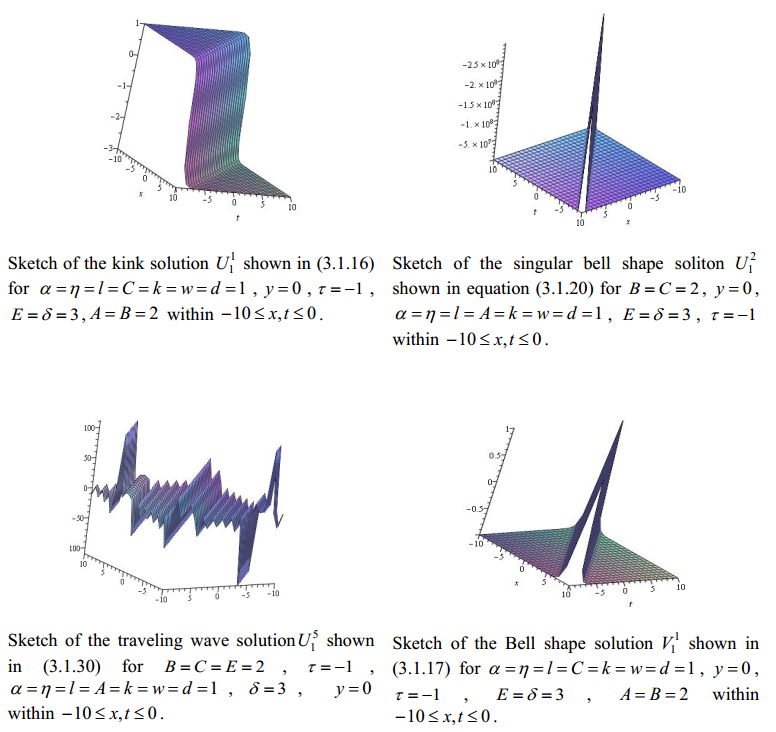
U11(ξ)=±1Ak3/2{k3(2dψ+B)∓Aw√k}∓k3/2A{2dψ+B+√Ωtanh√Ωξα2Aα}∓4ψk3/2A(d2ψ+Bd−E){2dψ+B+√Ωtanh√Ωξα2Aα}−1
|
(3.1.16)
|
|
V11(ξ)=−1+k2lA2(2dψ+B){2dψ+B+√Ωtanh√Ωξα2Aα}−k2l2A2{2dψ+B+√Ωtanh√Ωξα2Aα}2+4ψk2lA2(2dψ+B)(d2ψ+Bd−E)×{2dψ+B+√Ωtanh√Ωξα2Aα}−1−8ψ2k2lA2(d2ψ+Bd−E)2{2dψ+B+√Ωtanh√Ωξα2Aα}−2
|
(3.1.17)
|
where ξ=k1/αx+l1/αy+w1/αt.
When B≠0, ψ=A−C and Ω=B2+4Eψ<0
|
U12(ξ)=±1Ak3/2{k3(2dψ+B)∓Aw√k}∓k3/2A{2dψ+B+√−Ω−C1sinΦ+C2cosΦC1cosΦ+C2sinΦ}∓4ψk3/2A(d2ψ+Bd−E){2dψ+B+√−Ω−C1sinΦ+C2cosΦC1cosΦ+C2sinΦ}−1
|
(3.1.18)
|
|
V12(ξ)=−1+k2lA2(2dψ+B){2dψ+B+√−Ω−C1sinΦ+C2cosΦC1cosΦ+C2sinΦ}−k2l2A2{2dψ+B+√−Ω−C1sinΦ+C2cosΦC1cosΦ+C2sinΦ}2+4k2lψA2(2dψ+B)(d2ψ+Bd−E){2dψ+B+√−Ω−C1sinΦ+C2cosΦC1cosΦ+C2sinΦ}−1−8k2lψ2A2(d2ψ+Bd−E)2{2dψ+B+√−Ω−C1sinΦ+C2cosΦC1cosΦ+C2sinΦ}−2
|
(3.1.19)
|
where Φ=√−Ωξα2Aα.
In particular, if C1≠0 and C2=0, then Eqs. (3.1.18), (3.1.19) are simplified as
|
U12(ξ)=±1Ak3/2{k3(2dψ+B)∓Aw√k}∓k3/2A(2dψ+B−√−ΩtanΦ)∓4ψk3/2A(d2ψ+Bd−E)(2dψ+B−√−ΩtanΦ)−1
|
(3.1.20)
|
|
V12(ξ)=−1+k2lA2(2dψ+B)(2dψ+B−√−ΩtanΦ)−k2l2A2(2dψ+B−√−ΩtanΦ)2+4k2lψA2(2dψ+B)(d2ψ+Bd−E)(2dψ+B−√−ΩtanΦ)−1−8k2lψ2A2(d2ψ+Bd−E)2(2dψ+B−√−ΩtanΦ)−2
|
(3.1.21)
|
where Φ=√−Ωξα2Aα and ξ=k1/αx+l1/αy+w1/αt.
When B≠0, ψ=A−C and Ω=B2+4Eψ=0,
|
U13(ξ)=±1Ak3/2{k3(2dψ+B)∓Aw√k}∓k3/2A{2dψ+B+2ψαC2C1α+C2ξα}∓4ψk3/2A(d2ψ+Bd−E){2dψ+B+2ψαC2C1α+C2ξα}−1
|
(3.1.22)
|
|
V13(ξ)=−1+k2lA2(2dψ+B){2dψ+B+2ψαC2C1α+C2ξα}−k2l2A2{2dψ+B+2ψαC2C1α+C2ξα}2+4k2lψA2(2dψ+B)(d2ψ+Bd−E){2dψ+B+2ψαC2C1α+C2ξα}−1−8ψ2k2lA2(d2ψ+Bd−E)2{2dψ+B+2ψαC2C1α+C2ξα}−2
|
(3.1.23)
|
If C1=0 and C2≠0, then
|
U13(ξ)=±1Ak3/2{k3(2dψ+B)∓Aw√k}∓k3/2A(2dψ+B+2ψα/ξα)∓4ψk3/2A(d2ψ+Bd−E)(2dψ+B+2ψα/ξα)−1
|
(3.1.24)
|
|
V13(ξ)=−1+k2lA2(2dψ+B)(2dψ+B+2ψα/ξα)−k2l2A2(2dψ+B+2ψα/ξα)2+4k2lψA2(2dψ+B)(d2ψ+Bd−E)(2dψ+B+2ψα/ξα)−1−8ψ2k2lA2(d2ψ+Bd−E)2(2dψ+B+2ψα/ξα)−2
|
(3.1.25)
|
where ξ=k1/αx+l1/αy+w1/αt.
When B=0, ψ=A−C and Δ=ψE>0,
|
U14(ξ)=±1Ak3/2{2dψk3∓Aw√k}∓2Ak3/2{dψ+√ΔC1sinhL+C2coshLC1coshL+C2sinhL}∓2ψk3/2A(d2ψ−E){dψ+√ΔC1sinhL+C2coshLC1coshL+C2sinhL}−1
|
(3.1.26)
|
|
V14(ξ)=−1+4dψk2lA2{dψ+√ΔC1sinhL+C2coshLC1coshL+C2sinhL}−2A2k2l{dψ+√ΔC1sinhL+C2coshLC1coshL+C2sinhL}2+4dk2lψ2A2(d2ψ−E){dψ+√ΔC1sinhL+C2coshLC1coshL+C2sinhL}−1−2ψ2k2lA2(d2ψ−E)2{dψ+√ΔC1sinhL+C2coshLC1coshL+C2sinhL}−2
|
(3.1.27)
|
Consider the arbitrary constants as C1≠0 and C2=0, then
|
U14(ξ)=±1Ak3/2{2dψk3∓Aw√k}∓2Ak3/2(dψ+√ΔtanhL)∓2ψk3/2A(d2ψ−E)(dψ+√ΔtanhL)−1
|
(3.1.28)
|
|
V14(ξ)=−1+4dψk2lA2(dψ+√ΔtanhL)−2A2k2l(dψ+√ΔtanhL)2+4dψ2k2lA2(d2ψ−E)(dψ+√ΔtanhL)−1−2ψ2k2lA2(d2ψ−E)2(dψ+√ΔtanhL)−2
|
(3.1.29)
|
where L=√ΔξαAα and ξ=k1/αx+l1/αy+w1/αt.
When B=0, ψ=A−C and Δ=ψE<0,
|
U15(ξ)=±1Ak3/2{2dψk3∓Aw√k}∓2Ak3/2{dψ+√−Δ−C1sinM+C2cosMC1cosM+C2sinM}∓2k3/2ψA(d2ψ−E){dψ+√−Δ−C1sinM+C2cosMC1cosM+C2sinM}−1
|
(3.1.30)
|
|
V15(ξ)=−1+4dψk2lA2{dψ+√−Δ−C1sinM+C2cosMC1cosM+C2sinM}−2A2k2l{dψ+√−Δ−C1sinM+C2cosMC1cosM+C2sinM}2+4dψ2k2lA2(d2ψ−E){dψ+√−Δ−C1sinM+C2cosMC1cosM+C2sinM}−1−2k2lψ2A2(d2ψ−E)2{dψ+√−Δ−C1sinM+C2cosMC1cosM+C2sinM}−2
|
(3.1.31)
|
For particular case C1≠0 and C2=0,
|
U15(ξ)=±1Ak3/2{2dψk3∓Aw√k}∓2Ak3/2(dψ−√−ΔtanM)∓2k3/2ψA(d2ψ−E)(dψ−√−ΔtanM)−1
|
(3.1.32)
|
|
V15(ξ)=−1+4dψk2lA2(dψ−√−ΔtanM)−2A2k2l(dψ−√−ΔtanM)2+4dψ2k2lA2(d2ψ−E)(dψ−√−ΔtanM)−1−2k2lψ2A2(d2ψ−E)2(dψ−√−ΔtanM)−2
|
(3.1.33)
|
where M=√−ΔξαAα and ξ=k1/αx+l1/αy+w1/αt.
Following the same procedure as above for Eqs. (3.1.10)–(3.1.13) together with Eqs. (2.2.7)–(2.2.11), we might obtain more general closed form traveling wave solutions to the space time fractional (2+1)-dimensional dispersive long wave equations in terms of hyperbolic function, trigonometric function and rational function. To avoid the disturbance of readers the results have not been recorded here.
3.2. The (3+1)-dimensional space time fractional mKdV-ZK equation
Let us consider the (3+1)-dimensional space time fractional mKdV-ZK equation in the form
|
Dαtu+δu2Dαxu+D3αxu+Dαx(D2αyu)+Dαx(D2αzu)=0,
|
(3.2.1)
|
where 0<α⩽1 and δ is an arbitrary constant. This equation is derived for plasma comprised of cool and hot electrons and a species of fluid ions [44].
Using the fractional composite transformation
|
u(x,y,z,t)=U(ξ),ξ=l1/αx+m1/αy+n1/αz−ω1/αt,
|
(3.2.2)
|
where l,m,n and ω are non-zero parameters, Eq. (3.2.1) is turned into the ordinary differential equation
|
−ωDαξU+δlU2DαξU+(l3+lm2+ln2)D3αξU=0.
|
(3.2.3)
|
The anti-derivative of Eq. (3.2.3) with integral constant zero possesses
|
−ωU+δl3U3+(l3+lm2+ln2)D2αξU=0.
|
(3.2.4)
|
Considering the value of n obtained by homogeneous balance to Eq. (3.2.4), Eq. (2.2.4) takes the form
|
U(ξ)=a0+a1(d+DαξG/G)+b1(d+DαξG/G)−1,
|
(3.2.5)
|
where at least one of a1 and b1 is non-zero.
Substitute Eq. (3.2.5) with the help of Eq. (2.2.5) into Eq. (3.2.4), we obtain a polynomial in (d+DαξG/G). Equating each term of this polynomial to zero gives a set of algebraic equations for a0,a1,b0,b1,and ω. Solving these equations by Maple gives the following set of solutions:
|
Set−1:a0=±(2dψ+B)A√3(l2+m2+n2)−2δ,a1=±ψδA√−6δ(l2+m2+n2),b1=0,ω=−l(l2+m2+n2)(4Eψ+B)2A2
|
(3.2.6)
|
|
Set−2:a0=±(2dψ+B)2δA√−6δ(l2+m2+n2),ω=−l(l2+m2+n2)(4Eψ+B)2A2,a1=0,b1=∓(d2ψ+Bd−E)δA√−6δ(l2+m2+n2)
|
(3.2.7)
|
Utilizing Eqs. (3.2.6), (3.2.7) into Eq. (3.2.5) yields the following general expressions for solutions:
|
U1(ξ)=∓√−6δ(l2+m2+n2)2Aδ(B−2ψDαξG/G)
|
(3.2.8)
|
|
U2(ξ)=±√−6δ(l2+m2+n2)2Aδ{2dψ+B−2(d2ψ+Bd−E)(d+DαξG/G)−1},
|
(3.2.9)
|
where ξ=l1/αx+m1/αy+n1/αz−{−l(l2+m2+n2)(4Eψ+B)2A2}1/αt.
Eq. (3.2.8) along with Eqs. (2.2.7)–(2.2.11) provides the following solutions in terms of hyperbolic, trigonometric and rational:
When B≠0, ψ=A−C and Ω=B2+4Eψ>0,
|
U11(ξ)=±√−6δ(l2+m2+n2)2Aδ√ΩC1sinh(√Ωξα2Aα)+C2cosh(√Ωξα2Aα)C1cosh(√Ωξα2Aα)+C2sinh(√Ωξα2Aα)
|
(3.2.10)
|
The choices for arbitrary constants as C1≠0, C2=0, reduces Eq. (3.2.10) to
|
U11(ξ)=±√−6δ(l2+m2+n2)2Aδ√Ωtanh(√Ωξα2Aα)
|
(3.2.11)
|
where ξ=l1/αx+m1/αy+n1/αz−{−l(l2+m2+n2)(4Eψ+B)2A2}1/αt.
When B≠0, ψ=A−C and Ω=B2+4Eψ<0,
|
U12(ξ)=±√−6δ(l2+m2+n2)2Aδ√−Ω−C1sin(√−Ωξα2Aα)+C2cos(√−Ωξα2Aα)C1cos(√−Ωξα2Aα)+C2sin(√−Ωξα2Aα)
|
(3.2.12)
|
The choices for arbitrary constants as C1≠0, C2=0, reduces Eq. (3.2.12) to
|
U12(ξ)=∓√−6δ(l2+m2+n2)2Aδ√−Ωtan(√−Ωξα2Aα),
|
(3.2.13)
|
where ξ=l1/αx+m1/αy+n1/αz−{−l(l2+m2+n2)(4Eψ+B)2A2}1/αt.
When B≠0, ψ=A−C and Ω=B2+4Eψ=0,
|
U13(ξ)=±ψαC2√−6δ(l2+m2+n2)Aδ(C1α+C2ξα)
|
(3.2.14)
|
In particular, if C1=0, C2≠0, then
|
U13(ξ)=±ψαAδξα√−6δ(l2+m2+n2)
|
(3.2.15)
|
where ξ=l1/αx+m1/αy+n1/αz−{−l(l2+m2+n2)(4Eψ+B)2A2}1/αt.
When B=0, ψ=A−C and Δ=ψE>0,
|
U14(ξ)=±√−6Δδ(l2+m2+n2)Aδ{C1sinh(√ΔξαAα)+C2cosh(√ΔξαAα)C1cosh(√ΔξαAα)+C2sinh(√ΔξαAα)}
|
(3.2.16)
|
For C1≠0, C2=0, Eq. (3.2.16) becomes
|
U14(ξ)=±√−6Δδ(l2+m2+n2)Aδtanh(√ΔξαAα)
|
(3.2.17)
|
where ξ=l1/αx+m1/αy+n1/αz−{−4Eψl(l2+m2+n2)2A2}1/αt.
When B=0, ψ=A−C and Δ=ψE<0,
|
U15(ξ)=±√6Δδ(l2+m2+n2)Aδ{−C1sin(√−ΔξαAα)+C2cos(√−ΔξαAα)C1cos(√−ΔξαAα)+C2sin(√−ΔξαAα)}
|
(3.2.18)
|
If C1≠0, C2=0, Eq. (3.2.18) becomes
|
U15(ξ)=∓√6Δδ(l2+m2+n2)Aδtan(√−ΔξαAα)
|
(3.2.19)
|
where ξ=l1/αx+m1/αy+n1/αz−{−4Eψl(l2+m2+n2)2A2}1/αt.
Making use of Eq. (3.2.9) as above will also provide further new and general exact traveling wave solutions in terms of hyperbolic, trigonometric and rational. For convenience of readers we have not record these all solutions in this study. Guner et al. [45] obtained only four solutions by (G′/G)-expansion method where as our applied fractional generalized (DαξG/G)-expansion method has ensured many solutions which are further new and general. To the best of our knowledge, these solutions have not been visible in any earlier study.
3.3. The space time fractional modified regularized long-wave equation
The following nonlinear space-time fractional modified regularized long-wave equation is considered to be examined for further exact traveling wave solutions:
|
Dαtu+δDαxu+τu2Dαxu−ηDαtD2αxu=0,0<α⩽1
|
(3.3.1)
|
where δ,τand η are constants. This equation proposed by Benjamin et al. to describe approximately the unidirectional propagation of long waves in certain dispersive systems is supposed to be alternative to the modified KdV equation. Eq. (3.3.1) has been modeled to demonstrate some physical phenomena like transverse waves in shallow water and magneto hydrodynamic waves in plasma and photon packets in nonlinear crystals [46,47,48].
The fractional complex transformation
|
u(x,t)=U(ξ),ξ=x−v1/αt,
|
(3.3.2)
|
reduces Eq. (3.3.1) to the ODE
|
(δ−v)DαξU+τU2DαξU+vηD3αξU=0
|
(3.3.3)
|
Integrating Eq. (3.3.3) and setting integral constant to zero gives
|
(δ−v)U+τ3U3+ηvD2αξU=0
|
(3.3.4)
|
Taking homogeneous balance between highest order linear term and highest nonlinear term from Eq. (3.3.4) yields n=1 and the solution Eq. (2.2.4) is reduced to
|
U(ξ)=a0+a1(d+DαξG/G)+b1(d+DαξG/G)−1
|
(3.3.5)
|
where at least one of a1 and b1 is nonzero.
Eq. (3.3.4) with the help of Eq. (2.2.5) and Eq. (3.3.5) makes a polynomial in (d+DαξG/G). Set each coefficient of this polynomial to zero and obtain a system of equations for a0,a1,b1 and v. Calculating these equations by Maple gives the following solutions:
|
Set−1:a0=±3lηδ(2dψ+B)√−3τηδ(2A2+4l2ηEψ+l2ηB2),a1=∓6lηδψ√−3τηδ(2A2+4l2ηEψ+l2ηB2),b1=0,v=2lδA22A2+4l2ηEψ+l2ηB2
|
(3.3.6)
|
|
Set−2:a0=±3lηδ(2dψ+B)√−3τηδ(2A2+4l2ηEψ+l2ηB2),b1=∓6lηδ(d2ψ+Bd−E)√−3τηδ(2A2+4l2ηEψ+l2ηB2),a1=0,v=2lδA22A2+4l2ηEψ+l2ηB2
|
(3.3.7)
|
Inserting the values appearing in Eq. (3.3.6) and Eq. (3.3.7) into Eq. (3.3.5) possesses the following expressions for solutions:
|
U1(ξ)=±3lηδ√−3τηδ(2A2+4l2ηEψ+l2ηB2)(B−2ψDαξG/G)
|
(3.3.8)
|
|
U2(ξ)=±3lηδ(2dψ+B)−2(d2ψ+Bd−E)(d+DαξG/G)−1√−3τηδ(2A2+4l2ηEψ+l2ηB2)
|
(3.3.9)
|
where ξ=x−(2lδA22A2+4l2ηEψ+l2ηB2)1/αt.
Eq. (3.3.8) with the help of Eqs. (2.2.7)–(2.2.11) provides the following solutions:
Case 1: When B≠0, ψ=A−C and Ω=B2+4Eψ>0,
|
U11(ξ)=∓3lηδ√Ω√−3τηδ(2A2+4l2ηEψ+l2ηB2)×C1sinh(√Ωξα2Aα)+C2cosh(√Ωξα2Aα)C1cosh(√Ωξα2Aα)+C2sinh(√Ωξα2Aα)
|
(3.3.10)
|
Since C1 and C2 are arbitrary constants, one may chooseC1≠0, C2=0 and under simplification Eq. (3.3.10) becomes
|
U11(ξ)=∓3lηδ√Ω√−3τηδ(2A2+4l2ηEψ+l2ηB2)×tanh(√Ωξα2Aα)
|
(3.3.11)
|
where ξ=x−(2lδA22A2+4l2ηEψ+l2ηB2)1/αt.
Case 2: When B≠0, ψ=A−C and Ω=B2+4Eψ<0,
|
U12(ξ)=∓3lηδ√−Ω√−3τηδ(2A2+4l2ηEψ+l2ηB2)×−C1sin(√−Ωξα2Aα)+C2cos(√−Ωξα2Aα)C1cos(√−Ωξα2Aα)+C2sin(√−Ωξα2Aα)
|
(3.3.12)
|
In particular, if we choose C1≠0, C2=0, then under simplification Eq. (3.3.12) reduces to
|
U12(ξ)=±3lηδ√−Ω√−3τηδ(2A2+4l2ηEψ+l2ηB2)×tan(√−Ωξα2Aα)
|
(3.3.13)
|
where ξ=x−(2lδA22A2+4l2ηEψ+l2ηB2)1/αt.
Case 3: When B≠0, ψ=A−C and Ω=B2+4Eψ=0,
|
U13(ξ)=∓3lηδ√−3τηδ(2A2+4l2ηEψ+l2ηB2)×2ψαC2C1α+C2ξα
|
(3.3.14)
|
If C1=0, C2≠0, Eq. (3.3.14) is simplified to
|
U13(ξ)=∓6ψαlηδξα√−3τηδ(2A2+4l2ηEψ+l2ηB2)
|
(3.3.15)
|
where ξ=x−(2lδA22A2+4l2ηEψ+l2ηB2)1/αt.
Case 4: When B=0, ψ=A−C and Δ=ψE>0,
|
U14(ξ)=∓6lηδ√Δ√−3τηδ(2A2+4l2ηEψ)×C1sinh(√ΔξαAα)+C2cosh(√ΔξαAα)C1cosh(√ΔξαAα)+C2sinh(√ΔξαAα)
|
(3.3.16)
|
For particular values of the arbitrary constants as C1≠0, C2=0, Eq. (3.3.16) possesses
|
U14(ξ)=∓6lηδ√Δ√−3τηδ(2A2+4l2ηEψ)×tanh(√ΔξαAα)
|
(3.3.17)
|
where ξ=x−(2lδA22A2+4l2ηEψ)1/αt.
Case 5: When B=0, ψ=A−C and Δ=ψE<0,
|
U15(ξ)=±6lηδ√−Δ√−3τηδ(2A2+4l2ηEψ)×C1sin(√−ΔξαAα)+C2cos(√−ΔξαAα)C1cos(√−ΔξαAα)+C2sin(√−ΔξαAα)
|
(3.3.18)
|
The choice of the arbitrary constants as C1≠0, C2=0 forces Eq. (3.3.18) to turn into
|
U15(ξ)=±6lηδ√−Δ√−3τηδ(2A2+4l2ηEψ+l2ηB2)×tan(√−ΔξαAα)
|
(3.3.19)
|
where ξ=x−(2lδA22A2+4l2ηEψ)1/αt.
The obtained solutions in terms of hyperbolic function, trigonometric function and rational function are new and more general. In similar way, much more new and general solutions of the closed form can be constructed by using Eq. (3.3.9) along with Eqs. (2.2.7)–(2.2.11). The solutions obtained by modified simple equation method [49] and the improved fractional Riccati expansion method [50] are only in terms of hyperbolic, where as we achieved those in terms of hyperbolic function, trigonometric function and rational function in explicitly general form. We have not recorded these results to avoid the annoyance of the readers. On comparison, our solutions are general and much more in number than those of [49,50].
4. Graphical representations of the solutions
The complex physical mechanism of real world can be illustrated by means of graphical representations. The graphs (Figures 1–3) drown for the exact solutions obtained in this study has been appeared in different shape like kink type soliton, bell shape soliton, singular bell shape soliton, anti bell shape soliton, periodic solution, singular periodic solution etc. We have recorded here only few graphs rather than all for making it easily readable.
5. Conclusion
This article has been put in writing further new and general traveling wave solutions in closed form to the space time fractional (2+1)-dimensional dispersive long wave equations, the (3+1)-dimensional space time fractional mKdV-ZK equation and the space time fractional modified regularized long-wave equation. The solutions have successfully constructed in terms of hyperbolic function, trigonometric function and rational function by the newly established fractional generalized (DαξG/G)-expansion method. To the best of our knowledge, these results are not available in the literature. The obtained solutions might play important roles to analyze the mechanisms of complex physical phenomena of the real world. The performance of the suggested method is highly appreciable for its easiest productive behavior and worthy for revealing rare solutions to more fractional order nonlinear evolution equations. Since each nonlinear equation has its own anomalous characteristic, the future research might be how the suggested method is compatible for revealing the solutions to other fractional nonlinear evolution equations.
Conflict of interest
All authors have contributed to the manuscript equally. We all discussed the outcomes of the proposed method and approved the final manuscript.









 DownLoad:
DownLoad: 





