The intention and novelty in the presented study were to develop the regularity analysis for a parabolic equation describing a type of Eyring-Powell fluid flow in two dimensions. We proved that, under certain general conditions involving the space of bounded mean oscillation (BMO) and the Lebesgue space L2, there exist bounded and regular velocity solutions under the L2 space scope. This conclusion was additionally supplemented by the condition of a finite square integrable initial data (also some of the obtained expressions involved the gradient and the laplacian of the initial velocity distribution). To make our results further general, the proposed analysis was extended to cover regularity results in Lp(p>2) spaces. As a remarkable conclusion, we highlight that the solutions to the two dimensional Eyring-Powell fluid flow did not exhibit blow up behaviour.
Citation: José Luis Díaz Palencia, Saeed Ur Rahman, Saman Hanif. Regularity criteria for a two dimensional Erying-Powell fluid flowing in a MHD porous medium[J]. Electronic Research Archive, 2022, 30(11): 3949-3976. doi: 10.3934/era.2022201
| [1] | Tahereh Karamzadeh, Hamzeh Alipour, Marziae Shahriari-Namadi, Abbasali Raz, Kourosh Azizi, Masoumeh Bagheri, Mohammad D. Moemenbellah-Fard . Molecular characterization of the netrin-1 UNC-5 receptor in Lucilia sericata larvae. AIMS Genetics, 2019, 6(3): 46-54. doi: 10.3934/genet.2019.3.46 |
| [2] | Natalie J. Nokoff, Sharon Travers, Naomi Meeks . Two cases of androgen insensitivity due to somatic mosaicism. AIMS Genetics, 2015, 2(2): 104-109. doi: 10.3934/genet.2015.2.104 |
| [3] | Xiaochen Fan, David A F Loebel, Heidi Bildsoe, Emilie E Wilkie, Jing Qin, Junwen Wang, Patrick P L Tam . Tissue interactions, cell signaling and transcriptional control in the cranial mesoderm during craniofacial development. AIMS Genetics, 2016, 3(1): 74-98. doi: 10.3934/genet.2016.1.74 |
| [4] | Huong Thi Thu Phung, Hoa Luong Hieu Nguyen, Dung Hoang Nguyen . The possible function of Flp1 in homologous recombination repair in Saccharomyces cerevisiae. AIMS Genetics, 2018, 5(2): 161-176. doi: 10.3934/genet.2018.2.161 |
| [5] | Tú Nguyen-Dumont, Jenna Stewart, Ingrid Winship, Melissa C. Southey . Rare genetic variants: making the connection with breast cancer susceptibility. AIMS Genetics, 2015, 2(4): 281-292. doi: 10.3934/genet.2015.4.281 |
| [6] | Nusrat Masood, Saman Khan, Suaib Luqman, Shakil Ahmed . Thymoquinone disrupts the microtubule dynamics in fission yeast Schizosaccharomyces pombe. AIMS Genetics, 2016, 3(4): 239-251. doi: 10.3934/genet.2016.4.239 |
| [7] | Chiara De Santi, Sucharitha Gadi, Agnieszka Swiatecka-Urban, Catherine M. Greene . Identification of a novel functional miR-143-5p recognition element in the Cystic Fibrosis Transmembrane Conductance Regulator 3’UTR. AIMS Genetics, 2018, 5(1): 53-62. doi: 10.3934/genet.2018.1.53 |
| [8] | Cristiane Sá Roriz Fonteles, Richard H. Finnell, Timothy M. George, Raymond J. Harshbarger . Craniosynostosis: current conceptions and misconceptions. AIMS Genetics, 2016, 3(1): 99-129. doi: 10.3934/genet.2016.1.99 |
| [9] | Sergio Branciamore, Andrei S. Rodin, Grigoriy Gogoshin, Arthur D. Riggs . Epigenetics and Evolution: Transposons and the Stochastic Epigenetic Modification Model. AIMS Genetics, 2015, 2(2): 148-162. doi: 10.3934/genet.2015.2.148 |
| [10] | Dawei Liu, Zeeshan Shaukat, Rashid Hussain, Mahwish Khan, Stephen L. Gregory . Drosophila as a model for chromosomal instability. AIMS Genetics, 2015, 2(1): 1-12. doi: 10.3934/genet.2015.1.1 |
The intention and novelty in the presented study were to develop the regularity analysis for a parabolic equation describing a type of Eyring-Powell fluid flow in two dimensions. We proved that, under certain general conditions involving the space of bounded mean oscillation (BMO) and the Lebesgue space L2, there exist bounded and regular velocity solutions under the L2 space scope. This conclusion was additionally supplemented by the condition of a finite square integrable initial data (also some of the obtained expressions involved the gradient and the laplacian of the initial velocity distribution). To make our results further general, the proposed analysis was extended to cover regularity results in Lp(p>2) spaces. As a remarkable conclusion, we highlight that the solutions to the two dimensional Eyring-Powell fluid flow did not exhibit blow up behaviour.
Craniosynostosis is a cranial malformation occurring in approximately 1 in 2500 live births. In around 15% of these cases [1,2], it is part of a craniofacial syndrome associating typical facial features such as exorbitism and maxillary retrusion to the premature fusion of cranial sutures [3]. Common variable features also include secondary complications, such as hydrocephalus, intellectual disability, or sleep apnea. However, the diversity of phenotypes is not always straightforwardly explained by the genetic alteration. Knowing the phenotypical prognosis helps managing and preventing some complications, by proposing early adapted treatment.
FGFR2 (Fibroblast Growth Factor Receptor 2) is akey gene involved in craniosynostosis syndromes such as Crouzon and Pfeiffer syndromes. It codes for a membrane receptor with three extracellular immunoglobulin(Ig)-like domains, a transmembrane domain and an intracellular tyrosine kinase (TK) domain. It is expressed from gastrulation onwards in the developing skeleton, particularly in the frontal bones of the skull and in the limbs [4].
Since 1994, many FGFR2 mutations have been identified in patients with Crouzon syndromes [4,5,6,7,8]. Most of them are missense mutations affecting the extracellular domain [9,10]. Besides, rare mutations affect the intracellular TK domain of FGFR2 with subsequent constitutive activation [9,11]. The clinical phenotypes associated with these rare mutations have been described but there is little genotype-phenotype correlation regarding subtle findings. Therefore, all cases must still be centralized and described precisely.
From a cohort of patients affected by craniofacial syndromes, we identified three patients with missense mutations affecting the same amino acid Asn549, located in the FGFR2 TK domain, we discuss their molecular mechanism and compare their phenotypes.
Blood samples were drawn for diagnostic purposes after informed consent. DNA was extracted using a QIAamp blood kit (Qiagen, Courtaboeuf, France). FGFR2 exons 4, 6, 8 (IIIa), 10 (IIIc), 11, 14, 15, 16, 17 were amplified and sequenced directly on both strands (Life technologies, Courtaboeuf, France) then analyzed using Sescape (Life Technologies and Alamut software (Interactive Biosoftware, Rouen, France). The NCBI reference sequences were FGFR2 (NM_000141.4) for c.DNA and FGFR2 (NG_012449.1) for exons numbering. The mutations nomenclature is based on HGVS nomenclature guidelines (http://www.hgvs.org/mutnomen).
Patient 1 is a sixteen-year-old boy with Crouzon syndrome, showing facial retrusion and prominent forehead. His parents and four siblings show no clinical sign of craniosynostosis. Pregnancy was uneventful, head circumference at birth was 33 cm. He was born with isolated sagittal suture fusion. Hydrocephalus at birth required ventriculo-peritoneal shunt, that was removed at the age of ten, after decompression surgery. Other surgical history includes forehead advancement at one, and extensive frontal surgery at three, followed by frontal subcutaneous fat injection. He never presented papilledema. Recent brain imaging reveals asymptomatic cavum septum pellucidum, but no ventricular enlargement nor Chiari malformation, which is a displacement of cerebellar tonsils through the foramen magnum, sometimes associated with craniostenosis (Figure 1a). Recent clinical evaluation reveals frequent headaches, behavioral difficulties and intellectual disability (IQ 70), with normal neurological and sensory examination.
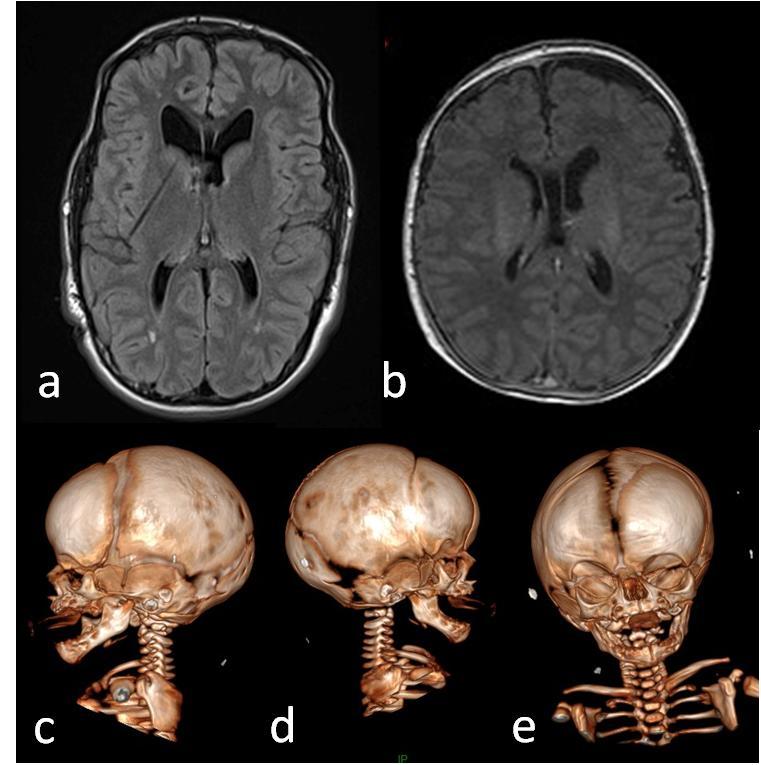 Figure 1. a) Case 1 at the age of 14, brain MRI (T1 sequence, axial) shows cavum septum pellucidum and the sequelae of a right ventricular catheter, as hydrocephalus had been treated with ventriculo-peritoneal shunting; b) c) d) e) Case 3 at the age of 1 before decompressive craniectomy was performed: b) Brain MRI (T1 sequence, axial) shows cavum septum pellucidum and mild ventricular dilatation. c) d) e) 3D CT scan shows right coronal suture fusion and lambdoid ridge.
Figure 1. a) Case 1 at the age of 14, brain MRI (T1 sequence, axial) shows cavum septum pellucidum and the sequelae of a right ventricular catheter, as hydrocephalus had been treated with ventriculo-peritoneal shunting; b) c) d) e) Case 3 at the age of 1 before decompressive craniectomy was performed: b) Brain MRI (T1 sequence, axial) shows cavum septum pellucidum and mild ventricular dilatation. c) d) e) 3D CT scan shows right coronal suture fusion and lambdoid ridge.This patient presented c.1646A > G, p.Asn549Ser mutation, which has been reported in the Human Gene Mutation Database (Cardiff University, 2015) but has never been described clinically (Figure 2).
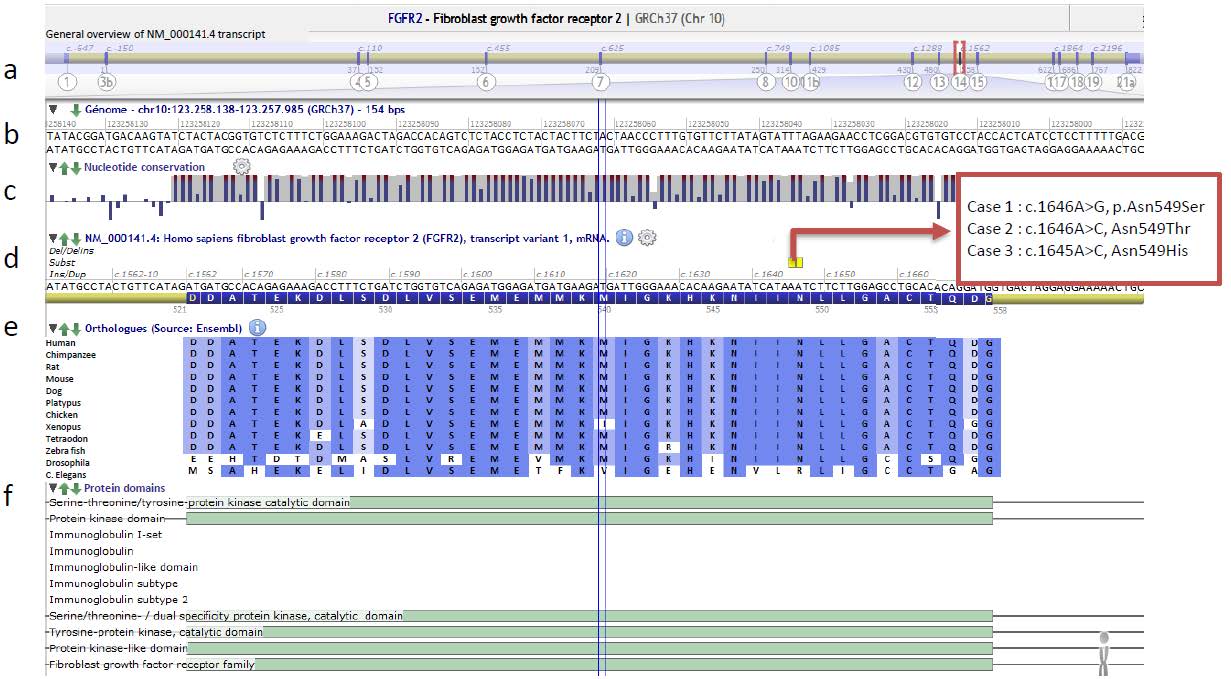 Figure 2. Localization of mutations in FGFR2 exon 14, coding for FGFR2 tyrosine kinase 1 domain (Alamut Visual Interactive Biosoftware, France). a) general overview of Humo Sapiens FGFR2 (NM_000141.4) transcript, composed of 18 exons with genomic numbering, exon 14 is shown in red brackets; b) exon 14 genomic localization; c) nucleotide conservation; d) amino-acid positions: the mutations localizations for the three cases are shown in yellow (red arrow); e) amino-acid conservation among different species: the mutations are located in highly conserved nucleotides; f) exon 14 transcript, this exon codes for tyrosine kinase domain.
Figure 2. Localization of mutations in FGFR2 exon 14, coding for FGFR2 tyrosine kinase 1 domain (Alamut Visual Interactive Biosoftware, France). a) general overview of Humo Sapiens FGFR2 (NM_000141.4) transcript, composed of 18 exons with genomic numbering, exon 14 is shown in red brackets; b) exon 14 genomic localization; c) nucleotide conservation; d) amino-acid positions: the mutations localizations for the three cases are shown in yellow (red arrow); e) amino-acid conservation among different species: the mutations are located in highly conserved nucleotides; f) exon 14 transcript, this exon codes for tyrosine kinase domain.Patient 2 is a fifteen-year-old girl presenting with exorbitism, maxillary retrusion, and broad thumbs that corresponds to Pfeiffer syndrome. Parents have a normal appearance and further family history is unknown. Pregnancy was uneventful. She was born with coronal fusion, then developed premature sagittal fusion. Ventriculoperitoneal shunt was placed at the age of six weeks for hydrocephalus, and was removed at ten. She underwent bilateral parietal decompression at the age of four and ten, posterior decompression with distractors at thirteen. Ophthalmological examination revealed strabismus, which was treated surgically, and right ptosis. Neurological imaging shows Chiari malformation, which was operated at the age of five, complicated with cervical C3-C7 syrinx, and no intracranial malformation. Clinical examination shows unilateral hypoacousia, upper limbs paresthesias and lower limbs weakness that progressively got better after occipital foramen surgery. She presents behavioral abnormalities treated with ritaline but no major intellectual disability. She has sleep apnea syndrome, which required CPAP therapy at night for years and resolved after tonsillectomy.
She was diagnosed with c.1646A > C, Asn549Thr mutation, reported once [12] (Figure 2).
Patient 3 is a four-year-old boy presenting with typical Crouzon syndrome with exorbitism and maxillary retrusion, associated with right coronal suture fusion and lambdoid ridge at birth (Figure 1c, d, e). His father and father’s mother had a crouzonoid appearance but were not followed. Pregnancy was uneventful, head circumference at birth was 38.5 cm. He underwent fronto-orbital advancement with decompressive craniectomy at the age of one, tonsillectomy at two. At the age of three, he presented premature bilateral coronal and sagittal fusion, for which he underwent parietal decompression. Ophthalmological examination at the time revealed bilateral papilledema, a sign of hydrocephalus, that resolved after surgery, and left ptosis. Recent head CT scan shows asymptomatic cavum septum pellucidum, no ventricular enlargement nor cerebellar tonsils malformation (Figure 1b). There is no neurological or sensory impairment, and no major intellectual disability. He developed moderate sleep apnea syndrome (apnea+hypopnea index 0.8/min).
He presented with c.1645A > C, Asn549His mutation, which has been described already [9] (Figure 2).
Mutations affecting FGFR2 TK domain are a subgroup of FGFR2 mutations found in syndromic craniosynostoses. They may correlate with a phenotypical subgroup, with particular characteristics and complications.
Although most FGFR2 mutations found in patients with Crouzon and Pfeiffer syndromes are located in exons 8 (IIIa) and 10 (IIIc) that encode the extracellular part of the protein [9,10], screening of patients with syndromic craniosynostosis has led to the identification of nine distinct mutations in FGFR2 intracellular TK domain (exons 14, 15, 16), accounting for~10% of patients with craniosynostosis [9,11,12,13,14]. In Necker-Enfants Malades Hospital, screening of FGFR2 in all patients with Crouzon and Pfeiffer syndromes led to the identification of 7.4% of TK domain mutations (5/67), 4 affecting Asn549 and one Lys659. Patients with other syndromic craniosynostoses did not present with TK domain mutations. Only three patients with Asn549 variants were available for complete clinical follow-up. The three mutations are localized in c.1645A and c.1646A, highly conserved nucleotides, which is consistent with their pathological impact (Figure 2). When screening FGFR2 for all patients with any syndromic craniosynostosis, Kan et al. found 6 mutations (7%, 6/85) occurring in the TK domain, in 8 patients (3%, 8/259) [9] which is consistent with our population. On the opposite, Roscioli et al. do not report any mutation in the TK domain in a review of 630 patients, but it is likely that they have not been screened for this domain [15].
The protein structure itself is not affected by the Asn549 changes, according to simulated Polyphen scores (score max=1 for both SIFT and Polyphen softwares). The mechanism by which these mutations lead to FGFR2 gain of function has been explored by Chen et al., who compared the crystal structures of wild-type FGFR2 kinase domain with those of N549H and N549T [11]. They found that these mutations lead to ligand-independent FGFR2 kinase activation by directly disengaging a molecular brake that is conserved in a wide range of receptors tyrosine kinase. More precisely, N549 maps onto the kinase hinge (the linker between β5 strand and αD helix). Crystal analysis of the hinge region of the N549H and N549T mutant kinases reveals the loss of the hydrogen bonds between mutated residue 549 and the backbone atoms of the loop between the αC helix and the β4 strand, relaxing the N-lobe to rotate towards the C-lobe. This mechanism prevents normal function of this molecular break and constitutively activates FGFR2 for p.Asn549His and p.Asn549Thr changes. We can hypothesize that the Asn549Ser mutation has the same effect.
On a phenotypical point of view, the three patients we report present with typical Crouzon or Pfeiffer syndrome: exorbitism, maxillary retrusion, premature suture fusion, and one patient with hand abnormalities. However, the three of them developed hydrocephalus, which happens in only 40% of patients with Crouzon and Pfeiffer syndrome in general [16]. Two patients have a cavum septum pellucidum, which is found in only 1.1% of general population. Among patients with syndromic craniosynostosis, cavum septum pellucidum has been reported in 25% of patients with Apert syndrome, a congenital disorder characterized by craniosynostosis associated with malformations of the hands and feet [17], but not in Crouzon patients. This finding was considered incidental, but may also be interpreted as obstructing cerebrospinal fluid circulation, and thus causing hydrocephalus. Hydrocephalus may cause intellectual disability, which could explain this tendency in our three patients, and in the cases reported by Wilkie et al. and Kan et al. [9,12].
The two patients with p.Asn549His mutations reported by Kan et al. display Crouzon appearance with developmental delay and hydrocephalus, and one of them has craniosynostosis with Chiari malformation, while the other has macrocephaly [9]. The newly reported p.Asn549Ser mutation is also associated, in our case, with hydrocephalus and secondary intellectual disability.
Overall, although no definitive conclusion can be drawn from so few cases, hydrocephalus seems to be an atypically frequent feature in patients with mutations in the FGFR2 TK domain: patients with p.Lys526Glu mutation display scaphocephaly with intellectual disability [18]. Kan et al. already reported that hydrocephalus and intellectual disability were over-represented in patients with TK domains mutations compared with typical Crouzon and Pfeiffer syndromes [9].
Patients with Crouzon and Pfeiffer syndromes presenting with missense mutations of Asn549 residue, located in FGFR2 TK domain, are at high risk of developing hydrocephalus. Therefore, regular imaging and clinical monitoring is useful to treat hydrocephalus as early as possible and prevent secondary intellectual disability.
All authors declare no conflict of interest in this paper.
| [1] |
R. E. Powell, H. Eyring, Mechanisms for the relaxation theory of viscosity, Nature, 154 (1944), 427–428. https://doi.org/10.1038/154427a0 doi: 10.1038/154427a0

|
| [2] |
A. Ara, N. A. Khan, H. Khan, F. Sultan, Radiation effect on boundary layer flow of an Eyring–Powell fluid over an exponentially shrinking sheet, Ain Shams Eng. J., 5 (2014), 1337–1342. https://doi.org/10.1016/j.asej.2014.06.002 doi: 10.1016/j.asej.2014.06.002

|
| [3] |
T. Hayat, Z. Iqbal, M. Qasim, S. Obaidat, Steady flow of an Eyring Powell fluid over a moving surface with convective boundary conditions, Int. J. Heat Mass Transfer, 55 (2012), 1817–1822. https://doi.org/10.1016/j.ijheatmasstransfer.2011.10.046 doi: 10.1016/j.ijheatmasstransfer.2011.10.046

|
| [4] |
A. Riaz, R. Ellahi, M. M. Bhatti, Study of heat and mass transfer in the Eyring–Powell model of fluid propagating peristaltically through a rectangular compliant channel, Heat Transfer Res., 50 (2019), 1539–1560. https://doi.org/10.1615/HeatTransRes.2019025622 doi: 10.1615/HeatTransRes.2019025622

|
| [5] |
M. Y. Malik, A. Hussain, S. Nadeem, Boundary layer flow of an Eyring–Powell model fluid due to a stretching cylinder with variable viscosity, Sci. Iran., 20 (2013), 313–321. https://doi.org/10.1016/j.scient.2013.02.028 doi: 10.1016/j.scient.2013.02.028

|
| [6] |
B. Mallick, J. C. Misra, Peristaltic flow of Eyring-Powell nanofluid under the action of an electromagnetic field, Eng. Sci. Technol. Int. J., 22 (2019), 266–281. https://doi.org/10.1016/j.jestch.2018.12.001 doi: 10.1016/j.jestch.2018.12.001

|
| [7] |
M. Ramzan, M. Bilal, S. Kanwal, J. D. Chung, Effects of variable thermal conductivity and non-linear thermal radiation past an Eyring Powell nanofluid flow with chemical Reaction, Commun. Theor. Phys., 67 (2017), 723. https://doi.org/10.1088/0253-6102/67/6/723 doi: 10.1088/0253-6102/67/6/723

|
| [8] |
J. Rahimi, D. D. Ganji, M. Khaki, Kh. Hosseinzadeh, Solution of the boundary layer flow of an Eyring-Powell non-Newtonian fluid over a linear stretching sheet by collocation method, Alexandria Eng. J., 56 (2017), 621–627. https://doi.org/10.1016/j.aej.2016.11.006 doi: 10.1016/j.aej.2016.11.006

|
| [9] |
N. S. Akbar, A. Ebaid, Z. H. Khan, Numerical analysis of magnetic field on Eyring-Powell fluid flow towards a stretching sheet, J. Magn. Magn. Mater., 382 (2015), 355–358. https://doi.org/10.1016/j.jmmm.2015.01.088 doi: 10.1016/j.jmmm.2015.01.088

|
| [10] |
T. Javed, Z. Abbas, N. Ali, M. Sajid, Flow of an Eyring–Powell nonnewtonian fluid over a stretching sheet, Chem. Eng. Commun., 200 (2013), 327–336. https://doi.org/10.1080/00986445.2012.703151 doi: 10.1080/00986445.2012.703151

|
| [11] | Y. Zhou, L. Zhen, Logarithmically improved criteria for Navier-Stokes equations, 2008. Available from: https://arXiv.org/pdf/0805.2784.pdf. |
| [12] | C. H. Chan, A. Vasseur, Log improvement of the Prodi-Serrin criteria for Navier-Stokes equations, 14 (2007), 197–212. https://dx.doi.org/10.4310/MAA.2007.v14.n2.a5 |
| [13] | Da Veiga, H. Beirao, A new regularity class for the Navier-Stokes equations in Rn, Chin. Ann. Math., 16 (1995), 407–412. |
| [14] |
C. Cao, E. S. Titi, Regularity criteria for the three-dimensional Navier–Stokes equations, Indiana Univ. Math. J., 57 (2008), 2643–2662. https://doi.org/10.1512/iumj.2008.57.3719 doi: 10.1512/iumj.2008.57.3719

|
| [15] |
Y. Zhou, On regularity criteria in terms of pressure for the Navier-Stokes equations in R3, Proc. Amer. Math. Soc., 134 (2006), 149–156. https://doi.org/10.1090/S0002-9939-05-08312-7 doi: 10.1090/S0002-9939-05-08312-7

|
| [16] |
L. C. Berselli, G. P. Galdi, Regularity criteria involving the pressure for the weak solutions to the Navier-Stokes equations, Proc. Amer. Math. Soc., 130 (2002), 3585–3595. https://doi.org/10.1090/S0002-9939-02-06697-2 doi: 10.1090/S0002-9939-02-06697-2

|
| [17] |
D. U. Chand, M. C. Alberto, S. Y. Jin, Perfect fluid spacetimes and gradient solitons, Filomat, 36 (2022), 829–842. https://doi.org/10.2298/FIL2203829D doi: 10.2298/FIL2203829D

|
| [18] |
M. A. Ragusa, Local Hölder regularity for solutions of elliptic systems, Duke Math. J., 113 (2002), 385–397. https://doi.org/10.1215/S0012-7094-02-11327-1 doi: 10.1215/S0012-7094-02-11327-1

|
| [19] |
S. J. Wang, M. Q. Tian, R. J. Su, A Blow-Up criterion for 3D nonhomogeneous incompressible magnetohydrodynamic equations with vacuum, J. Funct. Spaces, 2022 (2022), 7474964. https://doi.org/10.1155/2022/7474964 doi: 10.1155/2022/7474964

|
| [20] |
B. Manvi, J. Tawade, M. Biradar, S. Noeiaghdam, U. Fernandez-Gamiz, V. Govindan, The effects of MHD radiating and non-uniform heat source/sink with heating on the momentum and heat transfer of Eyring-Powell fluid over a stretching, Results Eng., 14 (2022), 100435. https://doi.org/10.1016/j.rineng.2022.100435 doi: 10.1016/j.rineng.2022.100435

|
| [21] |
S. Arulmozhi, K. Sukkiramathi, S. S. Santra, R. Edwan, U. Fernandez-Gamiz, S. Noeiaghdam, Heat and mass transfer analysis of radiative and chemical reactive effects on MHD nanofluid over an infinite moving vertical plate, Results Eng., 14 (2022), 100394. https://doi.org/10.1016/j.rineng.2022.100394 doi: 10.1016/j.rineng.2022.100394

|
| [22] |
A. Saeed, R. A. Shah, M. S. Khan, U. Fernandez-Gamiz, M. Z. Bani-Fwaz, S. Noeiaghdam, et al., Theoretical analysis of unsteady squeezing nanofluid flow with physical properties, Math. Biosci. Eng., 19 (2022), 10176–10191. https://doi.org/10.3934/mbe.2022477 doi: 10.3934/mbe.2022477

|
| [23] |
P. Thiyagarajan, S. Sathiamoorthy, H. Balasundaram, O. D. Makinde, U. Fernandez-Gamiz, S. Noeiaghdam, et al., Mass transfer effects on mucus fluid in the presence of chemical reaction, Alexandria Eng. J., 62 (2023), 193–210. https://doi.org/10.1016/j.aej.2022.06.030 doi: 10.1016/j.aej.2022.06.030

|
| [24] |
J. V. Tawade, C. N. Guled, S. Noeiaghdam, U. Fernandez-Gamiz, V. Govindan, S. Balamuralitharan, Effects of thermophoresis and Brownian motion for thermal and chemically reacting Casson nanofluid flow over a linearly stretching sheet, Results Eng., 15 (2022), 100448. https://doi.org/10.1016/j.rineng.2022.100448 doi: 10.1016/j.rineng.2022.100448

|
| [25] |
T. Hayat, M. Awais, S. Asghar, Radiative effects in a three dimensional flow of MHD Eyring-Powell fluid, J. Egypt. Math. Soc., 21 (2013), 379–384. https://doi.org/10.1016/j.joems.2013.02.009 doi: 10.1016/j.joems.2013.02.009

|
| [26] | V. A. Solonnikov, Estimates for solutions of nonstationary Navier–Stokes equations, Zap. Nauchn. Semin. Leningr. Otd. Mat. Inst. Steklova, 38 (1973) 153–231. Available from: https://zbmath.org/?q=an:0346.35083. |
| [27] |
J. Azzam, J. Bedrossian, Bounded mean oscillation and the uniqueness of active scalar equations, Trans. Amer. Math. Soc., 367 (2015), 3095–3118. https://doi.org/10.1090/S0002-9947-2014-06040-6 doi: 10.1090/S0002-9947-2014-06040-6

|