Heteroclinic orbits between static classes of time periodic Tonelli Lagrangian systems

1.   Introduction

Let $M$ be a closed connected smooth Riemannian manifold, and $L \in C^2(TM \times \mathbb {R}, \mathbb {R})$ be a Lagrangian satisfying the following conditions introduced by Mather ^[1]:

1. Periodicity: $L$ is $1$-periodic in time, i.e., $L(x, v, t) = L(x, v, t+1)$ for all $(x, v, t) \in TM \times \mathbb {R}$;

2. Positive definiteness: $\partial^2 L/\partial v^2(x, v, t)$ is positive definite, as a quadratic form, for all $(x, v, t) \in TM \times \mathbb {R}$;

3. Superlinear growth: $\lim_{\|v \|_x \to {+\infty}} \frac{L(x, v, t)}{\|v\|_x} = {+\infty}$, in each fiber, i.e., for each $A \in \mathbb {R}$, there exists $B(A) \in \mathbb {R}$ such that $L(x, v, t) \ge A\|v \|_{x} - B(A)$, for all $(x, v, t) \in TM \times \mathbb {R}$.

4. Completeness: Every orbit of the Euler-Lagrange flow introduced by $L$ is defined for all time.

Remark 1.1. $\|\cdot \|_x$ denotes the norm associated to the Riemannian metric on $M$. Since $M$ is compact, condition $(3)$ in the above definition is independent of which Riemannian metric is chosen on $M$. For any $x, y \in M$, we use $d(x, y)$ denotes the distance defined by the Riemannian metric.

For any compact interval $[a, b] \subset \mathbb {R}$, we denote ${\mathcal{C}}([a, b], M)$ by the set of all absolutely continuous curves defined on $[a, b]$. The action $A_L$ of $L$ on any ${\gamma} \in {\mathcal{C}}([a, b], M)$ is defined by

Given $x, y \in M$, we set ${\mathcal{C}}_{[a, b]}(x, y): = \{ {\gamma} \in {\mathcal{C}}([a, b], M): {\gamma}(a) = x, {\gamma}(b) = y\}$ and ${\mathcal{C}}_T(x, y): = {\mathcal{C}}_{[0, T]}(x, y)$ for any $T > 0$. The extremals of $A_L$ in ${\mathcal{C}}_{[a, b]}(x, y)$ are solutions of the Euler-Lagrange equation which in local coordinates is given by

Furthermore we assume $L$ is a critical Lagrangian. A Lagrangian is called critical if the infimum of the actions of all closed curves is $0$. Every Tonelli Lagrangian can be made critical by adding a proper constant, see ^[2].

For any $(x, a), (y, b) \in M \times \mathbb {R}$ with $a < b$, we define

The infimum above is actually a minimum, see Theorem 2.1.

For any $(x, {\alpha}), (y, {\beta}) \in M \times \mathbb {T}$, we define

The following propositions of the functions we just defined will be needed in this paper and we refer the interested readers to ^[3] for their proofs.

Proposition 1.1. 1. The function $h: M \times {\mathbb{R}} \times M \times {\mathbb{R}} \to {\mathbb{R}}; ((x, a), (y, b)) \to h((x, a), (y, b))$ is Lipschitz continuous and bounded on $\{ b-a \ge 1 \}$.

2. For any ${\alpha}, {\beta} \in {\mathbb{T}}$, ${h^{\infty}}((\ast, {\alpha}), (\ast, {\beta})): M \times M \to {\mathbb{R}}$ is Lipschitz continuous and satisfies triangle inequality

for any $(x, {\alpha}), (y, {\beta}), (z, \rho) \in M \times \mathbb {T}$.

3. We set ${\widetilde{d}}: M \times {\mathbb{T}} \times M \times {\mathbb{T}}: \to {\mathbb{R}}$ as

then ${\widetilde{d}}$ is non-negative.

Let $I \subset \mathbb {R}$ be an interval of time, a curve ${\gamma} \in {\mathcal{C}}(I, M)$ is called semi-static if

When $I = \mathbb {R}$, we say ${\gamma}$ is a global semi-static curve. When $I = [a, {+\infty})$ (or $I = ( {-\infty}, a]$) for some $a \in \mathbb {R}$, we say ${\gamma}$ is a forward (or backward) semi-static curve. Obviously a semi-static curve is a solution of (EL).

If ${\gamma}$ satisfies

we say it is static. When $I = \mathbb {R}$, we say ${\gamma}$ is a global static curve. By Proposition 1.1 it is not hard to see a static curve must be semi-static.

We define the Mañé set ${\widetilde{\mathcal{N}}} \subset TM \times \mathbb {T}$ and Aubry set ${\widetilde{\mathcal{A}}} \subset TM \times \mathbb {T}$ as

Similarly we define

It is easy to see

Let $\pi: TM \times \mathbb {T} \to M \times {\mathbb{T}}$ be the usual projection. We set ${\mathcal{N}} = \pi({\widetilde{\mathcal{N}}})$ and ${\mathcal{A}} = \pi({\widetilde{\mathcal{A}}})$. The famous Mather's graph theorem (see ^[1]) tells us $\pi|_{{\widetilde{\mathcal{A}}}}: {\widetilde{\mathcal{A}}} \to {\mathcal{A}}$ is bijective and its inverse $(\pi|_{{\widetilde{\mathcal{A}}}})^{-1}: {\mathcal{A}} \to {\widetilde{\mathcal{A}}}$ is Lipschitz.

Following Mather's graph theorem, for any $(x, {\alpha}) \in {\mathcal{A}} \subset M \times {\mathbb{T}}$, there is a unique global static curve, denoted by ${\gamma}_{(x, {\alpha})}$, satisfying ${\gamma}_{(x, {\alpha})}({\alpha}) = x$. Furthermore using ${\widetilde{d}}$ defined in Proposition 1.1, we can define an equivalence relation on ${\widetilde{\mathcal{A}}}$ by saying $(x, v, a), (y, w, b) \in {\widetilde{\mathcal{A}}}$ are equivalent iff ${\widetilde{d}}(\pi(x, v, a), \pi(y, w, b)) = {\widetilde{d}}((x, a), (y, b)) = 0$.

By this equivalence relation, we break ${\widetilde{\mathcal{A}}}$ into classes will be called static classes. Let ${\widetilde{\mathbb{A}}}$ be the set of static classes, through the entire paper ${\widetilde{\Lambda}}, {\widetilde{\Omega}}, {\widetilde{\Gamma}}$ and ${\widetilde{\Delta}}$ with or without super-index will be used to represent static classes.

Under the assumption that

we will prove the following two theorems.

Remark 1.2. $(\ast_1)$ is a generic condition in the sense of Mañé, see ^[4].

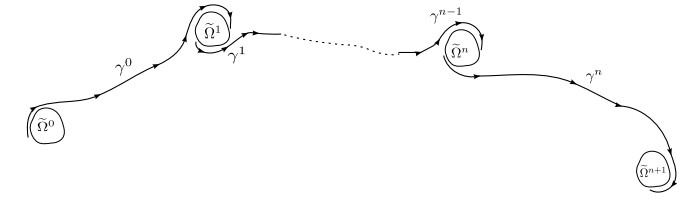
Theorem 1.1. For any two different static classes ${\widetilde{\Lambda}}^1, {\widetilde{\Lambda}}^2 \in {\widetilde{\mathbb{A}}}$, one of the following must be true:

1. There is a global semi-static curve ${\gamma}$ with the ${\alpha}$-limit set ${\alpha}(d{\gamma}) \subset {\widetilde{\Lambda}}^1$ and the ${\omega}$-limit set ${\omega}(d{\gamma}) \subset {\widetilde{\Lambda}}^2$;

2. There is a finite set of static classes $\{ {\widetilde{\Omega}}^1, \dots, {\widetilde{\Omega}}^n \} \subset {\widetilde{\mathbb{A}}}\setminus \{{\widetilde{\Lambda}}^1, {\widetilde{\Lambda}}^2 \}$ and global semi-static curves ${\gamma}^i: i = 0, \dots, n$ with ${\alpha}(d{\gamma}^i) \subset {\widetilde{\Omega}}^i$ and ${\omega}(d{\gamma}^i) \subset {\widetilde{\Omega}}^{i+1}$ for $i = 0, \dots, n$, where ${\widetilde{\Omega}}^0 = {\widetilde{\Lambda}}^1$ and ${\widetilde{\Omega}}^{n+1} = {\widetilde{\Lambda}}^2$.

By ${\alpha}(d{\gamma})$ (or ${\omega}(d{\gamma})$), we mean the ${\alpha}$-limit set (or ${\omega}$-limit set) of the orbit $\{ ({\gamma}(t), \dot{{\gamma}}(t), t{\; mod\; 1}): t \in {\mathbb{R}} \}$ of the Euler-Lagrange flow. Similarly we let ${\alpha}({\gamma})$ (or ${\omega}({\gamma})$) be the ${\alpha}$-limit set (or ${\omega}$-limit set) of $\{{\gamma}(t): t \in {\mathbb{Z}} \}$ in $M$.

When $L$ is time-independent the above theorem has been proved by Contreras and Paternain in ^[5].

Remark 1.3. Through the entire paper, for any subset $U \subset M$ and ${\delta} > 0$, by $U({\delta})$ we mean $U({\delta}): = \{x \in M: d(x, U)\le {\delta}\}$.

Let ${\mathcal{N}}_0: = {\mathcal{N}} \cap M \times \{0\}$ and ${\mathcal{A}}_0 : = {\mathcal{A}} \cap M \times \{0\}.$ Under an further assumption

We will prove along a chain of heteroclinic orbits obtained in Theorem 1.1, there is a real heteroclinic orbit connecting the two given static classes.

Theorem 1.2. If $(\ast_1), (\ast_2)$ are true, for any two different static classes ${\widetilde{\Lambda}}^1, {\widetilde{\Lambda}}^2 \in {\widetilde{\mathbb{A}}}$, there is a curve ${\gamma} \in C^2({\mathbb{R}}, M)$, such that $(d{\gamma}(t), t{\;mod\;1})$ is an orbit of the Euler-Lagrange system introduced by $L$ with ${\alpha}(d{\gamma}) \subset {\widetilde{\Lambda}}^1$ and ${\omega}(d{\gamma}) \subset {\widetilde{\Lambda}}^2$.

Similar variational method has been used in ^[6] and ^[7], where the authors established the existence of homoclinic orbits to the Aubry set under various conditions different from ours.

2.   Preliminary

By Mather's graph theorem, we can break ${\mathcal{A}}$ into a set of equivalent classes ${\mathbb{A}}: = \{ {\Lambda} = \pi({\widetilde{\Lambda}}): {\widetilde{\Lambda}} \in {\widetilde{\mathbb{A}}} \}$. By abusing of notation, they will also be called static classes and capital Greek letters ${\Lambda}, {\Omega}$ with or without super-index will be reserved to represent such static classes throughout this paper.

For all the sets ${\widetilde{\mathcal{A}}}, {\widetilde{\mathcal{N}}}, {\widetilde{\Lambda}}$ (${\mathcal{A}}, {\mathcal{N}}, {\Lambda}$), by putting a sub-index $t \in \mathbb {T}$ to them, we mean it is their intersection with $TM \times \{t\}$($M \times \{t\}$), for example ${\widetilde{\mathcal{A}}}_t = {\widetilde{\mathcal{A}}} \cap TM \times \{t\}$, ${\mathcal{A}}_t = {\mathcal{A}} \cap M \times \{t\}$.

For any $n \in {\mathbb{N}}$, we define $h^n: M \times M \to {\mathbb{R}}$ by

and ${h^{\infty}}: M \times M \to {\mathbb{R}}$, $\Phi: M \times M \to {\mathbb{R}}$ by

In some cases, we need to shift the time parameterization of a given curve for which we introduce the following operator.

Definition 2.1. Given $a < b \in {\mathbb{R}}$ for any $c \in {\mathbb{R}}$, we define an operator $\tau_c: {\mathcal{C}}([a, b], M) \to {\mathcal{C}}([a+c, b+c], M)$ by

The variational study of Tonelli Lagrangian $L$ depends on some standard results proved by Mather in ^[1].

Lemma 2.1. Given a real number $K$ and a compact interval $[a, b]$,

is compact for the topology of uniform convergence.

Theorem 2.1. (Tonelli Theorem) Given two points $x, y \in M$ and a compact interval $[a, b]$, there is a ${\gamma} \in {\mathcal{C}}_{[a, b]}(x, y)$ with $A_L({\gamma}) = h((x, a), (y, b))$ and ${\gamma}$ is a $C^2$ solution of (EL).

If a curve ${\gamma} \in {\mathcal{C}}_{[a, b]}(x, y)$ satisfies $A_L({\gamma}) = h((x, a), (y, b))$ we will call it a minimizer. Obviously a semi-static curve is a minimizer, but a minimizer is not necessarily a semi-static curve.

The next lemma is well-known to experts, however we can not locate a complete proof in the literature, therefore we give one at here.

Lemma 2.2. Given any $p, q \in M$ and two sequences of positive integers $\{T^1_k\}\nearrow {+\infty}, \{T^2_k\} \nearrow {+\infty}$, if $\{ {\gamma}_k \in {\mathcal{C}}_{[-T^1_k, T^2_k]}(p, q) \}$ is a sequence of minimizers, i.e., $A_L({\gamma}_k) = h^{T^1_k+T^2_k}({\gamma}_k(-T^1_k), {\gamma}_k(T^2_k)),$ for any $k \in {\mathbb{N}}$, satisfying

then there is a global semi-static curve ${\gamma}$, such that ${\gamma}_k$ converges to ${\gamma}$ uniformly on any compact interval along a subsequence.

Proof. By Proposition $1.1$ and Lemma 2.1, it is not hard to see for any $T > 0$, along a subsequence ${\gamma}_k$ converges uniformly to a ${\gamma}_T \in {\mathcal{C}}([-T, T], M)$ on $[-T, T]$. Apply this to a sequence of positive integers $\{T_n \} \nearrow {+\infty}$, then by a diagonal extraction, we can find a subsequence of ${\gamma}_k$, which we rename as ${\gamma}_k$, and a ${\gamma} \in {\mathcal{C}}({\mathbb{R}}, M)$, such that ${\gamma}_k$ converges uniformly to ${\gamma}$ on any compact interval.

We claim for any $T \in {\mathbb{Z}}^+$, $A_L({\gamma}|_{[-T, T]}) = \Phi({\gamma}(-T), {\gamma}(T))$, so ${\gamma}$ is a global semi-static curve.

Assume this is not true, then there is a $T \in {\mathbb{Z}}^+$, such that

Since ${\gamma}_k|_{[-T, T]}$ converges uniformly to ${\gamma}|_{[-T, T]}$, the lower semi-continuity of $A_L$ implies

By the definition of $\Phi$ there is a $S \in {\mathbb{Z}}^+$, such that

Because $h^S$ is Lipschitz,

As $\lim_{k \to {+\infty}}d({\gamma}_k(\pm T), {\gamma}(\pm T)) = 0$, for $k$ large enough we have

By Tonelli Theorem, for any $k \in {\mathbb{N}}$, there are $\xi_k \in {\mathcal{C}}_{[0, S]}({\gamma}_k(-T), {\gamma}_k(T))$ with

so by (2.4),

Combine this with (2.1), (2.2) and (2.3), we get

for $k$ large enough.

We define a new sequence of curves $\{ \widetilde {{\gamma}}_k \in {\mathcal{C}}_{T^1_k+T^2_k -2T+S}(p, q) \}$ by

For all $k$ large enough, $A_L(\widetilde {{\gamma}}_k) \le A_L({\gamma}_k) - \frac{{\varepsilon}}{4}$. Since $\{T^2_k+T^1_k -2T+S \}$ goes to infinity as $k \to {+\infty}$, we have

which is absurd and we proved our claim.

Remark 2.1. In the previous lemma, if we assume $\{T^1_k\}$ (resp. $\{T^2_k\}$) is bounded, by the same arguments it is not hard to see there is a forward semi-static curve (resp. backward semi-static curve) ${\gamma}$, such that, ${\gamma}_k$ converges uniformly to ${\gamma}$ on any compact interval in the domain of ${\gamma}$ along a subsequence.

In this paper a stronger version of Lemma 2.2 will be needed.

Lemma 2.3. Given any $p, q \in M$ and a sequence of positive integers $\{T_k\} \nearrow {+\infty}$, let $\{ {\gamma}_k \in {\mathcal{C}}_{T_k}(p, q) \}$ be a sequence of minimizers, i.e., $A_L({\gamma}_k) = h((p, 0), (q, T_k))$, satisfies $\lim_{k \to {+\infty}} A_L({\gamma}_k) = {h^{\infty}}(p, q)$.

If $\{a_k\} \nearrow {+\infty}, \{ b_k\} \nearrow {+\infty}$ are two sequence of positive integers satisfying

1. $0 \le a_k \le b_k \le T_k$, for all $k \in {\mathbb{N}}$;

2. $b_k - a_k \to {+\infty}$ as $k \to {+\infty}$;

3. there are $x, y \in M$, such that along a subsequences $d({\gamma}_k(a_k), x) \to 0$ and $d({\gamma}_k(b_k), y) \to 0$ as $k \to {+\infty}$,

then along a subsequence, $\lim_{k \to {+\infty}} A_L({{{\gamma}_k}}|_{[{{a_k}}, {{b_k}}]}) = {h^{\infty}}(x, y).$

Proof. Noticing that $\{ A_L({{{\gamma}_k}}|_{[{{a_k}}, {{b_k}}]})\}$ has a finite upper bound, passing to a subsequence if necessary, we can say

We claim $B = {h^{\infty}}(x, y)$ and the lemma follows immediately from this claim.

By Lipschitz continuity of $h^n$,

by passing to a proper subsequence, we can say $d({\gamma}_k(a_k), x) + d({\gamma}_k(b_k), y)) \to 0$ as $k \to {+\infty}$, then

Hence,

Assume ${\varepsilon} = B -{h^{\infty}}(x, y) > 0$, then there are non-negative integers $a'_k < b'_k$ with $b'_k -a'_k \to {+\infty}$ as $k \to {+\infty}$ satisfying

Then for $k$ large enough, we have

On the other hand, $B = \lim_{k \to {+\infty}} h^{b_k-a_k}({\gamma}_k(a_k), {\gamma}_k(b_k))$, so for $k$ large enough

Combine (2.6) and (2.7), we get

Again by the Lipschitz continuity of $h^n$ and $d({\gamma}_k(a_k), x) + d({\gamma}_k(b_k), y)) \to 0$ as $k \to {+\infty}$, for $k$ large enough we have

(2.8) and (2.9) imply

Now following the same argument as in the proof of Lemma 2.2, we can construct a new sequence $\{{\gamma}^*_k \in {\mathcal{C}}_{T_k-(b_k-a_k)+(b'_k -a'_k)}(p, q) \}$ with

which is a contradiction.

In next lemma we will strengthen the triangle inequality of ${h^{\infty}}$ given in Proposition $1.1$.

Lemma 2.4. Given a ${\Lambda} \in {\mathbb{A}}$ and a compact set $U \subset M$ with ${\Lambda}_0 \cap U = \emptyset$, then we can find an ${\varepsilon} > 0$ small enough and a ${\delta} = {\delta}({\varepsilon}) > 0$, such that

Proof. Because ${\Lambda}_0 \cap U = \emptyset$ and $U$ is compact, there is an ${\varepsilon}' > 0$, such that

Then for any $q \in {\Lambda}_0$, as ${h^{\infty}}$ satisfies triangle inequality,

so

the last equality is because of ${h^{\infty}}(p, q)+{h^{\infty}}(q, p) = {\widetilde{d}}(p, q) = 0$, as $p, q \in {\Lambda}_0$ are in the same static class.

Let ${\varepsilon} = \frac{{\varepsilon}'}{4}$ and ${\delta} = \frac{{\varepsilon}}{8C}$, then for any $x, z \in {\Lambda}_0({\delta})$, there are $p', q' \in {\Lambda}_0$ with $d(x, p') \le {\delta} \;{\rm{ and }}\; d(z, q') \le {\delta}.$ By the Lipschitz continuity of ${h^{\infty}}$, we have

combine these with (2.10), we get

Given an arbitrary $(x, {\alpha}) \in M \times {\mathbb{T}}$, by Fathi's weak KAM theory ^[8], there are at least one forward semi-static curve ${\gamma}^+ \in C^2([a, {+\infty}), M)$ with ${\gamma}^+(a) = x$, $a{\; mod\; 1} = {\alpha}$ and one backward semi-static curve ${\gamma}^- \in C^2(( {-\infty}, a], M)$ with ${\gamma}^-(a) = x$, $a {\; mod\; 1} = {\alpha}$.

One of the most important feature of these forward (or backward) semi-static curves is that the must asymptotic to a unique static class of ${\widetilde{\mathcal{A}}}$.

Lemma 2.5. If ${\gamma}$ is a forward (or backward) semi-static curve, then there is a unique static class ${\widetilde{\Lambda}} \in {\widetilde{\mathbb{A}}}$, such that ${\omega}(d{\gamma})$ (or ${\alpha}(d{\gamma})$) $\subset {\widetilde{\Lambda}}$.

Generally speaking there may be more than one forward (or backward) semi-static curves starting from (or ending at) a given point $(x, {\alpha}) \in M \times {\mathbb{T}}$, however if $(x, {\alpha})$ belongs to ${\mathcal{A}}$, then they are unique.

Lemma 2.6. If $(x, {\alpha}) \in {\mathcal{A}}$, then there is a unique $v \in T_xM$, such that $(x, v, {\alpha}) \in {\widetilde{\mathcal{A}}} \subset {\widetilde{\mathcal{N}}}^{\pm}.$

As a consequence there is a unique forward semi-static curve ${\gamma}^+ \in {\mathcal{C}}([{\alpha}, {+\infty}), M)$ with ${\gamma}^+({\alpha}) = x$ and a unique backward semi-static curve ${\gamma}^- \in {\mathcal{C}}(( {-\infty}, {\alpha}], M)$ with ${\gamma}^-({\alpha}) = x$, and ${\gamma}^+, {\gamma}^-$ must be static, with

where ${\gamma}_{(x, {\alpha})}$ is the unique global static curve passing $(x, {\alpha})$.

The proofs of the above two lemmas can be found in ^[2,5,8], which we will not repeat here.

3.   Heteroclinic chain

We will give the proof of Theorem 1.1 in this section. By assumption ($\ast_1$), we can fix a ${\delta}^* > 0$ small enough, such that for any two different static classes ${\Lambda}^1, {\Lambda}^2 \in {\mathbb{A}}$, ${\Lambda}^1_0({\delta}^*) \cap {\Lambda}^2_0({\delta}^*) = \emptyset$. In order to distinguish the two different cases in Theorem 1.1, we introduce the following definition

Definition 3.1. Given a ${\delta} > 0$ and a curve ${\gamma} \in {\mathcal{C}}([a, b], M)$, for any two static classes ${\Lambda}^1, {\Lambda}^2 \in {\mathbb{A}}$, we defined the following set

A similar idea was used by Maxwell ^[9] and Rabinowitz ^[10] on a special class of Hamiltonian systems including periodic forced multiple pendulum under time-reversibility assumption.

For the remainder of this section, we fix two arbitrary static classes ${\Lambda}^1 \neq {\Lambda}^2 \in {\mathbb{A}}$, and two points $p \in {\Lambda}^1_0, q \in {\Lambda}^2_0$. By Tonelli Theorem, there is a sequence of minimizers $\{ {\gamma}_k \in {\mathcal{C}}_{[-T^1_k, T^2_k]}(p, q) \}$ satisfying

1. $\{T^1_k \in {\mathbb{Z}}^+\} \nearrow {+\infty}, \{T^2_k \in {\mathbb{Z}}^+\} \nearrow {+\infty}$ as $k \to {+\infty}$;

2. $\lim_{k \to {+\infty}} A_L({\gamma}_k) = \lim_{k \to {+\infty}} h^{T^2_k +T^1_k} (p, q) = {h^{\infty}}(p, q).$

Let's consider the collection of sets $K({\gamma}_k, {\delta}, {\Lambda}^1, {\Lambda}^2)$, for all $k \in {\mathbb{N}}$ and ${\delta} > 0$, there are two possibilities:

Case 1: There is a ${\delta}_0 > 0$ small enough, such that for each $m \in {\mathbb{N}}$, there is a $k > m$ with $K({\gamma}_k, {\delta}_0, {\Lambda}^1, {\Lambda}^2) = \emptyset;$

Case 2: For each ${\delta} > 0$, there is a $m \in {\mathbb{N}}$, such that $K({\gamma}_k, {\delta}, {\Lambda}^1, {\Lambda}^2) \neq \emptyset, \quad \forall k > m$.

First we shall assume case 1 hold, then by passing $\{ {\gamma}_k\}$ to a subsequence, we may assume $K({\gamma}_k, {\delta}_0, {\Lambda}^1, {\Lambda}^2) = \emptyset$ for all $k \in {\mathbb{N}}$.

Proposition 3.1. If $\textrm{Case 1}$ hold, there is a global semi-static curve ${\gamma}$ satisfying

Proof. For each $k \in {\mathbb{N}}$, we set $S_k : = \min\{t \in [-T^1_k, T^2_k]\cap {\mathbb{Z}}: d({\gamma}_k(t), {\Lambda}^1_0) > {\delta}^* \}$. It is not hard to see, for each $k \in {\mathbb{N}}$, $S_k$ is a well-defined integer and $d({\gamma}_k(t), {\Lambda}^1_0) \le {\delta}^*, \;{\rm{ for \;all }}\; t \in [-T^1_k, S_k) \cap {\mathbb{Z}}$.

Lemma 3.2. Both $\{S_k+T^1_k \}$ and $\{ T^2_k- S_k\}$ go to infinity as $k$ goes to infinity.

Proof. (Lemma 3.2) We will only give the detailed proof for $S_k+T^1_k \to {+\infty}$, while $T^2_k -S_k \to {+\infty}$ can be proven similarly.

Suppose $\{S_k+T^1_k \}$ is bounded, then passing $\{{\gamma}_k\}$ to a subsequence, we can say $S_k+T^1_k \equiv T \in {\mathbb{Z}}^+$ for all $k \in {\mathbb{N}}$. For each $k \in {\mathbb{N}}$, we define ${\gamma}^*_k \in {\mathcal{C}}([0, T^1_k+T^2_k], M)$ by ${\gamma}^*_k = \tau_{T^1_k}({\gamma}_k)$, where $\tau_{T^1_k}$ is defined as in Definition 2.1, i.e., we shift the time parameterization on ${\gamma}_k$ forward by $T^1_k$.

Replace ${\gamma}^*_k$ by a proper subsequence, by Remark 2.1, there is a forward semi-static curve ${\gamma}^* \in {\mathcal{C}}([0, {+\infty}), M)$, such that ${\gamma}^*_k$ converges to ${\gamma}^*$ on any compact interval of $[0, {+\infty})$. Since

${\gamma}^*(T) \notin \Lambda^1_0$. At the same time ${\gamma}^*(0) = \lim {\gamma}^*_k(0) = p \in {\Lambda}^1_0$, then ${\gamma}^*$ can not be a static curve.

Because $p \in {\Lambda}^1_0 \subset {\mathbb{A}}_0$, there must be a global static curve $\xi$ with $\xi(0) = p$. As a result we have two different forward semi-static curves starting from $p$ and this is a contradiction to Lemma 2.6.

By Lemma 3.2, without loss of generality, we may assume $S_k \equiv 0$ for all $k \in {\mathbb{N}}$. Passing ${\gamma}_k$ to a subsequence, by Lemma 2.2, there is a global semi-static curve ${\gamma}$, such that ${\gamma}_k$ converges uniformly to ${\gamma}$ on any compact interval.

Since $d({\gamma}_k(t), {\Lambda}^1_0) \le {\delta}^*$, for all $t \in [-T^1_k, 0) \cap {\mathbb{Z}}$ and $k \in {\mathbb{N}}$, we have $d({\gamma}(t), {\Lambda}^1_0) \le {\delta}^*,$ for all $t \in ( {-\infty}, 0) \cap {\mathbb{Z}}$.

By Lemma 2.5, there is a unique ${\widetilde{\Lambda}} \in {\widetilde{\mathbb{A}}}$, such that ${\alpha}(d{\gamma}) \subset {\widetilde{\Lambda}}$, hence we must have ${\widetilde{\Lambda}} = {\widetilde{\Lambda}}^1$ and ${\alpha}(d{\gamma}) \subset {\widetilde{\Lambda}}^1$.

Because Case 1 is true, either ${\omega}(d{\gamma}) \subset {\widetilde{\Lambda}}^2$ or ${\omega}(d{\gamma}) \subset {\widetilde{\Lambda}}^1$ must be true. Assume ${\omega}(d{\gamma}) \subset {\widetilde{\Lambda}}^1$, then there is a sequence of positive integers $\{ T_j \} {\nearrow} {+\infty}$ with $\lim_{j \to {+\infty}} d({\gamma}(T_j), x) = 0$ for some $x \in {\Lambda}^1_0$.

On the other hand we can find a subsequence $\{{\gamma}_{k_j} \in {\mathcal{C}}_{[-T^1_{k_j}, T^2_{k_j}]}(p, q)\}$ of $\{{\gamma}_k\}$ with $T_j \le T^2_{k_j}$ for all $j \in {\mathbb{N}}$ and $d({\gamma}_{k_j}(T_j), {\gamma}(T_j))$ approaches to $0$ as $j \to {+\infty}$. Therefore $d({\gamma}_{k_j}(T_j), x)$ approaches to $0$ as $j \to {+\infty}$.

Replacing $\{{\gamma}_{k_j}\}$ by a proper subsequence, by Lemma 2.3

Since $\{T^1_{k_j}\}$ and $\{ T_j\}$ goes to infinity, as $j \to {+\infty}$, both sequences $\{{\gamma}_{k_j}|_{[-T^1_{k_j}, 0]}\}$ and $\{ {\gamma}_{k_j}|_{[0, T_j]}\}$ satisfy conditions of Lemma 2.3, passing $\{{\gamma}_{k_j}\}$ to a proper subsequence, we have

By (3.1) and (3.2), ${h^{\infty}}(p, {\gamma}(0))+{h^{\infty}}({\gamma}(0), x) = {h^{\infty}}(p, x)$.

However it is easy to see $d({\gamma}(0), {\Lambda}^1_0) \ge {\delta}^*$, at the same time $p, x \in {\Lambda}^1_0$, by Lemma 2.4, ${h^{\infty}}(p, {\gamma}(0)) + {h^{\infty}}({\gamma}(0), x) > {h^{\infty}}(p, x)$, which is a contradiction and we finished our proof.

Now we assume Case 2 is true, because of ($\ast_1$), by passing $\{{\gamma}_k\}$ to a subsequence, we can say that for a sequence of positive real numbers $\{ {\delta}_k \in (0, {\delta}^*) \} \searrow 0$, there is a finite set of static classes $\{ {\Omega}^1, \dots, {\Omega}^n\} \subset {\mathbb{A}} \setminus \{ {\Lambda}^1, {\Lambda}^2\}$ satisfying $K({\gamma}_k, {\delta}_k, {\Lambda}^1, {\Lambda}^2\}\equiv \{ {\Omega}^1, \dots, {\Omega}^n \}$ for all $k \in {\mathbb{N}}$.

We set ${\Omega}^0 = {\Lambda}^1$ and ${\Omega}^{n+1} = {\Lambda}^2$.

Proposition 3.3. If $\textrm{Case 2}$ is true, there is a chain of global semi-static curves ${\gamma}^i: i = 0, \dots, n$ satisfying ${\alpha}(d{\gamma}^i) \subset {\widetilde{\Omega}}^i$ and ${\omega}(d{\gamma}^i) \subset {\widetilde{\Omega}}^{i+1}$ for $i = 0, \dots, n$.

Proof. By Definition 3.1, for every $i = 1, \dots, n$ and $k \in {\mathbb{N}}$, we can find an $S^i_k \in (-T^1_k, T^2_k) \cap {\mathbb{Z}}$ with $d({\gamma}_k(S^i_k), {\Omega}^i_0) \le {\delta}_k$ and we set $S^0_k = -T^1_k$ and $S^{n+1}_k = T^2_k$ for all $k \in {\mathbb{N}}$.

Without loss of generality, we can assume $S^i_k \le S^{i+1}_k$ for all $i = 0, \dots, n$ and $k \in {\mathbb{N}}$. Furthermore by passing $\{{\gamma}_k\}$ to a proper subsequence, we can say there are $x_i \in {\Omega}^i_0$ for $i = 0, \dots, n+1$ with

where $x_0 = p$ and $x_{n+1} = q$.

Lemma 3.4. For every $i = 0, \dots, n$, $\{ S^{i+1}_k -S^i_k \} \to {+\infty}$ as $k \to {+\infty}$.

Proof. (Lemma 3.4) It can be proven similarly as we did in the proof of Lemma 3.2 and we will not repeat it here.

Lemma 3.5. There is a $\widetilde {{\delta}} \in (0, {\delta}^*)$ small enough, such that for every $k$ large enough

Proof. (Lemma 3.5) If not, without loss of generality we can assume there are $0 \le i_0 \neq i_1 \le n$ and a sequence of positive numbers $\{ \widetilde {{\delta}}_k \in (0, {\delta}^*)\} \searrow 0$ satisfying

for all $k$ large enough.

By the definition of $K$, we must have $i_1 \neq i_0 +1$. Let's assume $i_1 > i_0+1$ (the case of $i_1 < i_0$ can be proven similarly), then there is a sequence of integers $\{S_k \in (S^{i_0}_k, S^{i_0+1}_k)\}$, such that $d({\gamma}_k(S_k), {\Omega}^{i_1}_0) \le \widetilde {{\delta}}_k$.

First we will show that $\{ S^{i_0+1}_k - S_k\}$ approaches positive infinity as $k$ goes to ${+\infty}$. If this is not true, replacing $\{{\gamma}_k \}$ by a proper subsequence, we may assume $S^{i_0+1}_k -S_k \equiv S \in {\mathbb{R}}$ for all $k \in {\mathbb{N}}$.

We define a new sequence of minimizers $\{ {\gamma}^*_k = \tau_{-S_k}({\gamma}_k)\}$, then

Since $\widetilde {{\delta}}_k \to 0$ as $k \to {+\infty}$, passing $\{{\gamma}^*\}$ to a proper subsequence, we can say $\lim_{k \to {+\infty}} {\gamma}^*_k(0) = x$ for some $x \in {\Omega}^{i_1}_0$.

Again passing $\{ {\gamma}_k^* \}$ to a proper subsequence, by Lemma 2, there is a global semi-static curve ${\gamma}^*$ such that ${\gamma}_k^*$ converges to ${\gamma}^*$ on any compact interval. Hence

On the other hand

As ${\Omega}^{i_0+1}_0 \cap {\Omega}^{i_1}_0 = \emptyset$, ${\gamma}^*$ can not be a static curve. Since $(x, 0) \in {\Omega}_{i_1} \subset {\mathcal{A}}$, there is a global static curve ${\gamma}_{(x, 0)}$ with ${\gamma}_{(x, 0)}(0) = x$. Obviously ${\gamma}_{(x, 0)} \neq {\gamma}^*$ and we have two different forward semi-static curves starting from $x$, which is a contradiction to Lemma 2.6. Therefore $\{S^{i_0+1}_k -S_k\} \to {+\infty}$ as $k \to {+\infty}$.

At the same time by Lemma 3.4, $\{S^{i_1}_k-S^{i_0+1}_k\} \to {+\infty}$ as $k \to {+\infty}$. Noticing that $\{{\gamma}_k|_{[S_k, S^{i_1}_k]}\}$ is a sequence of minimizers with

by Lemma 2.3, passing $\{{\gamma}_k\}$ to a proper subsequence, we have

However $x, x_{i_1} \in {\Omega}^{i_1}_0$ and $x_{i_0+1} \in {\Omega}^{i_0+1}_0$, by Lemma 2.4,

which is absurd, so we are done.

Now we resume our proof of Proposition 3.3.

For each $i = 0, \dots, n$, by Lemma 3.4 and Lemma 3.5, we showed that $\{ {\gamma}|_{[S^i_k, S^{i+1}_k]} \}$ is a sequence of minimizers satisfying the following:

1. $S_k^{i+1}-S^i_k \to {+\infty}$ as $k \to {+\infty}$;

2. $\lim_{k \to {+\infty}} d({\gamma}_k(S^i_k), x_i) = 0$ and $\lim_{k \to {+\infty}} d({\gamma}_k(S^{i+1}_k), x_{i+1}) = 0$;

3. $K({\gamma}_k|_{[S^i_k, S^{i+1}_k]}, \widetilde {{\delta}}, {\Omega}^i, {\Omega}^{i+1}) = \emptyset$, for all $k$ large enough.

Let $\{ {\gamma}^i_k = \tau_{c_k}({\gamma}|_{[S^i_k, S^{i+1}_k]}) \}$, where $c_k = - \frac{S^i_k + S^{i+1}_k}{2}$, then following the same argument as in the proof of Proposition 3.1, we can show that along a subsequence $\{ {\gamma}^i_k\}$ converges uniformly on any compact interval to a global semi-static curve ${\gamma}^i$ satisfying ${\alpha}(d{\gamma}^i) \subset {\widetilde{\Omega}}^i$ and ${\omega}(d{\gamma}^i) \subset {\widetilde{\Omega}}^{i+1}$.

Hence $\{ {\gamma}^i: i = 0, \dots, n\}$ form a chain of heteroclinic orbits as we wanted and $\{x_i: i = 0, \dots, n\}$ satisfies $x_i \in {\omega}({\gamma}^{i-1}) \cap {\alpha}({\gamma}^i)\cap {\Omega}^i_0$ for $i = 1, \dots, n$, and $x_0 \in {\alpha}({\gamma}^0) \cap {\Omega}^0_0$, $x_{n+1} \in {\omega}({\gamma}^n) \cap {\Omega}^{n+1}_0$.

Furthermore we have

Hence,

Obviously Theorem 1.1 follows directly from Proposition 3.1 and Proposition 3.3.

4.   Heteroclinic Orbits

This section will be devoted to the proof of Theorem 1.2. In the previous section we proved that for any two different static classes, there is a chain of heteroclinic orbits connecting them. Under the assumption $(\ast_2)$, we will show that there is a real heteroclinic orbit connecting those two static classes along such a chain of heteroclinic orbits.

Such a heteroclinic orbits will be found as a constraint minimizer of the action of Lagrangian $L$. Using the minimizing properties of static curves and semi-static curves, we will show that the constraint minimizers we find will not bump up to the boundary conditions we posted and it is a real orbit.

First we will introduce some technical lemmas.

Lemma 4.1. There is a $\hat{{\delta}} \in (0, {\delta}^*)$ small enough, such that if $p, q \in {\Lambda}_0(\hat{{\delta}})$, for some ${\Lambda} \in {\mathbb{A}}$, then

and

Proof. Choose an arbitrary $p, q \in {\Lambda}_0({\delta}^*)$, first let's show ${h^{\infty}}(p, x)+{h^{\infty}}(x, q) = {h^{\infty}}(p, x')+{h^{\infty}}(x', q)$ if $x, x' \in {\Lambda}_0$. By the triangle inequality of ${h^{\infty}}$,

the last equality is due to the fact that $x, x'$ are contained in the same static class, which means

Therefore ${h^{\infty}}(p, x) + {h^{\infty}}(x, q) \le {h^{\infty}}(p, x') +{h^{\infty}}(x', q)$, the other direction of the inequality can be proven similarly.

First we will prove (4.1) under the assumption that both $p, q$ are contained in ${\Lambda}_0$.

For any $x \in {\Lambda}_0$, by triangle inequality

On the other hand, since $q, x$ are contained in the same static class $\Lambda_0$, ${\widetilde{d}}(q, x) = {h^{\infty}}(q, x)+{h^{\infty}}(x, q) = 0$, then

so

As a result, we proved equality (4.1) under the assumption $p, q \in \Lambda_0$.

Now we will drop our previous assumption. Without loss of generality, let's say $q \notin {\Lambda}_0$. Then there is a sequence of minimizers $\{ {\gamma}_k \in {\mathcal{C}}_{[0, T_k]}(p, q) \}$ with $\{ T_k \in {\mathbb{Z}}^+ \} {\nearrow} {+\infty}$, and a forward semi-static curve ${\gamma} \in {\mathcal{C}}([0, {+\infty}), M)$, such that ${\gamma}_k$ converges uniformly to ${\gamma}$ on any compact sub-interval of $[0, {+\infty})$.

Then ${\omega}({\gamma}) \subset {\Omega}$ for some ${\Omega} \in {\mathbb{A}}$. We can find a sequence of positive integers $\{ S_k \} {\nearrow} {+\infty}$ and a $x \in {\Omega}_0$, such that $\lim_{k \to {+\infty}} d({\gamma}(S_k), x) = 0$, then

. 0 We claim $T_k -S_k \to {+\infty}$ as $k \to {+\infty}$, if this is not true, passing to a subsequence, we may assume $T_k -S_k \equiv T \in {\mathbb{Z}}^+$. Let $\xi_k \in {\mathcal{C}}_{[-T_k, 0]}(p, q); \xi_k = \tau_{-T_k}({\gamma}_k)$ be a new sequence of minimizers.

Then passing to a subsequence $\xi_k$ converges uniformly to a backward semi-static curve $\xi$ on any compact sub-interval of $( {-\infty}, 0]$.

Noticing that $\xi_k(-T) = \xi_k(S_k -T_k) = {\gamma}_k(S_k)$ approaches to $x$ as $k$ goes to ${+\infty}$, so $\xi(-T) = \lim_{k \to {+\infty}}\xi_k(-T) = x \in {\Omega}_0$. Then by Lemma 2.6, $\xi$ must be part of a global static curve and $(\xi(t), 0) \in {\mathcal{A}}_0$ for any $t \in ( {-\infty}, 0] \cap {\mathbb{Z}}$. However $\xi(0) = \lim \xi_k(0) = \lim {\gamma}_k(T_k) = q \notin \Lambda_0$, which is a contradiction.

As we just showed, when $k$ goes to ${+\infty}$, $\{T_k-S_k \}$ approaches to ${+\infty}$, $\{S_k\}$ approaches to ${+\infty}$ and ${\gamma}_k(S_k)$ approaches to $x$, by Lemma 2.3, passing $\{{\gamma}_k\}$ to a proper subsequence, we have

Now we will show that for a small enough $\hat{{\delta}} > 0$, we must have ${\Omega} = {\Lambda}$, then $x \in {\Lambda}_0$ and (4.1) follows immediately from that.

Assume ${\Omega} \neq {\Lambda}$, then $x \in {\mathcal{A}}_0 \setminus {\Lambda}_0$, which is a compact set without any intersection with ${\Lambda}_0$, then by Lemma 2.4, we can find an $\hat{{\delta}} \in (0, {\delta}^*)$, such that for any $p, q \in {\Lambda}_0(\hat{{\delta}})$ and $y \in {\mathcal{A}}_0 \setminus {\Lambda}_0$, we have

This is a contradiction to to what we just proved. Therefore we must have ${\Omega} = {\Lambda}$.

Finally (4.2) follows directly from Lemma 2.4.

In section 2, we have mentioned that for any $(x, {\alpha}) \in M \times {\mathbb{T}}$, there is at least one forward semi-static curve ${\gamma}^+$ (or backward semi-static curve ${\gamma}^-$) starting from (or ending at) $(x, {\alpha})$ with its ${\omega}$-limit set (or ${\alpha}$-limit set) contained in a unique static class. Generally we can not determine which static class it will approach to, however by the above lemma we can determine where it asymptotic to in some special case.

Lemma 4.2. Let $\hat{{\delta}}$ be defined as in Lemma 4.1, if $p \in {\Lambda}_0(\hat{{\delta}})$, $q \in {\Lambda}_0$ for some ${\Lambda} \in {\mathbb{A}}$ and $\{ {\gamma}_k \in C_{T_k}(p, q) \}$ is a sequence of minimizers with $\lim_{k \to {+\infty}} A_{L}({\gamma}_k) = {h^{\infty}}(p, q)$ and $\{ T_k \} {\nearrow} {+\infty}$, then there is a forward semi-static curve ${\gamma}^+ \in C^2([0, {+\infty}), M)$ satisfying the following conditions

1. ${\gamma}^+(0) = p$;

2. $\{ {\gamma}_k \}$ converges uniformly to ${\gamma}^+$ along a subsequence on any compact interval;

3. ${\omega}(d{\gamma}^+) \subset {\widetilde{\Lambda}}$.

Proof. By Remark 2.1, there is a forward semi-static curve ${\gamma}$ satisfying conditions $(1), (2)$, we claim it also satisfies condition $(3)$. If not, by Lemma 2.5, there is another static class ${\Omega} \neq {\Lambda}$, such that ${\omega}(d{\gamma}) \subset {\widetilde{\Omega}}$.

Then there is a $x \in {\Omega}_0$ and a sequence of integers $\{ S_k \in (0, T_k) \} {\nearrow} {+\infty}$, such that

Hence passing $\{{\gamma}_k\}$ to a subsequence, we have

Similar to the proof of Lemma 4.1, we have $\{T_k - S_k \} \to {+\infty}$ as $k \to {+\infty}$.

Since $\{T_k - S_k\} \to {+\infty}$, $\{S_k\} \to {+\infty}$ and $\lim_{k \to {+\infty}} d({\gamma}_k(S_k), x) = 0$ as $k \to {+\infty}$, Lemma 2.3 tells us that along a subsequence of $\{ {\gamma}_k \}$,

Therefore

If $x \in {\Omega}_0 \neq {\Lambda}_0$, Lemma 4.1 tells us

which is a contradiction to (4.3). As a result we proved our claim and ${\gamma}$ is the forward semi-static curve ${\gamma}^+$ we are looking for.

Remark 4.1. It is not hard to see that similar argument can to be used to show the existence of a backward semi-static curve ${\gamma}^-$ with ${\gamma}^-(0) = p$ and ${\alpha}(d{\gamma}^-) \subset {\widetilde{\Lambda}}$.

Lemma 4.3. Given a global semi-static curve ${\gamma}$, if $p \in {\alpha}({\gamma}) \cap {\mathcal{A}}_0$ and $q \in {\omega}({\gamma}) \cap {\mathcal{A}}_0$, then

Proof. For arbitrary $p \in {\alpha}({\gamma}) \cap {\mathcal{A}}_0$ and $q \in {\omega}({\gamma}) \cap {\mathcal{A}}_0$, there are two sequences of integers $\{ S_k \} \searrow {-\infty}$ and $\{ T_k \} {\nearrow} {+\infty}$, such that $\lim_{k \to {+\infty}}{\gamma}(S_k) = p$ and $\lim_{k \to {+\infty}} {\gamma}(T_k) = q$.

Following Lemma 2.3, without loss of generality, we can say

Therefore

Lemma 4.4. Given a global semi-static curve ${\gamma}$, if there are two compact sets $U, V \subset M$ satisfying

1. ${\gamma}(S) \in U, \; {\gamma}(T) \in V$ for some $S \le T \in {\mathbb{Z}}$;

2. $\partial{U} \cap {\mathcal{N}}_0 = \emptyset, \quad \partial{V} \cap {\mathcal{N}}_0 = \emptyset$, where $\partial{U}, \partial{V}$ are the boundaries of $U, V.$

Then for any $p \in {\alpha}({\gamma})\cap {\mathcal{A}}_0$, $q \in {\omega}({\gamma}) \cap {\mathcal{A}}_0$ and $(x, y) \in U \times V.$, we have

Furthermore, if $x \in U \setminus {\mathcal{N}}_0$ or $y \in V \setminus {\mathcal{N}}_0$, then

and there is a ${\varepsilon} > 0$ such that

where $Int(U), Int(V)$ are the interiors of $U, V$.

Proof. Assume there are $x \in U$, $y \in V$ with ${\Delta}(p, x, y, q; {\gamma}) < 0$, then

By Remark 2.1, we can find two sequences of minimizers

satisfying

Let $\eta \in {\mathcal{C}}_{[S, T]}(x, y)$ be a minimizer, i.e., $A_L(\eta) = h^{T-S}(x, y)$. We define a new sequence of curves $\{ {\gamma}_k \in {\mathcal{C}}_{[-S_k, T-S+T_k]}(p, q) \}$ by

Obviously $S_k+T_k+T-S \to {+\infty}$ as $k \to {+\infty}$, and

However,

where the last inequality follows from (4.4). However this is absurd and we proved the first part of the lemma.

For the second part, without loss of generality we can assume there are $x \in U \setminus {\mathcal{N}}_0$ and $y \in V$ with ${\Delta}(p, x, y, q; {\gamma}) = 0$. Let $\{ {\gamma}_k\}$ be defined as above then

Although ${\gamma}_k$ is not necessary a minimizer, by (4.5), it is not hard to see, for any $T' \in {\mathbb{Z}}^+$, $\{ A_L({{{\gamma}_k}}|_{[{{-T'}}, {{T'}}]})\}$ has a finite upper bound, and the argument in the proof of Lemma 2.2 will still hold. Therefore along a subsequence $\{{\gamma}_k\}$ converges uniformly to a global semi-static curve ${\gamma}^*$ on any compact interval. Which means

and this is a contradiction to our assumption.

Hence ${\Delta}(p, x, y, q;{\gamma}) > 0$, if $x \in U \setminus {\mathcal{N}}_0$ or $y \in V \setminus {\mathcal{N}}_0$. By the Lipschitz continuity of $h^n$ and ${h^{\infty}}$, there is a ${\varepsilon} > 0$ such that

Now we are ready to prove Theorem 1.2.

Proof. (Theorem 1.2) We will follow the notations from the previous section, let $p \in {\Lambda}^1_0, \rm{ } q \in {\Lambda}^2_0$ and $\{ {\gamma}_k \in {\mathcal{C}}_{[-T^1_k, T^2_k]}(p, q) \}$ is a sequence of minimizers satisfying

Again there are two different cases as we discussed in the previous section.

If Case 1 is true, nothing needs to be done here.

If Case 2 is true, by the proof of Proposition 3.3, we have a set of finite static classes $\{ {\Omega}^1, \dots, {\Omega}^n \} \subset {\mathbb{A}} \setminus \{ {\Lambda}^1, {\Lambda}^2 \}$, a chain of global semi-static curves $\{{\gamma}^i: i = 1, \dots, n\}$ and $\{x_i \in {\Omega}^i_0: i = 0, 1, \dots, n+1\}$, where $x_0 = p, x_{n+1} = q,$ satisfying

1. ${\alpha}(d{\gamma}^i) \subset {\widetilde{\Omega}}^i$ and ${\omega}(d{\gamma}^i) \subset {\widetilde{\Omega}}^{i+1}$, for $i = 0, \dots, n$, where ${\Omega}^0 = {\Lambda}^1$ and ${\Omega}^{n+1} = {\Lambda}^2$;

2. $x_i \in {\omega}({\gamma}^{i-1}) \cap {\alpha}({\gamma}^i) \cap {\Omega}^i_0$, for $i = 1, \dots, n$, and $x_0 = p \in {\alpha}({\gamma}^0) \cap {\Omega}^0_0$, $x_{n+1} \in {\omega}({\gamma}^n) \cap {\Omega}^{n+1}_0$.

3. ${h^{\infty}}(x_0, x_{n+1}) = \sum_{i = 0}^{n} {h^{\infty}}(x_i, x_{i+1}).$

Let $\hat{{\delta}} > 0$ be defined as in Lemma 4.1, for each ${\gamma}^i$, we can choose $S^i < T^i \in {\mathbb{Z}}$ satisfying

Then by assumption ($\ast_2$), for each $i = 0, \dots, n$ there are compact sets $U^i, V^i \subset M$ satisfying

For each $(Y, Z): = \{(y_0, z_0), \dots, (y_n, z_n) \} \in \prod_{i = 0}^n U^i \times V^i$, we define a function $J$ by

For each $i = 0, \dots, n-1$, $z_i \in V^i \subset {\Omega}^{i+1}_0(\hat{{\delta}})$ and $y_{i+1} \in U^{i+1} \subset {\Omega}^{i+1}_0(\hat{{\delta}})$, by Lemma 4.1,

Hence the function $J$ can be rewritten as

For any $\tau = (\tau_i)_{i = 0}^{n-1}$ with each $\tau_i \in {\mathbb{Z}}^+$ define a $J_{\tau}: \prod_{i = 0}^n U^i \times V^i \to {\mathbb{R}}$, by

Let

by the compactness of $U^i, V^i$ and Lipschitz continuity of $h^n, {h^{\infty}}$, it is easy to see the above infimum is in fact a minimum.

Lemma 4.5. There is a $\tau$, such that if $(Y', Z') = \{(y'_0, z'_0), \dots, (y'_n, z'_n) \} \in \prod_{i = 0}^n U^i \times V^i$ satisfies $J_T(Y', Z') = c_T$, then

We postpone the proof of the above lemma for a moment. Now there is a

with $J_{\tau}(Y', Z') = c_{\tau}$. Meanwhile for each $i = 0, \dots, n$, there is a minimizer ${\zeta}_i \in {\mathcal{C}}_{[0, T^i-S^i]}(y'_i, z'_i)$ with $A_L({\zeta}_i) = h^{T^i -S^i}(y'_i, z'_i)$, and for each $j = 0, \dots, n-1$, there is a minimizer $\eta_j \in {\mathcal{C}}_{[0, \tau_j]}(z'_j, y'_{j+1})$ such that $A_L(\eta_j) = h^{\tau_j}(z'_{j+1}, y'_{j+1})$.

By Lemma 4.2, there is a forward semi-static ${\gamma}^+ \in {\mathcal{C}}([0, {+\infty}), M)$ with ${\gamma}^+(0) = z'_n$ and ${\omega}(d{\gamma}^+) \subset {\widetilde{\Omega}}^{n+1}$, and a backward semi-static curve ${\gamma}^- \in {\mathcal{C}}(( {-\infty}, 0], M)$ with ${\gamma}^-(0) = y'_0$ and ${\alpha}(d{\gamma}^-) \subset {\widetilde{\Omega}}^0$.

Gluing these curves together by the following order

we get a new curve ${\gamma} \in {\mathcal{C}}({\mathbb{R}}, M)$ with ${\alpha}(d{\gamma}) \subset {\widetilde{\Lambda}}^1$ and ${\omega}(d{\gamma}) \subset {\widetilde{\Lambda}}^2$.

By the standard variational argument, it is not hard to see ${\gamma}$ is a classical solution of (EL) and we are done.

Proof of Lemma 4.5. Set ${\{{\gamma}^i(S^i), {\gamma}^i(T^i) \}}: = \{ ({\gamma}^0(S^0), {\gamma}^0(T^0)), \dots, ({\gamma}^n(S^n), {\gamma}^n(T^n)) \}$. Since ${\{{\gamma}^i(S^i), {\gamma}^i(T^i) \}} \in \prod_{i = 0}^n Int(U^i) \times Int(V^i)$, it is enough to show, there is a $\tau$ such that

for all $(Y, Z) = \{(y_0, z_0), \dots, (y_n, z_n) \} \in \prod_{i = 0}^n U^i \times V^i \setminus \prod_{i = 0}^n Int(U^i) \times Int(V^i)$. Using the expression of $J$ given in (4.7), we get

Meanwhile by Lemma 4.3, for each $i = 0, \dots, n$,

Therefore

By Lemma 4.4, there is an ${\varepsilon} > 0$ independent of the choice of $(Y, Z)$, such that

By the compactness of $U^i, V^i$ and Lipschitz continuity of $h^n, {h^{\infty}}$, there is a $\tau' \in {\mathbb{Z}}^+$, such that for all $i = 0, \dots, n-1$, when $\tau_i \ge \tau'$,

Then (4.6) and (4.8) imply

Meanwhile for each $i = 0, \dots, n-1$, we can always find a $\tau_i \ge \tau'$, such that

Again by (4.6) and (4.8), we get

Combining the above inequality with (4.9) and (4.10), we have

This finishes our proof of the lemma.

Acknowledgments

This work is supported by the National Key R & D Program of China (2020YFA0713303), NSFC (No. 12171253), the Fundamental Research Funds for the Central Universities and Nankai Zhide Fundation.

Conflict of interest

The authors declare there is no conflicts of interest.