In this research we have attempted to measure vulnerability of the communities living in the flood prone area of Khyber Pukhtunkhwa province of Pakistan. Extensive literature review was conducted to identify the flood vulnerability indicators. Primary data were used to achieve the objective of this study. Questionnaires were used to collect the primary data from the selected households and from the director of Centre for Disaster Preparedness and Management. Subjective assessment technique was used to allocate weights to the selected indicators of vulnerability. A sample size of 280 respondents was taken from three selected locations of Charsadda, Nowshera and Peshawar. Simple random sampling was employed for the selection of respondents. Results revealed that overall vulnerability as well as component vulnerability for the selected locations was very high. The study therefore recommends preparedness, provision of funds for building houses with flood resistant materials and building houses in safer places. There is also a need for enhancing the adaptive capacities of the concerned communities through their socio-economic uplift. Implementation of these policies would lower the vulnerability of the communities to flood disasters.
1.
Brief historical development and motivation
Since the mid−20th century, the researchers have shifted their interest from classical matrix algebra to more general algebraic structure. They started exploring the properties of matrices in terms of general algebraic structures such as nonassociative algebras and rings. This resulted in the establishment of generalized matrix algebras with a binary operation (zero product) instead of the usual matrix multiplication. The study of Lie (Jordan) centralizers at zero products in generalized matrix algebras has its roots in the broader field of matrix theory and algebraic structures, as well as Lie algebras, operator theory, and nonassociative algebras.
The zero product operation introduces new challenges in understanding matrix behavior, leading the researchers to extend the concept of Lie (Jordan) centralizers to generalized matrix algebras, operator algebras, and alternative algebras. The motivation behind the study of Lie (Jordan) centralizers at zero products reflects the broader evolution of algebraic structures and their applications. The exploration of these centralizers has contributed to a deeper understanding of generalized matrix algebra. The analysis of centralizers and related concepts is essential for knowing the structure and properties of noncommutative multiplication, while Lie (Jordan) centralizers play a role in characterizing certain types of sub-algebras and their properties (see [22,23,28,29]). The Lie (Jordan) centralizer at zero products provides a framework for studying the algebraic properties and structures of matrices in generalized matrix algebras (see [16,17,18,19]).
Numerous researchers have been diligently investigating over the past few years the behavior of Lie (Jordan) centralizers for matrix algebras, triangular rings, nest algebras, and alternating algebras (see [1,11,12,13,14,26]). In 2021, Jabeen [10] investigated Lie centralizers on generalized matrix algebra and obtained the necessary and sufficient criteria for suitable Lie centralizers. Foˇsner and Xing [8] explored the relevancy of Lie centralizers on nest algebras and triangular rings. Liu [21] introduced nonlinear Lie centralizers for a particular class of generalized matrix algebra. Recently, many algebraists [4,5,25] examined certain specific Lie centralizers/σ−centralizers on generalized matrix algebras and triangular algebras. In 2023, Fadaee et al. [7] derived Jabeen's ideas to Lie triple centralizers on generalized matrix algebras. In 2023, Ashraf and Ansari [2] described Lee (Jordan) σ−centralizers of generalized matrix algebra. They demonstrated that each Lie σ−centralizer of a generalized matrix algebra can be expressed as a sum of centralizers and center-valued mappings under particular situations. Furthermore, in 2023, Ashraf and Ansari [3] argued that any Jordan σ−centralizer of a triangular algebra is a centralizer.
Motivated by recent works, the key objective of this manuscript is to investigate the structure of Lie (Jordan) σ−centralizers on generalized matrix algebra at zero products and to present the relationship between Lie (Jordan) σ−centralizers and generalized matrix algebra's centralizers.
2.
Key content and notations
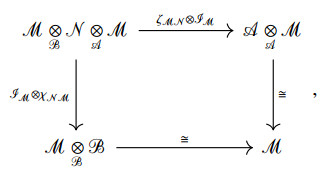
Let's keep in mind that R be a unital commutative ring, A be R−algebra and Z(A) be the center of A. Readers are referred to basic definitions and related characteristics [6,15,20]. Let us review numerous definitions and properties utilized throughout the article. A Morita context consists of two R−algebras A and B, two bimodules AMB and BNA, and two bimodule homomorphisms called the pairings ζMN:M⨂BN→A and χNM:N⨂AM→B satisfying the following commutative diagrams:
and
Let's call this Morita context (A,B,M,N,ζMN,χNM). For additional information on Morita contexts, look through [24]. If (A,B,M,N,ζMN,χNM) is a Morita context, then the collection
is an algebra when standard matrix operations are applied. An R−algebra of this type is known as a generalized matrix algebra of order two, and it is represented by G=G(A,M,N,B). G is referred to be a trivial generalized matrix algebra if ζMN and χNM are zero. Such a form of the algebra was initially proposed by Sands in [27]. Whenever M=0 or N=0, G immediately reduces to the identified triangular algebra. Generalized matrix algebras are isomorphic to all associative algebras with nontrivial idempotents. Natural generalized matrix algebra, semi-hereditary algebra, complete matrix algebra, and nested algebra are some typical examples of generalized matrix algebra [8]. A generalized matrix algebra is a unit algebra A over all matrices of rank n×n [9]. In case N=0, G is referred to as triangular algebra and denoted by Tri(A, M, B)=[AM0B]. Additionally, G=G(A,M,N,B) has unity if and only if R−algebra of A and B has unity 1A and 1B, respectively. Therefore, (A, B)−bimodule M is unital such that 1Am=m=m1B for every m∈M, and in the same manner, (B, A)−bimodule N is also unital [9]. Thus, the identity of generalized matrix algebra G is I=[1A001B]. On the other hand, it is easy to show that the triangular algebra is unital if and only if R−algebra of A and B are unital as well as the (A, B)−bimodule M is unital [9]. The center of G is Z(G) = {[a00b]|na=bn,am=mb,for everya∈Z(A), b∈Z(B),m∈M,n∈N}, where G is of order two.
Remark 2.1. Consider two projections πB:G→B and πA:G→A, which is defined as πB([amnb])=b and πA([amnb])=a. Additionally, πB(Z(G))⊆Z(B), πA(Z(G))⊆Z(A), and there is one, and only one, algebraic isomorphism τ:πA(Z(G))→πB(Z(G)) in which am=mτ(a), na=τ(a)n for every a∈πA(Z(G)),m∈M, and n∈N.
3.
Lie (Jordan) σ−centralizers at the zero products
Theorem 3.1. Suppose Φc:G → G is a linear mapping satisfying Φc(xy)=Φc(x)σ(y)=σ(x)Φc(y) for every x,y∈G, then
where Θ1:A→A,℧2:M→M,U4:B→B, and V3:N→N are linear mappings such that Θ1(mn)=℧2(m)ν(n) and U4(nm)=V3(n)μ(m) are satisfied.
Proof. Assume the map Φc on G takes the form
where ℧1:A→M, ℧2:M→M, ℧3:N→M, ℧4:B→M, Θ1:A→A, Θ2:M→A, Θ3:N→A, Θ4:B→A, V1:A→N, V2:M→N, V3:N→N, V4:B→N, and U1:A→B, U2:M→B, U3:N→B, U4:B→B are all linear mappings with automorphism σ.
If a and b are in A and B, respectively, then [a000][000b]=0. Additonally,
This equation implies
and, hence,
If we set b=1B, then ℧1(a)n0=0, ℧1(a)=Θ1(a)m0, and U1(a)=V1(a)m0. Again by (3.1), we have
Now taking a=1A in the above, we obtain Θ4(b)=−m0V4(b), ℧4(b)=−m0U4(b), and n0℧4(b)=0.
Again, applying a similar calculative procedure with
we get Θ4(b)=−℧4(b)n0, V4(b)=−U4(b)n0, V4(b)m0=0, m0V1(a)=0, V1(a)=n0Θ1(a), and U1(a)=−n0℧1(a). Therefore, by (3.1), (3.2), and [4, Proposition 2.1], we get U1(a)=0 and Θ4(b)=0.
If a1,a2∈A with a1a2=0, we have [a1000] [a2000]=0. Thus,
Then, Θ1(a1a2)=0=Θ1(a1)γ(a2)+℧1(a1)n0γ(a2)=γ(a1)Θ1(a2)+γ(a1)m0V1(a2). Hence, by (3.1) and (3.2), we have Θ1(a1a2)=0=Θ1(a1)γ(a2)=γ(a1)Θ1(a2). Therefore, Θ1 is a σ−centralizer at the zero product on A.
Similarly, if b1,b2∈B with b1b2=0, we have [000b1] [000b2]=0. Then, we get U4(b1b2)=0=−V4(b1)m0δ(b2)+U4(b1)δ(b2)=−δ(b1)n0℧4(b2)+δ(b1)+δ(b1)U4. Hence, by (3.1) and (3.2), we have U4(b1b2)=0=U4(b1)δ(b2)=δ(b1)+δ(b1)U4. Therefore, U4 is a σ−centralizer at the zero product on B.
If m and a are in M and A, respectively, then [0m00] [a000]=0. Furthermore,
This leads to
Put a=1A, and we have Θ2(m)=−℧2(m)n0 and V2(m)=−U2(m)n0. Similarly, [000b] [0m00]=0. Then,
From the above, we find that V2(m)=n0δ2(m) and U2(m)=n0℧2(m).
We recognize that [−1Am00] [0m01B]=0 for every m∈M. Therefore,
The above equation implies that
Hence, we get ℧2(m)n0=0, ℧2(m)=Θ1(1A)μ(m)−Θ2(m)μ(m), and U2(m)n0=0. By (3.4) and concerning that m∈M, we get Θ2(m)=0 and V2(m)=0. Also since we know Θ1 is a σ−centralizer at the zero product on A, then ℧2(am)=Θ1(1A)μ(am)=Θ1(1A)γ(a)μ(m)=Θ1(a)μ(m) for any m∈M with a=0. Therefore, M is a left faithful A−module.
Again by (3.6), we have 0= [−1A−m0+μ(m)−n00][0℧2(m)+℧4(B)V4(1B)U2(m)+U4(1B)]. Then, we find ℧2(m)=μ(m)U4(1B) and n0℧2(m)=0. Hence, by (3.4) and concerning that m∈M, we have U2(m)=0. Also, by (3.3) we have that U4 is a σ−centralizer at the zero product on B, then ℧2(mb)=μ(mb)U4(1B)=μ(m)δ(b)U4(1B)=μ(m)U4(b) for every m∈M, where b=0 implies that M is a right faithful B−module. Since [a000] [00n0]=0, for any a∈A and n∈N, we have
By (3.5), we deduce that
So, we get
Put a=1A, and we find that Θ3(n)=−m0V3(n) and ℧3(n)=−m0U3(n). Similarly, [00n0][000b]=0, for every n∈N and b∈B, we have
Hence, we find that ℧3(n)=Θ3(n)m0 and U3(n)=V3(n)m0. For any n∈N, [00n1B] [−1A0n0]=0, we have
Therefore, for any n∈N, we find these results: Θ3(n)m0=0, V3(n)m0=0, m0V3(n)=0, V3(n)=U4(1B)ν(n), and V3(n)=ν(n)Θ1(1A). Hence, from (3.7) and (3.8), we get ℧3(n)=0, U3(n)=0, and Θ3(n)=0. Also, in the case of Θ1 and U4 are σ−centralizers on A and B, respectively, we have the (B,A)−bimodule N as a faithful (B,A)−bimodule.
If m and n are in M and N, respectively, then [mnm0b][−10n0]=0. Then,
By (3.10), we obtain
This equation leads to Θ1(mn)=℧2(m)ν(n). Similarly, with [00nnm][0m0−1]=0, we have V3(n)μ(m)=U4(nm). □
Theorem 3.2. Suppose G is a generalized matrix algebra of 2−torsion free and a linear mapping ΦJc: G → G satisfies Φc(x∘y)=Φc(x)∘σ(y)=σ(x)∘Φc(y) for every x,y∈G, such that
where ρ1:A→A,r2:M→M,s3:N→N, and g4:B→B are linear mappings that hold
(i) r2(am)=γ(a)r2(m)=ρ1(a)μ(m) and r2(mb)=r2(m)δ(b)=μ(m)g4(b).
(ii) s3(na)=s3(n)γ(a)=ν(n)ρ1(a) and s3(bn)=δ(b)s3(n)=g4(b)ν(n).
(iii) ρ1(mn)=μ(m)s3(n)=r2(m)ν(n) and g4(nm)=s3(n)μ(m)=ν(n)r2(m).
Proof. Assume the map ΦJc on G takes the form
where ρ1:A→A, ρ2:M→A, ρ3:N→A, ρ4:B→A, r1:A→M, r2:M→M, r3:N→M, r4:B→M, s1:A→N, s2:M→N, s3:N→N, s4:B→N, and g1:A→B, g2:M→B, g3:N→B, g4:B→B are all linear mappings with automorphism σ.
If a and b are in A and B, respectively, then [a000] [000b]=0. Moreover,
This implies that
which is rewritten as
and gives
If we set b=1B, then r1(a)=ρ1(a)m0,s1(a)=n0ρ1(a), and g1(a)=0. Again with (3.9), the following matrix
is equal to zero. Evaluating with a=1A, we obtain ρ4(b)=0,r4(b)=−m0g4(b), and s4(b)=−g4(b)n0.
If m and a are in M and A, respectively, then [0m00] [a000]=0. Therefore,
This implies that
and, hence,
On taking a=1A in the above, we see that ρ2(m)=0,s2(m)=0,g2(m)=0, and r2(am)=γ(a)r2(m). Similar with [000b] [0m00]=0, we find that r2(mb)=ρ4(b)μ(m)+μ(m)g4(b)=r2(m)δ(b).
Since for any a∈A and n∈N, [a000] [00n0]=0, we obtain
By (3.12), we deduce that
which is rewritten as
This leads to
Set a=1A, and we find ρ3(n)=0,r3(n)=0,g3(n)=0, and s3(na)=g1(a)ν(n)+ν(n)ρ1(a)=s3(n)γ(a). Follow the similar steps with [00n0] [000b]=0, and we get s3(bn)=δ(b)s3(n)=ν(n)ρ4(b)+g4(b)ν(n).
For any m∈M and n∈N, [mnm00] [−10n0]=0, and we have
By (3.14), we obtain
This equation gives ρ1(mn)=r2(m)ν(n) and g4(nm)=ν(n)r2(m). Similarly for [00nnm] [0m0−1]=0, we have ρ1(mn)=μ(m)s3(n) and g4(nm)=s3(n)μ(m). □
From the above two results it is easy to conclude that:
Theorem 3.3. Every Jordan σ−centralizer is a σ−centralizer at zero products on generalized matrix algebras.
Theorem 3.4. Suppose Φlc:G→G is a linear mapping satisfying Φlc([x,y])=[Φlc(x),σ(y)]=[σ(x),Φlc(y)], then
where ρ1:A→A, ρ4:B→A, r1:A→M.r2:M→M, r4:B→M, s1:A→N, s3:N→N, s4:B→N, g1:A→B and g4:B→B are linear mappings such that
(i) r1(a)=ρ1(a)m0−m0g1(a) and r4(b)=−m0g4(b)+ρ4(b)m0.
(ii) s1(a)=−g1(a)n0+n0ρ1(a) and s4(b)=n0ρ4(b)−g4(b)n0.
(iii) r2(am)=γ(a)r2(m)=ρ1(a)μ(m)−μ(m)g1(a) and r2(mb)=μ(m)g4(b)−ρ4(b)μ(m)=r2(m)δ(b).
(iv) s3(na)=ν(n)ρ1(a)−g1(a)ν(n)=s3(n)γ(a) and s3(bn)=δ(b)s3(n)=g4(b)ν(n)−ν(n)ρ4(b).
(v) ρ1(mn)−ρ4(nm)=μ(m)s3(n)=r2(m)ν(n) and g1(mn)−g4(nm)=−s3(n)μ(m)=−ν(n)r2(m).
Proof. Assume the map Φc on G takes the form
where ρ1:A→A, ρ2:M→A, ρ3:N→A, ρ4:B→A, r1:A→M, r2:M→M, r3:N→M, r4:B→M, s1:A→N, s2:M→N, s3:N→N, s4:B→N, and g1:A→B, g2:M→B, g3:N→B, g4:B→B are all linear mappings with automorphism σ.
If a and b are in A and B, respectively, then [a000] [000b]=0. Therefore,
This equation implies
which is rewritten as
and gives
If we set b=1B, then
Again, by the other part of (3.15), we have
If m and a are in M and A, respectively, then [0m00] [a000]=0. Additionally,
This implies that
It follows that
Taking a=1A in the above, we see that ρ2(m)=0,s2(m)=0,g2(m)=0, and r2(am)=γ(a)r2(m)=−μ(m)g1(a)+ρ1(a)μ(m). Likewise with [000b] [0m00]=0, we have r2(mb)=−ρ4(b)μ(m)+μ(m)g4(b)=r2(m)δ(b).
If a and n are in A and N, respectively, then [a000] [00n0]=0, and we have
By (3.17), we deduce that
which is rewritten as
and gives
Set a=1A, and we find ρ3(n)=0,r3(n)=0,g3(n)=0, and s3(na)=−g1(a)ν(n)+ν(n)ρ1(a)=s3(n)γ(a). Similar with [00n0] [000b]=0, we have s3(bn)=δ(b)s3(n)=−ν(n)ρ4(b)+g4(b)ν(n).
Next, if m and n are in M and N, respectively, then [mnm00] [−10n0]=0. Therefore,
By (3.18), we obtain
This equation gives ρ1(mn)−ρ4(nm)=r2(m)ν(n) and g1(mn)−g4(nm)=−ν(n)r2(m). Likewise, for any m∈M and n∈N, we have [00nnm] [0m0−1]=0. Thus,
By (3.19), we deduce that ρ1(mn)−ρ4(nm)=μ(m)s3(n) and g1(mn)−g4(nm)=−s3(n)μ(m). □
The next theorem provides sufficient and necessary conditions under which a Lie σ−centralizer at the zero product is proper on an order two generalized matrix algebra.
Theorem 3.5. Let (B,A)−bimodule N and (A,B)−bimodule M on generalized matrix algebra G have the weaker condition as follows:
and let Φlc:G→G be a Lie σ−centralizer at the zero product on G such that Φlc([a000])= [∗∗∗g1(a)] and Φlc([000b])= [ρ4(b)∗∗∗] for every a∈A and b∈B. Then, the following arguments are identical:
(i) ϕlc(S)=λσ(S)+τ(S) for any S⊂G, where λ∈ Z(G) and τ:G→ Z(G) is a linear map in which τ([G1, G2]) =0, for any G1,G2 ∈ G with G1G2=0.
(ii) g1(A)⊆ πB(Z(σ(G))) and ρ4(B)⊆ πA(Z(σ(G))).
(iii) g1(1A)∈ πB(Z(σ(G))) and ρ4(1B)∈ πA(Z(σ(G))).
Proof. By Theorem 3.4, the form of ϕlc is as follows
where ρ1,ρ4,r1,r2,r3,s1,s3,s4,g1, and g4 are all linear maps and have properties in Theorem 3.4.
(ⅰ) ⇒ (ⅱ) Let m∈M, n∈N, and a∈A be arbitrary elements. Take G1=[0amna0], and we have σ(G1)= [0γ(a)μ(m)ν(n)γ(a)0] and
Let λ=[a100η(a1)], where a1∈πA(Z(σ(G))), τ(G1)= [a200η(a2)], and a2∈πA(Z(σ(G))). By assumption, we get
and comparing the last two results of ϕlc, we get
Therefore,
As m∈M, n∈N are arbitrary, focusing on Remark 2.1, we get g1(a)∈ πB(Z(σ(G))) for each a∈A. Now, we will use the same argument for arbitrary elements b∈B, m∈M, and n∈N. Upon taking λ=[a100η(a1)], G2= [0mbbn0], and τ(G2)= [a200η(a2)], we can conclude from hypothesis and Theorem 3.4 that
and
From the last two relations, we get
Hence,
Now, for b∈B, m∈M, and n∈N, in view of Remark 2.1, we obtain ρ4(b)∈πA(Z(σ(G))).
(ⅱ) ⇒ (ⅰ). We can define the following well-defined functions based on the hypothesis:
where the maps p′ and q′ are linear. Applied to Theorem 3.4 (ⅲ), we obtain
and
for every m∈M, a∈A, and b∈B. Therefore,
for every m∈M.
Now, consider a∈A, b∈B, n∈N, and by Theorem 3.4 (ⅲ), we get
and
By Remark 2.1, we find p′(1A)∈πA(Z(σ(G))), q′(1B)∈πB(Z(σ(G))), and η(p′(1A))=q′(1B).
Next, consider a,a′∈A, m∈M, n∈N, and by Theorem 3.4 (ⅲ) and (ⅳ), we have
and
Therefore, (p′(aa′)−γ(a)p′(a′))μ(m)=0 and, hence, (p′(aa′)−γ(a)p′(a′))M=0. Also, s3(naa′)=ν(n)p′(aa′) and r2(aa′m)=ν(m)γ(a)p′(a′). Thus, ν(n)(p′(aa′)−γ(a)p′(a′))=0. Since ν is an isomorphism, we have N(p′(aa′)−γ(a)p′(a′))=0. Now, by assumption we get p′(aa′)=γ(a)p(a′) for any a,a′∈A. So, p′(a)=p′(a1A)=γ(a)p′(1A), and since p′(1A)∈πA(Z(σ(G))), it follows that p′(a)=γ(a)p′(1A)=p′(1A)γ(a) for any a∈A. Similarly, it follows q′(b)=q′(1B)δ(b)=δ(b)q′(1B) for any b∈B.
If m and n are in M and N, respectively, then ρ1(mn)−ρ4(nm)=r2(m)ν(n)=p′(1A)μ(m)ν(n)=p′(mn)=ρ1(mn)−η−1(g1(mn)). Moreover, ρ4(nm)=η−1(g1(mn)) and ρ1(mn)−η−1(g1(mn))=r2(m)ν(n). Thus, p′(mn)=r2(m)ν(n) for any m∈M and n∈N. Using the same procedures as above and Theorem 3.4, we arrive to the conclusion that q′(nm)=s3(n)μ(m). Set λ=[p′(1A)00q′(1B)], since η(p′1A)=q′(1B); consequently, λ∈ Z(σ(G)).
Now, consider the linear map τ:G→G such that
We can conclude from our hypothesis τ(G)∈ Z(σ(G)) for every G∈ Z(σ(G)).
Now, for any G=[amnb]∈G, we obtain ϕlc(G)=λσ(G)+τ(G). Finally, by using Lie σ-centralizer at the zero product and the above results for any G1,G2∈G where G1G2=0, we have τ([G1,G2])=ϕlc([G1,G2])−λσ([G1,G2])=0. Next, (ⅱ) ⇒ (ⅲ) is obvious.
(ⅲ) ⇒ (ⅱ) Let a0=ρ1(1A)−η−1(g1(1A)) and b0=g4(1B)−η−1(P4(1B)). By assumption and Theorem 3.4 for any a∈A, m∈M, and n∈N, we have r2(m)=a0μ(m). Therefore, γ(a)r2(m)=γ(a)a0μ(m)=ρ1(a)μ(m)−μ(m)g1(a). So, (ρ1(a)−γ(a)a0)μ(m)=μ(m)g1(a). Similarly, s3(m)=ν(n)a0 and s3(n)γ(a)=ν(n)a0γ(a)=ν(n)ρ1(a)−g1(a)ν(n). Hence, ν(n)(ρ1(a)−a0γ(a))=g1(a)ν(n). From Remark 2.1, we get g1(a)∈πB(Z(σ(G))) and η−1(g1(a))=ρ1(a)−a0γ(a), for any a∈A. Similarly, by using the same argument and Theorem 3.4 for any b∈B, m∈M, and n∈N, we see that μ(m)(g4(b)−b0δ(b))=ρ4(b)μ(m). Also, (g4(b)−b0δ(b))ν(n)=ν(n)ρ4(b). By Remark 2.1, it follows that ρ4(b)∈πA(Z(σ(G))) and η(ρ4(b))=g4(b)−δ(b)b0, for any b∈B. □
4.
Conclusions
We studied the structure of Lie and Jordan σ−centralizers at zero products in order two generalized matrix algebras. We considered the case where (A,B) and (B,A) are bimodules of M and N, respectively, with A,B being unital R−algebras. The R−algebra G=G(A,M,N,B) is a generalized matrix algebra defined by the Morita context (A,B,M,N,ζMN,χNM). This study based on the present structure of generalized matrix algebras has produced numerous substantial results that enhance our understanding of these algebraic structures. One of the key results is that every Jordan σ−centralizer at the zero products on the order two generalized matrix algebra G is indeed a σ−centralizer at the zero product. This result establishes a fundamental connection between two classes of algebraic objects, shedding light on their connection within the context of generalized matrix algebras. Furthermore, we provided necessary and sufficient conditions under which a Lie σ−centralizer at the zero product is proper on the order two generalized matrix algebra G. This characterization is valuable, as it allows for a deeper understanding of the algebraic properties and structure of these Lie σ−centralizers. This work extends the theory of generalized matrix algebras and provides novel insights into the characteristics of Lie and Jordan σ−centralizers in this algebraic scenario.
Author contributions
Mohd Arif Raza: Conceptualization, Methodology, Supervision, Writing-review & editing; Huda Eid Almehmadi: Writing-original draft, Methodology. All the authors have read and approved the final version of the manuscript for publication.
Acknowledgments
The authors thank the referees for their useful and constructive remarks and recommendations.
Conflict of interest
The authors disclose that they have no conflicts of interest.









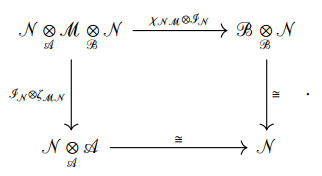




 DownLoad:
DownLoad: