1. Introduction

Typically, evaluation of the environmental hazard of a chemical, as may be elucidated through its persistence, bioaccumulation, and toxicity (PBT) characteristics, is performed for the ‘isolated’ chemical, possibly relative to others [1]. However, this procedure does not take into account the possible presence of substances or agents which one way or another may cause a change in the apparent P, B, and/or T values. Hence, it is well known that complexation may change individual values [2]. Recent and ongoing discussions on the possible use of nanomaterials as transporters for drug into the cells [3] and the role of microplastics [4] are further examples where complexation may change the inherent characteristics of organic molecules. In this respect, it should be emphasized that if sorption of drugs to nanoparticles can ease the transport of the drugs into the cell, a transport of highly unwanted substances into the cell could also be facilitated. It should be noted that the present study simply looks at the possible effects as a function of changed PBT characteristics of methoxychlor (MEC) without regard to how these changes have actually been introduced.

Little is known about such synergistic or antagonistic effects, although significant amounts of work have been devoted to the area [5]. In the present study a group of 12 "obsolete" pesticides (OPs), all banned by the Stockholm Convention [6], is studied. The mutual ranking of the 12 objects in this group of OPs has recently been studied by Sailaukhanuly et al. [1] based on P, B, and T data.

The objective of the study is the application of partial order methodology to elucidate and quantify how the mutual ranking of the OPs is subject to changes as a result of combination effects on the apparent P, B, or T characteristics of a single chemical, such as methoxychlor (MEC). MEC has been chosen arbitrarily, but serves as an exemplary example, as it ranks more or less in the middle when unperturbed indicators are applied [1], for example, in the absence of any combinatorial effects. To elucidate the effect, we followed the changes in rank of MEC as a function of the perturbation of P, B, or T indicators, respectively, where the mutual ranking of the compounds were a measure of the relative hazard. Obviously, the study could be further enlarged by perturbing two or three indicators simultaneously. However, this has not been included in the present paper in order not to introduce confuse.

2. Methods

2.1. Data and indicators

Quantitative Structure-Activity Relation (QSAR) generated data for the 12 obsolete pesticides (OPs), banned by the Stockholm Convention (2008), that was used as indicators. These comprise persistence (P), bioaccumulation (B), and toxicity (T) [1]. All indicators were obtained using the EPI Suite modeling tool [7]. Hence, the persistence was estimated by the BioWin module using the ultimate biodegradation as given by BDP3 of the BioWin module, the bioaccumulation by the BCF module, and the toxicity as the LC50 value for fish (LC50fish) by the EcoSAR module [7]. For the subsequent partial ordering, the persistence and the toxicity were applied as inverse values of BDP3 and LC50fish, respectively in order to assure a uniform direction (low to high) for all three indicators (Table 1).

Table 1. EPI Suite derived indicator values for the 12 OPs

ID	CAS No.	Trivial name	Short	Pers	BioA	Tox
				1/BDP3	logBCF	1/LC50fish
OP1	50-29-3	p,p-DDT	DDT	0.8361	4.2260	58.8235
OP2	72-55-9	p,p-DDE	DDE	0.6033	3.9620	9.8039
OP3	72-54-8	p,p-DDD	DDD	0.5758	3.6390	10.4167
OP4	72-43-5	methoxychlor	MEC	0.6611	3.0190	6.3291
OP5	309-00-2	Aldrin	ALD	1.3941	3.9560	37.0370
OP6	60-57-1	dieldrin	DIE	1.4852	3.0980	2.8169
OP7	76-44-8	heptachlor	HCL	1.9026	3.2760	6.4935
OP8	57-74-9	chlordane	CHL	3.6792	3.7710	12.8205
OP9	58-88-9	lindane (g-HCH)	LIN	0.6590	2.3990	0.4333
OP10	118-74-1	hexachlorbenzene	HCB	0.7518	3.4480	11.3636
OP11	82-68-8	pentachlor nitrobenzene	PCN	0.7441	2.7280	2.0492
OP12	87-86-5	pentachlor phenol	PCP	0.6120	3.0450	1.0060

 | Show Table

DownLoad: CSV

P was estimated using the ultimate biodegradation (BDP3) as obtained through the EPI Suite’s BioWin module [7, 8] (Table 1). The BioWin module estimates a chemical’s environmental biodegradation rate in hours, hours to days, days, days to weeks, and so on depending on the approximate amount of time needed for biodegradation to be "complete". These estimates were converted to half-lives by considering that 6 half-lives constituted "complete" or "ultimate" biodegradation and eventually to the biodegradation potential BDP. Chemicals with BDPs < 2 (1/BDP3 ˃ 0.5) are associated with a medium persistence potential, whereas chemicals with BDPs < 1.75 (1/BDP3 ˃ 0.57) are assigned a high persistence potential [8].

B, expressed as the logarithmic bioconcentration factor logBCF, was obtained applying the BCF module of the EPI Suite [7, 8] (Table 1). BCFs were estimated from the octanol-water partition coefficient and a series of structural correction factors. Chemicals with BCFs > 1000 (log BCF ˃ 3), but < 5000 (log BCF ˂ 3.67) were assigned a medium bioconcentration potential [8]. Under REACH BCF > 2000 (log BCF ˃ 3.3) are considered bioaccumulating, denoted B [9]. Chemicals with BCFs > 5000 (log BCF ˃ 3.67) were assigned a high bioconcentration potential [8], which under REACH is denoted vB (very bioaccumulating) [9].

In general, in order to be classified as toxic within the PBT regime requires a chronic NOEC ˂ 0.01 mg/L [9]. In the present study, the LC50 value for fish was adopted as measure of the T (Table 1). The toxicity data were estimated by the EcoSAR module of the EPI Suite [7].

2.2. Partial ordering

2.2.1 Overview

Partial order methodology is an alternative way to study a multi-indicator system (MIS), as it recently has been argued by Bruggemann and Carlsen [10]. Partial ordering can be considered as a non-parametric method, because in contrast to standard multidimensional analyses, no assumptions about linearity or distribution of the indicators are made nor are necessary.

2.2.2. Some technical explanations

In Partial Ordering, the only ma­thematical relation among the objects (in the present case, the 12 obsolete pesticides; Table 1) is "≤" [11, 12]. The "≤" relation is the basis for a comparison of the OPs and constitutes a graph. An OPx is connected with an OPy if and only if the relation y ≤ x holds. The crucial question is: under which conditions it can be claimed that x ≤ y? Thus, considering a system that can be described by a series of indicators—r_j, OP, OPx—and characterized by the set of indicators r_j(OPx), j = 1, ..., m, allowing for comparison to another OP, OPy, characterized by the indicators r_j(OPy), when

In the present study m equals 3 (section 2.1).

Equation 1 has a strict requirement for establishing a comparison. It demands that all indicators of OPy should be lower (or at least equal) than those of OPx through comparison of the single indicators, respectively. Note that in the present example, the lower the indicator values are, the ‘better’ they are considered to be, i.e., lower persistence, lower bioaccumulation and lower toxicity, respectively. Hence, let X be the group of OPs studied, i.e., X = {OP1, OP2, …, OP12}, OPx will be ordered higher (worse) than OPy, i.e., OPx > OPy, if at least one of the indicator values for OPx is higher (worse) than the corresponding indicator value for OPy and no indicator for OPx is lower (better) than the corresponding indicator value for OPy. However, if r_j(OPx) > r_j(OPy) for some indicator j and r_i(OPx) < r_i(OPy) for some other indicator i, OPx and OPy will be called incomparable (notation: OPx ǁ OPy) expressing the mathematical contradiction due to conflicting indicator values. When all indicator values for OPx are equal to the corresponding indicator values for OPy, i.e., r_j(OPx) = r_j(OPy) for all j, the two objects will have identical order and will be considered as equivalent, i.e., OPx ~ OPy. Note that in other studies applying partial order methodology, the term "order" is typically referred to as "rank" or "height".

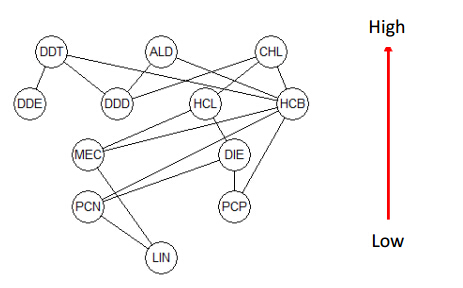
Equation 1 is the basis of the Hasse diagram technique (HDT) [11, 12], which is a special, statistically oriented portion of partial order theory. Thus, Hasse diagrams are visual representations of the partial orders. In the Hasse diagram, comparable objects are connected by a sequence of lines [12]. For construction of the Hasse diagram, a uniform orientation of the indicators should be secured, i.e., high indicator values correspond to "bad" objects and low values to "good" objects. In Figure 1, the Hasse diagram based on the data given in Table 1 is shown. Thus, in the present case, the higher an OP is placed in the Hasse diagram, the more hazardous and environmentally and human health damaging is it based on a simultaneous consideration of the PBT characteristics of the single OPs.

A Hasse diagram is characterized by it structure that comprises levels, chains, and anti-chains (Figure 1), where

Figure 1. Hasse diagram illustrating the partial ordering of the 12 OPs given in Table 1.

DownLoad: Full-Size ImgPowerPoint

• levels are the horizontal arrangement of objects within a Hasse diagram. Thus, the level structure gives a first approximation to a weak order of the objects from "good" (bottom) to "bad" (top).

• chains are a subset of X, such as X′ ⊆ X, where all objects in X′ fulfill Equation 1. A chain has a length, which is |X′|-1. For objects within a chain (e.g., from the bottom to the top of the chain), all indicators are simultaneously non-decreasing.

• Anti-chain: A subset X′ ⊆ X, where no object fulfills Equation 1; for example: if all objects in X′ are mutually incomparable, it is called an anti-chain. Thus, for any two objects within an anti-chain there is a conflict in indicator values.

The basic calculations were carried out applying the mHDCl2_8 module of the PyHasse software package.

2.2.3. Average orders

The level structure may be used as a first approximation to ordering. However, this will give rise to many tied orders, as all objects in a given level automatically will be assigned identical orders. Typically, it is desirable that the degree of tiedness should be as low as possible, i.e., ultimately looking for a linear ordering of the single objects. However, it is not immediately obtainable when incomparable objects are included.

Partial order methodology provides a weak order (tied orders are not excluded) by calculating the average order of the single objects [13]. In cases where only a relatively low number of objects are studied (typically < 25), an exact method for calculating average orders is available based on lattice theory [14, 15, 16]. However, for larger systems, approximations have been presented [17]. The calculations will assign an average order to the single objects. With the indicator orientation chosen as in the present study, the average orders will assigned from 1 (bottom) up to maximum n (top); n being the number of object (here 12). In the present study the average orders are calculated based on the exact method [14, 15, 16], as the study deals with only 12 objects.

The calculations to retrieve the average orders were carried out applying the avrank5 module of the PyHasse software package.

2.2.4. Perturbation of order characteristics

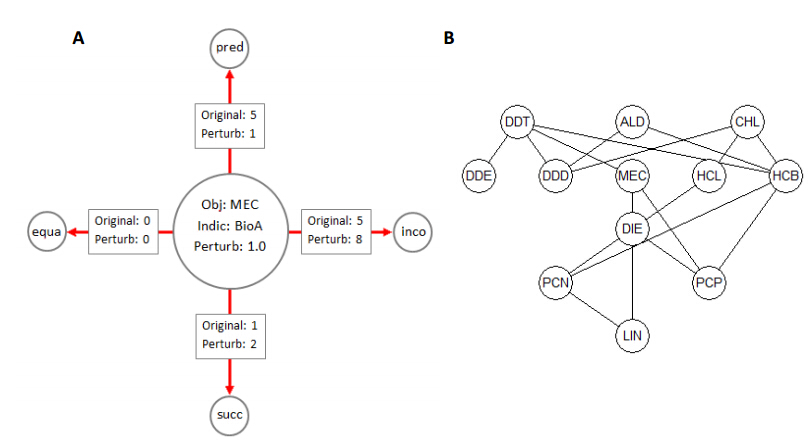
Each object in the Hasse diagram are characterized by what is called order characteristics, which are four values that state the number of equivalences, predecessors (number of upwards comparable objects), successors (number of downwards comparable objects), and incomparable elements, respectively [12].

Changes in one or more of the indicators may lead to changes in the order characteristics for the object under investigation. The module pooc6_3 of the PyHasse software package has been applied to visualize such changes, using MEC as an illustrative example.

2.2.5. PyHasse software

Partial order analyses were carried out applying the PyHasse software [18]. PyHasse was programmed using the interpreter language Python (version 2.6). The software package is continuously under further development and today contains more than 100 modules and is available upon request from the developer, Dr. R. Bruggemann (brg_home@web.de). The present study will apply only a few central modules such as mHDLc2_8, avrank5, pooc6_3. A simplified version of PyHasse operating on a web-based browser is under continuous development. Some tools are now available for use (www.pyhasse.org).

3. Results and Discussion

Based on the data presented in Table 1, the Hasse diagram for the 12 pesticides could be constructed (Figure 1). The diagram displays the mutual relation between the OPs as previously discussed by Sailaukhanuly et al [1].

From Figure 1 it can be seen that MEC is apparently incomparable to 5 OPs (DDE, DDD, DIE, PCN, PCP) and has 1 successor (LIN) and 5 predecessors (CHL, HCL, HCB, DDT, ALD). No OP was found equivalent to MEC.

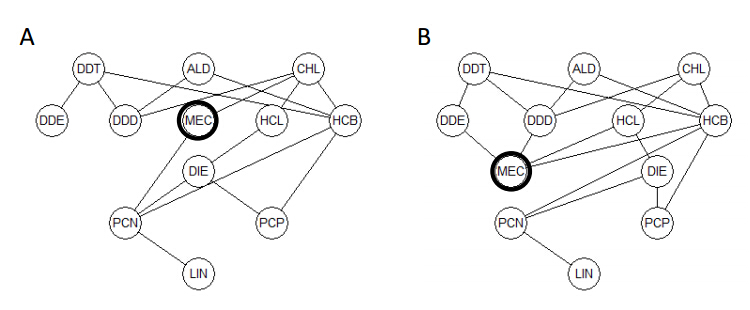
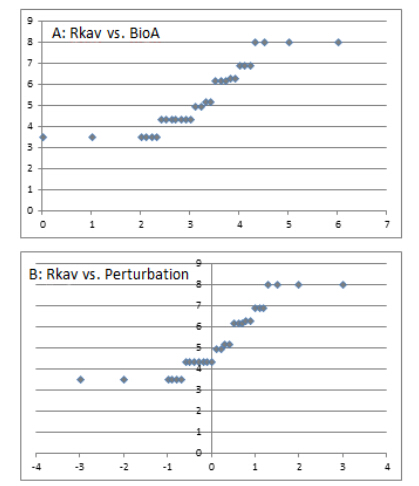
In order to visualize the effect of an apparent change in the value of a specific indicator, it appears obvious to initially look at the possible changes in the order characteristics. In Figure 2, a graphic displays the summary of a perturbation of the BioA indicator by +1 (Figure 2A), as well as the resulting Hasse diagram based on the perturbed value of BioA (MEC) (Figure 2B).

Figure 2. A: Graphics illustrating the effect of perturbation of the BioA indicator by +1 on the order characteristics of methoxychlor (MEC) (equa, pred, succ and inco denotes equalities, predecessors, successors and incomparabilities, respectively). B: The resulting Hasse diagram after perturbation.

DownLoad: Full-Size ImgPowerPoint

It is immediately seen by comparing the original Hasse diagram (Figure 1) and that following the perturbation (Figure 2B), MEC is now placed higher in the diagram and is now comparable (and worse) than DIE. This is directly reflected in the number of successors that after perturbation is 2 vs 1 in the original (Figure 2A). At the same time, it is noted that the number of predecessors is reduced from 5 to 1 and the number of pesticides now incomparable to MEC is increased from 5 to 8 (Figure 2A). It should be remembered that in this context, the sum of equa, pred, succ and inco (Figure 2A) is a constant equal to the number of compounds −1. Thus, any change in one aspect must imply a reduction in another aspect. In the present example (Figure 2A), pred is heavily reduced by perturbation (from 5 to 1). Hence, this value must be compensated by the other aspects, whereby the main compensation (and the most probable) is in inco.

However, despite the significant changes in the order characteristics, a further step is needed to disclose possible synergistic and/or antagonistic effects as a function of variations in the indicator value. For this purpose, it appears logical to apply the concept of average order (alternative notation average rank or height).

To elucidate the influence, synergistic or antagonistic of changes in the apparent indicator values three sets of calculations were performed, one for each of the three indicators. Hence, with the original value of BDP3, logBCF and LC50fish as starting points, the values were varied in both positive and negative directions. All variations were, as mentioned above, carried out using MEC as an illustrative example.

3.1. Persistence

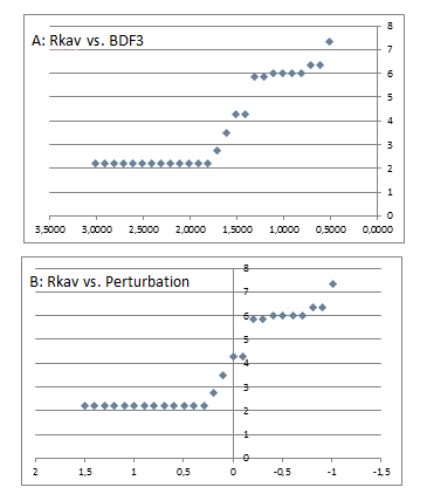
To study the effect on the ordering, with special focus on MEC, the BDP3 was varied from 0.5126 through the original value (1.5126) to 3.0126 in increments of 0.1 to disclose possible synergistic and antagonistic effects. In Figure 3, the average order of MEC as function of BDP3 (A) and the actual perturbation (B) is depicted.

Figure 3. Average order (Rkav) vs BDP3 (A) and the actual perturbation (B). Note the reversed axis for the BDP3 and the perturbation reflecting that the lower the BDP3 the higher the persistence.

DownLoad: Full-Size ImgPowerPoint

It is immediately noted that decreasing the apparent BDP3 value, such as by increasing the apparent persistency of "MEC", caused a significant increase in the average order. The actual increase being from 4.3 to 7.3 and is ordered as the 4^th worst OP after CHL (11.3), DDT (10.4), and ALD (10.0) (Figure 4A). These three (CHL, DDT, and ALD) still occupied the top level in the Hasse diagram (not shown), as was also the case in the unperturbed case (Figure 1).

Figure 4. Hasse diagrams displaying the location of MEC following a perturbation of the BDP3 by −1 (A) and +0.3 (B).

DownLoad: Full-Size ImgPowerPoint

It is further noted that a decrease in persistence only has an effect as for perturbed BDP3 values < 1.8126. For larger values of BDP3, the average order is constantly found to be 2.2, which is consistent with the fact that MEC for those values appears as a minimal element, as it has no successors (Figure 4B). In the unperturbed system, the order of MEC was found to be 4.3.

3.2. Bioaccumulation

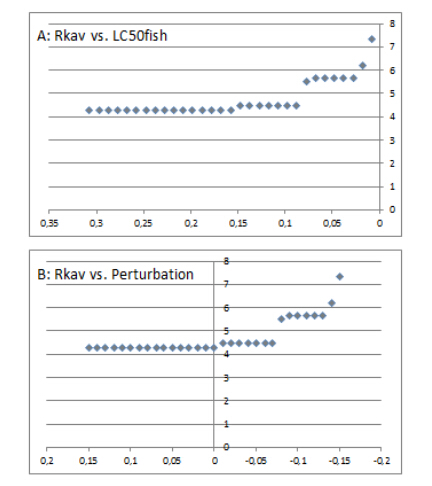
The effect on the ordering of MEC as a function of changes in the apparent bioaccumulating of the latter was studied varying the BioA (log BCF) indicator from 0.019 through the original value (3.019) to 6.019 in increments of 0.1. The average order of MEC as function of BioA (A) and the actual perturbation (B) is depicted in Figure 5.

Figure 5. Average order (Rkav) vs BioA (A) and the actual perturbation (B).

DownLoad: Full-Size ImgPowerPoint

By perturbing the MEC value by −0.7, a drop in the average MEC order from the original (4.3) to 3.5 was caused. Further lowering the BioA did not lead to a further reduction in the average order. It should be noted that MEC for perturbation ≤ −0.7 appears as a minimal element (Hasse diagram not shown).

On the other hand, by increasing the apparent bioaccumulation potential through the increase of the BioA indicator again lead to an increase in the average MEC order. Thus, the increase of BioA from 1.3 to 4.319 resulted in an increase in the average order to 7.9. Further increase by additional increases in the BioA was not observed. Despite the fact that MEC for BioA ≥ 4.319 was now a maximal element, it was still on an average basis ordered lower that DDT (10.3), CHL (11.0), and ALD (10.0).

3.3. Toxicity

The effect of a possible variation in the apparent toxicity of MEC as expressed through the LC50fish value was elucidated through a series of calculations where the LC50fish values were varied from 0.008 through the original value (0.158) to 0.308. In Figure 6, the average MEC orders as function of LC50fish (A) and the actual perturbation (B) are displayed.

Figure 6. Average order (Rkav) vs LC50fish (A) and the actual perturbation (B). Note the reversed axis for the LC50fish and the perturbation reflecting that the lower the LC50fish the higher the toxicity.

DownLoad: Full-Size ImgPowerPoint

It is immediately noted that decreasing the toxicity (such as by increasing the LC50fish value) did not cause any decrease of the average order of MEC, which is constantly found to be 4.3. In contrast, some increase in the average order is noted by increased toxicity as shown through decreased LC50fish. Thus, for LC50fish in the range 0.068-0.028, the average order of MEC was found to 5.6 and a further decrease in LC50fish to 0.008 caused a further increase in the average order to 7.3. In the latter case MEC is found as a maximal element. However, still fell below DDT (10.3), CHL (11.0), and ALD (10.0).

3.4. Relative indicator importance

In a previous paper [1], the relative importance of the three indicators was elucidated and it was unambiguously demonstrated that Pers ˃˃ BioA ˃ Tox. This is in agreement with the REACH concept which states that the persistence and the bioaccumulation outweigh the toxicity if the two former indicators are high enough, i.e., for the so-called vPvB substances, where the toxicity is not brought into play [9]. However, it should be noted that this finding is an empirical finding, based on one concrete set of data. It should also be noted that the PBT criteria serves a special purpose within REACH [19].

The above results are in agreement with the previous statements. Thus, through scrutinization of Figures 3, 4, and 6, it is noted that the major change in the apparent MEC average order was seen upon variation in the BDP3, followed by BioA; whereas, even significant changes in the LC50fish indicator lead only to relatively smaller variations in the MEC average order.

4. Conclusions

The possible synergistic and antagonistic effects on the relative hazard of chemicals have been elucidated applying simple partial order methodology. As an illustrative example, the relative hazard of methoxychlor (MEC) in a group of 12 obsolete chloro-containing pesticides was used.

The 12 pesticides were partially ordered by applying their persistence, bioaccumulation, and toxicity as indicators. The average order of MEC was estimated as function of a systematic variation in the three indicators. The ordering of the pesticides by simultaneously including these 3 indicators is believed to constitute an ordering according to the environmental hazard [19]. The present study thus demonstrates the advantageous use of partial ordering, which is an analytical approach that allows a simultaneous inclusion of all applied indicators. Partial ordering does not require any assumption on linearity or distribution of the indicators and such available data can be applied immediately. Hence, the information contained in the single indicator is maintained and not being hidden by a possible aggregation process, which could infer compensation effects [20].

It was found that increasing either the persistence, the bioaccumulation, or the toxicity caused a relative increase in the average order of MEC compared to the other 11 pesticides, resulting in an increased hazard. However, a decrease in the indicator values lead to a decreased relative hazard, apart from in the toxicity case, where a decrease in toxicity did not apparently cause any change in the relative average order of MEC.

It was further shown that the observed results are consistent with previous studies which demonstrated that the persistence and bioaccumulation indicators are the two dominating figures, but toxicity plays a somewhat less dominant role. This is further in agreement with the REACH regulation, where a distinction is made between PBT and vPvB compounds, which is to say that if persistence and bioaccumulation are both sufficiently high, the toxicity indicators are not taken into account.

In the present study, only the variation in one indicator at a time for one single compound, MEC, has been dealt with. Hence, a larger systematic study where all possible variations for single or multiple compounds and single or multiple indicators would be straightforward, but outside the scope of the present paper. However, the present study unambiguously demonstrates how partial order methodology can be applied as an advantageous tool in elucidating and quantifying synergistic and antagonistic effects which cause increased or decreased hazard of chemicals due to the possible presence of 'third party' agents. Such analyses thus contribute to the current discussion on the possible unwanted effects caused by factors such as nanomaterials and microplastics.

The partial order analytical tool presented here may serve as an initial analysis prior to elaborate, time consuming, a priori, and rather costly experimental studies.

Conflicts of interest

Author declares no conflicts of interest in this paper.