Conversion of crude palm oil to biofuels via catalytic hydrocracking over NiN-supported natural bentonite

1.   Introduction

Assuming that the underlying asset process follows a geometric Brownian motion, the Black-Scholes model was firstly proposed in 1973, where the option value satisfies a partial difference equation and depends only on the risk-free interest rate and the volatility of asset price ^[1]. In order to fit the empirical facts of practical financial markets, more extended models were introduced and studied, including jump-diffusion models ^[2,3], stochastic volatility models ^[4], fractional differential models ^[5,6,7] and regime-switching models ^[8].

The idea of switching regimes is prevalently applied in order to allow Lévy processes to switch in a finite state space by a Markov chain. In option pricing models, the parameters, such as interest rate, drift and volatility, are allowed to take diverse values in a finite number of regimes ^[9]. For instance, the option models based on exponential Lévy processes under switching regimes were proposed and widely discussed to capture the sudden state movement from the bull market to bear market, and deal with the non-stationary behavior ^[10,11,12]. Since the partial integro-differential equation (PIDE) derived from the regime-switching exponential Lévy processes is difficult to be solved in closed form, it is essential to develop effective numerical methods.

Recently, numerical solution of fractional option models under switching regimes attract much attention from the community of financial engineering. Cartea and del-Castillo-Negrete ^[13] proposed a first-order shifted Grünwald difference formula for the option pricing models, including the finite moment log stable (FMLS) model ^[6], CGMY model ^[7] and KoBoL model ^[5]. A first-order penalty method for fractional regime-switching American option pricing models, was constructed in ^[14]. Further, an implicit-explicit preconditioned direct method was developed in ^[12] for fractional regime-switching models which was of first order in spatial approximation.

In this paper, we consider a second-order numerical scheme for fractional regime-switching option pricing models, based on the weighted and shifted Grünwald difference (WSGD) formula and Crank-Nicolson scheme. Theoretical analysis on the stability and second-order convergence of the numerical scheme is studied in detail. A second-order ADI method is proposed to accelerate the computation with a preconditioned direct solver for the discrete linear system. Numerical experiments on both fractional PDE and multi-regime FMLS and CGMY models are presented to show the convergence and efficiency of the proposed approach.

The structure of this paper is organized as follows: A second-order numerical scheme for fractional regime-switching option pricing models is presented in Section 2. Numerical analysis of stability and the second-order convergence are shown in Section 3. In Section 4, we introduce the ADI method with preconditioned direct solver for the discrete linear system. Numerical experiments in Section 5 demonstrated the convergence and efficiency of the proposed method. Finally, conclusions are drawn in Section 6.

2.   A second-order finite difference method

Under the risk-neutral measure, assume that the stock price $S_t$ follows a geometric Lévy process

where $r$ is the risk-free rate, $\nu$ is a convexity adjustment and $\mathrm{d} L_t$ is the increment of a Lévy process under the equivalent martingale measure ^[15]. Below, we discuss the general fractional regime-switching option model derivated by three particular Lévy processes: LS, CGMY and KoBoL, see ^[13] for more details.

Let $V_s(x, t)$ be the value of an European option in state $s$, the fractional regime-switching option model is defined by

where $x = \ln S_t$, $1 < \alpha_s < 2, s = 1, 2, \ldots, \bar{S}$. The other parameters in Eq (2.1) depend on a certain state of a Markov process in the finite set $\{ 1, 2, \ldots, \bar{S} \}$. The constants $q_{s, j}$ represent the elements of the state transition matrix of the Markov process, which satisfy the conditions $\sum_{j = 1}^{\bar{S}} q_{s, j} = 0$ and $q_{s, j} \geq 0, \forall j\neq s$.

The left and right Riemann-Liouville tempered fractional derivatives $D_{+}^{\xi_s, \alpha_s}$ and $D_{-}^{\lambda_s, \alpha_s}$ are defined by

where $\Gamma(\cdot)$ is the Gamma function.

In the CGMY model, the parameters in the model (2.1) are given by

The model (2.1) also covers FMLS and KoBoL models by different choices, and we refer the readers to ^[16] for more details.

The terminal and boundary conditions for call options are given by

where $K$ is the strike price.

Let $N$ and $M$ be the number of the uniform discrete points in the space and time direction, respectively, and let $h = \left(x _ { r } - x _ { l } \right) / (N+1)$ and $\tau = T / M$ be the corresponding step length. Define $t _ { m } = m \tau (m = 0, 1, 2, \cdots, M), x _ { n } = x_ { l } + n h (n = 0, 1, 2, \cdots, N+1)$.

Assume that the function $V_s(x, t)$ is continuously differentiable and $\partial^2 V_s(x, t)/\partial x^2$ is integrable in the interval $[0, T)\times [x_l, x_r]$, then for every $\alpha \; (0 < \alpha < 2)$, the Riemann-Liouville derivative of $V_s(x, t)$ exists and coincides with the Grünwald-Letnikov type ^[17]. Hence, we can use the Grünwald difference approaches to approximate the tempered fractional derivatives in Eq (2.2) to avoid the strong singularity when $\zeta = x$.

The first-order shifted Grünwald difference scheme ^[18] was first proposed to approximate the fractional derivatives and used to solve the fractional option pricing models ^[12,14]. Now we consider the second-order weighted and shifted Grünwald difference scheme ^[19] in the discrete process of Eq (2.1).

Based on the weighted and shifted Grünwald difference scheme, the fractional derivative can be approximated by

where

Denote $V_{s, n}^m$ be the numerical solution at the discrete point $(x_n, t_m)$ of regime $s$. Discretising the convection term and the time term in Eq (2.1) by central differences, and the Crank-Nicolson scheme respectively, and introducing the time-reverse transformation $t^* = T - t$, dropping $*$ for simplicity, the following fully discrete scheme is derived:

Denote $V^m = \left(V_{1, 1}^m, V_{1, 2}^m, \ldots, V_{1, N}^m, V_{2, 1}^m, \ldots, V_{2, N}^m, \ldots, V_{\bar{S}, N}^m\right)^{T}$, $Q = \left[q_{s, j}\right]_{s, j = 1}^{\bar{S}}$ and $p^{m+\frac{1}{2}} = \frac{1}{2}\tau(p^{m+1}+p^{m})$, where

The matrix form of the numerical scheme (2.7) can be written as:

where

with

3.   Stability and convergence of the numerical scheme

In this section, the stability and convergence of the numerical scheme (2.8) are established.

A matrix is called positive definite if, and only, if its symmetric part is positive definite, that is, all the eigenvalues are positive.

Lemma 3.1. (Gerschgorin Disk Theorem) Suppose $A = \left[a_{i j}\right] \in \mathbb{C}^{n \times n}$, let

then

Theorem 3.1. (Stability) Assume that $1 < \alpha_s < 2$ and set

If

for all $s = 1, 2, \ldots, \bar{S}$, then the discretisation scheme (2.8) is stable.

Proof. Denote $B = -M_B-Q\otimes I_N$ and consider the matrix

In order to show the stability of the scheme (2.8), it suffices to prove that the eigenvalues $\lambda_Z$ of the matrix $Z$ satisfy the estimate $\left|\lambda_Z\right| < 1$. Or equivalently, that the eigenvalues $\lambda_B$ of matrix $B$ satisfy the estimate

The inequality (3.3) means that any $\lambda_B$ has a positive real part $\Re(\lambda_B)$. Therefore, the numerical scheme (2.8) is stable if the matrix $B$ is positive definite, i.e., its symmetric part $\mathcal{B}$ is positive definite.

Consider the symmetric Toeplitz matrix

and block diagonal Toeplitz matrix

thus,

Note that $c_{s, 2}, c_{s, 3}$ and $d_s$ are nonnegative, we have

where $1+(s-1)N\leq l \leq sN$, $s = 1, 2, \ldots, \bar{S}$.

Therefore, if the matrix $\mathcal{B}$ is strictly row diagonally dominant, then it is positive definite by Lemma 3.1, which means $\mathcal{B}$ satisfies the condition

for $1+(s-1)N\leq l \leq sN$ where $s = 1, 2, \ldots, \bar{S}$.

It is clear that the $l$th and the $(1+(2s-1)N-l)$th rows are the same. Without loss of generality, we choose $1+(s-1)N \leq l \leq (s-1)N+ \lceil\frac{N}{2} \rceil$, then

where $\ell = l-(s-1)N$. By rearranging the sequence $\{ g_k^{\alpha_s}\}$ from $\{ \omega_k^{\alpha_s}\}$ and according to the properties in Eq (2.6), we have

and

Thus, the condition (3.4) becomes

which can be written as

where $\eta_s(x)$ is defined in Eq (3.1).

It is similar that the stability condition in Theorem 3.1 from ^[16] is given by

Consider the specific parameters of the CGMY model from Eq (2.3), the stability condition (3.2) can be rewritten as

while condition (3.5) turns to

It is can be seen that the condition (3.2) allows a wider range of the parameters in Eq (2.1), which can describe more state movement as the financial markets change.

Consider now the convergence of the scheme (2.8). Due to the non-smoothness of the initial and boundary conditions in Eq (2.4), Eq (2.1) does not have a solution in the classical form. As a result, we consider the generalized solution, which satisfies the fractional PDE almost everywhere in $(0, T)\times (x_l, x_r)$. We define the viscosity solution of Eq (2.1) similar as Definition 2.4 in ^[20].

Theorem 3.2. (Convergence) Let ${V}_\ast^m$ be the viscosity solution of Eq (2.1). The scheme (2.8) is of second order convergence, i.e.,

if the matrix $B = -M_B-Q\otimes I_N$ is positive definite, i.e.,

where the norm $\|v \| = \sqrt{h\sum_{i = 0}^{\bar{S}N}v_i^2}$ and $C_0$ is a positive constant.

Proof. The proof is similar as Theorem 3.2 in ^[16], and we omit the specific process here.

4.   The ADI method

In this section, the ADI method will be used to solve scheme (2.7). The ADI method proposed by Peaceman and Rachford ^[21] in 1955 was widely used to solve two dimensional problems due to its computational effectiveness. Recently, the ADI method was also applied to solve two-asset option pricing problems under fractional models ^[22,23].

Denote

and

From Eq (2.7), it is easy to show

where

When the time step $\tau > 0$ is sufficiently small, we omit the term $R$ and define the following ADI scheme similar to that of the Peaceman–Rachford type ^[21]:

The following theorem illustrates the convergence order of the ADI scheme (4.3) and (4.4).

Theorem 4.1. Assume that the exact solution of the fractional PDE in Eq (2.1) is unique, and its partial derivatives are in $\mathcal{L}^1(\mathbb{R})$ and vanish outside $[0, T)\times [x_l, x_r]$. The ADI discretization for Eq (2.1) defined in Eqs (4.3) and (4.4) is also of second order convergence $\mathcal{O}(h^2+\tau^2)$.

Proof. From Theorem 3.2, we have proved that the Crank–Nicolson method has convergence of order $\mathcal{O}(h^2+\tau^2)$. In the ADI scheme, compared to the Crank–Nicolson scheme (2.7), the scheme (4.3) and (4.4) incurs an additional perturbation error $R$ defined in Eq (4.2).

Since

where

When $\tau$ is sufficiently small, the perturbation error $R$ is a higher-order term than the other terms in Eq (4.1). Therefore, the convergence order of the ADI scheme (4.3) and (4.4) is $\mathcal{O}(h^2+\tau^2)$.

In order to solve the ADI scheme (4.3)-(4.4), we need to define boundary conditions for $\widehat{V}_{s, n}$, which is accomplished by subtracting Eq (4.4) from Eq (4.3)

The corresponding algorithm is implemented as follows:

In Algorithm 1, denote $\widetilde{T}_s = I_N-\frac{\tau}{2} T_{s}$ to be the coefficient matrix of the linear system (4.6), which has Toeplitz structure. Using the preconditioned direct method proposed in ^[12,24], the computation process of solving the linear equations with coefficient matrix $\widetilde{T}_s$ can be accelerated by fast Fourier transformations (FFT). The total computation cost to solve Eq (4.6) for each $s = 1, 2, \ldots, \bar{S}$ is $\mathcal{O}(N\log N)$.

Since the order of the matrix $Q$ represents the number of the regime-switching states, which is far less than $N$, the linear system (4.7) can be quickly solved.

For more modern ADI approaches, we refer the readers to ^[25,26], which will be our future work to study them under fractional option pricing problems.

5.   Numerical experiments

In this section, numerical experiments on the fractional PDE, with known exact solution and European call options under multi-regime FMLS and CGMY models, are presented to show the convergence and efficiency of the proposed ADI approach.

Compared with the ADI method, GMRES and BiCGSTAB are used to solve the linear equation on every temporal layer, where the vector $V^{m-1}$ is taken as a initial guess and the iteration is terminated when the residual $r^{(k)}$ satisfies $\|r^{(k)} \|_2/\|r^{(0)} \|_2\leq 10^{-7}$. All numerical experiments are carried out by Matlab R2020a.

Example 5.1. Consider the following FPDE problem with source term:

with

where the exact solution is $V_s(x, t) = e^{-t-\lambda_s x} x^{2+\alpha_s}$.

The following two cases are considered as the settings in ^[12]:

(a) $\bar{S} = 2$, $\alpha = (1.9, 1.6)$, $\lambda = (0.92, 1.20)$, $Q = \left(\begin{array}{cc} -6 & 6\\ 8 & -8 \end{array}\right)$.

(b) $\bar{S} = 8,$$\alpha = (1.6, 1.1, 1.9, 1.8, 1.8, 1.3, 1.6, 1.1),$$\lambda = (2.04, 4.1, 3.6, 4.85, 2.66, 1.63, 0.53, 3.06),$

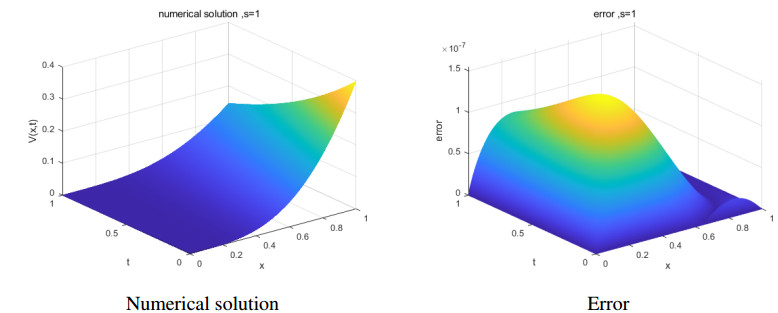
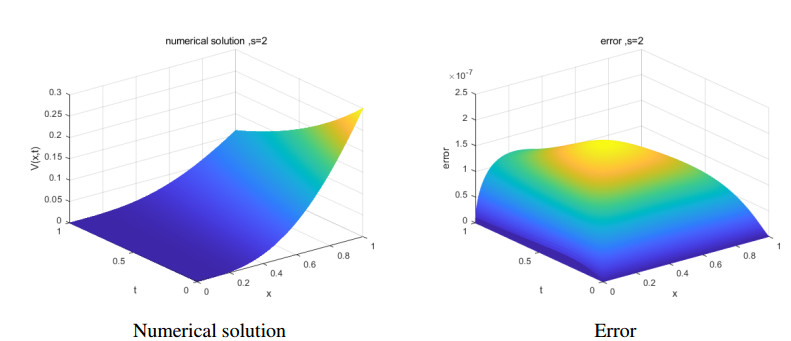
In Figures 1, 2, the surfaces of the numerical solution and error $|V^M-V_\ast^M|$ of case (a) are presented respectively, for $s = 1, 2$, when $M = N = 1024$.

Define the convergence order of the numerical scheme as

where $V_\ast^m$ is the exact solution on $t_m$ and $\|\cdot \|$-norm is defined in Theorem 3.2.

In Tables 1, 2, the error and convergence order of Crank-Nicolson scheme and ADI scheme are listed for case (a) and case (b), respectively. We use "D-ADI" to represent the ADI Algorithm 1 with preconditioned direct method.

From Tables 1, 2, it is seen that both the Crank-Nicolson and ADI schemes have second-order convergence. It is also observed that the convergence of the ADI scheme is more stable. Since the order from Tables 1, 2 represents the convergence on each regime, it can further verify the theoretical analysis in Theorem 3.2.

In Tables 3, 4, the average of the iteration number (denoted by "IT") and the total CPU time (in seconds, denoted by "CPU") of GMRES, BiCGSTAB and ADI methods are compared when the number of discrete points $N$ increases from $2^4$ to $2^9$ respectively.

From Tables 3, 4, it is observed that both GMRES and BiCGSTAB require more iteration step than ADI method, and so does the CPU time. By comparing the CPU time of the three methods, it is obvious that the preconditioned direct ADI method is fast, and can significantly reduce the computation time.

Then, the proposed preconditioned direct ADI method is applied to deal with the multi-regime European option pricing model in Example 5.3. The parameters in this example change in different regimes, by which the sudden state movement and the non-stationary behavior of the market is described.

In order to verify the convergence order for non-smooth payoff function as initial conditions in Eq (2.4), we demonstrate the results of an option pricing problem in Example 5.2.

Example 5.2. Consider the multi-regime FMLS model for pricing European call option, where $x_l = \ln(0.1), x_r = \ln(100), K = 50, r = 0.05, T = 1$. The regime-switching parameters are set as

In Table 5, we list the error and convergence order of ADI scheme. The viscosity solution is approximated by the numerical solution using a dense mesh with $N = M = 2^{13}$.

From Table 5, it is observed that the ADI scheme can keep the second-order convergence under the non-smooth initial conditions. The convergence orders are not as steady as those in Example 5.1 perhaps because of the discontinuity at the strike price $K$, which can be improved by the Padé schemes proposed in ^[27].

Example 5.3. Consider the multi-regime CGMY model for pricing European call option where $x_l = ln(0.1), x_r = \ln(200), K = 60, r = 0.05, T = 1, C = 0.1$.

Consider the following two cases:

(a) $\bar{S} = 4, \quad \alpha = (1.5, 1.7, 1.3, 1.8), \quad \sigma = (0.25, 0.5, 0.75, 0.5), \quad \xi = (2, 1, 5, 1), \quad\lambda = (1, 3, 2, 4),$

(b) $\bar{S} = 6$, $\alpha = (1.5, 1.2, 1.7, 1.3, 1.6, 1.8)$, $\sigma = (0.25, 0.5, 0.3, 0.75, 0.5, 0.2)$, $\xi = (1, 2, 1, 2, 3, 3)$, $\lambda = (3, 4, 3, 1, 2, 2)$,

The option values of four regimes and six regimes are depicted, respectively, in Figure 3 when $M = N = 512$, where the blue dashed line represents the payoff of the European call option and the other colored lines represent the option prices with different regimes at the value date.

6.   Conclusions

In this paper, a second-order finite difference method is proposed to discretise a class of fractional regime-switching option pricing models. In addition, the sufficient conditions of stability and convergence of the numerical scheme are studied in detail. The ADI scheme with preconditioned direct method is considered to deal with the multi-regime structure to accelerate the computation. Numerical experiments verify the theoretical convergence order and show the efficacy of the proposed method.

Acknowledgments

The authors are very grateful to the referees for their constructive comments and valuable suggestions, which greatly improved the original manuscript of the paper. This work is supported by the National Natural Science Foundation of China (No. 11971354 and No. 12171366).

Conflict of interest

The authors declare there is no conflicts of interest.