Abbreviations: LCOE: Levelized Cost of Energy; PES: Primary Energy Saving Index; SOFC: Solid Oxide Fuel Cell; GT: Turbogas or Gas Turbine Power Group; ST: Steam Turbine; SOFC/GT: overall hybrid system; HS: overall hybrid system; IIR: Indirect Internal Reforming; DIR: Direct Internal Reforming; CO-shift (WGS): Water Gas Shift process; RU: Recovery Unit; CHP: Combined Heat and Power Plant; C: Cracking; B: Boudouard; SP: Steam Production; LHV: Low Heat Value; HHV: High Heat Value; ORC: Organic Rankine Cycle
Superscripts: el: related to electro-reaction; fu.proc.: related to fuel processing; fc(r): related to real end compression; m: mechanical, related to mechanical power and/or efficiency; pump: water pump; fp(r): related to real end pumping; heat: related to preheating in the generic heat exchanger; exh: related to the exhaust of the generic component; comb, COMB: related to combustion; COMBn: related to oxygen necessary for Combustion; COMBext: related to external oxygen to be added for combustion; HS: overall hybrid system; CHP: Combined Heat and Power Plant; (r): real (power); (id): ideal (power); (lost): lost (power);
Symbols: F: Molar flowrates [mol·s-1]; Δ: variation; Uf: Fuel Utilization factor [-]; Uo: Oxidant Utilization factor [-]; x: quantity converted in the steam reforming reaction [mol·s-1]; y: quantity converted in the CO-shift (WGS) reaction [mol·s-1]; w (FH2r): quantity converted in hydrogen electroreaction [mol·s-1]; ˜h : molar enthalpy [J·mol-1]; V: real voltage [V]; EN: Nernst voltage [V]; η: polarization losses [V]; η:Efficiency [-], [%]; i: electric current [A]; j: electric current density [A·cm-2]; j0: exchange electric current density [A·cm-2]; αj: Tafel coefficient; ne: Number of electrons involved in the electro-reactions; Fa: Faraday Constant [C·mol-1]; R : Perfect gas constant [J·mol-1·K-1]; P: Power [W]; φ: Coefficient related to gas [-]; β: pressure ratio [-]; MW: Molecular Weight [g·mol-1]; k: gas coefficient [-]; ˜cp : Specific Heat [J·mol-1·K-1]; T: temperature [K]; LHV: Low Heat Value [[J·g-1]]; p: pressure [Pa], [bar]; ˜λeva : latent heat of vaporization [J·mol-1]; TIT: Inlet Turbine Temperature [K]; TOT: Outlet Turbine Temperature [K]; λ: excess air coefficient in combustion [-]; RP: Power ratio [-]; PES: Primary Energy Saving Index [%]; α: Parameter Carbon Deposition monitoring [-]; εT: computational error [-]; CCAP: Capital cost [$]*; CO & M: Operational & Maintenance cost [$]*; CFUEL: Fuel cost [$]*; EADE: Annualized Delivery cost [$]*; cr_co: coefficient of CO electro-reaction [-]; f: molar fraction [-]; e: Specific Energy (Work and/or Thermal Energy) [W·s-1·kg-1]; K: Thermochemical process Constant; G: Gibbs Free Energy [J·mol-1]; A: Fuel Cell Active Area [cm2]; αcomb: combustion coefficient [-]; τ: ratio between the inlet turbine temperature and the temperature at the compressors [-]; π: combustion efficiency; βGTopt : optimum pressure ratio for Turbogas [-]; βSOFC/GTopt : optimum pressure ratio for SOFC/GT [-]; ˙m : mass flowrate [kg·s-1]; s: entropy [j·kg-1·K-1]; H: Thermal transmittance [Wm-2·K-1]; Y: Head loss [m];
Subscripts: H2: Hydrogen; CO: Carbon Monoxide; CO2: Carbon Dioxide; H2O: Water/Steam; N2: Nitrogen; O2: Oxygen; i: generic term; IN (in): inlet term; OUT (out): outlet term; REAC: reaction; act: related to activation losses; ohm: related to ohmic losses; conc: related to concentration losses; an: related to anode; cat: related to cathode; k: SOFC layer; generic term; air: air; C: Compressor; id: ideal; env: environment; is: isoentropic; gas: related to the anodic gas; m: mechanical, related to mechanical power and/or efficiency; p, pump: water pump; el: electric, related to electric power; liq: related to H2O in the liquid phase; hyd: related to the hydraulic efficiency of the pump; ph: related to water preheating; vap: related to water vaporization; sh: related to steam superheating; eva: related di saturation temperature; HC: related to heat exchanger; exh: related to the exhaust; comb, COMB: related to combustion; RU: Recovery Unit; GT: Gas Turbine (Turbogas group); term related to excess air in combustion; cur: current variable related to excess air in combustion; tot: total, related to total flowrate; t, T: related to gas turbine isoentropic efficiency; turb: related to gas turbine; al: alternator; HS: overall hybrid system; CHP: Combined Heat and Power Plant; th: thermal; ref: reference, related to reference efficiency; C: Cracking; B Boudouard; SP: Steam Production; sys: overall system; r: related to gas reacted electrochemically; eq: equilibrium; fuel: fuel; biom: biomass; h: hot; c: cold;
*: Other contribution costs and details are reported in Table 3;
1.
Introduction
The ever-increasing demand for energy, associated with the consumption and therefore the outsized use of fossil fuels [1] which lead to an undoubted deterioration of the climate of the planet Earth [2], is increasingly pushing for the intelligent use of resources and the adoption of alternative production systems [3]. There is a growing interest in the class of high-temperature solid oxide fuel cells, since it has the virtue of being highly efficient, sustainable, and exercisable by a variety of fuels [4,5,6,7].
The high-temperature operation opens up the possibility of configuring hybrid systems by matching SOFC with steam (ST) and/or gas (GT) turbine, thus grafting a bottomed cycle, to further improve the energy efficiency [8,9,10,11,12]. Hybrid systems are considered by far the most promising technology in the search for maximum yields in the generation of electricity from fuels [13,14,15,16,17,18]. A market study by Research Dynamics Corporation concluded that hybrid systems could compete on the generated electricity cost with other distributed generation technologies [19].
Various arrangements can be made, even creating a complex SOFC/GT/ST system [20,21,22,23,24]. The most studied hybrid systems are those composed of solid oxide fuel cells and gas turbines SOFC/GT. They are currently the only ones to be in prototype and in a physical experimentation phase [25,26,27,28,29,30,31,32].
Many papers in the literature consider this technology and its progress. The study of Buonomano et al. [33] presents a comprehensive review. Various studies on different types of configurations are present [33]. Waste heat or part of it can be recovered at SOFC exhaust level, combustor exhaust level, and/or gas turbine exhaust level and can be employed for pre-heating entering fresh gases, preparing fuel processing stages, and transferring heat externally for co-trigenerative purposes [34,35]. Another variable much studied is the partial recirculation of the anode off-gas, especially when internal fuel processing is operated, demonstrating that it is a fundamental unit for high plant performance [36,37].
Feeding by fuel different from pure hydrogen has an impact on hybrid systems accordingly [38,39,40]. Hydrocarbon fuels must be subjected to fuel processing, requiring high amount of heat. The Fuel Processing can be operated inside the SOFC architecture, thus leading to an increase in system efficiency, as well as a reduction in overall dimensions and costs [41], give rise to Direct Internal Reforming (DIR) modality and/or by Indirect Internal Reforming (IIR) modality [42] which is more precautionary. In the case of steam reforming, the recirculation of the exhaust anodic streams enables the exploitation and the feeding of the contained steam [43,44]. However, externally reformed SOFC/GT layouts are also considered in the case of the more complex type of fuels [45], thus taking care of any problem of carbon deposition.
The layout most frequently studied is the one that shows the integration of a pressurized SOFC with a GT following a Brayton cycle. Various studies have also been conducted on atmospheric SOFC/GT hybrid cycles [46,47,48], demonstrating lower performance.
The selection of an SOFC/GT plant layout is determined by several design parameters, such as: operating temperature and pressure of the SOFC stack; type of fuel, and peculiarities of the fuel processing subsystem (steam reforming if internal or external, direct or indirect); anode recirculation; heat recovery systems for the heat supply of the endothermic processes; type of Brayton cycle if basic, inter-cooled and/or regenerative. A selection of papers describing the SOFC/GT system performance in relation to its management is reported to this purpose.
Calise et al. [49,50] studied an internally DIR reformed SOFC/GT power plant with an anodic recirculation, for which the GT cycle is a recuperative Brayton cycle. The system is fed with methane which is first pre-reformed and subsequently DIR reformed. The pressure ratio operated is about 8, the steam to carbon ratio and the fuel utilization factor are respectively 2 and 0.85. The calculations for this plant revealed a net total power of 1.5 MW and an electrical efficiency of 67.9%. Song et al. [51] investigated on a similar layout, but the fuel processing is operated adopting the IIR modality. As for the parameter setting, the Turbine Inlet Temperature is 840 ℃, the pressure ratio of about 3, steam to carbon ratio and fuel utilization factors of 2.5 and 0.85, respectively. The power plant resulted to be 840 kW, while calculations revealed an overall electric efficiency of 60.2%. Yang et al. [52] carried out an interesting comparison between internally and externally reformed SOFC/GT power systems. The investigated plant layout shows also an anodic recirculation system. For the externally reformed plant, it is heated by a heat exchanger by the SOFC cathode exhaust gases, while the internally reformed one receives heat directly from the SOFC. With the same parameters operated (steam to carbon ratio of 3; the pressure ratio and the utilization of respectively 3.5 and 0.70, SOFC temperature 700-1000 ℃, turbine inlet temperature 750-1050 ℃), the results showed that the internally reformed SOFC/GT power plant operates with better performance than the externally reformed one. In fact, in the first case, the efficiency ranges between 42% and 70%, while the efficiency of the externally reformed power plant varies between 32% and 60%. The authors concluded that the external reforming arrangement is penalized by the more complex thermal management since additional amounts of fuel are required to achieve comparable thermodynamic conditions. The absence of anodic recirculation is compensated by having a heat recovery system for steam generation, necessary to the fuel processing.
Huang and Turan [53] analyzed the effects of methane, carbon monoxide and hydrogen fed singularly to a pressurized SOFC/GT system, presenting an external reforming fuel processing. The analyses performed considered also the effect of the main operative parameters on performance. Results highlighted that the hybrid system reaches an optimized electric efficiency of 56.1%, 54.3%, and 60.7% when fueled by CH4, CO and H2 respectively based. Wang et al. [54] studied an SOFC/GT hybrid system combined with anode and combustor exhaust recirculation loops fed by farm biogas, varying also the main operating parameters. Results showed the rising of the electric efficiency and the technical performance by acting on the anode recycle loop can. The optimal recirculation ratios of 0.4 and 0.425 allowed the system to obtain the maximum power generation efficiency 62.21% and ensure the safe operation of SOFC with regards to carbon deposition. Chitgar and Moghimi [55] studied a novel integrated system based on solid oxide fuel cell-gas turbine (with anode off-gas recirculation) for the simultaneous production of electricity, freshwater and hydrogen. The system fed by natural gas was optimized through a genetic algorithm and it presented an energy efficiency of 56.9% for the SOFC/GT system.
A valid opportunity to generate energy at high efficiency, protecting the environment, is given when coupling biomass gasifier [56,57,58,59,60,61]. Lv et al. [62] presented the integration of an SOFC/GT system with biomass, studied via mathematical modeling. The authors analyzed the effects of changes of H2, CH4 and CO on the system performance. The energy efficiency of the system was evaluated as 60.78% at the design point using gasified wood chip gas. H2 concentration variation is the most influential factor for the energy system output power and efficiency, followed by CH4, and then CO. System efficiency increases significantly with H2 concentration increase, while it decreases slightly with a CO and CH4 increase. Ding et al. [62] presented a numerical analysis of a biogas-fueled SOFC/GT hybrid system with a recirculation process using combustor exhaust gas and an external reformer. The results show that the recirculation process could increase the electrical efficiency of the system from 58.18% to 62.8%, for an acceptable recirculation ratio between 0.17 and 0.32.
Recently, many researchers have studied SOFC-GT hybrid systems from economic points of view, besides technical and energy ones. Meratizaman et al. [64] proposed an SOFC/GT hybrid cycle fed by natural gas as an electrical and heating energy supplier for a residential area. The authors then carried out a sensitivity analysis of fuel cost and market price to find a solution for the substitution of a traditional power production system for four different climatic zones in Iran. The results of the economic analysis showed that the suggested system in a hot and humid climate has the best economic parameters including the Levelized Cost of Production of 0.0157 US$·kWh-1. Eveloy et al. [65] presented a techno-economic-environmental optimization of a pressurized SOFC/GT system, with an ORC bottomed process, coupled with a small-scale seawater reverse osmosis desalination unit. The SOFC/GT cycle is fed by natural gas, processed internally via direct internal reforming. The optimum solution assessed showed an overall exergy efficiency of 70.5% for a 2.4 MWe system and a cost rate of 0.0233 USD·s-1. Eisavi et al. [66] carried out performance and economic analyses on SOFC/GT layout-based systems fed by methane processed by internal reforming at a steam to carbon ratio of 2.5. The layouts differed from the base case by using two interacting SOFCs, The economic analysis lay on the estimate of the total expenses. The results showed energy efficiency ranging between 53-63%. The economic results showed the highest total cost, 24.95 $/h, for the base case while the least amount corresponds to the SOFC-GT series type, 18.5 $/h. Rao et al. [67] studied a 20 MW-electric power system based on SOFC/GT fed by gas coming from the steel industry from a thermodynamic and a Levelized Cost Of Electricity (LCOE) point of view. The SOFC/GT system layout presented an electric efficiency of 64%, operating at 0.25 A·cm2, steam to carbon ratio higher than 2.
Hou et al. [68] studied a 227 kW SOFC/GT system fed by methanol, from an energy and economic point of view, by using Aspen Plus. The study determined an electric efficiency of 59.7% and annual profits of 517 kYuan per year. Roy et al.'s study [69] involved a techno-economic-environmental assessment of a biomass gasification based power plant integrating an SOFC module, an externally fired gas turbine, and an organic Rankine cycle. The energy efficiency reached about 50%, while the economic analysis based on the Levelized Cost of Energy (LCOE) foresaw a minimum value of 0.086 $·kWh-1.
The analysis of the presented literature review highlights how this kind of hybrid system, based on the integration of SOFC/GT, shows higher energy efficiency compared to conventional power systems, and competitive economic indexes.
The motivation of this paper is that of performing a wide sensitivity analysis taking into consideration the technical, energy and economic aspect. Analyzing the recent papers, it was noticed that this kind of analyses can be of completion and so giving a valid contribution to the reference literature. The objective of this manuscript is pursued by means of an ad hoc numerical modeling and simulations. The originality of this work lies in a high accuracy model, which accounts on the thermochemical processes by a very high detail. In addition, the manuscript describes a likely Balance of Plant, up to consider its technical and technological limitations. All is focused on the concept of efficiency and sustainability, as well as the economic feasibility for employing this energy technology, by using possible alternative fuels.
This paper follows a previous one [69], from which inherits the tool of calculation about the SOFC. The internal thermo-electrochemical processes are modeled with a high degree of accuracy, with attention dedicated to the fuel utilization factor, Uf,, conversely to the majority of papers of the literature that uses it in an approximated way. The modeling considers the concurrent electro-reactions of hydrogen and carbon monoxide, besides the concurrent internal fuel processing.
The model efforts consist of organizing the system components with particular focus on not exceeding the technological constraints, besides being also energy efficient. Moreover, the computational exertion is in the communication between the various blocks that have to be organized and run harmoniously.
The calculation algorithm has the aim of calculating the flow rate of the entering gas at the required conditions. The computational burden associated with the resolution is very high since the main thermochemical variables are not known a priori. Iterative computational processes are necessary before convergence. The modeling is implemented and run in a Matlab calculation environment.
The layout of the system is composed of compressors for air and fuel, a pump for water flowing, direct internal fuel processing SOFC, post combustor for SOFC-exhaust fluids combustion, a gas turbine for turbo-expansion, and a final recovery unit for cogeneration purposes. Fresh gases are preheated after pressurization and before entering the SOFC. The heating-up system is made by flowing the combustion gases exhausted by the combustor into a proper heat exchanger, to lower their temperature and match the technological limit of the gas turbine material. This part of the layout represents another element of differentiation with the majority of SOFC/GT systems modeled and present in the scientific literature, for which the heat recovery for fresh gas preheating is made at the gas turbine discharge [71,72,73,74,75].
The analysis account on the influence on the system by investigating the change of the fuel composition (H2, CO, H2O, CO2, CH4 and N2), and by managing the main operating parameters, such as pressure and the fuel utilization factor. The paper reports on specific mass flow rates necessary to the purpose required, by assessing the SOFC outlet molar composition, specific energies (work) at main system elements, specific thermal energies at main system elements, energy and technical performance for SOFC energy unit; performance as electric and thermal efficiency, and temperatures at the main system elements. A final sensitivity analysis on performance, LCOE, and PES is made for completion. The overall investigation is also supported by a carbon deposition analysis on the SOFC anode section, in order to confirm or otherwise by considering the feeding and operating condition of the system.
2.
Plant layout
The configuration illustrated in Figure 1 is chosen for the SOFC/GT hybrid system, which is the main core of the modeling presented in this paper. The plant is composed of the gas compression sections (anodic gas and cathodic air), of the gas expansion section, represented by a gas turbine, of the section relating to the preheating of the incoming flows, preheating carried out by a series of heat exchangers, and of an SOFC module which is the core of the system and which carries out the energy conversion of the reacting flows.
The operating conditions of the SOFC (such as pressure, and composition of the gas mixture), the chemical and electrochemical processes that take place inside the SOFC, and, therefore, also the kinetics of the reactions, the utilization factor of the fuel and the oxidant strongly influence the operation of the entire hybrid system.
One of the most critical aspects of the design of a hybrid system concerns the methods of integrating the fuel cell with the gas turbine. In fact, the electric power generated as well as the electric efficiency of the hybrid system are also determined by the degree of interaction of the main components that make up the system, especially in terms of the recovery of mass and energy flows. In the configuration considered, the energy content of the flows leaving the combustor is used for preheating the air, the fuel, and the water (in this case for its evaporation and heating) up to the desired cathode and anode inlet temperatures. Since the gaseous output of the anodic compartment contains quantities of fuel electrochemically unreacted, it is considered to guide this flow directly into a combustor without adding an external fuel flow rate. Concerning the quantity of oxidant required, a possible integration of a certain quantity of air is envisaged from outside, in order to ensure combustion with excess air under the operating conditions of an ordinary gas turbine. This is the case when the content of output air from the cathode compartment of the SOFC is not sufficient to satisfy the development of the combustion, according to the required conditions.
The gaseous flows entering the system are technical air (consisting of 79% of N2 and 21% of O2) which is fed to the cathodic compartment of the solid oxide cell, and a gaseous mixture (generally consisting of CH4, CO2, CO, H2, H2O, N2) fed to the anode compartment. The air and anodic stream are first pressurized up to the system operating pressure. Air and anodic gas are pressurized by proper compressors. Subsequently, these streams are brought to the cathode inlet and anode inlet temperatures respectively, by being heated in heat exchangers. The heat exchangers are considered to be of the surface type, therefore, the gases remain physically separated from each other. HC_an and HC_cat are for anodic and cathodic gases, respectively, while water is treated apart. Water is pressurized by a proper pump and then heated up to the inlet temperature of the anodic compartment. To achieve this, water is treated in the dedicated heating section, made up of a preheater, PH, an evaporator, EVA, and a superheater SH. The importance of water refers to its role in the internal fuel processing stage; hence, this layout accounts for a provision of external water/steam in addition to that produced by the fuel cell itself. The streams are ready to be sent to the solid oxide fuel cell unit, in which thermochemical and electrochemical processes occur with the consequent generation of electric power. The gaseous flow leaving the anodic and the cathodic compartment of the solid oxide cell consists mainly of quantities of fuel that have not reacted in the cell, unreacted hydrogen, carbon monoxide, possible methane (anode side), and oxygen (cathode side) not reacted, as well as quantities of inert gases such as nitrogen, steam, and carbon dioxide. Therefore, the anodic and cathodic mixtures are then sent to a combustor, located downstream of the SOFC module.
The thermal content of the combustion gases is according to the type and composition of the mixture entering the hybrid system, the operating conditions of the SOFC (pressure, temperature, kinetics and degree of reaction of the chemical and electrochemical reactions that take place). The layout considered in this paper provides for the sending of the combustor exhaust flows to the above-mentioned heat exchangers. This solution is adopted to better shape the temperature of the gaseous flows with the entrance to the turbine, in order to ensure homogeneity with the thermal constraints of its materials. The thermal power from the combustor output is then used for the preheating of the gaseous flows entering the solid oxide cell. Subsequently, the combustion gases that have released thermal power to the exchangers are treated to lower the turbine inlet temperature and make it compatible, if too high. Therefore, they are prepared to expand into a gas turbine for the generation of additional electric power, in addition to that generated by the SOFC module. The expanded gaseous mixture, still possessing a high thermal content, can be used to provide thermal power to the outside. An additional section of the recovery unit, RU, is provided for the final heat recovery of the exhaust flows for cogeneration purposes.
3.
System modeling
The elaborated numerical model has the purpose of analyzing the performance of a hybrid system consisting of the integration of a planar SOFC stack with a gas turbine (Figure 1). The level of detail of the elaborated numerical model is zero-dimensional and stationary. The assumptions are: lumped elements; temperatures of the flows leaving the system elements equal to the temperatures of the system elements themselves; instantaneous and perfect combustion.
The input data consist of the cell geometry and the characteristic quantities relating to the components that make it up, the composition of the air and the feed gas mixture, the parameters relating to the fluid machinery (pump, compressors, and turbine), the combustor and the heat exchangers that complete the entire hybrid system.
Each main component of the system requires the implementation of specific lines of code in order to model its operation, as well as the interaction with the other subsystems that make up the system. Therefore, a continuous interaction between sub-models is necessary with a continuous exchange and updating of results and computational instructions.
The first phase of the numerical model concerns the section relating to the compression of air and the hydrogen-rich gas mixture that feed the system. In fact, it is necessary to compress the air and the gaseous mixture from the atmospheric pressure to the pressure in force in the cell. As for the water that enters the SOFC, it is necessary to model the pumping up to the cell operating pressure. The water enters the cell in the vapor phase, at a temperature equal to that of the entrance to the anode compartment. A preheating, evaporation, and overheating phases are therefore envisaged up to the conditions required by the cell. Therefore, the output data relating to the compression and pumping section are sent to the sub-model that describes the heating system of the reacting flows for entering the cell. The output is sent to the SOFC model.
The computational block of SOFC consists of modeling the thermo-electrochemical processes that take place inside it. Being an Internal Fuel Processing SOFC, the thermochemical reactions of fuel processing which occur simultaneously with the electrochemical reactions of electricity generation are extremely important. The SOFC block is the most important because it affects the calculation of the anodic and cathodic flow rates to be fed to the entire system. According to the aforementioned thermo-electrochemical processes, the molar flows and the composition of the gaseous mixture in output from the cell are evaluated.
A subset of the output of the SOFC model constitutes the set of input data for modeling the combustor. These are given by the flow rates and by the thermodynamic conditions of the flows leaving the SOFC model. The combustion process of the gases unreacted in the fuel cell, like hydrogen, carbon monoxide and possible methane, follows. Output flows from the combustor, combustion temperature, and thermal power associated with the combustion gases are then determined. This information is so used for heating the entering fresh fluids.
The sub-model relating to the preheating section allows determining the powers required to reach the imposed anode and cathode inlet temperatures. This follows the knowledge of the temperatures at the outlet compression sections, determined according to the required gas compression and the characteristics of the compressors.
The turbo expander modeling involves determining the thermodynamic conditions of the gas flow before and after expansion. The model for the gas turbo-expander aims to obtain the electrical power generated by the gas turbine, the values of the turbine inlet and outlet temperatures, and, consequently, the thermal power associated with the gases once the expansion phase is completed.
In general, each component is studied and investigated by employing at least two sub-models: the flow model, which calculates the flow rates and the gaseous compositions involved according to any thermo-electrochemical processes, and the thermal model, based on the thermal balance, which calculates the thermophysical properties (temperatures, energies, energy flows) at the remarkable stations of the plant. These sub-models are markedly sculpted for the SOFC block, to which the electrochemical model that allows obtaining the electrical characterization, and calculating both the voltage and current, and therefore the electrical power generated by the cell is added.
3.1. Solid Oxide Fuel Cell modeling
The computational block associated with the SOFC section is the most important since its resolution enables the determination of the flow rates to be fed to the global system for its operation.
The modeling of the solid oxide fuel cell is approached according to the direct internal fuel processing that involves an incoming mixture of CH4, CO2, CO, H2, H2O, N2, simultaneously with the electrochemical processes involved in the electro-reactions of H2 and CO, which generate electric and thermal energy and H2O and CO2 as fluids.
The fuel processing reactions consist of those processes related to the direct internal direct CO-shift when the methane content is null or negligible, or related to the direct internal steam reforming in the other cases.
The thermo-electrochemical processes occurring in the anode are reported in set (1), while those involving the oxygen reduction are presented in (2)
The SOFC simulation model is marked by the flow, thermal and electrochemical sub-models that interact with each other to determine the quantities that characterize the cell itself.
3.1.1. Flow model
The flow model determines the molar flows of the substances that make up the gaseous streams entering and leaving the SOFC and their composition.
The system of equations that describes the problem is constituted of the mass balance equations written for each gas species involved in the anodic and cathodic processes; according to (3), where the term ∆Fi indicates the variation of the molar flow of the i-th species due to the processes that occur at the anode and the cathode, therefore, due to the reaction in which it is involved.
The system of equations is a function of the unknown transformation quantities, x,y, (representing the amount of gaseous substance that reacts in the direct internal fuel processing. The input molar flow rate, FTOT, IN, to be fed is a function of the hydrogen reacted, w, of the hydrogen molar fraction at the inlet, of the fuel utilization factor operated, Uf, and of x and y; FTOT,IN=f(w,fH 2,Uf,x,y). The complexity of the procedure for the calculation of the inlet molar flow rate lies mainly in the fuel utilization factor, whose component terms are not known singularly beforehand. Uf=FH 2 rFH 2,IN + 3x+y is the ratio of the reacted fraction to the hydrogen present instantaneously in the anode bulk.
The sub-model considers the concurrent electro-reactions of hydrogen and carbon monoxide [76,77], while neglecting the possible CO2 reforming of the methane present in the mixture [78,79,80].
3.1.2. Thermal model
The thermal model has the purpose of determining the cell operating temperature (TSOFC). The molar flows resulting from the previous sub-model are sent to the thermal one. This sub-model is based on a power balance equation written for the cell, as in (4).
PelREAC and PFu.proc.REAC represent the powers associated with the fuel processing and that generated during the electrochemical reaction of hydrogen and carbon monoxide.
3.1.3. Electrochemical model
The electrochemical model uses as computational input data from the determination of all the unknown quantities involved in the flow and thermal models and it produces the electrical parameters as computational output useful to the numerical-electrical characterization of the solid oxide cell. The model enables the polarization curve (voltage vs electric current density (V-j)) to be built up, as well as the trends of all the electrical outcomes, as electric power density vs electric current density.
The electrochemical balance rises a system of non-linear Eq (5), where the real voltage is calculated starting from the Nernst voltage, diminished by the activation, ohmic, and concentration polarization losses.
Activation overpotentials are associated with the energy needed to establish the two reactions of hydrogen and carbon monoxide with oxygen ions at the anode side and electrons and oxygen at the cathode side, and they are calculated according to the Butler-Volmer Eq (6).
The ohmic polarization, caused by the ion conduction and resistance through the electrolyte and electrons through electrodes, follows the associated electric law.
Concentration losses are determined by making use of the known equations governing the gas diffusion in gas mixtures and porous media [81,82].
These models are applied to a conventional high-temperature solid oxide fuel cell. The anode material is based on nickel-cermets (Ni/YSZ), the cathode material is based on strontium-doped/lanthanum manganite (LSM), while the electrolyte material is based on yttria-stabilized zirconia (8YSZ).
More details, parameters of the aforementioned equations, cell stratigraphy, and technical insights, are reported in the authors' previous paper [69].
3.2. Anodic and cathodic gas compressors
The modeling of the overall Turbogas Group starts from the modeling of the single components that make it up. In the modeling of the processes that take place in the compressors and the turbine, irreversibility is taken into account through their isentropic efficiency. The pressure losses that occur mainly in some points of the thermodynamic cycle, such as at the compressor intake (filter, ducts, etc.), in the combustor, and in the exhaust ducts of the turbine (and which in they generally have a value between 1% and 3%), are neglected in the implemented model, as previously discussed.
Air and the incoming gas mixture must undergo compression up to the cell operating pressure, before being sent to the SOFC module.
Compression power and temperature at the outlet section of the air compression, Tfc(r)air are calculated by adopting the equation set, reported in (7).
The determination of the specific heat ˜cp,air (T), as a function of the air temperature is carried out by employing a fourth-degree polynomial relationship, in which the coefficients have been suitably evaluated for the air mixture, taking into account its constituent gases in the respective proportions.
Considering that the compressor is driven by the gas turbine, expression (8) is used to calculate the mechanical power that is actually absorbed, by considering the mechanical efficiency of the compression unit.
The power needed to compress the gaseous mixture entering the anodic compartment is determined in a similar way to the model steps presented for the air compression, and therefore also the actual temperature at the end of the compression (Tfc(r)gas_an) is calculated. The numerical expressions adopted are reported in the equation set (9).
Hence, the anodic compressor absorbs a mechanical power equal to (10).
3.3. Water pump
Water pressurization is delegated to a specific pump also responsible for its flushing. The expressions for calculating the pump power and the temperature of the water at its outlet are shown in (11-12).
Finally, the electric power required to operate the pump is given by (13), where the mechanical, electrical and hydraulic efficiencies appear in the denominator.
3.4. Heat exchangers
As shown in Figure 1 about the Plant Layout, a series of heat exchangers are used to obtain the preheating of the feeding flows, up to the conditions of the inlet temperature to the anodic and cathode compartments. Preheating is considered to be performed via the heat exchanger involving the combustion gases leaving the combustor. The heating of the water and its vaporization are carried out through a special evaporator, which also operates thanks to the thermal recovery of the combustion gases leaving the combustor. The list of expressions and thermal balances involved in the heat exchanger modeling is reported below (14-32).
The thermal power, Pheatair, required to heat the cathodic air from the temperature at the outlet section of the air compressor up to the cathode inlet temperature, Tcat,in, is presented in Eq (14).
The thermal power, Pheatgas_an, required to heat the anodic gas from the temperature at the outlet section of the gas compressor up to the anode inlet temperature, Tan,in, is presented in Eq (15).
The thermal power required for the evaporation of the feed water, Peva, and its heating up to the inlet temperature of the anode, Tan,in, are presented in Eq (16-17). Peva is considered as a function of three main rates: pre-heating (PH 2O,ph), vaporization (PH 2O,vap) and superheating (PH 2O,sh) contributions (16).
Clearly, the heating thermal powers transferred to the exchangers must be increased by a factor which is a function of the efficiency of the exchangers themselves. The expressions are reported in (18-23).
As discussed above, the fresh fluids are heated through the heat exchange with the gases exhausted by the combustor. The expressions reported in (24-28) allow the accomplishment of the calculation related to the thermophysical condition for the exhaust gases that yield part of their thermal power.
The thermal balance at heat exchangers combusted gases/cathodic air is shown in Eq (24).
The thermal balance at heat exchangers combusted gases/anodic gas is reported in Eq (25).
The thermal balance at heat exchangers of the water evaporator is presented in (26).
The thermal power given by the exhaust gases in output from the combustor is reported in set (27), where each contribution is emphasized.
Expression (27) can be written as in (28).
The above balance, (29), is necessary to calculate the turbine inlet temperature (TIT).
The thermal balance to the thermal recovery unit, heat exchanger exhaust gas-water, is given in (30-32).
This balance allows the determination of the water flow rate, FH 2O_RU, for the recovery of the thermal energy discharged from the system.
Some technical consideration for the preliminary design of the heat exchanger are reported as follows. In particular for what concerns the head losses occurring.
The pressure losses for a heat exchanger are very important in its dimensioning. The performance of a heat exchanger is identified with reference to a certain number of parameters that characterize the type of service. These parameters are usually the thermal length, the flow rates, the pressure drops, the fouling coefficients. Pressure drop increases as fluid flow velocity through the heat exchanger is increased, as does the convection heat transfer coefficient. A good design is therefore always a compromise of sufficiently heat transfer characteristics with acceptable pressure drop. Figure 2 illustrates the heat exchange.
The entropic graph well shows how the pressure losses impact on the heat exchange. The pressure losses occurring on the hot and cold fluid produce a heat loss, given by the areas shown in Figure 2 (b).
As known, the equations for the thermal exchange are given by Eq set (33-35)
The efficiency of the heat exchanger is in general the ratio between the real thermal power exchanged and the ideal thermal power (potentially exchangeable), as in (36).
Ultimately we can write the heat exchanger efficiency as in Eq (37).
By making the terms explicit, it becomes as in (38)
Therefore, by the former form the heat exchanger efficiency is function of: the mass flow rates of the cold and hot fluids, the thermal transmittance of the heat exchanger, the total heat exchange surface, and the head losses occuriing.
3.5. Combustor
The gas stream coming from the anode and cathode compartment of the cell enters the combustor located downstream of the SOFC module. The characteristics of these mixtures, in terms of temperature and composition, are conditioned by the type of mixture fed to the system and by the operating conditions of the SOFC. The temperature of the gas flow entering the combustor is considered equal to that of the SOFC, neglecting in the model the thermal losses that occur in the adduction ducts to the combustion chamber. As aforesaid, the thermal source is given by the amount of undepleted gas in the SOFC anode. The amount of hydrogen and carbon monoxide not oxidized in the cell can then be oxidized by the exhaust oxygen outgoing from the SOFC cathode. Also, traces of possible methane can be a potential thermal source, if present in the feeding stream. The more or less conspicuous quantities of inerts like steam and nitrogen can affect the combustion and, so, its temperature. The possible connection line to the gas turbine is determinrd by the technical constraints of the turbine material. A very high temperature can damage the first region of the turbo expander. Therefore, the idea of first lowering the temperature possessed by the gases in output from the combustor goes towards the direction of protecting the turbine itself. This can be accomplished by performing the useful effect of transferring part of the thermal power to fresh gases, thus lowering the temperature of the exhausted ones. The first control is effected on the combustion conduction, by means of the λ parameter, representing the air excess coefficient. The λ parameter is opportunely set by adopting the criterion of limiting the combustion temperature concerning its constituent material first, and to have a powerful gas in output, useful for fresh fluids heat up. λ is imposed as λGT. The exhaust oxygen from the cathode, which has a value of λ=λcur, cannot even present that value, λGT. In that case, a quantity of external air must be added.
The following reactions occur in the combustion chamber, as reported in (39).
The combustion is assumed as perfect, and therefore there are no traces of unreacted fuel exiting the combustor. Combustion must take place with an oxidant excess, in line with the operating conditions of the gas turbine. In this regard, the quantity of oxygen necessary, FCOMBnO2, for complete combustion is determined as in (40):
The generic term FSOFCi_out is the molar flow rate of the gaseous substance exiting the SOFC. The parameter λcur gives an indication of how the combustion takes place in terms of excess of O2, as aforesaid. It is defined as in (41).
This parameter is then compared with the equivalent parameter λGT. If λcur<λGT it is necessary to integrate a quantity of O2 from outside, given by expression (42). It is obviously accompanied by the amount of nitrogen (43) present in the ambient air (44).
The quantity of the integrated air is first subjected to compression to be brought to the condition of pressure set, then it bypasses the SOFC and is sent directly to the combustor.
The oxygen flow rate, FCOMBrO2, required by the combustion is therefore given by expression (45).
If λcur>λGT the combustion can take place without the necessity of external air integration.
The equation set reported in (46) illustrates the flow model for the combustion, based on the molar balance.
The temperature of the output flow from the combustor is determined by means of the energy balance equation of the combustor, which is formulated according to expression (47). The formulation reports the power released by the reaction of the gases involved, as well as the input and output power. Clearly, for this calculation, it is necessary to assess the specific heat for the possible integration of FCOMBextO2 and FCOMBextN2.
The thermal model, previously discussed, allows the calculation of the temperature TCOMB. In order to evaluate the conditions of the heat recovery section, and consequently the thermodynamic conditions of the gaseous current entering the turbine, it is necessary to determine the thermal power associated with the gaseous flow leaving the combustor (PCOMBGAS_OUT). It is convenient to use the expression in the form (48).
3.6. Gas turbine
Following the energy assessment of the preheating section, the turbine inlet conditions and therefore the turbine inlet temperature (TIT) are determined. The knowledge of the TIT is fundamental for the calculation of the power developed by the turbine. The equation set (49) is used for turbine power and temperature at machine outlet determination (TOT=Tft(r)turb).
For ˜cp,turb (T) is adopted a fourth-degree polynomial expression.
Turbine mechanical power is given by (50).
4.
System performance
The useful mechanical power developed by the overall Turbogas Group is reported in (51).
Compressor powers are negative as being an energy expense, so they are detracted from the turbine power to have useful value. While in expression (52) the net electric power of the Turbogas group is given.
In order to calculate the net power of the overall SOFC/GT energy system, all the electric powers are added. Clearly, the pump power is detracted, as being an absorption. The expression is reported as in (53).
Listed below are the electric efficiencies for SOFC (54), Gas Turbine (55), Turbogas Group (56), and overall SOFC/GT system (57). At the numerator, the useful power is represented by the electric power, while the available power is at the denominator and it is represented by the chemical power of the reactant fluids, possibly fed to the system.
A significant parameter that characterizes the performance of a hybrid system is represented by the ratio between the electrical power generated by the SOFC module and that generated by the gas turbine (58).
4.1. Primary Energy Saving analysis
The Primary Energy Saving (PES) analysis is performed for the completion of the energy analysis, to estimate the cogeneration goodness, according to the Italian Standards and Subsidies for Cogeneration Units.
The PES index expresses the relative saving of the primary energy achievable by a cogeneration plant compared to reference systems that generate the same heat and electricity separately, ηel, ref and ηth, ref. Autority for Electric Energy and Gas (AEEG) regulates its estimation. The reference terms, reference electric and thermal efficiencies in the AEEG, are estimated as 0.38 and 0.9. The PES formulation is reported in (59)
5.
Carbon formation analysis
The possible reactions that can lead to carbon formation must be taken into consideration in the high thermal regime environment of a reforming fuel conversion process. The carbon deposits on the reaction sites hinder the encounter between the gaseous reactants [83,84].
Carbon deposition mainly occurs due to methane cracking reactions (C) (60), to Bouduard (B) (61), and to Steam Production (SP) (62).
Operating with high-temperature SOFC materials could be very problematic since a study demonstrated the high selectivity of the Nickel for CH4 adsorption. The paper of Watanabe et al. [84] showed that carbon was formed on the surface after the CH4 adsorption on Ni surface and dissociation reactions. Therefore, special attention must be dedicated to this issue, especially to the Cracking phenomenon, given the possible presence of methane in the syngas. The phenomena are monitored by considering the alpha parameters (63-65).
The analysis is based on a thermodynamic method that helps to define the set of operating conditions, which would prevent the phenomena of carbon deposition from occurring. α is a function of pressure, temperature, and gas concentration as they compare the actual gas composition with the chemical equilibrium constant of the reactions involved. The α coefficients represent the ratio of the driving force to consume solid C to the chemical equilibrium constant of the reactions involved.
This parameter is, therefore, determined by the constants of the individual processes of carbonation, by the gas flows involved, and by the operating pressure. When α > 1, the system is not in equilibrium, this means that the member over the equal, excluding the constant K, is higher than the opposite value of the same constant (i.e., 1/KC), therefore, thermodynamic and chemical conditions are favorable to the production of products, and then carbon formation is observed. When α < 1, carbon formation is thermodynamically impossible.
6.
Algorithm flow chart
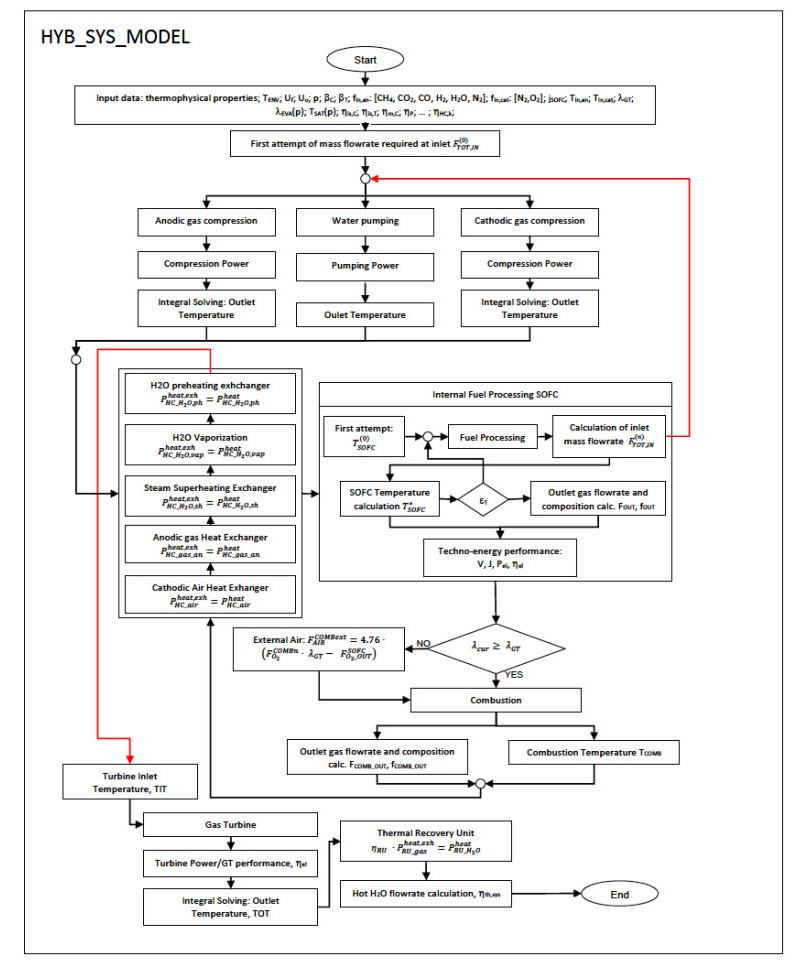
The Figure 3 shows the flow chart of the calculation algorithm for the SOFC/GT hybrid system.
The START conditions are constituted of the input data. It is necessary to provide the calculation algorithm with the operating parameters of the sub-systems, such as the fuel utilization factor, the oxidant utilization factor, the gas inlet temperatures and pressure for the fuel cell, the composition of the inlet gas mixtures (air and fuel), the parameters relating to the compressors such as mechanical and isentropic efficiency and compression ratio1, the information relating to the pump, such as pumping pressure and machine efficiency, the parameters relating to the heat exchangers, such as the heat exchange efficiencies, the parameters relating to the gas turbine, such as mechanical and isentropic efficiency and expansion ratio, the parameters relating to the combustor such as the coefficient of use of oxygen in combustion. Of course, this block must be accompanied by data relating to the thermophysical properties of the gases circulating in the system and with those relating to the thermophysical and geometric properties of the SOFC core.
1 Compression/Expansion ratio, or pressure ratio is meant as the ratio between the pressure operated and the atmospheric one.
The start of the computational flow coincides with the administration of the first attempt value for the anodic flow rate to be fed to the system, which is followed by a flow of cathodic air. Subsequently, the computational blocks, relating to the anodic and cathodic compressors, and to the water pumping system, are solved. No chemical reactions take place in these elements, therefore the molar flows of the constituent gases do not undergo any changes, so the thermal sub-model intervenes to calculate the powers used for the thermodynamic transformations of the flows and to calculate their temperatures at the respective outlet sections. Then, once the thermal conditions for entry to the SOFC core have been set, and controlled by the block relating to the input data, the SOFC model is solved. The computational block of the Internal Fuel Processing SOFC is the most delicate and the most important. It is determined by the calculation of the flow rate of anodic and cathode fluid to be fed to the entire energy system. As input, this block receives the flows heated to the set conditions and intervenes with the sub-model of the flows, with the thermal sub-model and with the electrochemical sub-model to determine the flow rates and the gaseous compositions, the temperature, and the electrical and thermal performance. The SOFC sub-algorithm has also the capability to perform technical analyses while monitoring and controlling the carbon deposition.
In the previous lines, the computational block related to Internal Fuel Processing SOFC is discussed in a simplified and impactful way, but actually, it involves a complex computational burden. More details are given in paper [69].
The computational flow containing information on discharge flows, gaseous compositions, and thermal information about the output of the SOFC sub-model constitutes the set of input data of the sub-model for the resolution of the combustor. This block allows the model to calculate the gas stream leaving the combustor, the new molar composition, and the temperature of the gas flow, taking into account the chemical reactions that take place in the associated element. The first check is made immediately at the discharge of the SOFC on the cathode oxygen as to whether it respects the combustion coefficient set (λcur>λGT). In the other case, an external integration of air suitably pressurized by the air compressor and sent to the combustor via a special bypass line is required. The sub-model of the combustor is then solved.
The output computational flow, containing information on flow rates and gaseous compositions and thermal properties, is then directed to the computational macroblock relating to the section of the heat exchangers. This macroblock contains a sub-block for the preheating of the anodic gas, of the cathodic air, and for the vaporization of the anodic water. It, therefore, has two inputs, it receives fresh fluids as well as burnt gases. These sections are strictly governed by the thermal model since it is necessary for determining the temperatures at the inlet and outlet sections of the single exchanger sub-blocks, both for the pre-heating flows and for the discharge flow of the combustor which transfers thermal energy. At the fresh fluids side-output of the "heat exchangers section" macroblock, the computational flow is adjusted according to the conditions set in the input data block, in order to be processed in the SOFC block. While at the other outlet the computational flow calculates the thermophysical properties of the exhaust gases (combustor exhaust gases), whose temperature (Turbine Inlet Temperature, TIT) is now adapted so that the latter can be subjected to the expansion that takes place in the gas turbine.
The computational flow is then sent to the block of the gas turbo-expander, which through the resolution of the associated model determines the thermodynamic conditions of the output gas flow, the mechanical power for driving the compressors. Consequently, the energy performance of the entire Turbogas Group is calculated, such as useful electrical power generated and electrical efficiency. The discharge flow, which has not undergone any changes in terms of gaseous composition, is at a turbine outlet temperature, TOT, still so high that it can still be subjected to a heat recovery process.
The computational flow is then sent to the "Thermal Recovery Unit" where the useful cogeneration effect is achieved by heating a water flow. This block calculates the flow of hot water and therefore the thermal efficiency of the SOFC/GT energy system.
The sequence of instructions and the strong interconnection between them (Figure 3) entails a very high computational burden. The interconnections between the various computational blocks often need to resort to recursive procedures. The passage to the next steps is then determined by the verification of a condition on the evaluation of the computational error. The computational blocks consist of the sets of equations shown in the previous paragraphs, while the algorithm instructions are determined by the functions that must fulfill the model's requests.
The objective of this calculation algorithm is to achieve the energy characterization of the SOFC/GT hybrid energy system under operating conditions imposed a priori. The fundamental operations of the same algorithm refer to the determination of the flow rate of anodic fluid and, therefore, of the flow rate of cathodic air to be fed to the SOFC/GT system (which are not known a priori), and to the determination of the temperatures (at the inlet and outlet sections of each component), of the flow rates and of the molar compositions at the same remarkable sections. The energy characterization is dependent on the calculation of the electric and thermal efficiency of the global system, as well as the energy performance of the system components.
7.
Levelelized Cost of Energy analysis
The present section is focused on economic analyses based on the Levelized Cost of Energy (LCOE), that ponders the goodness of an energy system based on the electric energy delivered. LCOE is the cost at which the electricity production of the power generation system is calculated, using the current investment and interest and inflation rates.
LCOE is computed as in (66).
CCAP represents the annualized capital cost, CO&M is the total operational and maintenance cost, CFuel is the cost of fuel. While EADE represents the annualized delivery of electric energy. All the single terms in the formulation are reported in Table 1. CCAP depends on CTOC and CRF, which are the total overnight cost and the capital recovery factor. CTOC depends on the total plant cost, CTPC, and on an adjustment factor, fTOC. CRF is a well-known parameter used in economic analyses, according to the yearly interest rate, iy. CTPC is a function of the total engineering, procurement, and construction costs, CEPCC, and of the associated adjustment factor, fTPC. CEPCC is a function of the equipment cost, CEQP, and of its associated adjustment factor, fEPCC. CO&M is determined as a percentage of CEQP and of the SOFC unit cost, CSOFC. Usually, this term is considered as 4% of CCAP. It is precautionary to account for an extra yearly operational cost, which is 5% of the SOFC unit cost and it is relative to the replacement of the device stack [85]. The number of 0.15 accounts for 3 possible replacements during a lifespan of 15-20 years. In EADE term the parameter CUF(1−α) is the capacity utilization factor. Table 1 also contains formulations to determine all the component cost.
The cost of fuel, CFuel, is calculated by considering the biomass (its quantity and so its cost) used to produce the gas feeding the system if the fuel is a syngas gasifier. When the fuel is a simulated mixture of single compounds, CFuel is calculated by considering the cost of the single gases.
Details are reported in the Appendix Section, e.g., the calculation of the biomass quantity, determined by using the generalized gasification reaction of biomass.
9.
Validation
The HYB_SOFC_Model is validated by first considering the model for the SOFC unit. The SOFC block is validated with both experimental and numerical data available in the literature. A proper paragraph was dedicated to this issue in a previous paper by the authors [69]. The SOFC block was validated by several different conditions of operations and of feeding [93,94,95,96,97]. The comparison with the cited references demonstrated a good agreement of the model results. The absolute percentage error showed a very low value ranging from 0.89-3.42%.
The turbogas group is validated also singularly. It is first validated by comparing the model results to the numerical results of [98]. The GT system is considered as a classic regeneration layout, with the combustor positioned downstream of the regenerator. The gas feeding is a syngas with the following composition: fH2: 0.535, fCH4: 0.072, fCO: 0.21, fCO2: 0.181. The same exercise conditions, considered as reference values, are recreated for comparison. From observing the graph in Figure 4, it can be concluded that model results are in good agreement with those of the reference paper.
Another comparison is made with paper [99], in which a turbogas system is considered fed with hydrogen. The model results show good agreement with the results achieved in the reference paper, with an electric efficiency of the turbogas of 44.5%.
10.
Settings and tests
This paragraph reports the settings and tests for the SOFC/GT plant system. The parameters set for the overall plant are presented in Table 2.
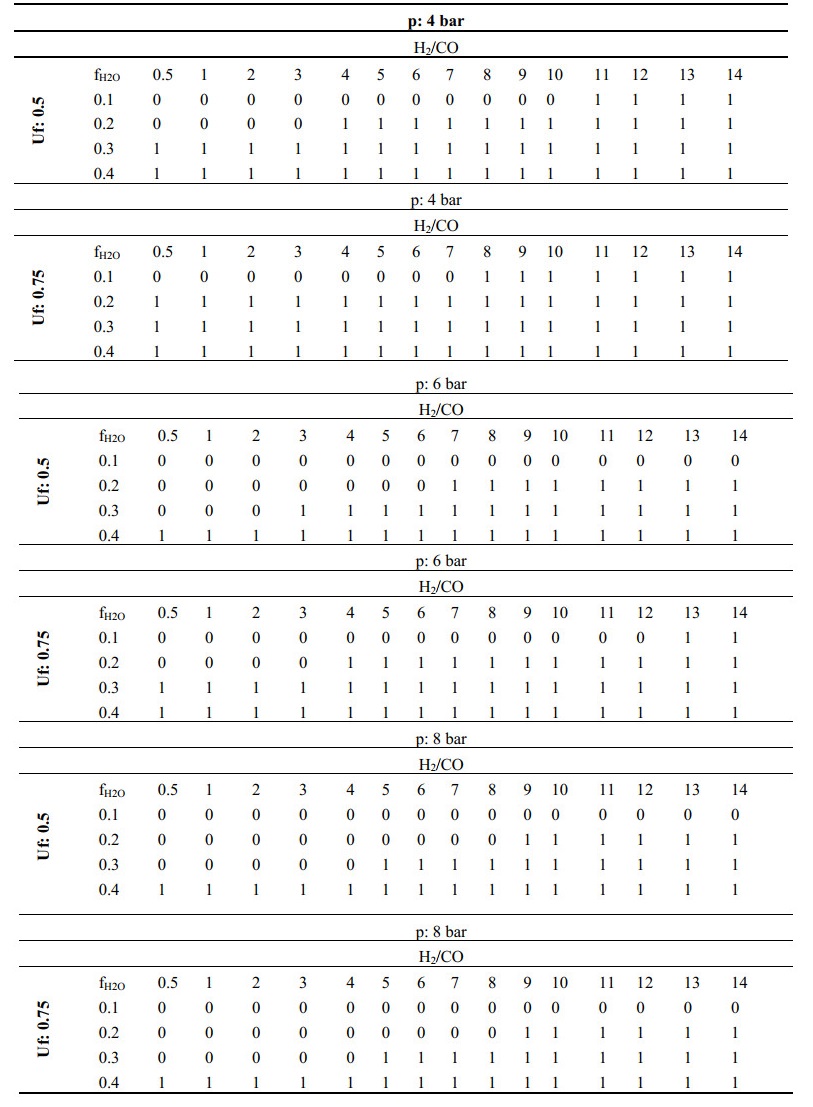
The simulation campaigns are conducted by varying the SOFC pressure, p, in the range 4-8, the fuel utilization factor, Uf, in the range 0.5-0.75 (the energy plant is thought to work at constant fuel utilization factor: variations are intended per simulation campaign), and by using several anodic gas mixtures, different in composition.
The analysis of the literature has shown that GT well matches SOFC when operating at low compression ratios. As well known from thermodynamics, internal fuel processing solid oxide fuel cells operate well when the pressure is close to atmospheric. Slightly higher pressure than atmospheric is necessary to consent good gas flowing and to overcome pressure drops. Pressure-related phenomena are, moreover, beneficial for polarization losses since they directly address this loss contribution by exercising more pushing to the flowing-reactant gas. Extreme increases in pressure can affect negatively the device sealing, the internal fuel processing by methane reforming (if methane is comprised in the feeding mixture). In addition, the Balance of Plant considered in this paper imposes to operate in pressurized modality, since the SOFC working operates at a pressure ratio higher than 1, as being strictly connected to the Turbogas group. Lower compression ratios consent the delivery of less useful power at the turbogas side, but consent the management of higher thermal potential to be recovered and used as thermal power. Vice versa, for higher compression ratios. An investigation of the pressure influence on carbon deposition is important. Its change can affect the mechanism contributions that cause the phenomena to a lesser or greater extent.
From performed preliminary tests, a range of pressure/compression ratio of 4-8 bar seems to be a good interval for operating the energy system.
The oxidant utilization factor is kept fixed at a value of 0.25. This value is motivated for the advantage of controlling the SOFC temperature according to protecting constituent layers from thermo-mechanical stresses, besides being a good value for guaranteeing a secure supply of air to the cathode.
As for the combustion control parameters, a parameter of λGT of 3 is used as a minimum value. If the air exhaust outgoing from the SOFC does not respect this value, the plant has to be supplied with external air.
Table 2 reports all the other settings such as the efficiency of heat exchangers, mechanical and isoentropic efficiencies of the machines, etc.
Some preliminary tests were performed to investigate the system under the assumptions previously discussed and to justify the choice of the range for the main operating parameters. The values within the range will be used to carry out a sensitive analysis to assess the system performance under different scenarios and conditions.
The first tests are reported in Figure 5. They are performed to understand the resulting windows of the fuel utilization factor, Uf, which can be considered energetically useful for the system, and the electric current density, j, on which setting the simulations of the hybrid system. Uf is varied in the range 0.5-0.78, while j up to 1 A/cm2. Pressure is set to 6 bar, as being the central value of the pressure range discussed above. A feeding mixture of H2, CO and H2O is preliminarily considered. H2/CO is fed in a ratio of 1.5, while a molar fraction of 0.3 is considered for H2O.
The fuel utilization factor represents the degree of reaction of hydrogen in the fuel cell. It is opportune to evaluate how Uf changes affect the performance of the plant components, whether more or less beneficial, and how the overall system is therefore affected. SOFC voltage, electric efficiency, SOFC/GT power ratio, feeding air, the fuel specific mass flowrate, and the SOFC exhaust molar fraction are assessed in these first tests.
As can be seen, Uf affects SOFC voltage positively, since it improves the degree of the electro-reaction (Figure 5 (a)). Voltage varies from 0.953 at j = 0.1 A·cm-2 to 0.399 at j = 1 A·cm-2 for Uf = 0.5. It varies from 0.994 at j = 0.1 A·cm-2 to 0.464 at j = 1 A·cm-2 for Uf = 0.78. This has repercussions on hybrid electric efficiency, which presents higher values at higher values of the fuel utilization factor. It varies from 49.37% at j = 0.1 A·cm-2 to 30.35% at j = 1 A·cm-2 for Uf = 0.5. It varies from 67.73% at j = 0.1 A·cm-2 to 38.23% at j = 1 A·cm-2 for Uf = 0.78. Figure 5 (b) and (c) graphs illustrate the specific cathodic and anodic mass flowrate to be fed to the system. The mass flowrates increase with electric current density since more electric current requires more gas to be converted. The profiles denote an 's' shape with a high slope at high electric current density. Air mass flowrate decreases with Uf. Vice versa is the case for fuel mass flowrate. It is also interesting to assess the electric efficiency of the overall system as a function of the power density developed by the SOFC (Figure 5 (d)).
Figure 5 (e) illustrates the SOFC/GT power ratio. It can be considered a fundamental parameter to set the working conditions of the overall plant. It diminishes with electric current density, and increases with the fuel utilization factor. It varies from 0.853 at j = 0.1 A·cm-2 to 0.357 at j = 1 A·cm-2 for Uf = 0.5. It varies from 1.247 at j = 0.1 A·cm-2 to 0.582 at j = 1 A·cm-2 for Uf = 0.78. The last graph of Figure 5 (f) reports the molar fractions at the SOFC anode discharge. Settling on hydrogen, a low fuel utilization factor implies a higher quantity of hydrogen at the SOFC exhaust, which is not reacted electrochemically and can be useful for combustion. Vice versa is the case for high fuel utilization factor. Hydrogen molar fraction passes from 0.25 at Uf = 0.5 to 0.115 at Uf = 0.78. Operating a power density of 0.3 W·cm-2, the electric efficiency goes from 42.2%, at Uf = 0.5, to 57.3 %, at Uf = 0.78.
About the fuel utilization factor, Uf, 0.78 is assessed to be an upper limit valued by these first tests. Uf values higher than 0.78 start to be problematic for the overall functioning since the low quantity of hydrogen exhausted from SOFC is not sufficient to keep on combustion and, so, the preheating of the fresh gases. It is not advisable to act with a fuel utilization factor lower than 0.5 in order not to affect much the SOFC performance.
Concerning the electric current density, SOFC works at a nominal condition near to an electric current density of 0.6 A·cm-2. At this value electric efficiency varies from 38.18% for Uf = 0.5, to 50.19% with an Uf = 0.78. A criterion to fix the working point can be the SOFC/GT power ratio. The energy plant can then be dimensioned on a value close to unity. An electric current density of 0.3 A·cm-2 is the condition aiming for this purpose.
At this value of j, the SOFC voltage remains at values significantly higher than 0.8 V. From the literature study, the latter is meant to be a performant choice. Uf of 0.75 will be considered as the maximum value, of good compromise to have sufficient fuel to subject to combustion and so sustain the gas. Results are in line with what expected from thermodynamics.
11.
Simulations for H2-CO-H2O mixture
The first simulation campaign was carried out with a variable anodic mixture composed of H2, CO, H2O, and cathodic mixture composed of technical air (N2 and O2 in the proportion 79/21). The anodic gas components were variable in proportions. H2 and CO depend on the H2/CO ratio, ranging between 0.5-14, while for H2O the change was imposed on its molar fraction ranging between 0.1-0.4.
The three gases considered are the main components of a real syngas produced by biomass hot-gasification. H2, H2O and CO are used to approach a potential gas where they are significantly higher compared to other possible compounds. Therefore, the change in compositions in the wide ranges presented above was adopted to assess the energy behavior of the SOFC/GT system to which they are fed, approaching a possible parallelism with a real syngas, where H2, CO, H2O are the predominant gases. The use of water/steam is related to its delicate role in the phase of fuel processing. The more or less H2O quantity affects the performance of the fuel processing, by consequently influencing the conversion to hydrogen. Moreover, it is considered of extremely great importance in the control of carbon deposition, which damages the fuel cell irreversibly.
11.1. Results
The results are organized by contour graphs reporting isolines of the variable currently analyzed. The graphs have the H2/CO ratio at 'x' axes and the molar fraction of H2O at 'y' axes. All the variables are presented in the specific modality, by relating to 1 kg of fuel fed. This consents the results to be extended easily to real application cases, hence determining the real needs.
The first paragraph is organized on assessing all the detailed parameters at all the significant stations of the SOFC/GT plant, at 6 bar of pressure for SOFC (compression and expansion ratio equal to 6) and 0.75 about fuel utilization factor. The section reports on specific mass flowrates and SOFC outlet molar compositions, specific energies (work) at main system components, specific thermal energies at main system components, energy and technical performance for SOFC energy unit, performance as electric and thermal efficiency, temperatures at main system components.
Finally, a section reporting on sensitivity analysis on performance, LCOE, and PES by changing pressure and fuel utilization factor, is presented.
Figure 6 relates to the specific mass flowrate that has to be supplied to the SOFC/GT energy system and on the molar fraction of the gases at the SOFC anode outlet. Specific mass flowrate is normalized to 1 kg·s-1 and to 1 kW of electric power produced, and with a unit of measure of [kg·s-1·kW-1] ([g·J-1]). As can be observed it ranges from 3e-5 to 1e-4 [kg·s-1·kW-1], as in Figure 6 (a). Operating at lower H2/CO ratios the hydrogen to satisfy the needs required has to be furnished using a higher mass flow rate since in the specific case the plant works at constant fuel utilization factor. Clearly, increasing the H2/CO ratio the mass flowrate to feed to the SOFC/GT plant can be diminished by about one magnitude order. A lower mass flow rate is required, when having a gas stream richer in hydrogen. The change in the molar fraction of the entering water does not imply significant changes. At higher H2/CO ratios the isolines tend to bend, higher water quantities slightly make the plant require more mass flowrate. It is interesting to observe the molar fraction exiting the SOFC anode. After the thermo-electrochemical processes, the gas stream at the anode outlet is composed of [CO2, CO, H2, H2O]. H2O and CO2 are the compounds most present since they are increased by the electro-reactions that converted H2 and CO.
CO molar fractions (Figure 6 (b)) at the SOFC anode outlet vary from about 0.15 to 0.02 at fH2O of 0.1, while they vary from about 0.07 to 0.01 at fH2O of 0.4. The conversion of CO is strictly linked to the fuel processing stage first (in this case CO shift reaction), which converts the same CO into hydrogen and then to the electro-reactions. As declared, this model also considers the electro-reaction of CO compared to that of hydrogen, according to the parameter (cr_co=FCOrFH 2 r) relating to the CO electro-reactions as functions of the ratio fCO/fH2. At lower external water introduction, i.e., fH2O of 0.1, CO is converted in the CO-shift process by the steam produced concurrently during the electro-reaction of hydrogen. Higher fH2O register a lower CO molar fraction, since they imply the dilution of the CO, as well as improving CO conversion with its consequent decreasing in the stream.
H2 molar fractions (Figure 6 (c)) at the SOFC anode outlet vary from about 0.1 to 0.21 at fH2O of 0.1, while they vary from about 0.1 to 0.15 at fH2O of 0.4. The discussion on the detailed quantities and/or their variations is somewhat critical since the fuel processing stage is internal to the fuel cell and occurs concurrently with the electro-reactions stage of the CO and H2. The fuel processing is strictly determined by the actual gas composition available at the bulk of the electrocatalytic sites. At the generic instant, the bulk contains a gas composition of H2, CO, H2O, CO2. As discussed above entering H2O and CO2 are varied by the additional quantities coming from the electro-reaction site during the phase of desorption. Therefore, the gas stream is strongly affected by these two incoming provisions. A more or less higher H2/CO ratio affects fuel processing in its turn. A lower ratio implies a less conversion of CO into H2, at lower entering H2O. Actually, this condition could act in the opposite direction of that desired. In fact, lower H2/CO ratios, at lower H2O content, could create the conditions of the Reverse Water Gas Shift Reaction (RWGS). A high amount of CO2 produced in the electro-reaction moves the reaction in favor of the reactants. This consumes the available hydrogen in favor of carbon monoxide production. The water provision is, therefore, necessary to oppose this effect. A more detailed study about the transformation quantities during a direct internal fuel processing is available in the paper by the authors [69]. From the observation of the graph, it can be concluded that an Uf of 0.75 provides an important amount of hydrogen to be used for other processes external to the SOFC unit, such as the combustion and the pre-heating.
CO2 at SOFC anode outlet (Figure 6 (d)) varies from about 0.34 to 0.04. The contribution of fH2O is not very significant since the isolines are almost vertical up to an H2/CO ratio of 10. A lower H2/CO ratio implies a significant amount of CO2.
H2O at the SOFC anode outlet(Figure 6 (e)) varies from about 0.46 to 0.72 at fH2O of 0.1, while it varies from about 0.5 to 0.8 at fH2O of 0.4. This means that the set Uf always guarantees a significant amount of H2O.
This flow analysis must be accompanied by the post-analysis on carbon deposition in order to verify whether the flow conditions (together with the thermodynamic ones) permit operation in safe mode, far from the undesired phenomenon.
Figure 7 relates to the specific energies at the main system components. The figure contains the graphs for air and gas compressor (Figure 7 (a-b)), pump (Figure 7 (c)), SOFC (Figure 7 (d)), Gas Turbine (Figure 7 (e)) and overall hybrid system SOFC/GT (Figure 7 (f)). The specific powers are expresses in [W·s·kgfuel-1] (J·kgfuel-1) as a unit of measure. This representation permits the power involved per element concerning the mass flow rate fed to the anode to be determined quickly.
The model then calculates the cathodic air beside the anodic stream to be fed. The cathodic air is calculated as a function of the Uo of 0.25. The air compressor requires higher power than the gas compressor to be moved. Its power ranges from 4000 to 16000 [W·s·kgfuel-1]. The anodic gas compressor ranges from 600 to 2400 [W·s·kgfuel-1]. The power required by the pump ranges from 0.1 to 0.6 [W·s·kgfuel-1] according to the fH2O operated. The SOFC unit generates a specific power in the window 10000-30000 [W·s·kgfuel-1] and is mainly determined by the H2/CO ratio. A better quality gas (higher content of hydrogen, higher H2/CO) directly affects the SOFC specific power. The same behavior is followed by the gas turbine that generates a specific power in the window 10000-30000 [W·s·kgfuel-1]. It has to be underlined that this value has to be diminished by the power required to move the air and fuel compressors, thus giving the useful value of the overall turbogas system. Finally, the last graph of Figure 7 reports the useful specific power generated by the overall SOFC/GT plant, ranging from 10000 to about 40000 [W·s·kgfuel-1].
Figure 8 shows the specific thermal energies at the heat exchangers. The figure contains the graphs for the anode (Figure 8 (a)) and cathode gas warmup (Figure 8 (b)), water preheating (Figure 8 (c)), evaporation and superheating; summary graph total heating (Figure 8 (d)), and a graph relating on the thermal power recovered in the Heat Recovery Unit that delivers it for cogeneration purposes. The specific thermal powers are expressed in [W·s·kgfuel-1] (J·kgfuel-1) as a unit of measure (Figure 8 (e)). Analogously to the previous case, this representation permits the power involved per element concerning the mass flow rate fed to the anode to be determined rapidly. The thermal power required to heat up the anode gas ranges from 200 to 800 [W·s·kgfuel-1]. A substantial amount of thermal power is the rate required to heat the cathode gas, ranging between 2000-8000 [W·s·kgfuel-1]. Also, the thermal power required for the preheating, evaporation and superheating of water is significant as that for cathode gas, as can be observed. This varies from 1000-8000 [W·s·kgfuel-1]. The total thermal power required to heat the anodic gas, the cathodic air, and the water/steam up to the thermal condition of the SOFC inlet set ranges 3000-18000 [W·s·kgfuel-1].
Finally, the specific thermal power recovered in the RU unit for cogeneration purposes is 6000-22000 [W·s·kgfuel-1]. This power is the one transferred from the exhaust stream in output from the gas turbine, which is composed of the total mass flow rates supplied to the plant (it is composed of hot H2O, CO2, N2, O2) and enters the RU at the turbine outlet temperature, TOT.
Figure 9 reports on the SOFC performance in terms of voltage (Figure 9 (a), power density (Figure 9 (b), and in terms of safe functioning relating to the carbon deposition analysis (Figure 9 (c). The SOFC voltage calculated at a simulated electric current density of 0.3 A·cm-2 ranges from 0.94 V at lower H2/CO ratios to 0.86 V at higher H2/CO ratios. As can be seen, the voltage is mainly influenced by the H2/CO ratio. The voltage is determined by several parameters, such as the working temperature, the partial pressure of the reactants, and overpotential. It should be underlined that the temperature shows an almost constant trend with the H2/CO ratio, as will be discussed in the proper part, therefore does not affect voltage change in this case. The main cause is therefore attributable to the higher partial pressure of the CO at low H2/CO ratios, compared to that of H2 at high H2/CO ratios. The SOFC power density ranges from 0.28 to 0.26 W·cm2.
The most significant analysis is that involving the carbon formation at the anode side. As aforesaid, the good and safe operation of the SOFC unit is strictly determined by the capacity of not producing solid carbon filaments, which are very harmful. Carbon deposition is monitored by the α parameter. Carbon deposition triggers when α > 1. Therefore the region of safe functioning for the SOFC anode is given by the area of the graph above the isoline of α = 1. The contribution to carbon deposition comes mainly from the "steam production" phenomenon that implies the reaction between hydrogen and carbon monoxide producing steam and solid carbon. The parameter associated with it is given by the formulation αSP=KSP (T)·pH 2·pCOpH 2O, hence depends on the process constant, KSP (T), and on the reactant partial pressures, pk. The constant process is a function of the temperature, since the generic formulation is Keq,k=exp(−∆GkR·T).
Steam Production tends to disappear as: the temperature decreases, the partial pressure of steam increases, and the partial pressures of hydrogen and carbon monoxide decrease. By writing the partial pressure as the Dalton law (pi=fi·ptot) α is written as αSP=KSP (T)·(fH 2·fCO·p totfH 2O ) . This means that steam is beneficial for the safe functioning of the SOFC. The results show that at fH2O higher than 0.25 each H2/CO ratio can be operated on the anodic mixture to be supplied. Conversely, at fH2O lower than 0.25, it is necessary to operate with the H2/CO ratio increasing with an almost linear trend as fH2O is decreased. At fH2O equal to 0.1 it is necessary to feed a gas mixture with an H2/CO ratio of at least 12.
Figure 10 reports on the performance of the hybrid SOFC/GT system in terms of electric and thermal efficiencies. The SOFC unit shows a very good electric efficiency, ranging from 43 to 51% (Figure 10 (a)). The main influence is given by the change in the H2/CO ratio. Clearly, at higher H2/CO ratios the SOFC unit receives a better quality gas. Also, fH2O affects electric efficiency more at lower H2/CO ratios since it is beneficial to aid the fuel conversion process. The single gas turbine efficiency shows an analogous behavior to the SOFC. Its electric efficiency varies from 40 to 46% (Figure 10 (b)). It is also important to discuss the useful electric efficiency of the overall Turbogas system (composed of gas Turbine, air, and gas-fuel compressor) since the compressors are moved by the turbine. This efficiency, illustrated in Figure 10 (c), goes from 11.5 to almost 13%. The fH2O affects this efficiency. Although the higher quantity of water implies a lower Turbine Inlet Temperature and a Turbine Outlet Temperature, overall, it improves the efficiency value. Finally, the overall hybrid system SOFC/GT efficiency can be detected. The overall system shows a very interesting electric efficiency, ranging from 53 to 63% (Figure 10 (d)). In the region where it can be operated safely, the system always shows an electric efficiency higher than 60%. Besides this, the thermal efficiency is calculated. Its value is around 37%, with few changes at different feeding conditions (Figure 10 (e)). Another useful parameter is the thermal/electric power ratio (Figure 10 (f)). It varies from 0.68 to 0.57. The last graph of Figure 10(g) reports the SOFC/Gas Turbine power ratio, being close to 1 as from preliminary choice.
Figure 11 reports on the temperatures determined at the main sections of the SOFC/GT plant. The gas at compressor output presents a temperature from about 615 K to 632 K (Figure 11(a)). Higher H2/CO ratios imply higher compressor output temperatures. While the cathode compressor presents air at a temperature of 670 K at its outlet.
As for the SOFC unit, the thermodynamic and feeding conditions imply a working temperature varying from 1330 to 1360 K (Figure 11 (b)). The temperature changes mainly with fH2O. As fH2O increases, the dilution of gas increases, thus lowering the temperature. The temperature does not present marked changes with varying H2/CO, as is observed from the graph. This is connected with the evidence that the quantity of hydrogen that is about to react is always the same (FH 2 r=1(1+cr_co)·j·Ane·Fa), since the system operates at constant fuel and oxidant utilization factor and a fixed electric current density, and the quantity of cathodic air being much higher than the anodic, as FAIR,IN=4.76·12·Uo·j·Ane·Fa, making negligible the fluctuations in the anodic composition.
The combustion temperature shows sidelong isolines, meaning that they are a function of both the H2/CO ratio and fH2O (Figure 11(c)). The combustion temperature varies from 1380 K at higher H2/CO ratios to 1450 K at lower H2/CO ratios, considering fH2O of 0.1. As fH2O increases, its influence diminishes. The combustion temperature varies from 1330 K at higher H2/CO ratios to 1360 K at lower H2/CO ratios. fH2O affects the temperature since it further dilutes the reactant gases. Lower H2/CO ratios are beneficial for combustion temperature since this condition allows the system to have high quantities of carbon monoxide that can be burnt, thus producing additional heat. During the simulation, the results demonstrated that no external air was necessary to carry on the combustion process.
The Turbine Inlet Temperature, TIT, is a consequence of the combustion temperature (Figure 11 (d)), presenting an analogous trend. The TIT is about 120 K lower than the combustion temperature since the combusted gases delivered part of their thermal power to the fresh fluids that have to be prepared and subjected to thermo-electrochemical processes occurring in the SOFC unit. This flow consents the thermal constraint related to the material of the gas turbine first stage to be respected. The gas entering the turbine shows a temperature trend in line with the usual TIT adopted in gas cycles.
The last graph presents the Turbine Outlet Temperature, TOT (Figure 11 (e)). As for the TIT, the TOT presents an analogous profile to the combustion temperature. Its value changes from 820 K to about 900 K. Hence, the temperature drop in the turbine is around 400 K.
11.2. Influence of pressure and fuel utilization factor
The present paragraph analyzes how system performance changes as the SOFC working pressure and fuel utilization factor change. Pressure changed by ± 2 bar, while the fuel utilization factor is set to the value of 0.5.
Figure 12 reports on the electric efficiency of the hybrid system by varying pressure and Uf. As already observed, electric efficiency has its value increasing as the H2/CO ratio and the fH2O increase. As an instance, the SOFC/GT plant shows an electric efficiency of 43% operating at p: 4 bar and Uf : 0.5, at a H2/CO ratio of 4 and an fH2O of 0.1 (Figure 12 (a)). Its electric efficiency increases by 2 percentage points by operating with an fH2O of 0.4, keeping the other conditions fixed. For example, to have an electric efficiency of 44%, when working at Uf: 0.5 and with a water molar fraction, fH2O, at anode inlet of 0.1, it is necessary to feed an anodic gas stream that presents an H2/CO ratio of almost 10 at p: 4 bar (Figure 12 (a)), a H2/CO ratio of almost 4 at p: 6 bar (Figure 12 (b)), a H2/CO ratio slightly higher than 3 at p: 8 bar (Figure 12 (c)). As can be seen, operating with an Uf of 0.5 does not produce high electric efficiencies which remain in the range of 40-47%. This is expected since the SOFC unit converts half of the reactant stream, thus sacrificing its contribution to efficiency. Conversely, the high amount of undepleted fuel in the SOFC is then used in the combustor to have more thermal power to recover in the RU, by increasing the thermal efficiency.
In general, it can be observed that a slight increase in the value of efficiency occurs by increasing the pressure from 4 bar to 6 bar. A turnaround occurs moving to 8 bar (Figure 12(d-f)). This can be better explained by means of the graphs illustrated in Figure 13. A feeding mixture of H2, CO, and H2O is still considered. H2/CO is fed with a ratio of 1.5, while a molar fraction of 0.3 is considered for H2O. The SOFC is considered to work at an electric current density of 0.3 A·cm2. The figure illustrates the electric efficiency for the SOFC unit (Figure 13 (a)) and Turbogas unit (Figure 13 (b)) singularly, as well as that of the global hybrid system (Figure 13 (c)), by considering a fuel utilization factor of 0.5 and 0.75 and pressure ratio (meant as the ratio between the pressure operated and the atmospheric one) in the range 3-12. The range of the pressure ratio has been enlarged to understand the efficiency trends better. The SOFC electric efficiency (Figure 13 (a)) obtains benefits from operating at high pressures, as know in theory. The SOFC polarization losses are mitigated and efficiency benefits from this. The SOFC efficiency profile shows an increasing trend with a horizontal asymptotic limit. The slopes are very high at a pressure close to atmospheric, and then they decrease. In the analyzed case, the SOFC efficiency increases its values from 27.3% to 28.01%, for Uf = 0.5, and from 44.5% to 45.7%, when the Uf is set to 0.75. From this evidence, it can be considered that the efficiency gain for the SOFC is more accentuated at higher fuel utilization factors. Besides that, the Turbogas Group efficiency is analyzed in the graph of Figure 13 (b). The efficiency has a parabolic profile with a maximum value.
This is, however, well known from the "Power Plants" theory, according to which the parabolic profile of the Turbogas Group efficiency is maximized at a precise value of pressure ratio β, βGTopt, whose expression is reported in (67).
α is the ratio between the air and the fuel mass flow rate operated in combustion, τ is the ratio of the inlet turbine temperature to the temperature at the inlet of the compressor (usually the ambient temperature), and π is the combustion efficiency. βGTopt=f(MWfuel,φfuel,α,π,τ), βGTopt according to the fuel fed to the system, to the operating combustion ratio, to the combustion efficiency, and to the maximum operating temperature.
In the specific case the fuel for the combustion is not chosen for this function, but it is determined by the thermo-electrochemical processes occurring in the SOFC. Therefore, it is a complex mixture of gas, composed of hydrogen, carbon monoxide, carbon dioxide, and steam. Moreover, this gas mixture is strictly determined by the fuel utilization factor operated in the SOFC. As can be observed from the second graph of Figure 13, the parabolic shape is determined by the fuel utilization factor, Uf. For Uf of 0.5, the parabola is more open and higher. For Uf = 0.5, the maximum for the Turbogas efficiency is close to 17% at a pressure ratio, β, of 7. For Uf = 0.75, the maximum for the Turbogas efficiency is close to 13% for a pressure ratio, β, of 4. The gas turbine would be so subjected to higher energy demands while moving to higher pressure ratios as to drag the compressors, slightly penalizing the turbogas group efficiency. Clearly, a higher gas quality corresponds to lower fuel utilization factors. A higher gas quality exiting from the SOFC moves the maximum turbogas efficiency to a higher pressure ratio. Finally, the graph of Figure 13 (c) incorporates all the contributions in the overall SOFC/GT energy system. The SOFC/GT system efficiency profile follows a sort of parabolic trend similar to the GT efficiency. At Uf of 0.5, the efficiency profile reveals a value of 41% at β of 3, to reach a maximum of 44.7% with a β of 7.5, then dropping slowly. With a β of 12, the efficiency is 43.5%. At Uf of 0.75, the efficiency profile presents a value of 56.72% at β of 3, to reach a maximum of 58% at β of 5.5, and then dropping to lower values. With a β of 12, considering this value of Uf, the efficiency is 54%. This demonstrates how lower pressure ratios can be beneficial for hybrid SOFC/GT systems: the SOFC/GT system has to be operated with a pressure ratio of 6 in order to maximize the energy performance in the specific case.
About the thermal efficiency, in general, it is noticed that it increases when both pressure and fuel utilization factors decrease (Figure 14). Pressure ratios decreases imply a more exploitable potential for thermal purposes. A lower fuel utilization factor limits the energy conversion of the reacting fluids in the SOFC unit and it makes them available at the combustor to be burnt and have a more thermal potential. Moving (Figure 14 (a-c)) from 8 bar to 4 bar the thermal efficiency even increases about 10 percentage points. The gain is not so prominent when passing from 0.75 to 0.5 for Uf. The gain in percentage points on thermal efficiency is approximately 2-3 at the expense of the loss of 15-20 points in electrical efficiency, as expected.
The operation must be confirmed by the analyses on carbon deposition monitoring. For more details, all the results of the analyses are reported in the appendix section.
11.3. Levelized Cost of Energy results
The present paragraph reports the results on the LCOE analysis, reported in Figure 15. Italian economic parameters have been considered for the simulations. The most marked influence on LCOE is given by the H2/CO ratio. LCOE varies from about 0.08 $·kWh-1, revealed at high H2/CO ratio, to 0.14 $·kWh-1 had at low H2/CO ratio. The steam content has a light influence as observed. LCOE increases by about 0.005 $·kWh-1, by changing the fuel utilization factor from 0.5 to 0.75. Also, the change in pressure ratio from 4 to 8 slightly affects the LCOE.
11.4. Primary Energy Saving results
The PES results are collected in Figure 16. In general, the PES parameter reveals changes in the range between 33-52%. The highest influence on it is given by the H2/CO ratio, which increases the PES by about 5 percentage points.
The steam content in the mixture also shows improvements in the PES values. The steam affected is predominant at low H2/CO ratio, where the PES has an improvement of about 4 percentage points.
Pressure increases do not produce benefits. Conversely, a change in the fuel utilization factor from 0.5 to 0.75 improves the PES by more than 10%. This is mainly due to the higher electric efficiency achieved at a higher fuel utilization factor. Anyway, the system shows substantial values of PES, meaning a positively marked cogeneration operation.
12.
Results for different syngas feedings
In this section, the performance analysis of the SOFC/GT energy system is reported when fed by different real syngases, produced by biomass gasification. The gases fed to the system are reported in Table 3. The table presents the gas composition, the additional steam to carbon ratio that is effected to stave off carbon deposition or simply to understand how performance is affected, and the actual steam to carbon ratio as the sum of the initial steam to carbon ratio of the entering mixture with the additional one; another column reports the hydrogen to carbon monoxide ratio of the mixture.
The syngases are all different by composition. Some samples (A, B, C) also account for the presence of methane. Methane is present in small percentages in the syngas, usually not higher than 10%. The samples, A, B, C contain methane, carbon dioxide, carbon monoxide, hydrogen, steam, and nitrogen; whilst D, E, F, G, are syngases that do not contain methane. E, F, G are the same gases but fed to the SOFC/GT system at different STC. Sample H is a mixture with a high content of hydrogen.
Table 4 reports on the performance achieved by the SOFC/GT plant, when fed with gases A-H. The table reports the main output parameter as electric efficiency, thermal efficiency, LCOE, and PES. Feeding the system with Gases A and B presents an important performance, with an electric efficiency of about 62%, at a favorable LCOE, as well as the anodic mass flow rate that has to be fed.
Gases C and D imply lower electric efficiencies, respectively of 56.4% and 55.72%, although they are still significant values. Concerning gas C, the small lower performance is due to the lower content of methane and the lower H2/CO ratio. It is necessary to operate with an additional STC of at least 1 to stave off carbon deposition for C and D.
The system fed with gas E shows an electric efficiency of 51.51%. This means that it is a poorer quality gas compared to the previous ones. The higher content of CO2 inhibits the hydrogen conversion in the fuel processing stage. This can be opposed by acting on an additional STC. In fact, the electric efficiency increases by about 3.4 points with an additional STC of 2 (Gas F), and by about 4.5 points with an additional STC of 3 (Gas G). This implies a little effort on the LCOE since it increases by about 0.02 $·kWh-1. Gas H shows the best performance: electric efficiency higher than 62%, the lowest LCOE (0.09 $·kWh-1), and a PES of about 52%.
It has to be noticed that gases that present higher H2/CO ratios imply a lower anodic mass flowrate at the system inlet. LCOE is higher for low quality gases, with a value of about 0.17 $·kWh-1. PES varies from 44% (for low quality gases) to about 52%, however showing very good values for considering the system as CHP.
13.
Results analysis
The analysis of the results achieved is conducted in this section to compare the performance of the SOFC/GT system at the various operating conditions. Table 5 summarizes the variations of the main performance variables as functions of the main working parameters.
The first simulations are conducted on a gas mixture of H2, CO, H2O, presenting the H2/CO ratio variable in the range 0.5-14, while the H2O variable in the range 0.1-0.4. H2, H2O, and CO are used to approach a possible syngas in which they are significantly high compared to other possible compounds. A Uf of 0.75 is evaluated as being the upper limit to provide an important amount of hydrogen to be further used for purposes external to the SOFC unit. Whilst it can be concluded that it is not convenient operating at a lower fuel utilization factor due to the high degradation of the overall electric efficiency, although the thermal one benefits.
The specific mass flowrate ranged from 3e-5 to 1e-4 [kg·s-1·W-1]. Lower H2/CO ratios imply a higher mass flowrate to furnish the hydrogen required. A lower mass flow rate is required, when having a gas stream richer in hydrogen.
As for electric efficiencies, the main influence is given by the H2/CO ratio, whose increasing values mean a better quality fuel. At an SOFC pressure of 6 bar, the SOFC unit electric efficiency ranging from 43 to 51% for which the main influence is attributed to the change in the H2/CO ratio. The electric efficiency of the overall Turbogas group ranges from 11.5 to almost 13%, thus giving an important contribution to the improvement of the overall performance. The overall system shows electric efficiency ranging from 53 to 63%, and thermal efficiency of about 37%. Steam quantity (fH2O) affects efficiency very slightly. The sensitivity analysis shows that the electric efficiency of the overall SOFC/GT system tends to increase with the pressure up to a maximum value to then decrease. This behavior is more affected by the Turbogas functioning which shows a parabolic profile vs pressure ratio, with a maximum value at βGTopt, although the SOFC efficiency profile shows an increasing trend with a horizontal asymptotic limit. The maximum value of the efficiency is located around a value of SOFC pressure of 6 bar (corresponding to a pressure ratio close to the optimum value βSOFC/GTopt), demonstrating and confirming the adoption of Turbogas system operating with a low-pressure ratio to build up more complex SOFC/GT hybrid systems.
About the temperatures at the main plant section, the SOFC unit presents a working temperature varying from 1330 to 1360 K, changing mainly with fH2O. Combustion temperature varies from 1380 K at higher H2/CO ratios to 1450 K at lower H2/CO ratios at low fH2O, while at high fH2O varies from 1330 K at higher H2/CO ratios to 1360 K at lower H2/CO ratios. Also, fH2O affects the temperature since it further dilutes the reactant gases. Lower H2/CO ratios are beneficial for combustion temperature since this condition consents having high quantities of carbon monoxide that can be burnt, thus producing additional heat. The results demonstrate that no external air is necessary to carry on combustion. The Turbine Inlet Temperature, TIT, shows analogous behavior to combustion temperature, changing from 820 K to about 900 K. The temperature drop in the turbine is around 400 K.
About the thermal efficiency, in general, it increased when both the SOFC pressure and fuel utilization factors decreased. The pressure decreases imply a more exploitable potential for thermal purposes. A lower fuel utilization factor limits the energy conversion of the reacting fluids in the SOFC unit and it makes them available at the combustor to be burnt and have a more thermal potential. Moving from 8 bar to 4 bar the thermal efficiency even increased by about 10 percentage points. The gain is not so prominent when passing from 0.75 to 0.5 for Uf. The gain obtained for the thermal efficiency does not sustain the losses related to the electrical efficiency. Higher H2/CO ratios and fH2O lowers the thermal efficiency slightly.
A carbon deposition analysis showed that not all the conditions can be operated. The results showed that the the feeding conditions are mainly affected, therefore on the fH2O and H2/CO ratio. At fH2O higher than 0.25 each H2/CO ratio can be operated on the anodic mixture. Conversely, at fH2O lower than 0.25, it is necessary to operate with the H2/CO ratio increasing with an almost linear trend as fH2O is decreased. At a fH2O of 0.1 it is necessary to feed a gas mixture showing an H2/CO ratio of at least 12. The pressure increase is not beneficial for carbon deposition. The gas stream containing methane needs additional attention due to the danger of cracking. This case must be mitigated by acting on the steam to carbon ratio of the mixture. A higher fuel utilization factor implies a higher conversion of hydrogen into steam, thus better controlling the phenomenon.
About the LCOE analysis, the strongest influence on the LCOE calculations was given by the H2/CO ratio. In general, the LCOE varied from about 0.08 $·kWh-1, revealed at high H2/CO ratios, to 0.15 $·kWh-1 had at low H2/CO ratio. The LCOE increased by about 0.005 $·kWh-1, by changing the fuel utilization factor from 0.5 to 0.75. Also, the change in pressure ratio from 4 to 8 had a slight influence on the LCOE.
The analysis based on Primary energy Saving is performed to assess the cogeneration goodness of the SOFC/GT system.The PES parameter reveals changes in the range 33-52. The gretest influence on it is noticed in the H2/CO ratio, which increases the PES by about 5 percentage points. The steam content in the mixture also allows improvements in the PES. The steam is predominantly affected at low H2/CO ratio, where the PES has an improvement of about 4 percentage points. The pressure increases do not produce benefits. Conversely, a change in the fuel utilization factor from 0.5 to 0.75 improves the PES by more than 10%.
A final performance analysis of the SOFC/GT energy system is based on considering real syngases produced by biomass gasification, which differ from each other in gas proportions. Some samples also account for the presence of methane. The gases at high H2/CO ratio are noticed as the best quality ones, revealing electric efficiency higher than 60%. The syngas with methane presence reveal also good performance, according to the fuel processing of methane itself to hydrogen. Low-quality syngases show electric efficiencies of about 51%. The analysis emphasizes the benefits of using an additional steam to carbon ratio up to 3 to these gases, by improving the electric efficiency by 4.5 percentage points. The LCOE varies from 0.09 (for high-quality gas) to 0.19 (for low-quality gas) $·kWh-1, while the PES from 44 to 52%.
14.
Conclusions
This paper was aimed at the comprehension of the SOFC/GT energy system performance when fed by syngases at different compositions, at several working conditions.
The SOFC/GT system, operating as a cogenerative unit, consisted of a pressurized SOFC combined with a Turbogas cycle, sustained by the combustion of SOFC exhaust gases. The fresh gases preheating is designed to be acted on by the exhaust combustion gases, with the aim of mitigating their temperature before entering the gas turbine and observing its techno-thermal constraints.
A totally in-house model was built to assess the SOFC/GT system techno-energy performance, whose calculation algorithm was implemented, validated, and run in a Matlab environment.
The analysis has reported on specific mass flowrate and the SOFC outlet molar composition, specific energies (work) for the main components of the system, specific thermal energies at main system elements, energy and technical performance for SOFC energy unit; performance as electric and thermal efficiency, temperatures at main system elements, the economic sustainability, by means of the LCOE analysis, and PES to assess the cogeneration goodness. Special attention has also been dedicated to the carbon deposition analysis to exercise the system safely.
Several simulations were performed first by varying the feeding conditions according to an anodic mixture composed of H2, CO, and H2O, presenting the H2/CO ratio variable in the range 0.5-14, while the H2O molar fraction variable in the range 0.1-0.4. Final simulations were instead carried out on real syngases, considering additional steam to carbon ratios by occurrence.
The anodic mixture of H2/CO/H20, presenting an H2/CO ratio of 1.5 and an fH2O of 0.3 is taken as an example in this conclusive paragraph. From the test, it was first concluded that a fuel utilization factor, Uf, of 0.78 represents an upper limit value. Uf values higher than 0.78 start to be problematic for the overall functioning, since the low quantity of hydrogen exhausted from the SOFC is not sufficient to keep on combustion, preheating the fresh gases and hence sustaining the Turbogas cycle. A slightly lower value of Uf than 0.75, was then assessed to be a good compromise for providing significant energy performance. The SOFC nominal conditions were assessed around an electric current density of 0.6 A·cm-2. At this value, the SOFC/GT electric efficiency is about 50%, by operating at an SOFC pressure 6 bar (corresponding to a pressure ratio of 6). Actually, an electric current density of 0.3 A·cm-2 was chosen as the working point, by using as a criterion the SOFC/GT power ratio close to unity. A test on considering a wide pressure ratio window 3-12 was conducted to understand the single system component performance. The SOFC efficiency profile showed an increasing trend with a horizontal asymptotic limit, with values from 44.5% to 45.7%. The Turbogas Group efficiency showed a parabolic profile with a maximum value at a precise pressure ratio, βGTopt close to 4, for which the efficiency is close to 13%. The efficiency profile of the overall SOFC/GT system followed a sort of parabolic trend similar to the GT efficiency, with the achievement of the maximum of 58% at βSOFC/GTopt between 5.5 and 6. This demonstrated and confirmed the adoption of lower pressure ratios operated for hybrid SOFC/GT systems, as well as demonstrating that the SOFC/GT system has to be operated at an SOFC pressure of 6 bar (β=6) to maximize the energy performance in the specific case. At these working conditions, the calculation algorithm calculated an anodic mass flowrate of 1e-4 kg·s-1·kW-1 to be fed to the system, evaluating an LCOE 0.13 $·kWh-1, and a PES higher than 50.5%.
Given the high thermal content discharged by the system at medium temperature, future development aimed at performance improvements will consist of assessing the combination with an Organic Rankine Cycle plant.
Appendix
Syngas generation from biomass gasification
The generalized gasification reaction of biomass is reported in (A.1) [103].
The molecular formula of dry biomass is reported as CHpNqOr, considering an aggregate of hydrogen, carbon, nitrogen, and oxygen. The values of 'p', 'q', 'r' are estimated from the elemental analysis of the biomass. 'yw' is the amount of moisture present per mole of biomass, 'yo' determines the amount of air needed for the gasification of 1 mole of biomass, while 'yH2', 'yCO', 'yH2O', 'yCH4', 'yN2' determine the mole of gases produced.
Biomass Low Heat Value
The Biomass Low Heat Value (LHVbiom) is determined by the correlations suggested by Arteaga-Perez et al. [104], reported in the set (A.2-A.3).
HHVbiom represents the high heat value for the biomass, CB, HB, OB, NB, Ab represent the mass fraction of carbon, hydrogen, nitrogen, and ash respectively. λeva is the latent heat of vaporization of water, while MC is the mass fraction of moisture.
Boolean Matrix for safe functioning feeding condition
1 is used to represent safe conditions. Viceversa 0.
Conflict of interest
The authors declare that there is no conflict of interest in this paper.
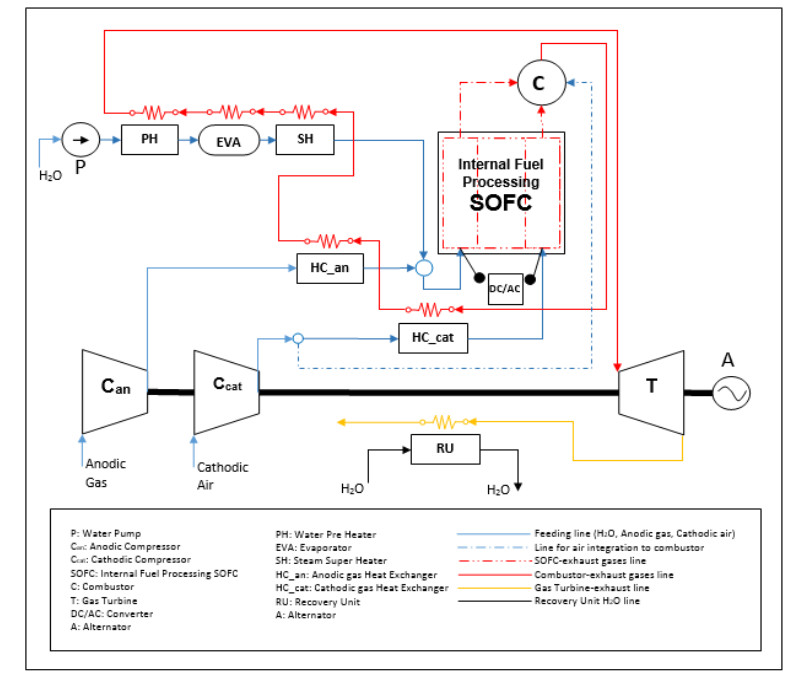









 DownLoad:
DownLoad: