Transient thermal characteristics of infrared window coupled radiative transfer subjected to high heat flux

Hong-Yu Pan; Chuang Sun; Xue Chen; Hong-Yu Pan; Chuang Sun; Xue Chen

doi:10.3934/energy.2021041

AIMS Energy

2021, Volume 9, Issue 5: 882-898. doi: 10.3934/energy.2021041

Previous Article Next Article

Research article Special Issues

Transient thermal characteristics of infrared window coupled radiative transfer subjected to high heat flux

School of Energy Science and Engineering, Harbin Institute of Technology, 92, West Dazhi Street, Harbin 150001, PR China

Received: 25 February 2021 Accepted: 05 July 2021 Published: 13 July 2021

In infrared detection system on aircrafts, the infrared window, as an essential part, always faces heating condition generated by aerodynamic effects. The accurate thermal analysis can ensure the safety and reliability of internal detection system. In this work, the transient thermal characteristics of infrared window-based encapsulation structure are investigated under a high heat flux loading. The physical model of coupled radiative-conductive heat transfer in the window is established while the spectral selectivity of the window to thermal radiation is considered. The transient temperature response is used to evaluate the thermal characteristics. The effect of the radiative heat transfer is firstly analyzed and compared with the pure heat conduction model. There is a temperature deviation (74.1 K) when the radiative heat transfer is ignored. Subsequently, the transient temperature response is simulated under three different kinds of heat flux respectively. It is found that the effect of external heat flux loading is significant. The highest temperature difference reaches 32.9% (299 K) when the heat flux is reduced by 0.5 times and achieves 86.3% (794 K) when the heat flux is increased by 2.5 times. Moreover, the geometric dimensions of window (shape of a truncated cone) generate an effect on its heat transfer characteristics. The temperature decreases significantly (37.8%) when the thickness rises from 10 mm to 20 mm (r = 25 mm) while the temperature decreases relatively small (8.1%) when the radius increases from 15 mm to 45 mm (d = 15 mm). The results reveal that the radiative heat transfer in the window should be carefully considered, especially under the high heat flux loading. Additionally, reducing heat flux or thickening window can improve insulation effectiveness so as to ensure the stable working of the internal equipment.

Keywords:

Citation: Hong-Yu Pan, Chuang Sun, Xue Chen. Transient thermal characteristics of infrared window coupled radiative transfer subjected to high heat flux[J]. AIMS Energy, 2021, 9(5): 882-898. doi: 10.3934/energy.2021041

Related Papers:

[1]	Yasong Sun, Jiazi Zhao, Xinyu Li, Sida Li, Jing Ma, Xin Jing . Prediction of coupled radiative and conductive heat transfer in concentric cylinders with nonlinear anisotropic scattering medium by spectral collocation method. AIMS Energy, 2021, 9(3): 581-602. doi: 10.3934/energy.2021028
[2]	Caliot Cyril, Flamant Gilles . Pressurized Carbon Dioxide as Heat Transfer Fluid: In uence of Radiation on Turbulent Flow Characteristics in Pipe. AIMS Energy, 2014, 1(2): 172-182. doi: 10.3934/energy.2014.2.172
[3]	Chao-Jen Li, Peiwen Li, Kai Wang, Edgar Emir Molina . Survey of Properties of Key Single and Mixture Halide Salts for Potential Application as High Temperature Heat Transfer Fluids for Concentrated Solar Thermal Power Systems. AIMS Energy, 2014, 2(2): 133-157. doi: 10.3934/energy.2014.2.133
[4]	Xiaofeng Zhang, Qing Ai, Kuilong Song, Heping Tan . Bidirectional monte carlo method for thermal radiation transfer in participating medium. AIMS Energy, 2021, 9(3): 603-622. doi: 10.3934/energy.2021029
[5]	Thomas Wetzel, Julio Pacio, Luca Marocco, Alfons Weisenburger, Annette Heinzel, Wolfgang Hering, Carsten Schroer, Georg Muller, Jurgen Konys, Robert Stieglitz, Joachim Fuchs, Joachim Knebel, Concetta Fazio, Markus Daubner, Frank Fellmoser . Liquid metal technology for concentrated solar power systems: Contributions by the German research program. AIMS Energy, 2014, 2(1): 89-98. doi: 10.3934/energy.2014.1.89
[6]	Chao Wei, Gabriel Alexander Vasquez Diaz, Kun Wang, Peiwen Li . 3D-printed tubes with complex internal fins for heat transfer enhancement—CFD analysis and performance evaluation. AIMS Energy, 2020, 8(1): 27-47. doi: 10.3934/energy.2020.1.27
[7]	Ruaa Al Mezrakchi . Investigation of various hybrid nanofluids to enhance the performance of a shell and tube heat exchanger. AIMS Energy, 2024, 12(1): 235-255. doi: 10.3934/energy.2024011
[8]	Jialin Song, Haoyi Zhang, Yanming Zhang, Zhongjiao Ma, Mingfei He . Research progress on industrial waste heat recycling and seasonal energy storage. AIMS Energy, 2025, 13(1): 147-187. doi: 10.3934/energy.2025006
[9]	Khadim Ndiaye, Stéphane Ginestet, Martin Cyr . Thermal energy storage based on cementitious materials: A review. AIMS Energy, 2018, 6(1): 97-120. doi: 10.3934/energy.2018.1.97
[10]	Kokou Aménuvéla Toka, Yawovi Nougbléga, Komi Apélété Amou . Optimization of hybrid photovoltaic-thermal systems integrated into buildings: Impact of bi-fluid exchangers and filling gases on the thermal and electrical performances of solar cells. AIMS Energy, 2024, 12(5): 1075-1095. doi: 10.3934/energy.2024051

Abstract

1. Introduction

The infrared window plays a key role in infrared detection systems (such as the satellite, aircraft and precision guided missile ^[1]), and can keep the signal detecting, imaging and other internal instruments working normally and is crucial for the whole detection progress ^[2]. It can isolate the internal instruments of the detection system from the external environment and prevent the external impurities from entering the interior. Moreover, as an important component in heat insulation, it can effectively weaken the impact of external thermal environment on the detection accuracy ^[3]. Generally, the infrared window is often used on high-speed aircrafts such as missiles, rockets, unmanned aerial vehicles, etc. An intensive high-temperature aerodynamic heat flux will be generated on the outer surface of the infrared window during the high-speed operation ^[4,5,6]. This can generate an amazing heating effect on the window and the temperature will rise rapidly. In serious cases, the high temperature can influence the working reliability and detecting accuracy of internal instruments. According to the physical properties of materials, the raw materials of the window can be roughly divided into new composite materials ^[7,8,9] and traditional materials such as fused silica (SiO₂) ^[10], sapphire (Al₂O₃) ^[11], diamond (C) ^[12], etc. In order to test whether the selected window is suitable, the thermal simulation in advance is inevitable ^[13]. For example, it will be very dangerous for the devices if the temperature of window close to melting point of the material. Therefore, the analysis of transient thermal characteristics in infrared window cannot be underestimated under high-temperature condition especially.

As a typical semitransparent medium, infrared window behaves radiative volumetric absorption characteristics and its transmissivity is above 0.90 in visible light. In the thermal analysis of a model containing a semitransparent medium, the coupled radiative-conductive heat transfer is obvious ^[14]. The radiation can be absorbed by the semitransparent medium (window) and plays a nonnegligible role in the simulation of the thermal characteristics. On the contrary, it is considered that there is almost no radiative heat transfer inside the opaque body and only the surface radiation participates in the heat transfer process ^[15]. For the investigation of coupled heat transfer, some work has been done ^{[16,17,18,19]}. Li et al. ^[20] studied the radiative characteristic of the open-cell foams, which reveals that the open-cell foam to be a typical semitransparent medium. Numerical simulation about transient coupled radiative-conductive heat transfer characteristics was conducted by Mendes et al. ^[21]. Fan and Xia et al. ^[22] performed the coupled radiative-conductive heat transfer characteristics in the 3D gray medium using the Monte Carlo method. Chen et al. ^[23,24] presented the experimental work of coupled heat transfer in the porous foam. A lot of simulation work about transient heat transfer characteristic was done with the whole system as main research object (such as satellites ^[25,26], space mapping camera ^[27], detection devices ^[28,29], hypersonic aircraft ^[30], etc.). Li and Xia et al. ^[31] calculated and analyzed the thermal characteristic of the solar receiver with the infrared window accurately, in which the semitransparent characteristic and spectral selectivity of the infrared window are considered under solar radiative flux. Therefore, the transient thermal characteristics of the window are studied under external transient high heat flux.

In this work, the transient thermal characteristics of the infrared window under external high aerodynamic heat flux are calculated. The infrared window is treated as a semitransparent medium with spectral selectivity. In the second section, mathematical and physical models of the infrared window with complex encapsulation structures are established. In the third section, the coupled radiative-conductive calculation model is compared with others to verify the availability of the model. In the fourth section, the effects of the radiative heat transfer in the window, the transient high-temperature heat flux loading, the ambient temperature and the geometric dimensions on the thermal characteristics of the window are analyzed respectively.

2. Physics model and numerical method

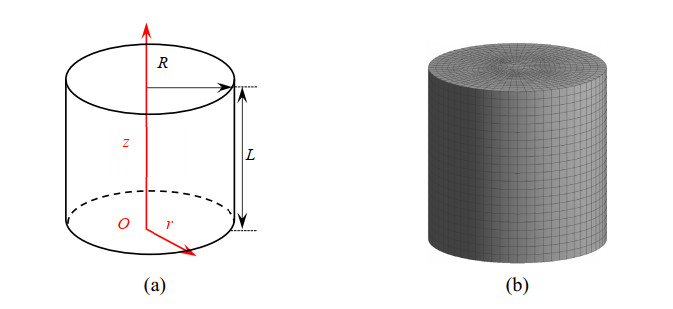
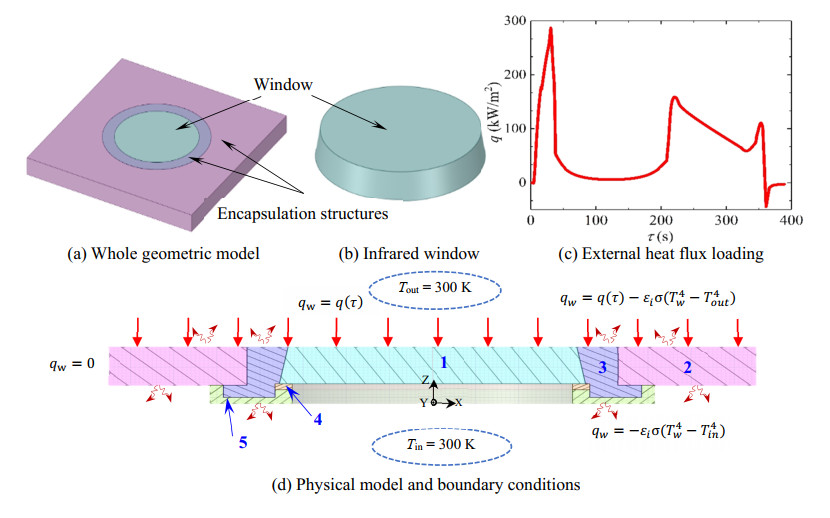
The geometric model is composed of the infrared window and complex encapsulation structures, which is shown in Figure 1(a). In detail, the infrared window is in the shape of a truncated cone (as shown in Figure 1(b)). Moreover, the window is regarded as close contacting with the encapsulation structures. The geometric model can be seen as a rotating body and the cross-sectional view of the model is shown in Figure 1(d). Part 1 is the infrared window, part 2 is the metal shell, parts 3 is the mounting frame, part 4 is the gasket, and part 5 is the pressing plate. Only the infrared window is regarded as a semitransparent medium while the other structures are regarded as opaque bodies with fixed emissivity.

Figure 1. Physical model of numerical simulation. Three-dimensional diagrams of (a) whole geometric model and (b) infrared window respectively; (c) external heat flux loading; (d) boundary conditions of the model.

DownLoad: Full-Size Img PowerPoint

In the simulation, the software Fluent is used to calculate the transient temperature response. Since the finite volume method (FVM) is based on the principle of conservation of physical quantities, the conservation of calculation is perfect and the unstructured grid can be used to discretize the computational domain ^[32,33]. Besides, in the discrete coordinate method (DOM), the radiative transfer equation is transformed into a differential expression, which is easy to be coupled with the general transport equation ^[34,35]. Therefore, the FVM and the DOM are used to calculate the conductive and radiative heat transfer respectively. In addition, it is assumed that the materials of each part are uniform and isotropic. The thermal properties of each part are listed in Table 1 according to Ref. ^[41].

Table 1. Thermal properties of each part in the model.

Part	Thermal conductivity (W·m⁻¹·K⁻¹)	Specific heat capacity (kJ·kg⁻¹·K⁻¹)	Density (kg·m⁻³)
1	1.7	1	2200
2	25	0.577	7800
3	0.48	1.2	1470
4	0.26	1.04	2070
5	14.9	0.477	7900

| Show Table

DownLoad: CSV

In view of the coupled radiative-conductive heat transfer in this model, the outside convective heat transfer is treated as the transient flux loading externally. It is considered that the external aerodynamic thermal environment is complex and the heat flux on the external surface has been obtained previously. In addition, the internal coupled radiative-conductive heat transfer is much more important than the outside convective one. Therefore, the coupled radiative-conductive heat transfer is calculated under transient heat flux loading. In the calculation of coupled radiative-conductive heat transfer, the semitransparent characteristics and the spectral selectivity of the window are considered simultaneously. The coupled radiative-conductive heat transfer is considered in the window (part 1). Instead, the encapsulation structures (part 2–5) are regarded as radiative nonparticipating medium in which only conductive and surface radiative heat transfer are considered.

The transient conductive heat transfer equation of the encapsulation structures is shown as follows ^[36].

ρ c \frac{\partial T}{\partial τ} = \nabla \cdot (λ \nabla T)

$\rho c\frac{{\partial T}}{{\partial \tau }} = \nabla \cdot (\lambda \nabla T)$

(1)

The infrared window is considered as radiative participating medium in which the coupled radiative-conductive heat transfer is conducted. The governing equation is shown as follows ^[37].

ρ c \frac{\partial T}{\partial τ} = \nabla \cdot (λ_{t} \nabla T) - \nabla \cdot {\overset{⇀}{q}}_{r}

$\rho c\frac{{\partial T}}{{\partial \tau }} = \nabla \cdot ({\lambda _t}\nabla T) - \nabla \cdot {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {q} _r}$

(2)

\nabla \cdot {\overset{⇀}{q}}_{r} = \int_{0}^{\infty} \int_{Ω = 4 π} \frac{I λ (s)}{d s} d λ d Ω

$\nabla \cdot {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {q} _r}{\rm{ = }}\int\limits_0^\infty {\int_{\Omega = 4\pi } {\frac{{I{\rm{\lambda }}(s)}}{{ds}}} } d\lambda d\Omega$

(3)

where T is the temperature, τ is the time, ρ is the density, c is the specific heat, λ_t is the thermal conductivity, q_r is the radiative heat flux, λ is the wavelength.

The infrared window is considered as non-scattering medium and the radiative transfer equation is shown as follows ^[37].

\frac{d I_{λ} (s)}{d s} = - k_{α λ} I_{λ} (s) + k_{α λ} I_{b λ} (s)

$\frac{{dI_{\rm{\lambda }}(s)}}{{ds}} = - k_{\rm{\alpha \lambda }}I_{\rm{\lambda }}(s) + k_{\rm{\alpha \lambda }}I_{\rm{b\lambda }}(s)$

(4)

where I_λ(s) is the spectral radiation intensity at position s, k_αλ is the spectral absorption coefficient, I_bλ(s) is the blackbody spectral radiation intensity at position s.

The initial temperature of the numerical simulation is T = 300 K. The external heat flux loading is shown in Figure 1(c). The heat flux roughly describes the flight process of hypersonic vehicle. Firstly, the heat flux rises rapidly with the vehicle launched through the atmosphere. Then the heat flux keeps stable during the gliding phase outside the atmosphere. Subsequently, the heat flux rises again when the vehicle reentry into the atmosphere. Finally, the heat flux decreases gradually until the end of the flight.

The boundary conditions of the model are shown in Figure 1(d). The heat transfer inside encapsulation structures is regarded as pure conduction and the heat transfer inside infrared window is considered as coupled radiative-conductive. Each part of the model conducts radiative heat transfer with the environment. The temperature and heat flux (T_window, q_window) at the contact surface between the window (T_evlop, q_evlop) and encapsulation structures are assumed as continuous, i.e., T_evlop = T_window and q_evlop = q_window.

Transient heat flux q(τ) is loaded on the external surface. Meanwhile, the thermal radiation transfers to the environment. The boundary condition is shown as follows.

q_{w} = q (τ) - ε_{i} σ (T_{w}^{4} - T_{o u t}^{4})

${q_w} = q(\tau ) - {\varepsilon _i}\sigma (T_w^4 - T_{out}^4)$

(5)

where q_w is the wall heat flux, T_w is the wall temperature, σ is Stefan-Boltzmann constant, ε_i (i = 2, 3, 4, 5) is the emissivity of different surfaces in Figure 1. Detailly, ε₂ = 0.4, ε₃ = 0.8, ε₄ = 0.65, ε₅ = 0.95.

The internal surface of the model is considered as radiative heat transfer with environment.

q_{w} = - ε_{i} σ (T_{w}^{4} - T_{i n}^{4})

${q_w} = - {\varepsilon _i}\sigma (T_w^4 - T_{in}^4)$

(6)

Surrounding surfaces are treated as adiabatic boundaries (q_w = 0). The internal ambient temperature T_in and the external one T_out are both assumed as a constant of 300 K.

3. Validation of model

3.1. Grid independence test of the model

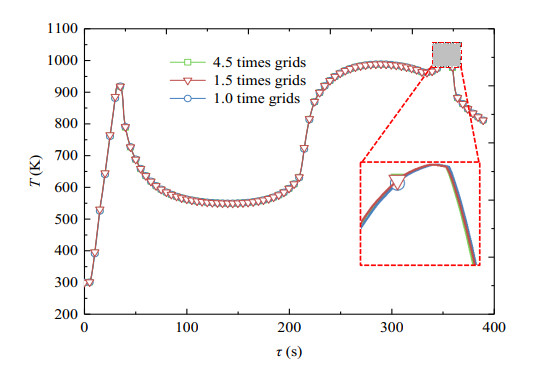
The computational domain of the whole model is discretized by the unstructured grids to calculate the temperature response. In order to verify the grid independence of numerical simulation, the transient temperature response with different grid numbers is checked. The grids are meshed into 62792 initially and are refined by 1.5 times (94199) and 4.5 times (284039) subsequently. Consequently, the comparison of the temperature responses with different configurations is shown in Figure 2. It can be seen that the temperatures under different grids are very similar to each other. This means, with the mesh refinement, the upmost temperature difference is far less than 1% and can be ignored in the calculation. Therefore, the 62792 grids are enough to obtain accurate numerical calculation results and the grid independence of calculation model can be satisfied.

Figure 2. Comparison of temperature responses with different grid numbers.

DownLoad: Full-Size Img PowerPoint

3.2. Validation of coupled model

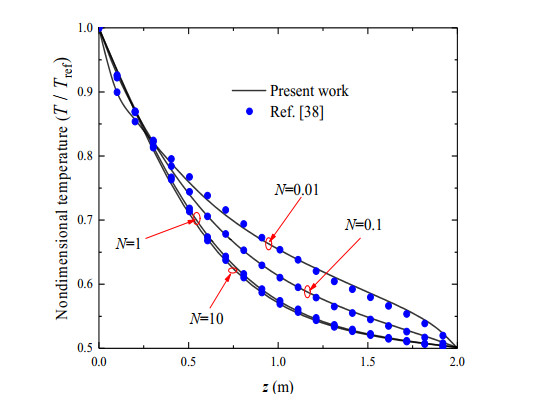
In order to verify the validation of the calculation model used in this work, a cylinder model is used (as shown in Figure 3). In the model, the aspect ratio of the height (L) to the radius (R) is 2, where L = 2R. Cylinder is regarded as a semitransparent and radiative participating medium, the attenuation coefficient (β) is assumed as 1 m⁻¹. The temperature of the cylinder bottom surface (T_ref) is twice that of the other surfaces (T_c), i.e., T_ref = 2T_c. Each surface is considered as the diffuse reflective black-body surface.

Figure 3. Illustration of cylinder model: (a) geometry; (b) meshing.

DownLoad: Full-Size Img PowerPoint

The radiative-conductive coefficient (N) of the model is used to represent the ratio of the radiative to the conductive heat transfer, and is defined as N = λβ/(4σn²T_re³) according to Ref. ^[38]. Different cases with various N are calculated and the comparison is presented in Figure 4. As can be seen, the results are in good agreement with the Monte Carlo calculation in Ref. ^[38]. Therefore, the validation of the calculation model and the feasibility of numerical simulation in this work can be proved.

Figure 4. Comparison of radiative-conductive coefficient N on centerline temperature with Ref. ^[38].

DownLoad: Full-Size Img PowerPoint

4. Results and discussion

4.1. Temperature response of infrared window

The transient temperature response of the infrared window is calculated as representation of the thermal characteristics. In the numerical simulation, the computational domain is discretized by 62792 grids and the transient time step is set to 0.1 s. The spectral selectivity of infrared window determines that its optical properties change with wavelength greatly in most cases. Therefore, the waveband appropriation is used to simulate the spectral properties of the window. In this work, fused silica is selected as the material of the window and its spectral optical properties have been measured by our group through experiments in Ref. ^[39]. The full spectrum is divided into 9 wavebands for approximate calculation with spectral selectivity according to Ref. ^[40], the detailed properties of each waveband are shown in Table 2.

Table 2. Spectral optical properties of fused silica window according to Ref. ^[40].

Waveband	Refractive index n	Absorption coefficient κ/m⁻¹
0.30 μm~1.30 μm	1.470	0.300
1.30 μm~2.52 μm	1.450	5.616
2.52 μm~2.70 μm	1.437	99.926
2.70 μm~2.85 μm	1.433	938.880
2.85 μm~3.55 μm	1.422	39.829
3.55 μm~3.80 μm	1.408	134.510
3.80 μm~4.20 μm	1.397	265.190
4.20 μm~5.00 μm	1.370	726.600
5.00 μm ~	1.349	15000.000

| Show Table

DownLoad: CSV

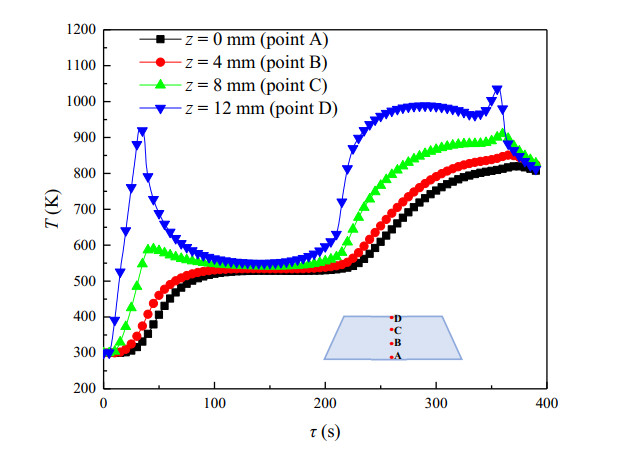
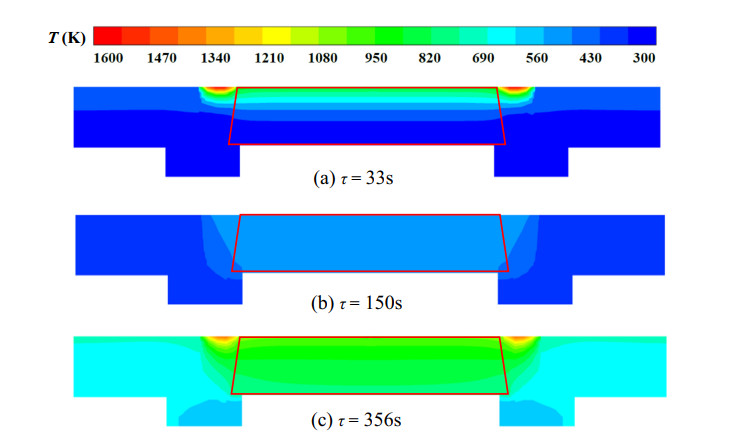
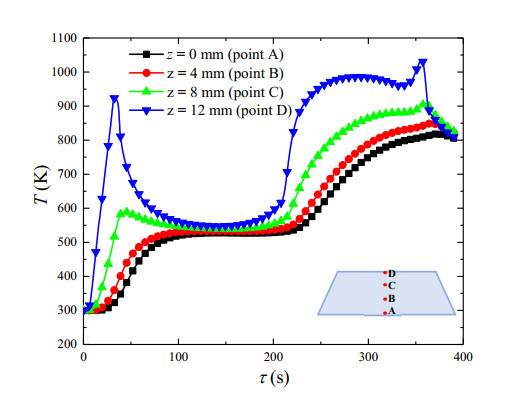
In order to characterize the temperature response of the infrared window, four points A (z = 0 mm), B (z = 4 mm), C (z = 8 mm), and D (z = 12 mm) on the central axial position are selected as characteristic points. The temperature response at different characteristic points is shown in Figure 5. Due to the high flux loading on the external surface, the temperature response at point D changes drastically over time. Additionally, there are two temperature peaks which are 925.3 K and 1038.6 K at τ = 33 s and τ = 356 s respectively.

Figure 5. Temperature response at characteristic points of the fused sapphire window.

DownLoad: Full-Size Img PowerPoint

As shown in Figure 5, the overall temperature response of the point D is similar to the trend of heat flux loading, which can also be divided into four stages. In the first stage, with the rapid rising of the heat flux, the temperature of the window increases sharply until the first peak (925.3 K) at τ = 33 s. Subsequently, with the sharp decrease of heat flux and the heat is gradually transferred from external to internal, the temperature decreases gradually. In the second stage, a relatively stable stage is performed. During this stage, the temperature of each characteristic point is around 550 K until about τ = 200 s. In the third stage, due to the rising of the heat flux, temperature increases rapidly again to the second peak (1038.6 K) at τ = 356 s. This temperature peak is also the highest value of the transient temperature response. In the fourth stage, the external heat flux stops heating and the temperature decreases slightly until the end of time. The transient temperature response of point C is similar to that of point D with two peaks and a stable stage. Furthermore, its maximal temperature is 916.02 K at τ = 362 s. However, the temperature responses of points B and A are not resembling with that of point D. Because the thermal conductivity of fused silica is relatively small, the temperature responses of points B and A generally show an upward trend with a stable stage at the middle time. Hence, there is only one temperature peak throughout the response. The maximal temperatures of points B and A are 851.00 K and 818.17 K at τ = 364 s and τ = 367 s.

According to the temperature response of point D, the temperature field distributions at τ = 33 s, τ = 150 s, and τ = 356 s are selected as representatives shown in Figure 6. At τ = 33 s, the heat has not yet been transferred into the window, but only generate an influence near the external surface. Meanwhile, the first temperature peak of 925.3 K is reached due to the raising heat flux. Then, the heat is transferred from the external surface to the internal of the window. At τ = 150 s, the overall temperature of the window is about T = 600 K and the temperature distribution is relatively uniform. With the rising of the heat flux, the temperature reaches the second peak (maximum) T = 1038.6 K at τ = 356 s. At this time, the overall temperature of the window is high and the temperature difference is also considerable, about T = 228.2 K.

Figure 6. Cross-section temperature distribution of the model at different times.

DownLoad: Full-Size Img PowerPoint

4.2. Effect of thermal radiation on the coupled heat transfer

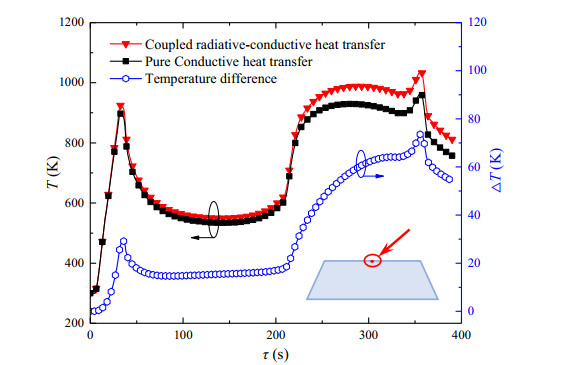
Considering the coupled radiative-conductive and the pure conductive heat transfer respectively, the comparison of temperature responses is shown in Figure 7. In the initial stage, the transient temperature response of the window only has little difference. Then, the temperature difference reaches the first peak of about 30 K at τ = 33 s. At this time, the effect of radiative heat transfer is relatively slight since the temperature of the whole window except near the external surface is not high as shown in Figure 6(a). However, with the increase of the whole window temperature, the effect of infrared radiative heat transfer on the temperature difference gradually increases after τ = 208 s. Then, the temperature reaches maximum (1038.6 K) and the temperature difference also reaches the second peak (maximum) T = 74.1 K. Subsequently, the temperature difference decreases a little. If the radiative heat transfer effect is not considered in the calculation, the highest deviation of 7.1% will be generated. It can affect the accuracy of thermal analysis. Therefore, the effect of radiative heat transfer is obvious and should not be ignored in the calculation.

Figure 7. Comparison of temperature response at point D in different conditions.

DownLoad: Full-Size Img PowerPoint

4.3. Effect of ambient temperature

For the space aircraft, the ambient temperature always keeps low. In order to explore the influence of low ambient temperature on the thermal characteristics of the window, the corresponding calculation and analysis are carried out. Assuming that the external ambient temperature is 250 K, the temperature response is shown in Figure 8. The two temperature peaks are 986.0 K and 1036.4 K at τ = 33 s and τ = 356 s. Compared with the results under 300 K ambient temperature, the temperature decreases slightly and the upmost temperature difference is only 3 K. The main reason is that the radiative heat transfer with environment has little effect on the window temperature compared with the high heat flux loading.

Figure 8. Temperature response at characteristic points under low-temperature ambient.

DownLoad: Full-Size Img PowerPoint

4.4. Effect of external heat flux

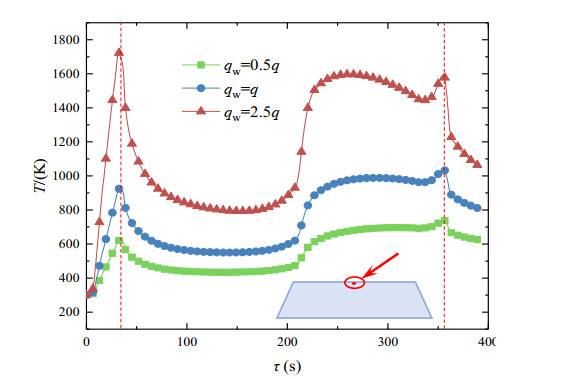
The infrared window on hypersonic vehicles often faces the problem of aerodynamic heating, the effect of the high heat flux loading on transient temperature response is investigated. According to the heat flux in Figure 1(c), three kinds of heat flux q_w = 0.5·q, q_w = q, and q_w = 2.5·q are selected as the conditions of numerical simulation.

As a representative, the temperature responses at point D under different heat flux loadings are shown in Figure 9. With the 0.5·q heat flux loading, in terms of the temperature response, there are two peaks 621.4 K and 739.9 K at τ = 33 s and τ = 356 s, respectively. Compared with the temperature peaks under q, these peaks decrease by about 300 K and the upmost difference (τ = 33 s) is about 32.9%. Obviously, the temperature rises rapidly with the increase of transient heat flux. With the 2.5·q heat flux loading, there are also two temperature peaks at τ = 33 s and τ = 356 s. However, the first peak (1723.4 K) is higher than the second one (1594.7 K), which is the maximal temperature. The reason is that the higher heat flux enhances the temperature of the window, which makes the radiative heat transfer between the window and the environment more significant. At τ = 33 s, there is only a high-temperature region near the external surface. But, at τ = 356 s, the temperature of the whole window is high and the radiative heat transfer with the environment is more intense. Therefore, the time of the maximal temperature moves from τ = 356 s to τ = 33 s. Compared with the temperature peaks under q, the temperature peaks increase by above 500 K and the upmost difference (τ = 33 s) is about 86.3%.

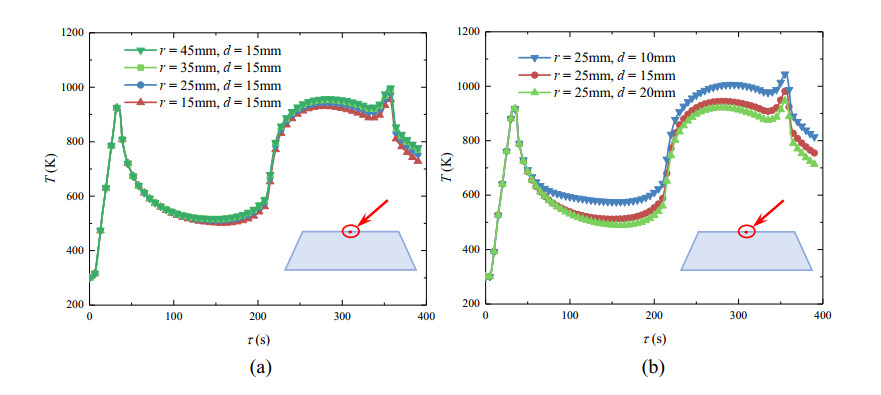
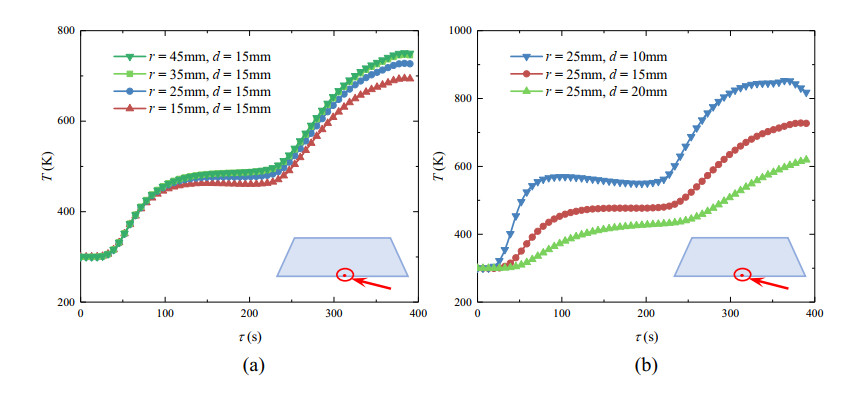
Figure 9. Comparison of temperature response under different heat flux.

DownLoad: Full-Size Img PowerPoint

4.5. Effect of geometric dimension

In order to study the effect generated by geometric dimensions of the infrared window on its temperature response, several cases in different dimensions (radius and thickness) are calculated and compared. The radius of the window is selected as r = 45 mm, 35 mm, 25 mm, 15 mm and the thickness of the window is selected as d = 20 mm, 15 mm, d = 10 mm. At points A and D, the temperature responses are shown in Figures 10 and 11 respectively. With the increase of the window radius, the temperature response changes slightly. However, with the increase of window thickness, the temperature response decreases significantly.

Figure 10. Comparison of temperature response of point D at external surface under different geometric dimensions: (a) effects of changing radius; (b) effects of changing thickness.

DownLoad: Full-Size Img PowerPoint

Figure 11. Comparison of temperature response of point A at internal surface under different geometric dimensions: (a) effects of changing radius; (b) effects of changing thickness.

DownLoad: Full-Size Img PowerPoint

Specifically, when the radius increases from 15 mm to 45 mm under the thickness of 15 mm, the maximum temperature difference is about 8.1% (56.5 K). The reason is that the increase of radius mainly influences the heat transfer characteristics in the radial direction of the window but donates little effect on the axial heat transfer characteristics. However, with the thickness increasing from 10 mm to 20 mm under the radius of 25 mm, the temperature decreases by 37.8% (307.5 K). The reason is that the heat transfer characteristics along the axial direction are greatly affected by the thickness of window. On the one hand, with the increase of thickness, the conductive heat transfer in the window is weakened so that the temperature responses decrease at both of points A and D. On the other hand, the optical thickness also increases with the increase of the thickness. The radiative absorption in the window is enhanced so that the temperature difference of point A is much higher than that of point D. The maximal temperature difference is 307.5 K at point A while it is only 101.1 K at point D.

5. Conclusions

In this work, the thermal characteristics of the infrared window are investigated under complex transient high heat flux in Figure 1(c). Besides, the temperature responses under different conditions are calculated. Consequently, the radiative heat transfer inside the window should be considered and the coupled radiative-conductive heat transfer model should be used in the simulation. In order to decrease the temperature of windows, the heat flux loading should be weakened and the windows with large thickness shall be adopted.

(1) The effect of the radiative heat transfer in the window has been performed. If only pure conductive heat transfer in the window is considered, the upmost temperature difference can reach 74.1 K. This deviation accounts for 7.1% of the temperature where radiative heat transfer is considered.

(2) The influence of external high heat flux is significant and the temperature rises sharply with the increase of heat flux. When the heat flux drops to 0.5·q, the temperature decreases by 32.9% (299 K) of that under q heat flux. When the heat flux rises to 2.5·q, the highest peak temperature increases by 86.3% (700 K) of that under q heat flux.

(3) The effect of different dimensions (radius and thickness) on its heat transfer characteristics has been discussed respectively. With the radius increasing from 15 mm to 45 mm (d = 15 mm), the maximum temperature decreases by 8.1% (56.5 K). Nevertheless, with the thickness increasing from 10 mm to 20 mm (r = 25 mm), the maximum temperature decreases by 37.8% (307.5 K).

The present work gives a thermal analysis of thermal characteristics in the infrared window under high heat flux. It will provide a guidance to the simulation and design of the infrared window on the hypersonic vehicle.

Acknowledgments

This work is supported by the National Natural Science Foundation of China (No. 51806046), the China Postdoctoral Science Foundation (No. 2018M630350), and Heilongjiang Postdoctoral Fund (NO. LBH-Z18081).

Conflict of interest

The authors declared that they have no conflicts of interest to this work.

References

[1]	Mahulikar SP, Sonawane HR, Rao GA (2007) Infrared signature studies of aerospace vehicles. Prog Aerosp Sci 43: 218-245. doi: 10.1016/j.paerosci.2007.06.002
[2]	Guo GM, Luo Q, Gong JJ (2021) Evaluation on aero-optical transmission effects caused by a vortex in the supersonic mixing layer. Opt Commun 483: 126631. doi: 10.1016/j.optcom.2020.126631
[3]	Fan ZG, Pei YW, He YL, et al. (2007) Analysis method of window light transmission in aerodynamic environment. J Astronaut 28: 255-258.
[4]	Chae JH, Mankodi TK, Choi SM, et al. (2020) Combined Effects of Thermal Non-equilibrium and Chemical Reactions on Hypersonic Air Flows Around an Orbital Reentry Vehicle. Int J Aeronaut Space Sci 21: 612-626. doi: 10.1007/s42405-019-00243-9
[5]	Tang W, Yang XF, Gui YW, et al. (2017) Review of hypersonic aerodynamics and aerothermodynamics for mars entries. J Astronaut 38: 230-239.
[6]	Li JW, Wang JF, Cheng KM, et al. (2019) Rapid method for calculating aero-heating coupled with structure heat transfer on hypersonic vehicles. Acta Aerodyn Sin 37: 956-965.
[7]	Nundy S, Mesloub A, Alsolami BM, et al. (2021) Electrically actuated visible and near-infrared regulating switchable smart window for energy positive building: A review. J Cleaner Prod 301: 126854. doi: 10.1016/j.jclepro.2021.126854
[8]	Xuan QD, Li GQ, Pei G, et al. (2021) Daylighting utilization and uniformity comparison for a concentrator-photovoltaic window in energy saving application on the building. Energy 214: 118932. doi: 10.1016/j.energy.2020.118932
[9]	Xuan QD, Li GQ, Pei G, et al. (2019) Design, optimization and performance analysis of an asymmetric concentrator-PV type window for the building south wall application. Sol Energy 193: 422-433. doi: 10.1016/j.solener.2019.09.084
[10]	Huang L, Wang T, Tang YB, et al. (2020) UV-to-IR highly transparent ultrathin diamond nanofilms with intriguing performances: Anti-fogging, self-cleaning and self-lubricating. Appl Surf Sci 527: 146733. doi: 10.1016/j.apsusc.2020.146733
[11]	Ma J, Thomas ME, McGuiggan P, et al. (2020) Weak absorption and scattering losses from the visible to the near-infrared in single-crystal sapphire materials. Opt Eng 59: 087101.
[12]	Wang WH, Dai B, Han JC, et al. (2020) Recent progress of diamond infrared window-related components. Mater Sci Technol 28: 42-57.
[13]	Nundy S, Ghosh A (2020) Thermal and visual comfort analysis of adaptive vacuum integrated switchable suspended particle device window for temperate climate. Renewable Energy 156: 1361-1372. doi: 10.1016/j.renene.2019.12.004
[14]	Chandrasekhar S (1960) Radiative Transfer, New York: Dover Publications.
[15]	Howell JR, Siegel R, Mengüç MP (2011) Thermal Radiation Heat Transfer, 5 Eds., Boca Raton: CRC Press.
[16]	Chen X, Xia XL, Sun C, et al. (2020) Performance evaluation of a double-pipe heat exchanger with uniform and graded metal foams. Int J Heat Mass Transfer 56: 291-302. doi: 10.1007/s00231-019-02700-3
[17]	Fan C, Li XL, Xia XL, et al. (2020) Tomography-based pore level analysis of combined conductive-radiative heat transfer in an open-cell metallic foam. Int J Heat Mass Transfer 159: 120122. doi: 10.1016/j.ijheatmasstransfer.2020.120122
[18]	Chen X, Sun C, Xia XL (2018) Numerical analysis on the Radiation-Convection coupled heat transfer in an Open-Cell foam filled annulus. Energy 11: 2713.
[19]	Chen X, Xia XL, Sun C, et al. (2017) Transient thermal analysis of the coupled radiative and convective heat transfer in a porous filled tube exchanger at high temperature. Int J Heat Mass Transfer 108: 2472-2480. doi: 10.1016/j.ijheatmasstransfer.2017.01.089
[20]	Li Y, Xia XL, Sun C, et al. (2019) Radiative characteristics of Voronoi open-cell foams made from semitransparent media. Int J Heat Mass Transfer 133: 1008-1018. doi: 10.1016/j.ijheatmasstransfer.2019.01.016
[21]	Mendes MAA, Talukdar P, Ray S, et al. (2014) Detailed and simplified models for evaluation of effective thermal conductivity of open-cell porous foams at high temperatures in presence of thermal radiation. Int J Heat Mass Transfer 68: 612-624. doi: 10.1016/j.ijheatmasstransfer.2013.09.071
[22]	Fan C, Li XL, Xia XL, et al. (2019) An unstructured Monte Carlo ray-tracing method for solving radiative heat transfer in 3D gray semitransparent medium. J Quant Spectrosc Radiat Transfer 225: 110-118. doi: 10.1016/j.jqsrt.2018.12.035
[23]	Xia XL, Chen X, Li XL, et al. (2018) Experiment and numerical simulation on transient heat transfer from SiC foam to Air-Flow in a high temperature tube. Therm Sci 22: S597-S606. doi: 10.2298/TSCI171103044X
[24]	Xia XL, Chen X, Sun C, et al. (2017) Experiment on the convective heat transfer from airflow to skeleton in open-cell porous foams. Int J Heat Mass Transfer 106: 83-90. doi: 10.1016/j.ijheatmasstransfer.2016.10.053
[25]	Yin YZ, Fu WC, Lu QR, et al. (2020) Thermal design of GF-7 satellite based on dimensional stability. Spacecr Eng 29: 82-88.
[26]	Li Q, Kong L, Zhang L, et al. (2020) Thermal design and validation of multispectral max width optical remote sensing satellite. Opt Precis Eng 28: 904-913.
[27]	Yin YZ, Fu WC, Huang JY, et al. (2020) Thermal design and verification for two-linear array stereo mapping camera of GF-7 satellite. Spacecr Eng 29: 131-137.
[28]	Huang JY, Pan FM, Fu WC, et al. (2020) Thermal design and verification of laser altimeter for GF-7 satellite. Spacecr Eng 29: 138-143.
[29]	Yu CW, Sui J, Chen C, et al. (2020) Thermal design and verification of multi-head very high accuracy star sensor onboard GF-7 satellite. Spacecr Eng 29: 144-150.
[30]	Li ZH, Sun C, Xia XL (2018) Numerical Simulation of aerodynamic heating over solid blunt configuration with porous spike. J Aerosp Eng 31: 04018083. doi: 10.1061/(ASCE)AS.1943-5525.0000901
[31]	Li XL, Sun C, Xia XL, et al. (2020) Modeling of coupled heat transfer in a windowed volumetric solar receiver. Sol Energy 201: 195-208. doi: 10.1016/j.solener.2020.02.073
[32]	Raithby GD, Chui EH (1990) A finite-volume method for predicting a radiant heat transfer in enclosures with participating media. ASME Trans J Heat Transfer 112: 415-423. doi: 10.1115/1.2910394
[33]	Chui EH, Raithby GD (1992) Implicit solution scheme to improve convergence rate in radiative transfer problems. Numer Heat Transfer Part B Fundam 22: 251-272. doi: 10.1080/10407799208944983
[34]	Sakurai A, Song TH, Maruyama S, et al. (2005) Comparison of radiation element method and discrete ordinates interpolation method applied to three-dimensional radiative heat transfer. JSME Int J 48: 259-264. doi: 10.1299/jsmeb.48.259
[35]	Aghanajafi C, Abjadpour A (2015) Discrete ordinates method applied to radiative transfer equation in complex geometries meshed by structured and unstructured grids. J Braz Soc Mech Sci Eng 38: 1-13.
[36]	Holman JP (2009) Heat Transfer, 10 Eds., New York: Mc-Graw Hill Higher Education.
[37]	Mahan JR (2002) Radiation Heat Transfer: A Statistical Approach, New Jersey: John Wiley & Sons Inc..
[38]	Fan C, Xia XL, Qiu J, et al. (2021) mcrtFOAM: A mesh-agglomeration Monte Carlo ray-tracing solver for radiative transfer in gray semitransparent solids. Comput Phys Commun 258: 107608. doi: 10.1016/j.cpc.2020.107608
[39]	Zhang SD, Sun C, Xia XL, et al. (2017) Spectral properties of an UV fused silica within 0.8 to 5 μm at elevated temperatures. Infrared Phys Technol 85: 293-299.
[40]	Li XL, Xia XL, Chen X, et al. (2019) Effects of double windows on optical and thermal performance of solar receivers under concentrated irradiation. Sol Energy 184: 331-344. doi: 10.1016/j.solener.2019.04.016
[41]	John H Lienhard IV, John H Lienhard V (2011) A Heat Transfer Textbook, 4 Eds, Cambridge: Phlogiston Press.

Reader Comments

Your name:*

Email:*
© 2021 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

AIMS Energy

1.8 3.8

Metrics

Article views(3075) PDF downloads(429) Cited by(0)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

Figures and Tables

Figures(11) / Tables(2)

AIMS Energy

Transient thermal characteristics of infrared window coupled radiative transfer subjected to high heat flux