1. Introduction
Offshore wind sector has become a primary energy policy among several European countries for decreasing carbon dioxide (CO2) emissions and attenuating climate change impacts, as was set by the EU key targets for the year 2020 and 2030. As a result, the corresponding share of the annual EU wind energy installations was increased from 13% in 2014 to 24% the next year [1]. In line with this target, offshore wind energy has gained ground against onshore wind installations during the past few years.
Offshore and onshore wind conditions have great distinctions as regards development and installation of wind farms; for instance, offshore winds are higher in magnitude and more stable (spatially and temporally) than onshore winds producing considerably higher power over time while there are available wide-open offshore areas in contrast with the satiated onshore spaces for large-scale wind projects adjacent to energy demanding centers. On the other hand, offshore wind projects share a higher total cost for their materialization than onshore projects and raise greater risks and uncertainties due to the immaturity of technology and the lack of knowledge as regards the impacts of offshore wind farms (OWFs) on the socio-economic and environmental features of a candidate area; see also [2,3,4,5]. Currently, the most rapidly growing sea basin in terms of offshore wind installations is the North Sea with 69.4% of offshore wind capacity by 2015 [6], mainly due to the favorable combination of high wind potential and shallow water depths at great distances from the shore. In the Mediterranean Sea, numerous offshore wind projects have been planned, however immediate implementation of OWFs is not foreseen yet.
One of the most important and fundamental problems in the design and development of an offshore wind project is the preliminary identification of appropriate areas that meet specific criteria. The selection of appropriate sites is neither a simple nor a straightforward process; on the contrary, the determination of the suitability of an OWF site is a multilateral and complex procedure based on various considerations that are not always aligned. Site selection is, in general, a three-fold procedure built on the following distinct frameworks: i) the technical/engineering framework, which is relevant with the assessment of technical and engineering aspects (such as wind resource availability, water depth and bottom suitability, distance from shore, etc.), ii) the environmental framework concerning sensitive marine habitats and protected areas, effects and impacts on seabirds, fish and marine mammals, etc. and iii) the socio-economic framework dealing with the effects on human life, other coastal and marine activities/uses (e.g. tourism, fisheries, shipping lanes, marine cultural heritage, military exercise areas), financial issues, European and national legislation, marine spatial planning, etc. An application integrating some of the above-mentioned factors into a single framework is given in [7].
Apart from wind availability, distance from shore and water depth are currently the most important technical and financial constraints in the selection of sites for OWF development. As distance from shore and bottom depth increase, the costs of underwater electrical grid connections, installation and maintenance also increase. On the other hand, a short distance from shore causes visual disturbances in the neighboring coastal areas. The importance of visual disturbance is crucial for areas of high touristic development like the majority of the Mediterranean coasts [8,9]. For example, due to the strong reaction of the coastal communities against fixed installations, France has recently considered, at a regional level, to develop OWFs based on floating wind turbines that can be deployed in deeper water depths and off the Mediterranean coasts; see [10], as well as the published planning document by the Préfet Maritime de la Méditerranée and the Préfet de la region-Provence-Alpes-Côte d'Azur [11]. Moreover, three demonstration floating wind farms in the Mediterranean have been awarded from the French Ministry of the Environment, Energy and Marine Affairs, see e.g. [12]. It is anticipated that, if this strategy is strongly supported and successfully adopted in France, it will probably have implications on national policies and environmental, socio-economic, technical and legislative considerations of other EU Mediterranean countries including Greece. Moreover, on the presumption that the technology readiness level of the, still immature, floating wind turbines will reach the final stage and will be headed towards commercialization, and the corresponding costs will be significantly reduced as well (for instance, the cost of the floating foundations are four to six times higher than the fixed ones [13]), the installation of bigger floating turbines far from the coastline may provide a viable solution to the visual disturbance problem and weaken the Not-In-My-Backyard (NIMBY) attitude. Conversely, in Westerberg et al. [14], it is suggested that the attitude of the tourist community may be influenced as regards OWFs that are visible from shore if the proper information on offshore wind energy is provided (e.g. effectiveness of renewable energies, actual cost of offshore wind energy compared to conventional fuels in terms of climate change, etc.). A feasibility study including an economic evaluation, social benefits and a cost-benefit analysis of the floating wind technology in the Mediterranean Sea is presented in [15].
Wind resource assessment studies require reliable long-term measurements of wind speed and direction. However, in situ measurements are inadequate for such extended areas like the Mediterranean Sea. Thus, the only solution to overcome the hindrance of spatial coverage is the use of high-resolution gridded wind data sets in order to estimate accurately the parameters of interest even at nearshore areas.
Although there are several recent research studies mapping offshore wind resource over the Mediterranean Sea based on various wind data sources (e.g. [16,17,18,19,20]), in order to identify hot-spots for OWF development, the Greek Seas have received little attention despite their favorable wind climatology with respect to the development of such projects, especially in deep water depths. For instance, in Kotroni et al. [18], the wind climatology of Greece for different height levels is presented based on simulations of the high-resolution MM5 model with 2 km × 2 km grid resolution since 2000. After the verification of the model results with onshore meteorological stations, annually and monthly statistics of wind speed are provided over the mainland and maritime areas of Greece, as well as annual wind potential density at 50 m height. The SKIRON atmospheric model, a high-resolution atmospheric modeling system, was adopted by Emmanouil et al. [19] for the simulation of wind speed and direction between 2001 and 2010 with 0.05° × 0.05° horizontal resolution. The obtained result regarding the spatial pattern of wind power potential resembles the corresponding one from Kotroni et al. [18] reaching annual values around 600 W/m2 (at 10 m height) in the eastern Aegean Sea. However, none of the above studies includes the spatial distribution of basic statistics of wind direction nor variability measures that are very useful in wind energy industry. The significance of assessing wind direction as well has been highlighted, among others, in [20,21,22] and is attributed to the minimization of wake effects in varying wind directions during the wind farm micrositing design. On the other hand, variability measures, such as mean annual and inter-annual variability, are essential parameters for the wind energy economics as was stressed by Watson [23] and references cited therein.
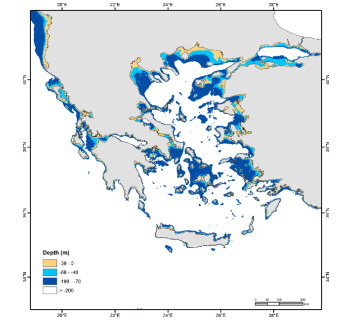
Nevertheless, OWF development in Greece is still at an infant stage. A rather important hindrance refers to the geomorphological features of the Greek Seas and, in particular, to the unfavorability of the bathymetric conditions. Specifically, the Greek continental shelf is very narrow; consequently, the effective water depths for OWF installations are located very close to the shore, increasing thus NIMBY attitudes. In Figure 1, a bathymetric map of the examined area is presented including specific depth ranges: ⅰ) 0-40 m ("shallow waters"), ⅱ) 40-70 m ("intermediate waters"), and ⅲ) 70-200 m ("deep waters"). Clearly, shallow and intermediate waters refer to monopile, gravity-based, tripod, jacket, and tri-pile supporting structure of offshore wind turbines. Deep waters (70-200 m) that have the highest spatial coverage over the examined sea areas, refer to floating wind turbines technologies, including tension leg platforms. Extended shallow water (0-40 m) areas are located in Northern Greece and at the north-eastern coasts of Limnos Isl. From this figure it is evident that bottom depth and, consequently, distance from shore are probably the most important technical parameters that should be considered in the development of OWFs in Greece.
This unfavorable situation (i.e. lack of Greek offshore wind projects) is also attributed to the financial crisis that, among others, prevented investments and the, until recently, unstable feed-in-tariff (FiT) scheme that caused additional doubt about the offshore industry and uncertainty to the potential investors; see, for example, [25]. However, on August 9, 2016 Law 4414/2016 was published in the Government Gazette [26], mainly containing a new support scheme for electricity from renewable energy sources (RES). This scheme aims to restructure the existing support scheme in order to promote better integration and participation of power generation from RES in the national electricity market, being also compatible with the European Commission's Guidelines on State aid for environmental protection and energy 2014-2020; see [27]. This new law introduces feed-in premiums (FiP), competitive tenders and virtual net metering. It is anticipated that Law 4414/2016 will rearrange the national energy sector by making relevant investments much more attractive; thus rendering OWF development in the Aegean and Ionian Seas more prosperous in the next few years.
The main objective of the present work is to provide the spatial distribution of offshore wind speed, wind direction and wind power density on an annual and seasonal scale over the Aegean and Ionian Seas, i.e. for two major sea areas where applications for production licenses have been submitted to the Greek Regulatory Authority for Energy (RAE). For this purpose, hindcast wind data, including wind speed and wind direction, with high spatial (0.1° × 0.1°) and temporal (3 h) resolution covering the period from 1995 to 2009 has been validated and analyzed. Moreover, variability measures of wind speed and direction are also provided for the examined areas leading to a more complete description of offshore wind climatology. Estimates of the equiprobable contours of the event [4 m/s ≤ wind speed ≤ 25 m/s] that resembles the wind turbine availability factor are also quantified and presented in an annual basis. The particular wind speed threshold values correspond to typical cut-in and cut-out wind speeds for most commercial offshore wind turbines. Finally, for selected potential offshore wind energy projects that are at the concept/planning phase the main wind climate wind power density characteristics are also provided.
The structure of this work is the following: Section 2 deals with the main methodological aspects followed in this work, including the validation procedure of the model results (regarding both wind speed and wind direction) using collocated wind data obtained from oceanographic buoys. Section 3 is focused on the description of the numerical model and the presentation of the results from the statistical analysis and the validation procedure. In Section 4 the detailed numerical results referring to the spatial distribution of wind speed and direction, as well as wind power density, are presented. Specifically, the main statistical parameters of the above-mentioned quantities along with some important variability characteristics and wind speed persistence analysis are provided. Moreover, the particular characteristics of some selected locations of the Aegean and Ionian Seas, where OWF development is at the concept/early planning phase are also presented. In the last section, the key findings of the presented analysis are summarized.
2. Methodology
In this work, the wind climate analysis and the assessment of offshore wind power potential are based on a high-resolution gridded wind dataset obtained from a numerical weather prediction (NWP) model.
Model outputs are subject to various uncertainties, mainly attributed to: i) the boundary and initial conditions that are not accurate enough due to measurement and assimilation errors; ii) the exclusion of specific interactions or less important variables for simplification reasons, and; iii) the chaotic nature of the atmosphere that renders the modelling of this system a very demanding and exacting procedure; for this reason, the validation of the model results is necessary. In this respect, measured wind speed and wind direction data, obtained from offshore oceanographic buoys, were used.
As regards wind speed, the statistical metrics that were used for the purpose of the model validation are the correlation coefficient (r), the bias (BIAS), the mean absolute error (MAE), the root mean square error (RMSE), the scatter index (SI) and the symmetrical mean absolute percentage error (SMAPE). The definition of all metrics can be found in [20] apart from SMAPE, which is defined as follows:
|
SMAPE=200NN∑i=1|uB,i−uM,iuB,i+uM,i|
|
(1)
|
where uB,i is the i-th measured wind speed from the buoy, uM,i is the i-th wind speed from the model and N is the sample size. The corresponding values are bounded to [0, 200]. The model performance is characterized as good if all the values of the adopted metrics are as close to zero as possible except for correlation coefficient that should be close to unity. The statistical metrics that were used for the purpose of the model validation as regards wind direction are the circular-circular correlation coefficient (rc), the bias (BIAS), the mean circular absolute error (MCAE), and the root mean error (RME); for the definition of these measures see [28]. If the values of BIAS, MCAE and RME are close to zero and rc is close to unity, then the model performance is good. See Section 3, where the wind data from both data sources are presented in detail along with the results of the validation procedure.
After the model validation, the spatial distribution of offshore wind speed and direction and wind power density evaluated at 80 m height asl is provided in the annual and the seasonal time scale. For the presentation of the main wind climate and wind power potential features for the Aegean and Ionian Seas various statistical quantities are assessed. As regards wind speed, apart from the standard statistical quantities, i.e. mean value and standard deviation, the mean annual variability (MAV) and the inter-annual variability (IAV) are estimated and presented herewith. These measures describe the variability of the variable of interest within a year and from one year to another, respectively, and constitute essential design parameters in wind energy applications (e.g. OWF planning). Their mathematical expressions are provided in [20]. Regarding wind direction, the description of the main statistical quantities (i.e. mean value, circular variance, circular standard deviation), which are less known, can be found in Section Ⅱ of Soukissian et al. [20] and standard reference books regarding circular statistics, such as [29] and [30]; see also [21], where wind (and wave) directions are modelled and examined in detail. In this work the circular variance instead of the circular standard deviation, is preferred since the former is bounded in [0, 1], in contrast to the latter, which ranges within [0, ∞].
The original time series of wind speed and direction that were extracted from the NWP model and analyzed are referred to 10 m height above sea level (asl). For the wind power estimation, the wind speed extrapolation at height of, say, h m asl (i.e. to a typical turbine hub height) is based on the log-law:
|
uh=u10ln(h/z0)ln(10/z0)
|
(2)
|
where uh is the wind speed at the examined height h asl, u10 is the wind speed at 10 m height asl (obtained from the NWP model results) and z0 is the roughness length that equals to 0.001 m for open sea areas [31]. The above equation has been compared with wind fields from LiDAR measurements, revealing its good performance [32].
Furthermore, the mean wind power density P (W/m2) is estimated directly by utilizing the long time series of wind speed at the model grid points. For a particular grid point, P is estimated by the following equation:
where N is the total sample size of the time series, ρ is the air density, considered to be constant and equal to 1.2258 kg/m3, and ui is the value of wind speed obtained from the corresponding time series. Without doubt, the accurate description of the wind climate in an area is a rather delicate issue, since rather small variations of u (from the actual value of u, if wind speed measurements were available) lead to very large variations in P due to the third power. The main variability characteristics of the above-mentioned quantities are also provided.
An additional factor that should be taken into account for the development of OWFs is the percentage of time that the wind speed is within the operational wind speed limits of any industrial offshore wind turbine. The majority of wind turbines are characterized by typical cut-in speed~4 m/s and cut-out speed~25 m/s. The examined event is denoted by A=[4⩽U80⩽25], where U80 denotes the wind speed at 80 m height asl, representing a typical turbine hub height. The probability of occurrence of A can be estimated from the following relation:
|
Pr[A]≈N∑i=11A(4⩽u80,i⩽25)N
|
(4)
|
where 1A(·) is the indicator function, u80,i is the particular i-th wind speed value (at 80 m height asl) and N is the considered sample size.
Finally, for some particular locations of the Aegean and Ionian Seas, the main wind climate and wind power density characteristics are also evaluated.
3. Wind Data Description and Validation
3.1. General
The hindcast wind data spanning 15-year period (1995-2009) was produced by downscaling European Centre for Medium-Range Forecasts (ECMWF) global reanalyses with the aid of the Eta-based NWP model of the POSEIDON system [33]. In Table 1, the main features of the model are presented. Details about the dynamical downscaling procedure, the relevant products and the data evaluation can be found in the work of Papadopoulos et al. [34].
Table 1. Main features of the ETA model configuration
| Main features of the ETA model configuration |
| Horizontal grid increment |
0.10 × 0.10 |
| Vertical levels |
38 |
| Time steps (s)
|
30 |
| Grid |
Arakawa E grid |
| Model output frequency (h)
|
3 |
| Cloud microphysics scheme |
Ferrier [35]
|
| Cumulus scheme |
Betts-Miller-Janjic [36]
|
| Surface layer scheme |
Monin-Obukhov-Janjic scheme [37]
|
| Land-surface model |
4-layer NOAH [38]
|
| Planetary boundary layer scheme |
Mellor-Yamada-Janjic Level 2.5 [37]
|
| Radiation scheme (shortwave; longwave)
|
GFDL [39,40]
|
In order to evaluate the model results, measured wind speed and wind direction data obtained from four offshore oceanographic buoys of the POSEIDON system, see [41], were used; see Table 2, where the geographical coordinates of each buoy are depicted. In the next subsection, the statistical analysis of the collocated wind data sets from the NWP model and the buoy measurements is presented, and then, the validation of the model results is performed.
Table 2. Wind speed statistics for the buoy measurements and model data in the Aegean and Ionian Seas
| Location name |
Latitude (deg) |
Longitude (deg) |
Data source |
N
|
m (m/s) |
s (m/s) |
min (m/s) |
max (m/s) |
CV (%) |
| Athos |
39.96 |
24.72 |
Buoy |
19971 |
5.185 |
3.585 |
0.000 |
23.098 |
69.130 |
| Model |
4.731 |
2.880 |
0.046 |
16.578 |
60.874 |
| Lesvos |
39.15 |
25.81 |
Buoy |
20436 |
6.811 |
3.711 |
0.000 |
24.998 |
54.490 |
| Model |
5.482 |
2.800 |
0.123 |
16.156 |
51.071 |
| Mykonos |
37.51 |
25.46 |
Buoy |
20824 |
7.623 |
4.014 |
0.001 |
21.306 |
52.656 |
| Model |
6.372 |
3.110 |
0.161 |
16.168 |
48.811 |
| Pylos |
36.83 |
21.61 |
Buoy |
5072 |
5.280 |
2.941 |
0.270 |
18.065 |
55.710 |
| Model |
4.622 |
2.658 |
0.094 |
14.769 |
57.510 |
3.2. Analysis and validation of collocated measured and model wind data
A typical procedure for a rational comparative assessment of buoy measurements and model results is to collocate wind speed data from both data sources in space and time. The spatial collocation is achieved by interpolating the four nearest model grid points to the exact buoy location via the implementation of the inverse squared distance weighting interpolation function to the simulated wind speed time series, while the temporal collocation is based on the simultaneous available wind speed data and refers to the common time steps 00, 03, …, 21 UTC. Furthermore, outlying observations were detected using Cook's distance and discarded from the collocated samples after thorough examination.
In Table 2, the main statistics (i.e. mean value m, standard deviation s, minimum and maximum values: min, max, and coefficient of variation CV) of the collocated wind speed data are presented. The sample sizes N correspond to a consecutive wind time series of two to seven year-long. The values of m, s, max and CV are consistently higher for the buoy measurements (except for CV of Pylos), compared to the model.
In Table 3, the main directional statistics parameters (i.e. mean value ˉθW and circular variance Vθ) of the collocated wind direction data are presented. Mean wind direction for all selected locations is confined to the northern sector (roughly from NW to NE for both data sources). The smallest value of circular variance is exhibited for Mykonos, while the variance values for the model results are consistently higher, except for Pylos.
Table 3. Wind direction statistics for the buoy measurements and model data in the Aegean and Ionian Seas
| Location name |
Data source |
N |
ˉθW (deg) |
Vθ (-) |
| Athos |
Buoy |
19971 |
36.268 |
0.692 |
| Model |
14.160 |
0.699 |
| Lesvos |
Buoy |
20436 |
23.232 |
0.596 |
| Model |
7.000 |
0.625 |
| Mykonos |
Buoy |
20824 |
323.013 |
0.567 |
| Model |
324.169 |
0.597 |
| Pylos |
Buoy |
5072 |
334.119 |
0.722 |
| Model |
306.537 |
0.690 |
In Table 4, the obtained results for each statistical metric are presented for the four selected buoy locations. From the values of r, it is evident that the linear relationship between buoy and model wind speed data is strong with the highest value observed for Mykonos (0.874) and the lowest one for Pylos (0.796). The absolute values of BIAS range from 0.455 m/s (corresponding to Athos) to 1.329 m/s (Lesvos) while the lowest (1.922 m/s) and the highest (2.563 m/s) values of RMSE are provided by Pylos and Lesvos. SMAPE, which is more sensitive when the model underestimates wind speed with respect to buoy measurements, takes the minimum value (35.264%) for Mykonos; the same holds true for SI (0.308).
Table 4. Statistical metrics applied for the validation of wind speed data from the model with reference to buoy measurements in the Aegean and Ionian Seas. Boldface numbers denote the best value for each metric
| Location name |
r (-) |
BIAS (m/s) |
RMSE (m/s) |
MAE (m/s) |
SI (-) |
SMAPE (%) |
| Athos |
0.832 |
0.455
|
2.041 |
1.614 |
0.394 |
45.505 |
| Lesvos |
0.809 |
1.329 |
2.563 |
2.081 |
0.376 |
42.565 |
| Mykonos |
0.874
|
1.251 |
2.351 |
1.909 |
0.308 |
35.264
|
| Pylos |
0.796 |
0.658 |
1.922
|
1.552
|
0.364
|
40.082 |
In Table 5 the obtained results for each statistical metric are presented for the four selected buoy locations. From the values of rc, it is evident that the (circular) association between buoy and model wind direction data is fair with the highest value observed for Mykonos (0.708) and the lowest one for Pylos (0.447). The values of the other adopted metrics are consistently lower also for Mykonos.
Table 5. Statistical metrics applied for the validation of wind direction data from the model with reference to buoy measurements in the Aegean and Ionian Seas. Boldface numbers denote the best value for each metric
| Location name |
rc (-) |
BIAS (deg) |
MCAE (deg) |
RME (-) |
| Athos |
0.539 |
-22.108 |
38.247 |
0.472 |
| Lesvos |
0.639 |
-16.232 |
29.315 |
0.381 |
| Mykonos |
0.708
|
1.156
|
22.706
|
0.330
|
| Pylos |
0.447 |
-27.583 |
33.340 |
0.428 |
In the work of Kotroni et al. [18], the performance of another high-resolution model was evaluated with reference to six onshore observing stations based on four evaluation statistics and the results were presented both for the complete and operational datasets, referring though only to wind speed (see Table 2 of [18]). Comparing the values of the common adopted metrics, i.e. r, RMSE and MAE, for the complete datasets, it seems that the performance of the present model is better since the lower values of RMSE and MAE, and the highest one of r suggest more accurate estimates of the wind field. Let us note though, that such comparisons should be made with caution since they refer to different reference measurements and different lengths of collocated wind data.
4. Numerical Results
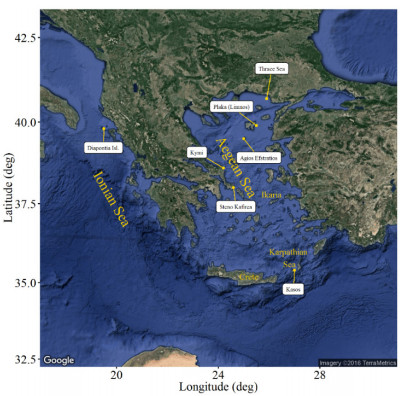
In this section, the obtained results by applying the above methodology are presented. The color gradation for the following figures, used for representing the spatial distribution of offshore wind speed and wind power density, at the different time scales was kept the same for facilitating comparison purposes while the location of the main names that are mentioned throughout the analysis are shown in Figure 8.
4.1. Wind speed and direction
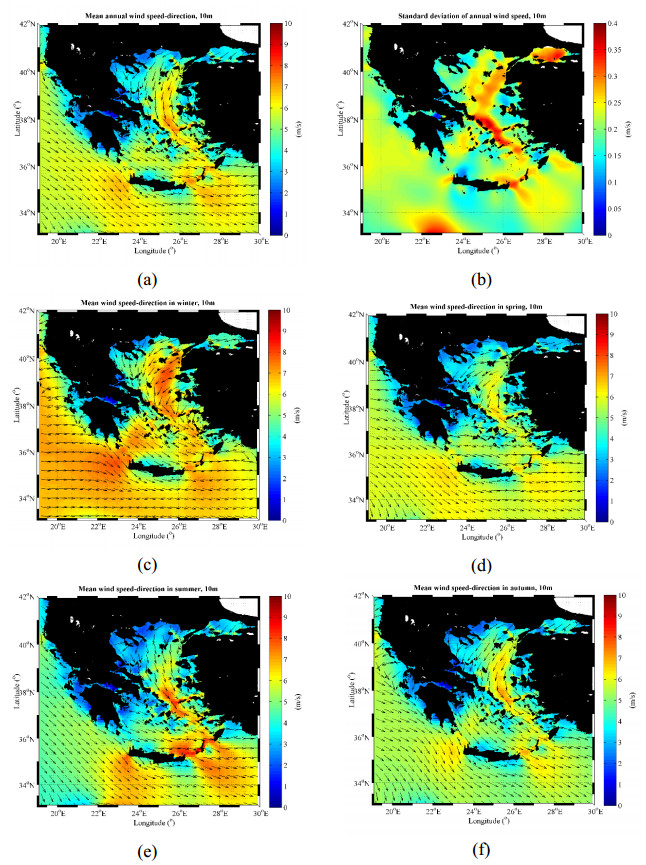
The mean annual offshore wind speed and direction (at 10 m height asl) are presented in Figure 2a. It is noticed that the winds blow in the mean from the north-eastern directions for the N. Aegean Sea, while the north-western directions are the most characteristic over the Ionian Sea. The maximum value of the mean annual wind speed (at 10 m height asl) is observed in the central Aegean Sea (37.5°N, 25.6°E) reaching the value of 7.57 m/s with associated mean wind direction 327°. A gross comparison of the Aegean and Ionian Seas reveals that the Aegean is clearly windier. In Figure 2b, the standard deviation of the mean annual wind speed is depicted. The maximum standard deviation (0.38 m/s) is observed again at the central Aegean Sea (37.8°N, 25.3°E).
The rest panels of Figure 2 exhibit the seasonal spatial distribution of wind speed and direction. Summer wind speeds are characterized by the highest values with maximum value around 9 m/s over the Karpathian Sea (35.5°N, 27°E) and mean wind direction 304°, then winter follows with maximum value up to approximately 8 m/s over the N. Aegean Sea (39.3°N, 25.4°E) with mean wind direction 50°, then autumn with maximum value up to 7.35 m/s over the central part of the Aegean Sea (37.5°N, 25.6°E) and mean wind direction 329°, and finally, spring with maximum value up to 7.03 m/s over the E. Aegean Sea (37.7°N, 26.5°E) and mean wind direction 303°. Let us note though, that regarding the entire area of interest (i.e. the Aegean and Ionian Seas) winter wind speeds are, in the mean, clearly higher than summer wind speeds.
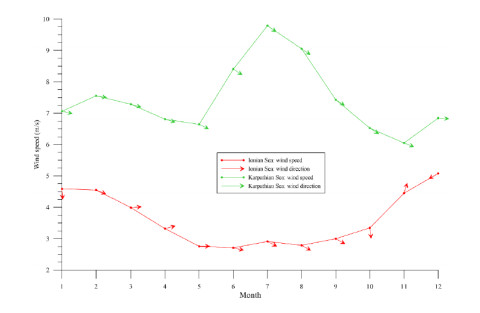
From the monthly analysis (not presented here) the overall windiest month for the Aegean Sea is February and then, December and January follow. However, the largest monthly values of wind speed are observed during July and August. Specifically, the largest mean monthly value (9.80 m/s) is observed during July over the Karpathian Sea (35.5°N, 27°E), and the second largest (9.0 m/s) during August at the same area. This distinct seasonality feature is clearly revealed when compared with the typical wind seasonality pattern observed at another location in the Ionian Sea. See, for example, Figure 3, where the seasonality curves of both mean monthly wind speed and direction for two selected locations in the Karpathian and Ionian Seas (37.5°N, 21°E) are depicted.
From Figure 3 it is evident that a remarkable stability of wind direction is present as regards the location of the Karpathian Sea. The mean monthly wind directions are totally restricted in the sector [270°, 305°], suggesting a rather unidirectional wind pattern. The most intense months as regards wind speed in this area are July, August and June. On the other hand, for the location of the Ionian Sea, the monthly wind speed curve follows the classical U shape; however, the wind direction exhibits a large fluctuation between 200° and 360°, except for December where the mean wind direction is around 60°.
From the above-mentioned results, the determinant role of the etesian winds, which blow over the Aegean Sea during June, July, August and September, is verified as regards the formation of the offshore wind climate of the area. The etesian winds shape to a large extent the corresponding wind climate and contribute significantly to the rich wind potential of the area.
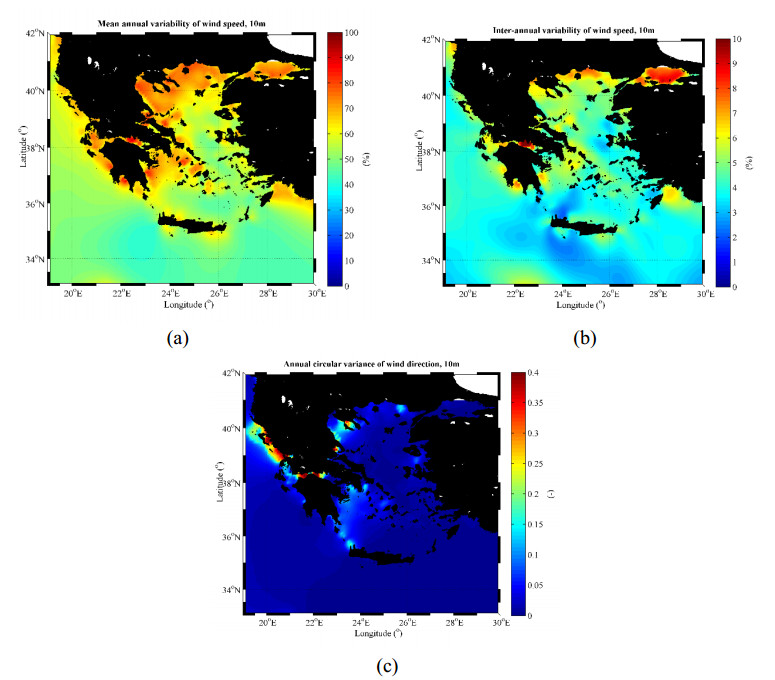
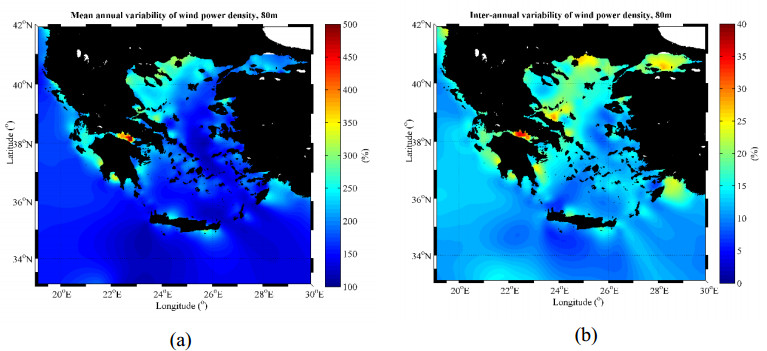
The mean annual variability (MAV) and the inter-annual variability (IAV) of wind speed are depicted in Figure 4. The highest values of MAV and IAV are observed over the southern coasts of Peloponnesus (36.8°N, 22.2°E) with values~88% and~8%, respectively. The corresponding lowest values are observed over the south-western part (34.9°N, 23.1°E) and the northern part (36.8°N, 22.2°E) of Crete Isl., with values~41% and~2%, respectively. Clearly, areas with values of MAV and IAV as low as possible, combined with high mean values of wind speed, are favorable for the development of OWFs. Finally, in Figure 4c, the spatial distribution of the circular variance of the annual wind direction is shown. For the offshore areas, the corresponding values are very low (close to zero), while for some particular coastal areas, especially in the N. Ionian Sea, the circular variance may reach values up to 0.4.
4.2. Wind power density
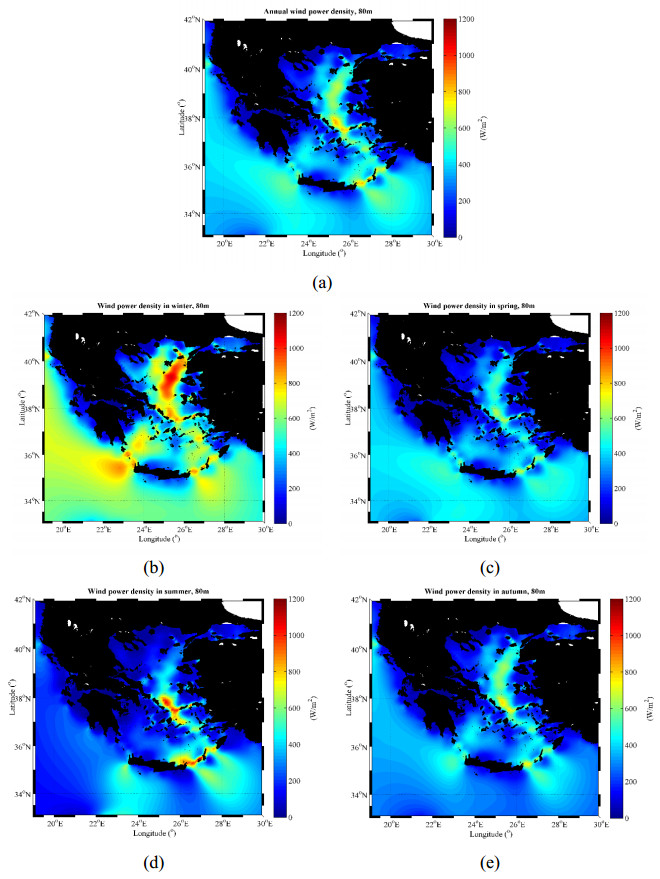
In Figure 5, the offshore wind power density is presented at 80 m height asl for the annual and seasonal scale. The overall highest value of the mean annual wind power density (~885 W/m2) is depicted in the central Aegean Sea (37.7°N, 26.5°E). The behavior of wind power density at the seasonal scale can be described as follows: the overall highest value is observed during summer reaching peak values around 1172 W/m2 over the south-eastern Aegean Sea (35.5°N, 27°E); winter follows with highest value~1090 W/m2 over the N. Aegean Sea (39.3°N, 25.4°E), then autumn with peak value~806 W/m2 over the central part of the Aegean Sea, and finally, spring with peak value~773 W/m2 over the E. Aegean Sea (37.7°N, 26.5°E).
In the Ionian Sea, the wind power density reaches values up to~584 W/m2 over the northern part (40.2°N, 19.3°E) and~490 W/m2 over the southern part (35.5°N, 22°E). During winter, the corresponding maximum wind power density values are~790 W/m2 and~780 W/m2. Overall, the lowest values of wind power density in the Ionian Sea are observed during summer.
The spatial distribution of offshore wind power potential resembles qualitatively the results of Kotroni et al. [18] (see Figure 3 of [18]), stressing that the Aegean Sea is clearly more energetic than the Ionian Sea with values higher than 600 W/m2 at 50 m height asl. The same holds true for the results of a higher resolution atmospheric model presented in Emmanouil et al. [19] (see Figure 5 of [19]), where offshore wind power potential is presented at 10 m height asl.
MAV and IAV of wind power density are presented in Figure 6. For MAV, the highest value (~375%) is depicted at the same location with the corresponding measure for wind speed (36.8°N, 22.2°E) while the lowest one (~114%) is very close (spatially) with the corresponding location for wind speed (33°N, 23.1°E). The highest value of IAV (~30%) is located over the W. Aegean Sea (38.8°N, 23.8°E) and the lowest one (~6%) over the northern part of Crete Isl. (34.8°N, 23.7°E).
4.3. Equiprobable contours of wind speed at 80 m above sea level
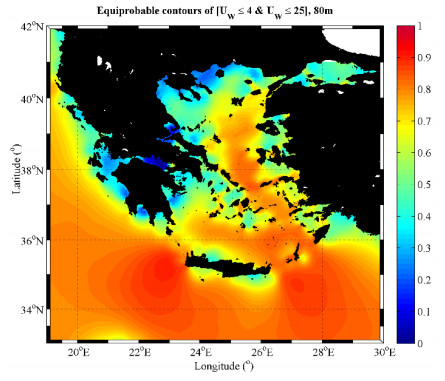
In Figure 7, the spatial distribution of the frequency of the event [4 m/s ≤ U80 ≤ 25 m/s] is depicted. As can be seen in this figure extended areas of the central Aegean Sea, the S. Karpathian Sea and the area at the southwestern part of Crete Isl., are characterized by frequencies of occurrences close to 0.9. The corresponding seasonal features (not presented here) suggest that the persistence of wind speeds within the wind turbine operational limits in the southern part of the Aegean Sea takes its maximum values during summer. On the other hand, autumn seems to be the period of the year with the smallest persistence of the examined wind speeds. For the Ionian Sea, the highest persistence is observed at the northern and offshore southern part.
4.4. Wind climate and wind power density characteristics for specific locations in the Aegean and Ionian Seas
In this section, the main statistical characteristics of wind climate and wind power density are provided for seven locations where OWF development is at the concept/planning phase. Six of these locations cover the entire Aegean Sea and one is located in the N. Ionian Sea; see also Figure 8. In Table 6, the mean annual wind speed (U80), the corresponding standard deviation (sU80) along with MAV and IAV, and the annual mean wind power density (ˉP80) at 80 m height asl are provided. As is seen in this table, the location in Kasos (Karpathian Sea) is the most favorable as regards wind resource availability; the mean annual wind speed is 8.03 m/s, the values of MAV (49.83%) and IAV (4.09%) are the lowest amongst the examined locations and the available wind potential is 570.9 W/m2. The second best location is Steno Kafirea with an annual wind speed of 7.51 m/s, a rather high value of IAV (5.51%) while the available wind potential is 545.6 W/m2. The lowest wind availability is exhibited at the location in the Thrace Sea (with mean annual wind speed at 3.33 m/s); the same location exhibits also the highest value of MAV (72.55%) and IAV (6.09%). Overall, it seems that the available wind resource characteristics at Kasos location are superior rendering the location favorable for a future potential OWF development.
Table 6. Wind climate and wind power density characteristics of selected locations in the Aegean and Ionian Seas
| Location name |
Latitude (deg) |
Longitude (deg) |
ˉUW,80−sW,80 (m/s) |
MAV (%) |
IAV (%) |
ˉP80 (W/m2) |
| Agios Efstratios |
39.5 |
25.0 |
6.941-0.336 |
59.75 |
4.84 |
468.2 |
| Diapontia Isl. |
39.8 |
19.5 |
5.089-0.222 |
62.09 |
4.36 |
191.4 |
| Kymi |
38.6 |
24.2 |
6.620-0.319 |
58.77 |
4.81 |
383.4 |
| Kasos |
35.4 |
27.0 |
8.029-0.328 |
49.83 |
4.09 |
570.9 |
| Thrace Sea |
40.7 |
25.9 |
3.339-0.203 |
72.55 |
6.09 |
71.7 |
| Plaka (Limnos) |
39.9 |
25.5 |
6.692-0.319 |
61.38 |
4.77 |
430.3 |
| Steno Kafirea |
38.0 |
24.6 |
7.513-0.414 |
57.34 |
5.51 |
545.6 |
It is important to remind that except for wind resource availability other important criteria should be also considered such as bottom depth, distance to shore and to the power grid, type of sediments, distance to ports, etc. On the other hand, socio-economic and environmental considerations may alter significantly the final decisions as regards the feasibility of OWFs in any location. Finally, since the results presented in this work are based on the analysis of hindcast data, they are always subject to numerical model uncertainties as is already mentioned in Section 2.
5. Conclusions
In this study, the offshore wind power potential of the Aegean and Ionian Seas is analytically examined and presented in order to rationalize and facilitate the preliminary identification of promising candidate sites for future offshore wind farm development. Since offshore in situ measurements are scarce and cannot cover the spatial scale of the examined sea areas, the analysis performed was based on a 15-year hindcast of wind data spanning from 1995 to 2009. The hindcast data was produced by a high-resolution atmospheric downscaling of the ECWMF reanalysis, exhibiting fine scale features in the coastal zone and allowing the analysis even close to the land/sea boundary. An analytic validation of the model results with respect to offshore in situ measurements obtained from four oceanographic buoys was implemented, confirming its suitability for the purpose of this study. Regarding the Greek Seas, validation of wind direction, apart from wind speed, is presented here for the first time as far as the authors are aware of. The validation results suggest that the model performance is overall good: as regards wind speed, the correlation coefficient ranges between 0.874 and 0.796, the absolute BIAS between 0.455 m/s and 1.329 m/s and RMSE between 1.922 m/s and 2.563 m/s; as regards wind direction, the circular-circular correlation coefficient ranges between 0.708 and 0.447, the absolute BIAS between 1.156 deg and 27.583 deg and the circular absolute error between 22.706 deg and 38.247 deg.
From the statistical analysis of offshore wind speed and direction (at 10 m height asl) it can be highlighted that the etesian winds are the most distinct wind feature for the Aegean Sea, blowing mainly during summer, when the wind conditions of the rest Mediterranean Sea are considerably calmer while, simultaneously, energy demand tends to be higher due to tourism and recreation activities. Moreover, variability measures referring to wind speed, wind direction and wind power potential as well as persistence statistics for wind speed that are important for the offshore wind energy community are provided. Overall, it seems that the wind potential (at 80 m height asl) mainly in the Aegean Sea and, secondarily, in the Ionian Sea, is adequately exploitable at specific locations; offshore deep water locations, especially in the Aegean Sea, are characterized by high values of offshore wind resource (mean annual wind power density up to 885 W/m2 in the central Aegean). The overall highest value is observed during summer reaching peak values around 1172 W/m2 over the south-eastern Aegean Sea. In addition, the persistence of wind speeds within the wind turbine operational limits in the Aegean Sea is very suitable for offshore wind energy projects since extended areas of the Aegean Sea are characterized by frequencies of occurrences close to 0.9.
However, some of the examined shallow-water locations (see Section 4.4) do not seem to meet the required standards for the efficient exploitation of offshore wind resource. On the other hand, expansion of the offshore wind energy industry in deep water areas requires a significant progress towards commercialization of floating wind turbines and reduction of costs.
The presented results are expected to give insight to the offshore wind energy sector as regards wind energy potential estimates and variability measures in the Aegean and Ionian Seas while such analysis can form the basis of a preliminary assessment study for the potential exploitation of offshore wind in the future. Furthermore, wave energy assessment studies and meteorological applications can be benefited from relevant analyses. Let us though point out that the local in-depth assessment of any candidate area is the only robust means to provide final conclusions as regards the suitability of the area from all considered frameworks (i.e. technical/engineering, socio-economic and environmental aspects). For example, a detailed wind resource assessment, requires at least 2-year in situ wind measurements for the most accurate estimation of the wind power potential in a candidate area for OWF development.
At the end of the day, it remains to be seen whether the new law 4414/2016 for RES will provide the impetus needed for the development of the offshore wind energy industry in Greece.
Acknowledgments
This research has been funded from the Greek General Secretariat for Research and Technology and the European Regional Development Fund under Grant Agreement no. 09SYN-32-598 for the project "National programme for the utilization of offshore wind potential in the Aegean Sea: preparatory actions" (AVRA).
Conflict of Interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: