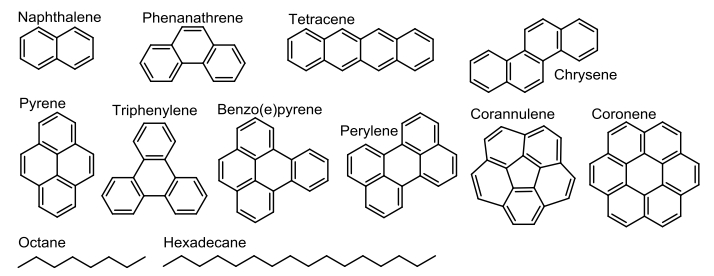
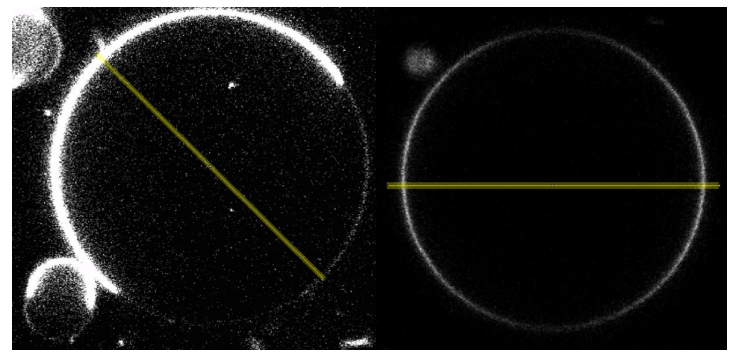
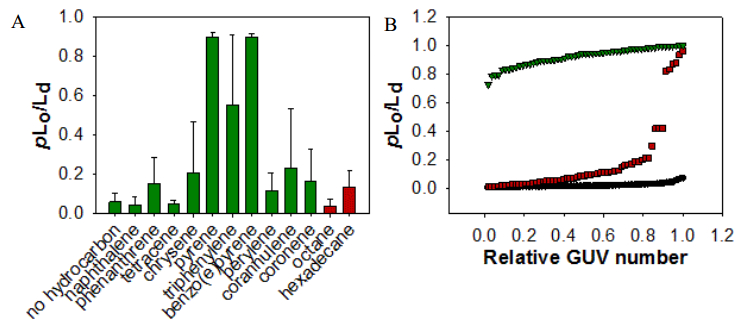
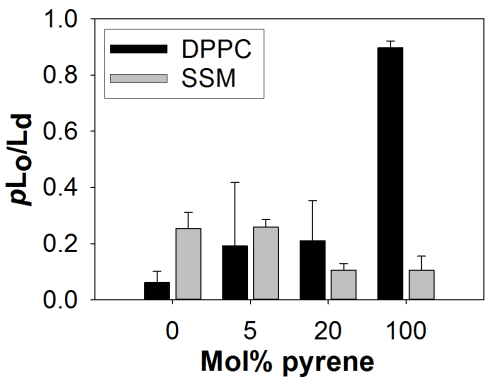
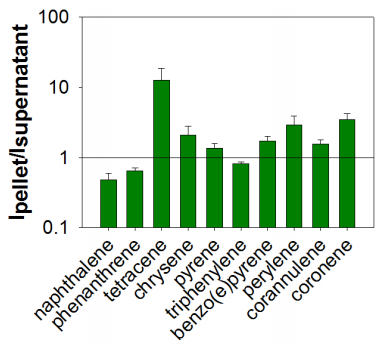
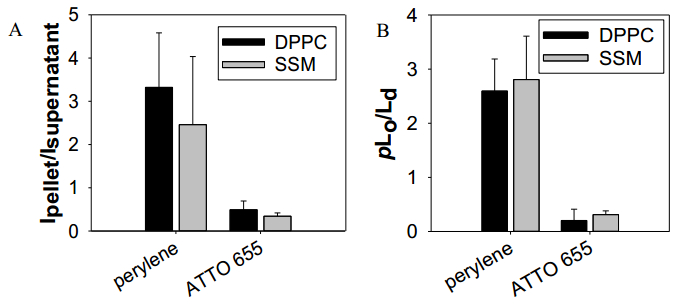
Hydrophobic hydrocarbons are absorbed by cell membranes. The effects of hydrocarbons on biological membranes have been studied extensively, but less is known how these compounds affect lipid phase separation. Here, we show that pyrene and pyrene-like hydrocarbons can dissipate lipid domains in phase separating giant unilamellar vesicles at room temperature. In contrast, related aromatic compounds left the phase separation intact, even at high concentration. We hypothesize that this behavior is because pyrene and related compounds lack preference for either the liquid-ordered (Lo) or liquid-disordered (Ld) phase, while larger molecules prefer Lo, and smaller, less hydrophobic molecules prefer Ld. In addition, our data suggest that localization in the bilayer (depth) and the shape of the molecules might contribute to the effects of the aromatic compounds. Localization and shape of pyrene and related compounds are similar to cholesterol and therefore these molecules could behave as such.
1.
Introduction and outline
The Pell and Pell-Lucas polynomials have unique values and applications in various branches of mathematics [1,2,3,4]. They are defined as follows [5]:
● Recurrence relations
● Boundary conditions
● Binet formulae
and
where α=α(x)=x+√x2+1 and β=β(x)=x−√x2+1 are the roots of an associated quadratic equation y2−2xy−1=0.
● Special values
where Pn,Qn,Fn and Ln are the Pell, Pell-Lucas, Fibonacci, and Lucas numbers, respectively.
There are several kinds of Chebyshev polynomials, which have extensive research and application value in mathematics, engineering, and physics [6,7]. In particular, the first kind and the second kind polynomials are defined as follows [5,8,9]:
● Recurrence relations
● Boundary conditions
● Binet formulae
and
where η=η(x)=x+√x2−1 and γ=γ(x)=x−√x2−1 are zeros of the quadratic characteristic equation y2−2xy+1=0.
The binomial coefficients are hot topics in combinatorial mathematics. Recently, Othsuka [10] conjectured the following identities about Fibonacci and Lucas numbers:
and
Inspired by Eqs (1.5) and (1.6), we shall investigate, in this paper, the following two sums:
where δ∈N0 is a fixed integer, ⌊⋅⌋ and ⌈⋅⌉ are the floor and the ceiling functions [11], respectively. Φn(x) is assigned to one of the four polynomials below:
Then we will obtain several binomial sums for four types of polynomials involving the floor and ceiling functions.
The rest of the paper will be organized as follows: In the next four sections, we present summation formulae for the four types of polynomials, respectively. Considering the special values of the Pell and Pell-Lucas polynomials, in Section 6, we provide several identities regarding the Fibonacci-Lucas numbers. Finally, we provide a summary and further observation.
It is worth noting that certain binomial coefficients identities and theorems play significant roles in our derivation:
They will be utilized in the proof processes for each type of polynomial. Compared with the two identities of Othsuka [10], our results can not only derive them when x takes special values but also obtain some conclusions about Pn, Qn, Fn, and Ln that have similarly elegant forms.
2.
The Pell polynomials Pn(x)
In this section, we will explore the sums when Φn(x) is the Pell polynomials Pn(x), that is, the following two sums:
The main results are enunciated in the following theorem.
Theorem 1.
Proof of (i).
For the first summation (2.1), we can evaluate it in the following manner:
By recalling equation (1.7), we can rewrite it as follows:
Then, by making use of the Binet formula of Pn(x) (1.1), it is not hard to make the following calculation:
Finally, using the binomial Theorem (1.9), we can reformulate the final expression below
where the product of α and β satisfies the relationship αβ=−1.
This completes the proof of (i). □
Proof of (ii).
Analogous to the derivation of (2.3), the second sum (2.2) can be transformed into
By making use of Binet's formula of Pn(x) (1.1), we obtain
In conjunction with (1.10),
the last expression can be rewritten as
This completes the proof of (ii). □
Taking x=12 and x=1, the polynomials Pn(x) correspond to the Fibonacci numbers Fn and the Pell numbers Pn. Considering the Binet formulae of Fn, Pn, and Qn, we derive the following corollaries from the two equations in Theorem 1.
Corollary 2.
Corollary 3.
When δ=0 in Corollary 2(ii), we obtain the identity (1.5) proposed by Othsuka [10].
We need to pay attention that there are some cases where Pn,Qn, and Fn have negative subscripts in corollaries 2 and 3. For example, when δ=0, Pδ−1=P−1,Qδ−1=Q−1. Here we point that when Pn,Qn,Fn, and Ln have negative subscripts, they can be extended through recursive relations below [12,13]: (n≥0)
3.
The Pell-Lucas polynomials Qn(x)
In this section, we will explore the sums when Φn(x) is the Pell-Lucas polynomial Qn(x), that is, the following two sums:
The main results are enunciated in the following theorem.
Theorem 4.
Proof of (i).
For the first summation (3.1), referring to (2.3), we can rewrite it as
Then, by making use of the Binet formula of Qn(x) (1.2), we obtain
Finally, applying the identity (1.9), the last expression can be rewritten as
This completes the proof of (i). □
Proof of (ii).
Similar to (2.3), summation (3.2) can be transformed into the following form:
By making use of Binet's formula of Qn(x) (1.2), it is not hard to make the following calculation:
Applying the identity (1.10), the last expression can be rewritten as
This completes the proof of (ii). □
Taking x=12,x=1, respectively, and considering the Binet formulae of Fn, Pn, and Qn, we derive the following corollaries from the two equations in Theorem 4.
Corollary 5.
Corollary 6.
When δ=0 in Corollary 3(ii), it's just the identities (1.6) proposed by Othsuka [10].
4.
The first kind of Chebyshev polynomials Tn(x)
In this section, we will explore the sums when Φn(x) is the first kind of Chebyshev polynomials Tn(x), that is, the following two sums:
The main results are enunciated in the following theorem.
Theorem 7.
Proof of (i).
For the first summation (4.1), referring to (2.3), we have
Then, by making use of the Binet formula of Tn(x) (1.3), there has
Finally, applying (1.9), the last expression can be rewritten as
where the product of η and γ satisfies the relationship ηγ=1.
This completes the proof of (i).
Proof of (ii).
Analogous to the derivation of (2.3), the second sum (4.2) can be transformed into
By making use of Binet's formula of Tn(x) (1.3), we obtain
Applying (1.10), the last expression can be rewritten as
This completes the proof of (ii).
When x=1, the first kind of Chebyshev polynomials Tn(1) reduce to the constant sequence {1}. Thus, Theorem 7 reduces to the familiar binomial identity
5.
The second kind of Chebyshev polynomials Un(x)
In this section, we will explore the sums when Φn(x) is the second kind of Chebyshev polynomials Un(x), that is, the following two sums:
The main results are enunciated in the following theorem.
Theorem 8.
Proof of (i).
Similarly to (2.3), we can rewrite (5.1) as
Then, by making use of the Binet formula of Un(x) (1.4), it is not hard to make the following calculation:
Finally, applying the identity (1.9), the last expression can be rewritten as
This completes the proof of (i). □
Proof of (ii).
Similar to (2.3), summation (5.2) can be transformed into the following form:
By making use of Binet's formula of Un(x) (1.4), there has
Applying the identity (1.10), the last expression can be rewritten as
This completes the proof of (ii). □
Up to now, for the above four types of polynomials, we found that the results obtained from their summation formulae are not straightforward. As we all know, the extended Fibonacci-Lucas numbers play important roles in combinatorial mathematics [2,4]. Therefore, we carried out similar calculations for the extended Fibonacci-Lucas numbers. Surprisingly, we obtained relatively concise results.
6.
The extended Fibonacci-Lucas numbers Gn
For two complex numbers a, b, and a natural number n∈N0, define the following extended Fibonacci-Lucas numbers {Gn(a,b)}n≥0 by the recurrence relation [14]:
with the initial values being given by G0(a,b)=a and G1(a,b)=b.
By means of the usual series manipulation [5], it is not hard to show the following explicit formula:
where
as well as
The well-known Fibonacci and Lucas numbers are the following particular cases: Gn(0,1)=Fn and G_n(2, 1) = L_n . For the sake of brevity, they will be shortened as G_n = G_n(a, b) .
In this section, we consider the sums that \Phi_{n} is G_{n} , that is, the following two sums:
In fact, we can easily derive the results of these two summations using a method similar to that in the previous sections. Consequently, we will omit the derivation process and present the results directly in the following theorems.
Theorem 9.
Now, we consider the recurrence relation of Fibonacci numbers and the next identity[13]
for n\geq1 . It is easy for us to deduce the identity
which will be used to deduce the identities of Corollaries 10 and 11.
Taking a = 0, \; b = 1 , and a = 2, \; b = 1 in Theorem 9, respectively, we get the following corollaries.
Corollary 10.
When \delta = 0 in the last corollary, the identities reduced to the results of (1.5) and (1.6) proposed by Othsuka [10].
Corollary 11.
7.
Conclusions and further observations
In this paper, we successfully generalized the two identities conjectured by Othsuka [10] by introducing four types of polynomials. Additionally, we also obtained some conclusions about the Pell numbers P_{n} , the Pell-Lucas numbers Q_{n} , and the extended Fibonacci-Lucas numbers G_{n} that have similarly elegant forms when x = 1 . Interested readers are encouraged to explore the results of similar sums of other polynomials by the method used in this paper.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
This research was funded by the National Natural Science foundation of China (No.12426531, 12026245).
Conflict of interest
The authors declare there is no conflicts of interest.













 DownLoad:
DownLoad: