An insight into the biomaterials used in craniofacial tissue engineering inclusive of regenerative dentistry

1.   Introduction

The non-stationary Stokes and Navier-Stokes equations are the cornerstone of fluid mechanics and have been widely applied in numerous engineering fields. The non-stationary Stokes equations serve as an abridged form of the Navier-Stokes equations, and their numerical solutions are indispensable for fluid dynamics design and analysis in engineering environments.

The finite volume element method (FVEM) is a powerful numerical method widely employed for tackling partial differential equations (PDEs) encountered in fluid dynamics, heat conduction, and various other disciplines dealing with continuous materials. Its capacity to preserve local conservation laws, adapt to complex geometries, and provide accurate and efficient results has earned it popularity among researchers and engineers. Additionally known as the finite volume method ^{[1, 2]}, the control volume method, the mixed co-volume method ^{[3, 4]}, the box method ^{[5, 6]}, or the first-order generalized difference method ^[7], the FVEM is also recognized as a variant of the control volume finite element (CVFE) method without overlapping control volumes ^{[8, 9, 10]}. Essentially, the FVEM can be regarded as a numerical solution method that bridges the finite element method (FEM) and the finite difference method (FDM). In the past two decades, significant progress has been made in the application of FVEMs to solving the Stokes and Navier-Stokes equations. The rapid development of FVEMs has resulted in a wealth of research achievements, especially with a significant focus on theoretical aspects such as stability and convergence, as described in ^[11]. However, there is a significant gap in theoretical analysis compared to the extensive theoretical research of FEMs. This paper will theoretically discuss the stability and error estimation of a fully discrete spatial-temporal FVEM scheme for solving non-stationary incompressible Stokes equations.

Currently, the research focus on solving non-stationary Stokes equations using FVEMs is mainly on the adoption of spatially low-order finite volume techniques. These techniques approximate the velocity in the Stokes equations using piecewise linear polynomial functions. This preference arises from the lower computational complexity of low-order methods, which is beneficial for theoretical research, easy to implement, and thus enhances their attractiveness to researchers and professionals. The paper ^[12] proposed a semi-discrete FVEM scheme for the spatial discretization of the non-stationary Stokes equations, utilizing the $\mathcal{P}_1-\mathcal{P}_0$ macro-element. By employing a post-processing technique, this method enhances the convergence order for the $\mathbf{H^1}$ norm of the velocity and improves the $\mathrm{L}^2$ norm accuracy of the pressure. The paper ^[13] established the optimal estimates for a low-order spatial-temporal fully discrete method for the non-stationary Navier-Stokes equations. It uses a semi-implicit Euler method for time and a special finite volume scheme for space, with the $\mathcal{P}_1-\mathcal{P}_0$ trial function pair for spatial discretization and macro elements for stability. A low-order semi-discrete scheme for non-stationary Navier-Stokes equations was presented in ^[14], followed by a new fully discrete FVEM scheme using macroelements. Error estimates for the FVEM solutions were obtained via standard FEM techniques. Utilizing the lowest equal-order finite element space pairs, based on two local Gauss integrals, the paper ^[15] constructed a stabilized FVEM scheme for the transient Stokes equations. In this approach, both the velocity and pressure were approximated with piecewise linear polynomial functions, and this paper achieved the optimal error estimates in the $\mathbf{H^1}$ norm for the velocity and in the $\mathrm{L}^2$ norm for the pressure. In ^[16], a stabilized FVEM scheme for transient Navier-Stokes equations was presented, which maintains conservation and yields optimal velocity and pressure estimates through error analysis derived from the FVEM scheme. This scheme offers convergence similar to the stabilized linear FEM under the same solution regularity and source term conditions. For a more in-depth understanding of solving incompressible flow problems using the FVEM, readers can refer to the latest relevant research literature on FVEM studies.

According to our current understanding, there is a clear lack of research literature regarding the application of spatially high-order FVEMs to study non-stationary Stokes or Navier-Stokes equations. In this work, we propose a full-discrete scheme where the spatial discretization employs quadratic FVEM for velocity and discontinuous piecewise linear elements for pressure, coupled with a first-order temporal discretization. As widely recognized, the quadratic FVEM for velocity approximation offers distinct advantages over lower-order spatial methods, such as offering more precise discrete velocity solutions, especially when dealing with smooth situations or high-precision requirements. Compared to linear methods, the quadratic methods also converge faster to the actual solution, which is very helpful for dealing with complex geometries or boundary conditions. Consequently, developing a fully discrete FVEM that employs quadratic polynomials to approximate velocity in the non-stationary Stokes equations, and performing theoretical analysis on its stability and error estimates, holds significant theoretical importance and practical utility.

As is well known, the continuity equation for incompressible fluids is generally considered to embody the law of mass conservation for fluid velocities. The Hood-Taylor finite element space pairs are extensively applied in the numerical solution of the Stokes equations, and their theoretical foundations have been thoroughly investigated in numerous scholarly works ^{[17, 18]}. Nonetheless, the Hood-Taylor finite element space pairs are typically based on continuous pressure spaces, which can only weakly ensure the mass conservation of discrete velocity solutions on the whole domain. In contrast, the use of discontinuous pressure spaces can lead to local mass conservation for discrete velocity solutions, as they could ensure theoretically that the average of the divergence is zero within each individual element. To guarantee the local mass conservation of the discrete velocity solution, many research efforts have adopted a modification of the Hood-Taylor finite element space pairs as the approximation spaces for the velocity and pressure components in the Stokes equations. A distinguishing feature of this modification is the addition of piecewise constant functions in the continuous pressure space. This idea was first introduced in ^[19], and the stability of these methods has been demonstrated in subsequent studies by ^{[20, 21]}. The LC finite element space pair ^{[22, 23]} happens to be a modification of the lowest-order Hood-Taylor finite element space pair, and it was originally designed to cater to the FEMs for solving stationary Stokes problems. This paper will employ the LC element to approximate the velocity and pressure in the Stokes equations so that the proposed FVEM scheme would be classified as a pressure-robust method ^[24]. This selection constitutes the major distinction between the current work and the paper ^[25], who employed the lowest-order classical Hood-Taylor finite element space pairs to deal with the velocity-pressure pairs of the Stokes problem. Therefore, these two FVEM schemes exhibit significant differences in their stability analysis. Specifically, for the Taylor-Hood elements, the equivalence of bilinear forms derived from gradient and divergence operators is generally valid in any dual partition of the test space with respect to the velocity, while for the LC elements, equivalence requires careful design of the dual partition of the test space with respect to the velocity to ensure the stability of the FVEM scheme. It is observed that in the FVEM scheme using the LC element, the velocity is approximated with a continuous piecewise quadratic polynomial, while the pressure is approximated using a discontinuous piecewise linear polynomial on the same meshes. This implies that the divergence of the discrete velocity solutions lies within the discontinuous pressure space, and thus it can be inferred that the integral average of the divergence of the discrete velocity solution in the FVEM over each element will vanish. This property inherently guarantees the local mass conservation property of the discrete velocity solutions, preserving the original physical characteristics of incompressible fluid flows ^{[26, 27]}. Thus, the proposed FVEM scheme is demonstrated to be a stable and local mass conservation numerical method on the barycenter-refined triangular meshes. This is one of the primary contributions of this paper.

We note that, despite paper ^[28] employing the discontinuous finite element spaces as the trial spaces for the FVEM in solving the Stokes equations with respect to velocity and pressure, the stability and convergence analysis relies on an interior penalty term. In spite of the analysis in paper ^[29], which considered the mixed FVEM for the Stokes problem on triangular meshes, utilizing the MINI element for the velocity-pressure trial spaces and piecewise constant functions for the test spaces, the proposed scheme is classified as a low-order numerical method.

The mapping, which connects the trial space of FVEMs with their test spaces, plays a crucial role in the stability analysis of the FVEMs. Many studies are now focused on introducing novel mappings to check the stability of these methods. To investigate the stability and error estimates for the space of the fully discrete FVEM scheme, we employ the one-to-many mapping identified in the literatures ^{[30, 31, 32]}. This technique results in the FVEM scheme, when equipped with this mapping, being equivalent to the conventional FVEM scheme that does not utilize such a mapping. In this paper, we first propose a semi-discrete first-order temporal scheme for the non-stationary Stokes equations, and then derive a fully discrete FVEM scheme by starting directly from the semi-discrete temporal scheme, utilizing the FVEM based on dual partitions for spatial discretization. The reason we are compelled to develop the semi-discrete scheme for time before achieving the fully discrete spatial-temporal FVEM scheme is due to the fact that the introduced one-to-many mapping differs from the conventional one-to-one mapping and it does not possess the self-adjoint property with respect to the $\mathrm{L}^2$ inner product. By introducing the one-to-many mapping and utilizing classical finite element analysis techniques, the theoretical analysis of the existence, uniqueness, and error estimation of the fully discrete FVEM solution has been derived in this paper.

The plan of this article is as follows. In the next section, we will introduce the non-stationary Stokes equations and establish their variational forms. Then, in Section 3, a semi-discrete scheme for the non-stationary Stokes equations with respect to time is provided. Section 4 proposes the fully discrete FVEM scheme for the non-stationary Stokes equations and proves its stability. Section 5 gives the optimal order estimate of the scheme. Finally, Section 6 provides numerical experiments to verify the obtained theoretical results, and the last section gives the conclusion of this paper.

2.   Variational forms for the non-stationary Stokes equations

In this section, we will discuss the non-stationary Stokes equations and present their classical variational formulations.

In the context of a bounded and connected domain $\Omega \subset\mathbb{R}^{2}$, characterized by a boundary $\partial\Omega$ that is Lipschitz continuous, we consider the following incompressible, time-dependent Stokes equations, which are subject to homogeneous boundary conditions. We seek to determine the velocity ${\bf{u}}$ and the pressure $p$ for all $T > 0$ such that

Here, ${\bf{u}}(\mathbf{x}, t) = ({u}_1(\mathbf{x}, t), {u}_2(\mathbf{x}, t))$ denotes the velocity vector of the fluid, $p(\mathbf{x}, t)$ represents the pressure, $T$ is the duration of the time interval, ${\bf{f}}(\mathbf{x}, t)$ is the prescribed body force, ${\bf{u}}_0(\mathbf{x})$ is the initial velocity distribution, $\mu$ is the coefficient of viscosity, and ${\mathbf{u}}_t = \frac{\partial {\bf{u}}}{\partial t}$ signifies the partial derivative of the velocity with respect to time.

We now present the variational form for the problem (2.1). For any subdomain $\mathcal{D}\subset\Omega$ and any integer $r\geqslant0$, we use $(\cdot, \cdot)_{\mathcal{D}}$ to represent the $\mathrm{L}^2(\mathcal{D})$ inner product, $\|\cdot\|_{r, \mathcal{D}}$ for the $\mathrm{H}^{r}(\mathcal{D})$ norm, and $|\cdot|_{r, \mathcal{D}}$ for the $\mathrm{H}^{r}(\mathcal{D})$ semi-norm. When $\mathcal{D} = \Omega$, the subscript $\mathcal{D}$ is omitted for clarity. We define ${\mathrm{L}}_0^2(\Omega)$ as the set of functions $p$ in $\mathrm{L}^2(\Omega)$ with the property that $\int_\Omega{p {\mathrm{d}}\mathbf{x} = 0}$, ${\mathrm{H}}_0^1(\Omega)$ as the set of functions $v$ in $\mathrm{H}^1(\Omega)$ that vanish on the boundary $\partial\Omega$, and ${\bf{H}}^\mathbf{r}(\Omega)$ as the square of the Sobolev space $\mathrm{H}^r(\Omega)$. The standard variational form for addressing the problem (2.1) is given by: Find $\left(\mathbf{u}(t), p(t)\right)\in\left(\mathbf{H_0^1}(\Omega), {\mathrm{L}_0^2}(\Omega)\right)$ for all $t\in (0, T]$ such that

where $a\left({{\mathbf{u, v}}}\right) = \mu \left({\nabla{\mathbf{u}}, \nabla{\mathbf{v}}}\right)$ and $b({\mathbf{u}}, p) = \left(p, \mathrm{div} \mathbf{u}\right)$. It is a well-established fact that the problem (2.1) is valid for sufficiently smooth solutions $\mathbf{u}$ and $p$ if and only if the variational form (2.2) holds for almost every $t\in (0, T]$.

In this paper, we will employ $C$ and $c$ as arbitrary positive constants, whose values are determined by the data $(\mu, T, \mathbf{u}_0, \Omega)$ and may vary in different situations. We assume that the initial velocity ${\mathbf{u}}_0(\mathbf{x})$ and the body force $\mathbf{f}(\mathbf{x}, t)$ in (2.1) are sufficiently smooth and compatible to fulfill the following conditions:

Furthermore, we ensure that, as in ^{[33, 34]}, for any arbitrary $T > 0$, there exists a unique solution pair $(\mathbf{u}, p)$ for the problem (2.1) that has the following regularity requirements:

with $\tau(t) = \min \{1, t\}$. These estimates (2.3) and (2.4) will serve as the foundation for the theoretical analysis presented in the subsequent sections.

We remark that the bilinear form $a({\cdot}, {\cdot})$ possesses the following properties:

for all $\mathbf{{u}}, {\mathbf{v}}\in {\mathbf{H_0^1}}(\Omega)$. Additionally, the bilinear form $b({\cdot}, {\cdot})$ satisfies the $\inf-\sup$ stability condition ^[35]

For any $\mathbf{u}\in{\mathbf{H_{0}^1}}(\Omega)$, the Poincaré inequality implies the following inequalities:

These inequalities will be recurrently employed in the subsequent discussion.

3.   Semi-discrete schemes about time

In this section, we will present a semi-discrete variational scheme about time for problem (2.1), and then examine its stability properties and derive error estimates.

We next introduce the semi-discrete temporal scheme. Given a positive integer $M \geqslant 1$, we define the time increment as ${\Delta t} = \frac{T}{M}$, and denote ${\mathbf{u}}^n$ as the semi-discrete approximation of ${\mathbf{u}}$ at the time point $t_n = n{\Delta t}$. The approximation of the temporal derivative ${\mathbf{u}}_t$ is given by

where $n\in\mathbb{Z}_M$ and $\mathbb{Z}_M: = \{1, 2, \ldots, M\}$. We define $\mathbf{f}^n = \mathbf{f}(\mathbf{x}, t_n)$, which represents the value of $\mathbf{f}(\mathbf{x}, t)$ at the time $t_n$ due to the smoothness of the body force $\mathbf{f}$. The semi-discrete temporal scheme reads as follows: For any $t \in (0, T]$, find $(\mathbf{u}^n, p^n) \in ({\mathbf{H_{0}^1}}(\Omega), \mathrm{L}_0^2(\Omega))$, $n\in\mathbb{Z}_M$, such that

The following theorem holds for the semi-discrete scheme (3.1). To clarify our main points, the proof has been moved to Appendix A.

Theorem 1. If ${\mathbf{u}}_0\in {\mathbf{H_{0}^1}}(\Omega)$ and $\mathbf{f}\in {\mathbf L^2}(\Omega)$ for any $t\in (0, T]$, then the semi-discrete scheme (3.1) has a unique sequence of solutions $(\mathbf{u}^n, p^n)\in\left({\mathbf{H_{0}^1}}(\Omega), \mathrm{L}_0^2(\Omega)\right)$, $n\in\mathbb{Z}_M$, which satisfies the following stability conditions:

with $C$ being a constant that is independent of the parameter ${\Delta t}$.

This theorem indicates the temporal stability of the proposed semi-discrete scheme (3.1).

Next we examine the error estimates for the semi-discrete scheme presented in (3.1). For any time point $t\in(0, T]$, Taylor's theorem provides the following expansion:

which combining the time step ${\Delta t} = t_n - t_{n-1}$, where $n\in \mathbb{Z}_M$, derives the following expression for ${\mathbf{u}}_t(t_n)$:

By employing similar methods as in ^[34], it can be proven that the solution to the scheme (3.1) satisfies the following theorem. To clarify our main points, the proof has been moved to Appendix B.

Theorem 2. Let $(\mathbf{u}, p)\in \left({\mathbf{H_{0}^1}}(\Omega), \mathrm{L}_0^2(\Omega)\right)$ denote the solution pair for the problem (2.1) at any time $t\in (0, T]$, and the solution pair $(\mathbf{u}^n, p^n)\in \left({\mathbf{H_{0}^1}}(\Omega), \mathrm{L}_0^2(\Omega)\right)$ results from the semi-discrete scheme (3.1) for all $n\in\mathbb{Z}_M$. If $\mathbf{u}_0\in {\mathbf{H_{0}^1}}(\Omega)$ and $\mathbf{f}\in {\mathbf L^2}(\Omega)$ for every $t\in (0, T]$, then the following error estimates are valid:

where $C$ represents a constant that is independent of the discretization parameter ${\Delta t}$.

The theorem provides an error estimation of the convergence order of the semi-discrete scheme (3.1) about time, and the theoretical result of this theorem may not be the optimal convergence order about time. The primary focus of this paper is to analyze the stability and convergence order of the FVEM scheme using the LC element in the spatial discretization for solving non-stationary Stokes equations.

4.   Fully discrete FVEM schemes

In this section, we will present a fully discrete spatial-temporal FVEM scheme for the time-dependent Stokes problem as stated in (2.1), and examine its stability.

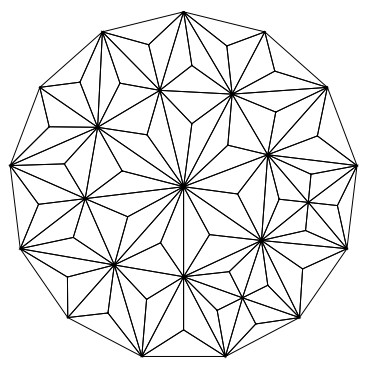
To elucidate the construction of the FVEM scheme, we first present the primary partition $\mathcal{T}$ and its associated dual partition $\mathcal{T}_*$ for the domain $\Omega$. In this paper, we utilize a distinctive triangular mesh as the primary partition $\mathcal{T}$. We define $\mathcal{T}_M = \{M\}$ as a macro-element partition of the polygonal region $\Omega$, with each macro-element being a triangle, as shown in Figure 1. This indicates that the polygonal domain $\Omega$ is divided into a finite number of macro triangles. Then the primary partition $\mathcal{T} = \{K\}$ is derived by subdividing each macro triangle $M\in \mathcal{T}_M$ into three smaller triangles $K\in \mathcal{T}$, in the spirit of connecting the vertices of the macro triangle to its barycenter, as illustrated in Figure 2. The meshes generated by $\mathcal{T}$ are termed barycenter-refined triangular meshes. In numerous studies, including the references ^{[36, 37, 38]}, the primary partition $\mathcal{T}$ is alternatively referred to as the Clough-Tocher refinement of the macro-element partition $\mathcal{T}_M$. It is evident that the smaller triangles $K\in \mathcal{T}$ are nested within the macro triangle $M\in \mathcal{T}_M$, and the collective union of all these smaller triangles constitutes the primary partition $\mathcal{T}$ of the domain $\Omega$. We denote by $h_K$ the diameter of the element $K$ and by ${\rho_K}$ the diameter of the largest ball contained in $K$, and set $h: = \mathop {\max }_{K \in \mathcal{T}}{h_K}$. Let $\mathfrak{T} = \{\mathcal{T}\}$ be a family of the triangulations of $\Omega$, and assume the family of primary partitions $\mathfrak{T} = \{\mathcal{T}\}$ to be a regular triangulation. For such triangulations, there exits a constant $\sigma > 1$ such that ${h_K} \leqslant \sigma{\rho_K}$, for all $K \in \mathcal{T}$, $\mathcal{T}\in \mathfrak{T}$. For a subset $\mathcal{D}\subset \mathbb{R}^2$, the notation ${\mathcal{P}_{r}(\mathcal{D})}$ refers to the set of all polynomials of degree at most $r$ defined on $\mathcal{D}$. The trial space ${\mathbf{U}}_{\mathcal {T}}$ for the velocity is selected to be a quadratic conforming finite element space, which is defined as follows:

where ${\mathrm{U}}_{\mathcal{T}} = \{u: u\in{\mathrm{H}_{0}^1}(\Omega)\cap {\mathrm{C}}(\Omega), u|_K\in {\mathcal{P}_{2}(K)}, \ \mbox{for all} \ K\in \mathcal{T} \}.$ This implies that the velocity is approximated using continuous piecewise quadratic polynomial functions.

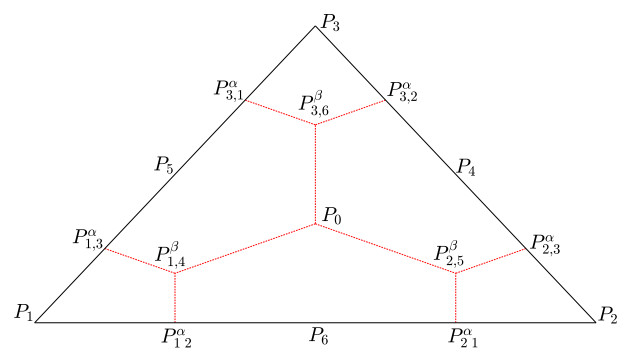
We then present the dual partition ${\mathcal {T}_{\ast}}: = \left\{{K}^*\right\}$ associated with the primary partitions $\mathcal{T}$. In the context of a triangle $K = \Delta P_1 P_2P_3$, we identify the three midpoints as ${P_4}$, ${P_5}$, and ${P_6}$, and the barycenter as ${P_0}$, as depicted in Figure 3. To delineate the dual elements, we define the mesh parameters $\alpha\in (0, \frac{1}{2})$ and $\beta\in (0, \frac{2}{3})$. For any distinct indices $m$ and $n$ with $m, n\in \mathbb{N}_3$, we denote the point $P_{m, n}^\alpha$ on the boundary $\overline{{P_m}{P_n}}$ such that ${{\left| {\overline {{P_m}P_{m, n}^\alpha } } \right|}} = \alpha {{\left| {\overline {{P_m}{P_n}} } \right|}}.$ The point $P_{m, m + 3}^\beta$, where $m \in \mathbb{N}_3$, is defined as the point on the midline $\overline{{P_m}{P_{m + 3}}}$ such that ${{\left| {\overline {{P_m}P_{m, m + 3}^\beta } } \right|}} = \beta {{\left| {\overline {{P_m}{P_{m + 3}}} } \right|}}.$ By connecting the points $P_{m, m + 3}^\beta$ to the barycenter $P_0$ and joining the points $P_{m, m + 3}^\beta$ with $P_{m, n}^\alpha$ for all $m, n\in \mathbb{N}_3$ where $m\ne n$, using straight lines, we construct the dual partition of $K$ as illustrated in Figure 3. Consequently, the dual partitions ${\mathcal{T}_\ast} = \{K^*\}$ of the domain $\Omega$ are formed by the dual partitions of all elements $K\in {\mathcal {T}}$.

In light of the dual partitions ${\mathcal{T}_\ast}$ of the domain $\Omega$, the test space $\mathbf{U}_{\mathcal{T}_*}$ associated with the velocity is defined as follows:

with the definition of ${\mathrm{U}_{\mathcal {T}_* } }: = \mathrm{span}\{\chi_{K^*}: K^*\in \mathcal{T}_* \}$ where $\chi_{E}$ represents the scalar characteristic function defined on the dual element ${E}\in {\mathcal{T}}_*$. The variations of the mesh parameters $\alpha$ and $\beta$ lead to a distinct FVEM scheme. In our discussion, we choose $\alpha\in \left({\frac{1}{6}, \frac{1}{2}} \right)$ and $\beta = 1-\frac{1}{6\alpha}$. It is evident that $\beta\in \left({0, \frac{2}{3}} \right)$.

We define the trial and test spaces for the pressure as ${\mathrm{Q}}_{\mathcal{T}}\subset \mathrm{L}_0^2(\Omega)$ and by

Specifically, the pressure space ${\mathrm{Q}}_{\mathcal{T}}$ is defined as follows, as described in ^{[22, 23, 26]}:

This space is characterized by augmenting the continuous linear space with piecewise constant functions within each element of the partition $\mathcal{T}$, and thus it can be seen as composed of discontinuous piecewise linear polynomial functions defined on each element $K\in \mathcal{T}$, thereby ensuring that the divergence of the trial space for the velocity remains a subspace of it. This contrasts with the selection of the pressure space ${\mathrm{Q}}_{\mathcal{T}}$ presented in ^[25].

The finite element space pair $({\mathbf{U}}_{\mathcal{T}}, {\mathrm{Q}}_{\mathcal{T}})$ is referred to as the LC finite element space pair, and the space ${\mathrm{Q}}_{\mathcal{T}}$ defined above is called the continuous linear plus constant pressure element, as noted in ^{[22, 23]}. Observe that the primary partition $\mathcal{T}\in \mathfrak{T}$ is constructed by joining the vertices and barycenter of every macro triangle $U\in \mathcal{T}_M$. It is documented in references ^{[22, 23]} that the spaces ${\mathbf{U}}_{\mathcal{T}}$ and ${\mathrm{Q}}_{\mathcal{T}}$ satisfy the following discrete $\inf-\sup$ inequality:

with $c$ being a constant that is invariant with respect to the mesh size $h$ and the time step ${{\Delta t}}$.

Next, we present the fully discrete scheme for the problem as stated in (2.1). For all $(\mathbf{u}, p) \in \left({\mathbf{U}}_{\mathcal{T}}, {\mathrm{Q}}_{\mathcal{T}}\right)$ and $(\mathbf{v}, q) \in \left({\mathbf{U}}_{\mathcal{T}_*}, {\mathrm{Q}}_{\mathcal{T}}\right)$, we define the following discrete bilinear forms:

where ${\mathrm{int} K}$ refers to the interior region of the element $K$, and $\mathbf{n}$ represents the outward-pointing unit normal vector on the boundary $\partial {K}$ or $\partial {K}^*$. Let $\Pi_{h}$ be the interpolation projection that maps functions from the space $\mathrm{H^1}(\Omega)$ onto the finite element space ${\mathrm{U}}_{\mathcal{T}}$, and $\Gamma_{h}$ serves as the interpolation projection from the space $\mathrm{L^2_0}(\Omega)$ to the finite element space ${\mathrm{Q}}_{\mathcal{T}}$. Given that the family of primary partitions $\mathfrak{T} = \{\mathcal{T}\}$ is regular, the interpolation theory on finite element spaces guarantees the following inequalities. For any $w \in \mathrm{H^3}(\Omega)$, $m\in\{0, 1\}$, we have

Similarly, for any $q \in \mathrm{H^2}(\Omega)$, $m\in\{0, 1\}$, the inequality

holds. We now suggest a fully discrete FVEM scheme for the problem defined in (2.1), which is formulated as follows: Find $(\mathbf{u}_h^n, p_h^n)\in \left({\mathbf{U}}_{\mathcal{T}}, {\mathrm{Q}}_{\mathcal{T}}\right)$ for all $n\in\mathbb{Z}_M$ such that it satisfies the following conditions:

where $\mathbf{f}^n$ represents the value of the function $\mathbf{f}(\mathbf{x}, t)$ at the time point $t_n$.

We remark that the velocity trial space ${\mathbf{U}}_{\mathcal{T}}$ is defined as the continuous piecewise quadratic finite element space, while the pressure trial space ${\mathrm{Q}_{\mathcal{T}}}$ is defined as the sum of a continuous piecewise linear finite element space and a local constant function space, and this characterization explicitly clarifies its inherent discontinuity. This ensures that the divergence of ${\mathbf{U}}_{\mathcal{T}}$ is contained within ${\mathrm{Q}_{\mathcal{T}}}$. As a result, the discrete velocity solution derived from (4.3) is provided with the property that the integral average of the divergence over each element will automatically vanish. Consequently, the scheme presented in (4.3) is guaranteeing local mass conservation of the discrete velocity within each element $K\in \mathcal{T}$ and the pressure-robustness. In other words, any modifications to the function $\mathbf{f}(\mathbf{x}, t)$ at the right end of the problem (2.1) that solely impact the pressure will only influence the variation of the discrete pressure solution in (4.3).

We find that the mapping from the trial space ${\mathrm{U}_{\mathcal{T}}}$ to the test space ${\mathrm{U} _{\mathcal{T}_*}}$ can facilitate the theoretical analysis of the FVEM scheme. We now present the mapping $\Pi_{\mathcal{T}_*}:{\mathrm{U}_{\mathcal{T}}}\to {\mathrm{U} _{\mathcal{T}_*}}$ that is discussed in ^[25]. For any $v\in {\mathrm{U}_{\mathcal{T}}}$, the mapping $\Pi_{\mathcal{T}_*}$ is defined such that for each vertex $P_i$ of $K$, $i\in\mathbb{N}_3$,

and for each interior midpoint $M_{i, j}$ of $K$, $i$, $j\in\mathbb{N}_3$ with $i < j$,

with $\omega$ being a non-zero constant. The specific relationships between the nodal points are depicted in Figure 3, with $M_{1, 2} = P_6$, $M_{1, 3} = P_5$, and $M_{2, 3} = P_4$. The mapping $\Pi_{\mathcal{T}_*}$ can be constructed from the linear mappings ${\Pi_{\mathcal{T}_*}}$ defined on each element $K\in \mathcal{T}$. For any non-zero real number $\omega$, it can be readily demonstrated that $\Pi_{\mathcal {T}_*}$ is a linear invertible mapping from the space ${\mathrm{U}_{\mathcal {T}}}$ onto ${\mathrm{U}_{\mathcal{T}_*}}$.

By employing the linear invertible mapping $\Pi_{\mathcal {T}_*}$ as previously defined, for any non-zero coefficient $\omega \in \mathbb{R}$, the fully discrete FVEM scheme (4.3) for the problem given in (2.1) is equivalent to the following formulation. Find $(\mathbf{u}_h^n, p_h^n)\in \left({\mathbf{U}}_{\mathcal{T}}, {\mathrm{Q}}_{\mathcal{T}}\right)$, where $n\in \mathbb{Z}_M$, satisfying

with the notation $\Pi_{\mathcal {T}_*} {\bf w} : = \left(\Pi_{\mathcal {T}_*}{w}_{1}, \Pi_{\mathcal {T}_*}{w}_{2}\right)$ for any vector ${\bf w}: = (w_1, w_2)\in {{\bf U}_{\mathcal {T}}}$.

We will now examine the stability of the fully discrete scheme presented in (4.4). This scheme must satisfy the abstract theories of generalized saddle-point problems as outlined in ^{[39, 40]}. To facilitate this analysis, we select the mapping coefficient $\omega$ as $\omega = \frac{1}{1-3\alpha\beta}$ in the subsequent discussion. It is important to note that the mesh parameters are defined as $\beta = 1 - \frac{1}{6\alpha}$, where $\alpha\in\left(\frac{1}{6}, \frac{1}{2} \right)$. This choice results in $\omega = \frac{2}{1-6\alpha}$. From the references ^{[25, 41]}, it can be seen that the choice of mapping coefficient $\omega$ does not affect the numerical solution of the FVEM scheme.

We define a block matrix $\bf{A}$ as follows:

where $\omega_0 = \frac{1-\omega}{2}$, $\mathbf{E} = \mathbf{1} - \mathbf{I}$, $\mathbf{I}$ is the $3 \times 3$ identity matrix, and $\mathbf{1}$ is a $3 \times 3$ matrix with all entries equal to 1. By employing proof techniques similar to those in references ^{[25, 42]}, the following conclusion can be obtained.

Lemma 1. For all $v \in \mathcal{P}_{2}(K)$ and $u \in \mathcal{P}_{0}(K)$, the following equations hold for any $K \in \mathcal{T}$:

and

As a direct result of Lemma 1, we derive the following proposition.

Proposition 1. For all $\mathbf{u}\in {{\bf U}_{\mathcal {T}}}$ and $\mathbf{v}\in {{\bf U}_{\mathcal {T}}}$, and for all $q\in {\mathrm{Q}_{\mathcal {T}}}$, the following equations hold:

Proof. Note that the space ${\mathrm{Q}}_{\mathcal{T}}$ is the discontinuous function space. According to the definition of $b_{\mathcal{T}}(\cdot, \cdot)$, for any ${\mathbf{v}}\in{\bf U}_{\mathcal{T}}$ and $q\in \mathrm{Q}_{\mathcal{T}}$, we have

Since $\Pi_{\mathcal {T}_*}{\bf{v}}\in{{\bf U}_{\mathcal{T}_*}}$ and ${{\bf U}_{\mathcal{T}_*}}$ consists of piecewise constant functions, it follows that

which simplifies the bilinear form $b_{\mathcal{T}}(\cdot, \cdot)$ to

Applying Green's formulae to the above expression results in

From the definition of $d_{\mathcal{T}}(\cdot, \cdot)$, it is confirmed that for any ${\mathbf{v}}\in{\bf U}_{\mathcal{T}}$ and $q\in \mathrm{Q}_{\mathcal{T}}$,

Given that for any $K\in \mathcal{T}$, $q|_K\in \mathcal{P}_{1}(K)$, $\nabla q|_K \in \left(\mathcal{P}_{0}(K), \mathcal{P}_{0}(K)\right)$, and $\mathbf{v}|_K\in \left(\mathcal{P}_{2}({K}), \mathcal{P}_{2}({K})\right)$, and using the result of (4.6) in Lemma 1, it is evident that

Now, let us examine the final term on the right-hand side of (4.9). Due to the discontinuity of $q\in \mathrm{Q}_{\mathcal{T}}$ on the boundaries of adjacent elements ${K}\in{\mathcal{T}}$, it is typically the case that

Given that for any $q\in \mathrm{Q}_{\mathcal{T}}$, $q = q_1+q_0$ with $q_1\in C(\Omega)$ and $q_1|_{K} \in {\mathcal{P}_{1}(K)}$, $q_0|_{K} \in {\mathcal{P}_{0}(K)}$ for each $K\in \mathcal{T}$, we have

The fact that $q_1\in C(\Omega)$ and the result of (4.7) in Lemma 1 imply

This shows that for any ${\mathbf{v}}\in{\bf U}_{\mathcal{T}}$ and $q\in \mathrm{Q}_{\mathcal{T}}$,

Consequently, it follows that $b_{\mathcal{T}}\left(\Pi_{\mathcal {T}_*}{\bf{v}}, q\right)+d_{\mathcal{T}}\left({\bf{v}}, q \right) = 0$ for any $({\mathbf{v}, q }) \in ({\bf U}_{\mathcal{T}}, \mathrm{Q}_{\mathcal{T}})$, and thus the Eq (4.8) is established.

Noticing that according to the definitions of the bilinear forms $d_{\mathcal{T}}(\cdot, \cdot)$ and $b(\cdot, \cdot)$, the verification of the following equation can be readily achieved by applying Green's formulae. That is, it holds for all $\mathbf{u}, \mathbf{v}\in {{\bf U}_{\mathcal {T}}}$ and $q\in {\mathrm{Q}_{\mathcal {T}}}$ that

This completes the proof of the proposition. □

Proposition 1 elucidates that the discrete bilinear forms $b_{\mathcal{T}}\left(\Pi_{\mathcal {T}_*}\cdot, \cdot\right)$ and $d_{\mathcal{T}}\left(\cdot, \cdot\right)$ in the FVEM scheme with an LC element are equivalent to those in the FEMs when the mapping coefficient is set to $\omega = \frac{1}{1-3\alpha\beta}$, with $\beta = 1-\frac{1}{6\alpha}$. It is important to note that although the conclusion of Proposition 1 is consistent with Proposition 5.10 as referenced in ^[25], the conditions required for these theorems are distinct. This proposition chooses the space ${\mathrm{Q}}_{\mathcal{T}}$ to be a space of discontinuous pressures.

We note that the following equalities inherently hold for all $(\mathbf{v}, q) \in (\mathbf{U}_{\mathcal{T}}, \mathrm{Q}_{\mathcal{T}})$ when $\mathrm{Q}_{\mathcal{T}}$ is selected as a continuous linear finite element space, that is,

This result has been previously established in ^[25]. In these conditions, the validity of Eq (4.8) is ensured only by Eq (4.6) from Lemma 1, and thus obviating the need for the restrictive Eq (4.7) which is derived from $\beta = 1-\frac{1}{6\alpha}$. For details, refer to ^[25]. This implies that when $\mathrm{Q}_{\mathcal{T}}$ is a continuous finite element space, Equation (4.8) can be valid for a broader range of $\alpha \in \left({0, \frac{1}{2}} \right)$ and $\beta \in \left({0, \frac{2}{3}} \right)$, provided that $\omega = \frac{1}{1-3\alpha\beta}$.

From the preceding conclusions, it is evident that for a map coefficient $\omega$ defined as $\omega = \frac{1}{1-3\alpha\beta}$, the fully discrete FVEM scheme for the problem described in (2.1) can be expressed in the following forms: Find $(\mathbf{u}_h^n, p_h^n)\in\left({\mathbf{U}}_{\mathcal{T}}, {\mathrm{Q}}_{\mathcal{T}}\right)$, where $n\in\mathbb{Z}_M$, such that

It is important to note that the FVEM scheme (4.3) is fundamentally the same as the FVEM scheme (4.4) when the linear mapping $\Pi_{\mathcal {T}_*}:{\mathbf{U}_{\mathcal{T}}}\to {\mathbf{U}_{\mathcal{T}_*}}$ is applied, regardless of any map coefficient $\omega\in \mathbb{R}^*$. The FVEM scheme (4.10) is a specific instance of the FVEM scheme (4.4) that arises from the choice of $\omega = \frac{1}{1-3\alpha\beta}$. This implies that the FVEM scheme (4.10) is inherently equivalent to the FVEM scheme (4.3). Given that the discrete velocity solution in (4.10) is the local mass conservation within each element $K\in \mathcal{T}$, the numerical solution of the FVEM scheme (4.3) also maintains the local mass conservation. Therefore, to investigate the stability of (4.3), it is sufficient to focus on the analysis of (4.10).

To this end, we need to establish some preliminary conclusions. For the mesh parameters $\alpha\in (0, \frac{1}{2})$ and $\beta\in (0, \frac{2}{3})$, we define the following expressions:

We introduce the matrices

where $\mathbf{E} = \mathbf{1}-\mathbf{I}$ is a $3\times3$ matrix as defined in (4.5). For every $w\in {\mathrm{U}}_{\mathcal{T}}$, we define the norm $|||w|||_0$ as $\left(w, \Pi_{\mathcal {T}_*}w\right)^{\frac{1}{2}}$. This norm $|||\cdot|||_0$ can be demonstrated to be equivalent to $\|\cdot\|_0$ on the subspace ${\mathrm{U}}_{\mathcal{T}}$.

Proposition 2. There exist two positive constants $c$ and $C$ such that for all ${w}\in {\mathrm{U}}_{\mathcal {T}}$,

Proof. To establish the proposition, it is enough to show that there are constants $c$ and $C$ such that for all $K\in \mathcal{T}$,

For every $w\in{\mathrm{U}}_{\mathcal {T}}$, we define $w$ restricted to $K$ as the linear combination $w|_K = \sum_{i = 1}^{6}w_{i, K}\varphi_{i, K}$, where $\varphi_{i, K}$ are the basis functions associated with the nodal points $P_{i}$ on the element $K$. From the definition of $\Pi_{\mathcal {T}_*}$ on each $K \in {\mathcal {T}}$, it follows that

Through a direct calculation, we obtain

with ${\bf w} = [{w} _{i, K}, i\in \mathbb{N}_6]$ and ${\bf D} = \frac{{\bf AC}+ ({\bf AC})^T}{2}$. Noting that $\omega = \frac{1}{1-3\alpha\beta}$ and $\beta = 1-\frac{1}{6\alpha}$ for $\alpha \in \left({\frac{1}{6}, \frac{1}{2}} \right)$, it is straightforward to confirm that the matrices $\mathbf{D}$ and $\mathbf{B}$ are positive definite. This guarantees the existence of positive constants $c$ and $C$ that are independent of the mesh size $h$ and the time step ${{\Delta t}}$, satisfying

for all ${\bf w}\in {{\mathbb{R}}^{6}}$. Consequently, the inequality (4.11) is verified, and the proof of the proposition is complete. □

In this section, we note that the inner product $\left(\cdot, \Pi_{\mathcal {T}_*}\cdot\right)$ defined on the mapping $\Pi_{\mathcal{T}_*}$ presented in this paper is not self-adjoint in general, unlike the linear FVEMs. Specifically, the equality

holds if and only if $w = v \in \mathrm{U}_{\mathcal{T}}$. This non-self-adjointness necessitates the development and analysis of semi-discrete temporal schemes for the problem (2.1) before we can proceed to the fully discrete FVEM scheme. Referring to the works of ^{[25, 41]}, we present the following properties of the mapping $\Pi_{\mathcal{T}_*}$.

Proposition 3. There exist positive constants $c$ and $C$ such that for all $w \in \mathrm{U}_{\mathcal{T}}$, the following inequalities hold:

This proposition demonstrates the equivalence between the discrete norms and the error estimates on $\Pi_{\mathcal{T}_*}$.

It is widely recognized that the coercivity of the bilinear forms $a_{\mathcal{T}}(\cdot, \Pi_{\mathcal {T}_*} \cdot)$ as presented in (4.4) is dependent on the geometric characteristics of the primary triangular meshes $K\in \mathcal{T}$. To streamline our discussion, we shall hereafter assume that the primary partition family $\mathfrak{T} = \{\mathcal{T}\}$ is of shape regularity, ensuring the existence of a positive constant $c_0$ such that

Furthermore, as demonstrated in ^{[25, 41]}, there exists a constant $C$ for all $\mathcal{T} \in \mathfrak{T}$ such that the following uniform boundness holds:

Our theoretical exploration will employ the following discrete Gronwall lemma, as outlined in ^{[43, 44]}.

Lemma 2. Consider the nonnegative sequences $a_n$, $b_n$, $c_n$, and $d_n$. If they satisfy

then it follows that

with $\tau$ and $C$ being positive constants that are independent of the mesh size $h$ and the time step ${{\Delta t}}$.

After the above preparations, we establish the stability of the fully discrete FVEM scheme presented in (4.10).

Theorem 3. If ${\mathbf{u}}_0\in {\mathbf{H_{0}^1}}(\Omega)$ and $\mathbf{f}\in {\mathbf{L^2}}(\Omega)$ for all $t \in (0, T]$, there exists a unique sequence of solutions $(\mathbf{u}_h^n, p_h^n)\in \left({\mathbf{U}}_{\mathcal{T}}, {\mathrm{Q}}_{\mathcal{T}}\right)$, where $n \in \mathbb{Z}_M$, for the fully discrete FVEM scheme (4.10), and the solutions satisfy the following stability conditions:

where $C$ denotes a positive constant that is independent of the mesh size $h$ and the time step ${\Delta t}$.

Proof. For all $(\mathbf{u}_h^n, p_h^n)\in\left({\mathbf{U}}_{\mathcal{T}}, {\mathrm{Q}}_{\mathcal{T}}\right)$ and $(\mathbf{v}, q)\in\left({\mathbf{U}}_{\mathcal{T}}, {\mathrm{Q}}_{\mathcal{T}}\right)$, where $\left({\mathbf{U}}_{\mathcal{T}}, {\mathrm{Q}}_{\mathcal{T}}\right)\subset \left(\mathbf{H_0^1}(\Omega), {\mathrm{L}_0^2}(\Omega)\right)$, we set

The inequalities (4.12) and (4.13) imply that the discrete bilinear form $a_{\mathcal{T}}\left(\mathbf{u}_h^n, \Pi_{\mathcal{T}_*}\mathbf{v}\right)$ is uniformly bounded and coercive. Specifically, it satisfies the following conditions:

The discrete bilinear form $b(\mathbf{u}_h^n, q)$ also satisfies the discrete $\inf-\sup$ condition (4.1). From Proposition 2 and Proposition 3, we have the following inequalities:

By applying the same proof technique as in Theorem 1, we can establish the existence of solutions for the FVEM scheme (4.10).

For the stability estimates, we first demonstrate the estimate (4.14). From the scheme (4.10), we have for all $(\mathbf{v}, q) \in ({\mathbf{U}}_{\mathcal{T}}, {\mathrm{Q}}_{\mathcal{T}})$,

By choosing $\mathbf{v} = \mathbf{u}_h^n$ and $q = p_h^n$, we obtain

Applying the Cauchy-Schwarz inequality, Poincaré inequality, and Yang's inequality to the right-hand side of the above equation, we get

From this inequality, we can conclude that

where $\delta \geqslant 1$ is a positive constant independent of $h$ and ${\Delta t}$. By summing the above inequality from $1$ to $n$ and applying the discrete Gronwall lemma, we obtain

Noting that for any $\mathbf{v} \in \mathbf{U}_{\mathcal{T}}$,

we derive the estimate (4.14) from the above inequalities.

To demonstrate the second estimate (4.15), we first provide the estimate for $\|d_t{\mathbf{u}}_h^n\|_0$. It is noted that the pair $(\mathbf{u}_h^n, p_h^n)\in \left({\mathbf{U}}_{\mathcal{T}}, {\mathrm{Q}}_{\mathcal{T}}\right)$, where $n\in\mathbb{Z}_M$, constitutes a unique sequence of solutions for the fully discrete FVEM scheme in (4.10). This implies that for any $(\mathbf{v}, q)\in \left({\mathbf{U}}_{\mathcal{T}}, {\mathrm{Q}}_{\mathcal{T}}\right)$, the following holds

By selecting $\mathbf{v} = d_t{\mathbf{u}}_h^n$ and $q = p_h^n$ in the above equation, we obtain

which results in

Considering again that $|{\mathbf{u}}_h^0|_1 \leqslant C\|{\mathbf{u}}_0\|_1$ and $c\|\mathbf{v}\|_0\leqslant |||\mathbf{v}|||_0\leqslant C\|\mathbf{v}\|_0$ for any $\mathbf{v} \in {\mathbf{U}}_{\mathcal{T}}$, summing the above inequality from $1$ to $n$ and applying the discrete Gronwall lemma gives

By employing a technique similar to that used to derive the estimate of $\|p^n\|_0$ in Theorem 1, the estimate (4.15) can be derived. This concludes our proof. □

This theorem elucidates that the fully discrete FVEM scheme, as described in (4.10), being equivalent to the FVEM scheme in (4.3), possesses a unique series of solutions and meets the necessary stability requirements.

5.   Error estimates

This section is dedicated to deriving error estimates for the fully discrete FVEM scheme presented in (4.10). To streamline the theoretical investigation, we focus on the FVEM in (4.10) with the mesh parameter as follows:

This specific choice of $\alpha$ allows for an easier analysis. Similar approaches can be applied to other cases. Given $\alpha = \bar{\alpha}$, it can be deduced that $\beta = 1-\frac{1}{6\alpha}$ and $\omega = \frac{1}{1-3\alpha\beta}$ yield $\beta = \alpha$ and $\omega = \frac{2}{\sqrt{3}}$.

The following results are then derived from the work of ^{[25, 42]}.

Proposition 4. For every $v\in \mathcal{P}_{2}(K)$ and $u\in\mathcal{P}_{1}(K)$, it is shown that

which consequently implies that for all $\mathbf{u}\in {{\bf U}_{\mathcal {T}}}$ and $\mathbf{v}\in {{\bf U}_{\mathcal {T}}}$,

In this context, the fully discrete FVEM scheme, as presented in (4.10), with $\alpha = \bar{\alpha}$, can be expressed as follows: Find $(\mathbf{u}_h^n, p_h^n)\in\left({\mathbf{U}}_{\mathcal{T}}, {\mathrm{Q}}_{\mathcal{T}}\right)$, for $n\in\mathbb{Z}_M$, satisfying

The primary objective of the subsequent discussion is to investigate the error estimates for the equations given in (5.3).

To streamline the verification of error estimation, we first present the Stokes projection, which was initially proposed in ^[33] within the context of the FEM. We denote the Stokes projection of the solutions $(\mathbf{u}^{n}, p^n)\in \left({\mathbf{U}}_{\mathcal{T}}, {\mathrm{Q}}_{\mathcal{T}}\right)$ for the semi-discrete scheme (3.1) as $(S_h\mathbf{u}^{n}, Q_h p^n)$, where $n\in \mathbb{Z}_M$. This projection ensures that for the solutions $(\mathbf{u}^n, p^n)\in \left({\mathbf{H_{0}^1}(\Omega)}, \mathrm{L}_0^2(\Omega)\right)$, there exists the corresponding $(S_h\mathbf{u}^{n}, Q_h p^n)\in \left({\mathbf{U}}_{\mathcal{T}}, {\mathrm{Q}}_{\mathcal{T}}\right)$ satisfying the following conditions

Following the standard FEM technique for the Stokes equations as outlined in ^[35], we derive the following proposition.

Proposition 5. Let $(\mathbf{u}^n, p^n)$, $n\in\mathbb{Z}_M$, be the solutions of the semi-discrete scheme (3.1) with $(\mathbf{u}^n, p^n)\in\left({\mathbf H_{0}^1}(\Omega)\cap {\mathbf H^3}(\Omega), \mathrm{L}_0^2(\Omega)\cap {\mathrm H^2}(\Omega)\right)$, and assume that ${\mathbf{u}}_0\in {\mathbf{H_{0}^2}}(\Omega)$. Then, the following error estimates are valid:

where $C$ is a positive constant that is independent of the mesh size $h$ and the parameter ${\Delta t}$.

Proof. Employing a proof technique similar to Theorem 1, it follows that there is a unique sequence of solutions $(\mathbf{\tilde{u}}_h^n, \tilde{p}_h^n)\in \left({\mathbf{U}}_{\mathcal{T}}, {\mathrm{Q}}_{\mathcal{T}}\right)$, where $n\in\mathbb{Z}_M$, for the system of equations given by

We now examine the error estimates. Similar to standard mixed finite element analysis, for any $q\in {\mathrm{Q}}_{\mathcal{T}}$, we select $\mathbf{\tilde{w}}_h^n\in{\mathbf{U}}_{\mathcal{T}}$ such that $b(\mathbf{\tilde{w}}_h^n, q) = 0,$ where the $\inf-\sup$ condition is satisfied by the space pair $\left({\mathbf{U}}_{\mathcal{T}}, {\mathrm{Q}}_{\mathcal{T}}\right)$. It is worth noting that $b(\mathbf{\tilde{u}}_h^n, q) = 0$, which implies $b(\mathbf{\tilde{u}}_h^n-\mathbf{\tilde{w}}_h^n, q) = 0$ for all $q\in {\mathrm{Q}}_{\mathcal{T}}$. By substituting $\mathbf{v} = \mathbf{\tilde{u}}_h^n-\mathbf{\tilde{w}}_h^n$ into Eq (5.5), we obtain

Subtracting Eq (3.1) from the above equation, we get

with the observation that $b(\mathbf{v}, \Gamma_h p^n) = b(\mathbf{\tilde{u}}_h^n-\mathbf{\tilde{w}}_h^n, \Gamma_h p^n) = 0$ since $\Gamma_h p^n\in {\mathrm{Q}}_{\mathcal{T}}$ and $p^n\in \mathrm{L}_0^2(\Omega)\cap {\mathrm H^2}(\Omega)$. Thus we have

Considering $\mathbf{v} = \mathbf{\tilde{u}}_h^n-{\mathbf{u}}^n +{\mathbf{u}}^n-\mathbf{\tilde{w}}_h^n$, the following equation is derived:

Next, we examine each term located at the right-hand side of the above equation. By utilizing the Cauchy-Schwarz inequality, Poincaré inequality, and Yang's inequality for each term, we obtain the following:

and

By substituting the above inequalities into the right-hand side of (5.6), we obtain the following result:

It is observed that $\mathbf{v} = \mathbf{\tilde{u}}_h^n-\mathbf{\tilde{w}}_h^n$ leads to the inequality

This implies that

which, when combined with the inequality (5.7), results in

By utilizing the given information

and $\|p^n-\Gamma_h p^n\|_0 \leqslant Ch^2\|{p}^n\|_2,$ we can deduce that

Define the projection $\mathbf{\tilde{u}}_h^0 = \Pi_h{\mathbf{u}}^0 = S_h{\mathbf{u}}^0$, and observe the inequality

By summing the above inequality from $1$ to $n$ and applying the discrete Gronwall inequality, we obtain

with the condition ${\Delta t} \leqslant T$ being utilized. In the context of the above inequalities, let $S_h\mathbf{u}^{n} = \mathbf{\tilde{u}}_h^n$ and $Q_h p^n = p_h^n$ for all $n \in \mathbb{Z}_M$. This leads to the first estimate of the proposition.

Next, we examine the second estimation. Define $\eta^n = p^n-\Gamma_h p^n$ and $\eta^n_h = Q_h p^n-\Gamma_h p^n$. This implies that $\eta^n-\eta^n_h = p^n-Q_h p^n$. For any $(\mathbf{v}, q)\in \left({\mathbf{U}}_{\mathcal{T}}, {\mathrm{Q}}_{\mathcal{T}}\right)$, subtracting Eq (5.5) from Eq (3.1) under the conditions $S_h\mathbf{u}^{n} = \mathbf{\tilde{u}}_h^n$ and $Q_h p^n = p_h^n$, for all $n\in\mathbb{Z}_M$, results in

By utilizing the discrete $\inf-\sup$ condition (4.1), we derive the following inequality:

By applying the first estimate of this proposition to the right-hand side of the above inequality, we derive the following inequality:

and thus we have

Here, the interpolation estimate $\|\eta^n\|_0 = \|p^n - \Gamma_h p^n\|_0 \leqslant Ch^2\|p^n\|_2$ and the condition ${\Delta t} \leqslant T$ are utilized. This completes the proof of the proposition. □

Utilizing the results of Proposition 5 concerning the Stokes projection, we derive the following error estimates for the solutions $(\mathbf{u}_h^n, p_h^n)$ obtained from the fully discrete FVEM scheme presented in (5.3), where $(\mathbf{u}_h^n, p_h^n)\in\left({\mathbf{U}}_{\mathcal{T}}, {\mathrm{Q}}_{\mathcal{T}}\right)$ and $n\in\mathbb{Z}_M$. The fully discrete FVEM scheme proposed by (5.3) is equivalent to the FVEM scheme in (4.10) when $\alpha$ is set to $\alpha = \bar{\alpha}.$ We then establish the following theorem.

Theorem 4. We are given that $(\mathbf{u}_h^n, p_h^n)\in \left({\mathbf{U}}_{\mathcal{T}}, {\mathrm{Q}}_{\mathcal{T}}\right)$ represents the solutions for the fully discrete FVEM scheme as described in (5.3), with $n\in\mathbb{Z}_M$, and that $(\mathbf{u}^n, p^n)\in \left({\mathbf H_{0}^1}(\Omega)\cap {\mathbf H^3}(\Omega), \mathrm{L}_0^2(\Omega)\cap {\mathrm H^2}(\Omega)\right)$ are the solutions for the semi-discrete scheme in (3.1), with $n\in\mathbb{Z}_M$. If ${\mathbf{u}}_0\in {\mathbf{H_{0}^2}}(\Omega)$ and $\mathbf{f}\in {\mathbf{ H^1}}(\Omega)$ for all $t\in (0, T]$, the following error estimates are valid:

with $C$ being a positive constant that is independent of the mesh size $h$ and the time step ${\Delta t}$.

Proof. We begin by examining the first estimate. By subtracting (5.3) from (3.1), we obtain the error equation for all $(\mathbf{v}, q)\in\left({\mathbf{U}}_{\mathcal{T}}, {\mathrm{Q}}_{\mathcal{T}}\right)$. The equation is presented as follows:

which can be rewritten as

We select $\Pi^0_\mathcal{T}{\mathbf{w}}\in \mathbf{U}_\mathcal{T}$ as the piecewise constant interpolation function for $\mathbf{w}\in{\mathbf{H^2}}(\Omega)$ associated with the primary partitions $\mathcal{T}\in \mathfrak{T}$. By applying the first outcome of Lemma 1 to the above equation, it follows that for all $(\mathbf{v}, q)\in\left({\mathbf{U}}_{\mathcal{T}}, {\mathrm{Q}}_{\mathcal{T}}\right)$,

We define $\mathbf{e}^n$ as $\mathbf{e}^n = \mathbf{u}^n-S_h \mathbf{u}^n$, and denote $\eta^n$ as $\eta^n = p^n-Q_h p^n$. We introduce $\mathbf{e}_h^n = \mathbf{u}_h^n-S_h\mathbf{u}^n$ and $\eta^n_h = p_h^n-Q_h p^n$, which allows us to express the following relationships:

Based on these definitions, the given equation can be rewritten as follows:

Observe that for any integer $n \in \mathbb{Z}_M$, the pairs $(\mathbf{u}^n, p^n)\in \left({\mathbf H_{0}^1}(\Omega), \mathrm{L}_0^2(\Omega)\right)$ and $(S_h\mathbf{u}^{n}, Q_h p^n)\in \left({\mathbf{U}}_{\mathcal{T}}, {\mathrm{Q}}_{\mathcal{T}}\right)$ satisfy the Eq (5.4). Thus for any $(\mathbf{v}, q) \in \left({\mathbf{U}}_{\mathcal{T}}, {\mathrm{Q}}_{\mathcal{T}}\right)$, the following holds:

This simplifies the Eq (5.9) to the following form:

We now evaluate each term on the right-hand side of the above equality by setting $\mathbf{v} = \mathbf{e}_h^n$ and $q = \eta^n_h$. By applying the Cauchy-Schwarz inequality, the Poincaré inequality, and Yang's inequality on each individual term, we obtain the following inequalities:

and

The second inequality in Proposition 3 is employed in the derivation of these estimates. Next, we delve into a more detailed analysis of the estimate for the term $h^2|\mathbf{u}_h^n-\mathbf{u}_h^{n-1}|_1|\mathbf{e}_h^n|_1$. Utilizing Taylor's theorem, we obtain the following inequality for all $n\in\mathbb{Z}_M$,

Based on the result of Theorem 2, we have $|{\mathbf{u}}(t_n)-{\mathbf{u}}^n|_1 \leqslant C{\Delta t}$ for every $n\in\mathbb{Z}_M$. This implies that for any $n\in\mathbb{Z}_M$, the following inequality holds:

Thus, we derive the following inequality:

By utilizing the inverse inequality in finite element theory and Yang's inequality, we can deduce the following inequality from the previous one:

Consequently, for sufficiently small values of $h$, we obtain

By substituting the above estimates into (5.10), with $\mathbf{v} = \mathbf{e}_h^n$ and $q = \eta^n_h$, we obtain

This simplifies to

It is observed that $\|\mathbf{e}_h^{0}\|_0\leqslant Ch^2$. By summing the above inequality from $1$ to $n$ and applying the discrete Gronwall lemma, we have

Note that the equation $\mathbf{u}^n-\mathbf{u}_h^n = \mathbf{e}^n-\mathbf{e}_h^n$ and the results of Proposition 5 hold, and by employing the trigonometric inequality and the interpolation theorem of finite elements, the first estimate can be derived.

We now examine the second estimation. Observe that for every $q \in {\mathrm{Q}}_{\mathcal{T}}$, the following equality holds:

Thus from Eq (5.8), we deduce that for all $(\mathbf{v}, q) \in\left({\mathbf{U}}_{\mathcal{T}}, {\mathrm{Q}}_{\mathcal{T}}\right)$, the following relationship is valid:

Given the expressions $\eta^n = p^n-Q_h p^n$, $\eta^n_h = p_h^n-Q_h p^n$, and thus $\eta^n-\eta^n_h = p^n-p_h^n$, we can derive the following equality:

This equation is derived by expanding the difference between the bilinear forms involving $\eta^n$ and $\eta^n_h$, and then rearranging the terms. Applying the discrete $\inf-\sup$ condition (4.1), we derive the following inequality from the above equation:

This inequality, when combined with the results of the first estimate in this theorem, leads to the following result:

By utilizing the inverse inequality and the results of the first estimate of this theorem, it can be deduced from estimate (5.11) that

Substituting this into (5.12), we obtain

Applying the triangle inequality, we have

This is achieved using the estimation $\|\eta^n\|_0\leqslant Ch^2\|{p}^n\|_2$ and the condition ${{\Delta t}} \leqslant T$. This completes the proof. □

This theorem demonstrates that the fully discrete FVEM scheme, as detailed in (5.3), achieves optimal order error estimates for the spatial variables associated with the velocity in the $\mathbf{{H}^1}$-norm and the pressure in the $\mathrm{L}^2$-norm, aligning with the error estimates of the corresponding FEMs.

It is worth noting that the smoothness of the solution to problem (2.1) guarantees that the semi-discrete scheme (3.1) maintains the same level of smoothness in the temporal domain. By combining Theorem 2 with Theorem 4, we arrive at the following principal results.

Theorem 5. Let $(\mathbf{u}, p)$ be a solution to (2.1) with $(\mathbf{u}, p) \in \left({\mathbf{H_{0}^1}}(\Omega) \cap {\mathbf{H}}^3(\Omega), \mathrm{L}_0^2(\Omega) \cap \mathrm{H}^2(\Omega)\right)$ for all $t \in (0, T]$, and $(\mathbf{u}_h^n, p_h^n)\in\left({\mathbf{U}}_{\mathcal{T}}, {\mathrm{Q}}_{\mathcal{T}}\right)$ for $n\in\mathbb{Z}_M$ is the solution for the fully discrete FVEM scheme (5.3). If $\mathbf{u}_0 \in {\mathbf{H_{0}^2}}(\Omega)$ and $\mathbf{f} \in {\mathbf{H^1}}(\Omega)$ for every $t \in (0, T]$, the following error estimates are valid:

where $C$ denotes a constant that is independent of the mesh size $h$ and the time step ${{\Delta t}}$.

Regarding the FVEM scheme presented in (4.10), with different values of the mesh parameter $\alpha\in \left(\frac{1}{6}, \frac{1}{2} \right)$, similar theoretical estimates can be achieved through analogous approaches. However, the proof process may be somewhat intricate and laborious. Readers interested in exploring this further are encouraged to attempt it independently. It is worth noting that the FVEM scheme (4.10) is equivalent to the FVEM scheme (4.3). This equivalence demonstrates that the FVEM scheme (4.3) also possesses optimal order error estimates. The subsequent section will provide numerical results that elucidate this point.

6.   Numerical experiments

This section provides two numerical experiments designed to validate the theoretical results discussed in the preceding sections. Additionally, a cavity flow test is executed to demonstrate the practicality and effectiveness of the FVEM scheme (4.3) for solving non-stationary Stokes equations numerically. Throughout these experiments, the mesh parameters associated with the dual partition $\mathcal{T}_*$ are set to $\alpha\in \left(\frac{1}{6}, \frac{1}{2} \right)$, and the corresponding value of $\beta$ is calculated as $\beta = 1-\frac{1}{6\alpha}$. The experiments were conducted on a personal computer running Ubuntu OS version 16.04, equipped with an Intel(R) Xeon(R) Silver 4110 CPU operating at 2.10 GHz and a Quadro P4000 GPU.

In our first example, we examine the error estimations for spatial variables in the FVEM scheme presented in (4.3), and compare them with those of a fully discrete FEM scheme as follows:

As established in ^[35], the FEM scheme (6.1) is known for its stability and possesses optimal error estimates for the non-stationary Stokes equations. The numerical outcomes were achieved using MATLAB software version 7.11.0 (R2023a), which solved the linear systems derived from the FVEM scheme (4.3) and the FEM scheme (6.1).

Example 1. We consider the non-stationary Stokes equations (2.1), which are defined within the domain $\Omega = (0, 1)\times (0, 1)$. The viscosity of the fluid is set to $\mu = 1$, and the body force $\mathbf{f}(\mathbf{x}, t)$ is specified such that the exact solution is given by $\mathbf{u}(\mathbf{x}, t) = (u_1(x, y, t), u_2(x, y, t))$ where

and

The initial condition $\mathbf{u}_0$ is selected to be the exact solution evaluated at $t = 0$, i.e., $\mathbf{u}_0 = \mathbf{u}(\mathbf{x}, 0)$.

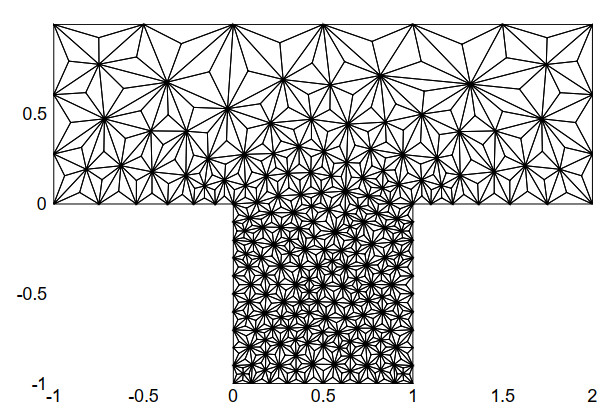
Figure 4 illustrates the primary partition $\mathcal{T}$ of the unit square domain $\Omega$, featuring a mesh size of $h = \frac{8}{25}$. This partition was generated by the GMSH software version 2.5.0 (2016) through the application of barycentric refinement methods, ensuring that the primary partition $\mathcal{T}\in \mathfrak{T}$ exhibits good shape regularity.

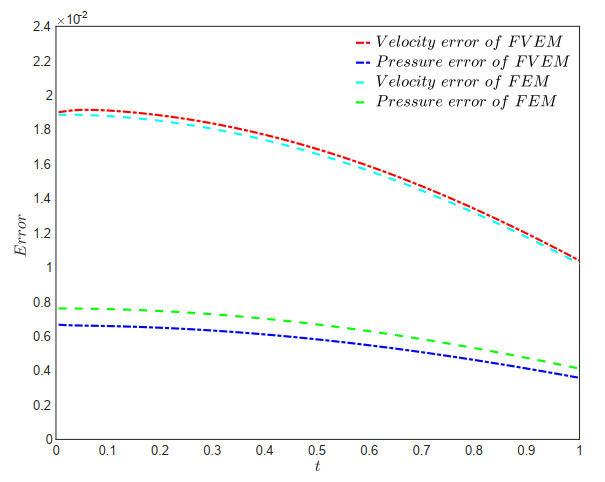
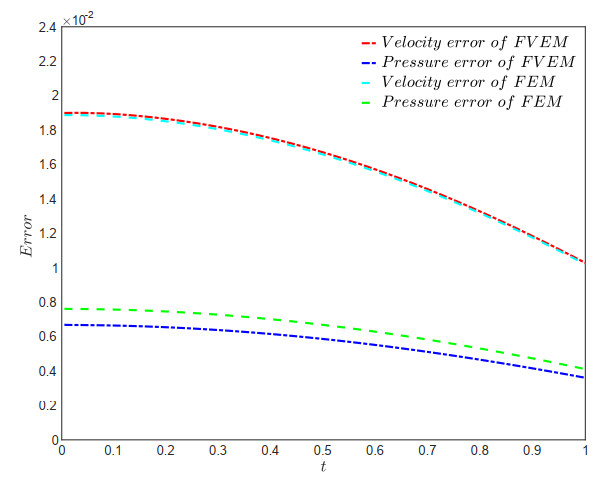
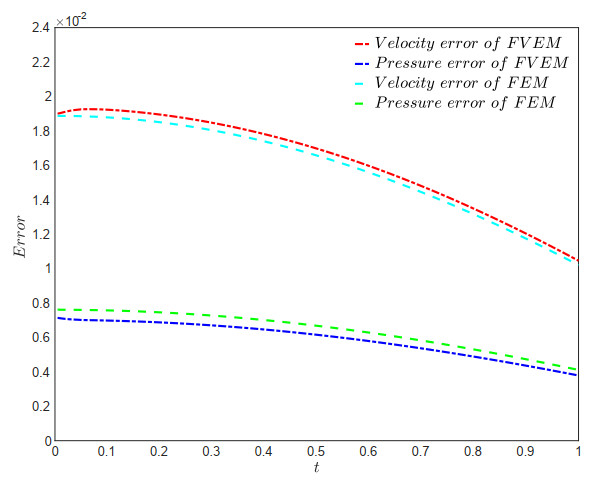
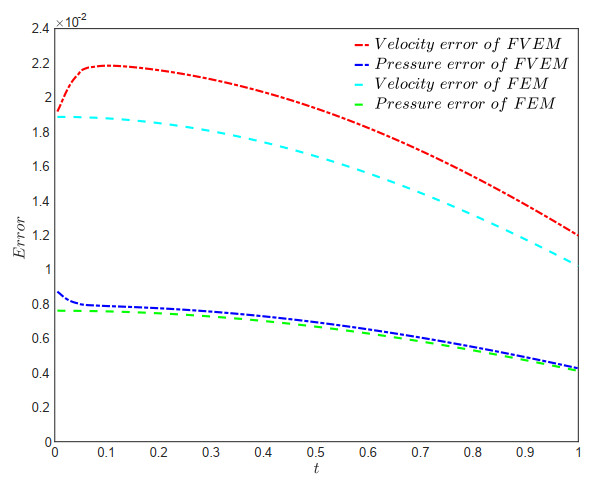
The subsequent figures, Figures 5, 6, 7, and 8, depict the error curves for the velocity ($\mathbf{H^1}$-norm) and pressure ($\mathrm{L}^2$-norm) approximations resulting from the FVEM scheme (4.3). These curves are plotted for various values of the mesh parameter $\alpha\in \left(\frac{1}{6}, \frac{1}{2} \right)$ and at time points $t \in (0, 1]$, with a time step size of ${{\Delta t}} = 0.005$. It is evident from the figures that both the FVEM scheme (4.3) and the FEM scheme (6.1) exhibit decreasing errors for velocity and pressure approximations as the time level advances, confirming the stability of the FVEM scheme (4.3) as predicted theoretically. It is easy to understand that, due to the interpolation error of the initial values constructed here decaying over time, the velocity and pressure errors will also show a decreasing trend over time. The numerical results presented in the figures demonstrate that these FVEM schemes exhibit no significant difference in velocity approximation errors compared to the corresponding FEM scheme, except for the FVEM scheme with $\alpha = \frac{1}{3}$, which displays slightly higher numerical errors. This indicates that the FVEM schemes achieve computational accuracy comparable to the corresponding FEM scheme, while additionally preserving local physical conservation on dual elements - an inherent advantage of the finite volume framework that is absent in FEM implementations.

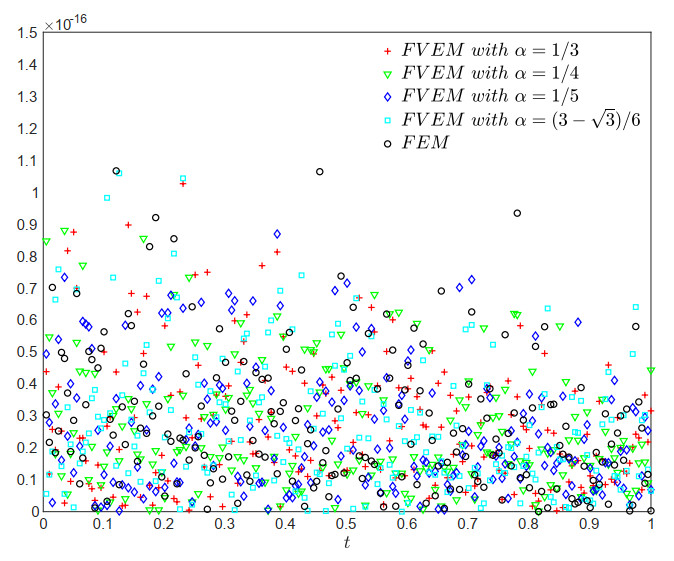
To demonstrate the local mass conservation property of the discrete velocity solutions in the FVEM schemes, Figure 9 presents a scatter plot of the absolute values of the integral of the divergence for velocity solutions versus times obtained by the FVEM schemes (under different dual partitions) and the FEM scheme. Considering that in practical numerical computations, factors such as discretization errors, integration approximations, and mesh conditions collectively prevent the divergence integral of the discrete solution from being strictly zero, the results in the figure reveal that the divergence integral of the velocity solutions generated by FVEM schemes with varying dual partitions remains at the level of round-off errors, specifically on the order of $10^{-16}$, which is equivalent to the corresponding FEM scheme, consequently achieving local mass conservation of the velocity.

Our second numerical example aims to verify that the numerical results from the FVEM scheme presented in (4.3) achieve the optimal convergence order for the error estimates in the $\mathbf{H^1}$-norm for the velocity and the $\mathrm{L}^2$-norm for the pressure within the spatial discretization.

Example 2. This example supposes that the viscosity of the fluid in the non-stationary Stokes equations (2.1) is $\mu = 1$ and the exact solution is given by $\mathbf{u}(\mathbf{x}, t) = (u_1(x, y, t), u_2(x, y, t))$, where

and $p(\mathbf{x}, t) = 10e^{-t}(2x-1)(2y-1)$. The initial condition $\mathbf{u}_0$ is selected as the exact solution evaluated at $t = 0$, and the computational domain $\Omega$ is identical to that used in Example 1.

Figure 10 illustrates the initial primary partition $\mathcal{T}$ of the unit square domain $\Omega$, utilizing a mesh size of $h = \frac{1}{10}$. In contrast, Figure 11 depicts the final refined primary partition, which employs a finer mesh with $h = \frac{1}{20}$.

The convergence order of the FVEM scheme with the spatial mesh size $h$ is determined using the following formula:

where $E_i$ and $E_{i+1}$ denote the errors associated with the FVEM scheme for mesh sizes $h_i$ and $h_{i+1}$, respectively.

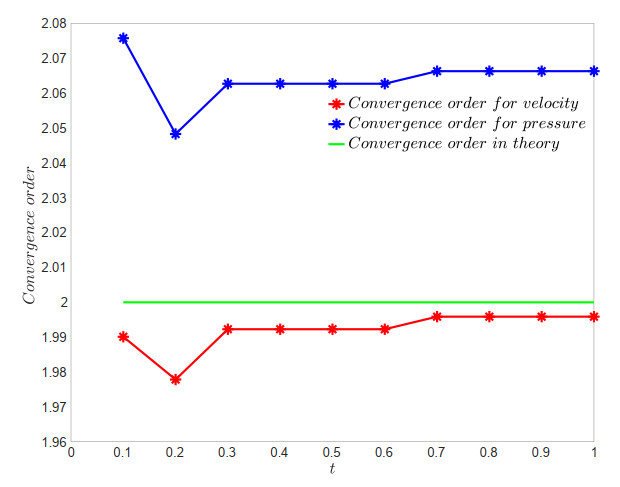
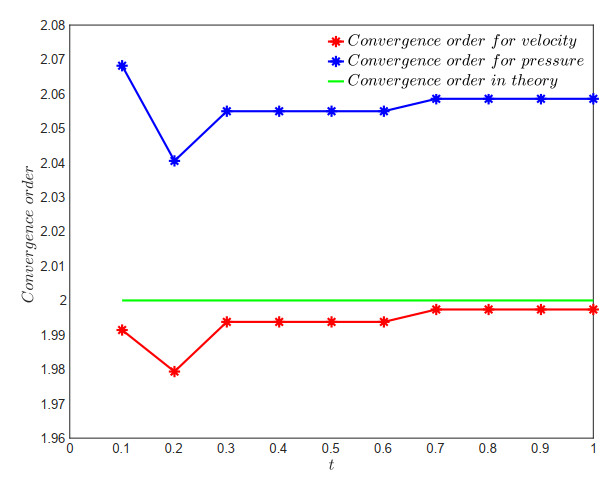
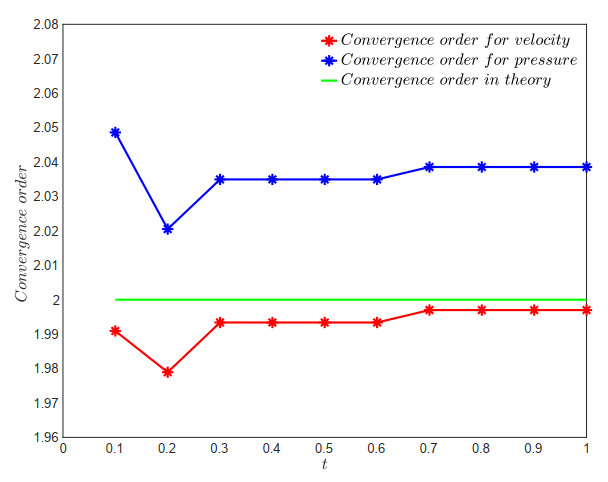
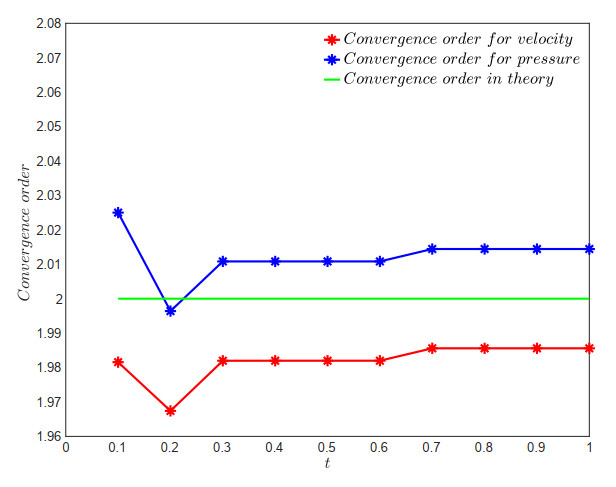
In Table 1, we define $N = \frac{1}{h}$. The table presents the optimal convergence order $\mathcal{O}(h^2)$ for the error estimates of the $\mathbf{H^1}$-norm of the velocity and the $\mathrm{L}^2$-norm of the pressure, considering various mesh parameters $\alpha\in\left(\frac{1}{6}, \frac{1}{2} \right)$, and a time step size of ${{\Delta t}} = h^2$ at the time level $t = 1$. This validates the convergence analysis of the FVEM scheme (4.3) for the non-stationary Stokes equations.

Furthermore, the error order curves depicted in Figures 12–15 below, respectively, indicate that the numerical solutions of (4.3) exhibit optimal error estimates at the time levels $t\in [0.1, 1]$ for various values of the mesh parameter $\alpha\in \{\frac{1}{5}, \ \frac{1}{2}-\frac{\sqrt{3}}{6}, \ \frac{1}{4}, \ \frac{1}{3}\}$. These numerical findings align perfectly with our theoretical predictions, confirming that the proposed FVEM scheme is capable of achieving the optimal error convergence order that matches the corresponding FEM schemes.

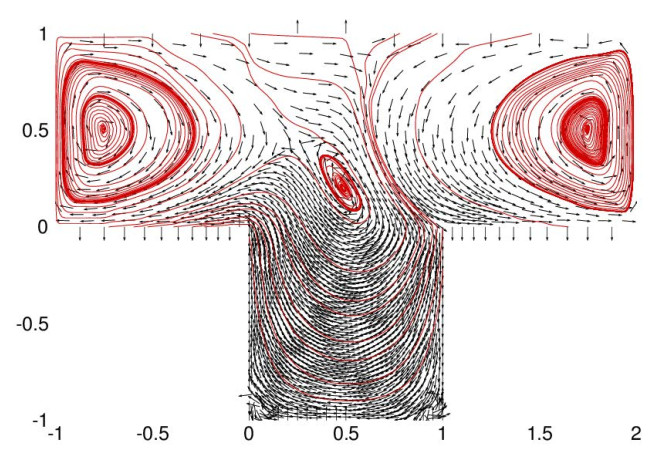
In our concluding numerical example, we will conduct a cavity flow analysis to demonstrate the efficiency and practicality of the FVEM scheme in tackling non-stationary Stokes equations. To visualize the numerical results resulting from the FVEM scheme, we will utilize the software TECPLOT version 360EX.

Example 3. This example considers the cavity flow for the problem defined in (2.1), under the conditions of $\mu = 1$ and $\mathbf{f} = \mathbf{0}$ on the domain $\Omega = \left([-1, 2]\times[0, 1]\right)\cup \left([0, 1]\times[-1, 0]\right)$. At the left entrance, where $x = -1$, the initial function ${\mathbf{u}}(\mathbf{x}, 0)$ and the boundary value function ${\mathbf{u}}(\mathbf{x}, t)$ are both set to ${\mathbf{u}}_0(\mathbf{x}) = (0, y(1-y))$. Similarly, at the right exit, where $x = 2$, these functions are set to ${\mathbf{u}}_0(\mathbf{x}) = (0, 2)$. Elsewhere on the boundary, the boundary velocities are maintained at 0.

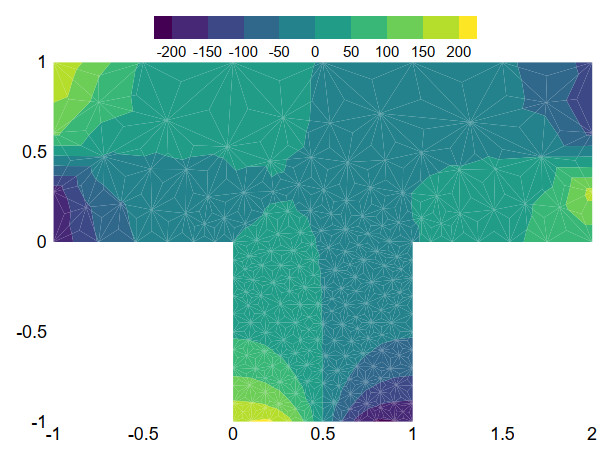
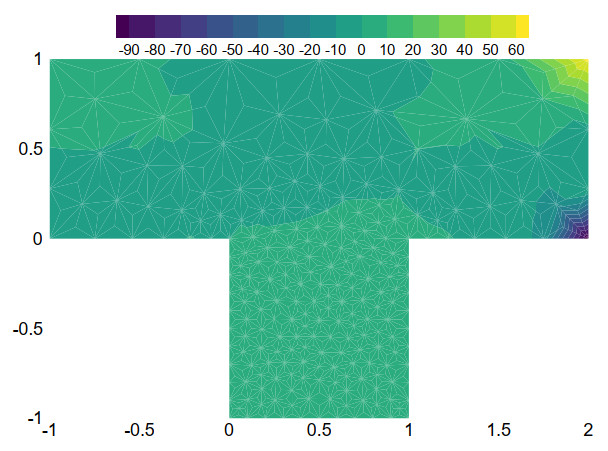
In this example, we utilize unstructured triangular meshes as the primary partition $\mathcal{T}$ for the domain $\Omega$, as illustrated in Figure 16. For the dual partitions ${\mathcal{T}_*}$ of the FVEM scheme, we select the mesh parameter to be $\alpha = \frac{1}{2}-\frac{\sqrt{3}}{6}$. The time step size remains at ${{\Delta t}} = 0.005$. Figures 17 and 18 present the pressure contours obtained through the FVEM scheme at time points $t = 0.01$ and $t = 1$, respectively. Comparing these figures, it is evident that the pressure contour lines have become less pronounced.

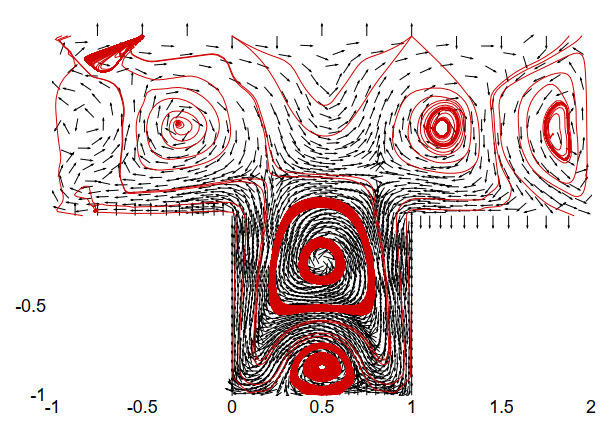
Figures 19 and 20 illustrate the streamline and flow patterns at time instances $t = 0.01$ and $t = 1$, respectively. Comparing Figure 19 with Figure 20, it can be intuitively observed that the streamline and flow field obviously and deterministically shift from the bottom wall of the cavity to the two side walls. This observation suggests that the FVEM scheme we propose is both stable and efficient in tackling the non-stationary Stokes equations. To learn more information on the fluid mechanics of driven cavities, readers are encouraged to consult ^[45] and its related references.

7.   Conclusions

In this paper, a novel fully discrete spatial-temporal FVEM scheme, utilizing the LC element pair, has been developed and investigated for solving the non-stationary Stokes equations on barycenter-refined triangular meshes. We first derived a semi-discrete temporal scheme for the non-stationary Stokes equations, followed by directly constructing the fully discrete FVEM scheme from the semi-discrete temporal scheme, thereby avoiding the establishment of a semi-discrete spatial FVEM scheme. Employing the theoretical analysis techniques of classical FEMs, we established the stability of the fully discrete FVEM scheme, as well as the existence and uniqueness of the discrete solution, and derived the optimal order error estimate for spatial variables. The discrete velocity solution obtained from the FVEM scheme exhibits the property of local mass conservation. Numerical experiments have been conducted to confirm that the numerical errors between the discrete FVEM solutions and the exact solutions align with the theoretical findings presented earlier. Furthermore, a numerical simulation of flow within a cavity demonstrates the feasibility and efficiency of the fully discrete FVEM scheme in computing numerical solutions for the non-stationary Stokes equations. The methods and concepts presented in this paper can be extended to other time discretization schemes, such as the Crank-Nicolson FVEM scheme with second-order temporal accuracy. Given the benefits of higher-order approximations in fluid dynamics applications, the proposed scheme deserves further investigation. Future research should extend the application of this scheme to the non-stationary Navier-Stokes equations and broader computational fluid dynamics problems, while systematically addressing potential singularities caused by geometric discontinuities near the corners of the computational domain.

Use of Generative-AI tools declaration

The author(s) declare(s) they have no used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The author would like to express the deepest gratitude to the anonymous referees for their careful reading of the manuscript, several valuable comments, and suggestions for its improvement. This work is partly supported by the Foundation Research Project of Kaili University (grant no. 2024ZD007) and by the Famous Teacher Studio Project of Guizhou Province (grant no. MSGZS-SJ-2024003).

Conflict of interest

The author declares that he has no potential conflict of interest or personal relationships that could have appeared to influence the work reported in this paper.

A.   The proof of Theorem 1

Proof. We first present the existence of the solution to Eq (3.1). Let $\mathbf{A}\left(\mathbf{u}^n, \mathbf{v}\right) = ({\mathbf{u}}^n, \mathbf{v}) +{{\Delta t}} a\left(\mathbf{u}^n, \mathbf{v}\right)$ and $\mathbf{F}(\mathbf{v}) = ({{\Delta t}}\mathbf{f}^n+\mathbf{u}^{n-1}, \mathbf{v})$ for any $(\mathbf{v}, q)\in\left({\mathbf{H_{0}^1}}(\Omega), \mathrm{L}_0^2(\Omega)\right)$. It is easy to see that $\mathbf{A}\left(\mathbf{u}^n, \mathbf{v}\right)$ is a bounded bilinear form satisfying $\mathbf{A}\left(\mathbf{u}^n, \mathbf{v}\right) \leqslant C\|\mathbf{u}^n\|_1\|\mathbf{v}\|_1,$ and there exists a positive constant $c$ such that $\mathbf{A}\left(\mathbf{u}^n, \mathbf{u}^n\right) = {{\Delta t}}\mu|\mathbf{u}^n|^2_1+\|\mathbf{u}^n\|^2_0 \geqslant c\|\mathbf{u}^n\|^2_1.$ For given $\mathbf{u}^{n-1}$ and $\mathbf{f}$, we know $\mathbf{F}(\mathbf{v})$ is a continuous function on $\mathbf{L^2}(\Omega)$. It follows from (2.5) that $b(\mathbf{u}^n, q)$ satisfies the $\inf-\sup$ stability condition for any $(\mathbf{u}^n, q)\in\left({\mathbf{H_{0}^1}}(\Omega), \mathrm{L}_0^2(\Omega)\right)$. Thus from the theory of existence and uniqueness of the solution for the mixed variational problem, Equation (3.1) has a unique series of solutions $(\mathbf{u}^n, p^n)\in\left({\mathbf{H_{0}^1}}(\Omega), \mathrm{L}_0^2(\Omega)\right)$, $n\in\mathbb{Z}_M$.

We next consider the estimates. Choosing $\mathbf{v} = \mathbf{u}^n$, $q = p^n$ in (3.1), we have

Applying the Cauchy-Schwartz inequality, Yang's inequality and the Poincaré inequality to the right-hand term of the equation above yields

and thus $\|\mathbf{u}^n\|_0^2+{{\Delta t}}\mu|\mathbf{u}^n|_1^2 \leqslant {{\Delta t}}\mu^{-1}\|\mathbf{f}^n\|^2_0+\|\mathbf{u}^{n-1}\|^2_0.$ Observe that $\mathbf{u}^0 = \mathbf{u}_0$. Summing the above inequalities from $1$ to $n$ yields the first estimate of this theorem, which implies

We now analyze the second estimate. To this end, we first show the estimate $\|d_t{\mathbf{u}}^n\|_0$. Note that $(\mathbf{u}^n, p^n)\in\left({\mathbf{H_{0}^1}}(\Omega), \mathrm{L}_0^2(\Omega)\right)$ for any $n\in\mathbb{Z}_M$ is the solution of (3.1), and this means $b\left(\mathbf{u}^n, q\right) = b\left(\mathbf{u}^{n-1}, q\right) = 0,$ for all $q\in \mathrm{L}_0^2(\Omega)$. This combines with (3.1) to yield that for all $(\mathbf{v}, q)\in\left({\mathbf{H_{0}^1}}(\Omega), \mathrm{L}_0^2(\Omega)\right)$,

Choosing $\mathbf{v} = d_t{\mathbf{u}}^n$, $q = p^n$ in the above equation gives us

which is equivalent to ${{\Delta t}} \|d_t{\mathbf{u}}^n\|_0^2 +a\left(\mathbf{u}^n, \mathbf{u}^n\right) -a\left(\mathbf{u}^n, \mathbf{u}^{n-1}\right) = {{\Delta t}}(\mathbf{f}^n, d_t{\mathbf{u}}^n).$ Applying the Cauchy-Schwartz and Young inequality to the above equation, we get

Summing the above inequalities from $1$ to $n$ yields

which implies

It is our turn to present the estimate $\|p^n\|_0$. Applying the $\inf-\sup$ condition (2.5) to the first equality in (3.1), it yields $\|p^n\|^2_0 \leqslant C\left(\|d_t{\mathbf{u}}^n\|^2_0 + \mu |{\mathbf{u}}^n|^2_1 +\|{\mathbf{f}}^n\|^2_0\right).$ By summing the above inequalities from $1$ to $n$, we obtain

Applying the results of (A.1) and (A.2) to the above right-hand term yields the second desired result. This completes our proof. □

B.   The proof of Theorem 2

Proof. Note that $\left({{\mathbf{u}}, p} \right)\in\left({\mathbf{H_{0}^1}}(\Omega), \mathrm{L}_0^2(\Omega)\right)$ for any $t\in (0, T]$ is the solution of the problem (2.1) and thus satisfies the variational form (2.2). Taking $t = t_n$ in (2.2) yields

Subtracting (3.1) from (B.1), and then taking $\mathbf{v} = \mathbf{u}(t_n)-\mathbf{u}^n$ and $q = p(t_n)-p^n$, we obtain

where we used the fact that $\mathbf{f}(t_n) = \mathbf{f}^n$. Denote $\mathbf{e}^n = \mathbf{u}(t_n)-\mathbf{u}^n$, using the definition of $d_t{\mathbf{u}}^n$ and the result of (3.2), and it follows that

Note that $t-t_{n-1}\leqslant {{\Delta t}}$ and $t-t_{n-1}\leqslant \tau(t)$ for any $t\in [t_{n-1}, t_{n}]$, $n\in\mathbb{Z}_M$. An application of the Cauchy-Schwartz inequality, Yang's inequality, and the Poincaré inequality to the right end term of the above equation obtains

where we used the fact that

Note that $\frac{1}{2{{\Delta t}}} \left(\|\mathbf{e}^n\|^2_0 - \|\mathbf{e}^{n-1}\|^2_0 \right) \leqslant \frac{1}{{{\Delta t}}} \left(\mathbf{e}^n-\mathbf{e}^{n-1}, \mathbf{e}^n\right).$ By substituting the above two inequalities into the right and the left ends of equation (B.2) respectively, we obtain

By summing the inequality above from $1$ to $n$ and using the fact that $\mathbf{e}^0 = \mathbf{0}$, we gain

which implies for any $n\in\mathbb{Z}_M$,

We next consider the estimate of $\mathbf{\eta}^n = p(t_n)-p^n$. Note that $(\mathbf{u}^n, p^n)\in\left({\mathbf{H_{0}^1}}(\Omega), \mathrm{L}_0^2(\Omega)\right)$ for any $n\in\mathbb{Z}_M$ is the solution of (3.1), and $\left({{\mathbf{u}}(t), p(t)} \right)\in\left({\mathbf{H_{0}^1}}(\Omega), \mathrm{L}_0^2(\Omega)\right)$ for any $t\in (0, T]$ satisfies the variational form (2.2), which leads to $b\left(\mathbf{e}^n-\mathbf{e}^{n-1}, q\right) = 0$ for all $q\in \mathrm{L}_0^2(\Omega)$. Subtracting (3.1) from (B.1) again, and then choosing $\mathbf{v} = \mathbf{e}^n-\mathbf{e}^{n-1}$ and $q = p(t_n)-p^n$, yields $\left({\mathbf{u}}_t(t_n)-d_t{\mathbf{u}}^n, \mathbf{e}^n-\mathbf{e}^{n-1}\right) +a\left(\mathbf{e}^n, \mathbf{e}^n-\mathbf{e}^{n-1}\right) = 0$. Then it holds that

Again an application of the Cauchy-Schwartz inequality, Yang's inequality, and the inequality (B.3) to the right end term of the above equation obtains

This means the inequality (B.5) can be written as

By summing the inequality above from $1$ to $n$ and using the fact that $\mathbf{e}^0 = \mathbf{0}$, we gain

On the other side, the difference between (3.1) and (B.1) leads to

where the equality (3.2) was used. Note that

and observing the $\inf-\sup$ condition (2.5) yields

Then applying inequality (B.3) again, we have

Considering the estimates (B.4) and (B.6), summing the above inequalities from $1$ to $n$ yields

This finishes the proof of this theorem. □