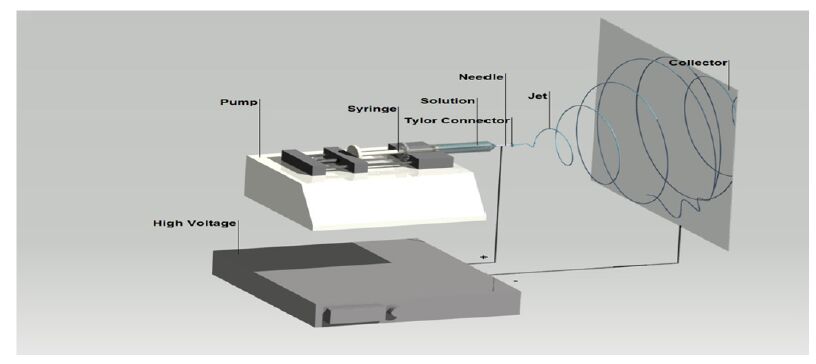
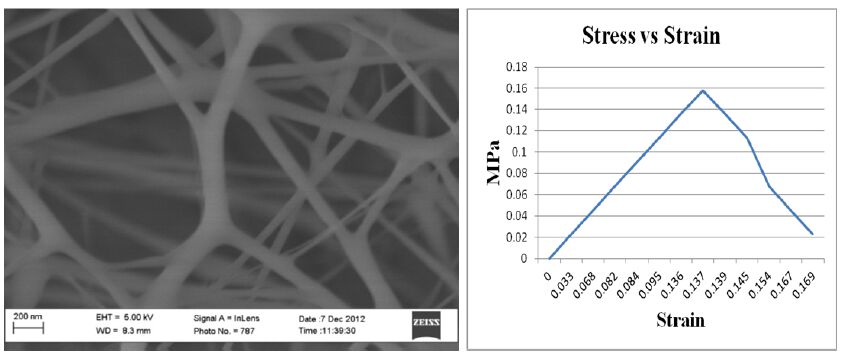
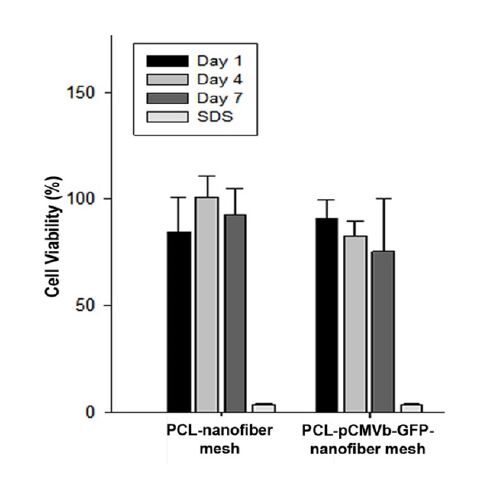
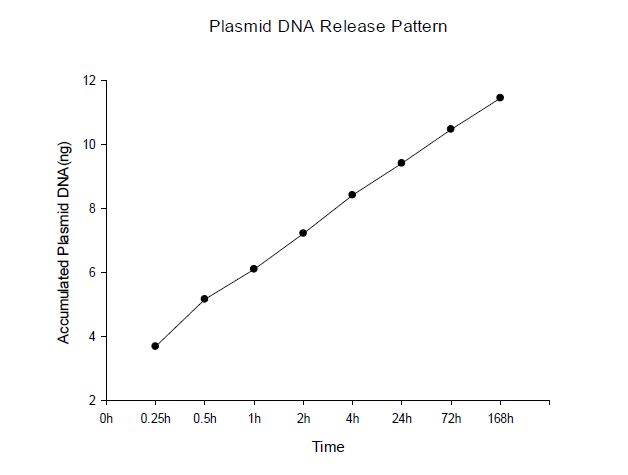
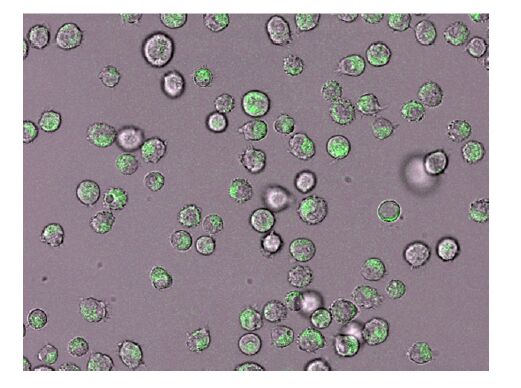
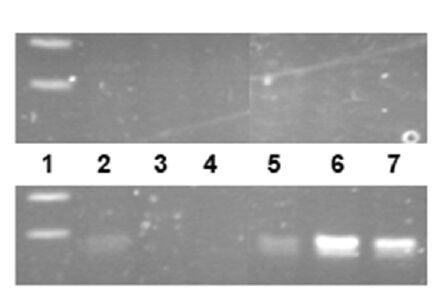
Poly-ε-caprolactone electrospun nanofiber mesh as a gene delivery tool

1.   Introduction

The biological sciences have advanced at a breakneck pace during the last few decades, and it's reasonable to predict that this trend will continue, aided by massive technological advancements in a long time. Mathematics has always both contributed to and benefited society. There is huge progress in the natural sciences because of mathematics, and it can do the same for biological science ^[1]. Biology generates intriguing problems, and mathematics develops models to help us understand them, and biology then tests the mathematical models. The handling of complex mathematical systems has been made easier thanks to recent improvements in computer algebra systems. This has allowed scientists to concentrate on understanding mathematical biology rather than the mechanics of solving problems ^[2].

Cancer has always been considered a complex system as it causes different diseases around two hundred with different characteristics. Therefore, many scientists are still trying to investigate the interactions between tumor cells and immune cells by employing different strategies to better understand the dynamics of cancer ^[3,4]. Research is devoted to understanding the interaction between the immune system and tumor cells ^[5]. Ordinary differential equations mathematical models have been proven valuable to understand the dynamics of the tumor-immune system how host immune cells and cancerous cells evolve interact; See e.g. ^[6,7,8]. However, fractional-order differential equations have more characteristics than classical derivatives in mathematical modeling.

Accordingly, the subject of fractional calculus has gained popularity and importance due to its demonstrated applications in system biology ^[9], and different fields of sciences ^[10]. Derivatives and integrals of any non-negative order are allowed in fractional calculus. The benefit of fractional derivatives (integral as well) is that they are not a local (or point) attribute (or quantity) ^[11]. We noticed that in epidemiology, mathematical models are frequently employed to comprehend the complexity of infectious diseases. The stability theory of differential equations is used to study the dysentery modeling approach with controls ^[12]. The most often employed operators, such as Caputo-Fabrizio, and Atangana-Baleanu, involve a local derivative with an exponential function, power-law, and a Mittag-Leffler function, respectively. On the other hand, real-world processes display intricate fractal behavior, including volatility, aquifers, porous media, biomedicine, and Darcy's law. In this context, it is necessary to have operators involving nonlocal differentiation in the kernel, which Atangana provided in the form of fractional fractal operators ^[13]. In the field of mathematical biology, epidemiological models design has been examined using classical and certain fractional-order operators such as conformable derivatives, Caputo-Fabrizio, Atangana-Baleanu, beta derivatives, and a few more. Dengue fever, tuberculosis, measles, Ebola, and other diseases are among the epidemiological designs supported by fractional operators. Nevertheless, fresh real-life applications studied on fractal-fractional operators have shown that the operator's effectiveness is best suited to curves derived under Caputo type fractal operators using actual banking data ^[14]. Fractal-fractional derivative and integration analysis develop complicated behaviors of diarrhoeal sickness. These operators have created the best curve of the actual data of the diseased population, and the model of diarrhea proves that these novel operators have a unique solution ^[15]. Some application of fractional order model with the local and nonlocal, nonsingular kernel is also studied in ^{[16,17,18,19,20,21]} having memory results for a dynamical system.

Fractional derivative in the Caputo sense is studied in ^[29,30,31]. A vitro model of HER 2 + breast cancer cells dynamics resulting from many dosages and timing of paclitaxel and trastuzumab combination regimens was proposed in ^[30]. Study the pattern and the trend of spread of this disease and prescribe a mathematical model which governs COVID-19 pandemic using Caputo type derivative ^[32]. Fractal-fractional operator in the Caputo sense, the condition for Ulam's type of stability of the solution to the models and its related work is in ^{[33,34,35,36]}. Distributed order time-fractional constitution model is put forward to analyze the unsteady natural convection boundary layer flow and heat transfer, in which the magnetic field effect is considered and its related work is in ^[37,38,39].

This paper, in Sections 1 and 2, consists of an introduction and basic definitions for analysis. Section 3 is for the Ulam-Hyres stability and uniqueness of the proposed scheme of the fractional order cancer model with the fractal fractional operator by using generalized Mittag-Leffler Kernel. A numerical algorithm for simulation and results is developed in Section 4. Description and conclusion of results are described in Sections 5 and 6.

2.   Preliminaries

We consider some basic refinement of fractional calculus ^{[22,23,24,25]} in this section which are helpful for analysis and simulation of the problem.

Definition 2.1. Let $0\leq \xi$, $\eta \leq 1$, then $U(t)$ in the Riemann-Liouville for fractal-fractional with power-law kernel and the fractal-fractional integral have been given as ^[26]:

and

Definition 2.2. Let $0\leq \xi$, $\eta \leq 1.$ Then $U(t)$ in the Riemann-Liouville for fractal fractional operator having exponentially decaying kernel and fractal-fractional integral have been presented by ^[26,27]:

and

Definition 2.3. Let $0\leq \xi$, $\eta \leq 1$ then $U(t).$ Then the Riemann-Liouville for fractal fractional operator with generalized Mittag-Leffler kernel and fractal-fractional integral have been presented by ^[26,27]:

and

3.   Cancer model with fractal-fractional operator

Recently, many researchers studies to examine the mathematical model of cancer-immune ^[27,28]. By this motivation, IL-12 cytokine is used to increase it ability by increasing the number of CD4+T, CD8+T lymphocytes, and the help of anti-PD-L1 inhibitor with effect of CD8+T cells are added in Castiglione-Piccoli model. So, ^[27,28] explains the new time-dependent ordinary differential system. Equation (1) tells about components of immune system against cancer cells, which is made by adding IL-12 and anti-PD-L1 to components of immune system. The main objective of adding new variables in (1) is to fight cancer cells for the immune system more effectively. The system of nonlinear fractional order with Fractal Fractional operator is given as

where

Here $H, C, M, D, I L - 2, I L-12$ and $Z$ symbolize $CD_4^+T$ and $CD_8^+T$ lymphocytes, cancer cells, dendritic cells, IL-2 and IL-12 cytokine, anti-PD-L1, respectively given in ^[27,28]

Theorem 1. The solution of the given cancer fractal-fractional model (3.1) along initial conditions is unique and bounded in $R_+^7$.

Proof. We obtain

If $(S(0), U(0), C(0), C_{a}(0), R(0), B(0) \in R_+^6$, then according to Eq (3.2) thee solution cannot escape from the hyperplane. Also on each hyperplane bounding the non-negative orthant, the vector field points into $R_+^7$, i.e., the domain $R_+^7$ is a positively invariant set.

Stability and existences of proposed operator

Here, we consider stability and existences with proposed operator,

For existence, we have

where

We can write system (3.4) as:

By replacing $^{ABR}_{0}D^{\xi, \eta}_{0}$ by $^{ABC}_{0}D^{\xi, \eta}_{0}$ and applying fractional integral, we get

where

For the existence theory, we define a Banach space $B = C\times C\times C\times C\times C\times C\times C$, where $C = [0, T]$ under the norm

Define an operator $\wp:B \rightarrow B$ as:

Now, we suppose that $\Lambda(t, (\Omega(t))$ is the non-linear function with growth and the Lipschitz conditions.

● For each $\Omega\epsilon B, \; \exists$ constants $A_{\Lambda}$ and $P_{\Lambda}$ such that

● For each $\Omega$, $\overline{\Omega}\epsilon B, \exists\; a$ constant $K_{\Lambda} > 0$ such that

Theorem 2. For the set of continuous function $\Lambda = [0, T]\times B\rightarrow R$ there exists at least single outcome for system (3.1) if the condition (3.6) holds.

Proof.

Let

Now for any $\Omega\epsilon B$, we have

Hence, $\wp$ is uniformly bounded, for equicontinuity of $\wp$, let us take $t_{1} < t_{2}\leq T$. So, we have

when $t_{1}\rightarrow t_{2}$ then $|\wp(\Omega)(t_{2}-\wp(\Omega)(t_{1}|$. Consequently, we can say that,

Hence, $\wp$ is equicontinuous. So, theorem is proved. Thus, system has at least one solution.

Theorem 3. Assume that (3.7) holds. If $\varrho < 1$, where

Then the considered model has a unique solution.

Proof. For $\Omega, \overline{\Omega} \epsilon B$, we have

Hence, $\wp$ is a contraction. So, system has unique solution by using Banach contraction principle.

Definition 3.1. The proposed model is Ulam-Hyres stable if $\exists\; \wp_{\xi, \eta} \geq 0$ such that for any $\varepsilon > 0$ and for every $\Omega \in (C[0, T], R)$ satisfies the following inequality:

and there exists a unique solution $\Upsilon \in (C[0, T], R)$ such that

Consider a small perturbation $\Psi \in C[0, T]$ such that $\Psi(0) = 0$. Let

Theorem 4. The solution of the perturbed model

fulfills the relation given below

where

Proof. Under condition (3.7) along with Theorem 3.5, the solution of the proposed model is Ulam-Hyres stable if $\varrho < 1$.

Let $\Upsilon\in B$ be a unique solution and $\Omega\in B$ be any solution of the proposed model, then

Consequently, one can write

We can write the above relation is

where $\wp_{\xi, \eta} = \frac{\xi^{\ast}_{\xi, \eta}}{1-\varrho}$. Hence, proposed scheme is Ulam-Hyres stable.

4.   Proposed scheme with fractional operator

In this section, The numerical scheme is establish for developed fractional order model, we get

Now, we derive the numerical scheme at $t = t_{x+1}$, we have

On system (4.2), we have

Using Lagrangian piece-wise interpolation with in the finite interval $[t_f, t_{f+1}]$, we get

We have

5.   Numerical results and discussion

The mathematical analysis of the tumor-immune system consisting of a fractional differential equation has been presented. In order to conduct a credible study, several $\alpha$ values are evaluated. By using non-integer parameter values, surprising reactions are achieved from the compartments of the proposed fractional-order model. Solution for $H(t), M(t), C(t)$, $I_{2}(t)$ and $I_{12}(t)$ start decreasing by decreasing the fractional values while $D(t)$ and $Z(t)$ start increasing by decreasing fractional values respectively and can be seen easily from Figures 1–7 which converges to steady state with dimension 0.7. Solution for $H(t), M(t), D(t)$, $I_{2}(t)$, $I_{12}(t)$ and $Z(t)$ start increasing by decreasing the fractional values while $C(t)$ start decreasing by decreasing fractional values respectively and can be seen easily from Figures 8–14 which converges to steady state with dimension 0.9. It is easily observed from Figure 3 and Figure 9 that cancer cell start decreasing by decreasing the fractional with both dimensions. But Fractal-fractional technique with dimension 0.9 gives better results for all the compartments which converges rapidly to steady state as compare to dimension 0.7. It is easily observed from simulation that fractional order model check the relationship between cancer cells and immune system which further increase the immune system of CD4+T and CD8+T lymphocytes production and decrease the cancer cell by adding IL-12 cytokine and anti-PD-L1 inhibitor. The variable anti-PD-L1 inhibitor was introduced to catch cells escaping from the immune system and destroy these cells which can be seen in Figures 7 and 14 with both dimensions. Also the variable IL-12 cytokine is used to increase the number of CD4+T and CD8+T lymphocytes production which can be seen in Figures 1, 2 and 8, 9 with dimension 0.7 and 0.9 respectively. This kind of study helps to analyze the effect of cancer cell and its anti-PD-L1 inhibitor in human body. Numerical simulations are important in sense for developing algorithm of treatment cell and impact of vaccination to control the disease. This kind of study is helpful for physician for planing and decision making for treatment cells.

6.   Conclusions

We developed a scheme for the analytical solution of the fractional order cancer model by using the Fractal Fractional operator. The model represents population dynamics during the disease as a set of non-linear fractional-order ordinary differential equations. The Fractional-order system is analyzed qualitatively to verify the state of the disease as well as determine the unique positive solutions. Uniqueness and boundedness for solution are proved using the fixed point theory. The solution is obtained for the fractional-order cancer model using the Fractal Fractional operator. Numerical simulations are carried out to check the actual behavior of the cancer outbreak using a developed scheme for fractional-order model, which will be helpful in future understanding of this disease and control strategics. The simulation easily observed that the fractional-order model examines that IL-12 cytokine and anti-PD-L1 inhibitor are used to check the relationship between the immune system and cancer cells, which cause to increase the immune system and decrease the cancer cell is due to IL-12 cytokine and anti-PD-L1 inhibitor with the impact of fractional parameters. Results show significant changes using different fractional values with different dimensions. Numerical simulations are important for developing an algorithm of treatment cells and the impact of vaccination to control the disease. In the future, the other cytokineses are also added to the mathematical model, which can further check with different types of derivatives and different types of techniques.

Conflict of interest

All authors declare no conflicts of interest in this paper.