From genetic circuits to industrial-scale biomanufacturing: bacterial promoters as a cornerstone of biotechnology

1.   Introduction

Uncertainty has long been considered as a significant factor that influences investors' behavior (Menzly et al., 2004; Bekaert and Hoerova, 2016).¹ Hansen, Sargent and Tallarini (1999) and Bloom (2009) note that a sudden rise in uncertainty will impede business prospects and households' consumption, which can threaten future cash flows and weaken stock market performance. A popular approach for examining the negative effect of uncertainty on stock prices has been a regression analysis that regresses (excess) stock returns on a conditional variance generated by a GARCH-type model as pioneered by French et al. (1987). Follow-up studies of this issue are summarized by Bollerslev et al. (1992) and Engle (1995). In general, the literature supports the notion that conditional volatility is a good proxy for a risk variable that explains excess stock returns (Bali and Engle, 2010; Bali and Peng, 2006), confirming the risk-return tradeoff hypothesis (Lettau and Ludvigson, 2010.)

¹ Hillen et al. (2017) survey definitions of uncertainty, which vary substantially and mainly refer to possibility that a potentially harmful event may occur (Dugas et al., 2000). With different diverse definitions of uncertainty, however, they share a common feature, which is the indeterminacy of future outcomes (Carleton et al., 2010). Economic policy uncertainty (EPU) helps to narrow down the scope. Yet, EPU in this study is tied to the news-based definition that contains trio terms of economic, policy, and uncertainty. This approach is pertinent to empirical analysis.

Since conditional variance is characterized by a long memory, the conditional variance series appears to be too smooth to capture the impact of a jump in stock prices. In fact, investors often reveal an aversion to loss due to a downside movement of stock prices. Subsequent work in the field refocused on the use of value-at-risk (VaR) as a measure of downside risk. Bali et al. (2009) and Chen and Chiang (2016) demonstrate that the VaR is a significant factor in explaining excess stock returns, supporting the downside risk premium hypothesis.

Spikes in volatility in financial market often spillovers to the global markets due to cross market correlations. The U.S. subprime crisis attests to the fact that financial turmoil can rapidly disturb not only a country's domestic business sectors but also spread to those in other countries. The speed at which information travels is accelerated by the digital circulation and reputation of major newspapers as well as different types of media instruments. Stirred by financial gurus, politicians, and Trumpian type twitter statements and comments, investors are often motivated to make rush investment decisions that regularly disrupt stock market tranquility.² The attention that market participants place on uncertainty changes (Peng and Xiong, 2006) as revealed in newspapers or media apparently is an integral part of inputs in accessing financial market behavior. An analysis of news headlines by Kirange and Deshmukh (2016) finds that the way in which emotions are classified based on financial news has significant information content in predicting stock market prices. The study of Tetlock, Saar-Tsechansky, and Macskassy (2008) also uses a broad sample of articles from Wall Street Journal and Dow Jones News Service to analyze stock market behavior.

² For instance, following the Fed's decision on December 19, 2018 to raise rates, Trump criticized the move by tweeting, "The only problem our economy has is the Fed. They don't have a feel for the market…The Fed is like a powerful golfer who can't score because …he can't putt!" (Trump, December 24, 2018). This statement caused the Dow to drop 650.17 points, which led to a 1,010.45-point drop of the Japanese Nikkei the following day.
Trump's twitter is available at: https://www.thestreet.com/politics/trump-continues-trash-talking-federal-reserve-over-twitter-14819895.

Recent publications show that the economic policy uncertainty (EPU) index constructed by Baker et al. (2016) is capable of explaining stock market behavior. Following this line of inquiry, studies by Christou et al. (2017), Balli et al. (2017), Bahmani-Oskooee and Saha (2019a), and Chiang (2019a) demonstrate that stock returns are negatively correlated with a change of EPU. The current study is motivated by this line of research and attempts to expand its scope by using a broad category of uncertainty measures in examining stock market behavior.

This paper differs from existing studies in the following ways. First, in the test equation, this study adds several categorical policy uncertainties as independent variables rather than use a single measure of financial market risk, such as VIX. This specification helps to alleviate the impact of a spurious correlation if a single set of variables is used. As noted earlier, the current literature tends to use a given measure of uncertainty such as EPU in examining the uncertainty-return relation (Ozoguz, 2009; Antonakakis et al., 2013; Brogaard and Detzel, 2015; Tsai, 2017). Employing multiple uncertainty indices is likely to provide more insights on the impact of different parametric measures based on various sources of uncertainty.

Second, the focus of this study is on the Japanese stock market, which is used because of the size of its capital market and its unique ability to link other Asian markets to the U.S. capital market.³ Viewed in retrospect, Japan has historically played a vital position in carrying transactional information of stock prices among Japan and global markets as noted in a number of studies (Becker et al., 1990; Karolyi and Stulz, 1996; Connolly and Wang, 2003; Chong et al., 2008; Hamao, 2018). Moreover, after "Japan's lost decade"⁴, the Japanese Prime Minister Shinzo Abe attempted to adopt a series of expansionary monetary and fiscal policies and structural reforms designed to resolve Japan's earlier macroeconomic problems. By implementing Abenomics, which entailed open-ended asset purchases along with stimulus packages, the central bank of Japan was able to weaken the Japanese yen in the first half of 2013, which helped to boost the Nikkei index (Zhang, 2018).⁵ Investors, however, are concerned about whether the Bank of Japan's easy monetary policy could cause rampant speculation during an economic boom that could lead to a debt crisis.

³ By the end of 2018, the U.S. had the top market capitalization of 30436.31 billion U.S. dollars, followed by China with 6,323.88 billion U.S. dollars and Japan with 5,296.81 billion U.S. dollars.
https://www.theglobaleconomy.com/rankings/stock-market-capitalization-dollars/

⁴ Japan experienced a period of economic stagnation and price deflation from 1991 through 2001, which is known as "Japan's Lost Decade." A survey of historical price movements in the Japanese stock market can be found in Hamao (2018).

⁵ Abe's fiscal stimulus, which included a 10.3 trillion-yen package in 2013 and an increase in the consumption tax to 10% in 2014–2015 to finance government spending, however, have created a great deal of uncertainty about their economic consequences.

Third, the study's focus on the U.S. and Japanese markets is based on the data constraint as only these two countries provide a broader range of categorical policy uncertainty indices. Use of these new indices also allows us to revisit the dynamics of a stock return-volatility relation between the U.S. and Japan and to connect this research to earlier studies by Hamao et al. (1990), Karolyi and Stulz(1996), Zhang (2018). The availability of the uncertainty indices also affords this study the ability to investigate international uncertainty spillovers and to compare the relative strength from different categories of policy uncertainty changes (Arbatli et al., 2017). The empirical research of Japan's policy uncertainty on stock markets is a timely study that helps to shed some light on the policy evaluations gained in other countries.

This study contributes to the literature in the following aspects. First, this study employs both financial risk variables and different uncertainty measures to test Japanese stock market behavior. Evidence indicates that excess stock returns in the Japanese market are negatively related to changes of equity volatility, downside risk and policy uncertainties. Second, this paper demonstrates a significant positive intertemporal relation between (excess) stock returns and the level of lagged volatility/downside risk, which supports the risk-return tradeoff hypothesis as noted by Bali et al. (2009) and Chen and Chiang (2016). Third, the evidence shows that a rise in EPU leads to an increase in excess stock returns in the subsequent month, supporting the uncertainty premium hypothesis. Moreover, the evidence also supports the existence of uncertainty changes from fiscal policy, monetary policy, trade policy and global markets as a whole, which generally confirms the policy uncertainty premium hypothesis. Fourth, while testing the interactions between the U.S. and Japanese markets, evidence indicates the presence of strong uncertainty premiums associated with total uncertainty and different types of policy uncertainties for the U.S. own market, but offers very little support for spillover from the Japanese market to the U.S. market. The only exception is in monetary policy uncertainty, where this study indicates a negatively significant effect of spillover from the Japanese market to the U.S. market. Fifth, testing of the asymmetrical impacts of an upward and downward shift in uncertainty indicates the presence of inverse relations between uncertainty changes and stock returns. Yet, the degree of asymmetry from uncertainty changes on stock returns is more significant from the Japanese own market as compared with the U.S. influence.

Following this introduction, this paper is organized as follows. Section 2 reviews the literature on the relation between policy uncertainty and stock returns. Section 3 presents regression models relevant to the empirical estimations. Section 4 describes the data and related variables of empirical estimations. Section 5 presents the empirical evidence. Section 6 conducts robustness tests using different measures of variables. Section 7 concludes the empirical findings.

2.   Literature review

Empirical investigations of policy uncertainty on stock prices mainly adopt the use of regression models that test the parametric significance between stock returns and policy surprises. A proxy for the uncertainty measure is derived from the residual series of a stated variable (Mishkin, 1982; Cornell, 1983; Pearce and Roley, 1983). Some studies, however, prefer to employ the Vector Autoregressive (VAR) model and track policy uncertainty shocks by displaying the impulse response function (Arbatli et al., 2017; Christou et al., 2017; Trung, 2019) to articulate the effect of policy uncertainty on stock returns. These studies in general reach a conclusion that policy uncertainty produces a destructive effect on consumption, investments, and cash flows, driving stock prices down.

Recognizing the value of using a newspaper-based measure of policy uncertainty developed by Baker et al. (2016), a number of studies demonstrate that heightened uncertainty will produce a negative effect on stock returns. This proposition has been confirmed by the studies of Brogaard and Detzel (2015), Arouri et al. (2016) and Carriero et al. (2017), Bahmani-Oskooee and Saha (2019b) and Chiang (2019b).

However, with a different research orientation that emphasizes the impact of uncertainty on stock market volatility, Pastor and Veronesi (2012), Liu and Zhang (2015), Tsai (2017) and Chiang (2019a) find that the inclusion of EPU can enhance the predictability of stock returns. The evidence is consistent with the proposition that an upward shift in stock volatility due to escalating policy uncertainty would lead to a demand for higher returns as a way to compensate for a systematic risk (Hansen et al., 1999).

Some researchers test the impact of EPU on Bitcoin market. Demir et al. (2018) and Phan et al. (2018) find that the EPU has a predictive power on Bitcoin returns. Wang et al. (2019) and Phan et al. (2018) document significant evidence to support that Bitcoin can serve as a hedging tool against EPU shocks. Testing the dynamic conditional correlations between the equity and commodity returns for G7 countries, Izadi and Hassan (2018) find the correlations between the gold/equity pairs are negative during the financial crisis. This finding suggests the benefit of hedging stock portfolios with gold futures whenever the EPU rises.

Influenced by the literature on the international financial contagion (Bae et al., 2003; Chiang et al., 2007; Forbes, 2012), some research articles pay particular attention to the cross-country effects of uncertainty. For instance, using the policy uncertainty indices for investigating six developed countries, Klößner and Sekkel (2014) find a significant spillover effect of policy uncertainty from the U.S. and U.K. to other countries, which are the recipients of policy uncertainty shocks during and after the crisis period. Christou et al. (2017) investigate international spillovers and find U.S. EPU produces a negative and significant effect on stock market prices in Canada, China, Japan and S. Korea. Chiang (2019b) examines the cross-country spillover effect and finds when EPU escalates in the U.S. market, shocks from this uncertainty soon spread to China's stock markets, causing stock price volatility. Li and Zhong (2019) report that the US EPU appears to be the most significant exogenous cause of the fall of China's financial conditions index. Trung (2019) tests the impact of U.S. uncertainty on emerging economies and documents that an upward shift in U.S. policy uncertainty inhibits international capital inflows and investment activity, which causes stock prices to fall in emerging economies.

Several points concerning these studies deserve further investigation. First, a commonly shared feature in these empirical works is that the uncertainty variable is based on a single measure of risk (French et al., 1987; Zhang, 2018) or uncertainty, EPU(or ΔEPU) (Li et al., 2015; Li, 2017; Chen et al., 2017, Bahmani-Oskooee and Saha, 2019a)⁶, which serves as a regressor. As a result, the nature of uncertainty is unable to be identified precisely. Recently, Davis (2016) and Arbatli et al. (2017) expand the category of uncertainty indices for the U.S. and Japanese markets, respectively, to cover the measures of fiscal policy uncertainty (FPU), monetary policy uncertainty (MPU), trade policy uncertainty (TPU) and global economic policy uncertainty (GEPU). These news-based uncertainty indices allow us to investigate the responses of stock prices to different policy uncertainty changes. Further, these data allow us to re-access some early literature on the U.S.-Japan market interactions observed by Hamao et al. (1990) and Karolyi and Stulz (1996). Thus, this study will provide more updated information on the response of stock market behavior to different types of policy uncertainties.

⁶ Bahmani-Oskooee and Saha (2019a) employ an error-correction model (Engle and Granger, 1987) to explain the stock prices, so both the level of EPU and ΔEPU are included in their models.

A second common feature presented in the literature is that certain risk factors are excluded from the test equation when examining the impact of uncertainty on stock returns even though they control for liquidity risk or conditional variance. The exclusion of a risk variable is likely to inflate the effect of policy uncertainty. Thus, it is appropriate to employ both stock market risk variables and an uncertainty variable in a test framework.

Third, the existing study shows that volatility in the U.S. market has a significant effect on the world markets (Karolyi and Stulz, 1996, Chiang et al., 2007; Diebold and Yilmaz, 2009), including the Japanese market. But the study finds no evidence to support the presence of volatility spillovers from Japan to the U.S. (Hamao et al., 1990; Karolyi and Stulz, 1996; Connolly and Wang, 1999). By the same token, the evidence suggests that EPU spillovers from the U.S. to Japan markets (Christou et al 2017; Chiang, 2019a); however, the evidence does not demonstrate that the same patterns apply to the impact from U.S. fiscal policy, monetary policy or trade policy uncertainties. In addition, it is of interest to investigate whether the asymmetric uncertainty spillover patterns also present from the Japanese market to the U.S. market.

3.   Models for estimations

3.1.   Risk model

The conventional study of the risk/uncertainty-return relation is derived from the notion of an intertemporal capital asset pricing model (Merton, 1980) and posits that excess stock returns are a linear function of stock return volatility and other investment opportunities. Following Bali et al. (2009), the representation is written as:

where R_t is the (excess) expected stock market return at time t. $\Delta Vo{l_t}$ is the log-difference in stock volatility, which is the monthly volatility calculated as the realized variance of the daily returns using the window size of returns for 22 trading days (see French et al., 1987).The estimated coefficient β₁ is anticipated to be negative based on the fact that –($\Delta Vo{l_t}) = - \left({Vo{l_t} - Vo{l_{t - 1}}} \right), $ which implies a negative impact from ${Vo{l_t}}$ on R_t and a positive effect from $Vo{l_{t - 1.}}$ It follows that if the statistical result shows a positive intertemporal coefficient for $Vo{l_{t - 1}}$, the result would be consistent with a positive relative risk aversion behavior and would support the risk-return trade off hypothesis.⁷ Evidence by French et al. (1987), Baillie and DeGennaro (1990), Ghysels et al. (2005), and Bali and Engle (2010) supports this parametric relation.

⁷ It has been argued that the expected return has an additional component reflecting a hedge demand for investment opportunities. Merton (1980) indicates that under certain conditions, the hedge component of excess returns is negligible. However, Harvey et al. (2010) find higher moments of stock returns are significant. Scruggs (1998) and Guo and Whitelaw (2006) provide evidence to argue that the hedge component is nontrivial.

However, the literature suggests that investors often place a high priority on portfolio safety to avoid big losses (Roy, 1952). Bali et al. (2009) use value-at-risk (VaR) to capture the downside risk behavior under extreme market conditions. By applying the Cornish-Fisher expansion (Cornish and Fisher, 1937), Chen et al. (2018) show that the inclusion of $ {VaR}_{t} $ helps to capture information of the higher moments of stock returns.⁸ It is anticipated that $ {\beta }_{2} < 0 $, which indicates that a rise in downside risk will induce investors to sell off their stocks, and cause stock prices to plunge (Bali et al., 2009; Chen and Chiang, 2016). However, rational traders see this situation as an opportunity to purchase stocks at declining process; however, if investors decide to place new orders will be reward by higher returns to compensate them for the downside risk. Thus, a positive estimated coefficient of $ { VaR}_{t-1} $ is consistent with the notion of a downside risk premium (Bali et al., 2009, Chen and Chiang, 2016). Moreover, the lagged dividend yield ($ {DY}_{it-1}) $ is used as a proxy for the economic fundamentals as suggested by Campbell, Lo and MacKinlay (1997). In priori, $ \delta $ > 0 reflects the fact that a higher dividend yield provides information for projecting a higher stock return.

⁸ Much evidence has supported that the use of downside risk as an argument to explain a positive risk-return relation. (Bali et al., 2009; Chen and Chiang, 2016; Chen et al., 2018).

3.2.   Uncertainty model

In applying Equation (1) to the empirical investigation, some control variables, such as the dividend yield, liquidity risk, or market sentiment (Kirange and Deshmukh, 2016) were often added to it. These additions seem insufficient due to the omission of relevant news variables.⁹ Recent empirical studies suggest the factors that influence stock return performance go beyond the scope of financial factors. Evidence by Baker et al. (2016), Arbatli et al. (2017) and Chiang (2019a) ¹⁰ demonstrates that EPU index can significantly affect stock market returns because the information content of an EPU index is more effective and covers broad news about the fundamentals of economy, policy, and uncertainty. This notion is expressed as:

⁹ Scruggs (1998) finds that the long-term government bond return is significantly related to investment opportunities. This result implies that the estimated risk-return relation can be biased if a significant variable is omitted from the mean equation or the variance equation (Kennedy, 2008).

¹⁰ Knight (1921) argue that only quantifiable uncertainty is considered as a risk and defined uncertainty as peoples' inability to forecast the outcome of events happening (Bloom 2014). The availability of EPU indices (Baker et al., 2016) and Japan's policy uncertainty indices (Arbatli et al., 2017) help to quantify the measurability of uncertainty.

where $ ∆ $ denotes the difference operator; $ ∆{EPU}_{t} $ is the first difference in natural logarithm of the EPU at time t; $ { w}_{t} $ is the random error term. Some researchers prefer to use the level of $ { EPU}_{t} $ (Chen et al., 2017; Gu et al., 2018); this study, however, uses a natural log-differenced form for two reasons. First, the differenced form helps to reduce the problem that arises from the first order serial correlation. Second, the coefficient of a differenced form summarizes the parametric effects of two-period performance. In priori, $ \mathrm{\gamma } $, the coefficient of $ {∆EPU}_{t} $, is expected to be negative. This equation has been widely used in the literature (Chen et al., 2017; Li et al., 2015; Li, 2017; Chiang, 2019a, among others).

3.3.   A risk cum uncertainty model

Several channels have been identified to explain that a heightened uncertainty could produce damaging effects on economic activities. First, an increase in uncertainty tends to interrupt investment decision and in turn jeopardizes production (Bloom, 2014), which causes prospects regarding future cash flows to be pessimistic and lowers expectations about stock prices. Second, uncertainty provokes worry, fear, and anxiety, inducing noise traders to selloff stocks, which results in a decline in stock prices (Koutmos, 2014). Third, growing uncertainty increases precautionary savings among economic agents, which reduces the availability of funds (Johannsen, 2014). Fiscal policy uncertainty arising from changes in legislation or the tax code can impede output production and household spending that further affect employment (Fernandez-Villaverde et al., 2015). Deterioration in production and consumption could threaten a firm's cash flows and lead to stock prices decline. For a country like Japan that depends heavily on foreign trade, an increase in trade policy uncertainty will affect the investment in export capacity and hence future cash flows. In summary, a number of economic arguments point to the direction that heightened uncertainties in economic policy, fiscal policy, monetary and trade channels could interrupt investment decision and hence frustrate stock prices. The following equation combines all the risk and uncertainty innovations in a regression model as:

with $ {\beta }_{1} < 0 $, $ {\beta }_{2} < 0 $, $ {\gamma }_{i} < 0, \delta >0 $ and $ {\epsilon }_{t} $│ $ {I}_{t-1}\backsim \mathrm{G}\mathrm{E}\mathrm{D}(0, {\sigma }_{t-1}^{2}, \nu) $.

where $ { ∆XPU}_{t} $ refers to a change in X-type policy uncertainty. The $ {\gamma }_{i} $ is parametric measures the effect of changes in X-type uncertainty, $ {∆XPU}_{t} $: {$ {∆EPU}_{t}, {∆FPU}_{t}, {∆MPU}_{t}{, ∆TPU}_{t} $, $ {∆GEPU}_{t}\} $ denotes a vector of changes in policy uncertainty, including changes in economic policy uncertainty, fiscal policy uncertainty, monetary policy uncertainty, trade policy uncertainty and global economic policy uncertainty. The coefficient of $ {\gamma }_{i} $ is expected to be negative, reflecting that a rise in uncertainty will impede economic activities and drive stock prices down (Bloom, 2014; Arbatli et al., 2017).

Economic rationales and prior empirical analysis in the literature guide the selection of the above explanatory variables. The choice of financial variables of $ {∆Vol}_{t} $ and $ {∆VaR}_{t} $ are based on established empirical evidence (Bali, et al., 2009; Chen et al., 2018). These variables are measured directly by financial time series available in the public domain. In a traditional model specification, risk is associated with "news", which is an unpredictable component of a state variable that is derived from time series models (Mishkin, 1982; Edwards, 1982; Cornell, 1983). The policy uncertainty variable in Equation (3), however, is constructed on a news-based measurement of uncertainty derived from major newspapers, the words used reflect the impacts of the White House, Congress, the U.S. Treasury, the Fed (Baker et al., 2016) and the Bank of Japan (Arbatli et al., 2017), among other constituencies and institutions.¹¹ As the result, news released from these government agents can be interpreted, at least in part, as impacts of government policy uncertainty. A comparison with two previous model specifications, it is clear that the Equation (1) and Equation (2) are nested in Equation (3).

¹¹ Traditional analysis in the literature defines "news" as the unexpected component of a state variable to serve as a measure of risk (see Edwards, 1982; Cornell, 1983; Pearce and Roley, 1983). In this study, news variables as constructed by Baker et al. (2016) serve as a proxy of uncertainty. Appendix II provides major term sets for categorical policy uncertainty indices.

To test the joint significance of the categorical policy uncertainties on stock returns, one can perform a Chi-squared test by examining the null of $ {\gamma }_{i} $ = 0. A rejection of the null in the test equation suggests that the categorical policy uncertainties are significant in explaining the (excess) stock return, and the presence of a negative sign suggests the existence of uncertainty premiums. Equation (3), therefore, provides a general equation pertinent for testing the change in economic policy uncertainty, $ {∆EPU}_{t} $ (Ozoguz, 2009; Chen et al., 2017), the change of global EPU, $ ∆{GEPU}_{t} $ (Chiang, 2009a) and other forms of change in policy uncertainty while controlling for conditional volatility, $ {∆Vol}_{t} $ (French et al., 1987), downside risk, $ {∆VaR}_{t} $ (Bali et al., 2009) and the lagged dividend yield, $ {DY}_{t-1} $ (Campbell et al., 1997).

To close the model, I specify the variance equation by using a GARCH (1, 1) process as popularized by Bollerslev et al. (1992), which is expressed by:¹²

¹² In this study, the Asymmetric GARCH (1, 1) models (Glosten et al., 1993) and an EGARCH (1, 1) model (Nelson, 1991) were tested in an experimental stage; no significant evidence was found in the asymmetric coefficient specification. The use of GARCH (1, 1) was recommended by Bollerslev et al. (1992) for its consistency with most stock return series. Bollerslev (2010) provides details of alternative GARCH model forms.

The GED distribution (Nelson, 1991; Li et al., 2005) is employed to model stock return error series. This GED distribution is appealing, since the error series can be transformed from a normal distribution to a leptokurtotic distribution. As a result, the GED can accommodate the thickness of the tails of a distribution. Moreover, the GED distribution is able to model the fat-tail.

4.   Data

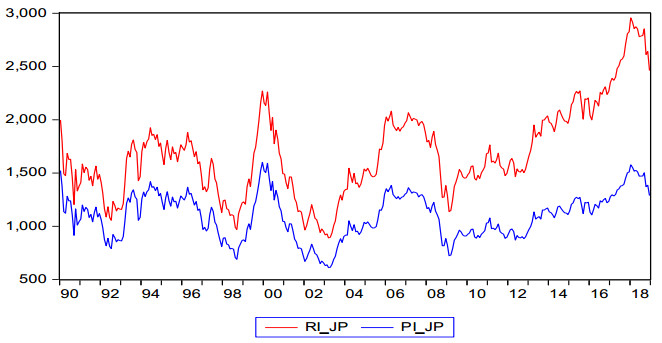
This study employs stock indices in the Japanese (JP) and United States (US) markets.¹³ A return index (RI) and price index (PI) are both used to construct stock returns. RI in Datastream is defined as stock price index ($ {PI}_{t } $) adjusted for dividend yields. The stock returns are calculated by taking the natural log-difference of RI or PI times 100. As shown in Figure 1, the time series of RI and PI indices are measured in the vertical axis and the monthly unit is given in the horizontal axis. The time series plots of RI and PI in Figure 1 indicate that both series exhibit a high degree of comovements and typically capture major turning points. However, the vertical difference of the two series reflects the extent of time-varying for dividend yields as they change over time. Besides RI and PI, the data also include implied volatility variables (VIX) of the 1-month stock options volatility for both the Japanese and U.S. markets used in the robustness test.¹⁴

¹³ The data used in this study can be obtained in the link: Data_to_APFM_Japan_Policy_Uncertainty.

¹⁴ Appendix 1 provides a summary of notations in this paper and Appendix 2 gives terms for measuring EPU and categorical uncertainties in newspapers.

The excess return is constructed by subtracting 1-month Eurocurrency rates ($ {r}_{1m, t}) $and 10-year government bond yields ($ {\mathrm{r}}_{10\mathrm{y}, \mathrm{t}}) $from the stock return at time t for the U.S and Japan, respectively. The dividend yields (DY) is used to serve as the economic fundamental (Campbell et al., 1997; Campbell and Hamao, 1992). The stock indices cover both the daily and the monthly data; monthly data are measured by the closing price at the end of the month for RI and PI. Daily data are used to calculate the volatility and downside risk. All of the above-mentioned data were obtained from Datastream for the period from January 2, 1990 through October 31, 2018. Following the literature, the stock indices are measured by U.S. dollars, which enable us to make cross-market comparisons and without concerning for exchange rate risk (Bekaert and Harvey, 1995; Bali and Cakici, 2010).

The U.S. $ EPU $ index is downloaded from the website at www.PolicyUncertainty.com (Baker et al., 2016 and Davis, 2016). The index is constructed from three components: (ⅰ) newspaper coverage of policy-related economic uncertainty based on 10 large newspapers; (ⅱ) the number of federal tax code provisions set to expire in future years; (ⅲ) disagreement among economic forecasters which serves as a proxy for uncertainty. Basically, a search of the digital archives of each newspaper for a monthly count of articles that contain a trio of terms: "uncertainty" or "uncertain"; "economic" or "economy"; and one or more of the terms "deficit, " the Fed, " or "White house, " and "uncertainties" or their variants. Baker et al. (2016) find this EPU index is reliable, unbiased, and consistent. By using the same approach, Davis (2016) constructs a categorical policy uncertainty index. Major term sets for categorical policy uncertainty indices are contained in Appendix 2.

Following a similar method to construct a measure of global EPU market using data from major newspapers for each local market, Davis (2016) constructs a global EPU index, which is calculated as a GDP-weighted average of monthly EPU index values for a group of international markets based on their local major newspapers. The data can be downloaded from the following link. http://www.policyuncertainty.com/media/Global_Annotated_Series.pdf.

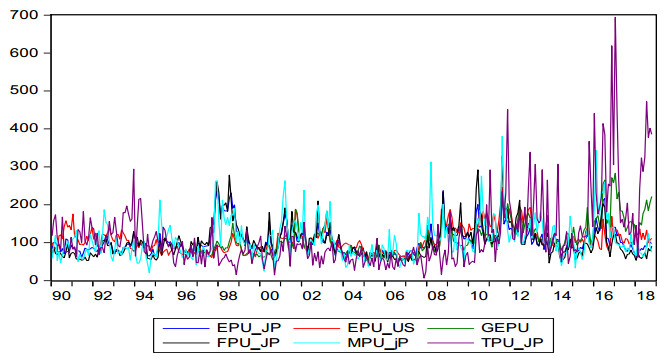
Arbatli et al. (2017) construct several newspaper-based policy uncertainty measures for Japan following the methods of Baker et al. (2016). Arbatli et al. (2017) count articles in four major newspapers (Yomiuri, Asahi, Mainichi and Nikkei) that contain at least one term in each of three categories: (E) "economic" or "economy"; (P) "tax", "government spending", "regulation", "central bank" or certain other policy-related terms; and (U) "uncertain" or "uncertainty". They find that the EPU index spiked as a reaction to the failure of Lehman Brothers in 2008, the U.S. debt-ceiling fight in 2011, the Brexit referendum in 2016 and the deferral of a hike in the consumption tax rate in 2017. Arbatli et al. (2017) also construct categorical uncertainty indices for fiscal policy, monetary policy, and trade policy. The information is given in Appendix 2. Figure 2 presents time series plots for the natural logarithms of Japan's EPU, U.S. EPU, GEPU and various categories of Japanese policy uncertainties series over time. One observation from these time series is that they display some sort of comovements, indicating that to some extent these uncertainty series are positively correlated; yet, they deviate from each other due to their distinct characteristics, which reflect their different sensitivity toward news or policy changes.¹⁵ The trade policy uncertainty exhibits a higher degree of deviation from the other indices since 2011. This result may stem from the uncertainty of political conflicts over Japan's participation in TPP talks (Arbatli et al., 2017), the tension from the impact of Brexit and the threat of escalating U.S. tariffs.

¹⁵Arbatli et al. (2017) note that among all articles that satisfy the E, P and U criteria in the Japanese market, 57 percent reference fiscal policy matters, 27 percent reference monetary policy, 8 percent reference trade policy.

Table 1 reports the correlation matrix for the changes in uncertainty variables. A common phenomenon of the pairwise relations for each variable coefficient is that the correlations are positive; correlations range from 0.01 ($ ∆{TPU}_{t}^{JP}\mathrm{v}\mathrm{s}.{∆VaR}_{t}^{JP}\mathrm{a}\mathrm{n}\mathrm{d}{∆VIX}_{t}^{JP} $) to 0.85 ($ ∆{FPU}_{t}^{JP} $vs. $ {∆EPU}_{t}^{JP} $). The statistics also indicate that the correlation between $ ∆{FPU}_{t}^{JP} $ and $ ∆{EPU}_{t}^{JP} $is 0.85 which is rather high and may generate a multicollinearity problem if both variables are simultaneously included in the test equation. In practice, dynamic relations among these uncertainty time series are very complex, since they may commonly change in response to shocks that bring about covarying over time. However, these series may move in opposite directions due to different levels of dynamic sensitivity to news developments. This complexity is observed by Arbatli et al. (2017), who note that "the presence of automatic fiscal stabilizers diminishes the need for discretionary fiscal stimulus, and the political conflicts and policy uncertainty that often accompanies efforts to deploy discretionary fiscal tools".

5.   Empirical results

The Newy-West procedure (Newey and West, 1987) is applied to estimate the impacts of risk factors and each individual policy uncertainty variable on stock returns. The independent variable for each simple regression model includes $ ∆{Vol}_{t}^{JP} $, $ {∆VaR}_{t}^{JP} $, $ ∆{EPU}_{t}^{JP} $, $ ∆{FPU}_{t}^{JP} $, $ ∆{MPU}_{t}^{JP} $, $ ∆{TPU}_{t}^{JP} $ and $ {∆GEPU}_{t}^{*} $, which is a residual series developed by regressing $ ∆{GEPU}_{t} $ on $ ∆{EPU}_{t}^{JP} $.

Table 2 reports the estimates by regressed stock return in Japan for different independent variables, respectively. The estimated coefficients are placed in the first column for each model, and the absolute values of t-statistics are in parentheses. The evidence indicates that the independent variable for each model exhibits a negative sign and is statistically significant at the 5% level, revealing that all risk/uncertainty variables have a dampening effect on stock return with an upsurge in risk/uncertainty. Obviously, the estimated coefficients vary from each other, and the absolute values for the financial risk variables are higher than those of policy uncertainty variables. This may be attributable to the fact that from investors' perspective, volatility and downside risk changes are more visible and appear to be perceived as a directly observable indicator, making their responses more sensitive to these changes.

In market practice, it is hard to believe that a single variable could sufficiently summarize all relevant information to describe stock return behavior. To relax the single explanatory variable assumption, the estimation process is carried out by adding one uncertainty variable at a time in Table 3 while treating $ ∆{Vol}_{t}^{JP}, {∆VaR}_{t}^{JP} $, and $ {DY}_{t-1} $as control variables. Note that both $ ∆{Vol}_{t}^{JP} $and $ {∆VaR}_{t}^{JP} $ are included in the test equation, which helps to reduce the spurious correlation arising from the correlation between risk factors and policy uncertainty.

The inclusion of $ ∆{Vol}_{t}^{JP}, {∆VaR}_{t}^{JP} $ and $ { DY}_{t-1}^{JP} $ as independent variables is compatible to the specifications of Bali at al. (2009) and Chen at al. (2018), who highlight the significance of market volatility, downside risk and dividend yield on stock returns. Adding the $ ∆{EPU}_{t} $, however, allows us to independently identify the incremental impact of policy efficiency as given in studies by Liu and Zhang (2015), Arouri et al. (2016), Li (2017) and Chiang (2019a). Another special feature of the model presented in Table 3 is the addition of news variables for other policy uncertainties, including $ ∆{MPU}_{t}^{JP} $, $ ∆{TPU}_{t}^{JP} $ and $ {∆GEPU}_{t}^{*}. $¹⁶ It is evident that all the incremental variables associated with categorical policy uncertainty changes present negative signs and are statistically significant, which supports the uncertainty premium hypothesis.

¹⁶ $\Delta FPU_t^{JP}$ is excluded from the current model due to its high correlation with the $\Delta EPU_t^{JP}$. However, in the robustness check, the $\Delta EPU_t^{JP}$ will be replaced by $\Delta FPU_t^{JP}$ in the estimated equation.

Since the full model in the last two columns has more information content and the specifications of other models in table 3 are nested in this full model, the interpretation shall focus on the full model. The main findings are summarized as follows. First, consistent with the finding by Campbell and Hamao (1992) for the period 1971–1989 and the result by Aono and Iwaisako (2010) for the post-1990 period in the Japanese market, a rise in dividend yield contributes the ability to predict monthly stock returns. This is shown in the positive coefficient of $ {DY}_{t-1}^{JP} $and the significant t-statistic.

Second, evidence shows that the variance of the Japanese stock returns is time-varying as characterized by a positive autocorrelation and a highly significant t-ratio. This implies the Japanese return series exhibits a volatility clustering phenomenon, which is consistent with the studies documented by Bollerslev et al. (1992), Bali and Engle (2010) and Chiang (2019a).

Third, the test result in the mean equation indicates that the coefficient of volatility innovation is negative and highly significant. This outcome reveals a market phenomenon that as greater volatility hits the market, risk-averse investors tend to short their stocks to prevent further price depreciation. This result is comparable to the finding provided by Chiang et al. (2015).

Fourth, the coefficient of $ ∆{VaR}_{t}^{JP} $ indicates a negative sign and the t-statistic of this variable is highly significant. This outcome is plausible and reflects that a rise in downside risk will spawn an agammaavation of fear in market condition that causes stock prices to fall off. The evidence is consistent with the results documented by Bali et al. (2009) and Chen and Chiang (2016).

Fifth, the coefficient for the $ ∆ $EPU_t is significantly negative, which indicates a damaging effect on stock returns associated with an escalation in higher $ ∆ $EPU_t. Note that $ -∆{EPU}_{t}^{JP} $implies $ (-{EPU}_{t}^{JP} $+ $ {EPU}_{t-1}^{JP}) $, which shows that the coefficient of $ {EPU}_{t}^{JP} $ has a negative sign in the current period and a positive sign in the lagged period. This outcome is consistent with the behavior of investors who sell off stocks as uncertainty spikes, which depresses stock prices. However, rational traders, who bought stocks at a time of high uncertainty, will be rewarded by premiums if prices rebound in the next period. This phenomenon is consistent with the studies documented by Antonakakis et al. (2013) and Chiang (2019a).

Sixth, the estimates for testing incremental efficiency for $ ∆{MPU}_{t}^{JP}, ∆{TPU}_{t}^{JP}\mathrm{a}\mathrm{n}\mathrm{d}{∆GEPU}_{t}^{*} $on stock returns turn out to have significant evidence comparable to that of $ ∆ $EPU_t, as noted by slopes that are negative and statistically significant. This finding provides more statistical support of the impact of categorical policy uncertainties that would produce destructive effects on the Japanese stock market. The evidence is consistent with the investigations of Arbatli et al. (2017), who use a VAR model and show these policy innovations have a negative impact on Japan's economic performance. However, evidence here further indicates that deteriorations in Japan's macroeconomic performance further impinge on the stock market performance.

Among these uncertainty shocks, the upward disturbance of $ {∆GEPU}_{t}^{* } $turns out to depress Japanese stock prices more than one perceived. A general conclusion from this study leads us to believe that a rise in uncertainty shocks, regardless of its origin, tends to create fear that leads investors to sell off their stocks and causes a plunge in stock prices. Further testing the incremental efficiency of uncertainty changes involves a Wald test, which is used to examine $ ∆{EPU}_{t}^{JP} = ∆{MPU}_{t}^{JP} = ∆{TPU}_{t}^{JP} = {∆GEPU}_{t}^{*} = 0 $. The calculated 𝜒²(k) statistic 267.44 for k = 4 indicates a rejection of the null as indicated by the P-value in brackets. The test result, therefore, supports the joint hypothesis that changes in uncertainty in economic policy, monetary policy, trade policy and global EPU have significant effects on the stock returns.

6.   Robustness tests

6.1.   Evidence from excess stock returns

The empirical estimations in Table s show that a stock return and financial risk/policy uncertainty changes are negatively correlated. However, the studies in the financial literature (Scruggs, 1998; Chiang, 2019a) contend that it is more appealing to use the excess-return rather than the stock return to serve as the dependent variable in testing the uncertainty-return relation. Thus, it is worthwhile to conduct robustness test on whether the parametric relations still hold when the stock return is replaced by excess stock returns. To address this issue, a measure of excess stock return, $ {R}_{t}^{JP}-{r}_{10y, t}^{JP} $, is achieved by subtracting the 10-year Japanese bond yield from the stock return. The results, which are derived by employing ($ {R}_{t}^{JP}-{r}_{10y, t}^{JP} $) as a dependent variable in estimating stock return equations, are reported in Table 4.

The evidence in Table 4 indicates that the test equation is robust. All the coefficients show signs as anticipated and are statistically significant. The evidence is consistent with the results obtained in Table 3. Focusing on the last two columns of the full model, the evidence suggests that the estimated coefficients of $ ∆{Vol}_{t}^{JP} $and $ ∆{VaR}_{t}^{JP} $display negative signs and are highly significant, supporting the risk aversion hypothesis. For the $ ∆{EPU}_{t}^{JP} $and categorical uncertainty variables, all the coefficients are negative and statistically significant at the 1% level. As discussed in the previous section, the negative sign is consistent with the existence of the uncertainty premium hypothesis. Further testing of the joint hypothesis of $ ∆{EPU}_{t}^{JP} $ = $ ∆{MPU}_{t}^{JP} $ = $ ∆{TPU}_{t}^{JP} $ = $ ∆G{EPU}_{t}^{*} $ = 0 leads us to decisively reject the null based on $ {\chi }^{2}(k = 4) $ = 211 as indicated by the P-value at the 1% level (shown in the brackets). It can be confirmed that the excess returns changes are negatively correlated to policy uncertainties and should earn excess premiums.

6.2.   Different explanatory variables

The regression estimations are sensitive to the measure of the variables under investigation (Kennedy, 2008). Let's consider the following three cases. First, due to high correlation (0.85) between $ ∆{EPU}_{t}^{JP} $ and $ ∆{FPU}_{t}^{JP} $as shown in Table 1, only $ ∆{EPU}_{t}^{JP} $ is used in the test equation rather than both to avoid a multicollinearity problem (see Tables 3 and 4). In model 1 shown in Table 5, the $ ∆{FPU}_{t}^{JP} $ is used to replace $ ∆{EPU}_{t}^{JP} $. The estimated coefficient of $ ∆{FPU}_{t}^{JP} $shows a negative sign and is significant at the 1% level. In contrast, all the other variables keep the same qualitative results of the equation using $ ∆{EPU}_{t}^{JP} $as reported in the last model in Table 4. This result for $ ∆{FPU}_{t}^{JP} $is consistent with the evidence reported by Fernandez-Villaverdeet al. (2015) who estimated U.S. data and supports the finding as reported by Arbatli et al (2017).

Second, rather than relying on the 10-year bond yield as a proxy for the risk free-rate, the 1-month deposit rate can be applied to calculate the excess stock returns. The estimates in the next two models examine the difference by using either $ {R}_{t}^{JP}-{r}_{1m, t}^{JP} $ or $ {R}_{PI, t}^{JP}-{r}_{1m, t}^{JP} $in the test equation. Evidence in Table 5 shows whether the excess returns are based on $ {R}_{t}^{JP}-{r}_{1m, t}^{JP} $ or $ {R}_{PI, t}^{JP}-{r}_{1m, t}^{JP} $as dependent variable; no significant difference is found in performance.

Third, the literature shows that the implied volatility, $ ∆{VIX}_{t}^{JP}, $ is a good measure of market risk, which may be part of the reason that it is viewed as a significant argument to be included in the asset pricing model as noted by Whaley (2009). Evidence shown in Table 1 suggests that $ ∆{VIX}_{t}^{JP} $ is positively correlated with $ ∆{Vol}_{t}^{JP} $. Thus, I proceed in making estimations by replacing $ ∆{Vol}_{t}^{JP} $with $ ∆{VIX}_{t}^{JP} $. The estimated results for the last model are also reported in Table 5. Consistent with the existing literature (Whaley, 2009; Chiang et al., 2015), the coefficients of $ ∆{VIX}_{t}^{JP} $clearly produce negative signs and are statistically significant as the dependent variable is based on ($ {R}_{PI, t}^{JP}-{r}_{1m, t}^{JP} $)¹⁷. On the other hand, all other variables produce comparable qualitative results as previously noted. It can be concluded from the test results in Table 5 that the model is robust across different measures of market returns, risk-free rates, and market volatility after controlling for $ {DY}_{t-1}^{JP} $.

¹⁷ A comparable result will be achieved by using either $R_{PI, t}^{JP}$ or $R_t^{JP}$.

Another important observation emerging from Table 5 stems from the joint test for $ ∆{EPU}_{t}^{JP} $ (or $ ∆{FPU}_{t}^{JP}) $ = $ ∆{MPU}_{t}^{JP} $ = $ ∆{TPU}_{t}^{JP} $ = $ ∆G{EPU}_{t}^{*} $ = 0. A check of the P-value for the $ {\chi }^{2}\left(k\right) $ statistic clearly indicates that the null should be rejected based on the P-values (in brackets) for all the models in Table 5. Therefore, it can be concluded that the uncertainty premiums are significant and should be priced in the stock prices regardless of whether the source the uncertainty comes from $ ∆{EPU}_{t}^{JP} $, $ ∆{FPU}_{t}^{JP} $, $ ∆{MPU}_{t}^{JP} $, $ ∆{TPU}_{t}^{JP} $or $ ∆G{EPU}_{t}^{*} $.

6.3.   Impact of U.S. policy uncertainties

The dominant role of the U.S. financial position over the global markets was witnessed during the 2008–2009 U.S. subprime crisis and confirmed by academic research publications (Karolyi and Stulz, 1996; Chen et al., 2003; Rapach et al., 2013). It is of interest to examine how significant the response of Japanese stock market behavior was to the shocks originating from the U.S. market. Thus, the estimation process includes all equivalent measures of risk and categorical policy uncertainty variables from the U.S. market. This set of variables is: $ \{∆{VaR}_{t}^{US} $, $ ∆{EPU}_{t}^{US} $, $ ∆{MPU}_{t}^{US}\mathrm{a}\mathrm{n}\mathrm{d}∆{TPU}_{t}^{US}\}. $ The estimated results, which factor into these U.S. variables, are reported in Table 6.

The evidence indicates the estimated statistics are comparable with the previous findings using the Japanese variables alone. After adding the information set of the U.S. variables, the statistics show an incremental efficiency and suggests that all the estimated coefficients display negative signs, and the corresponding t-statistics are highly significant. This outcome is consistent with the literature that changes in EPU in the U.S. are negatively related to Japanese stock returns on the Nikkei 225 (Sum, 2012). The findings, however, indicate that the impact stems not just from $ ∆{EPU}_{t}^{US} $but also from a broad category of measures of $ ∆{MPU}_{t}^{US}\mathrm{a}\mathrm{n}\mathrm{d}∆{TPU}_{t}^{US} $. These results lead to the conclusion that all economic policy uncertainty changes from the U.S. market produce a harmful effect on Japanese stocks, and investors should incorporate the impact of U.S. policy uncertainties in pricing the Japanese stocks.

One related question, which arises from this study, is whether the U.S. stock market also has a symmetric effect from the Japanese market? Table 7 reports the results in reverse country order for regressing the U.S. excess stock return against its own financial risk, changes in policy uncertainty and global EPU change plus the Japanese market's policy uncertainty changes.

The evidence from Table 7 shows that U.S. excess stock returns are negatively correlated to their own financial risk and different types of policy uncertainty changes, including the variables of $ \{∆{VaR}_{t}^{US} $, $ ∆{EPU}_{t}^{US} $, $ ∆{MPU}_{t}^{US}, ∆{TPU}_{t}^{US} $and $ ∆{GEPU}_{t}^{*}{^{18}}\} $, which are statistically significant. However, in reviewing the performance of Japanese risk and uncertainty variables in the test equation, the results show that only a change in monetary policy uncertainty produces a significant negative sign; no evidence supports a significant effect on the other Japanese's variables associated with financial risk factors or changes in policy uncertainty. This may result from the fact that changes in monetary policy are regularly disseminated, and implementation of policies for the Bank of Japan and the U.S. Fed are effectively coordinated. In general, there is no strong evidence to reveal that VaR/uncertainties from the Japanese market could produce damaging effects on U.S. stocks. Thus, the asymmetric uncertainty spillover patterns between the U.S. and Japan in this study are consistent with asymmetric volatility spillover reported by Hamao et al. (1990) and Connolly and Wang (1999).

¹⁸ The U.S. EPU effect has been neutralized from the GEPU measure. This variable differs from the one in the Japanese market, which is neutralized from the Japan's EPU.

6.4.   Asymmetry of uncertainty on stock returns

As stated earlier, a rise in uncertainty tends to provoke fear, pessimism, and risk aversion that disrupt investment decisions and the stock market. If this were the case, then would a reduction in uncertainty relieve investors' tensions help to improve the stock market? Thus, it is worthwhile to examine the impact on stock prices with respect to a downturn in uncertainty vis-à-vis an increase in uncertainty (Bahmani-Oskooee and Saha, 2019b). To simplify the estimation, let us define total uncertainty, TU, which is the sum of categorical policy uncertainty, since information regarding categorical uncertainties comes from different terms, and employing a measure of TU can avoid the over parameterization in estimation that could occur from using all categorical policy uncertainty variables. The test model is expressed as:

where $ { R}_{t} $ is (excess) stock returns for the Japanese market. The other variables are unchanged. The new variable in Equation (5) is the $ ∆{TU}_{t}^{JP} $, the change of Japanese total uncertainty defined as: $ ∆{TU}_{t}^{JP} = ∆{MPU}_{t}^{JP} $ + $ ∆{FPU}_{t}^{JP}+∆{TPU}_{t}^{JP}. $ The $ ∆{TU}_{t}^{JP} $series is divided into two regimes: $ ∆{TU}_{t}^{+, JP} $ = $ ∆{TU}_{t}^{JP} $ > 0, and = 0 otherwise; $ ∆{TU}_{t}^{-, JP} $ = $ ∆{TU}_{t}^{JP} < 0 $, and = 0 otherwise. By the same token, the $ \{U.S.Variablesof∆{TU}_{t}^{US}\} $ represent their counterparts for the related variables in the U.S. The $ ∆{TU}_{t}^{+, JP} $ and $ ∆{TU}_{t}^{-, JP} $series capture the information of an upward shift in total uncertainty vis-à-vis a downward shift in uncertainty. Before running the regression, the original $ ∆{TU}_{t}^{-, JP} $and $ ∆{TU}_{t}^{-, US} $series are multiplied by −1. Thus, $ {\beta }_{4} $ > 0 means that as total uncertainty increasingly declines, stock returns are expected to rise. However, $ {\beta }_{3} $ < 0 reflects a market response that shows as total uncertainty increases, the stock return goes down.

The estimations of Equation (5) are conducted based on both stock return and excess stock returns as dependent variables. The results are reported in Table 8. The asymmetric effects can be captured by focusing on the estimated coefficients of total uncertainty. As predicted by prior expectations, the evidence shows that the estimated coefficients of $ ∆{TU}_{t}^{+, JP} $ and $ ∆{TU}_{t}^{+, US} $present a negative sign, while the coefficients of $ ∆{TU}_{t}^{-, JP} $ and $ ∆{TU}_{t}^{-, US} $ display a positive sign, all of estimated coefficients are statistically significant based on the t-statistics. These findings are consistent with the phenomenon that a heightened total uncertainty in current period could signify a tendency for further worsening in policy uncertainty, which would induce investors to sell off their stocks and cause stock prices to decline. On the other hand, declining total uncertainty can be interpreted as a slowdown in the adverse environment. Under this scenario, investors may perceive the possibility of a market rebound, which would motivate them to place new orders that cause stock prices to rise. Testing of the impacts for an equal magnitude between $ ∆{TU}_{t}^{+} $ and $ ∆{TU}_{t}^{-} $ presents $ {\chi }_{1}^{2, JP} $statistics, which decisively indicate a rejection of the null for three equations in the Japanese market; however, testing for the U.S. variables, $ {\chi }_{1}^{2, US} $ statistics shows that only in the case of excess stock returns, $ {(R}_{t}^{JP}-{r}_{1m, t}^{JP}) $, which uses 1-month interest rate, the null is rejected, suggesting that the Japanese market presents a stronger asymmetric effects than that from the U.S. market.¹⁹

¹⁹ Lagged values of $\Delta TU_t^ + $ and $\Delta TU_t^ - $ may be added to the model. The use of a current period model is to maintain a consistency with previous estimated models. Bahmani-Oskooee and Saha (2019b) model uses an error–correcting model so the asymmetric effects were test based on a country's own uncertainty effect. This study's test includes the cross–market asymmetric effects of uncertainty.

7.   Conclusions

This paper presents a coherent framework that incorporates both risk and uncertainty to test the risk/uncertainty-return relations. Testing the month data on the Japanese markets achieves several empirical findings. First, evidence indicates that a rise in volatility/downside risk will generate a negative effect on (excess) stock prices, confirming the risk premium hypothesis. This finding is consistent with the behavior of noise traders who will sell stocks as risk hits the market. On the other hand, negative feedback traders would take an opposite position by buying stocks at current low prices and benefiting from the risk premiums when prices reverse in the future (Koutmos, 2014).The evidence is in agreement with the findings reported by Bali et al. (2009) and Chen and Chiang (2016).

Second, this paper finds evidence of a negative coefficient for the change in economic policy uncertainty ($ ∆ $EPU_t) in the stock return equation. This finding implies that EPU_t is negatively correlated with the excess stock return at the current period but positively correlated with the EPU_t–1. This result is consistent with the market phenomenon that an increase in EPU will spawn fear in investors, which would prompt them to sell off stocks, bring down prices. However, rational traders who place orders at this moment of high uncertainty would reap uncertainty premiums as prices reverse in the future.

Third, this study finds evidence that (excess) returns are negatively correlated with changes in fiscal policy uncertainty, monetary policy uncertainty, trade policy uncertainty, and global market uncertainty, which implies that premiums ought to be accounted for in pricing as investors perceive a rise in categorical policy uncertainties.

Fourth, beside the domestic factors, (excess) stock returns in the Japanese market are negatively correlated with the U.S. $ ∆ $EPU as well as different forms of categorical policy uncertainties that spillover from the U.S. market. This is analogous to global financial contagion where a rise in uncertainty in the U.S. market soon spreads to the Japanese markets, disturbing the market tranquility. However, uncertainty shocks in the Japanese market do not produce a comparable result to the U.S. market.

Fifth, this study also examines whether investors' reactions could be different with respect to an increase in policy uncertainty as compared to a decline in uncertainty. Evidence derived from this paper suggests that symmetric effects of changes in policy uncertainty on stock investment are strongly rejected in the Japanese market; however, the evidence is less significant for the presence of asymmetric effects on Japanese stocks if the uncertainty change originated from the U.S. markets.

Sixth, a main finding from this study is that the stock returns are negatively correlated with the EPU. However, the literature (Pham et al., 2018; Demir et al., 2018; Wang et al., 2019) suggests that the correlation between Bitcoin returns and the EPU is positive and significant at both lower and higher quantiles. In the light of these findings, commodity such as gold futures or Bitcoin can serve as a hedging tool against uncertainty.

Conflict of interest

The author would like to declare that no conflicts of interest involves in this paper.