1.
Introduction
Hydraulic jumps are frequently observed in lab studies, river flows, and coastal environments. The shallow water equations, commonly known as Saint-Venant equations, have important applications in oceanography and hydraulics. These equations are used to represent fluid flow when the depth of the fluid is minor in comparison to the horizontal scale of the flow field fluctuations [1]. They have been used to simulate flow at the atmospheric and ocean scales, and they have been used to forecast tsunamis, storm surges, and flow around constructions, among other things [2,3]. Shallow water is a thin layer of constant density fluid in hydrostatic equilibrium that is bordered on the bottom by a rigid surface and on the top by a free surface [4].
Nonlinear waves have recently acquired importance due to their capacity to highlight several complicated phenomena in nonlinear research with spirited applications [5,6,7,8]. Teshukov in [9] developed the equation system that describes multi-dimensional shear shallow water (SSW) flows. Some novel solitary wave solutions for the ill-posed Boussinesq dynamic wave model under shallow water beneath gravity were constructed [10]. The effects of vertical shear, which are disregarded in the traditional shallow water model, are included in this system to approximate shallow water flows. It is a non-linear hyperbolic partial differential equations (PDE) system with non-conservative products. Shocks, rarefactions, shear, and contact waves are all allowed in this model. The SSW model can capture the oscillatory character of turbulent hydraulic leaps, which corrects the conventional non-linear shallow water equations' inability to represent such occurrences [11]. Analytical and numerical techniques for solving such problems have recently advanced; for details, see [12,13,14,15,16,17] and the references therein.
The SSW model consists of six non-conservative hyperbolic equations, which makes its numerical solution challenging since the concept of a weak solution necessitates selecting a path that is often unknown. The physical regularization mechanism determines the suitable path, and even if one knows the correct path, it is challenging to construct a numerical scheme that converges to the weak solution since the solution is susceptible to numerical viscosity [18].
In the present work, we constructed the generalized Rusanov (G. Rusanov) scheme to solve the SSW model in 1D of space. This technique is divided into steps for predictors and correctors [19,20,21,22,23]. The first one includes a numerical diffusion control parameter. In the second stage, the balance conservation equation is retrieved. Riemann solutions were employed to determine the numerical flow in the majority of the typical schemes. Unlike previous schemes, the interesting feature of the G. Rusanov scheme is that it can evaluate the numerical flow even when the Riemann solution is not present, which is a very fascinating advantage. In actuality, this approach may be applied as a box solver for a variety of non-conservative law models.
The remainder of the article is structured as follows. Section 2 offers the non-conservative shear shallow water model. Section 3 presents the structure of the G. Rusanov scheme to solve the 1D SSW model. Section 4 shows that the G. Rusanov satisfies the C-property. Section 5 provides several test cases to show the validation of the G. Rusanov scheme versus Rusanov, Lax-Friedrichs, and reference solutions. Section 6 summarizes the work and offers some conclusions.
2.
Mathematical formulation for the shear shallow water model
The one-dimensional SSW model without a source term is
while $ \mathrm{R_{11}} $ and $ \mathrm{R_{12}} $ are defined by the following tensor $ \mathrm{R_{ij}} = \mathrm{h p_{i j}} $, and also, $ \mathrm{E_{11}} $, $ \mathrm{E_{12}} $ and $ \mathrm{E_{22}} $ are defined by the following tensor $ \mathrm{E_{i j}} = \frac{1}{2}\mathrm{R_{ij}}+\frac{1}{2}\mathrm{\mathrm{h v_i v_j}} $ with $ i\ge 1, j\le 2 $. We write the previous system 2.1 in nonconservative form with non-dissipative $ (C_f = 0, D_{11} = D_{12} = D{22} = 0) $, see [24], which can be written as follows
Also, we can write the previous system as the following
with
and
System (2.3) is a hyperbolic system and has the following eigenvalues
3.
The G. Rusanov scheme for SSWE
In order deduce the G. Rusanov scheme, we rewrite the system (2.1) as follows
Integrating Eq (3.1) over the domain $ [t_n, t_{n+1}]\times[x_{i-\frac{1}{2}}, x_{i+\frac{1}{2}}] $ gives the finite-volume scheme
in the interval $ [x_{i-1/2}, x_{i+1/2}] $ at time $ t_n $. $ \mathrm{W_i^n} $ represents the average value of the solution $ \mathrm{W} $ as follows
and $ \mathit{F}(\mathrm{W_{i\pm1/2}^n)} $ represent the numerical flux at time $ t_n $ and space $ x = x_{i\pm1/2} $. It is necessary to solve the Riemann problem at $ x_{i+1/2} $ interfaces due to the organization of the numerical fluxes. Assume that for the first scenario given below, there is a self-similar Riemann problem solution associated with Eq (3.1)
is supplied by
The difficulties with discretization of the source term in (3.2) could arise from singular values of the Riemann solution at the interfaces. In order to overcome these challenges and reconstruct a $ \mathrm{W_{i+1/2}^n} $ approximation, we created a finite-volume scheme in [19,20,21,22,23,25,26,27] for numerical solutions of conservation laws including source terms and without source terms. The principal objective here is building the intermediate states $ \mathrm{W_{i\pm1/2}^n} $ to be utilized in the corrector stage (3.2). The following is obtained by integrating Eq (3.1) through a control volume $ [t_n, t_{n}+\theta^n_{i+1/2}]\times[x^-, x^+] $, that includes the point $ (t_n, x_{i+1/2}) $, with the objective to accomplish this:
with $ \mathrm{W_{i\pm1/2}^n} $ denoting the approximation of Riemann solution $ \mathrm{R_s} $ across the control volume $ [x^-, x^+] $ at time $ t_{n}+\theta^n_{i+1/2} $. While calculating distances $ \Delta x^- $ and $ \Delta x^+ $ as
$ \mathrm{Q^n_{i+\frac{1}{2}}} $ closely resembles the average source term $ \mathrm{Q} $ and is given by the following
Selecting $ x^- = x_i $, $ x^+ = x_{i+1} $ causes the Eq (3.5) to be reduced to the intermediate state, which given as follows
where the approximate average value of the solution $ \mathrm{W} $ in the control domain $ [t_n, t_{n}+\theta^n_{i+1/2}]\times[x_{i}, x_{i+1}] $ is expressed by $ \mathrm{W_{i+1/2}^n} $ as the following
by selecting $ \theta^n_{i+1/2} $ as follows
This choice is contingent upon the results of the stability analysis[19]. The following represents the local Rusanov velocity
where $ \alpha^n_{i+1/2} $ is a positive parameter, and $ \lambda^n_{k, i} $ represents the $ k^{th} $ eigenvalues in (2.3) evaluated at the solution state $ \mathrm{W^n_{i}} $. Here, in our case, $ k = 6 $ for the shear shallow water model. One can use the Lax-Wendroff technique again for $ \alpha^n_{i+1/2} = \frac{\Delta t}{\Delta x S^n_{i+1/2}} $. Choosing the slope $ \alpha^n_{i+1/2} = \tilde\alpha_{i+1/2}^n $, the proposed scheme became a first-order scheme, where
and
In this case, the control parameter can be written as follows:
where $ \mathrm{\tilde \alpha_{i+1/2}^n} $ is given by (3.11), and $ \Phi_{i+1/2} = \Phi\left(r_{i+1/2}\right) $ is a function that limits the slope. While for
and
One may use any slope limiter function, including minmod, superbee, and Van leer [28] and [29]. At the end, the G. Rusanov scheme for Eq (2.3) can be written as follows
4.
How the source term is treated
With a definition of the C-property [30], the source term in (2.1) is discretized in the G. Rusanov method in a way that is well-balanced with the discretization of the flux gradients. According to [30,31], if the following formulas hold, a numerical scheme is said to achieve the C-property for the system (3.1).
When we set $ v_1 = v_2 = 0 $ in the stationary flow at rest, we get system (3.1), which can be expressed as follows.
We can express the predictor stage (3.14) as follows after applying the G. Rusanov scheme to the previous system
Also, we can write the previous equations as follows
and the stage of the corrector updates the solution to take on the desired form.
The solution is stationary when $ \mathrm{W}^{n+1}_i = \mathrm{W}^n_i $ and this leads us to rewrite the previous system (4.5) as follows
This lead to the following
Afterward, when the source term in the corrector stage is discretized in the earlier equations, this leads to the G. Rusanov satisfying the C-property.
5.
Numerical simulation for the SSW model
In order to simulate the SSW system numerically, we provide five test cases without a source term using the G. Rusanov, Rusanov, and Lax-Friedrichs schemes to illustrate the effectiveness and precision of the suggested G. Rusanov scheme. The computational domain for all cases is $ \mathbb{L} = [0, 1] $ divided into $ 300 $ gridpoints, and the final time is $ t = 0.5s $, except for test case $ 2 $, where the final time is $ t = 10s $. We evaluate the three schemes with the reference solution on the extremely fine mesh of $ 30000 $ cells that was produced by the traditional Rusanov scheme. Also, we provide one test case with a source term using the G. Rusanov scheme in the domain $ [0, 1] $ divided into $ 200 $ gridpoints and final time $ t = 0.5 $. We select the stability condition [19] in the following sense
where a constant $ \mathrm{CFL} = 0.5 $.
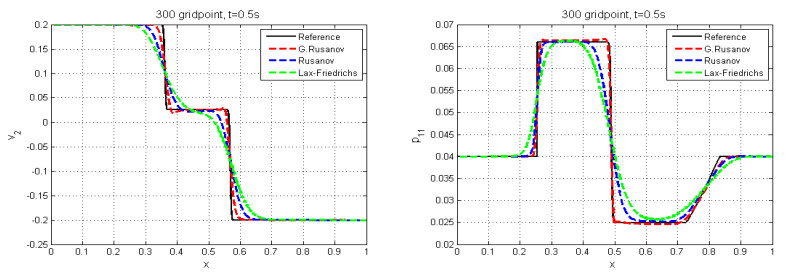
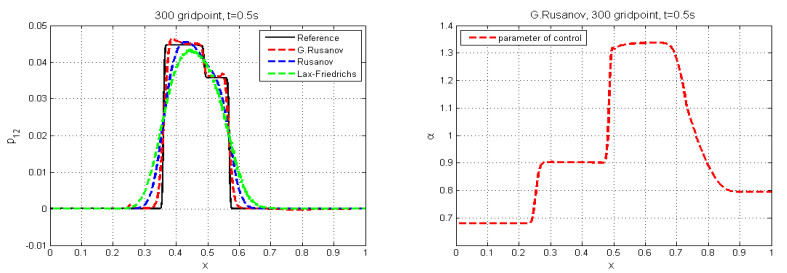
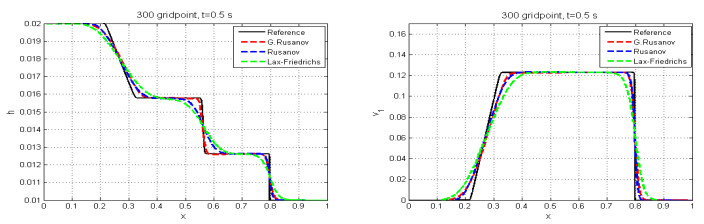
5.1. Test case 1
This test case was studied in [24] and [32], and the initial condition is given by
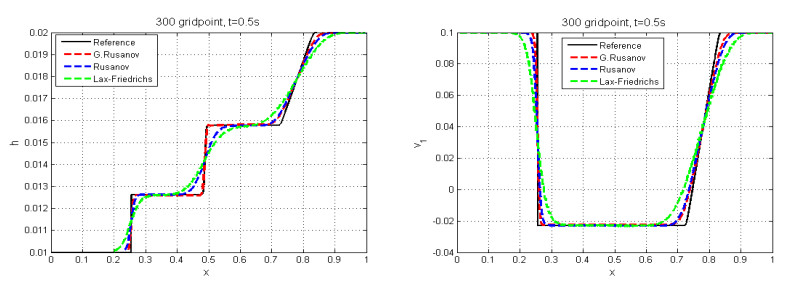
The solution include five waves, which are represented by $ 1- $ shock and $ 6- $ rarefaction. We compare the numerical results with the reference solution, which is calculated with the Rusanov scheme with very fine mesh of $ 30000 $ cells. Figures 1–3 show the numerical results and variation of parameter of control. We note that all waves are captured by this scheme and the numerical solution agrees with the reference solution. Table 1 shows the CPU time of computation for the three schemes by using a Dell i5 laptop, CPU 2.5 GHZ.
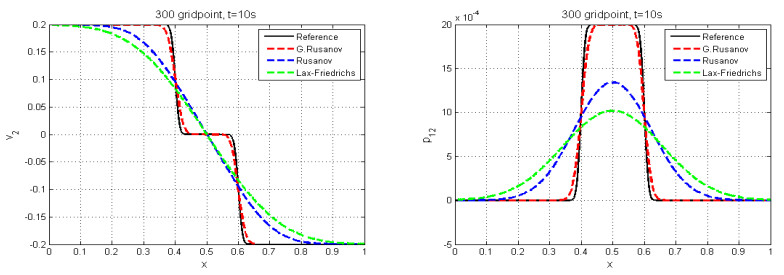
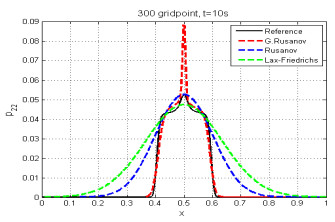
5.2. Test case 2
This test case (the shear waves problem) was studied in [24] and [32], and the initial condition is given by
The solution is represented by two shear waves with only transverse velocity discontinuities, the $ p_{12} $ and $ p_{22} $ elements of a stress tensor. We compare the numerical results by G. Rusanov, Rusanov, and Lax-Friedrichs with the reference solution, which is calculated with the Rusanov scheme with very fine mesh of $ 30000 $ cells and a final time $ t = 10s $, see Figures 4 and 5. We observe that Figure 5 displays a spurious rise in the central of the domain of computation, which has also been seen in the literature using different methods, see [24,32].
5.3. Test case 3
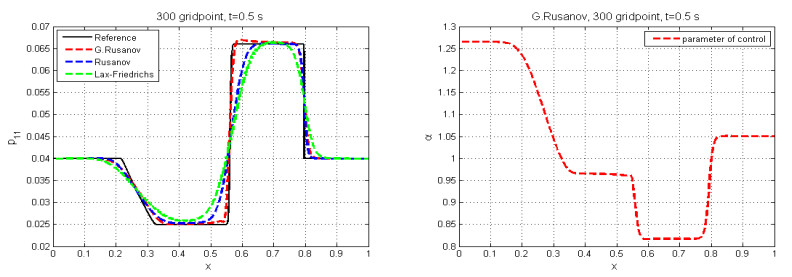
This test case was studied in [24] with the following initial condition
The solution for $ h $, $ v_1 $, and $ p_{11} $ consists of two shear rarefaction waves, one moving to the right and the other moving to the left, and a shock wave to the right. See Figures 6 and 7 which show the behavior of the height of the water, velocity, pressure, and variation of the parameter of control.
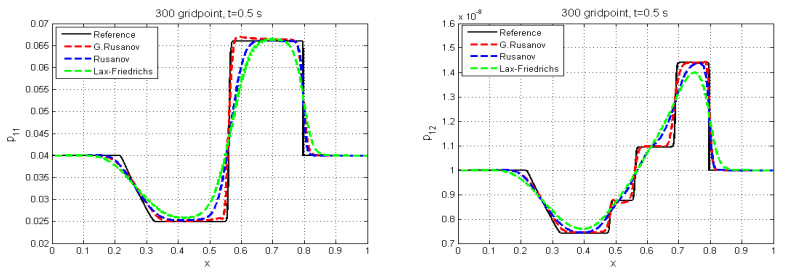
We take the same example, but with another variant of the modified test case, where $ p_{12} = 1\times 10^{-8} $ is set to a small non-zero value. We notice that the behavior of $ h $, $ v_1 $, and $ p_{11} $ is the same, but there is a change in the behavior of $ p_{12} $ such that it displays all of the five waves (four rarefaction and one shock) of the shear shallow water model, see Figures 8 and 9.
5.4. Test case 4
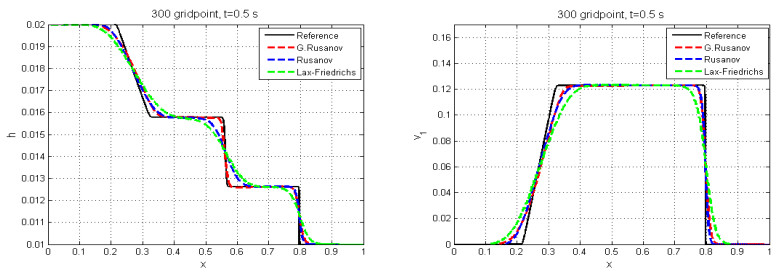
This test case was studied in [24] with the following initial condition
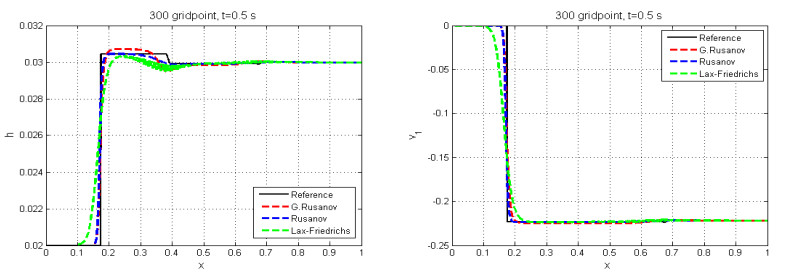
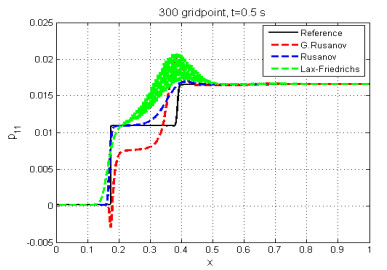
The solution for this test case consists of a single shock wave. We compare the numerical results with the reference solution, which is calculated with the Rusanov scheme with very fine mesh of $ 30000 $ cells and a final time $ t = 0.5s $. Figures 10 and 11 show the numerical results, and we note that all waves are captured by this scheme and the numerical solution agrees with the reference solution, but the solution of $ p_{11} $ does not agree with the exact solution [24]. There is an oscillation with Lax-Friedrichs scheme in the water height $ h $ and the pressure $ p_{11} $.
5.5. Test case 5
This test case (the shear waves problem) was studied in [24] and [32] with the following initial condition
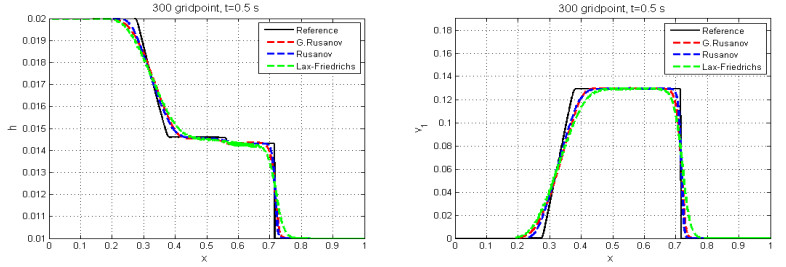
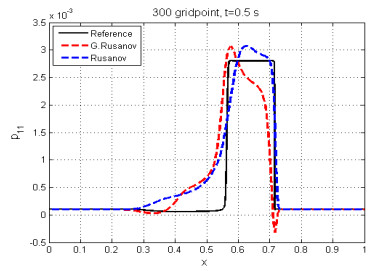
The solution of this test case has a single shock wave and a single rarefaction wave, separated by a contact discontinuity. We compare the numerical results with the reference solution, which is calculated with the Rusanov scheme with very fine mesh of $ 30000 $ cells and a final time $ t = 0.5s $. Figures 12 and 13 show the numerical results, and we note that all waves are captured by this scheme and the numerical solution agrees with the reference solution, but the solution of $ p_{11} $ does not agree with the reference solution [24].
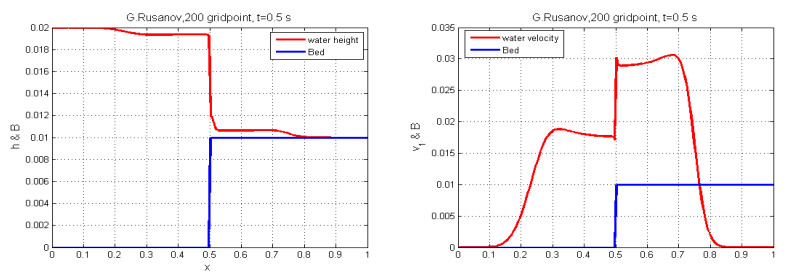
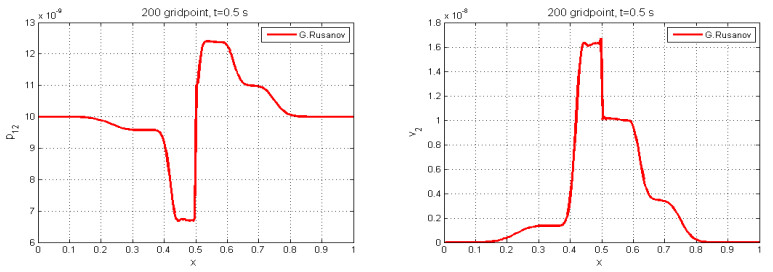
5.6. Test case 6 with a source term
In this test case, we take the previous test case 3 and we added the discontinuous fond topography with the following initial condition
We simulate this test case with the G. Rusanov scheme with $ 200 $ gridpoints on the domain $ \mathbb{L} = [0, 1] $ at the final time $ t = 0.5s $, and we note that the behavior of the solution for $ h $ consists of one shear rarefaction wave moving to the left, a contact discontinuity after that two shear rarefaction waves, one moving to the right and the other moving to the left (see the left side of Figure 14. The right side of the Figure 14 shows the behavior of the velocity $ v_1 $, which it consists of a rarefaction wave, a contact discontinuity after that, and two shear rarefactions. The left side of Figure 14 displays the behavior of the velocity $ v_{1} $. It is composed of two shear rarefactions followed by a contact discontinuity and three rarefaction waves moving to the right. The the right side of Figure 14 displays the behavior of the velocity $ v_2 $. It is composed of two shear rarefactions moving to the left followed by a contact discontinuity after that, and two rarefaction waves moving to the right.
In summary, we have reported five numerical examples to solve the SSW model. Namely, we implemented the G. Rusanov, Rusanov, and Lax-Friedrichs schemes. We also compared the numerical solutions with the reference solution obtained by the classical Rusanov scheme on the very fine mesh of $ 30000 $ gridpoints. The three schemes were capable of capturing shock waves and rarefaction. Also, we have given the last numerical test with a source term. Finally, we discovered that the G. Rusanov scheme was more precise than the Rusanov and Lax-Friedrichs schemes.
6.
Conclusions
The current study is concerned with the SSW model, which is a higher order variant of the traditional shallow water model since it adds vertical shear effects. The model features a non-conservative structure, which makes numerical solutions problematic. The 1D SSW model was solved using the G. Rusanov technique. We clarify that this scheme satisfied the C-property. Several numerical examples were given to solve the SSW model using the G. Rusanov, Rusanov, Lax-Friedrichs, and reference solution techniques. The simulations given verified the G. Rusanov technique's high resolution and validated its capabilities and efficacy in dealing with such models. This approach may be expanded in a two-dimensional space.
Author contributions
H. S. Alayachi: Conceptualization, Data curation, Formal analysis, Writing - original draft; Mahmoud A. E. Abdelrahman: Conceptualization, Data curation, Formal analysis, Writing - original draft; K. Mohamed: Conceptualization, Software, Formal analysis, Writing - original draft.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
The authors extend their appreciation to the Deputyship for Research & Innovation, Ministry of Education in Saudi Arabia for funding this research work through the project number 445-9-753.
Conflict of interest
The authors declare that they have no competing interests.









 DownLoad:
DownLoad: