Closer is more important: The impact of Chinese and global macro-level determinants on Shanghai crude oil futures volatility

1.   Introduction

Since China laughed at the RMB-based crude oil futures in Shanghai International Energy Exchange on 26 March 2018, scholars began to study Shanghai crude oil futures, which is sometimes referred to as INE crude oil futures or Chinese crude oil futures from various perspectives. These emerging literatures studies can be summarized into the following categories. The first string of studies focuses on price discovery efficiency (Shao & Hua, 2022; Yang et al., 2020; Yu et al., 2023) and market maturity (Corbet et al., 2022; Joo et al., 2021). The second string of studies interests in the arbitrage strategy of Shanghai crude oil futures (Wu et al., 2022; Niu et al., 2023). The third string of literature concentrates on its price volatility and forecasting (Guo et al., 2023; Liu & Lee, 2021; Jin et al., 2022; Bei et al., 2023; Wang et al., 2022; Gong et al., 2022; Lu et al., 2022; Jiang et al., 2023). The fourth string of studies investigates the co-movements or spillover effects between Shanghai crude oil futures market and other financial markets, e.g., stock market (He et al., 2021; Li et al., 2023; Sun et al., 2023; Wang & Wang, 2019; Wang et al., 2023; Lv et al., 2020; Yu & Xiao, 2022), bond market (Sun et al., 2023), gold market (He et al., 2021), foreign exchange market (He et al., 2021; Sun et al., 2022), and commodity market (Dai et al., 2022). The fifth string of studies pays attention on the influence of Shanghai crude oil futures on the global and domestic oil markets (Wang et al., 2022; Zhang et al., 2021; Dai et al., 2022; Luo & Ji, 2018; Sun et al., 2023; Yang et al., 2021; Zhang et al., 2022; Sun et al., 2023; Wei et al., 2022; Fu & Qiao, 2022). Besides, there are few researchers focusing on the impact of extreme event such as COVID-19 pandemic on Shanghai crude oil futures market (Zhu et al., 2022; Hu & Jiang, 2023).

In this paper, we continue to enrich the literature on Shanghai crude oil futures. Using a sample spanning from March 2018 to February 2023, we investigate the impact of Chinese and global economic determinants on the return volatility of Shanghai crude oil futures to determine which macro-level determinant is the most informative: Chinese crude oil fundamentals, global crude oil fundamentals, Chinese or global economic policy uncertainty, or global crude oil speculation? For this purpose, supposing that macro-level factors affect the return volatility via its long-term volatility component, the adjusted Generalized Autoregressive Conditional Heteroscedasticity Mixed Data Sampling (GARCH-MIDAS) models are used to conduct our study, in which we used the macro-level variables to replace the original realized volatility variable in the original GARCH-MIDAS model proposed by Engle et al. (2013). Specifically, twelve macro-level economic factors are included, namely, four Chinese macro-level economic determinants (i.e., Chinese crude oil demand, Chinese crude oil production, Chinese crude oil import, and Chinese economic policy uncertainty), four global macro-level economic factors (i.e., global crude oil demand, global crude oil production, global crude oil speculation, and global economic policy uncertainty), and four composite macro-level factors constructed by the method of principal component analysis (i.e., the composite macro-level factor constructed by the four Chinese macro-level economic determinants and global crude oil speculation, the Chinese composite macro-level factor constructed by the four Chinese macro-level economic determinants, the global composite macro-level factor constructed by the four global macro-level economic determinants, and the composite macro-level factor constructed by the eight Chinese and global macro-level economic determinants).

We start with estimating the GARCH-MIDAS models to investigate whether the 12 macro-level variables have significant impact on the return volatility of Shanghai crude oil futures. Then, we employ the recursive scheme to generate one-step-ahead forecasts, and further take the DM test proposed by Diebold & Mariano (1995) and the Fluctuation test proposed by Giacomini & Rossi (2010) to statically and dynamically compare the out-of-sample predictive power of the 12 different GARCH-MIDAS models, respectively. The in-sample empirical results show that there are five individual macro-level determinants (i.e., Chinese crude oil demand, Chinese crude oil production, Chinese economic policy uncertainty, and global crude oil speculation) and two composite factors (i.e., the composite macro-level factor constructed by these five individual macro-level determinants and the Chinese composite macro-level factor) being found having a significant impact on the long-term volatility component of Shanghai crude oil futures at the significance levels more than 10%. The out-of-sample prediction results show that Chinese crude oil production has the best predictive power for the return volatility of Shanghai crude oil futures, followed by the composite macro-level factor constructed by the five macro-level determinants (i.e., Chinese crude oil demand, Chinese crude oil production, Chinese economic policy uncertainty, and global crude oil speculation). Compared with global crude oil production, global economic policy uncertainty and Chinese crude oil import, Chinese crude oil production, Chinese economic policy uncertainty, and global crude oil speculation have stronger impact and higher predictive power on the return volatility of Shanghai crude oil futures, respectively. These findings above are supported by both the statically DM test and the dynamical Fluctuation test results. However, there is no consistent evidence suggesting the much better predictive power of Chinese crude oil demand than global crude oil demand.

Our study contributes to the literature on Shanghai crude oil futures from following aspects. First, different from the previous studies mentioned in the first paragraph (e.g., Shao & Hua, 2022; Corbet et al., 2022; Niu et al., 2023; Gong et al., 2022; Sun et al., 2023; He et al., 2021; Dai et al., 2022; Luo & Ji, 2018), we investigate the influential factors for the return volatility of Shanghai crude oil futures from the macro-level economic perspectives since there is little relevant literature on the macro-economic determinants for the return volatility of Shanghai crude oil futures. Second, different from the researchers who investigated China's macro-financial factors (e.g., exchange rate, interest rate, treasury bonds rate, etc.), determining the Shanghai crude oil futures market (Lin & Su, 2021), we examine the impact of crude oil fundamentals, economic policy uncertainty, and crude oil speculation on its return volatility. Third, different from Huang et al. (2023) and Yang et al. (2021), who focused on the linkage of economic policy uncertainty and China's crude oil futures market, we compare the forecast power of economic policy uncertainty for the return volatility of Shanghai crude oil futures with that of several other macro-level factors, including crude oil fundamentals, global crude oil speculation, and these composite factors. Fourth, we consider both Chinese and global macro-level determinants related to crude oil futures market, including individual and composite factors, to determine which determinant is most informative to the volatility of Shanghai crude oil futures. Last, we take both statical and dynamical methods, namely, the DM test and the Fluctuation test, to compare the relative forecast performance for the return volatility of Shanghai crude oil futures, which is also one innovation of our study.

The remainder of this paper is organized as follows. In Section 2, we introduce the methodology, including the GARCH-MIDAS model, the principal component analysis, the DM test, and the Fluctuation test. In Section 3, we describe data sources and descriptive statistics. In Section 4, we present the empirical results, which mainly show the in-sample parameter estimation and the out-of-same prediction performance of different models. Finally, in Section 5, we conclude the study.

2.   Methodology

2.1.   GARCH-MIDAS model

Our purpose of this study is to figure out whether the volatility of Shanghai crude oil futures can be affected by Chinese domestic economic activities and global economic activities. Considering that the frequency of data for financial markets is daily or higher frequency while that for economic activities is monthly or lower frequency, we use the Generalized Autoregressive Conditional Heteroscedasticity Mixed Data Sampling (GARCH-MIDAS) model suggested by Engle et al. (2013) to link economic activity and the volatility of Shanghai crude oil future market. The advantage of the GARCH-MIDAS model is that it can involve low-frequency and high-frequency sample data into one model, which can be specified as below.

where ${{\text{r}}_{i, t}}$ is the log return of Shanghai crude oil futures on day $i$ during month $t$. ${{{P}}_{{i}}}$ and ${{{P}}_{{{i - 1}}}}$ are the closing price of Shanghai crude oil futures on day $i$ and $i - 1$, respectively. ${N_t}$ is the number of trading days in month $t$. The total volatility of daily return is defined as $\sigma _{i, t}^2\left({\sigma _{i, t}^2 = {\tau _t} \times {g_{i, t}}} \right)$, where ${\tau _t}$ and ${g_{i, t}}$ are the long-term component and the short-term component of the total volatility, respectively. The short-term component ${g_{i, t}}$ follows a daily GARCH (1, 1) process (Equation 2). The long-term component ${\tau _t}$ is specified by smoothing economic variables in the MIDAS regression (Equation 3), of which the weighting scheme is specified by one-parameter beta polynomial (Equation 4). Notably, $E{V_{{t}}}$ (${{E}}{{{V}}_{{t}}} = 100 \times \left[ {{{ln }}\left({{{{E}}_{{t}}}} \right){{ - ln }}\left({{{{E}}_{{{t - 1}}}}} \right)} \right]$), represents the monthly change rates of selected economic activities, including Chinese economic policy uncertainty (CEPU), Chinese crude oil demand(COD), Chinese crude oil production(COP), Chinese crude oil import amount(COI), global crude oil demand(GEPU), global crude oil production(GOP), global crude oil speculation (GOS) and the composite proxy variable for these economic fundamentals.

2.2.   Principal component analysis

Since the GARCH-MIDAS model is computationally complex, we use one variable at a time in the MIDAS equation, in case of identification or convergence problems caused by the inclusion of several economic variables in one model. In this study, there are eight types of economic activity considered, including Chinese economic policy uncertainty (CEPU), Chinese crude oil demand (COD), Chinese crude oil production (COP), Chinese crude oil import amount (COI), global crude oil demand (GEPU), global crude oil production (GOP), and global crude oil speculation (GOS). To incorporate the information contained in different variables in the same equation, we also refer to Stock & Watson (2002) to construct principal components to extract the combined information from several economic variables. We take four ways to construct composite proxy variables. First, we use the correlation matrix to extract the first principal component of all the eight economic variables. Second, we divide the eight economic variables into two groups: Chinese factors (namely, Chinese economic policy uncertainty, Chinese crude oil demand, Chinese crude oil production, and Chinese crude oil import amount), and global factors (namely, global economic policy uncertainty, global crude oil demand, global crude oil production, and global crude oil speculation). For each group, using the correlation matrix, we extract the first principal component of Chinese and global economic factors, respectively. In the last, we construct a composite proxy variable by extracting the first principal component for all the economic variables which have statistically significant impact on the volatility Shanghai crude oil futures, depending on the estimation results of GARCH-MIDAS models with these economic variables.

2.3.   Loss function and DM test

In this study, we use the square forecast error as the loss function to evaluate the volatility predictive power of a specific model by comparing the estimated predicted variance with the realized volatility. It can be described as follows:

where $e_{i, t}^2$ denotes the square forecast error of model $i$ at time $t$. ${Y_t}$ is the realized volatility of Shanghai crude oil futures (${Y_t} = {r_t}^2$), and ${\hat Y_{i, t}}$ is the estimated predicted variance of Shanghai crude oil futures by model $i$ at time $t$.

We employ the Diebold and Mariano (DM) test, suggested by Diebold & Mariano (1995) to compare the prediction accuracy of completive models. The DM test can be described as below:

where $e_{1, t}^2$ means the square forecast error of the benchmark model at time t. $e_{2, t}^2$ means the squared forecast error of the completing model at time t, and ${d_t}$ means the square forecast error differences of the two completive models at time t. $T$ is the total number of forecasts, $\overline d$ is the mean square forecast error (MSFE) differences computed over the whole forecasting sample, and $\text{var} \left(d \right)$ is the variance of ${d_t}$. The null hypothesis of the DM test is $E(d){\text{ }} = {\text{ }}0$, preferring non-difference in the forecasting abilities of the two completive models. When the DM statistic is positive, it indicates that the completing model has better forecasting power than the benchmark model.

2.4.   Fluctuation test

The Diebold and Mariano (DM) test can compare the average forecasting performance of different models in the out-of-sample period, but the relative performance of the two competitive models may be time-varying in real life. Thus, considering the fact that using the static DM test to averaging the evolution over time could result in loss of information, we further employ the Fluctuation test proposed by Giacomini & Rossi (2010) to compare the out-of-sample forecasting performance of different models in the presence of possible instabilities.

The Fluctuation test can be performed by following these steps. First, we assume that the variable ${Y_{\text{t}}}$ can be estimated by two models, which are respectively characterized by parameters $\chi$ and $\gamma$. The total sample of size T is assumed to be divided into two parts, namely, an in-sample portion and an out-of-sample portion. The size of the in-sample portion and the out-of-sample portion is marked as M and P, respectively. Second, for comparing the two h-step-ahead forecasts for the variable ${Y_{\text{t}}}$, the local relative loss for the two completive models is defined as the sequence of out-of-sample loss differences computed over centered rolling windows of size m. It can be described as below:

where $R{L_{{{t, m}}}}$ the local relative loss for the two competitive models over rolling window of size m. ${L^{(1)}}({Y_t}, {\widehat \chi _{t - h, M}})$ is the loss function computed by the in-sample parameter estimates ${\widehat \chi _{t - h, M}}$ for the first model. ${L^{(2)}}({Y_t}, {\widehat \gamma _{t - h, M}})$ is the loss function computed by the in-sample parameter estimates ${\widehat \gamma _{t - h, M}}$ for the second model. $\Delta {L_t}({\widehat \chi _{t - h, M}}{\widehat {, \gamma }_{t - h, M}})$ is the forecast loss difference of the two model. Corresponding to the DM test, we also take the square forecast error (SFE) as the loss function here. However, different from the DM test, the models' local relative performance is calculated by the out-of-sample mean square forecast error (MSFE) differences over rolling windows rather that the whole sample.

Third, the Fluctuation test statistic can be specified as follows:

where ${F_{t, m}}$ is the test statistic for Fluctuation test at time t. ${\widehat \sigma ^2}$ is a HAC estimator of ${\sigma ^2}$ and $q(P)$ is a bandwidth that grows with P. If preferring non-difference in the forecasting abilities of the two completive models. If the Fluctuation test statistic ${F_{t, m}}$ is positive, it means that the second model (completing model) has better forecasting accuracy than the first model (benchmark model) at time t. The null hypothesis of Fluctuation test is $E\left[ {\Delta {L_t}({{\widehat \chi }_{t - h, M}}{{\widehat {, \gamma }}_{t - h, M}})} \right] = 0$ for all $t = M + h, ..., T$.The null hypothesis is rejected against the two-sided alternative $E[\Delta {L_t}({\widehat \chi _{t - h, M}}{\widehat {, \gamma }_{j - h, M}})] \ne 0$ when ${\max _t}\left| {{F_{t, m}}} \right| > {k_\alpha }$, where ${k_\alpha }$ is the critical value for a significant level $\alpha$.

3.   Data

3.1.   Data sources

We collect daily closing prices of Shanghai crude oil futures from the Wind database. We collect the monthly macro-level determinants of oil price volatility from three ways. The monthly Chinese Economic Policy Uncertainty (CEPU) Index which is based on mainland newspapers, and the monthly Global Economic Policy Uncertainty (GEPU) Index which is based on current-price GDP-weighted average of national EPU indices for 21 countries, are obtained from the Economic Policy Uncertainty website (http://www.policyuncertainty.com/). The data of Chinese crude oil demand, Chinese crude oil production, Chinese crude oil import, global crude oil demand, and global crude oil production are collected from the Wind database. Notably, since the original data frequency of Chinese crude oil demand and global crude oil demand that can be available is quarterly, we convert quarterly data to monthly data based on the actual number of days in each month. Following the methods of Kilian & Murphy (2014) and Wei et al. (2017), the global oil speculation index is calculated by the ratio of OECD petroleum stocks over U.S. petroleum stocks, of which data are also collected via the Wind database from the U.S. Energy Information Administration.

Our sample data spans from March 2018 to February 2023, of which the daily price data of Shanghai crude oil futures is from 30 March 2018 to 28 February 2023. Supposing that there are five trading days for each week, we use interpolation to fill in the missing values. We calculate the logarithm growth rates for all the variables. Consequently, there are 1282 daily observations for the log returns of Shanghai crude oil futures and 59 monthly data for the logarithm growth rate of each macro-level variable in our final sample.

3.2.   Descriptive analysis

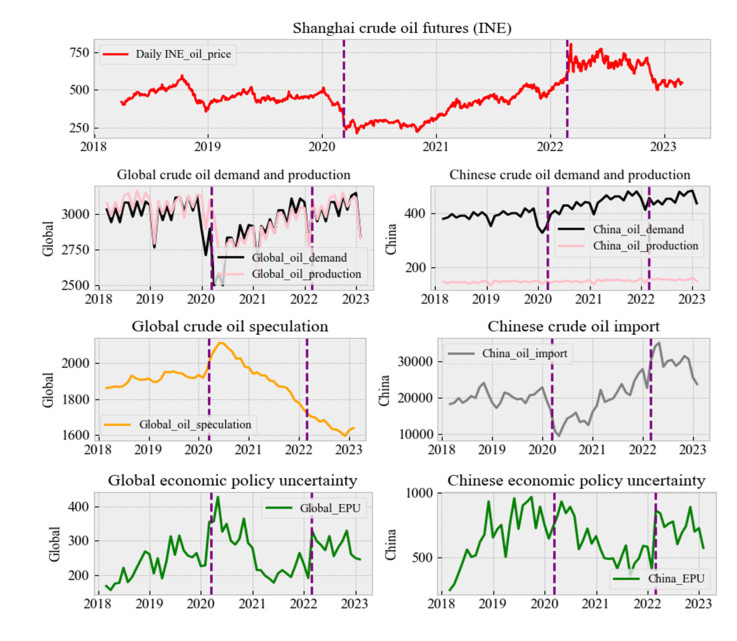
Figure 1 plots the daily evolution of Shanghai crude oil futures' price and the monthly evolution of the eight macro-level economic factors, namely, Chinese crude oil demand and production, global crude oil demand and production, Chinese crude oil import, global oil speculation, Chinese economic policy uncertainty index, and global economic policy uncertainty index. As we can see in the figure, both the crude oil price and the macro-level economic activities reacted to the important events during recent years, including the COVID-19 pandemic and Russia-Ukraine war. Specifically, when the COVID-19 pandemic broke out in 2020, both Chinese and global economic policy university indexes reached a peak, along with a peak in the global oil speculation. However, global and Chinese crude oil fundamentals (including global crude oil demand and production, Chinese crude oil demand and production, and Chinese crude oil import amount) experienced sharp decreases, along with a low point in the price of Shanghai crude oil futures. When the Russia-Ukraine war broke out in 2022, both Chinese and global economic policy university indexes also experienced a smaller peak, while the global oil speculation index did not increase. It seems that global crude oil demand and production experienced a small dip and then quickly recovered. Chinese crude oil demand increased and its crude oil import rose sharply, and the price of Shanghai crude oil futures sharply increased when Russia-Ukraine war broke out in 2022. Besides, as seen in Figure 1, China's crude oil demand is much greater than its crude oil production, so it is very dependent on crude oil imports. That is also why we consider whether Chinese crude oil import is an important factor to influence the volatility of Shanghai crude oil futures' returns in this study.

Figure 1.  Time evolution of Shanghai crude oil future prices and macro-level determinants.

(Notes: This figure plots daily evolution of Shanghai crude oil future prices and monthly evolution of macro-level determinants from 26^th March 2018 to 28^th February 2023. This upper subgraph plots daily prices and returns of Shanghai crude oil futures. Notably, the first purple dashed vertical line marks the date when WHO announced the COVID-19 pandemic on 11 March 2020, the second one marks the date when Russia launched military attack against Ukraine on 24 February 2022.)

DownLoad: Full-Size Img PowerPoint

Table 1 shows descriptive statistics of daily log returns of Shanghai crude oil futures and monthly change rates of the eight macro-level determinants in our final sample. Seen from this table, the mean value of daily log returns of Shanghai crude oil futures ($INE\_oil\_return$) during March 2018 to February 2023 is 0.021, indicating the overall upward trend of the crude oil futures' price, which is in line with Figure 1. The mean values of $C{{hina\_EPU}}$ and $Global\_{{EPU}}$ are 1.438 and 0.649, respectively. It means that the change rate of Chinese economic policy uncertainty is larger than global economic policy uncertainty. The mean values of $China\_oil\_demand$, $China\_oil\_production$, $China\_oil\_import$, $Global\_oil\_demand$, and $Global\_oil\_production$ are 0.236, 0.027, 0.446, −0.109 and −0.143, respectively, suggesting that the he average growth rates of Chinese crude oil demand, production and import are positive while those of global crude oil demand and production are negative during March 2018 to February 2023.

Table 1.  Descriptive statistics for all the variables.

	Freq.	Obs.	Mean	S.D.	Min	Max	Skew.	Kurt.
$INE\_oil\_return$	Daily	1282	0.021	2.294	−14.132	9.732	−0.392	3.151
$C{{hina\_EPU}}$	Monthly	59	1.438	22.370	−50.975	75.471	0.114	1.115
$China\_oil\_demand$	Monthly	59	0.236	5.847	−17.583	12.287	−0.348	0.517
$China\_oil\_production$	Monthly	59	0.027	4.993	−11.941	12.560	0.065	0.867
$China\_oil\_import$	Monthly	59	0.446	12.964	−43.007	28.534	−0.445	1.238
$Global\_{{EPU}}$	Monthly	59	0.649	16.880	−27.099	54.074	0.603	0.869
$Global\_oil\_demand$	Monthly	59	−0.109	5.549	−14.845	12.628	−0.140	0.171
$Global\_oil\_production$	Monthly	59	−0.143	5.168	−13.796	13.755	−0.028	0.641
$Global\_oil\_speculation$	Monthly	59	0.071	0.725	−2.028	1.563	−0.566	0.520
Notes: This table reports descriptive statistics of all the variables in this study. Daily data covers the period from 2 April 2018 to 28 February 2023.Monthly data covers the period from April 2018 to February 2023. $INE\_oil\_return$ is the daily return series of Shanghai crude oil futures. $C{{hina\_EPU}}$ denotes the monthly change rate of Economic Policy Uncertainty Index for China based on mainland newspapers. $Global\_{{EPU}}$ is the monthly change rate of Global Economic Policy Uncertainty (GEPU) Index based on current-price GDP-weighted average of national EPU indices for 21 countries. $China\_oil\_demand$, $China\_oil\_production$, and $China\_oil\_import$ are monthly growth rates of Chinese crude oil demand, production and import amount, respectively. $Global\_oil\_demand$ and $Global\_oil\_production$ are monthly growth rate of global crude oil demand and production, respectively. $Global\_oil\_speculation$ denotes the growth rate of global crude oil speculation, which is calculated by the ratio of OECD petroleum stocks over U.S. petroleum stocks.

---

 | Show Table

DownLoad: CSV

Table 2 reports the results of the unit root test, normality test, and ARCH effect test for the variables. All the statistics of Dickey-Fuller (DF) test, Augmented Dickey-Fuller (ADF) test, Phillips-Perron (PP) test, and Vratio (VR) test are statistically significant at 1% or 5% levels, rejecting the unit root null hypothesis and indicating that these time series are stationary. The Jarque-Bera (JB) test for Shanghai crude oil future return series is significant at the 1% level, implying that it does not follow the normal distribution. Similarly, the Jarque-Bera (JB) tests for global economic policy uncertainty, Chinese crude oil import and global oil speculation are statistically significant at the 10% level, in favor of non-normal distributions. Contrarily, the Jarque-Bera (JB) tests for Chinese economic policy uncertainty, Chinese and global crude oil demand, Chinese and global oil production cannot reject the null hypothesis of normal distribution. Besides, the ARCH test for Shanghai crude oil future return series is significant at 1% level, indicating that there is significant heteroskedastic effect and GARCH-type models are proper to capture its volatility.

Table 2.  Stationary test and normality test.

	DF	ADF	PP	VR	JB	ARCH
$INE\_oil\_return$	−34.504***	−23.766***	−34.504***	−11.427***	557.322***	45.158***
	(0.001)	(0.001)	(0.001)	(0.000)	(0.001)	(0.000)
$C{{hina\_EPU}}$	−10.230***	−7.895***	−10.230***	−3.185***	2.215	0.524
	(0.001)	(0.001)	(0.001)	(0.001)	(0.201)	(0.470)
$Global\_{{EPU}}$	−10.313***	−6.497***	−10.313***	−3.652***	4.585*	0.080
	(0.001)	(0.001)	(0.001)	(0.000)	(0.059)	(0.778)
$China\_oil\_demand$	−9.841***	−6.704***	−9.841***	−4.122***	1.475	0.364
	(0.001)	(0.001)	(0.001)	(0.000)	(0.358)	(0.546)
$Global\_oil\_demand$	−14.084***	−7.701***	−14.084***	−4.632***	0.190	0.373
	(0.001)	(0.001)	(0.001)	(0.000)	(0.500)	(0.541)
$China\_oil\_production$	−13.957***	−8.820***	−13.957***	−3.848***	0.593	6.480**
	(0.001)	(0.001)	(0.001)	(0.000)	(0.500)	(0.011)
$Global\_oil\_production$	−19.523***	−12.481***	−19.523***	−3.980***	1.227	13.782***
	(0.001)	(0.001)	(0.001)	(0.000)	(0.432)	(0.000)
$China\_oil\_import$	−6.644***	−5.447***	−6.644***	−2.374**	4.485*	0.532
	(0.001)	(0.001)	(0.001)	(0.018)	(0.062)	(0.466)
$Global\_oil\_speculation$	−7.039***	−5.152***	−7.039***	−2.983***	3.336*	1.338
	(0.001)	(0.001)	(0.001)	(0.003)	(0.099)	(0.247)
Notes: This table reports results of unit root test, normality test and ARCH effect test for all the variables in this study. Daily data cover the period from 2 April 2018 to 28 February 2023. Monthly data cover the period from April 2018 to February 2023. $INE\_oil\_return$ is the daily return series of Shanghai crude oil futures. $C{{hina\_EPU}}$ denotes the monthly change rate of Economic Policy Uncertainty Index for China based on mainland newspapers. $Global\_{{EPU}}$ is the monthly change rate of Global Economic Policy Uncertainty (GEPU) Index based on current-price GDP-weighted average of national EPU indices for 21 countries. $China\_oil\_demand$, $China\_oil\_production$, and $China\_oil\_import$ are monthly growth rates of Chinese crude oil demand, production and import amount, respectively. $Global\_oil\_demand$ and $Global\_oil\_production$ are monthly growth rate of global crude oil demand and production, respectively. $Global\_oil\_speculation$ denotes the growth rate of global crude oil speculation. The Dickey-Fuller (DF) test, Augmented Dickey-Fuller (ADF) test, Phillips-Perron (PP) test and Vratio (VR) test are used to test the stationarity of time series. The Jarque-Bera (JB) tests is for testing whether a given time series follows the normal distribution, and the ARCH test is for testing the heteroskedastic effect. The numbers in parentheses are the p-values corresponding to the test statistics. 0.000 means that the value is less than 0.001. ***, ** and * respectively denote the significance at 1%, 5%, and 10% levels.

---

 | Show Table

DownLoad: CSV

Table 3 shows the correlation between monthly observations about macro-level economic variables and the monthly realized volatility of Shanghai crude oil futures return (RV). The correlation coefficient between Chinese and global economic policy uncertainty ($C{{hina\_EPU}}$ and $Global\_{{EPU}}$) is 0.694, which is highly correlated. The correlation coefficient between Chinese crude oil demand ($China\_oil\_demand$) and Chinese crude oil production ($China\_oil\_production$) is 0.665, and that between global crude oil demand ($Global\_oil\_demand$) and global crude oil production ($Global\_oil\_production$) is 0.871, highlighting that the correlation between crude oil demand and production in China is lower than that on the global level. Except for Chinese economic policy university ($C{{hina\_EPU}}$), the growth rate of global crude oil speculation index ($Global\_oil\_speculation$) negatively correlates to all the growth rates of the other macro-level economic variables.

Table 3.  Correlation between variables.

	$C{{hina\_EPU}}$	$China\_oil\_demand$	$China\_oil\_production$	$China\_oil\_import$	$Global\_{{EPU}}$	$Global\_oil\_demand$	$Global\_oil\_production$
$C{{hina\_EPU}}$	1
$China\_oil\_demand$	0.399	1
$China\_oil\_production$	0.383	0.665	1
$China\_oil\_import$	0.146	0.072	0.329	1
$Global\_{{EPU}}$	0.694	0.408	0.436	0.075	1
$Global\_oil\_demand$	0.349	0.732	0.829	0.373	0.428	1
$Global\_oil\_production$	0.350	0.749	0.878	0.358	0.420	0.871	1
$Global\_oil\_speculation$	0.112	−0.118	−0.097	−0.005	−0.007	−0.038	−0.111
Notes: This table reports the correlation between monthly observations about macro-level economic variables and the monthly realized volatility of Shanghai crude oil futures return (RV). The monthly realized volatility of Shanghai crude oil futures return is calculated by the sum of daily realized volatility in a given month, namely, $R{V_{{t}}} = \sum\limits_{{{i}} = 1}^N {{{{r}}_{{i}}}^2}$.The macro-level economic variables are the growth rates of Chinese Economic Policy Uncertainty Index ($C{{hina\_EPU}}$), Global Economic Policy Uncertainty Index ($Global\_{{EPU}}$), Chinese crude oil demand ($China\_oil\_demand$), Chinese crude oil production ($China\_oil\_production$), Chinese crude oil import ($China\_oil\_import$), global crude oil demand ($Global\_oil\_demand$), global crude oil production ($Global\_oil\_production$), and global crude oil speculation ($Global\_oil\_speculation$).Data cover the period from April 2018 to February 2023.

---

 | Show Table

DownLoad: CSV

Compared with the growth rate of global crude oil demand, the growth rate of global crude oil speculation index has a closer correlation with the growth rate of global crude oil production ($\left| { - 0.111} \right| > \left| { - 0.038} \right|$). Except Chinese crude oil import (−0.033), the monthly realized volatility of Shanghai crude oil futures return (RV) is positively correlated with the change rates of other macro-level economic variables, namely, Chinese economic policy uncertainty index (0.319), Chinese crude oil demand (0.310), Chinese crude oil production (0.218), global economic policy uncertainty index (0.445), global crude oil demand (0.059), global crude oil production (0.219), and global crude oil speculation (0.015).

4.   Empirical results

4.1.   In-sample estimation

Table 4 shows the estimated parameters of the GARCH-MIDAS models, spanning from April 2018 to February 2023. Panel A and B of this table reports the estimation results for the different models with the eight individual economic variables in the MIDAS equation. Most parameters in the equations for the short-term variance component (${g_{i, t}}$, Equation 3) are statistically significant at the 1% level, suggesting a clustering pattern in the short-term return volatility of Shanghai crude oil futures. Turning to the impact of macro-level economic factors on the long-term variance component (${\tau _t}$, Equation 4), we can see that the estimated parameter ($\theta$) for $C{{hina\_EPU}}$ and $Global\_oil\_speculation$ are significant at the 5% level, and that for $China\_oil\_demand$, $China\_oil\_production$, and $China\_oil\_import$ are significant at the 10% level, indicating that the growth rates of Chinese economic policy uncertainty, Chinese crude oil demand, Chinese crude oil production, Chinese crude oil import and global crude oil speculation index have significant impact on the long-run return volatility of Shanghai crude oil futures. As shown in Panels A and B of Table 4, the estimation results do not provide evidence that global economic policy uncertainty index ($Global\_{{EPU}}$), global crude oil demand ($Global\_oil\_demand$) and global crude oil production ($Global\_oil\_production$) have significant impact on the return volatility of Shanghai crude oil futures, for the corresponding estimated parameters ($\theta$) are not significant at a level less than 10%. If we divide the eight macro-level determinants into two groups, namely Chinese factors and global factors, of which corresponding estimation results respectively shown in Panel A and B of Table 4, we can find that the number of Chinese factors which significantly affect the long-term return volatility of Shanghai crude oil futures is more than that of global factor. In detail, the shocks from Chinese economic policy uncertainty, Chinese crude oil demand and production are respectively stronger than the shocks from global economic policy uncertainty, global crude oil demand and production. Interestingly, the shock from global crude oil speculation is stronger than that from Chinese crude oil import, in that the estimation parameter ($\theta$) for $Global\_oil\_speculation$ is larger than that for $China\_oil\_import$.Among the four global factors, namely, global economic policy uncertainty, global crude oil demand, global crude oil production and global crude oil speculation, only global crude oil speculation index has significant impact on the return volatility of Shanghai crude oil futures.

Table 4.  Estimated parameters of the GARCH-MIDAS model with individual macro-level variables of the MIDAS equation.

Model	$\mu$	$\alpha$	$\beta$	$\theta$	$\omega$	$\upsilon$	Obs. /L.L.	AIC/BIC
Panel A: Chinese macro-level factors
CEPU	0.0762	0.1232***	0.8316***	−0.0256**	1.0313***	1.7173***	1282	5452
	(0.0543)	(0.0163)	(0.0195)	(0.0104)	(0.0487)	(0.1441)	−2720	5483
COD	0.0670	0.0531***	0.9469***	−0.0421*	4.7684	−0.1050	1282	5513
	(0.0465)	(0.0049)	(0.0045)	(0.0232)	(2.9654)	(0.2492)	−2750	5544
COP	0.0716	0.0654***	0.9346***	−0.0714*	7.7409	0.2370	1282	5497
	(0.0452)	(0.0059)	(0.0054)	(0.0395)	(7.3988)	(0.4170)	−2742	5528
COI	0.0696	0.1367***	0.8109***	0.0335*	1.0010***	1.6731***	1282	5151
	(0.0583)	(0.0185)	(0.0227)	(0.0177)	(0.0312)	(0.1400)	−2569	5182
Panel B: Global macro-level factors
GEPU	0.0776	0.1286***	0.8322***	0.0129	1.0010***	1.6710***	1282	5457
	(0.0539)	(0.0162)	(0.0191)	(0.0154)	(0.0601)	(0.1647)	−2723	5488
GOD	0.0767	0.1299***	0.8314***	0.0901	1.0010***	1.6810***	1282	5456
	(0.0545)	(0.0160)	(0.0184)	(0.0811)	(0.0283)	(0.1653)	−2722	5487
GOP	0.0787	0.1308***	0.8280***	0.0849	1.0010***	1.6785***	1282	5457
	(0.0543)	(0.0166)	(0.0191)	(0.0856)	(0.0316)	(0.1592)	−2722	5488
GOS	0.0796	0.1315***	0.8184***	0.4806**	1.0010***	1.6182***	1282	5456
	(0.0546)	(0.0172)	(0.0224)	(0.2258)	(0.0391)	(0.1376)	−2722	5486
Notes: The table shows the estimated parameters of the GARCH-MIDAS model with different specifications of the MIDAS equation. Panel A of this table reports the results of the model with the growth rates of Chinese macro-level determinants in the MIDAS equation, namely, Chinese economic policy uncertainty index ($C{{hina\_EPU}}$), Chinese crude oil demand ($China\_oil\_demand$), Chinese crude oil production ($China\_oil\_production$), and Chinese crude oil import ($China\_oil\_import$), of which the corresponding GARCH-MIDAS models are marked as CEPU, COD, COP, and COI, respectively. Panel B of this table reports the results of the model with the growth rates of global macro-level determinants in the MIDAS equation, namely, global economic policy uncertainty index ($Global\_{{EPU}}$), global crude oil demand ($Global\_oil\_demand$), global crude oil production ($Global\_oil\_production$), and global crude oil speculation ($Global\_oil\_speculation$), of which the corresponding GARCH-MIDAS models are marked as GEPU, GOD, GOP, and GOS, respectively. The parameter space for the short-term component of the total volatility is Θ = { $\mu$, $\alpha$, $\beta$ }, corresponding to Equation (3). The parameter space for the long-term component of the total volatility is Θ = { $\theta$, $\omega$, $\upsilon$ }, corresponding to Equations (4) and (5). The numbers in parentheses are standard errors. Obs. is the number of daily observations in the estimated sample. L.L.is the optimal log-likelihood function, AIC is the Akaike information criterion and BIC is the Bayesian information criterion. ***, ** and * respectively denote the significance at 1%, 5%, and 10% levels.

---

 | Show Table

DownLoad: CSV

In order to further test the relationship between Chinese as well as global macro-level factors and the long-term return volatility of Shanghai crude oil futures, we further estimate the GARCH-MIDAS models with the composite factors which consist of the principal components extracted from these individual determinants, which can incorporate the information contained in different determinants. Table 5 reports the corresponding estimation results. The estimated parameter ($\theta$) for ${{Total\_PCA}}$ is not statistically significant while that for ${{macro\_PCA}}$ is statistically significant at the 5% level. This indicates that the composite factor (${{macro\_PCA}}$) constructed by the five determinants ($C{{hina\_EPU}}$, $China\_oil\_demand$, $China\_oil\_production$, $China\_oil\_import$, $Global\_oil\_speculation$) which have been found to have a significantly estimated parameter ($\theta$) as shown in Panels A and B of Table 4, has stronger impact on the long-term return volatility of Shanghai crude oil futures, compared with the composite factor (${{Total\_PCA}}$) constructed by all the eight determinants in this study.

Table 5.  Estimated parameters of the GARCH-MIDAS model with composite macro-level variables of the MIDAS equation.

Model	Long-run variables	$\mu$	$\alpha$	$\beta$	$\theta$	$\omega$	$\upsilon$	Obs. /L.L.	AIC/BIC
TPCA	${{Total\_PCA}}$	0.0757	0.1252***	0.8323***	0.0237	1.1501	1.6979***	1282	5456
		(0.0542)	(0.0164)	(0.0195)	(0.0155)	(0.7969)	(0.1501)	−2722	5487
MPCA	${{macro\_PCA}}$	0.0750	0.1230***	0.8332***	0.0372**	1.2316**	1.7233***	1282	5454
		(0.0544)	(0.0165)	(0.0197)	(0.0165)	(0.5120)	(0.1470)	−2721	5485
CPCA	${{China\_PCA}}$	0.0754	0.1226***	0.8313***	−0.0661**	1.0604***	1.8014***	1282	5451
		(0.0541)	(0.0165)	(0.0204)	(0.0266)	(0.1796)	(0.1520)	−2719	5482
GPCA	${{Global\_PCA}}$	0.0373	0.0491***	0.9509***	−0.0087	4.4338	−0.1051	1282	5520
		(0.0470)	(0.0041)	(0.0039)	(0.0229)	(15.8790)	(0.2767)	−2754	5551
Notes: The table shows the estimated parameters of the GARCH-MIDAS model with composite macro-level variables of the MIDAS equation. There are four composite macro-level variables, which are respectively constructed by the first principal component of all the eight macro-level variables (${{Total\_PCA}}$), the first principal component of the five macro-level variables which have been found having statistically significant relationship with the long-term volatility component of Shanghai crude oil futures as shown in Table 4 (${{macro\_PCA}}$), the first principal component of the four Chinese macro-level variables (${{China\_PCA}}$), the first principal component of the four global macro-level variables (${{Global\_PCA}}$), which are specified as following equations: $\begin{array}{l} {{Total\_PCA = - 0}}{{.32 * Global\_EPU + - 0}}{{.29 * China\_EPU + - 0}}{{.41 * China\_oil\_demand + - 0}}{{.45 * Global\_oil\_demand + }} \hfill \\ {{ - 0}}{{.46 * Global\_oil\_production + - 0}}{{.45 * China\_oil\_production + - 0}}{{.19 * China\_oil\_import + 0}}{{.04 * Global\_oil\_speculation }} \hfill \\ {{macro\_PCA = - 0}}{{.46 * China\_EPU + - 0}}{{.57 * China\_oil\_demand + - 0}}{{.61 * China\_oil\_production + }} \hfill \\ {{ - 0}}{{.29 * China\_oil\_import + 0}}{{.07 * Global\_oil\_speculation }} \hfill \\ {{China\_PCA = 0}}{{.47 * China\_EPU + 0}}{{.57 * China\_oil\_demand + 0}}{{.61 * China\_oil\_production + 0}}{{.29 * China\_oil\_import }} \hfill \\ {{Global\_PCA = - 0}}{{.45 * Global\_EPU + - 0}}{{.63 * Global\_oil\_demand + - 0}}{{.63 * Global\_oil\_production + 0}}{{.08 * Global\_oil\_speculation }} \hfill \\ \end{array}$ These composite variables are respectively involved in the MIDAS equation and the corresponding GARCH-MIDAS models are marked as TPCA, MPCA, CPCA and GPCA, respectively. The parameter space for the short-term component of the total volatility is Θ = { $\mu$, $\alpha$, $\beta$ }, corresponding to Equation (3). The parameter space for the long-term component of the total volatility is Θ = { $\theta$, $\omega$, $\upsilon$ }, corresponding to Equations (4) and (5). The numbers in parentheses are standard errors. L.L.is the optimal log-likelihood function, AIC is the Akaike information criterion and BIC is the Bayesian information criterion. ***, and ** respectively denote the significance at 1% and 5% levels.

---

 | Show Table

DownLoad: CSV

The estimated parameter ($\theta$) for the composite factor (${{China\_PCA}}$) constructed by the four Chinese determinants ($C{{hina\_EPU}}$, $China\_oil\_demand$, $China\_oil\_production$, and $China\_oil\_import$) is statistically significant at the 5% level, while that for the composite factor (${{Global\_PCA}}$) constructed by the four global determinants ($Global\_{{EPU}}$, $Global\_oil\_demand$, $Global\_oil\_production$, and $Global\_oil\_speculation$) cannot be statistically significant at the 10% level. It suggests that the long-term return volatility of Shanghai crude oil futures is strongly exposed to the change of Chinese macro-level determinants but weakly affected by corresponding macro-level global factors.

Figure 2 illustrates the estimated total and long-term volatility from the GARCH-MIDAS models corresponding to different specifications in the MIDAS equation and the daily realized volatility of Shanghai crude oil futures during from April 2018 to February 2023. It shows that the estimated variances from the 12 GARCH-MIDAS models mostly follow a similar pattern with the realized volatility, which successfully capture the abnormally high volatility of Shanghai crude oil future returns when the COVID-19 pandemic and the Russia-Ukraine war broke out. Except for the estimated variances from the models, which includes Chinese crude oil demand (COD), Chinese crude oil production (COP), and the joint proxy variable of the four global macro-level determinants (GPCA), respectively, we observe that the long-term component volatility is below the total volatility most of the time. Besides, the peak of estimated long-term volatility comes later than the peak of estimated total volatility and the realized volatility.

Figure 2.  Plot of the daily realized volatility and the estimated total and long-term volatilities from different GARCH-MIDAS models.

(Notes: This figure illustrates the total and long-term variances estimated by the GARCH-MIDAS model and the daily realized volatility calculated by daily squared returns of Shanghai crude oil futures ($R{V_i} = {{{r}}_{{i}}}^2$). Corresponding to Table 4, the MIDAS equation respectively includes the corresponding macro-level variable as shown in the subtitle for each subgraph. The estimation period covers the period from April 2018 to February 2023, while a sample of 30 observations is used to calculate the moving average of the included variables in the MIDAS equation. Notably, the first black dashed vertical line marks the date when WHO announced the COVID-19 pandemic on 11 March 2020, the second one marks the date when Russia launched military attack against Ukraine on 24 February 2022.)

DownLoad: Full-Size Img PowerPoint

To compare the estimated long-term volatilities from different models more clearly, we further depict the estimated long-term variance components in one graph, which is shown in Figure 3. Some interesting findings can be observed from this figure. First, the estimated long-term volatilities obtained from the three models that includes Chinese crude oil demand (COD), a model that includes Chinese crude oil production (COP), and the joint proxy variable of the four global macro-level determinants (GPCA), respectively, which are higher than those obtained from the other nine models. Second, the long-term volatility estimated by Chinese crude oil production (COP) is lower than that estimated by Chinese crude oil demand (COD) and the global composite factor (GPCA). Third, the long-term volatility estimated by Chinese crude oil demand (COD) is higher than that estimated by the global composite factor (GPCA) at most of time. Fourth, when the COVID-19 pandemic broke out in 2020, the long-term volatility estimated by the global composite factor (GPCA) once outpaced the long-term volatility estimated by Chinese crude oil demand (COD) and then gradually fell back. Besides, the long-term volatility estimated by the global composite factor (GPCA) outpaced that that estimated by other macro-level variables once again when the breakout of Russia-Ukraine war in 2022.

Figure 3.  Estimated long-term volatilities from different GARCH-MIDAS models.

(Notes: The figure plots the estimated long-term volatility, based on twelve alternative specifications of the MIDAS equation, namely, a model that includes Chinese economic policy uncertainty index (CEPU), a model that includes Chinese crude oil demand (COD), a model that includes Chinese crude oil production (COP), and a model that includes Chinese crude oil import (COI), a model that includes global economic policy uncertainty index (GEPU), a model that includes global crude oil demand (GOD), a model that includes global crude oil production (GOP), a model that includes global crude oil speculation (GOS), a model that includes the first principal component of all the eight macro-level variables (TPCA), a model that includes the first principal component of the five macro-level variables which have been found having statistically significant relationship with the long-term volatility component of Shanghai crude oil futures as shown in Table 4 (MPCA), a model that includes the first principal component of the four Chinese macro-level variables (CPCA), and a model that includes the first principal component of the four global macro-level variables (GPCA). The estimation period covers the period from April 2018 to February 2023, while a sample of 30 observations is used to calculate the moving average of the included variables in the MIDAS equation. Notably, the first black dashed vertical line marks the date when WHO announced the COVID-19 pandemic on 11 March 2020, and the second one marks the date when Russia launched military attack against Ukraine on 24 February 2022 in this figure.)

DownLoad: Full-Size Img PowerPoint

4.2.   Out-of-sample prediction

Next, we further compare the forecast performance of different GARCH–MIDAS models for the total daily return volatility of Shanghai crude oil futures. Following Yu et al. (2021), we use the recursive scheme to generate one-step-ahead forecast, in which the initial estimation date is fixed while an additional observation is added at a time to the estimation period. The DM test is employed to statically compare the forecasting accuracy of different GARCH-MIDAS models, while the Fluctuation test is used to dynamically compare the forecasting accuracy of the models. Three out-of-sample forecasting horizons (i.e., 120 days, 250days, and 500 days of the total sample) are considered for obtaining robust model evaluation results, ranging from approximately 6 months to 3 years.

4.2.1.   DM test

Table 6 reports the Diebold and Mariano (DM) testing results for comparing the predictive accuracy of the eight GARCH-MIDAS models with individual macro-level determinants, namely, the Chinese economic policy uncertainty index (CEPU), Chinese crude oil demand (COD), Chinese crude oil production (COP), Chinese crude oil import (COI), global economic policy uncertainty index (GEPU), global crude oil demand (GOD), global crude oil production (GOP), and global crude oil speculation (GOS). As shown in Table 6, all the DM statistics are statistically significant at the 5% or 1% levels, suggesting different forecast performance between the eight models. As discussed in Section 2.3, positive DM statistics indicate that the completing model in the row has better forecast performance than the benchmark model in the corresponding column, while the negative DM statistics means the better forecast performance of the benchmark models in the column comparing the completing model in the row.

Table 6.  Results of DM test for the out-of-sample forecasting performance of GARCH-MIDAS models with individual macro-level determinants.

Model	Long-run variables	CEPU	COD	COI	COP	GEPU	GOD	GOP	GOS
Panel A: 120-day forecasting horizon
CEPU	$C{{hina\_EPU}}$		−1.193***	−0.276***	−0.990***	1.257***	−0.900***	−0.138***	−0.638***
COD	$China\_oil\_demand$	1.193***		0.609***	0.596**	1.541***	0.548***	0.253***	0.069***
COI	$China\_oil\_production$	0.276***	−0.609***		−0.163***	1.358***	−0.648***	−0.045***	−0.430***
COP	$China\_oil\_import$	0.990***	−0.596**	0.163***		1.626***	−0.303***	0.009***	−0.378***
GEPU	$Global\_{{EPU}}$	−1.257***	−1.541***	−1.358***	−1.626***		−1.565***	−0.787***	−1.215***
GOD	$Global\_oil\_demand$	0.900***	−0.548***	0.648***	0.303***	1.565***		0.097***	−0.223***
GOP	$Global\_oil\_production$	0.138***	−0.253***	0.045***	−0.009***	0.787***	−0.097***		−0.266***
GOS	$Global\_oil\_speculation$	0.638***	−0.069***	0.430***	0.378***	1.215***	0.223***	0.266***
Panel B: 250-day forecasting horizon
CEPU	$C{{hina\_EPU}}$		0.520***	1.708***	−0.740***	1.613***	0.810***	0.869***	0.691***
COD	$China\_oil\_demand$	−0.520***		0.439***	−0.842***	1.038***	0.152***	0.010***	−0.206***
COI	$China\_oil\_production$	−1.708***	−0.439***		−1.280***	1.190***	−0.159***	−1.070***	−2.147***
COP	$China\_oil\_import$	0.740***	0.842***	1.280***		1.606***	1.922***	0.963***	0.867***
GEPU	$Global\_{{EPU}}$	−1.613***	−1.038***	−1.190***	−1.606***		−0.733***	−1.533***	−1.834***
GOD	$Global\_oil\_demand$	−0.810***	−0.152***	0.159***	−1.922***	0.733***		−0.165***	−0.341***
GOP	$Global\_oil\_production$	−0.869***	−0.010***	1.070***	−0.963***	1.533***	0.165***		−0.516***
GOS	$Global\_oil\_speculation$	−0.691***	0.206***	2.147***	−0.867***	1.834***	0.341***	0.516***
Panel C: 500-day forecasting horizon
CEPU	$C{{hina\_EPU}}$		−0.003***	0.688***	−1.218***	1.521***	−0.303***	−0.131***	−0.091***
COD	$China\_oil\_demand$	0.003***		0.577***	−0.871***	1.534***	−0.271***	−0.118***	−0.070***
COI	$China\_oil\_production$	−0.688***	−0.577***		−1.401***	1.749***	−0.469***	−1.610***	−1.814***
COP	$China\_oil\_import$	1.218***	0.871***	1.401***		1.988***	0.252***	0.917***	0.987***
GEPU	$Global\_{{EPU}}$	−1.521***	−1.534***	−1.749***	−1.988***		−0.911***	−2.241***	−2.228***
GOD	$Global\_oil\_demand$	0.303***	0.271***	0.469***	−0.252***	0.911***		0.243***	0.254***
GOP	$Global\_oil\_production$	0.131***	0.118***	1.610***	−0.917***	2.241***	−0.243***		0.091***
GOS	$Global\_oil\_speculation$	0.091***	0.070***	1.814***	−0.987***	2.228***	−0.254***	−0.091***
Notes: The table shows the Diebold and Mariano (DM) test for the different models' out-of-sample forecast performance. The DM method is applied to examine the null hypothesis of equal forecasting performance. The DM statistic in each cell is calculated by the model given in the row comparing with the benchmark model given in the column. The positive DM statistics indicate that the completing model in the row has better forecast performance than the benchmark model in the corresponding column, while the negative DM statistics means the better forecast performance of the benchmark models in the column comparing the completing model in the row. *** and ** denote significance at the 1%, and 5% level, respectively.

---

 | Show Table

DownLoad: CSV

Panel A in Table 6 shows the comparing results for the 120-day out-of-sample horizon. First, we can observe that the model with Chinese crude oil demand (COD) has the best forecast performance in that all the DM statistics in the corresponding column are negatively significant at the 5% or 1% levels, while the model with global economic policy uncertainty index (GEPU) has the worst forecast performance in that all the DM statistics in the corresponding column are positively significant at the 1% significance level. Second, when we compare the models including Chinese macro-level variables with the models including corresponding global macro-level variables, the results show that Chinese crude oil demand (COD), Chinese crude oil production (COP), and Chinese economic policy uncertainty respectively have better forecast performance than global crude oil demand (GOD), global crude oil production (GOP), and global economic policy uncertainty index (GEPU). However, the model with global crude oil speculation (GOS) outperforms than that with Chinese crude oil import (COI).

When the out-of-sample forecasting period is extended to 250 trading days (Panel B, Table 6), the model with global economic policy uncertainty index (GEPU) still performs worst, while the model which has the best predictive accuracy is turned from the model with Chinese crude oil demand (COD) to that with Chinese crude oil production (COP). In line with the DM testing results for the out-of-sample forecasting period which has 120 trading days (Panel A, Table 6), the model with Chinese crude oil demand (COD) performs better than that with global crude oil demand (GOD), the model with Chinese crude oil production (COP) performs better than that with global crude oil production (GOP), and the model with Chinese economic policy uncertainty (CEPU) performs better than that with global economic policy uncertainty index (GEPU), which is in line with the parameter estimation results shown in Table 4. Besides, global crude oil speculation (GOS) has better predictive accuracy for the volatility of Shanghai crude oil futures than Chinese crude oil import (COI), in spite that both the estimated parameters for global crude oil speculation and Chinese crude oil import are statistically significant in Table 4.

We extend the out-of-sample forecasting period to 500 trading days, of which the corresponding DM testing results are reported in Panel C in Table 6. Like the 250-day forecasting horizon, the model with Chinese crude oil production (COP) performs best while the model with global economic policy uncertainty index (GEPU) performs worst. The models with Chinese crude oil production (COP), Chinese economic policy uncertainty (CEPU), and global crude oil speculation (GOS) have better forecast power for the volatility of Shanghai crude oil futures than corresponding models with global crude oil production (GOP), global economic policy uncertainty (GEPU), and Chinese crude oil import (COI), respectively. The only expectation is that global crude oil demand (GOD) has better predictive power for Shanghai crude oil futures' return volatility than Chinese crude oil demand (COD) when the forecasting period extended to around 2 years (500 trading days).

Next, we use the DM test to compare the out-of-sample forecast performance of GARCH-MIDAS models with composite macro-level determinants. As shown in Table 7, the model with the composite factor constructed by the five macro-level variables, which have been found having statistically significant relationship with the long-term volatility component of Shanghai crude oil futures, as shown in Table 4 (MPCA), has relatively best predictive accuracy for the volatility of Shanghai crude oil futures according to the fact that all the DM statistics are negative and statistically significant at the 1% level when taking it as the benchmark. The model with the composite factor constructed by the four global macro-level variables (GPCA) has relatively worst predictive accuracy, according to the fact that all the DM statistics are positive and statistically significant at the 1% level when taking it as the benchmark. Compared with both the global composite macro-level factor (GPCA) and the total composite macro-level factor (TPCA), the Chinese composite macro-level factor (CPCA) has better predictive power. These findings can hold for all the three out-of-sample forecasting horizons (i.e., 120 days, 250 days, and 500 days of the total sample).

Table 7.  Results of DM test for the out-of-sample forecast performance of GARCH-MIDAS models with composite macro-level determinants.

Model	Long-run variables	CPCA	GPCA	MPCA	TPCA
Panel A: 120-day forecasting horizon
CPCA	${{China\_PCA}}$		1.369***	-0.457***	0.941***
GPCA	${{Global\_PCA}}$	−1.369***		-1.258***	-0.143***
MPCA	${{macro\_PCA}}$	0.457***	1.258***		1.199***
TPCA	${{Total\_PCA}}$	−0.941***	0.143***	-1.199***
Panel B: 250-day forecasting horizon
CPCA	${{China\_PCA}}$		1.504***	-1.687***	0.496***
GPCA	${{Global\_PCA}}$	−1.504***		-2.443***	-1.382***
MPCA	${{macro\_PCA}}$	1.687***	2.443***		1.804***
TPCA	${{Total\_PCA}}$	−0.496***	1.382***	-1.804***
Panel C: 500-day forecasting horizon
CPCA	${{China\_PCA}}$		1.337***	-2.054***	0.943***
GPCA	${{Global\_PCA}}$	−1.337***		-1.845***	-1.014***
MPCA	${{macro\_PCA}}$	2.054***	1.845***		1.461***
TPCA	${{Total\_PCA}}$	−0.943***	1.014***	-1.461***
Notes: This table shows the Diebold and Mariano (DM) test for the out-of-sample forecast performance of different models with composite macro-level determinants, namely, the composite determinant constructed by all the eight macro-level variables (TPCA), the composite determinant constructed by the five macro-level variables which have been found having statistically significant relationship with the long-term volatility component of Shanghai crude oil futures as shown in Table 4 (MPCA), the composite determinant constructed by the four Chinese macro-level variables (CPCA), and the composite determinant constructed by the four global macro-level variables (GPCA). The DM method is applied to examine the null hypothesis of equal forecasting performance. The DM statistic in each cell is calculated by the model given in the row comparing with the benchmark model given in the column. The positive DM statistics indicate that the completing model in the row has better forecast performance than the benchmark model in the corresponding column, while the negative DM statistics means the better forecast performance of the benchmark models in the column comparing the completing model in the row. *** denotes significance at the 1% level.

---

 | Show Table

DownLoad: CSV

Table 8 summarizes the DM testing results for the 12 GARCH-MIDAS models with different macro-level variables. Panel A of this table shows the ranking results according to the out-of-sample predictive accuracy of the eight GARCH-MIDAS models which include individual macro-level factors (i.e., CEPU, COD, COP, COI, GEPU, GOD, GOP, and GOS) for the three forecasting horizons (i.e., 120 days, 250 days, and 500 days), while Panel B in this table shows the ranking results according to the out-of-sample predictive accuracy of the for GARCH-MIDAS models, which include composite macro-level factors (i.e., TPCA, MPCA, CPCA, and GPCA). Since we have discussed the comparing results reported in Table 6 and Table 7 corresponding to Panels A and B in Table 8, respectively, we focus on further analyzing the comparing results between GARCH-MIDAS models with composite macro-level factors (i.e., TPCA, MPCA, CPCA, and GPCA) and GARCH-MIDAS models with individual macro-level factors that have been found having statistically significant relationship with the long-term volatility component of Shanghai crude oil futures as shown in Table 4 (i.e., CEPU, COD, COP, COI, and GOS). Notably, in these five individual variables, there are four variables that have better forecast performance than other given macro-level variables as reported in Table 6. Namely, CEPU performs better than GEPU, COD performs better than GOD, COP performs better than GOP, and GOS performs better than COI.

Table 8.  Summary of the DM testing results.

Ranking number	120-day forecasting horizon		250-day forecasting horizon		500-day forecasting horizon
	Model	Long-run variables	Model	Long-run variables	Model	Long-run variables
Panel A: Comparing results among GARCH-MIDAS models with individual macro-level factors
1	COD	$China\_oil\_demand$	COP	$China\_oil\_production$	COP	$China\_oil\_production$
2	GOS	$Global\_oil\_speculation$	CEPU	$C{{hina\_EPU}}$	GOD	$Global\_oil\_demand$
3	GOD	$Global\_oil\_demand$	GOS	$Global\_oil\_speculation$	GOP	$Global\_oil\_production$
4	COP	$China\_oil\_production$	COD	$China\_oil\_demand$	GOS	$Global\_oil\_speculation$
5	GOP	$Global\_oil\_production$	GOP	$Global\_oil\_production$	COD	$China\_oil\_demand$
6	COI	$China\_oil\_import$	GOD	$Global\_oil\_demand$	CEPU	$C{{hina\_EPU}}$
7	CEPU	$C{{hina\_EPU}}$	COI	$China\_oil\_import$	COI	$China\_oil\_import$
8	GEPU	$Global\_{{EPU}}$	GEPU	$Global\_{{EPU}}$	GEPU	$Global\_{{EPU}}$
Panel B: Comparing results among GARCH-MIDAS models with composite macro-level factors
1	MPCA	${{macro\_PCA}}$	MPCA	${{macro\_PCA}}$	MPCA	${{macro\_PCA}}$
2	CPCA	${{China\_PCA}}$	CPCA	${{China\_PCA}}$	CPCA	${{China\_PCA}}$
3	TPCA	${{Total\_PCA}}$	TPCA	${{Total\_PCA}}$	TPCA	${{Total\_PCA}}$
4	GPCA	${{Global\_PCA}}$	GPCA	${{Global\_PCA}}$	GPCA	${{Global\_PCA}}$
Panel C: Comparing results between GARCH-MIDAS models with composite macro-level factors and GARCH-MIDAS models with individual macro-level factors
1	COD	$China\_oil\_demand$	COP	$China\_oil\_production$	COP	$China\_oil\_production$
2	GOS	$Global\_oil\_speculation$	MPCA	${{macro\_PCA}}$	MPCA	${{macro\_PCA}}$
3	COP	$China\_oil\_production$	CEPU	$C{{hina\_EPU}}$	GOS	$Global\_oil\_speculation$
4	COI	$China\_oil\_import$	CPCA	${{China\_PCA}}$	COD	$China\_oil\_demand$
5	CEPU	$C{{hina\_EPU}}$	GOS	$Global\_oil\_speculation$	CEPU	$C{{hina\_EPU}}$
6	MPCA	${{macro\_PCA}}$	COD	$China\_oil\_demand$	CPCA	${China\_PCA}$
7	CPCA	${{China\_PCA}}$	TPCA	${{Total\_PCA}}$	COI	$China\_oil\_import$
8	TPCA	${{Total\_PCA}}$	COI	$China\_oil\_import$	TPCA	${{Total\_PCA}}$
9	GPCA	${{Global\_PCA}}$	GPCA	${{Global\_PCA}}$	GPCA	${{Global\_PCA}}$
Notes: This table summarizes the DM testing results for the 12 GARCH-MIDAS models with different macro-level variables. Panel A of this table shows the ranking results according to the out-of-sample predictive accuracy of the eight GARCH-MIDAS models which include individual macro-level factors (i.e., CEPU, COD, COP, COI, GEPU, GOD, GOP, and GOS) for the three forecasting horizons (i.e., 120 days, 250 days, and 500 days), while Panel B of this table shows the ranking results according to the out-of-sample predictive accuracy of the for GARCH-MIDAS models which include composite macro-level factors (i.e., TPCA, MPCA, CPCA, and GPCA). Panel C shows the ranking results according to the comparing results between GARCH-MIDAS models with composite macro-level factors and GARCH-MIDAS models with individual macro-level factors.

---

 | Show Table

DownLoad: CSV

Panel C in Table 8 shows the ranking results according to the comparing results between GARCH-MIDAS models with composite macro-level factors and GARCH-MIDAS models with individual macro-level factors for predicting the volatility of Shanghai crude oil futures, of which the specifical DM statistics are reported in Appendix A. When the forecasting horizon is 120 days (around half of one year) of the total sample, the models with individual macro-level factors performs better than the models with composite factors, in which the model with Chinese crude oil demand (COD) performs best, followed by the model with global crude oil speculation (GOS) and that with Chinese crude oil production (COP), etc.

The ranking result changes when the forecasting period is extended. Specifically, the predictive accuracy of the model with Chinese crude oil production (COP) is better than that with Chinese crude oil demand (COD) and becomes the model that has the best predictive power, along with the forecasting period extended from 120 days to 250 days. Thus, the model with the composite macro-level factor (MPCA) constructed by Chinese crude oil demand, Chinese crude oil production, Chinese crude oil import, Chinese economy policy uncertainty, and global crude oil speculation has an excellent predictive power, which is only worse than the model with Chinese crude oil production (COP). This highlights the important role of global crude oil speculation activity in the return volatility of Shanghai crude oil futures, except the domestic macro-level determinants of China. These major results can hold when the forecasting period is extended to 500 days. In addition, no matter which forecasting period (120 days, 250 days, or 500 days) is considered, the predictive power of the model with the global composite macro-level factor remains worst, as shown in Panel C in Table 8.

4.2.2.   Fluctuation test

Observing the DM testing results summarized in Table 8, we find that the ranking results for predictive abilities of all the GARCH-MIDAS models are not consistent in three forecasting horizons, except that the major findings mentioned in the previous subsection can be obtained. This indicates that the relative predictive power of these models is possibly time-varying, highlighting the necessity for comparing their forecast performance dynamically.

Figure 4 depicts the Fluctuation statistics for relative forecast performance among the twelve GARCH-MIDAS models, which include different macro-level variables in this study. The Fluctuation test statistics are constructed following Equations (8)-(10) with a moving window of 120 days, where the whole forecasting period is 500 trading days. Positive statistic values demonstrate that the competing model has better predictive power than the benchmark model. As shown in Figure 4, as our expectation, the relative forecast performance among the GARCH-MIDAS models involving different macro-level variables is time-varying, with the Fluctuation test statistics waving all the time (sometimes positive while sometimes negative).

Figure 4.  Plots of Fluctuation test statistics.

(Notes: This figure plots the Fluctuation testing results for relative forecast performance among 12 GARCH-MIDAS models specified in this study.The forecasting period is set as 500 days of the total sample and the Fluctuation test statistics are calculated by using a moving window of 120 days. In each subgraph, blue or red lines are used to plot the Fluctuation testing statistics of the competing model marked in the y-axis relative to the benchmark model marked in the title. Positive values of the test statistics imply that the competing model marked in the y-axis is better than the benchmark model marked in the title. Blue line demonstrates that the competing model marked in the y-axis is better than the corresponding benchmark model marked in the subgraph title at most of time, while red line demonstrates that the benchmark model marked in the subgraph title is better than the competing model marked in the corresponding y-axis at most of time, corresponding to the statistical results shown in Table 9.)

DownLoad: Full-Size Img PowerPoint

Table 9 summarizes the Fluctuation test results via calculating the number of positive statistics and corresponding percent ratios. Combined with Figure 4 and Table 9, we can observe following results.

Table 9.  Summary of the Fluctuation test results for dynamically comparing relative out-of-sample forecast performance among different GARCH-MIDAS models.

Model	Ranking number	COP	MPCA	GOD	GOS	GOP	COD	CEPU	CPCA	COI	TPCA	GEPU	GPCA
COP	1		260##	271##	206##	273##	258##	377##	368##	317##	371##	336##	335##
			(68%)	(71%)	(54%)	(72%)	(68%)	(99%)	(97%)	(83%)	(97%)	(88%)	(88%)
MPCA	2	121		203##	216##	278##	293##	298##	368##	320##	381##	339##	378##
		(32%)		(53%)	(57%)	(73%)	(77%)	(78%)	(97%)	(84%)	(100%)	(89%)	(99%)
GOD	3	110	178		195##	253##	195##	345##	326##	292##	360##	318##	336##
		(29%)	(47%)		(51%)	(66%)	(51%)	(91%)	(86%)	(77%)	(94%)	(83%)	(88%)
GOS	4	175	165	186		197##	197##	209##	290##	348##	308##	315##	344##
		(46%)	(43%)	(49%)		(52%)	(52%)	(55%)	(76%)	(91%)	(81%)	(83%)	(90%)
GOP	5	108	103	128	184		227##	208##	280##	254##	353##	303##	352##
		(28%)	(27%)	(34%)	(48%)		(60%)	(55%)	(73%)	(67%)	(93%)	(80%)	(92%)
COD	6	123	88	186	184	154		257##	331##	341##	346##	309##	375##
		(32%)	(23%)	(49%)	(48%)	(40%)		(67%)	(87%)	(90%)	(91%)	(81%)	(98%)
CEPU	7	4	83	36	172	173	124		260##	213##	261##	239##	319##
		(1%)	(22%)	(9%)	(45%)	(45%)	(33%)		(68%)	(56%)	(69%)	(63%)	(84%)
CPCA	8	13	13	55	91	101	50	121		195##	303##	265##	330##
		(3%)	(3%)	(14%)	(24%)	(27%)	(13%)	(32%)		(51%)	(80%)	(70%)	(87%)
COI	9	64	61	89	33	127	40	168	186		313##	269##	308##
		(17%)	(16%)	(23%)	(9%)	(33%)	(10%)	(44%)	(49%)		(82%)	(71%)	(81%)
TPCA	10	10	0	21	73	28	35	120	78	68		198##	320##
		(3%)	(0%)	(6%)	(19%)	(7%)	(9%)	(31%)	(20%)	(18%)		(52%)	(84%)
GEPU	11	45	42	63	66	78	72	142	116	112	183		292##
		(12%)	(11%)	(17%)	(17%)	(20%)	(19%)	(37%)	(30%)	(29%)	(48%)		(77%)
GPCA	12	46	3	45	37	29	6	62	51	73	61	89
		(12%)	(1%)	(12%)	(10%)	(8%)	(2%)	(16%)	(13%)	(19%)	(16%)	(23%)
Notes: This table summarizes the Fluctuation test results for dynamically comparing relative out-of-sample forecast performance among different GARCH-MIDAS models. The Fluctuation test statistics are constructed following Equations (8)-(10) with a moving window of 120 days, where the whole forecasting period is 500 trading days, consequently generating 381 observations. Positive statistic values demonstrate that the competing model has better predictive power than the benchmark model. The right 12 columns of the table report the number of positive Fluctuation test statistics of the competing models in the row, relative to the benchmark models in the corresponding column. The number in parentheses is the percent ratio of the number of positive statistics to the total number of Fluctuation test statistics (381 observations) in each cell. ## denotes that the model in the row has better forecast performance relative to the benchmark model in the corresponding column at most of time (more than 50%). The second column of this table shows the ranking result according to the Fluctuation test.

---

 | Show Table

DownLoad: CSV

First, the GARCH-MIDAS model involving Chinese crude oil production (COP) has the best predictive power for the return volatility of Shanghai crude oil futures in that its Fluctuation test statistics relative to other 11 models are positive more than 50% of the time. Specifically, as shown in the first row of Table 9, relative to the benchmark models with Chinese economic policy uncertainty (CEPU), Chinese composite factor (CPCA), the total composite factor (TPCA), global economic policy uncertainty (GEPU), Chinese crude oil import (COI), global crude oil production (GOP), global crude oil demand (GOD), Chinese crude oil demand (COD), the composite factor (MPCA), and global crude oil speculation (GOS), the ratios of the number of positive statistics to the total number of Fluctuation test statistics are 99%, 97%, 97%, 88%, 88%, 83%, 72%, 71%, 68%, 68%, and 54%, respectively.

Second, following the GARCH-MIDAS model involving Chinese crude oil production (COP), the predictive power of the model which includes the composite macro-level factor constructed by Chinese economic policy uncertainty, Chinese crude oil import, Chinese crude oil demand, and production, can rank in the second place, as shown in the second row of Table 9. Third, following a similar analysis method, we find that the model with the global composite macro-level factor (GPCA) has the worst predictive power, comparing with other models. These three findings are consistent with the DM testing results for 120-day and 500-day forecasting horizons, which are shown in Panel C of Table 8.

Due to space limitation, we do not describe the Fluctuation test results in Table 9 one by one. Thus, we concentrate on whether other major findings obtained from the DM test can hold when time-varying relative forecast performance is considered. As reported in Table 9 and Figure 4, the GARCH-MIDAS model involving global oil speculation index (GOS) performs better than the model with Chinese oil import (COI) 91% of the time, the model involving Chinese crude oil production (COP) performs better than the model with global crude oil production (GOP) 72% of the time, the model involving Chinese economic policy uncertainty index (CEPU) performs better than global economic policy uncertainty index (GEPU) at 63% of the time, and the model involving Chinese composite macro-level factor (CPCA) performs better than global composite macro-level factor (GPCA) 87% of the time, providing robust evidence for the corresponding comparing results obtained from the DM test. However, inconsistent with the DM test, there is no obvious evidence for the better predictive power of Chinese crude oil demand (COD) compared with global crude oil demand (GOD) in that the ratio of the positive Fluctuation test statistics for GOD relative to COD is 51%. Summarily, these findings suggest that the return volatility of Shanghai crude oil futures is more affected by the domestic macro-level factors in China than the global macro-level factors.

4.3.   Robustness check

In the previous subsections, we found that the current growth rates of Chinese economic policy uncertainty($C{{hina\_EPU}}$), Chinese crude oil demand ($China\_oil\_demand$), Chinese crude oil production($China\_oil\_production$), Chinese crude oil import($China\_oil\_import$) and global crude oil speculation index($Global\_oil\_speculation$) have significant impact on the long-run return volatility of Shanghai crude oil futures. However, the market price of the Shanghai crude oil futures is always available immediately while the monthly or quarterly data always have delay in real life. In order to check whether this kind of delay would impact the empirical results, we further re-estimate the GARCH-MIDAS models in which the macro-level economic variables are one-monthly lagged, investigating how the macro-factors in the previous month affect the return volatility of Shanghai crude oil futures in current month.

As seen in Table 10, when the macro-level economic factors are one-monthly lagged, the estimated parameter ($\theta$) for $C{{hina\_EPU}}$, $China\_oil\_demand$, $Global\_oil\_production$, and $Global\_oil\_speculation$ are significant at the 5% level, indicating that the previous monthly growth rates of Chinese economic policy uncertainty, Chinese crude oil demand, global crude oil production, and global crude oil speculation index also have significant impact on the long-run return volatility of Shanghai crude oil futures. Connected with the empirical results shown in Table 4, it can be summarized that the long-run return volatility of Shanghai crude oil futures is significantly influenced by Chinese crude oil production in current month and global previous oil production in the last month. In addition, the current long-run return volatility of Shanghai crude oil futures is not only affected by Chinese economic policy uncertainty, Chinese crude oil demand, and global crude oil speculation index in current month, but also affected by the growth rates of these three macro-factors in the last month.

Table 10.  Estimated parameters of the GARCH-MIDAS models when the macro-level variables are one-monthly lagged.

Model	$\mu$	$\alpha$	$\beta$	$\theta$	$\omega$	$\upsilon$	Obs. /L.L.	AIC/BIC
Panel A: Chinese factors
CEPUt-1	0.0762	0.1232***	0.8317***	−0.0258**	1.0318***	1.7184***	1282	5452
	(0.0543)	(0.0163)	(0.0195)	(0.0104)	(0.0491)	(0.1442)	−2720	5483
COD t-1	0.0242	0.0526***	0.9474***	−0.0498**	4.7179*	−0.0650	1282	5211
	(0.0494)	(0.0049)	(0.0045)	(0.0241)	(2.4759)	(0.3182)	−2599	5242
COP t-1	0.0536	0.0686***	0.9314***	−0.0591	10.1040	0.3429	1282	5496
	(0.0451)	(0.0060)	(0.0057)	(0.0363)	(16.2190)	(0.4318)	−2742	5527
COI t-1	0.0440	0.0674***	0.9326***	−0.0259	1.0069***	−0.3490	1282	5211
	(0.0466)	(0.0056)	(0.0052)	(0.0181)	(0.0329)	(0.3403)	−2599	5242
Panel B: Global factors
GEPU t-1	0.0002	0.0410***	0.9590***	0.0095	4.0962	−0.6169***	1282	5232
	(0.0487)	(0.0035)	(0.0035)	(0.0087)	(3.9815)	(0.2348)	−2610	5263
GOD t-1	0.0767	0.1298***	0.8314***	0.0895	1.0010***	1.6799***	1282	5457
	(0.0545)	(0.0160)	(0.0184)	(0.0813)	(0.0285)	(0.1651)	−2722	5487
GOP t-1	0.0190	0.0544***	0.9456***	0.1692**	1.0022***	0.1069	1282	5521
	(0.0462)	(0.0045)	(0.0043)	(0.0718)	(0.0111)	(0.2836)	−2754	5552
GOS t-1	0.0796	0.1315***	0.8186***	0.4765**	1.0012***	1.6182***	1282	5456
	(0.0545)	(0.0172)	(0.0223)	(0.2258)	(0.0396)	(0.1378)	−2722	5487
Panel C: Composite factor
TPCA t-1	0.0669	0.1336***	0.8175***	−0.0022	7.4495	1.7096***	1282	5153
	(0.0582)	(0.0182)	(0.0226)	(0.0091)	(58.2020)	(0.1447)	−2571	5184
MPCA t-1	−0.0055	0.0422***	0.9578***	0.0083	16.3260	−0.7132***	1282	5230
	(0.0485)	(0.0037)	(0.0035)	(0.0068)	(142.3600)	(0.2330)	−2609	5261
CPCA t-1	0.0437	0.0422***	0.9578***	−0.0278	4.6998	0.2594	1282	5518
	(0.0492)	(0.0038)	(0.0037)	(0.0190)	(4.0895)	(0.3135)	−2753	5549
GPCA t-1	0.0785	0.1299***	0.8289***	−0.0104	9.6282	1.6733***	1282	5457
	(0.0542)	(0.0164)	(0.0196)	(0.0218)	(29.5690)	(0.1567)	−2723	5488
Notes: The table shows the estimated parameters of the GARCH-MIDAS model with different specifications of the MIDAS equation. In these models, the macro-level variables are one-monthly lagged, which are respectively marked as CEPUt-1, COD t-1, COP t-1, COI t-1, GEPU t-1, GOD t-1, GOP t-1, GOS t-1, TPCA t-1, MPCA t-1, CPCA t-1, and GPCA t-1. Please see the footnotes of Tables 4 and 5 for more details on these variables. The parameter space for the short-term component of the total volatility is Θ = { $\mu$, $\alpha$, $\beta$ }, corresponding to Equation (3). The parameter space for the long-term component of the total volatility is Θ = { $\theta$, $\omega$, $\upsilon$ }, corresponding to Equations (4) and (5). The numbers in parentheses are standard errors. the variables, namely, Obs. is the number of daily observations in the estimated sample. L.L.is the optimal log-likelihood function, AIC is the Akaike information criterion and BIC is the Bayesian information criterion. ***, ** and * respectively denote the significance at 1%, 5%, and 10% levels.

---

 | Show Table

DownLoad: CSV

Next, we concentrate on whether other major findings about the out-of-sample forecast performance obtained in previous subsections can hold when the macro-level variables are one-monthly lagged. Table 11 shows the time-varying relative forecast performance of the GARCH-MIDAS models involving the one-monthly lagged macro-level variables in the MIDAS speculation. As seem from this table, different from the results shown in Table 9, the GARCH-MIDAS model involving Chinese oil import (COI_t-1) has the best predictive power for the return volatility of Shanghai crude oil futures, followed by the models with Chinese crude oil production (COP _t-1) and global oil speculation index (GOS _t-1), respectively. Although the ranking numbers for different models slightly changed when the lagged macro-level variables are involved, compared with the results shown in Table 9, the main finding that the return volatility of Shanghai crude oil futures is more affected by the domestic macro-level factors in China than the global macro-level factors can hold. Specifically, when the macro-level variables are one-monthly lagged, the model with Chinese oil import (COI_t-1) performs better than global oil speculation index (GOS _t-1) 62% of the time, the model involving Chinese crude oil production (COP _t-1) performs better than the model with global crude oil production (GOP _t-1) 75% of the time, the model involving Chinese economic policy uncertainty index (CEPU _t-1) performs better than global economic policy uncertainty index (GEPU _t-1) 52% of the time, and the model involving Chinese crude oil demand (COD _t-1) performs better than global crude oil demand (GOD _t-1) 54% of the time.

Table 11.  Summary of the Fluctuation test results when the macro-level variables are one-monthly lagged.

Model	COI t-1	COP t-1	GOS t-1	GPCA t-1	CPCA t-1	GOP t-1	COD t-1	GEPU t-1	CEPU t-1	MPCA t-1	GOD t-1	TPCA t-1
COI t-1		241##	237##	340##	211##	291##	330##	203##	256##	290##	249##	345##
		(63%)	(62%)	(89%)	(55%)	(76%)	(87%)	(53%)	(67%)	(76%)	(65%)	(91%)
COP t-1	140		236##	305##	254##	284##	308##	230##	247##	315##	232##	346##
	(37%)		(62%)	(80%)	(67%)	(75%)	(81%)	(60%)	(65%)	(83%)	(61%)	(91%)
GOS t-1	144	145		208##	254##	171	219##	196##	321##	220##	294##	243##
	(38%)	(38%)		(55%)	(67%)	(45%)	(57%)	(51%)	(84%)	(58%)	(77%)	(64%)
GPCA t-1	41	76	173		203##	240##	214##	192##	227##	267##	200##	266##
	(11%)	(20%)	(45%)		(53%)	(63%)	(56%)	(50%)	(60%)	(70%)	(52%)	(70%)
CPCA t-1	170	127	127	178		192##	236##	217##	217##	212##	281##	281##
	(45%)	(33%)	(33%)	(47%)		(50%)	(62%)	(57%)	(57%)	(56%)	(74%)	(74%)
GOP t-1	90	97	210##	141	189##		185	206##	228##	257##	213##	316##
	(24%)	(25%)	(55%)	(37%)	(50%)		(49%)	(54%)	(60%)	(67%)	(56%)	(83%)
COD t-1	51	73	162	167	145	196##		183	189##	229##	204##	268##
	(13%)	(19%)	(43%)	(44%)	(38%)	(51%)		(48%)	(50%)	(60%)	(54%)	(70%)
GEPU t-1	178	151	185	189##	164	175	198##		184	183	191##	299##
	(47%)	(40%)	(49%)	(50%)	(43%)	(46%)	(52%)		(48%)	(48%)	(50%)	(78%)
CEPU t-1	125	134	60	154	164	153	192##	197##		179	235##	180
	(33%)	(35%)	(16%)	(40%)	(43%)	(40%)	(50%)	(52%)		(47%)	(62%)	(47%)
MPCA t-1	91	66	161	114	169	124	152	198##	202##		177	290##
	(24%)	(17%)	(42%)	(30%)	(44%)	(33%)	(40%)	(52%)	(53%)		(46%)	(76%)
GOD t-1	132	149	87	181	100	168	177	190	146	204##		209##
	(35%)	(39%)	(23%)	(48%)	(26%)	(44%)	(46%)	(50%)	(38%)	(54%)		(55%)
TPCA t-1	36	35	138	115	100	65	113	82	201##	91	172
	(9%)	(9%)	(36%)	(30%)	(26%)	(17%)	(30%)	(22%)	(53%)	(24%)	(45%)
Notes: This table summarizes the Fluctuation test results for dynamically comparing relative out-of-sample forecast performance among different GARCH-MIDAS models, in which the macro-level variables are one-monthly lagged. The Fluctuation test statistics are constructed following Equations (8)-(10) with a moving window of 120 days, where the whole forecasting period is 500 trading days, consequently generating 381 observations. Positive statistic values demonstrate that the competing model has better predictive power than the benchmark model. The right 12 columns of the table report the number of positive Fluctuation test statistics of the competing models in the row, relative to the benchmark models in the corresponding column. The number in parentheses is the percent ratio of the number of positive statistics to the total number of Fluctuation test statistics (381 observations) in each cell. ## denotes that the model in the row has better forecast performance relative to the benchmark model in the corresponding column at most of time (more than 50%).

---

 | Show Table

DownLoad: CSV

5.   Discussion and conclusion

To determine which macro-level determinant is the most informative in affecting Shanghai crude oil futures' return volatility, we investigate the impact of Chinese and global macro-level economic activities on Shanghai crude oil futures. There are twelve macro-level economic factors considered in this study, including four Chinese macro-level economic determinants (i.e., Chinese crude oil demand, Chinese crude oil production, Chinese crude oil import, and Chinese economic policy uncertainty), four global macro-level economic factors (i.e., global crude oil demand, global crude oil production, global crude oil speculation, and global economic policy uncertainty), and four composite macro-level factors constructed by the method of principal component analysis (i.e., the composite macro-level factor constructed by the four Chinese macro-level economic determinants and global crude oil speculation, the Chinese composite macro-level factor constructed by the four Chinese macro-level economic determinants, the global composite macro-level factor constructed by the four global macro-level economic determinants, and the composite macro-level factor constructed by the eight Chinese and global macro-level economic determinants). Based on the GARCH-MIDAS model proposed by Engle et al. (2013), we suppose that Chinese and global macro-level economic activities affect the return volatility of Shanghai crude oil futures via the long-term component of the total volatility, using the macro-level variables to replace the original realized volatility variable in the model.

We take three steps to carry out this study. In the first step, we estimate the GARCH-MIDAS models with different macro-level variables during from April 2018 to February 2023, to find out which macro-level factor significantly affects the return volatility of Shanghai crude oil futures. In the second step, we use the recursive scheme to generate one-step-ahead forecasts and take the Diebold and Mariano (DM) test to statically compare the out-of-sample predictive power of the 12 different GARCH-MIDAS models, considering three forecasting horizons (i.e., 120 days, 250 days, and 500 days of the total sample). In the last step, we further employ the Fluctuation test proposed by Giacomini & Rossi (2010), to dynamically compare the out-of-sample forecasting performance of the twelve GARCH-MIDAS models in the presence of possible instabilities.

Some interesting findings are obtained from this study. First, the growth rates of Chinese economic policy uncertainty, Chinese crude oil demand, Chinese crude oil production, Chinese crude oil import and global crude oil speculation have a significant impact on the long-run return volatility of Shanghai crude oil futures, in that the corresponding estimated coefficients of these variables in the GARCH-MIDAS models are statistically significant. The current composite factor constructed by these five macro-level variables and the current composite factor constructed by the four Chinese macro-level variables also have statistically significant impact on the long-run return volatility of Shanghai crude oil futures. Second, the DM testing results show that the GARCH-MIDAS model involving Chinese crude oil production has the best predictive power for the return volatility of Shanghai crude oil futures, followed by the model involving the composite macro-level factor constructed by the four Chinese macro-level determinants and the global crude oil speculation, when the current monthly macro-factors are considered. Compared with global crude oil demand, global crude oil production, and global economic policy uncertainty, the models respectively with Chinese crude oil demand, Chinese crude oil production, Chinese economic policy uncertainty and global crude oil speculation have relative better predictive power, respectively. This highlights that the return volatility of Shanghai crude oil futures is more affected by the domestic macro-level factors in China and the global crude oil speculation activity rather than global oil fundamentals. Thirdly, the results of Fluctuation test show that the relative forecast capabilities among the GARCH-MIDAS models involving different macro-level variables are indeed time-varying, but even so, the main results obtained from the DM test still can be supported. Specifically, the GARCH-MIDAS model involving Chinese crude oil production (COP) has the best predictive power for the return volatility of Shanghai crude oil futures, in that its Fluctuation test statistics relative to other 11 models are positive at least more than 50% of the time. In addition, the Fluctuation test results show that Chinese crude oil production and Chinese economic policy uncertainty have better predictive power more than 70% of the time relative to global crude oil production and global economic policy uncertainty, respectively, which are in line with the DM testing results. Especially when the macro-level variables are one-monthly lagged, all the GARCH-MIDAS models with Chinese domestic factors have better predictive performance than the corresponding models with global factors. In the last, our empirical results show that the global crude oil speculation is the global macro-level determinant which has strongest influence on the volatility of Shanghai crude oil futures.

This study has following incremental contributions to the literature on Shanghai crude oil futures in China. First, it is the first study to systematically investigate the impact of Chinese and global macro-level economic factors on the return volatility of Shanghai crude oil futures, including Chinese and global crude oil demand, Chinese and global crude oil production, Chinese and global economic policy uncertainty, Chinese crude oil import, and global crude oil speculation. Second, both the individual macro-level economic factors and the composite factors constructed by all or parts of these individual variables are considered to figure out the most informative determinant for predicting the volatility of Shanghai crude oil futures. Third, we not only take the DM test to statically compare the forecast performance of different determinants for the volatility of Shanghai crude oil futures in different forecasting horizons, but also use the Fluctuation test to dynamically compare the time-varying relative forecast performance of these determinants. Fourth, the findings of this study are very helpful for understanding Chinese and global macro-level economic determinants on Shanghai crude oil futures. Although there have been several studies on the impact of economic policy uncertainty and traditional determinants (e.g., global oil demand, supply, and speculation) on global crude oil futures such as WTI and Brent crude oil markets (Zagaglia, 2010; Wei et al., 2017; Dai et al., 2022; Kang et al., 2020; Diaz-Rainey et al., 2017; Bu, 2014; Ma et al., 2019), we find some special features for the emerging Shanghai crude oil futures. For example, we found that global crude oil speculation has closer linkage with Shanghai crude oil futures volatility than global economic uncertainty has, which is inconsistent with the study by Wei et al. (2017) that argue the stronger predictive capacity of global economic uncertainty. Besides, the volatility of Shanghai crude oil futures is more exposed to the changes of Chinese global oil fundamentals and economic policy uncertainty than global oil fundamentals and economic policy uncertainty, in which the Chinese crude oil production is the most informative determinant.

This study has some important implications for investors and policymakers related to Shanghai crude oil futures market. Based on the empirical results in this study, we suggest investors and policymakers to pay more attention to Chinese domestic macro-level determinants, but also to not ignore the shocks from global factors. For example, we found that Chinese crude oil production, Chinese crude oil import, and global crude oil speculation activity have a significant impact on Shanghai crude oil futures in this study. If one investor notices a shape decrease of Chinese crude oil production while shape increases of China crude oil import and global crude oil speculation index in the last month, it possibly implies a sharp increase of the price of Shanghai crude oil futures, vice versa. Although this paper has some important contributions to the literature on Shanghai crude oil futures by providing new knowledge about its volatility, there are some limitations of this study, implying some further research directions in future. First, in our paper, the original data of Chinese and global crude oil demand are quarterly while all the data of other macro-factors are monthly. Limited by the data availability, we choose to convert quarterly oil demand to monthly data by simply based on the actual number of days in each month. However, this smoothing methodology would impact the empirical results, suggesting that it could be interesting to re-study this topic when more specifical sample data can be obtained in the future. Second, we concentrate only on the impact of Chinese and global macro-factors on the volatility of Shanghai crude oil futures, trying to compare the strength of different factors and their predictive abilities in this study. Further comparison between the volatility of Shanghai crude oil futures and other major global crude oil futures markets also could be an interesting research topic in the future. Third, the research object of this study is Shanghai crude oil futures, which was first launched in March, 2018. There are only 12 monthly observations for each macro-level variables after the Russia-Ukraine war broke out in 2022; thus, it is not appropriate to depart the total sample into two groups for comparing the changes before and after Russia-Ukraine war. Therefore, it could be interesting to investigate how geopolitical events to affect the volatility of Shanghai crude oil futures, by using other methodology such as the Event Study. Fourth, we do not investigate the impact of some specific economic policy on the volatility of Shanghai crude oil futures, but only take the economic policy uncertainty index as one of macro-factors to examine economic policies' impact on the volatility of Shanghai crude oil futures. Moreover, estimated parameter for the monthly changes of Chinese economic policy uncertainty is negative in this study, contrary to some previous literature that found positive relationship between changes of EPU and the volatility of financial markets. Thus, there are also potential topics for future study. Besides, there have been many researchers investigating the co-movements among different financial markets. Thus, there may be some reasons to speculate that the macro-level determinants on Shanghai crude oil futures volatility would have some influence to other commodities traded in China, which is also one potential research direction of our study in the future.

Author contributions

Xiaoling Yu: Conceptualization, Writing – review & editing, Writing – original draft, Validation, Methodology, Investigation, Formal analysis. Kaitian Xiao: Conceptualization, Writing – original draft, Formal analysis. Javier Cifuentes-Faura: Writing – review & editing, Validation.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this work.

Acknowledgements

This study is supported by the 14th Five-Year Plan Project of Philosophy and Social Science Development in Guangzhou granted by Guangzhou Social Science Planning Leading Group Office (NO. 2023GZQN46), the Research Project of the Party's 20th National Congress granted by Foshan University (NO. 2023DXKT06), the Annual Research Project in 2023 granted by the Commerce Economy Association of China (NO. 20231063), and the 14th Five-Year Plan Project granted by Guangdong Planning Office of Philosophy and Social Science (NO. GD24CYJ17).

Conflict of interest

All authors declare no conflicts of interest in this work.

Data availability

Data will be made available on request.