Investigating the risk spillover from crude oil market to BRICS stock markets based on Copula-POT-CoVaR models

1.   Introduction

The international crude oil demand and its price trends always draw the attention of the world, and in the history, the flucturation of international crude oil price usually have a huge impact on the world macroeconomic performance. Since the stock market has usually been regarded as a national economy barometer, whether or not crude oil market volatility will have a spillover effect on the stock market has always been an important subject in academic research. From the perspective of the mechanism of stock market volatility caused by fluctuations in oil prices, rising oil prices will raise the level of domestic prices, reduce the level of income of residents, thereby inhibiting consumption which is not conducive to economic growth, the stock market will also be affected. What's more, rising oil prices will also lead to an increase in the cost of enterprises in the middle and lower reaches, the reduction in corporate profits will reduce production enthusiasm, which is not conducive to economic growth and the development of the stock market.

Over the past decade, BRICS countries have contributed about 50% to global economic growth and remain an important engine for global economic growth, but BRICS countries' rapid economic growth was accompanied by their corresponding increase in crude oil consumption. Additionally, China, the most competitive country in the BRICS, as the world's largest crude oil importer and consumer, both domestic and foreign investors are very much concerned about the spillover effects of international crude oil price on China's A-share market. Given the important role of BRICS countries in the global economic growth and their increasing crude oil consumption, it is worth investigating the spillover effects between BRICS stock market and crude oil market, especially for China's stock market. Also, such kind of empirical study has important theoretical and practical significance.

Ever since the 1970s, a considerable amount of literature has focused on the interaction between oil prices and stock market prices. Using a multi-factor model, Kling (1985) analyzes the impact of an oil price shock on American stock market and finds that oil price changes have a significant impact on the stock market. Jones and Kaul (1996) studies the reaction of four well-developed markets to the oil shock and show that the fluctuation of stock returns can be somehow explained by the effect of these shocks on cash flows of different companies. Adopting a VAR-GARCH model, Sadorsky (1999) concludes that compared with the explanation of the interest rate, the volatility of oil price plays a more and more important role in explaining the error variance of stock market prediction. Miller and Ratti (2009) examines that oil price changes have a significant impact on the stock price of OECD countries in the long term.

The recent researches shift attention to study the relationship between oil prices and stock market prices at the volatility spillover effect level. Applying VAR-GARCH method to analyze the optimal weights and hedging ratios of oil-stock portfolios, Arouri et al. (2011) documents that the international oil price and the stock market have a persistent volatility spillover effect in the GCC countries. Utilizing multivariate GARCH approach, Sadorsky (2012) analyzes the correlation and volatility spillover effect between oil price and the price of clean energy companies and technology companies stock. Taking advantage of four different models (the CCC model, the VARMA-GARCH model, the VARMA-AGARCH model, the DCC model). Chang et al. (2013) examines the conditional correlation and volatility spillover effects between crude oil price and stock market index by employing a wavelet-based approach. Khalfaoui et al. (2015) investigates the mean and volatility spillover effect between WTI crude oil price and G7 stock markets in different time spans. Using ARMAX-GARCH method to fit the conditional mean and conditional variance of yield rate, Bouri (2015) tests the volatility spillover effect of oil prices on the stock market in the oil importing countries such as Lebanon and Jordan. Utilizing bivariate GARCH model based on structural change, Ewing and Malik (2016) finds that there is a significant volatility spillover effect between oil price and the stock market. Adopting wavelet method, Boubaker and Raza (2017) studies the spillover effect between oil price changes and the BRICS stock market from diverse time spans. Employing a wavelet-based GARCH-BEKK approach, Liu et al. (2017) investigate the evolution of spillover effect between oil price changes and stock market index of USA and Russia. Al-Yahyaee et al. (2019) uses DECO-FIAPARCH model to analyze dynamic return and risk spillover between energy and GCC (Gulf Cooperation Council) stock markets. These methods mainly use the linear correlation to investigate the spillover effect. By judging the coefficients, the degree of co-movement between oil market and the stock market can be estimated, but it is difficult to identify the direction of the risk spillover. Thus, we can not conclude whether oil market causes the fluctuation of a stock market. Meanwhile, the linear correlation is not capable of describing the nonlinear relationship among markets, and this limitation decreases the accuracy of risk spillover estimation.

To solve the above problems, some scholars have applied Copula-CoVaR to investigate the spillover effect and tail dependence between two financial markets (e.g., Bernardino et al., 2015; Avdulaj and Barunik, 2015; Reboredo and Ugolini, 2015; Mensi et al., 2017; Lourme and Maurer, 2017; Bernardi et al., 2017). Dičpinigaitienė and Novickytė (2018) points out that the Copula-CoVaR can investigate how a group of distress institution can affect the systematic risk. Ji et al. (2019) using dynamic copula-CoVaR to analyze the risk dependence between oil prices and exchange rates. Uner the framework of CoVaR (Conditional Value-at-Risk), spillover effect usually refers to that the change of one market condition will transfer to other related markets, causing the price fluctuation of another market. Also, the nonlinear relationship among financial markets could be captured by Copula function. Therefore, by judging the value of the Copula-CoVaR, we can determine not only the degree of the risk spillover but also the direction of risk spillover among financial markets.

Despite the advantages of the Copula-CoVaR, some critical features of financial markets are not incorporated in this method. Among those features, the extreme risk or event is recently considered by scholars when they explore the financial risk. For example, Liu et al. (2011) considers the extreme risk and develops an EVT-Copula-CoVaR model to describe the risk spillover among stock markets. Singh et al. (2013) points out that the economic model should consider the rare financial events when Black Swan events seem to be more apparent in global financial markets. Du and He (2015) suggests that the extreme events may have the power to predict the spillover between oil and stock market. Wang et al. (2016) finds that the transmission velocity of extreme risk becomes faster after the 2008 global financial crisis. Belhajjam et al. (2017) proves that the extreme risk has a significant impact on portfolio management, and the assumption that the returns obey normal distribution is not appropriate for modeling portfolio risk. Muela et al. (2017) argues that the VaR models based on extreme value theory could be more sophisticated. Yu et al. (2018) use extreme value theory to improve the Value-at-Risk model, and their results show that GARCH-type-EVT models can generate an accurate estimation of oil portfolios. The existing literatures prove that the extreme risk should be incorporated in risk spillover evaluation models. However, to our knowledge, there are few study to investigate the extreme risk spillover between crude oil markets and BRICS stock market. Thus, the initial aim of this paper is to examine the feasibility of the Copula-CoVaR models incorporating the extreme risk spillovers.

As for the risk spillover effect among the oil market and BRICS stock markets, Bildirici and Badur (2018) investigates the relationship between oil price, business confidence and stock return for China, Inida and Russia by adopting Markov Switching Vector Auto Regressive (MS-VAR) methods. Xiao et al. (2018) provides evidence that there is a significant negative effect on the agammaegate and sectoral stock returns in the bearish market. Wang et al. (2019) examines the causal links between crude oil and BRICS stock markets, and finds that negative and positive shocks have asymmetric impact on stock price fluctuations. Zhou et al. (2019) investigates the oil volatility and stock return in BRICS countries by using quantile dependence. Although some works have already investigated the impact of extreme shocks, such as Wang et al. (2019) provides a method to detect whether there is a Granger cause between extreme negative shocks and BRICS stock market. However, most of the current literatures in this field do not provide the degree of extreme risk spillover between these two categories of markets.

In this paper, we apply the Copula-POT-CoVaR model and investigate the spillover from crude oil market to BRICS stock markets. By using the crude oil market and BRICS stock market data from 2006 to 2016 as the sample, we find that the Copula-POT-CoVaR model is a convenient and precise method to evaluate the market risk spillover, and there is a significant risk spillover from crude oil market to BRICS stock markets. Moreover, the degree of risk spillover effect varies among five BRICS stock markets, and the rank of this degree is Russia, South Africa, India, Brazil and China. Our contributions are two folds. On the one hand, we verify that the Copula-Copula-CoVaR model is capable of depicting the extreme risk spillover between crude oil market and BRICS stock markets. On the other hand, by conducting the empirical study, we systematically examine the risk spillover from crude oil market and BRICS stock market, and find the degree and characteristic of conditional risk, thus, provide useful empirical experience for the global portfolio management.

The remainder of the article is organized as follows. Section 2 presents our empirical methodology and the Copula-POT-CoVaR model. Section 3 shows data sources and descriptive statistics. Section 4 describes empirical results of the spillover effect from the crude oil market to BRICS's stock markets. Section 5 is the conclusions.

2.   Methodology

2.1.   The marginal distribution and POT model

To capture the dependence structure, we adopt the EVT (Extreme Value Theory) method to fit the marginal distribution of each financial time series data. The EVT method fit the tail behavior of a loss distribution by using extreme values rather than all data. Thus, it has the advantage of acquiring an asymptotic distributional form for independent observations from any of a large class of so-called max-stable distributions (Kotz and Nadarajah, 2000). According to the EVT theory, we use POT (Peak-over-Threshold) model, which is based on Generalized Pareto Distribution(GPD), to obtain the threshold value of the financial time series data.

Consider X₁, X₂, …to be a sequence of i.i.d. random variables representing losses with unknown cumulative distribution function F(x), then we choose a sufficiently large value threshold u and the exceedances of that threshold value u are considered as POT model. The conditional probability is defined as:

where x_F is the right endpoint of the cumulative distribution function F(x). When the threshold u is large enough then cumulative distribution function F_u(x) will converge to Peak Over Threshold model (POT), the corresponding cumulative distribution function is as follows:

where ξ and β are called shape parameter and scale parameter respectively.

An appropriate threshold u should satisfy two conditions: (a) the value of u must be large enough so that the POT data has converged to the GPD, and (b) the value of u cannot be too large to leave inadequate data to estimate the distribution. Failure of condition (a) brings about a bias error, and the failure of the condition (b) enlarges the variance error. To choose the most suitable threshold value, we have to balance the relationship between bias and variance well. Graphical diagnosis methods, such as the Mean residual life plot and the assessment of parameters stability, are two approaches frequently utilized to identify the suitable threshold (Coles, 2001), but these methods demand the users to own a great deal of expertise, and the result could be subjective. To avoid this disadvantage, we introduce the exponential regression model proposed by Beirlant et al. (1999). The exponential regression model can be represented by:

where constant $\gamma \ge 0$ and $\rho \le 0$, k defines as the number of sample points beyond a certain threshold, ${b_{n, k}}$ represents as a positive ratio function which can be expressed as:

where function b(x) satisfies that when $x \to \infty$ then $b(x) \to 0$, and ${f_1}, {f_2}, \cdot \cdot \cdot, {f_k}$ are random variables from an independent identically distributed a standard exponential sample of size k. To choose an appropriate value k, we make our choice according to the minimum asymptotic mean square error (AMSE) criterion for Hill estimation, expressed as:

Additionally, the optimal value k can be obtained by the following equation:

When the optimal value k is obtained, we can compute the optimal threshold value by the formula: u = X_{n-k, n.}

2.2.   Copula-CoVaR method

2.2.1.   Copula approach

This paper employs bivariate Copulas to capture the average and tail dependence structure between crude oil returns and stock market index returns. The bivariate Copula method is usually considered as a joint distribution F_XY(x, y) of two continuous random variables X and Y, and this kind of joint distribution F_XY(x, y) could be represented on the basis of a Copula function C(u, v) and each random variable's marginal distribution function F_X(x) and F_Y(y). The relationship can be denoted by the formula below:

The joint probability density of the two random variables could be gained with the help of the Copula density, expressed as:

where u = F_X(x) and v = F_Y(y). According to the formula above, if we want to construct the joint distribution of two random variables, the information about each random variable's marginal distribution function will be needed.

2.2.2.   CoVaR approach

The VaR (Value at Risk) method has been well recognized as an useful tool in financial risk management, it measures the maximum loss which an investor will suffer within a specific time horizon and with a confidence interval. Given the returns $x_t^i$ of a market i and the confidence interval α, then $VaR_{\alpha, t}^i$ is defined as αquantile of the market's return distribution, The relationship can be formulated as:

where α = 0.05, $VaR_{0.05, t}^i$ means the 5th quantile of the market's return distribution. If the market's return distribution F(x) is continuous and define F^-1(x) as its inverse function, then we can estimate the $VaR_{\alpha, t}^i$ value through the formula below:

Introduced by Adrian and Brunnermeier (2011) and generalized by Girardiand Ergün (2013), $CoVaR_{\alpha, t}^{i\left| j \right.}$ (Conditional Value-at-Risk) method is defined as that the VaR of a market i conditional on another market j running into financial difficulties. The whole definition can be represented by the formula below

And we can draw a conclusion that market i's risk contribution to market j is defined as the formula below:

The $\Delta CoVaR_{\alpha, t}^{i\left| j \right.}$ method can quantify how much risk contribution one market adds to another market. In order to make this relationship be more intuitive, we can obtain another formula:

2.2.3.   Copula-CoVaR method

Define ${f_X}(x)$ and ${f_Y}(y)$ as the marginal density of variable X and Y, respectively. And the variable X and Y, represent the losses time series of market i and j. Define ${f_{XY}}(x, y)$ as the joint distribution of variable X and Y, finally we can estimate $CoVaR_{\alpha, t}^{i\left| j \right.}$ value that satisfies the following equation:

On the basis of the formula above, we gain another formula as below:

Since the conception that $CoVaR_\alpha ^{i\left| j \right.}$ is defined as VaR of a market i conditional on another market j running into financial distress. Define $F_{X\left| Y \right.}^{ - 1}\left({x\left| y \right.} \right)$ as the inverse function of ${F_{X\left| Y \right.}}\left({x\left| y \right.} \right)$, and then we can obtain the formula which can calculate the $CoVaR_\alpha ^{i\left| j \right.}$ value:

However, it's difficult to solve the $F_{X\left| Y \right.}^{ - 1}$ explicit expression. Therefore, we have to calculate the $CoVaR_\alpha ^{i\left| j \right.}$ value through solving the equation below:

Finally, the value of $CoVaR_\alpha ^{i\left| j \right.}$ equals $x_t^i$, and the represents the magnitude of risk spillover from crude oil market to stock markets.

3.   Data

This study utilizes daily price data for crude oil and stock market indices of the BRICS countries (Brazil, Russia, India, China and South Africa) from January 1, 2006, to December 31, 2016. For the crude oil market, we adopt the Europe Brent spot prices, collected from the Energy Information Administration, to stand for the international crude oil price since they frequently function as reference prices for reasonable pricing crude oil. Meanwhile, we choose Brazil's Bovespa index, Russia's RTS index, India's BSE Sensex index, China's Shanghai composite index and South Africa's iShares MSCI index to calculate the volatility of the stock markets. All the stock market data are obtained from the Wind Economic Database.

The returns of the daily crude oil prices and stock market index are all defined as the natural logarithm of the ratio of two successive daily closing price and in order not to make this value too small, take those ratios and multiply by a hundred. Expressed as:$x_t^i = 100 \times \ln ({{P_t^i} \mathord{\left/ {\vphantom {{P_t^i} {P_{t - 1}^i}}} \right. } {P_{t - 1}^i}})$, where $P_{t - 1}^i$ and $P_t^i$ are the crude oil price or closing price of the stock market i for days t-1 and t, respectively. For each stock market and crude oil market return pair, we exclude these data which are not in the same trading day from two markets and then employ the Copula-POT-CoVaR model to estimate the spillover effect value by using the remaining data.

As we can see, Table 1 provides descriptive statistics for the returns of crude oil prices and stock market indices. The average returns of six markets are all close to zero, and the differences between the maximum and minimum returns show that return range of China's stock market is smaller than the other five return series. Skewness shows that positive shocks are more common in Brazilian and Indian markets, while negative shocks are more common to other BRICS markets. Kurtosis coefficient of six return series is far greater than 3, which thus exhibit that all six return series has a higher peak and heavy-tailed distribution and that the probability of observing extreme negative returns is higher than that of a normal distribution. Apparently, the Jarque-Bera statistic rejects the null hypothesis of normality at the 1% level for all return series, which confirms the conclusion of heavy-tailed distribution again. The Ljung-Box Q statistic indicates that all these six return series are not random and independent over time, or in other word, serial correlations are found in all the six markets. The Lagrange multiplier test suggests that ARCH effects could be found in all these six return series. The unit root test implies that all six return series are stationary. At last, results of the unconditional correlation between the stock market and crude oil are weak and positive which indicates that there is volatility transmission between BRICS stock market and crude oil at a certain extent. And the correlation of returns on China is the smallest of these coefficients, which suggest that the impact of crude oil on China's stock market may be the smallest among the BRICS countries. All of these findings justify that it is necessary for calculating the CoVaR by employing the POT and Copula approach to fit the return series of six markets and considering the extreme structure dependence between crude oil and the stock market.

4.   Results and discussions

4.1.   The structure of marginal distribution model

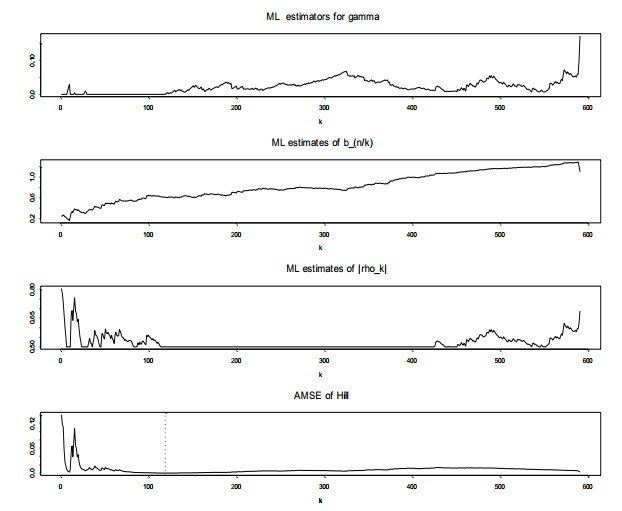
In this subsection, we apply the POT approach to fit the higher peak and heavy-tailed return distribution. The parameter estimations of the exponential regression model and the corresponding POT models are presented in Table 2. For all these six market return series, the parameter ${\gamma _k}$, ${b_{n, k}}$ of the exponential regression model are both positive, and ${\rho _k}$ is negative, which confirms that the exponential regression model is capable of determining the appropriate threshold. To verify the rationality of k-value selection, we take the threshold selecting of the lower tail in China's stock market return as an example which is shown in Figure 1. Apparently, Hill estimated trend line intersects with the dashed lines in the Hill estimation of the asymptotic mean square error of the minimum, dotted lines represent the optimal k-value is 119. When k is less than 119, the trends of the maximum likelihood estimates of the gamma curves and the Hill estimated curve are just as the same. When k is larger than 119, the maximum likelihood estimates of the gamma curves and Hill estimated curves are very different, which means that k equals to the value of 119 is a reasonable choice. Also, the other two curves also support the above views.

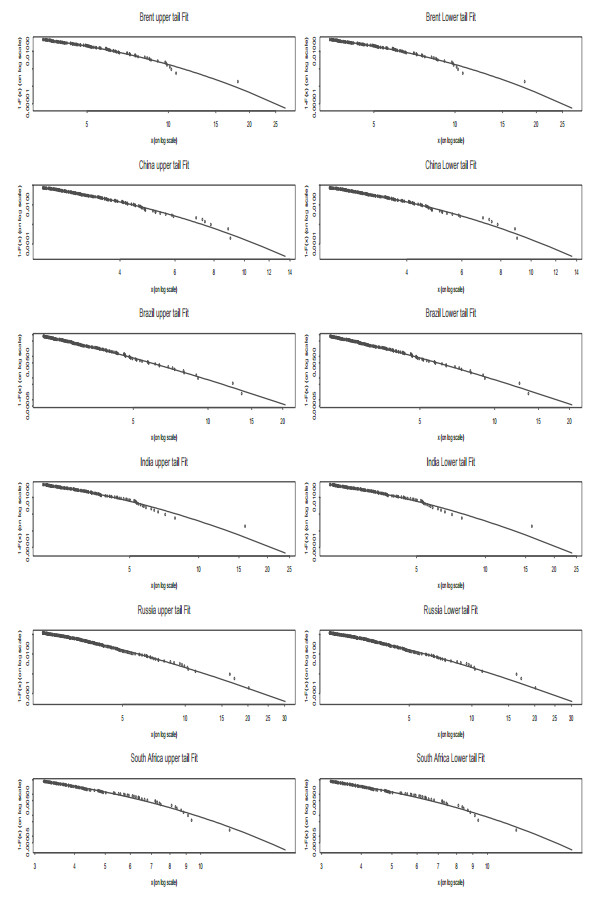
Using the threshold estimated by the exponential regression model and presented in Table 2, we diagnose the fitting condition of POT model through the upper tail and lower tail perspectives. To visually demonstrate how well the POT models fit the tails of return distribution, we plot the empirical distribution of exceedances along with the cumulative distribution simulated by POT approach, and the fitting degree between the simulated results and measured values are shown in Figure 2.

For almost all these six market returns, the empirical distribution of exceedances verify that the POT can fits the exceedances. Furthermore, the threshold value of the POT model is effective to fit the tail distribution of six market returns (as shown in Figure 2).

4.2.   Copula model results

In this section, we implement fourteen different Copula family to capture various tail dependence properties: Normal Copula, Gumbel Copula, Tawn Copula, Frank Copula, Joe Copula, BB1 Copula, BB2 Copula, BB3 Copula, BB6 Copula, BB7 Copula, BB4 Copula, Husler and Reiss Copula, Clayton Copula and Galambos Copula. All these Copula functions belong to Archimedean Copula, elliptical copula and extreme value copula family, and those three categories of copula family are able to describe the upper tail, lower tail, heavy-tail, symmetry dependence structure. Given that the best suitable Copula class is confirmed, the function could be easily obtained to construct the joint cumulative distribution function and also the probability density function. Moreover, by using the maximum likelihood approach, we can compute the Copula parameters and the tail-dependence coefficients.

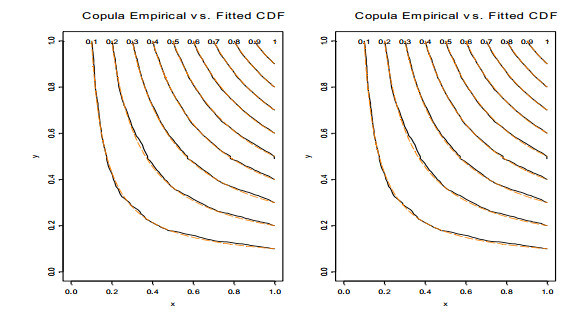
On the basis of the estimated marginal distribution model reported in Table 2, we employ different bivariate Copula models to capture the tail dependence of the BRICS stock market and crude oil market return pairs. To verify the rationality of the best suitable Copula selection, we take the China stock market and crude oil market return pair as an example. The estimated parameter values are presented in Table 3. Apparently, among all the single parameter and two-parameter Copula functions given below, the maximum likelihood value of BB7 Copula is the largest one, but its AIC value and BIC value are the smallest one, followed by BB3 Copula. By further comparing the BB7 Copula fitting graph with the BB3 Copula fitting graph, which is both displayed in Figure 3. By judging Figure 3, we find that the goodness-of-fit of BB7 Copula is better than that of BB3 Copula, and this result suggests that BB7 Copula is more appropriate to construct the tail dependence between the stock market and oil market.

According to AIC criteria, BIC criteria and the log-likelihood value, we can obtain the most suitable Copula model for all five BRICS stock markets and crude oil market pairs. The results for each pair are reported in Table 4. We can observe that the value of the entire four dependence measures statistic is positive, which suggests there is a positive dependence structure between crude oil market and BRICS stock markets. According to the degree of dependence that the four dependence measures statistic indicates the degree of dependence for Brent and China pair is the smallest one, and Brent and Russia pair is the largest one.

As the Table 4 shows, the four dependence statistic indicates that the degree of dependence for Brent & China pair is the smallest one and Brent & Russia pair is the largest one. Moreover, for all market pairs, the tail dependence coefficients all suggest the significant correlations between stock markets and crude oil market, and for the stock market risk management, the attention should be paid to extreme events in crude oil market both in good market condition or bad market condition, which is represented by the upper tail dependence (λ_U) and lower tail dependence (λ_L).

4.3.   CoVaR results and spillover effect analysis

Adopting Copula models with highest goodness-of-fit for each pair of BRICS stock market and crude oil market, we can compute the CoVaR, △CoVaR and %CoVaR according to the method designed in Section 2.1 and 2.2. The results are displayed in Table 5.

Judging from the results shown in Table 5, we can find there is significant risk spillover between crude oil market and BRICS stock markets. The value of CoVaR and △CoVaR are all above zero, and this indicates that the stock markets and oil market are closely connected in BRICS countries. When there is market slump in crude oil market, the BRICS stock markets also face extreme risk. Meanwhile, %△CoVaR of each match is greater 50%, showing that the extreme risk of crude oil market significantly contributes to BRICS stock markets. Thus, the Copula-POT-CoVaR model can capture the extreme risk spillover between crude oil market and BRICS stock markets. These risk spillover effects could be explained from the following aspects. Firstly, the BRICS countries develop very quickly, and they demand large amount of the oil to support their real economy. According to the statistics of the Statistics Portal (www.statista.com), the daily oil consumption for BRICS countries are respectively 3018, 3203, 4489, 12381 and 560 thousand barrels, and the oil price can affect the different industries and real economy, therefore, the price volatility in oil market can cause the fluctuation of stock market, which is the barometer of the country's economy. Secondly, crude oil has become an important financial asset during the recent decades. The risk of oil market can be transmitted to stock market through the trading of oil-related stocks, futures, options and other financial derivative products, or merely the change of investors' market expectation or risk tolerance. Oil and oil-related energy sectors are important component of the equity market in those countries, in Brazil and Russia, the sectoral distribution of oil and raw materials stock in whole stock market index is 50.2% and 60.2% (Bouoiyour and Selmi, 2016). In India, some largest energy companies, such as Adani Transmission Ltd., Bharat Petroleum Corporation Ltd., GAIL (India) Ltd., Hindustan Petroleum Corporation Ltd., Indian Oil Corporation Ltd., NTPC Ltd., Oil & Natural Gas Corporation Ltd and other companies which are the constituents of Nifty Energy Index are among the top companies in terms of the market capitalization, and according to the data released by National Stock Exchange of India Ltd. (https://www.nseindia.com/) on Sep-01-2018, the total market capitalization of those companies is 235.8 billion US dollars. In China, the total market capitalization of energy companies are 263.69 billion US dollars, and according to the report of Global top 100 companies 2019 released by PwC Global, company PetroChina is the 40th largest listed companies worldwide. Because of the relative importance of oil-related companies in equity market, combining with the close nexus of oil price and oil-related companies and the investor confidence and behavior in those markets (Bildirici and Badur, 2018), the extreme risk of crude oil market could exert an significant influence on BRICS stock markets.

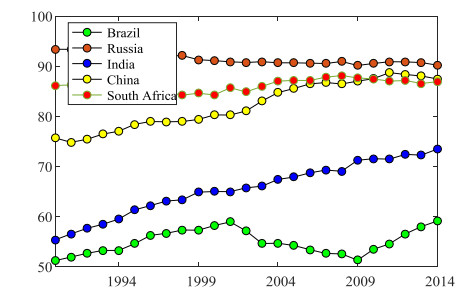
Furthermore, the degree of risk spillover between crude oil market and BRICS stock markets is different for each pair. We can find the Russia's stock market are shocked most severely by the extreme events of the crude oil market, then the degree of risk spillover is followed by the market of South Africa, India, Brazil, and China, and this result is consistent with the value of lower tail dependence as shown in Table 4. The degree of risk spillover could be the result of the reliance of fossil fuel in their domestic economy. According to the World Bank's data, the average percentage of fossil fuel consumption to total energy consumption from 1990 to 2014 for BRICS countries is 54.97%, 91.40%, 65.57%, 82.24% and 86.26% (the specific ratio of each year is displayed in Figure 4). By comparing the rank of this ratio and risk spillover degree, we can find they are basically consistent except for the China's stock market.

The Russia's economy are heavily rely on the oil exportation, this makes the whole national economy be very susceptible to international oil price fluctuations, which have a relatively large risk spillover effect on the stock market. Although China is a net oil import country, the risk of crude market has caused weaker impact on stock market compared to Russia, South Africa, India and Brazil. This result could be due to the following reasons. Firstly, the volume of China's economy and stock market is larger than other BRICS countries. The GDP value of China in 2016 is 11218 billion USD dollars and ranks after the USA and European Union. Moreover, its stock market capitalization has reached to 9045 billion USD dollars in November 2017. Thus, the comparative larger economy can absorb and bear a larger shock without causing a high volatility in stock market. Secondly, the price of domestic retail oil prices can be adjusted by the National Development and Reform Commission (NDRC). If the international crude oil price changes by more than 50 Yuan for tone over a period of 10 working days, the domestic retail oil price can be adjusted by NDRC, and this pricing mechanism can be helpful for buffering the adverse risk shocks from crude oil market, making the impact of international crude oil price fluctuation on China's stock market has been significantly weekend. Finally, the connection between China's stock market and international markets is restricted by the management of the capital account. The quota volume of Qualified Foreign Institutional Investors (QFII), Shenzhen-Hong Kong Stock Connect, Shanghai-Hong Kong Stock Connect and other forms of capital flow channel are relatively small for Chinese stock market, thus, part of the risk in international crude market can be blocked and extreme risk events will cause lighter impact on China's stock market.

5.   Conclusions

In this paper, we try to investigate the risk spillover from crude oil market to BRICS stock market by using the Copula-POT-CoVaR models. We find that the Copula-POT-CoVaR model can depict the extreme risk of the oil market and BRICS stock markets, and it is an effective way to measure the risk spillover effect of financial markets. Meanwhile, the oil market has significantly transmitted risk to the stock market, and a large part of stock market risk can be explained by the volatility of crude oil market when crude oil market is in extreme condition. Furthermore, the magnitude of response to oil market varies within five BRICS stock markets. The crude oil market most severely influences Russia's stock market, and then followed by South Africa, India, Brazil, and China. This ranking could be the result of energy consumption, economic structure, and other complex financial factors.

The practical implications of our paper are helpful and critical for the international investors and the policymakers. The existence of risk spillover effect of crude oil market on BRICS stock market suggests that information from crude oil market improve the accuracy of forecasts the fluctuation in the stock market. The investors should take the information of crude oil market into account to better construct the suitable oil & BRICS stock portfolios and better formulate their hedging strategies. The policymakers should also pay attention to the risk spillover from crude oil market to stock markets, especially when the crude oil market is in extreme condition. To maintain the stability of the financial markets, policymakers should oversee the extreme risk in crude oil market, and implement countermeasures, such as building firewalls, increasing national oil reserves, or increasing stock market depth to cope with the adverse shocks from crude oil market. Meanwhile, since the reliance of oil may affect the degree of risk spillover, the policymakers could also diversify the energy consumption, optimize the economic structure to lower the dependence on crude oil, thus to increase the immunity to risk from the crude oil market.

Acknowledgments

This work is supported by the National Social Science Foundation of China (Grant No.17ATJ005), National Natural Science Foundation of China (Grant No. 71503078) and the program for Science and Technology Innovative Research Team in Higher Educational Institutions of Hunan Province (Grant No. [2014] 103).

Conflict of interest

All authors declare no conflicts of interest in this paper.