Global recessions and booms: what do Probit models tell us?

1.   Introduction

One of the greatest challenges of empirical business cycle research is the detection and modelling of business cycle turning points. In the US and the euro area, there are the Business Cycle Dating Committees of the NBER and the CEPR, respectively, which date the turning points in the dynamics of economic activity. However, at a global level—be it worldwide, advanced economies, emerging market economies—such dating does not exist and the business cycle analysis is quite limited. Due to globalisation and internationalisation of business as well as potential international policy coordination, such a global perspective might be helpful. The 2009 great recession has increased awareness that economic crises can be global phenomena. Additionally, an indicator of turning points in global real economic activity can be used to model the dynamics of the world economy. To detect as well as model the turning points in a global context, we make use of dynamic and non-linear bivariate Probit models.

Dynamic Probit models estimate a multi-regime variable directly with the help of one or more economic variables (Haltmaier, 2008; Christiansen et al., 2014; Boysen-Hogrefe, 2012; Abberger and Nierhaus, 2010; Fornari and Lemke, 2010).¹ The application of probit models requires the definition of a binary variable that distinguishes expansions from recessions. There are various ways to specify the upswings and downswings to construct the binary variable. These include simple rules of thumb (e.g., two consecutive declines in quarterly GDP growth as indicative of a recession) or more formal rules like the Bry-Boschan-algorithm (Harding, 2008).

¹ An alternative would be Markov Switching models which define and estimate two or more regimes where the evolution of economic activity is regime-dependent (see, e.g., Hamilton, 1989). A comparison of both model types with regard to business cycles may be found in Layton and Katsuura (2001).

There are only few papers on turning points in global economic activity. Ferrara and Marsilli's (2014) approach builds on a Factor-Augmented Mixed Data Sampling model of various countries and sectors worldwide. As Ferrara and Marsilli (2014), Ravazzolo and Vespignani (2015) also concentrate on growth rates. They evaluate the quality of world steel production compared to Kilian's index of global economic activity and the index of OECD world industrial production. Stratford (2013) uses linear models to investigate several global indicators' ability to nowcast world trade and world GDP. He finds that the indicators are most helpful during periods of large swings in world growth. However, their usefulness fluctuates greatly over time. The only paper which addresses turning points directly and on a global level within a non-linear framework is Camacho and Martinez-Martin (2015). They propose a two-state Markov-switching dynamic factor model to produce short-term forecasts of world GDP and to compute business cycle probabilities.

Our analysis differs in several aspects from these papers. First, and in contrast to Ferrara and Marsilli (2014), Ravazzolo and Vespignani (2015) and Stratford (2013), we concentrate solely and directly on turning points of global GDP growth. Second, we also analyse advanced and emerging economies. Third, we use Probit models to capture the turning points on a global level. So far, these methods have been predominantly applied to a national level. Fourth, we use several business cycle turning point dating methods to evaluate the models. Fifth, the indicator variables are included individually, not as factors as in Camacho and Martinez-Martin (2015) and Ferrara and Marsilli (2014).

Our results reveal that lagged GDP growth rates and activity-based variables are the best indicators of upswing and downswing periods. The emerging market economies are the hardest to model. The remainder of the paper is structured as follows. Section 2 describes the independent and dependent variables used. Following this, section 3 introduces the Probit models and presents results. Section 4 summarises and concludes.

2.   Data

We use seasonally-adjusted quarterly data for the sample 1980Q1–2016Q4. World activity is measured by real quarterly world GDP, derived from a PPP-weighted agammaegation of national GDP data based on national sources. We also distinguish between real quarterly GDP for advanced economies and emerging economies (see Appendix A for details).

The independent variables considered can be grouped as follows:

● Activity data: industrial production in OECD countries and emerging market economies, world steel production (see Ravazzolo and Vespignani, 2015), the Kilian index of real world economic activity, the Goldman Sachs Global Leading Indicator, the Composite Leading Indicator by the OECD, a global factor derived by Delle Chiaie, Ferrara and Giannone (2017) and the Conference Board US Leading Economic Index.

● Survey data: consumer confidence in OECD countries and the US.

● Financial data: the US term spread (10 years minus 3 month), the US BBB bond spread, the S & P500, M1 and M3 for OECD countries.

● Commodity prices: oil prices in USD and indices of metal prices and non-oil commodity prices.

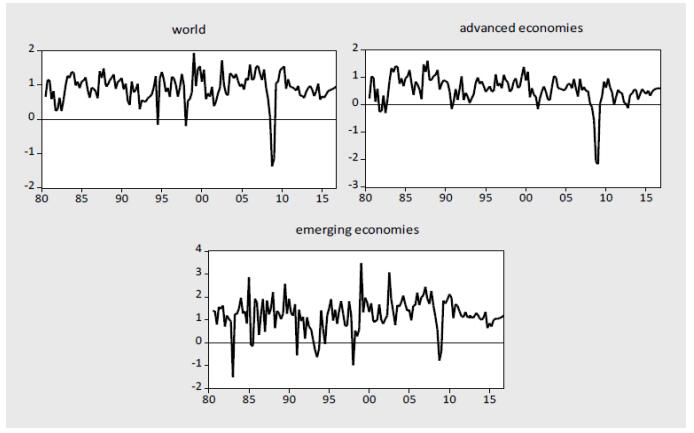
Figure 1 plots quarterly world, advanced economy and emerging economy real GDP growth from 1980Q1 to 2016Q4. We distinguish two types of periods with different mean growth rates: (ⅰ) negative or slightly positive, but low growth rates; (ⅱ) periods of robust growth (either briefly following recessions or on a more prolonged basis). The only common recession in all three country groupings is the great recession 2009 which affected global economies, advanced economies (AE) as well as emerging economies (EME), although the latter to a lesser extent.

In what follows, our aim is to use model-based techniques and judgmental approaches to detect these alternative episodes, and thereafter to estimate probabilities of staying in a regime or moving to a different one.

3.   Probit models

3.1.   Methodology

One methodology commonly used to analyse turning points in economic activity is the Probit model. A textbook treatment may be found in Verbeek (2012). Recent business cycle applications are, inter alia, Chauvet and Potter (2010), Christiansen et al. (2014), Nyberg (2014), Fossati (2015), Hsu (2016), and Proaño (2017). In our case, a value of the binary variable of "0" signals a "downswing" whereas the value "1" indicates an "upswing". The objective of the analysis is to assess with what probability the variable changes its value at a specific date.

Formally, the probit model can be represented as follows:

where P_i represents the probability that a specific event (e.g. an upswing) will occur; Φ(.) is the distribution function of the standard normal distribution (the so-called probit function); u indicates the normally distributed residuals. X_i is the vector of the independent variables, in our analysis specifically the potential variables that explain an upswing or a downswing or, more specifically, a turning point. The ß coefficients of the independent variables of this non-linear estimation approach can only be determined by iteration. To estimate these coefficients, we use the Newton-Raphson method with Marquardt steps to obtain parameter estimates. The standard errors are estimated by the inverse of the estimated information matrix. The latter is computed by the observed Hessian.

A precondition for the empirical application of Probit models is the specification of the binary variable. As there is neither an official business cycle dating available at the global level nor for advanced or emerging economies as a whole (as, for example, for the US from the NBER), we rely on our own dating. For that purpose, we use four variants:

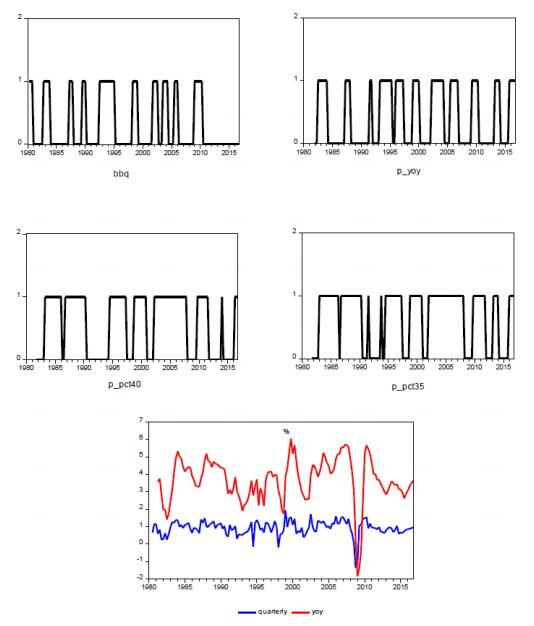
● "Acceleration" is defined as 1 if there is an acceleration in year-on-year real GDP growth in at least three out of five quarters (measured on a centred rolling basis), and 0 otherwise (p_yoy),

● "High growth" is 1 in any period if the centred five-quarter moving average quarterly growth rate in real GDP is above the 40^th (35^th) percentile of the series, and 0 otherwise (p_pct40(35)),

● "Bry/Boschan" is a quarterly analogue to the Bry-Boschan algorithm to detect turning points in time series (bbq) (see Bry and Boschan, 1971; Harding and Pagan, 2002). This methodology identifies a turning point by using the definition that a peak happens at time t if y(t-k), .., y(t-k+1) < y(t) > y(t+1), …, y(t+k), where k is the so-called symmetric window parameter (turnphase). It needs to be set. For for quarterly data, usually k = 2.

Figure 2 shows the four binary variables together with the quarterly and year-over-year growth rates for the world economy. The Figure illustrates that all indicators capture the worldwide recession in 2009 quite well. Since then, however, the picture is mixed. Whereas the Bry-Boschan index does not show signs of an upswing, the other three variables indicate some, but no clear-cut, hints of an acceleration in growth since about 2013. The problem in getting an unambiguous assignment is evident in the growth figure in the lower right part of the Figure. It shows that after 2010 the growth rates declined in the first years (until 2013). Afterwards they exhibit ups and downs, but increased on a quarterly and annual basis since 2015.

Figures 2a and 2b in Appendix B present the same information for advanced and emerging economies. All binary indicators point to an improved economic situation in the advanced economies in the last few years. This pattern is also apparent in the rising annual growth rates. In contrast, two out of the four indicators for the emerging countries do not show any signs of a turning point in the direction of an upswing. The year-over-year method and the one where we calculate the cut-off rate with the 35^th percentile present evidence of a turning point in 2016. What is also evident is that the year-over-year growth rates in the advanced economies declined to a lesser extent compared to the emerging world in the Great Recession. In the former, growth rates declined to around −5%, while they did not turn into negative territory in the latter.

In what follows, we describe in detail the results for the best model(s) of one indicator and refer to similarities and differences of the others in footnotes and separate paragraphs. Our preferred indicator is the year-over-year procedure as it looks especially at turning points and yields in most of the cases—economically and statistically—the most promising results.

3.2.   Results

3.2.1.   Model selection

The various variables that we consider (outlined in section 2) and the possibility of different combinations of these variables leads to a large number of possible models out of which we need to choose the best ones. We use a combination of econometric/model-based and economic criteria for model selection. The statistical-econometric criteria are (ⅰ) the statistical significance of the variables; (ⅱ) information criteria (Akaike and Bayesian); (ⅲ) forecast quality with respect to turning points; (ⅳ) regime qualification with respect to a simple constant probability benchmark model; and (ⅴ) the economic interpretation of the estimated regimes. For that purpose and for the sake of parsimony, we take at most one of the variables of each category (see section 2) up to lag 4 into account. For the endogenous variable, we also consider up to four lags. To select the variables entering the final model, we use the General-to-Specific methodology. Statistics for the criteria (ⅰ) to (ⅳ) are summarised in the sections that follow. The economic criterion to be fulfilled by variables entering the final model is that the signs of the coefficients should be in line with economic theory.

3.2.2.   Global GDP

The explanatory variables in the best model include the contemporaneous and lagged Goldman Sachs Global Leading Indicator (gs_gli).² This is also true for the other binary variables. The equation reads as

² Alternative models which do, however, not perform as good, only include lagged GDP growth rates or OECD consumer confidence (results available upon request).

Note: Sample: 1985q3–2016q4; observations with dependent variable = 0: 71; observations with dependent variable = 1: 55; absolute z-statistic in parentheses below coefficients; McFadden R² = 0.31; SE = 0.40; SSR = 20.1; LR = 53.5 (0.0).³

³ SE: standard error of regression; SSR: sum of squared residuals; LR: Likelihood Ratio statistic on the overall significance of the model (p-value in parentheses).

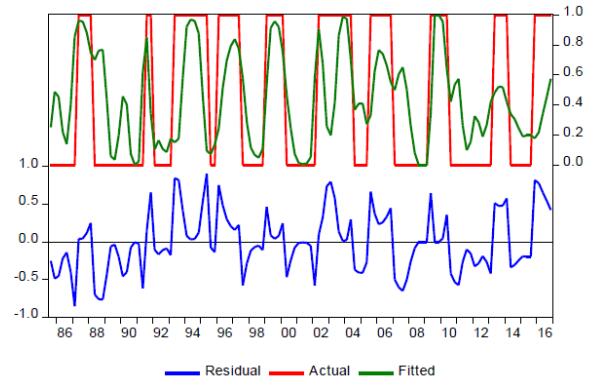
As can be seen from the residual analysis (see Figure 3), the model is quite a good predictor of the turning points. Most residual fluctuations are located at the regime edges, i.e. the model becomes restless around the turning points and, therefore, signals that a regime change is approaching. One "unpleasant" aspect is, however, the false signals during the downswing phases in the beginning and the middle of the 1990s and during the upswing phase at the beginning of the new century. Here, the model user would have erroneously suspected a regime change, even though none materialized (type-2 error).

Table 1 highlights once again the model's goodness of fit and its uncertainty. In this table, the 126 total observations are broken down by deciles. The columns labeled "Risk deciles" depict the high and low value of the predicted probability for each decile. Also depicted is the actual and expected number of observations in each group, as well as the contribution of each group to the overall Hosmer-Lemeshow (H-L) statistic. High values indicate large differences between the actual and predicted values for that decile. If the predicted values for the binary variables are in the 1st-5th or the 8th–10th decile, the model performs rather well in discriminating between the two different regimes (upswing or downswing). Most of the forecast errors are in the 7th decile. In this decile, if the model user were to assume that a predicted value of greater than 0.5 signals an upswing or a value of smaller than 0.5 a downswing, he would achieve a hit probability of only about 50%, i.e. in this decile he could basically toss a coin and then decide which regime is present. However, overall, the null that the observed and expected values are the same across all the deciles cannot be rejected, as indicated by the Hosmer-Lemeshow test (p-value > 90%). This test groups observations on the basis of the predicted probability that y = 1.

These conclusions are underscored by Table 2. Here, an assessment based on the model is correct if the predicted probability is below the cut-off value of C = 0.5 in the case of y = 0 or above 0.5 in the case of y = 1. It is obvious that in 76.2% of the cases the model prediction is correct (the specificity, i.e. the correct y = 0 observations, is 81.7%; the sensitivity, i.e. the correct y = 1 observations, is 69.1%). For comparative purposes, the right part of Table 2 shows the results of a model with a constant probability, which arises when one estimates the model only with a constant. It reveals that our preferred model is over 49% better (calculated as the percent of incorrect predictions corrected by the equation, i.e. (0.778 − 0.563)/(1 − 0.563)) than the model with constant probability, which generates 56.3% correct values.

For the other classification schemes of upswings and downswings, the statistical properties and the economic interpretation are not as good as for p-yoy.⁴ However, they all lead to an improvement compared to a model with constant probability.

⁴ Results available upon request.

3.2.3.   Advanced economies

For the advanced economies (ae), the optimal Probit model consists of lagged GDP growth rates (gdp_aet-i) and again the Goldman Sachs Global Leading indicator (gs_gli), see Equation 3.⁵ This is also true for the other binary variables. The inclusion of a leading indicator in the detection of turning points is in line with Haltmaier (2008) who finds that in six of the eight considered OECD countries at least one (monthly) lag of the leading indicator is significant. Moreover, it is also significant in her panel setup. Financial variables, especially the yield spread, and narrow monetary agammaegates which often are found helpful in this respect for (individual) advanced economies and within the Probit methodology (see, e.g., Fornari and Lemke, 2010; Boysen-Hogrefe, 2012) do not enter our preferred specification. Our best equation reads as

⁵ A model with only three lags of GDP growth performs slightly worse than the one presented (results available upon request). See appendix A for the list of advanced countries included in the analysis.

Note: Sample: 1985q2–2016q4; observations with dependent variable = 0: 68; observations with dependent variable = 1: 59; absolute z-statistic in parentheses below coefficients; McFadden R² = 0.33; SE = 0.40; SSR = 19.7; LR = 58.2 (0.0). Explanations see footnote 3.

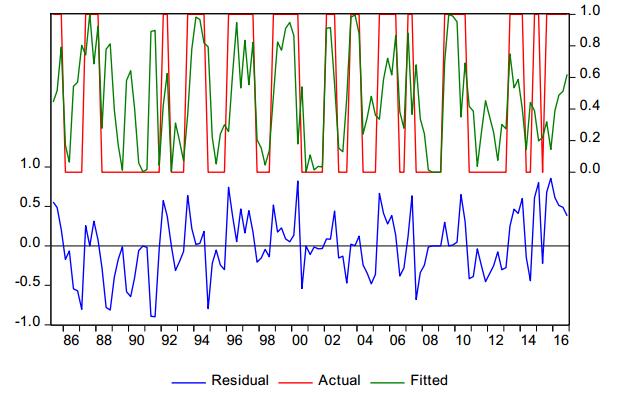
The residual analysis in Figure 4 shows a slightly better behaviour compared to the results for the global economy. The model reveals problems during the downswing at the end of the 1980s and beginning of the 1990s, but behaves quite well in the other episodes.⁶ At the end of the sample (2015/16) our preferred model indicates a steadily improving economic situation.

⁶ The latter is also true for the Bry-Boschan model. The "High growth" specification, in contrast, exhibits problems at the end of the 1990s and beginning of the new century (results available upon request).

Table 3 compares the fitted expected to the actual values by group (ten deciles) and calculates the Hosmer-Lemeshow test statistic. This test of goodness-of-fit shows that, in general, the model behaviour is quite good. There are some problems in the 5^th decile in which the accuracy is only slightly above 50%. In general, however, differences between "actual" and "expected" are not too large. Therefore, we do not reject the model as providing a sufficient fit to the data.

Table 4 reveals that in 78% of all cases our model delivers the correct classification (specificity: 82%; sensitivity: 73%). Compared to a model with constant probability which indicates 53% correct values, this is an improvement of more than 50 %.

The model with the binary variable specified by "High growth (40)" performs slightly better in discriminating between regimes and with regard to the overall fit of the model. In contrast, the results of all others binary variable specifications are worse than the one presented.

3.2.4.   Emerging markets

All in all, the emerging market economies (ee) were the hardest to model.⁷ As with advanced economies, the best model includes lagged quarterly GDP growth rates (gdp_ee_t-i), but in the emerging market case together with industrial production in emerging markets (ip_ee), see Equation 4. This result is in line with Baumann et al. (2019) who use a three regime classification to analyse emerging market economies within a Markov Switching framework. Overall, we have 140 observations, of which 77 belong to regime 0 and 63 to regime 1. The model has the lowest R² and the highest standard error of all the regional models considered.

⁷ See appendix A for the list of emerging market countries included in the analysis.

Note: Sample: 1982q1–2016q4; observations with dependent variable = 0: 77; observations with dependent variable = 1: 63; absolute z-statistic in parentheses below coefficients; McFadden R² = 0.12; SE = 0.50; SSR = 28.7; LR = 23.9 (0.0). Explanations see footnote 3.

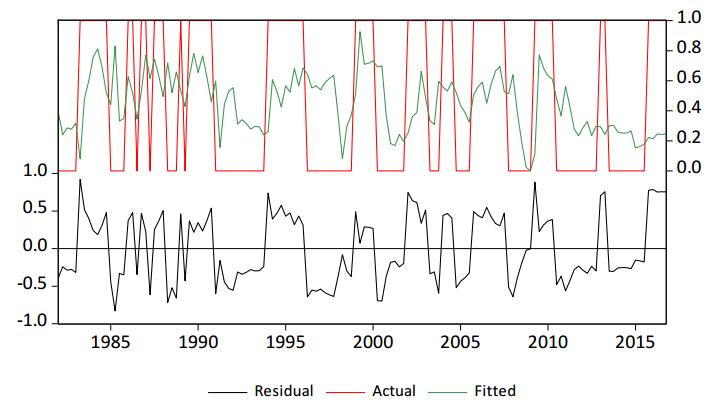
Figure 5 and Tables 5 and 6 summarize the statistical properties of the model. At the sample end (2016), the model indicates a slow movement in the direction of a possible regime turning point from downswing to upswing. The Hosmer-Lemeshow test on the equality of observed and expected values is significant (p-value: 0.13). With more than 70% correct predictions, our model is better than the one with constant probability which in turn does only forecast correctly in 55% of all cases.

The "Bry-Boschan" and the "high growth" regime classifications include the Goldman Sachs global leading indicator instead of industrial production. This corresponds to the preferred model in the multinomial logit case of Baumann et al. (2019). In terms of predictive accuracy, the best model is "high growth" which, in both cases (cut-off of 35 or 40) has about 80% of correct classifications (specificity: between 50% and 60%; sensitivity: > 90%). The improvement relative to the model with only a constant (which has 70% of correct predictions) is between 32% and 41%.

4.   Conclusions

In this paper, we tried to shed light on the question what determines the turning points of world GDP on the one side and economic activity in advanced as well as emerging economies on the other from the beginning of the 1980s onwards. For that purpose, we constructed different binary variables to capture upswings and downswings. These, in turn, were analysed with the help of Probit models. It seems that world and advanced economy activity can be better captured than that in emerging markets. This could be due to the poor data quality. The most important variables in these exercises are lagged GDP growth rates and activity-based indicators.

Interestingly, the yield spread does not yield significant results in detecting turning points. However, against the background that we neither have yield data on a global level nor for advanced and emerging economies as a whole, this is not too surprising.

It might be interesting to combine our approach with the Markov-Switching methodology to identify the turning points. These models might also be helpful to decide whether the two-regime case is really the correct one or whether we should take more than two regimes into account. This is left to a separate paper, see Baumann et al. (2019).

Acknowledgments

We are indebted to Bernd Schnatz for suggestions and comments. Moreover, we thank A. Loukas for excellent research assistance and the participants at an ECB seminar as well as two referees for helpful comments. The opinions expressed in the paper are those of the authors and do not necessarily reflect the views of the ECB. All errors and omissions remain the authors' responsibility.

Conflict of interest

The authors declare no conflict of interest in this paper.