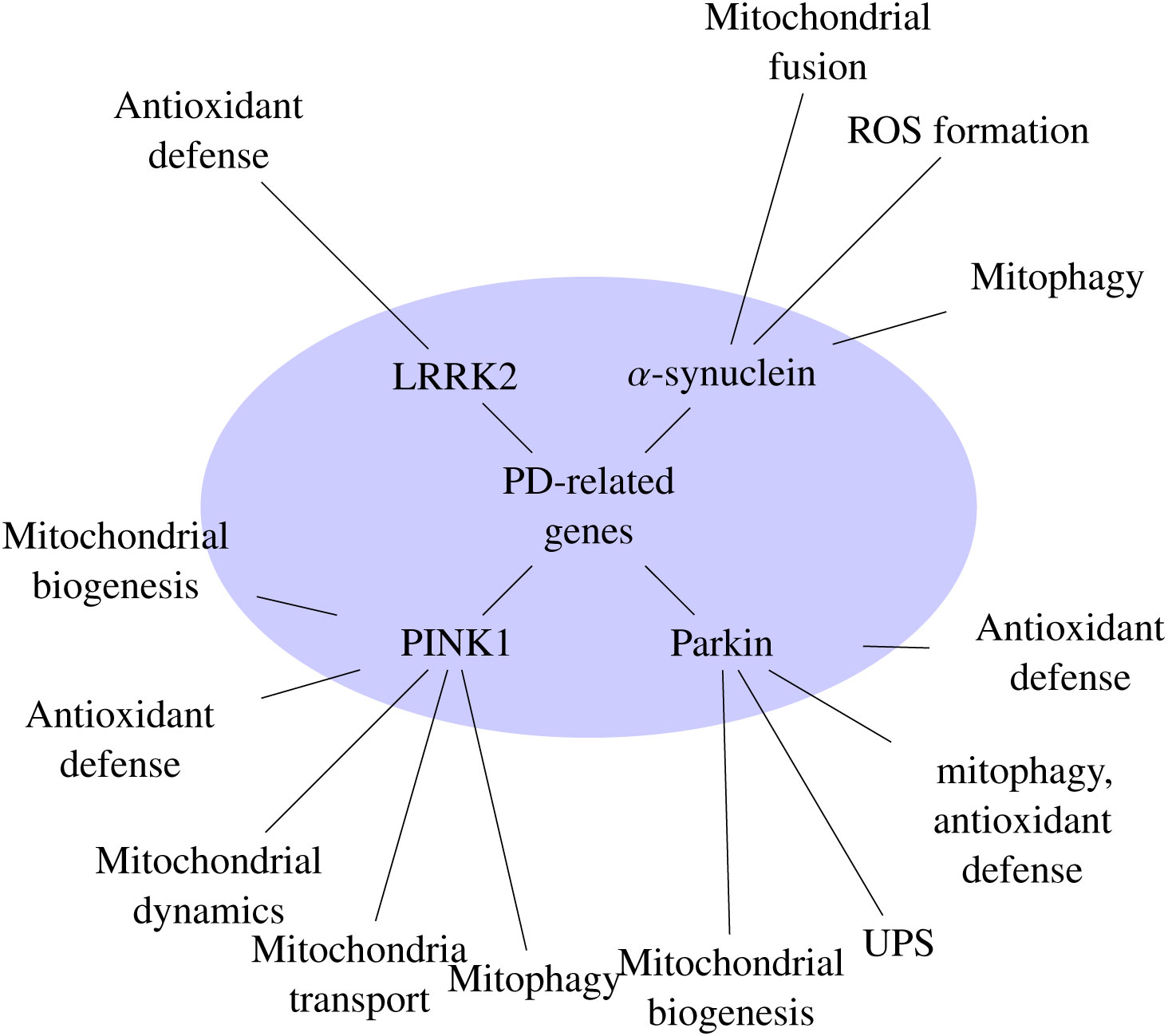
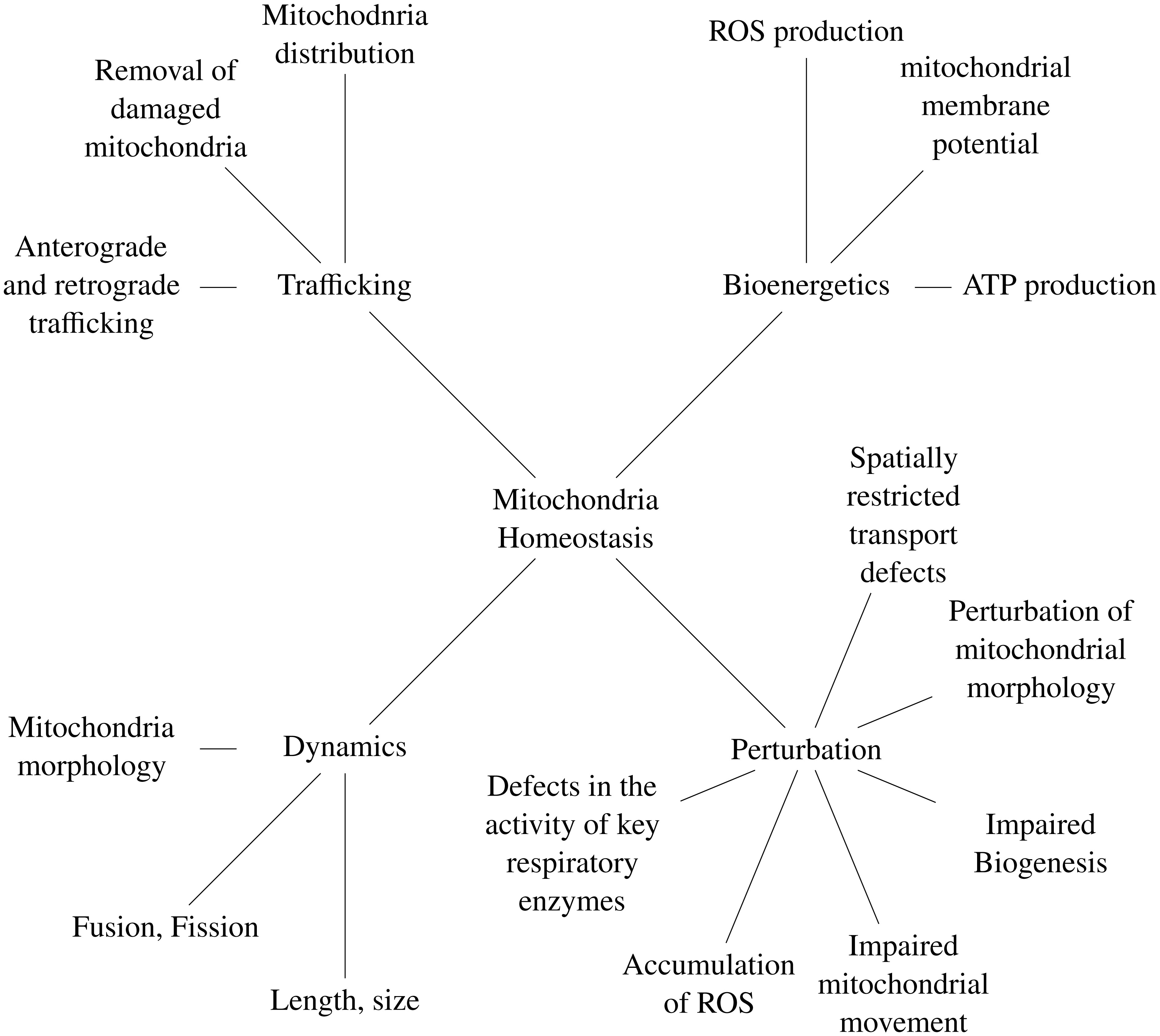
Orderly mitochondrial life cycle, plays a key role in the pathology of neurodegenerative diseases. Mitochondria are ubiquitous in neurons as they respond to an ever-changing demand for energy supply. Mitochondria constantly change in shape and location, feature of their dynamic nature, which facilitates a quality control mechanism. Biological studies in mitochondria dynamics are unveiling the mechanisms of fission and fusion, which essentially arrange morphology and motility of these organelles. Control of mitochondrial network homeostasis is a critical factor for the proper function of neurons. Disease-related genes have been reported to be implicated in mitochondrial dysfunction. Increasing evidence implicate mitochondrial perturbation in neuronal diseases, such as AD, PD, HD, and ALS. The intricacy involved in neurodegenerative diseases and the dynamic nature of mitochondria point to the idea that, despite progress toward detecting the biology underlying mitochondrial disorders, its link to these diseases is difficult to be identified in the laboratory. Considering the need to model signaling pathways, both in spatial and temporal level, there is a challenge to use a multiscale modeling framework, which is essential for understanding the dynamics of a complex biological system. The use of computational models in order to represent both a qualitative and a quantitative structure of mitochondrial homeostasis, allows to perform simulation experiments so as to monitor the conformational changes, as well as the intersection of form and function.
1.
Introduction
The panel data model has been widely used in economics and finance, as it can provide more information compared to the time series and cross-section model [1,2,3,4]. Also, it can relieve the problem that the important variables are not included in the model by adding individual and time effects to represent the heterogeneity and commonality of units respectively. Therefore, it is very important to test whether the individual and time effects are in the model, see, e.g., Breush and Pagan [5], Honda [6], Baltagi and Li [7], Bera et al. [8] and Baltagi et al. [9], etc.
If the model contains variables that should not present the estimators of this model will be inconsistent and even the statistic inference will be unreliable. For example, when the ture model is a linear panel data model with individual effect but a linear panel data model is incorrectly specified, the bias estimate of regression parameters will mislead policy makers. This motivated us to test whether the individual and time effects exist in the model.
Many scholars studied the testing methods of the existence of random effects. Breush and Pagan [5] proposed the Lagrange multiplier (LM) test under the assumption of normality of error terms, but Honda [6] found that the LM test was also robust under the assumption of non-normality and proposed two one-way tests on the basis of LM test. Baltagi and Li [7] further applied the LM test to the unbalanced panel. Bera et al. [8] used LM to test the individual effect when the idiosyncratic errors have autocorrelation. However, the above models they studied contain only one effect in the error term. For example, when we need to test individual effect, the test results will be distorted if the time effect exists. Baltagi et al. [9] used the LM test method based on the existence of two effects in the model. But LM test requires normality hypothesis and uncorrelation among explanatory variables, random effects and error term. Therefore, when the individual or time effect in the model is related to the explanatory variables, the estimation results will be biased when the ordinary least square (OLS) or general least square (GLS) estimation is used. We know that the individual or time effect is often related to the explanatory variables in the real econometric problem. Wu and Li [10] proposed a test method for individual and time effects based on moment estimation without making assumptions about the distribution of error terms and the independence between random effects and explanatory variables. The main idea is to construct the difference between the two variance estimators of the error terms of the model. One of the variance estimators of the error term is consistent regardless of whether there is an individual or time effect. Another variance estimator of the error term is only consistent under the null hypothesis. Therefore, the difference between them can be used to construct the test statistics, that is to say, the test statistics are close to zero under the null hypothesis and large under the alternative one. Also, the proposed test statistics are robust when testing one effect and the other effect exists.
In real economics applications, when factors such as age and race are considered, time-invariant variables should be included in the regression model. Pesaran [11], Sebastian and Claudia [12] and many other scholars studied the panel data model with time-invariant regressors. On the basis of Wu and Li [10], Chen et al. [13] further proposed the individual and time effect tests for the two-way error panel model with time-invariant regressors, which also combined with Pesaran [11]'s proposed estimation method when the time-invariant variables are endogenous. However, previous literature has not studied the test for an unbalanced panel with time-invariant variables.
Due to the complex external environment, panel data is often unbalanced or incomplete and the missing data may be random or non random. It is necessary to directly study the estimation and statistical inference of the unbalanced panel in order to get a precise conclusion. In the unbalanced panel model, the estimation and test methods for model contained one or two effects and for the different types of missing data are different. For example, on the basis of the testing idea put forward by Wu and Li [10] mentioned above, if the data is monotonically missing (the data of an individual after a certain time point is missing) and it is a linear panel model with only individual effect, the test method proposed by Wu and Li [10] can still be used in the unbalanced panel [14]. However, if the time effect also exists in the model, it is necessary to classify the cross-section individuals with the same missing type into one group. The main reason is that the common time effect can only be removed within the group when using OLS or other estimation methods to obtain accurate estimators. Besides, the interference of individual (time) effects should be avoided during the construction of test statistics [15]. If the data is random missing, the cross-sectional units with the same missing type need to be divided together, that is, the individuals can be differentiated in pairs to eliminate the time effect [16]. To sum up, many scholars have studied the test of parametric models in the unbalanced panel, but the test for individual and time effects in the unbalanced panel has not been studied. Therefore, we use a moment-based method to test the individual and time effects in the unbalanced panel data model with time-invariant regressors.
The contribution of this paper is the following two aspects. First, considering the difficulty to obtain the whole balanced panel data sample, we study a two-way error component time-invariant regressors model with an unbalanced panel. Also, a effective estimation method is given. Second, referring to Wu and Li [10]'s method, we have build the moment-based test statistics for individual and time effects in the unbalanced panel data model by using the difference of the two variance estimators of the error term. The test for individual (time) effect is robust no matter the existence of time (individual) effect and robust in regards to the correlation between the explanatory variable and individual or time effect. Furthermore, it is unnecessary to make a distributional assumption for the error in advance. The simulations demonstrate that the power of the test statistics is high in various situations.
The rest of this paper is organized as follows. In the Section 2, we introduce the basic model and the estimation process. Tests for individual and time effects are shown in Sections 3 and 4 respectively. Section 5 is the jointly test for two effects in the basic model and Section 6 is Monte Carlo simulations and a real example analysis. The conclusion is in Section 7. The proof of the relevant theorems will be presented in Appendix.
2.
Model and estimation
Consider a two-way error component panel data model with time-invariant regressors,
where yit is the response variable at unit i and time t, Xit=(Xit,1,⋯,Xit,p)′ is a p×1 vector of time varying explanatory variables, X′it is the transpose of Xit, β is a p×1 vector of parameter. Zi is a m×1 time-invariant exogenous variables* and γ is also a parameter. The error term vit contains unobservable individual effect μi and time effect ηt, which are both random effects. μi is assumed to be independent and identically distributed with mean zero and finite variance σ2μ. ηt, like μi, has mean zero and finite variance σ2η. Also, The idiosyncratic error ϵit is assumed to be identified independent distribution with mean zero and variance σ2ϵ.
*We only consider that Zi is exogenous for simplicity.
It is difficult to obtain all the sample data due to several factors including migration. In application, we often get unbalanced panels. However, the traditional methods for balanced panels are not suitable for unbalanced panel data models. We have to propose other effective methods for incomplete data model. It is worth noting that, in unbalanced panel data, if we use normal centering transformation for all units, the time effect will not be removed completely. The reason is that the individuals have different length of time T. Therefore, we can regard each group as a balanced panel data that they also have the same length of time by referring the grouping method of Wu et al. [15]. So, we can solve this problem by centering in each group.
Divide n cross-section units into L disjoint groups N1,⋯,NL such that the observed time periods are identical for each i∈Nl with l=1,2,⋯,L. There are nl units with time Tl in group Nl. The whole number of the sample is N=∑Ll=1nlTl. For each group Nl,
where yli=(yli,tl,1,yli,tl,2⋯,yli,tl,Tl)′, ιTl is a vector of one with dimension Tl and the other right-hand-side variables are stacked accordingly. Next, estimate the unbalanced panel data model.
First, we estimate β by making a centering transformation in each group to remove the time effect,
where ˜yli=yli−1nl∑nli=1yli. ˜Xli, ˜Z′i, ˜μli and ˜ϵli are defined similarly. We can find matrix QTl such that (T−1/2lιTl,QTl) is a Tl×Tl orthogonal matrix (e.g., Wu and Li [10]). Denote the jth column vector of matrix QTl by qlj=(qlj1,⋯,qljTl)′, l=1,⋯,L,j=1,⋯,Tl−1. Then, multiplying model (2.3) with Q′Tl, we have
where Q′TlιTl=0, so the time-invariant regressors and individual effect are also removed. We can use OLS to obtain the consistent estimator of β,
where PTl=QTlQ′Tl=ITL−1TLιTLι′TL that ITL is TL×TL identity matrix and Q′TlQTl=ITl−1.
Theorem 2.1. Under some mild conditions, |Σ1|>0 and as n→∞ with fixed time period, ˆβ has the following asymptotic normal distribution,
where Σ1=∑Ll=1ml[E(X′liPTlXli)−EX′liPTlEXli], Σ2=∑Ll=1mlE[(Xli−EXli)′PTlϵliϵ′li(Xli−EXli)] and ml=limn→∞nln, see Shao et al. [25]. Note that the result is based on the large individuals and short time period.
The proof of the asymptotic distribution of ˆβ can refer Wu et al. [10] since the time-invariant variables are removed after the transformation.
Second, estimate γ. Peseran and Zhou [11] used the filtered method to obtain the estimator of γ by the regression of ˆuit on Zi and mentioned that the estimator is still consistent under unbalanced panel data model. Details of estimating procedure are as follow. For each group Nl, the average over time of ˆuit,
where ˉˆuli=1Tl∑Tlt=1uit, ˉXli=1Tl∑Tlt=1Xit ˉvli=1Tl∑Tlt=1ϵli and ˆuit can be estimated by yit−X′itˆβ. Next, we can make the centering transformation over cross-section units in each group. Thus, the estimator of γ is
where ˉZ=1nl∑nli=1Zli, ˉˆu=1nl∑nli=1ˉˆuli. For the identifying assumption of γ, the time-invariant variables are not correlated to the individual effect in this paper and the endogenous regressors can be considered in the future study.
Assumption 2.1. The error term ϵit is cross-sectional uncorrelated and unrelated with explanatory variables Xit for i=1,⋯,nl and t=1,⋯,Tl, E(ϵitϵjs|X,Z)=0 for t, s and i≠j, E(ϵitXit,p)=0 for i, j and p.
Assumption 2.2. The ϵit can be heterogeneous, E(ϵitϵis)=ri(t,s), where ri(t,t)=r2i and ri(t,s)<K, K is the nonzero constant and K<∞.
Assumption 2.3. The time-invariant variable Zli is uncorrelated to the individual effect μli and the error term ˉϵli and also μli and ˉϵli are independently distributed. The fourth moment of Zi is finite. E(Ziμli)=0, E(Ziˉϵli)=0, E(||Zi||2μ2li)=0, E(||Zi||2ˉϵ2li)=0, E(Ziμi)=0 and E(||Zi||2μiˉϵli)=0 for all i, j.
These assumptions are similar to Peseran and Zhou [11].
Theorem 2.2. Under the Assumptions 2.1–2.3 and suppose that |Σ3|>0, as n→∞ with fixed time period, the estimator γ has the following asymptotic distribution,
where the definition of Σ3, Σ4, Ω1 and Ω2 can be seen in Eqs (A.8), (A.10), (A.14) and (A.15) in the Appendix.
3.
Test for individual effect
In this section, we construct a test statistic for individual effect in model (2.2). The hypothesis is:
After the transformation of original model, we obtain model (2.4) and the moment condition of Q′Tl˜ϵli:
where c1=∑Ll=1c1l with c1l=(nl−1)(Tl−1). Then, the estimator of σ2ϵ is:
where the ˆβ is obtained from Eq (2.5). ˆσ20ϵ is a consistent estimator of σ20ϵ under the null hypothesis, alternative hypothesis, and irregardless of the existence of μi and ηt (see Wu et al. [10]).
We can construct the fourth-order moment of the variance of error σϵ by referring Wu and Zhu [17] and Wu et al. [15].
where λ4ϵ=Eϵ4it.
Thus, the estimator of the λ4ϵ,
is consistent under some mild conditions.
Next, we should obtain the consistent estimator of β under the null hypothesis. Under the null hypothesis, the original model (2.2) becomes
We just need to remove the time effect by centering in each group,
It holds that
where c4=∑Ll=1c4l with c4l=(nl−1)Tl. Similarly,
where the ˆγ is obtained in Eq (2.8). However, ˆσ21ϵ is only consistent under Hμ1 (see Wu et al. [10]) while ˆσ20ϵ is both consistent under Hμ0 and Hμ1. Therefore, we can construct a test statistic by following Hausman [18],
where ωn=anˆλ4ϵ+bn(ˆσ20ϵ)2 is used to standardize the test statistic. The
That Tμ will be close to zero under the Hμ0 but large under Hμ1.
Assumption 3.1. The individual effect μi=n−14μ0i, where μ0i is i.i.d. with zero mean and finite variance σ21>0.
Assumption 3.2. E(μiϵit)=0,n12E(μ2iϵ2it)<∞,E(n14Xit,pμi)<∞ for each i, t and p.
The assumptions can refer to Wu et al. [15].
Theorem 3.1. Suppose the explanatory variable Xit, time-invariant variable Zit and error term ϵit are i.i.d sequence with EX4it<∞, |Σ1|>0, EZ4it<∞, |Σ3|>0 and Eϵ5it<∞. Under the Assumptions 3.1 and 3.2, we have the following asymptotic distribution,
where Φn=anλ4ϵ+bn(σ20ϵ)2, a=limn→∞an, b=limn→∞bn.
The proof of the above theorem is in Appendix.
4.
Test for time effect
In this section, we will test the time effect of model (2.2). Consider the heteroscedasticity of η, the hypothesis is as follows,
where T is the largest number of time of all groups. Similar to the test for individual, under Hη0, the model (2.2) reduces to,
We obtain the variance estimator of error by eliminating the individual effect and the time-invariant variables by the same orthogonal transformation mentioned in the Section 2. We have
It also holds that
where c5=∑Ll=1c5l with c5l=(Tl−1)nl. So,
That ˆσ22ϵ is consistent under the null hypothesis Hη0 but inconsistent under Hη1 (see Wu et al. [10]). The difference between ˆσ22ϵ and ˆσ20ϵ should be small under Hη0. A test statistic for time effect is
Then, we set some assumptions to study the properties of Tη (refer to Wu et al. [15]).
Assumption 4.1. The time effect ηt=n−1/2η0t, where η0t is random variable with mean zero and finite variance Eη20t>0.
Theorem 4.1. Suppose that EX2it,p<∞, Eϵ2it<∞, |Σ1|>0 and E(Xit,pϵ2is) for i, t, p, s. If the Assumption 4.1 holds, we have
where η=(η0tl,1,η0tl,2,⋯,η0tl,Tl), Σ8l=Σ9l+Σ′9l−Σ10l with Σ9l=mlQ′TlE(ϵliϵ′liPTl(Xli−EXli))Σ−11EX′liQTl and Σ10l=mlQ′TlEXliΣ−11Σ2Σ−11×EX′liQTl.
See Wu et al. [15] for similar discussion and the proof is omitted in this paper.
We can obtain that Σ8l=0 if the EXit is independent over time period. Then, the time effect test statistic Tη follows chi-distribution under the null hypothesis, which is very efficient in real application. In order to satisfy this condition, we consider two transformations as same as Wu et al. [15]. Firstly, centralize the Xit in the original model by deducing 1nl∑nli=1Xli in each group. Secondly, transform the explained variable yli,t into yli,t−Xl⋅,tˆβ. Theorem 4.1 still holds after the above transformation.
5.
Test jointly for two effects
In this section, we consider the jointly test for the two effects of model (2.2). The hypothesis is as follows,
Under the null hypothesis Hμη0, the original model becomes
We have
The estimator of the variance of the error term is
where ˆβ and ˆγ are obtained from (2.5) and (2.8). Referring to Pesaran and Zhou [11], the consistent estimator of α is that ˆα=1N∑Ll=1∑nli=1ι′Tl(yli−Xliˆβ−(ιTlZ′i)ˆγ). ˆσ23ϵ is only consistent under Hμη0. The test statistic can be similarly constructed based on the difference between ˆσ23ϵ and ˆσ20ϵ,
where ωn is as same as (3.11).
Theorem 5.1. Under the Assumptions 3.1, 3.2 and 4.1 mentioned above, EX4it<∞, |Σ1|>0, EZ4it<∞, |Σ3|>0 and Eϵ5it<∞, we have the following asymptotic distribution,
where Φn=anλ4ϵ+bn(σ20ϵ)2 and σ1 is defined in Assumption 3.1.
The proof of the theorem is similar to Theorem 3.1 and omitted in this paper since we can also refer to Wu et al. [15].
6.
Simulations
In order to evaluate the performance of the test method, Monte Carlo simulations are used to compute the empirical power of the test statistics based on 1000 replications.
6.1. Monte Carlo
We consider the data generating process as follows,
where the explanatory variables and time-invariant variables are two-dimensional, Xit=(Xit,1,Xit,2)′, Zi=(Zi,1,Zi,2)′, β=(β1,β2)′ with β1=1 and β2=1, γ=(γ1,γ2)′ with γ1=1 and γ2=1, {μi} and {ηt} are i.i.d. with mean zero, finite variance var(μi)=σ2μ and var(ηt)=σ2η. In this unbalanced panel data model, we assume that it has three groups with different time periods Ti, which is $ T = [4,8,12] $. The number of cross-section units in each group is random (see Wu et al. [15]). Referring to Chen et al. [13], we also set time-varying variables generated by
where k and h are constant and we can use them to control the correlations between Xit and individual effect μi and time effect η respectively. The correlation form has no effect on the results. For simplicity, we only set this form. g1t and g2t are uniformly distributed U(1,2), w(1)it and w(2)it are i.i.d. normal distribution with mean zero and one variance. In this paper, we assume that the time-invariant variable Zi is exogenous.
where ˉwi1=T−1∑Tt=1w(1)it, ˉwi2=T−1∑Tt=1w(2)it, ε(1)i and ε(2)i are i.i.d. N(0,1). Next, we describe the estimators of two parameters and the power of the test statistics in different situations. And we choose n=50,100,150,200 to evaluate the performance of the test statistics as the cross-section units increase. First, we summarize the performance of the estimators in Table 1 when the individual and time effects exist simultaneously. The value of the ˆβ1 and ˆβ2 (ˆγ1 and ˆγ2) is very close, so we just show the result of ˆβ1 and ˆγ1. Both ˆγ and ˆβ have small deviations and variances. The standard deviations of the two estimators also decrease when the sample size increases. We can see that the estimator is very close to the true value.
Second, we evaluate the empirical power of individual test statistic Tμ in two different distributions of error term. They are εit∼N(0,1) and εit∼√12 χ2(1). Table 2 shows that power of the Tμ is still high even the time effect η exists and we omit the result here because the results are same as that when the time effect does not exist. The individual effect test statistic is robust under two types of distribution and also robust to the correlation between the explanatory variables and individual effect. Besides, the empirical power of Tμ increases with the increase of sample size.
Next, we evaluate the time effect test statistic Tη. Table 3 shows that the power of Tη is higher than the individual effect test statistic Tμ. When the individual effect μ>0, the power of the Tη is as same as the result of Tμ>0 and we omit here. Besides, the power of the Tη increases as the sample size increases. Also, Tη is robust to the correlation between the explanatory variables and time effect.
Table 4 displays the empirical power of the Tμη when the explanatory variables are not related to the time effect (h=0). The test statistics becomes larger as the sample size increases. According to the Tables 2 and 3, the power of Tη is higher than Tμ. So the value of ση will have a greater impact on Tμη than σμ. When ση is large, such as ση=0.4, the power of Tμη is high at different values of σμ. When the sample size is small like n=50,100, the power is also very high. Thus, we just simulate n=50 and 100.
Table 5 displays the empirical power of the Tμη when the explanatory variables are not related to the individual effect (k=0). Tμη is robust under h=0 and h=1. When σμ=ση=0, Tμη is as same as Table 4 no matter h=0 or h=1 and k=1 or k=1 and Tμη just increases with the sample data increases. So, we omit this case here.
To sum up, three test statistics proposed in this paper are robust and have good power under several unique situations. Furthermore, many studies verified that these types of moment-based test methods have higher power than LM tests proposed by Breush and Pagan, [5], Honda's test [6] and conditional LM tests proposed by Baltagi et al. [9], see, e.g., Wu and Li [10], wu et al. [15], Chen et al. [13], etc, for more details.
6.2. A real example
Economic development is of great importance to countries and regions. There are many factors affecting the economic growth, see, e.g., Oleg[19], Iuliana[20], Carlsen[21], etc. The impact of foreign direct investment (FDI) on economic growth has been one of the focuses in economics. It can provide some useful suggestions for policymakers. Richard et al. [22] studied nine OECD countries and seven industries by using the cross-section data and concluded that FDI promotes economic growth through technology spillover. Borenztein et al. [23] studied 69 developing countries and found that FDI can only promote economic growth of host countries when advanced technology has sufficient absorptive capacity, and this impact depends on human capital. Besides, there are many other factors have effects on economic growth.
In order to study the relationship between FDI and economic growth, Kottardi and Stengos [24] considered the traditional linear model,
where yit is per capita GDP growth rate in ith province and tth time point, (FDI/Y)it is the ratio of foreign direct investment to total output, (DI/Y)it is the ratio of local investment to total output, nit is natural population growth rate, hit is human capital and ϵit is the idiosyncratic error. However, it is widely accepted that the effect of FDI on economic growth has the cross-sectional units heterogeneity due to the environment and some relevant policies on different provinces and regions. Also, the economic growth may have a trend over time, which cannot be captured by other variables. So, the model may contain the individual and time effects (μi and ηt). Then, one may wonder whether the individual and time effects exist. Therefore, the possible model for this example is as follows,
In this section, the model (6.5) can also be used to study the effect on economic growth of China. Our model utilized the panel data of 30 provincial regions in China from 1992 to 2017 (excluding Tibet) and the data are from China Statistical Yearbook and statistical yearbooks of various regions.
Since the proposed test method is very general, it can also be used for two-way error component panel data model without time-invariant variables. In order to illustrate the efficiency of the proposed test, we chose three types of unbalanced panel data sample with T=[10,18,26] from the original database and the number of cross-section units are random.
Table 6 gives the results of the test statistics in three different cases. The p-value of Tμ, Tη and Tμη are all less than 0.0001. So, we have to reject the null hypothesis at a significance level of 0.05. Similarly, the time effect test statistic Tη is larger than Tμ, which has the same result we obtained in the simulation. Thus, we conclude that the effect of FDI on economic growth has the heterogeneity over provinces and the time effect should be included in the model to get the correct estimator when studying this problem.
7.
Conclusions
In this paper, we construct three test statisitics for individual effect, time effect and jointly effects in unbalanced panel data models which include the time-invariant variables. The test is based on the moment method using the difference of two variance estimators of error. When we test the individual effect, the test statistic is efficient no matter the existence of the time effect, and vice versa. Furthermore, three test statistics are robust to the correlations between the explanatory variables and individual or time effect. There is no need to make some distributional assumption on error term. The simulation results show that the proposed test statistics are robust under various situations and they all have good finite sample properties. We also studied the relationship between FDI and economic growth, and found that the effect of FDI on economic growth has heterogeneity and common time characteristics.
In fact, traditional linear models are not efficient in actual application. The nonparametric model has been widely used for several years and we can consider a more effective test method of various nonparametric panel models in the future. In addition, the time-invariant variables could be endogenous. We can study the estimation and test methods for this kind of situation such as embedding the instrumental variable method or system generalized method of moments.
Acknowledgments
This work was supported by the Innovation Research for the Postgraduates of Guangzhou University under Grant number 2021GDJC-D01.
Conflict of interest
The authors declare there is no conflicts of interest.
Appendix
The proof of the theorems is as follows.
Proof. For theorem 2.2. We can refer the proof of Pesaran [11]. For each group Nl, according to the estimation,
where ˉμ=1nl∑nli=μli, ˉϵ=1nl∑nli=ϵli. For the identification, we have ∑Ll=1∑nli=1(Zli−ˉZ)(ˉμ+ˉϵ)=0. On the basis of the estimator ˆγ, we have
where ζli=μli+ˉϵli−(ˉXli−ˉX)′(ˆβ−β). For each group Nl, noting that ˆβ is consistent to β, we have
For i=1,⋯,nl, Z and X is the matrix that contains Zi and Xit respectively, and μ is the vector that contains μli. Under the Assumption 2.3, E((Zli−ˉZ)μli)=0. We have E(ˆγ)=γ that ˆγ is consistent to γ.
Then, we will proof that the ˆγ is a √n consistent estimator of γ.
Under the Assumptions 2.2 and 2.3, 1n∑Ll=1∑nli=1(Zli−ˉZ)(ˉXli−ˉX)′ will converge to finite value. In this paper, we assume that the individual effects in each group are the same, so the variance of the effect is constant σ2μ.
where ωliTl=σ2μ+r2iTl+1T2lΣri(s,t). Then we have
We know that ˆβ−β=Op(N−1/2). Then,
Next, obtain the asymptotic variance of the estimator ˆγ. According to the Eq (A.2), the first term of right side,
where ml=limn→∞nln, this setting is commonly used in Shao et al.[25].
The variance of the first term of above formula,
where Σ4=var[∑Ll=1√nln1√nl∑nli=1(Zli−ˉZ)μli]. First, we know that
where Σ5=∑Ll=1ml[E(ZliˉX′li)−E(Zli)E(ˉXli)′]. Then, the second term,
where ξli=[(Zli−ˉZ)T−1lι′Tl−Σ5Σ−11(Xli−EXli)′PTl]ϵli. According to Assumption 2.3, we have
and
The covariance of the two term in Eq (A.9),
where Σ6=∑Ll=1mlE[μliˉϵli(Zli−EZli)(Zli−EZli)′] and Σ7=∑Ll=1mlE[(Zli−EZli)μliϵ′liPTl(Xli−EXli)].
Following the central limit theorem, we have
Therefore, we can obtain the asymptotic distribution of ˆγ,
Lemma 7.1. Suppose that Eϵ4it<∞, EXit4<∞ and under the Assumption 2.1 for each i, t, ˆσ20ϵ and ˆλ4ϵ is consistent estimator of σ2ϵ and λ4ϵ respectively. The proof can be seen the proof of Lemma 2 of Wu et al. [15]. This is because the time-invariant variables are removed after the centering transformation.
Proof. For theorem 3.1. According to the lemma 7.1 and Eq (2.4), we have
and
Note that √n(ˆβ−β)=Op(1) and √n(ˆγ−γ)=Op(1). Besides, use some limit theorems and the proof in Appendix of Chen et al. [13] and we suppose the explanatory variable Xit and time-invariant variable Zit are i.i.d sequence and EX4it<∞, EZ4it<∞. We have
where σ21 is defined in Assumption 3.2.
where ςli=nc4ϵ′liϵli−nc1ϵ′liPTlϵli and ςli is independent cross units. It holds that limn→∞1n∑Ll=1∑nli=1Eςli=0 and
where ωn=anλ4ϵ+bn(σ20ϵ)2 is used to standardize the test statistics. The
The above proof process is the same as Wu et al. [15] and we also have the same result ω−1/2n√n(ˆσ21ϵ−ˆσ20ϵ)−Φ−1/2nσ21→dN(0,1). Thus, the proof of theorem is complete.









 DownLoad:
DownLoad: