Learning process for identifying different types of communication via repetitive stimulation: feasibility study in a cultured neuronal network

Yoshi Nishitani; Chie Hosokawa; Yuko Mizuno-Matsumoto; Tomomitsu Miyoshi; Shinichi Tamura; Yoshi Nishitani; Chie Hosokawa; Yuko Mizuno-Matsumoto; Tomomitsu Miyoshi; Shinichi Tamura

doi:10.3934/Neuroscience.2019.4.240

AIMS Neuroscience

2019, Volume 6, Issue 4: 240-249. doi: 10.3934/Neuroscience.2019.4.240

Previous Article Next Article

Research article

Learning process for identifying different types of communication via repetitive stimulation: feasibility study in a cultured neuronal network

1.
Department of Radiology, Graduate School of Medicine, Osaka University, Suita 565-0871, Japan
2.
Graduate School of Science Osaka City University, Osaka, 558-8585, Japan
3.
Graduate School of Applied Informatics, University of Hyogo, Kobe 650-0044, Japan
4.
Department of Integrative Physiology, Graduate School of Medicine, Osaka University, Suita 565-0871, Japan
5.
NBL Technovator Co., Ltd., 631 Shindachimakino, Sennan 590-0522, Japan

Received: 04 July 2019 Accepted: 23 September 2019 Published: 16 October 2019

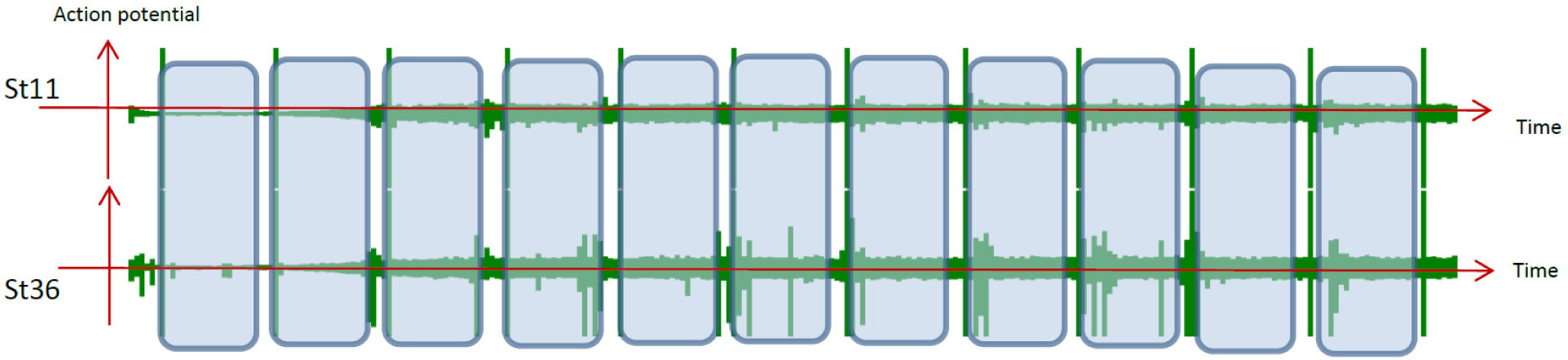
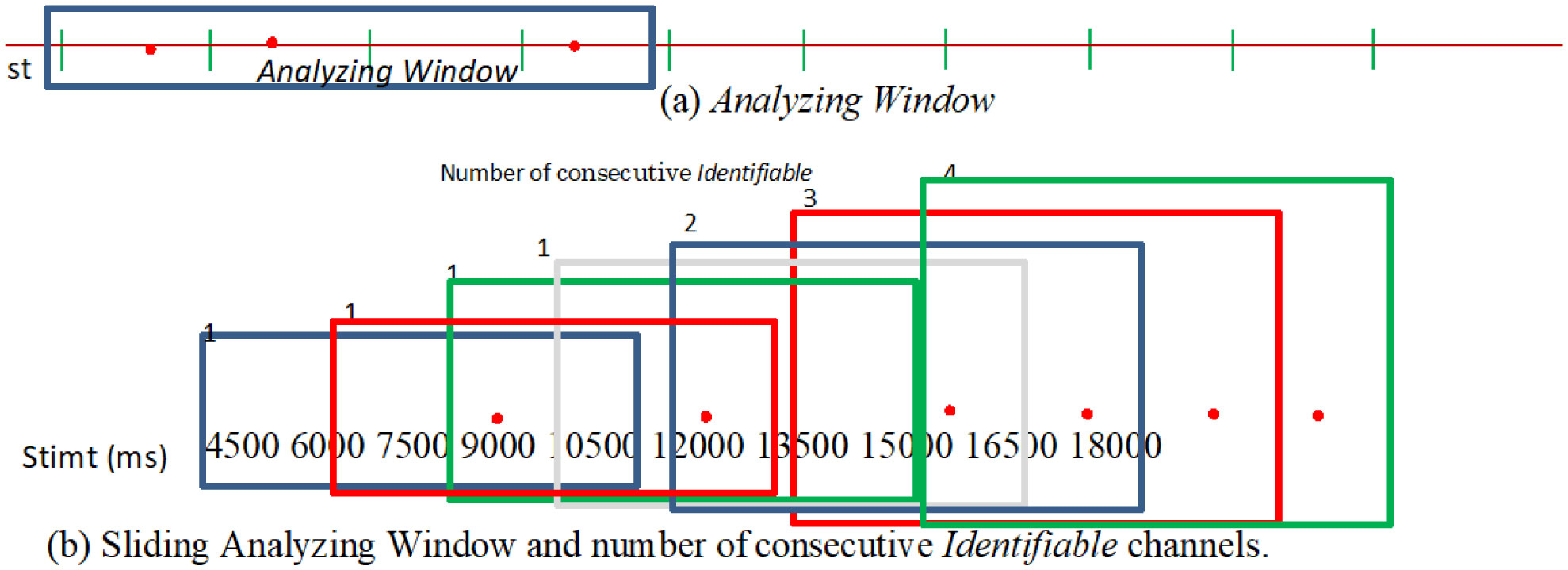
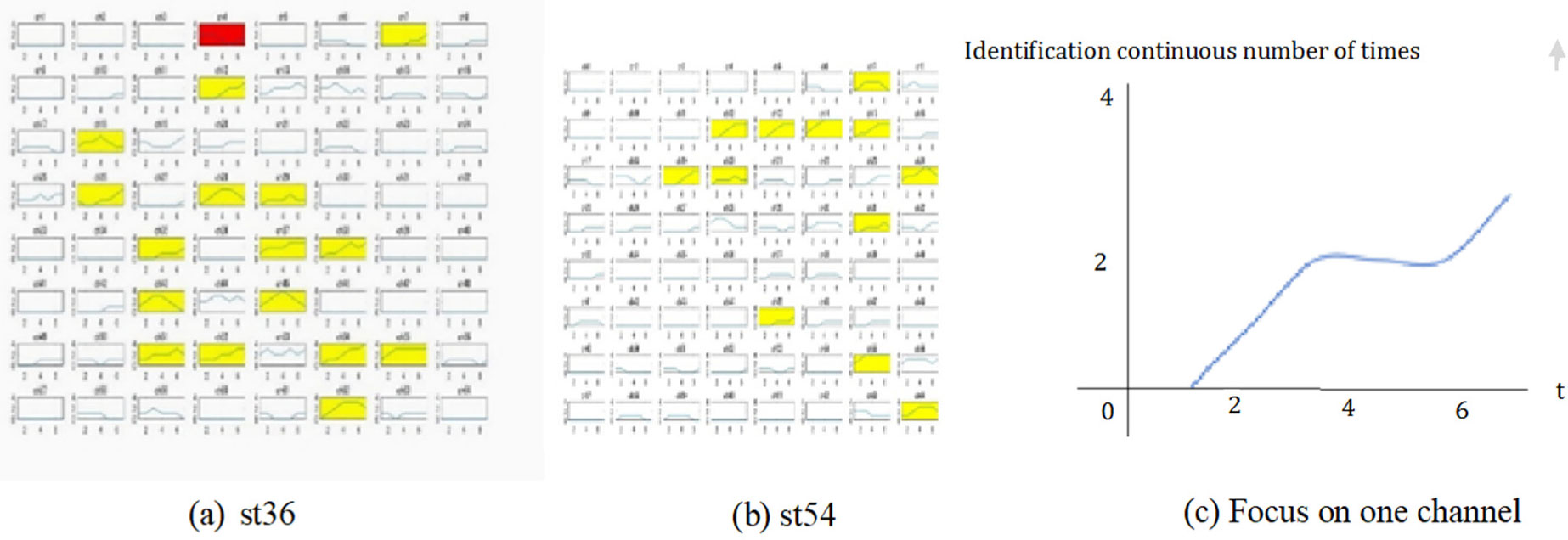
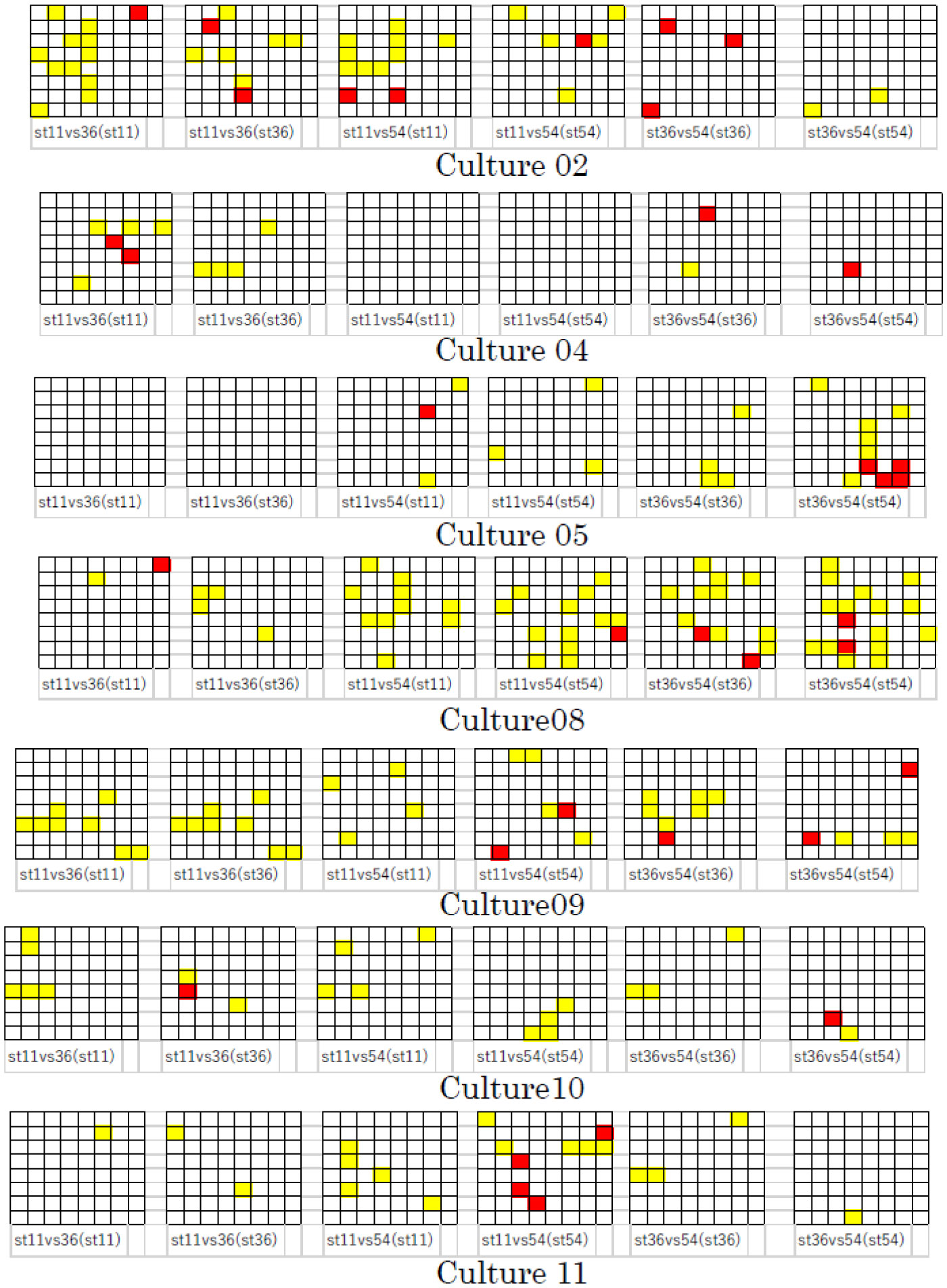
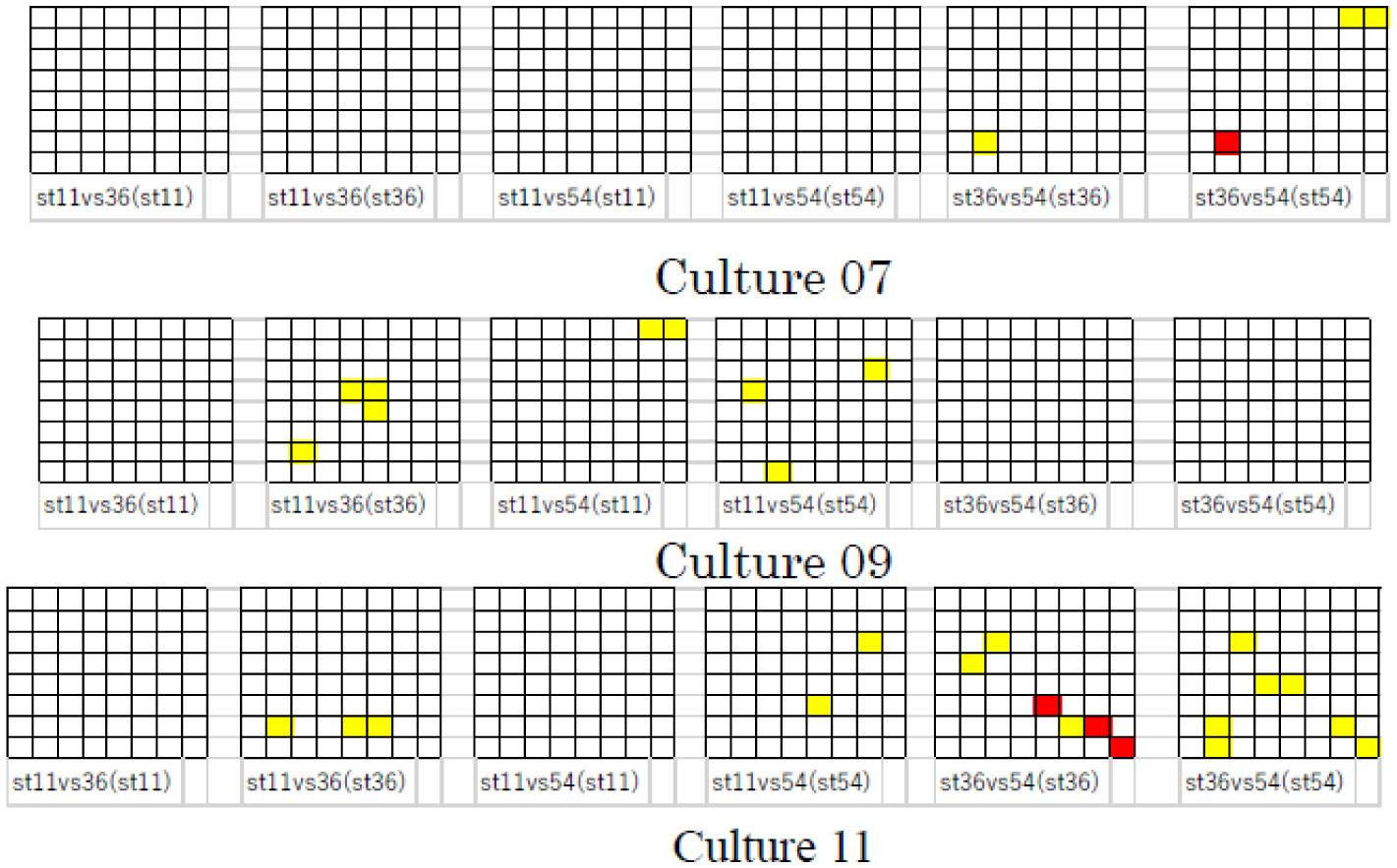
It is well known that various types of information can be learned and memorized via repetitive training. In brain information science, it is very important to determine how neuronal networks comprising neurons with fluctuating characteristics reliably learn and memorize information. The aim of this study is to investigate the learning process in cultured neuronal networks and to address the question described above. Previously, we reported that the spikes resulting from stimulation at a specific neuron propagate as a cluster of excitation waves called spike wave propagation in cultured neuronal networks. We also reported that these waves have an individual spatiotemporal pattern that varies according to the type of neuron that is stimulated. Therefore, different spike wave propagations can be identified via pattern analysis of spike trains at particular neurons. Here, we assessed repetitive stimulation using intervals of 0.5 and 1.5 ms. Subsequently, we analyzed the relationship between the repetition of the stimulation and the identification of the different spike wave propagations. We showed that the various spike wave propagations were identified more precisely after stimulation was repeated several times using an interval of 1.5 ms. These results suggest the existence of a learning process in neuronal networks that occurs via repetitive training using a suitable interval.

Keywords:

Citation: Yoshi Nishitani, Chie Hosokawa, Yuko Mizuno-Matsumoto, Tomomitsu Miyoshi, Shinichi Tamura. Learning process for identifying different types of communication via repetitive stimulation: feasibility study in a cultured neuronal network[J]. AIMS Neuroscience, 2019, 6(4): 240-249. doi: 10.3934/Neuroscience.2019.4.240

Related Papers:

[1]	Kai Friebertshäuser, Christian Wieners, Kerstin Weinberg . Dynamic fracture with continuum-kinematics-based peridynamics. AIMS Materials Science, 2022, 9(6): 791-807. doi: 10.3934/matersci.2022049
[2]	Hanh C. Nguyen, Shigeru Nagasawa, Kensei Kaneko . Strength estimation of silicon nitride ceramics using a round-notched specimen subjected to shearing-tool indentation. AIMS Materials Science, 2020, 7(5): 518-533. doi: 10.3934/matersci.2020.5.518
[3]	Samaneh Nasiri, Michael Zaiser . Rupture of graphene sheets with randomly distributed defects. AIMS Materials Science, 2016, 3(4): 1340-1349. doi: 10.3934/matersci.2016.4.1340
[4]	Yanmei Zhang, Mu Fan, Zhongmin Xiao . Nonlinear elastic-plastic stress investigations on two interacting 3-D cracks in offshore pipelines subjected to different loadings. AIMS Materials Science, 2016, 3(4): 1321-1339. doi: 10.3934/matersci.2016.4.1321
[5]	A.-V. Phan . Dynamic stress intensity factor analysis of the interaction between multiple impact-loaded cracks in infinite domains. AIMS Materials Science, 2016, 3(4): 1683-1695. doi: 10.3934/matersci.2016.4.1683
[6]	R. Citarella, M. Lepore, M. Perrella, C. Calì . Multiple crack propagation by DBEM in a riveted lap-joint. AIMS Materials Science, 2016, 3(4): 1577-1586. doi: 10.3934/matersci.2016.4.1577
[7]	R.R.Bhargava, Kamlesh Jangid, Pavitra Tripathi . A Mode-III strip saturation model for two collinear semi-permeable cracks in a piezoelectric media. AIMS Materials Science, 2016, 3(4): 1507-1519. doi: 10.3934/matersci.2016.4.1507
[8]	Pawan Kumar, B B Verma . Propagation of corrosion induced fatigue crack in aluminum alloy. AIMS Materials Science, 2022, 9(3): 512-521. doi: 10.3934/matersci.2022030
[9]	Tomoya Kawabata, Shuji Aihara, Yukito Hagihara . Coalescence judgment criteria for the interaction between two close surface cracks by WES2805 and its safety margin for brittle fracture assessment. AIMS Materials Science, 2016, 3(4): 1665-1682. doi: 10.3934/matersci.2016.4.1665
[10]	Genshichiro Katsumata, Valéry Lacroix, Yinsheng Li . Effect of interaction of embedded crack and free surface on remaining fatigue life. AIMS Materials Science, 2016, 3(4): 1748-1758. doi: 10.3934/matersci.2016.4.1748

Abstract

1. Introduction

The SARS-CoV-2 virus triggered a pandemic worldwide. SARS-CoV-2, a spike protein virus, is the pathogen that causes widespread Coronavirus infections. Coronaviruses make up a broad family of viruses. The first serious disease attributed to a coronavirus is the severe acute respiratory syndrome (SARS) an epidemic that began in China in 2003. Saudi Arabia was home to a second epidemic, middle east respiratory syndrome (MERS), first reported in 2012 ^[1]. In December 2019, Wuhan, China, announced a SARS coronavirus 2 outbreak (COVID-19). The World Health Organization (WHO) classified COVID-19 as a worldwide epidemic in March 2020. As of 8 January 2023, over 659 million cases have been confirmed worldwide, resulting in over 6.6 million deaths ^[2]. Typically, The disease is contracted through exposure to infected respiratory droplets from breathing, coughing, sneezing, and talking ^[3,4,5,6,7]. The disease is transmissible through the air, according to further research ^{[8,9,10,11,12,13]}. The risk of infection is also present when contact is made with objects that are contaminated with Covid-19. It has been observed that COVID-19 can cause a coughing fit, pain in the muscles, vertigo, high temperature, an inability to smell, throat irritation, weakness, and nasal congestion after 2–14 days of incubation of the virus.

The Omicron variant has been characterized by its high transmissibility and numerous mutations, which have raised concerns about its potential to evade immunity conferred by vaccines or prior infection. In response, India has implemented measures such as booster doses and vaccine mix-and-match regimens to enhance protection against the new variant. Furthermore, the Indian government has also imposed stricter quarantine rules for international travelers, particularly those arriving from countries with high Omicron prevalence. Despite these efforts, challenges remain, particularly in remote or under-resourced areas where healthcare infrastructure and resources may be limited. Additionally, the emergence of new variants underscores the need for ongoing surveillance and research to better understand the virus and its behavior. To that end, India has continued to invest in genomic sequencing efforts, which have played a crucial role in tracking the spread of different variants. As India continues to navigate the ongoing COVID-19 pandemic, the situation with Omicron remains dynamic, and it is important to remain vigilant and adaptable in the face of new developments.

Globally, the COVID-19 pandemic continues to pose a serious threat to public health. Three recent publications offer insight into the crucial elements that ought to direct disease containment efforts. A risk assessment of COVID-19 reappearance in connection to SARS-CoV-2 mutations and vaccine success is provided by Krueger et al.^[14] in 2022. They place a strong emphasis on the value of immunization and the necessity of ongoing surveillance of the disease's spread. The necessity for a coordinated European response to the omicron version of COVID-19 is highlighted by Calero Valdez et al. ^[15] in 2022. To slow the spread of the variation and prevent a spike in cases, the authors contend that concerted action is required. In the meanwhile, Markovi et al.^[16] (2021) provide evidence that socio-demographic and health characteristics are important contributors to the spread of the COVID-19 outbreak and recommend that vaccination regimens should consider these aspects for efficient disease control. Collectively, these papers highlight the significance of a thorough, evidence-based strategy for COVID-19 regulation that considers both individual and population-level determinants.

Dynamical systems have become increasingly complex, and fractional calculus (FC) has become an increasingly useful tool. The process of differentiation and integration in FC is generalized to non-integer orders. FC has been applied to research in a variety of fields. In order to gain a deeper understanding of a disease, fractional order differential equations (FODs) are used. For various diseases, mathematical models have been formulated and studied, for example, ^{[17,18,19,20,21,22]}. In order to overcome the deficiencies of the ordinary operator, fractional order derivatives have been developed ^[23]. Riemann-Liouville proposed the concept of the fractional derivative (FD). Caputo later reformulated and improved FD. The formula of Caputo FD is based on the singular power-law kernel. FDs are commonly used to study real problems, but they often yield singularities that are dissatisfactory. Following decades, and for this reason, Caputo-Fabrizio (CF) operators is created through nonsingular kernels ^[24]. CF, however, has a kernel locality problem. As a solution to this shortcoming, Atangana and Baleanu (AB) ^[25] proposed Mittag-Leffler kernels as a novel type of FD.

Several works ^[26,27,28] have proposed fractional operators with singular and nonsingular kernels, and recent publications such as ^{[29,30,31,32,33,34,35]} explore the research related to these topics and their applications. Additionally, mathematical modeling studies have recently emerged to address social issues, such as criminal activity, using FC. In order to convert the proposed fractional-order crime transmission model to the delayed model and account for the lag between the crime and judgment, Bansal et al. ^[36] established the time-delay coefficient. Pritam et al. ^[37] studied a fractional-order mathematical model of crime transmission that includes the memory property inherited from the previous impact of the input while predicting the crime growth rate in analyzing crime congestion. By using the actual initial conditions for the subgroups of the USA, Partohaghighi et al. ^[38] designed and compared the fractional-order crime systems for the first time using the Atangana-Baleanu-Caputo (ABC), Caputo, and Caputo-Fabrizio derivatives and to obtain approximate solutions to the proposed models, they developed some numerical methods. Rahman et al. ^[39] presented a study on the dynamics of a fractional mathematical model of serial killing under the Mittag-Leffler kernel, ^[39] discovered the approximate solution and numerically simulated it for multiple control techniques in various fractional orders using the iterative fractional-order Adams-Bashforth approach.

Haar wavelet numerical methods are a family of mathematical techniques used to solve differential equations with fractional derivatives. These methods are based on the Haar wavelet, a simple wavelet function that provides a piecewise constant approximation of a signal. The Haar wavelet is well suited for the numerical solution of fractional differential equations due to its simplicity, local support, and orthogonality. One of the main advantages of Haar wavelet numerical methods is their ability to provide efficient and accurate solutions to fractional differential equations. Unlike traditional numerical methods, which can be time-consuming and prone to errors when solving problems with fractional derivatives, Haar wavelet methods are computationally efficient and produce accurate solutions. Haar wavelet numerical methods have been applied to a wide range of problems in various fields, including physics, engineering, and finance. For example, they have been used to study the diffusion of heat in porous media, to model the dynamic behavior of financial markets, and to analyze the spread of infectious diseases. Haar wavelet numerical methods have gained significant attention in the past few years for solving problems associated with the COVID-19 pandemic. These methods have been employed to model the virus's propagation over time while accounting for the multiple factors influencing its transmission. Through these studies, useful information has been obtained regarding the pandemic's dynamics, its evolution, and its impact, which has helped in developing public health policies and strategies aimed at managing its spread.

The use of Haar wavelet numerical methods has gained popularity in various fields, including numerical analysis, image processing, quantum field theory, and statistics. Haar wavelets have been applied in communication, physics research, differential equations, and nonlinear problems ^[40]. They are preferred among all wavelet families because they are the simplest wavelet family that comprises pairs of piecewise constant functions. Additionally, they can be integrated analytically at random times. Recent research has employed Haar wavelets to solve various fractional-order mathematical models ^[41,42]. The Haar wavelet technique is not only fast but also more stable, making it an excellent option for numerical computation.

The innovative aspects of the paper include the application of Haar wavelet collocation methods and fractional order COVID-19 models to the simulation of the Omicron variant of the SARS-CoV-2 virus and the dynamics of the COVID-19 pandemic as well as the evolution of its variants. The results of the study can help shape public health policies and actions targeted at reducing its impact since they provide a more precise and effective solution to the fractional derivatives employed in the model. The importance of this work in furthering our understanding of COVID-19 is increased by the inclusion of parameter estimates and stability analysis. The remainder of the article is structured as follows: In Section 2, the basic concepts of the fractional differential, integral operator, and Haar wavelets have been presented. In Section 3, the fractional extension of the model has been formulated, and the equilibrium point and threshold number have been calculated. In Section 4, the existence and uniqueness of the solution of the model have been established and the numerical scheme is described. Section 5 provides parameter estimation for the COVID-19 reported data in India from 13 July to 25 August 2021. The sensitivity analysis of the model is cared out in Section 6. The numerical scheme and graphical results are presented in Section 7. Conclusions and future research direction have been offered in Section 8.

2. Preliminaries

In recent years, significant progress has been made in the definition of fractional derivatives. This progress has been documented in various sources, including ^{[30,31,43,44,45]}. The updated definitions encompass non-singular kernel derivatives, as well as the Riemann-Liouville fractional derivative without a singular kernel and the two-parameter derivative with non-singular and non-local kernels. Out of these, the following two definitions are widely accepted in the field:

Definition 1. Riemann-Liouville's definition characterizes the fractional derivative of $ \mathcal{F} $ with order $ \delta $. The definition can be expressed as follows:

$\begin{equation} \mathbb{D}_{\ast}^{\delta}\mathcal{F}(t) = \begin{cases} \frac{1}{\Gamma(s-\delta)}\left( \frac{d}{dt}\right) ^{s}\int _{0}^{t}\frac{\mathcal{F}(\nu)}{(t-\nu)^{\delta-s+1}}d\nu, & 0\leq s-1 < \delta < s,\quad s\in\mathbb{N},\\ (d/dt)^{s}\mathcal{F}(t), & \delta = s,\quad s\in\mathbb{N}. \end{cases} \end{equation}$ $

(2.1)

Definition 2. The function $ \mathcal{F} $ can be differentiated with respect to the fractional order $ \delta $ using the Caputo fractional derivative, which is defined in the following manner:

$\begin{equation} \mathbb{D}_{\ast}^{\delta}\mathcal{F}(t) = \begin{cases} \frac{1}{\Gamma(s-\delta)}\int_{0}^{t}\frac{(d/d\nu)^{s} \mathcal{F}(\nu)}{(t-\nu)^{\delta-s+1}}d\nu, & 0\leq s-1 < \delta < s,\quad s\in\mathbb{N},\\ (d/dt)^{s}\mathcal{F}(t), & \delta = s,\quad s\in\mathbb{N}. \end{cases} \end{equation}$ $

(2.2)

The study also employs the RL representation of the fractional integral operator $ \mathbb{D}_{\ast}^{-\delta} $ with order $ \delta $. This operator can be defined in the following manner:

$\begin{equation} \mathbb{D}_{\ast}^{-\delta}\mathcal{F}(t) = \frac{1}{\Gamma (\delta)}\int_{0}^{t}\mathcal{F}(\nu)(t-\nu)^{\delta-1}d\nu \end{equation}$ $

(2.3)

2.1. Haar wavelets

According to ^[46,47], the mother Haar wavelet function (on the real line) is denoted as $ \mathbb{\psi}(t) $, while the Haar scaling function is represented by $ \mathbb{\tilde{\psi}}_{0}(t) $:

$\begin{align} \mathbb{\psi}(t) & = \begin{cases} 1, & \text{ if }t\in\left[ 0,\frac{1}{2}\right) ,\\ -1, & \text{ if }t\in\left[ \frac{1}{2},1\right) ,\\ 0, & \text{ elsewhere, } \end{cases} \end{align}$ $

(2.4)

$\begin{align} \mathbb{\tilde{\psi}}_{0}(t) & = 1\text{, if }t\in\lbrack0,1). \end{align}$ $

(2.5)

Multiresolution analysis generates multiple Haar wavelets on the interval $ [0, 1) $, which can be denoted as $ \mathbb{\tilde{\psi}}_{m}(t) $. As a consequence, the following relationship holds:

$\begin{equation} \mathbb{\tilde{\psi}}_{m}(t) = 2^{j/2}\mathbb{\psi}\left( 2^{j}t-p\right) ,m = 1,2,\ldots; \end{equation}$ $

(2.6)

where $ m = 2^{j}+p:p = 0, 1, \ldots, 2^{j}-1;j = 0, 1, \ldots. $ Further, we can translate the Haar functions on $ u-1\leq t < u $ as

$\begin{equation} \mathbb{\tilde{\psi}}_{u,m}(t) = \mathbb{\tilde{\psi}}_{m}(t+1-u),m = 0,1,2,\ldots ,\quad u = 1,2,\ldots,\varrho,\quad\varrho\in\mathbb{N}. \end{equation}$ $

(2.7)

According to ^[47], the sequence $ \left\{ \mathbb{\tilde{\psi}}_{m}(t)\right\} _{m = 0}^{\infty} $ forms a complete orthonormal system in $ \mathcal{L} ^{2}[0, 1) $, while the sequence $ \left\{ \mathbb{\tilde{\psi}} _{u, m}(t)\right\} _{m = 0}^{\infty}, u = 1, 2, \ldots, \varrho $, forms a complete orthonormal system in $ \mathcal{L}^{2}[0, \varrho) $. This implies that any function $ \mathcal{F}(t) $ belonging to $ \mathcal{L}^{2}[0, \varrho) $ can be expressed as a series of Haar orthonormal basis functions.

$\begin{equation} \mathcal{F}(t) = \sum\limits_{u = 1}^{\varrho}\sum\limits_{m = 0}^{\infty}\mathcal{G} _{u,m}\mathbb{\tilde{\psi}}_{u,m}(t). \end{equation}$ $

(2.8)

Additionally, after truncating this series $ \mathcal{F}(t) $, we obtain the equivalent approximation $ y_{p}(t) $ of $ \mathcal{F}(t) $ as

$\begin{equation} \mathcal{F}(t)\approx y_{p}(t) = \sum\limits_{u = 1}^{\varrho}\sum\limits_{m = 0}^{p-1} \mathcal{G}_{u,m}\mathbb{\tilde{\psi}}_{u,m}(t) = B_{\varrho p\times1} ^{T}\mathbb{\tilde{\psi}}_{\varrho p\times1}(t), \end{equation}$ $

(2.9)

where the coefficients $ \mathcal{G}_{u, m} $ can be expressed by inner product

$\begin{equation} \begin{split} & \langle \mathcal{F}(t),\mathbb{\tilde{\psi}}_{u,m}(t)\rangle = \int_{u-1}^{u}\mathcal{F}(t)\mathbb{\tilde{\psi}}_{u,m}(t)dt,\quad m = 1,2,\ldots,(p-1),u = 1,2,\ldots,\varrho,\\ & B_{\varrho p\times1} = \left[ \mathcal{G}_{1,0},\ldots,\mathcal{G} _{1,p-1},\mathcal{G}_{2,0},\ldots,\mathcal{G}_{2,p-1},\ldots,\mathcal{G} _{\varrho,0},\ldots,\mathcal{G}_{\varrho,p-1}\right] ^{T},\\ & \mathbb{\tilde{\psi}}_{\varrho p\times1} = \left[ \mathbb{\tilde{\psi} }_{1,0},\ldots,\mathbb{\tilde{\psi}}_{1,p-1},\mathbb{\tilde{\psi}} _{2,0},\ldots,\mathbb{\tilde{\psi}}_{2,p-1},\ldots,\mathbb{\tilde{\psi} }_{\varrho,0},\ldots,\mathbb{\tilde{\psi}}_{\varrho,p-1}\right] ^{T}, \end{split} \end{equation}$ $

(2.10)

and superscript $ T $ indicates the transpose of a matrix.

3. Mathematical model

Mathematical modeling plays a crucial role in understanding and predicting the spread of infectious diseases. By using mathematical equations and algorithms, researchers can simulate the behavior of diseases and their transmission within populations. This allows them to make predictions about the future spread of the disease and to test various intervention strategies. Mathematical models can also provide valuable insights into the basic mechanisms of disease transmission, helping to identify risk factors and to inform public health policies. However, it is important to note that the accuracy of these models depends on the quality of data input and the assumptions made in the model, and they should always be used in conjunction with other sources of information. Considering the work of ^[7,11], the model applied takes the form of the following ODEs:

$\begin{equation} \left\{ \begin{split} & \frac{d\mathbb{S}(t)}{dt} = B-\theta \mathbb{S}(t) \mathbb{I}(t)(1+\tau \mathbb{I}(t))-(\varepsilon_{1}+\rho+\eta)\mathbb{S}(t),\\ & \frac{d\mathbb{E}(t)}{dt} = \theta \mathbb{S}(t) \mathbb{I}(t)(1+\tau \mathbb{I}(t))-(\varepsilon_{2}+\rho +\varphi){\mathbb{E}}(t),\\ & \frac{d \mathbb{I}(t)}{dt} = \varphi{\mathbb{E}}(t)-(\lambda+\epsilon +\rho+\varepsilon_{3}){\mathbb{I}}(t),\\ & \frac{d \mathbb{Q}(t)}{dt} = \varepsilon_{1}\mathbb{S}(t)+\varepsilon _{2}{\mathbb{E}}(t)+\varepsilon_{3}{\mathbb{I}}(t)-(\rho+\sigma){\mathbb{Q} }(t),\\ & \frac{d\mathbb{R}(t)}{dt} = \eta\mathbb{S}(t)+\sigma{\mathbb{Q}} (t)+\lambda{\mathbb{I}}(t)-\rho{\mathbb{R}}(t),\\ & \mathbb{S}(t)\geq{0},\quad{\mathbb{E}}(t)\geq{0},\quad{\mathbb{I}} (t)\geq{0},\quad{\mathbb{Q}}(t)\geq{0},\quad{\mathbb{R}}(t)\geq0. \end{split} \right. \end{equation}$ $

(3.1)

where,

$ \mathbb{N}(t) = \mathbb{S}(t)+\mathbb{E}(t)+\mathbb{I}(t)+\mathbb{Q} (t)+\mathbb{R}(t). $

According to the five categories, the total population at time $ t $ is represented by $ \mathbb{N}(t) $ in model (3.1). The individuals who are susceptible to infection are designated as $ \mathbb{S}(t) $; exposed individuals are designated as $ \mathbb{E}(t) $; infectious individuals are designated as $ \mathbb{I}(t) $; and quarantined individuals are designated as $ \mathbb{Q}(t) $; and recovered individuals are designated as $ \mathbb{R}(t) $. The parameters $ \theta $ and $ \tau $ are positive constants, whereas $ B $ is the constant birth rate, $ \theta $ is the coefficient of disease transmission, $ \rho $ is the natural death rate, and$ \epsilon $ is the mortality rate from infectious disease in humans and $ \varphi, \lambda, \varepsilon _{3}, \varepsilon_{2}, \varepsilon_{1}, \sigma $ are the state transition rates. The term $ \eta $ refers to the transmission rate from the class of persons who are immune system-strong to those who are susceptible to it.

3.1. Formulation of fractional model

The Caputo fractional derivative offers a significant advantage over classical models in the context of COVID-19 modeling by allowing for a more accurate representation of complex phenomena, such as the long-lasting effects of the disease on patients. Unlike classical models that assume instant recovery after an infection, Caputo fractional derivatives account for the memory effect of the disease, which can persist even after recovery, enabling more precise predictions and better decision-making regarding healthcare resource allocation and pandemic control measures. Additionally, using the Caputo derivative often requires less computational resources and less data, making it a more cost-effective solution in disease modeling. Furthermore, time memory effect can be found in most natural phenomena, such as epidemiological dynamics. Model (3.1) is expressed in integral form as:

$\begin{equation} \left\{ \begin{split} & \frac{d\mathbb{S}(t)}{dt} = \int_{t_{0}}^{t}\varsigma(t-\vartheta)\left[ B-\theta\mathbb{S}(t) {\mathbb{I}(t)}(1+\tau \mathbb{I}(t))-(\varepsilon_{1}+\rho +\eta)\mathbb{S}(t)\right] d\vartheta,\\ & \frac{d \mathbb{E}(t)}{dt} = \int_{t_{0}}^{t}\varsigma(t-\vartheta)\left[ \theta\mathbb{S}(t){\mathbb{I}(t)}(1+\tau \mathbb{I}(t))-(\varepsilon _{2}+\rho+\varphi){\mathbb{E}}(t)\right] d\vartheta,\\ & \frac{d \mathbb{I}(t)}{dt} = \int_{t_{0}}^{t}\varsigma(t-\vartheta)\left[ \varphi{\mathbb{E}}(t)-(\lambda+\epsilon+\rho+\varepsilon _{3}){\mathbb{I}}(t)\right] d\vartheta,\\ & \frac{d \mathbb{Q}(t)}{dt} = \int_{t_{0}}^{t}\varsigma(t-\vartheta)\left[ \varepsilon_{1}\mathbb{S}(t)+\varepsilon_{2} \mathbb{E}(t)+\varepsilon_{3}{\mathbb{I}}(t)-(\rho+\sigma){\mathbb{Q}}(t)\right] d\vartheta,\\ & \frac{d \mathbb{R}(t)}{dt} = \int_{t_{0}}^{t}\varsigma(t-\vartheta)\left[ \eta\mathbb{S}(t)+\sigma{\mathbb{Q}}(t)+\lambda{\mathbb{I}} (t)-\rho{\mathbb{R}}(t)\right] d\vartheta. \end{split} \right. \end{equation}$ $

(3.2)

Incorporating the Caputo derivative we get,

$\begin{equation} \left\{ \begin{split} & ^{C}D_{t}^{\delta-1}\left[ \frac{d\mathbb{S}(t)}{dt}\right] = ^{C}D_{t}^{\delta-1}I^{-(\delta-1)}\left[ B-\theta \mathbb{S}(t){\mathbb{I}(t)}(1+\tau \mathbb{I}(t))-(\varepsilon_{1}+\rho +\eta)\mathbb{S}(t)\right] ,\\ & ^{C}D_{t}^{\delta-1}\left[ \frac{d \mathbb{E}(t)}{dt}\right] = ^{C}D_{t}^{\delta-1}I^{-(\delta-1)}\left[ \theta \mathbb{S}(t){\mathbb{I}(t)}(1+\tau \mathbb{I}(t))-(\varepsilon_{2}+\rho +\varphi){\mathbb{E}}(t)\right] ,\\ & ^{C}D_{t}^{\delta-1}\left[ \frac{d \mathbb{I}(t)}{dt}\right] = ^{C}D_{t}^{\delta-1}I^{-(\delta-1)}\left[ \varphi {\mathbb{E}}(t)-(\lambda+\epsilon+\rho+\varepsilon_{3}){\mathbb{I}}(t)\right] ,\\ & ^{C}D_{t}^{\delta-1}\left[ \frac{d \mathbb{Q}(t)}{dt}\right] = ^{C}D_{t}^{\delta-1}I^{-(\delta-1)}\left[ \varepsilon _{1}\mathbb{S}(t)+\varepsilon_{2}{\mathbb{E}}(t)+\varepsilon_{3}{\mathbb{I} }(t)-(\rho+\sigma){\mathbb{Q}}(t)\right] ,\\ & ^{C}D_{t}^{\delta-1}\left[ \frac{d \mathbb{R}(t)}{dt}\right] = ^{C}D_{t}^{\delta-1}I^{-(\delta-1)}\left[ \eta \mathbb{S}(t)+\sigma{\mathbb{Q}}(t)+\lambda{\mathbb{I}}(t)-\rho{\mathbb{R} }(t)\right] . \end{split} \right. \end{equation}$ $

(3.3)

After calculations, we reaches

$\begin{equation} \left\{ \begin{split} & ^{C}D_{t}^{\delta}\mathbb{S}(t) = B-\theta\mathbb{S}(t){\mathbb{I}(t)} (1+\tau{\mathbb{I}(t)})-(\varepsilon_{1}+\rho+\eta)\mathbb{S}(t),\\ & ^{C}D_{t}^{\delta} \mathbb{E}(t) = \theta\mathbb{S}(t){\mathbb{I}(t)} (1+\tau{\mathbb{I}(t)})-(\varepsilon_{2}+\rho+\varphi){\mathbb{E}}(t),\\ & ^{C}D_{t}^{\delta}{\mathbb{I}(t)} = \varphi{\mathbb{E}}(t)-(\lambda +\epsilon+\rho+\varepsilon_{3}){\mathbb{I}}(t),\\ & ^{C}D_{t}^{\delta}{\mathbb{Q}(t)} = \varepsilon_{1}\mathbb{S} (t)+\varepsilon_{2}{\mathbb{E}}(t)+\varepsilon_{3}{\mathbb{I}}(t)-(\rho +\sigma){\mathbb{Q}}(t),\\ & ^{C}D_{t}^{\delta}{\mathbb{R}(t)} = \eta\mathbb{S}(t)+\sigma {\mathbb{Q}}(t)+\lambda{\mathbb{I}}(t)-\rho{\mathbb{R}}(t). \end{split} \right. \end{equation}$ $

(3.4)

3.2. Equilibrium point and threshold number $ R_{0} $

A crucial element of epidemiological modeling is the basic reproductive number $ R_0 $, which expresses the typical number of secondary infections brought on by a single infected person in a population that is fully susceptible. In the context of epidemiological modeling, $ R_0 $ offers numerous benefits:

● It provides a clear measure of the transmissibility of a disease: A high $ R_0 $ indicates that a disease is easily transmitted, while a low $ R_0 $ suggests that it is less contagious.

● It helps to predict the potential spread of an outbreak: By estimating $ R_0 $, epidemiologists can predict the potential size and duration of an outbreak and identify the most effective control measures.

● It can be used to evaluate the effectiveness of interventions: By comparing the $ R_0 $ before and after an intervention, such as the implementation of a vaccine or quarantine measures, epidemiologists can determine the effectiveness of the intervention in reducing transmission.

● It can be used to identify the critical control points: $ R_0 $ can be used to identify the critical points in the transmission of an infection, such as the number of infected individuals in a population.

● It can be used to predict the herd immunity threshold: The herd immunity threshold is the proportion of the population that needs to be immune to a disease in order to achieve herd immunity. $ R_0 $ helps to predict the herd immunity threshold and thus the overall effectiveness of vaccination programs.

The DFE of the model (3.4) is denoted by $ E^{0}(\mathbb{S} _{0}, 0, 0, \mathbb{Q}_{0}, \mathbb{R}_{0}) $, where

$ \mathbb{S}_{0} = \frac{B}{\eta+\rho+\varepsilon_{1}},\; \; \; \; \; \mathbb{Q}_{0} = \frac{\varepsilon_{1}\mathbb{S}_{0}}{\rho+\tau},\; \; \; \; \; \mathbb{R}_{0} = \frac{\eta\mathbb{S}_{0}+\tau\mathbb{Q}_{0}}{\rho}. $

Our proposed model is split in two matrices ^[48].

$ \tilde{U} = \left[

$\begin{array} [c]{cc} 0 & \theta\mathbb{S}_{0}\\ 0 & 0 \end{array}$ \right] ,\; \tilde{V} = \left[

$\begin{array} [c]{cc} \varphi+\rho+\varepsilon_{2} & 0\\ -\varphi & \rho+\epsilon+\lambda+\varepsilon_{3} \end{array}$ \right] , $

$ \tilde{V}^{-1} = \frac{1}{(\varphi+\rho+\varepsilon_{2})(\rho+\epsilon +\lambda+\varepsilon_{3})}\left[

$\begin{array} [c]{cc} \rho+\epsilon+\lambda+\varepsilon_{3} & 0\\ \varphi & \varphi+\rho+\varepsilon_{2} \end{array}$ \right] , $

$ \tilde{U}\tilde{V}^{-1} = \left[

$\begin{array} [c]{cc} \frac{\theta\mathbb{S}_{0}\varphi}{(\varphi+\rho+\varepsilon_{2} )(\rho+\epsilon+\lambda+\varepsilon_{3})} & \frac{\theta\mathbb{S}_{0}} {\rho+\epsilon+\lambda+\varepsilon_{3}}\\ 0 & 0 \end{array}$ \right] . $

Hence

$ R_{0} = \frac{\varphi\theta B}{(\eta+\rho+\varepsilon_{1})(\varphi +\rho+\varepsilon_{2})(\rho+\epsilon+\lambda+\varepsilon_{3})}. $

4. Existence and uniqueness

The existence and uniqueness of a solution to a mathematical problem is a fundamental concept in many areas of mathematics. In order for a solution to exist, the problem must have at least one solution that satisfies all the given conditions. Uniqueness, on the other hand, refers to the fact that there is only one solution to the problem that satisfies all the given conditions. This is important because it means that any method used to solve the problem will always give the same answer. In many cases, the existence and uniqueness of a solution can be proven through the use of mathematical theorems and techniques such as the existence and uniqueness theorem.

In this section, we describe the existence, uniqueness, and solution of the system (3.4) using the Caputo operator. We assume that the Banach space $ \mathcal{A}(Y) $ is a continuous real-valued function with the sup-norm property on $ J = [0, b] $, and that $ Y = [0, \kappa] $ and $ P = \mathcal{A}(Y)\times\mathcal{A}(Y)\times\mathcal{A}(Y)\times\mathcal{A}(Y)\times\mathcal{A}(Y) $ has the norm $ \left\Vert \left(\mathbb{S}, {\mathbb{E}}, \mathbb{Q}, \mathbb{I}, \mathbb{R}\right) \right\Vert = \Vert\mathbb{S}\Vert+\Vert{\mathbb{E}}\Vert+\left\Vert \mathbb{Q}\right\Vert+\left\Vert \mathbb{I}\right\Vert+\Vert\mathbb{R}\Vert $. Here, $ \Vert\mathbb{S}\Vert $, $ \Vert{\mathbb{E}}\Vert $, $ \left\Vert \mathbb{Q}\right\Vert $, $ \left\Vert \mathbb{I}\right\Vert $, and $ \left\Vert \mathbb{R}\right\Vert $ are defined as $ \sup_{t\in Y}|\mathbb{S}(t)| $, $ \sup_{t\in Y}|{\mathbb{E}}(t)| $, $ \sup_{t\in Y}|\mathbb{Q}(t)| $, $ \sup_{t\in Y}|\mathbb{I}(t)| $, and $ \sup_{t\in Y}|\mathbb{R}(t)| $, respectively. Using the Caputo fractional integral operator on both sides of (3.4), we obtain the following equation:

$\begin{equation} \left\{ \begin{split} & \mathbb{S}(t)-\mathbb{S}(0) = ^{C}{\mathbb{D}_{0,t}^{\delta} }\mathbb{S}(t)\left\{ B-\theta\mathbb{S}{\mathbb{I}}(1+\tau \mathbb{I})-(\varepsilon_{1}+\rho+\eta)\mathbb{S}(t)\right\} ,\\ & {\mathbb{E}}(t)-{\mathbb{E}}(0) = ^{C}{\mathbb{D}_{0,t}^{\delta}\mathbb{E}}(t)\left\{ \theta\mathbb{S}{\mathbb{I}}(1+\tau \mathbb{I})-(\varepsilon_{2}+\rho+\varphi){\mathbb{E}}(t)\right\} ,\\ & {\mathbb{I}}(t)-{\mathbb{I}}(0) = ^{C}{\mathbb{D}_{0,t}^{\delta}\mathbb{I}}(t)\left\{ \varphi{\mathbb{E}}(t)-(\lambda+\epsilon +\rho+\varepsilon_{3}){\mathbb{I}}(t)\right\} ,\\ & {\mathbb{Q}}(t)-{\mathbb{Q}}(0) = ^{C}{\mathbb{D}_{0,t}^{\delta}\mathbb{Q}}(t)\left\{ \varepsilon_{1}{\mathbb{S}}(t)+\varepsilon _{2}{\mathbb{E}}(t)+\varepsilon_{3}\mathbb{I}(t)-(\rho+\sigma)\mathbb{Q}(t)\right\} ,\\ & {\mathbb{R}}(t)-{\mathbb{R}}(0) = ^{C}{\mathbb{D}_{0,t}^{\delta}\mathbb{R}}(t)\left\{ \eta\mathbb{S}(t)+\sigma{\mathbb{Q}}(t)+\lambda {\mathbb{I}}(t)-\rho{\mathbb{R}}(t)\right\} . \end{split} \right. \end{equation}$ $

(4.1)

After calculation

$\begin{equation} \begin{array} [c]{l} \mathbb{S}(t)-\mathbb{S}(0) = {\mathcal{H}}(\delta)\int_{0} ^{t}(t-\vartheta)^{-\delta}{\mathcal{B}}_{1}(\delta,\vartheta,\mathbb{S}(\vartheta))d\vartheta,\\ \\ {\mathbb{E}}(t)-{\mathbb{E}}(0) = {\mathcal{H}}(\delta)\int_{0} ^{t}(t-\vartheta)^{-\delta}{\mathcal{B}}_{2}(\delta,\vartheta,{\mathbb{E}}(\vartheta))d\vartheta,\\ \\ {\mathbb{I}}(t)-{\mathbb{I}}(0) = {\mathcal{H}}(\delta)\int_{0} ^{t}(t-\vartheta)^{-\delta}{\mathcal{B}}_{4}\left( \delta,\vartheta,{\mathbb{I}}(\vartheta)\right) d\vartheta,\\ \\ {\mathbb{Q}}(t)-{\mathbb{Q}}(0) = {\mathcal{H}}(\delta)\int_{0} ^{t}(t-\vartheta)^{-\delta}{\mathcal{B}}_{3}\left( \delta,\vartheta,{\mathbb{Q}}(\vartheta)\right) d\vartheta,\\ \\ {\mathbb{R}}(t)-{\mathbb{R}}(0) = {\mathcal{H}}(\delta)\int_{0} ^{t}(t-\vartheta)^{-\delta}{\mathcal{B}}_{5}(\delta,\vartheta,{\mathbb{R}}(\vartheta))d\vartheta, \end{array} \end{equation}$ $

(4.2)

where

$\begin{equation} \left\{ \begin{split} & \mathbb{S}(t)-\mathbb{S}(0) = ^{C}{\mathbb{D}_{0,t}^{\delta} }\mathbb{S}(t)\left\{ B-\theta\mathbb{S}{\mathbb{I}}(1+\tau{\mathbb{I} })-(\varepsilon_{1}+\rho+\eta)\mathbb{S}(t)\right\} ,\\ & {\mathbb{E}}(t)-{\mathbb{E}}(0) = ^{C}{\mathbb{D}_{0,t}^{\delta }\mathbb{E}}(t)\left\{ \theta\mathbb{S}{\mathbb{I}}(1+\tau{\mathbb{I} })-(\varepsilon_{2}+\rho+\mathbb{\varphi}){\mathbb{E}}(t)\right\} ,\\ & {\mathbb{I}}(t)-{\mathbb{I}}(0) = ^{C}{\mathbb{D}_{0,t}^{\delta }\mathbb{I}}(t)\left\{ \varphi{\mathbb{E}}(t)-(\lambda+\epsilon +\rho+\varepsilon_{3}){\mathbb{I}}(t)\right\} ,\\ & {\mathbb{Q}}(t)-{\mathbb{Q}}(0) = ^{C}{\mathbb{D}_{0,t}^{\delta }\mathbb{Q}}(t)\left\{ \varepsilon_{1}{\mathbb{S}}(t)+\varepsilon _{2}{\mathbb{E}}(t)+\varepsilon_{3}\mathbb{I}(t)-(\rho+\sigma){\mathbb{Q} }(t)\right\} ,\\ & {\mathbb{R}}(t)-{\mathbb{R}}(0) = ^{C}{\mathbb{D}_{0,t}^{\delta }\mathbb{R}}(t)\left\{ \eta\mathbb{S}(t)+\sigma{\mathbb{Q}}(t)+\lambda {\mathbb{I}}(t)-\rho{\mathbb{R}}(t)\right\} . \end{split} \right. \end{equation}$ $

(4.3)

$\begin{equation} \begin{array} [c]{l} {\mathcal{B}}_{1}(\delta,t,\mathbb{S}(t)) = B-\theta\mathbb{S} {\mathbb{I}}(1+\tau{\mathbb{I}})-(\varepsilon_{1}+\rho+\eta)\mathbb{S}(t),\\ \\ {\mathcal{B}}_{2}(\delta,t,{\mathbb{E}}(t)) = \theta\mathbb{S} {\mathbb{I}}(1+\tau{\mathbb{I}})-(\varepsilon_{2}+\rho+\varphi){\mathbb{E} }(t),\\ \\ {\mathcal{B}}_{3}\left( \delta,t,{\mathbb{I}}(t)\right) = \varphi{\mathbb{E}}(t)-(\lambda+\epsilon+\rho+\varepsilon_{3}){\mathbb{I} }(t),\\ \\ {\mathcal{B}}_{4}\left( \delta,t,{\mathbb{Q}}(t)\right) = \varepsilon_{1}{\mathbb{S}}(t)+\varepsilon_{2}{\mathbb{E}}(t)+\varepsilon _{3}\mathbb{I}(t)-(\rho+\sigma){\mathbb{Q}}(t),\\ \\ {\mathcal{B}}_{5}(\delta,t,{\mathbb{R}}(t)) = \eta\mathbb{S} (t)+\sigma{\mathbb{Q}}(t)+\lambda{\mathbb{I}}(t)-\rho{\mathbb{R}}(t). \end{array} \end{equation}$ $

(4.4)

The symbols $ \mathcal{B} _{1}, $\mathcal{B} _{2},$ \mathcal{B} _{3}, $$ \mathcal{B} _{4} $ and $ \mathcal{B} _{5} $ have to hold for the Lipschitz condition only if $ \mathbb{S}(t), {\mathbb{E}}(t), {\mathbb{Q} }(t), {\mathbb{I}}(t) $ and $ {\mathbb{R}}(t) $ possess an upper bound. Summarizing that $ \mathbb{S}(t) $ and $ \mathbb{S}^{\ast}(t) $ are couple functions, we reach

$\begin{equation} \begin{array} [c]{l} \left\Vert {\mathcal{B}}_{1}(\delta,t,\mathbb{S}(t))-{\mathcal{B} }_{1}\left( \delta,t,\mathbb{S}^{\ast}(t)\right) \right\Vert = \left\Vert -\left( \theta{\mathbb{I}}(1+\mathbb{\tau}{\mathbb{I}})+\eta +\rho+\varepsilon_{1}\right) \left( \mathbb{S}(t)-\mathbb{S}^{\ast }(t)\right) \right\Vert . \end{array} \end{equation}$ $

(4.5)

Taking into account $ \Lambda_{1} = \left\Vert -\left(\theta{\mathbb{I}} (1+\tau{\mathbb{I}})+\eta+\rho+\varepsilon_{1}\right) \right\Vert $ one reaches

$\begin{equation} \left\Vert {\mathcal{B}}_{1}(\delta,t,\mathbb{S}(t))-{\mathcal{B} }_{1}\left( \delta,t,\mathbb{S}^{\ast}(t)\right) \right\Vert \leq\Lambda_{1}\left\Vert \mathbb{S}(t)-\mathbb{S}^{\ast}(t)\right\Vert . \end{equation}$ $

(4.6)

Similarly

$\begin{equation} \begin{array} [c]{l} \left\Vert {\mathcal{B}}_{2}(\delta,t,{\mathbb{E}}(t))-{\mathcal{B} }_{2}\left( \delta,t,{\mathbb{E}}^{\ast}(t)\right) \right\Vert \leq\Lambda_{2}\left\Vert {\mathbb{E}}(t)-{\mathbb{E}}^{\ast}(t)\right\Vert ,\\ \\ \left\Vert {\mathcal{B}}_{3}\left( \delta,t,{\mathbb{Q}}(t)\right) -{\mathcal{B}}_{3}\left( \delta,t,{\mathbb{Q}}^{\ast}(t)\right) \right\Vert \leq\Lambda_{3}\left\Vert {\mathbb{Q}}(t)-{\mathbb{Q}}^{\ast }(t)\right\Vert ,\\ \\ \left\Vert {\mathcal{B}}_{4}\left( \delta,t,{\mathbb{I}}(t)\right) -{\mathcal{B}}_{4}\left( \delta,t,{\mathbb{I}}^{\ast}(t)\right) \right\Vert \leq\Lambda_{4}\left\Vert {\mathbb{I}}(t)-{\mathbb{I}}^{\ast }(t)\right\Vert ,\\ \\ \left\Vert {\mathcal{B}}_{5}(\delta,t,{\mathbb{R}}(t))-{\mathcal{B} }_{5}\left( \delta,t,\mathbb{R}^{\ast}(t)\right) \right\Vert \leq\Lambda_{5}\left\Vert {\mathbb{R}}(t)-{\mathbb{R}}^{\ast}(t)\right\Vert . \end{array} \end{equation}$ $

(4.7)

Where

$\begin{split} \Lambda_{2} = & \left\Vert -\left( \varphi+\rho+\varepsilon_{2}\right) \right\Vert \\ & \\ \Lambda_{3} = & \left\Vert -\left( \rho+\epsilon+\lambda+\varepsilon _{3}\right) \right\Vert \\ & \\ \Lambda_{4} = & \left\Vert -\left( \rho+\tau\right) \right\Vert \\ & \\ \Lambda_{5} = & \left\Vert -\left( \rho\right) \right\Vert . \end{split}$ $

These results suggest that the Lipschitz condition holds for all five functions. By iteratively utilizing the equations in (4.2), we can derive the following expressions

$\begin{equation} \begin{array} [c]{l} \mathbb{S}_{n}(t) = {\mathcal{H}}(\delta)\int_{0}^{t}(t-\vartheta)^{-\delta}{\mathcal{B}}_{1}\left( \delta,\vartheta,\mathbb{S}_{n-1}(\vartheta)\right) d\vartheta,\\ \\ {\mathbb{E}}_{n}(t) = {\mathcal{H}}(\delta)\int_{0}^{t} (t-\vartheta)^{-\delta}{\mathcal{B}}_{2}\left( \delta,\vartheta,{\mathbb{E}}_{n-1}(\vartheta)\right) d\vartheta,\\ \\ {\mathbb{Q}}_{n}(t) = {\mathcal{H}}(\delta)\int_{0}^{t} (t-\vartheta)^{-\delta}{\mathcal{B}}_{3}\left( \delta,\vartheta,{\mathbb{Q}}_{n-1}(\vartheta)\right) d\vartheta,\\ \\ {\mathbb{I}}_{n}(t) = {\mathcal{H}}(\delta)\int_{0}^{t} (t-\vartheta)^{-\delta}{\mathcal{B}}_{4}\left( \delta,\vartheta,{\mathbb{I}}_{n-1}(\vartheta)\right) d\vartheta,\\ \\ {\mathbb{R}}_{n}(t) = {\mathcal{H}}(\delta)\int_{0}^{t} (t-\vartheta)^{-\delta}{\mathcal{B}}_{5}\left( \delta,\vartheta,{\mathbb{R}}_{n-1}(\vartheta)\right) d\vartheta, \end{array} \end{equation}$ $

(4.8)

together with $ \mathbb{S}_{0}(t) = \mathbb{S}(0), {\mathbb{E}}_{0}(t) = {\mathbb{E} }(0), {\mathbb{Q}}_{0}(t) = {\mathbb{Q}}(0), {\mathbb{I}}_{0}(t) = {\mathbb{I}}(0) $ and $ {\mathbb{R}}_{0}(t) = {\mathbb{R}}(0) $. When the successive terms difference is taken, we get

$\begin{equation} \begin{split} \Psi_{\mathbb{S},n}(t) = & \mathbb{S}_{n}(t)-\mathbb{S}_{n-1}(t)\\ = & {\mathcal{H}}(\delta)\int_{0}^{t}(t-\vartheta)^{-\delta}\left( {\mathcal{B}}_{1}\left( \delta,\vartheta,\mathbb{S}_{n-1}(\vartheta)\right) \right. \left. -{\mathcal{B}}_{1}\left( \delta,\vartheta,\mathbb{S} _{n-2}(\vartheta)\right) \right) d\vartheta,\\ \Psi_{{\mathbb{E}},n}(t) = & {\mathbb{E}}_{n}(t)-{\mathbb{E}} _{n-1}(t)\\ = & {\mathcal{H}}(\delta)\int_{0}^{l}(t-\vartheta)^{-\delta}\left( {\mathcal{B}}_{2}\left( \delta,\vartheta,{\mathbb{E}}_{n-1}(\vartheta)\right) \right. \left. -{\mathcal{B}}_{2}\left( \delta,\vartheta,{\mathbb{E}} _{n-2}(\vartheta)\right) \right) d\vartheta,\\ \Psi_{{\mathbb{I}},n}(t) = & {\mathbb{I}}_{2n}(t)-{\mathbb{I}} _{n-1}(t)\\ = & {\mathcal{H}}(\delta)\int_{0}^{t}(t-\vartheta)^{-\delta}\left( {\mathcal{B}}_{4}\left( \delta,\vartheta,{\mathbb{I}}_{n-1}(\vartheta)\right) \right. \left. -{\mathcal{B}}_{4}\left( \delta,\vartheta,{\mathbb{I}} _{n-2}(\vartheta)\right) \right) d\vartheta,\\ \Psi_{{\mathbb{Q}},n}(t) = & {\mathbb{Q}}_{1n}(t)-{\mathbb{Q}} _{n-1}(t)\\ = & {\mathcal{H}}(\delta)\int_{0}^{t}(t-\vartheta)^{-\delta}\left( {\mathcal{B}}_{3}\left( \delta,\vartheta,{\mathbb{Q}}_{n-1}(\vartheta)\right) \right. \left. -{\mathcal{B}}_{3}\left( \delta,\vartheta,{\mathbb{Q}} _{n-2}(\vartheta)\right) \right) d\vartheta,\\ \Psi_{{\mathbb{R}},n}(t) = & {\mathbb{R}}_{n}(t)-{\mathbb{R}} _{n-1}(t)\\ = & {\mathcal{H}}(\delta)\int_{0}^{t}(t-\vartheta)^{-\delta}\left( {\mathcal{B}}_{5}\left( \delta, \vartheta,{\mathbb{R}}_{n-1}(\vartheta)\right) \right. \left. -{\mathcal{B}}_{5}\left( \delta,\vartheta,{\mathbb{R}} _{n-2}(\vartheta)\right) \right) d\vartheta. \end{split} \end{equation}$ $

(4.9)

It is vital to observe that

$\begin{align*} \mathbb{S}_{n}(t) & = \sum\limits_{m = 0}^{n}\Psi_{\mathbb{S},m}(t),\quad {\mathbb{E}}_{n}(t) = \sum\limits_{m = 0}^{n}\Psi_{{\mathbb{E}},m}(t),\quad {\mathbb{Q}}_{n}(t) = \sum\limits_{m = 0}^{n}\Psi_{{\mathbb{Q}},m}(t),\\ \quad{\mathbb{I}}_{n}(t) & = \sum\limits_{m = 0}^{n}\Psi_{{\mathbb{I}} ,m}(t),\quad{\mathbb{R}}_{n}(t) = \sum\limits_{m = 0}^{n}\Psi_{{\mathbb{R}},m}(t). \end{align*}$ $

Additionally, by using Eqs (4.6) and (4.7) and considering that

$\begin{split} & \Psi_{\mathbb{S},n-1}(t) = \mathbb{S}_{n-1}(t)-\mathbb{S} _{n-2}(t),\quad\Psi_{{\mathbb{E}},n-1}(t) = {\mathbb{E}}_{n-1} (t)-{\mathbb{E}}_{n-2}(t),\quad\Psi_{{\mathbb{Q}},n-1}(t) = {\mathbb{Q} }_{n-1}(t)-{\mathbb{Q}}_{n-2}(t),\\ & \Psi_{{\mathbb{I}},n-1}(t) = {\mathbb{I}}_{n-1}(t)-{\mathbb{I}} _{n-2}(t),\quad\Psi_{{\mathbb{R}},n-1}(t) = {\mathbb{R}}_{n-1} (t)-{\mathbb{R}}_{n-2}(t), \end{split}$ $

we reach

$\begin{equation} \begin{array} [c]{l} \left\Vert \Psi_{\mathbb{S},n}(t)\right\Vert \leq \mathcal{H}(\delta)\Lambda_{1}\int_{0}^{t}(t-\vartheta)^{-\delta }\left\Vert \Psi_{\mathbb{S},n-1}(\vartheta)\right\Vert d\vartheta,\\ \\ \left\Vert \Psi_{{\mathbb{E}},n}(t)\right\Vert \leq{\mathcal{H} }(\delta)\Lambda_{2}\int_{0}^{t}(t-\vartheta)^{-\delta}\left\Vert \Psi_{{\mathbb{E}},n-1}(\vartheta)\right\Vert d\vartheta,\\ \\ \left\Vert \Psi_{{\mathbb{I}},n}(t)\right\Vert \leq{\mathcal{H} }(\delta)\Lambda_{4}\int_{0}^{t}(t-\vartheta)^{-\delta}\left\Vert \Psi_{{\mathbb{I}},n-1}(\vartheta)\right\Vert d\vartheta,\\ \\ \left\Vert \Psi_{{\mathbb{Q}},n}(t)\right\Vert \leq{\mathcal{H} }(\delta)\Lambda_{3}\int_{0}^{t}(t-\vartheta)^{-\delta}\left\Vert \Psi_{{\mathbb{Q}},n-1}(\vartheta)\right\Vert d\vartheta,\\ \\ \left\Vert \Psi_{{\mathbb{R}},n}(t)\right\Vert \leq{\mathcal{H} }(\delta)\Lambda_{5}\int_{0}^{t}(t-\vartheta)^{-\delta}\left\Vert \Psi_{{\mathbb{R}},n-1}(\vartheta)\right\Vert d\vartheta. \end{array} \end{equation}$ $

(4.10)

Theorem 3. If the following condition holds

$\begin{equation} \frac{{\mathcal{H}}(\delta)}{\delta}\kappa^{\delta }\Lambda_{m} < 1,m = 1,2,\ldots,5. \end{equation}$ $

(4.11)

Then, (3.4) has a unique solution for $ t\in\lbrack0, \kappa] $.

Proof It is shown that $ \mathbb{S}(t), {\mathbb{E}}(t), {\mathbb{Q} }(t), {\mathbb{I}}(t) $ and $ {\mathbb{R}}(t) $ are bounded functions. In addition, as can be seen from Eqs (4.6) and (4.7), the $ \mathcal{B} _{1}, $\mathcal{B} _{2},$ \mathcal{B} _{3}, $$ \mathcal{B} _{4} $ and $ \mathcal{B} _{5} $ hold for Lipchitz condition. Therefore, utilizing Eq (4.10) together with a recursive hypothesis, we arrive at

$\begin{equation} \begin{array} [c]{l} \left\Vert \Psi_{\mathbb{S},n}(t)\right\Vert \leq\left\Vert \mathbb{S}_{0}(t)\right\Vert \left( \frac{{\mathcal{H}}(\delta )}{\delta}\kappa^{\delta}\Lambda_{1}\right) ^{n},\\ \\ \left\Vert \Psi_{{\mathbb{E}},n}(t)\right\Vert \leq\left\Vert {\mathbb{E}}_{0}(t)\right\Vert \left( \frac{{\mathcal{H}}(\delta )}{\delta}\kappa^{\delta}\Lambda_{2}\right) ^{n},\\ \\ \left\Vert \Psi_{{\mathbb{I}},n}(t)\right\Vert \leq\left\Vert {\mathbb{I}}_{0}(t)\right\Vert \left( \frac{{\mathcal{H}}(\delta )}{\delta}\kappa^{\delta}\Lambda_{4}\right) ^{n},\\ \\ \left\Vert \Psi_{{\mathbb{Q}},n}(t)\right\Vert \leq\left\Vert {\mathbb{Q}}_{0}(t)\right\Vert \left( \frac{{\mathcal{H}}(\delta )}{\delta}\kappa^{\delta}\Lambda_{3}\right) ^{n},\\ \\ \left\Vert \Psi_{{\mathbb{R}},n}(t)\right\Vert \leq\left\Vert {\mathbb{R}}_{0}(t)\right\Vert \left( \frac{{\mathcal{H}}(\delta )}{\delta}\kappa^{\delta}\Lambda_{5}\right) ^{n}. \end{array} \end{equation}$ $

(4.12)

As a result, it is evident that sequences fulfill and exist

$ \left\Vert \Psi_{\mathbb{S},n}(t)\right\Vert \rightarrow0,\left\Vert \Psi_{{\mathbb{E}},n}(t)\right\Vert \rightarrow0,\left\Vert \Psi_{{\mathbb{I}},n}(t)\right\Vert \rightarrow0,\left\Vert \Psi_{{\mathbb{Q}},n}(t)\right\Vert \rightarrow0,\quad\left\Vert \Psi_{{\mathbb{R}},n}(t)\right\Vert \rightarrow0\text{ as } n\rightarrow \infty. $

Additionally, using Eq (4.12) and the triangle inequality, for any $ s $, we have

$\begin{equation} \begin{array} [c]{l} \left\Vert \mathbb{S}_{n+s}(t)-\mathbb{S}_{n}(t)\right\Vert \leq\sum _{j = n+1}^{n+s}X_{1}^{j} = \frac{X_{1}^{n+1}-X_{1}^{n+s+1}}{1-X_{1}},\\ \\ \left\Vert {\mathbb{E}}_{n+s}(t)-{\mathbb{E}}_{n}(t)\right\Vert \leq \sum\nolimits_{j = n+1}^{n+s}X_{2}^{j} = \frac{X_{2}^{n+1}-X_{2}^{n+s+1}}{1-X_{2}},\\ \\ \left\Vert {\mathbb{I}}_{n+s}(t)-{\mathbb{I}}_{n}(t)\right\Vert \leq \sum\nolimits_{j = n+1}^{n+s}X_{3}^{j} = \frac{X_{3}^{n+1}-X_{3}^{n+s+1}}{1-X_{3}},\\ \\ \left\Vert {\mathbb{Q}}_{n+s}(t)-{\mathbb{Q}}_{n}(t)\right\Vert \leq \sum\nolimits_{j = n+1}^{n+s}X_{4}^{j} = \frac{X_{4}^{n+1}-X_{4}^{n+s+1}}{1-X_{4}},\\ \\ \left\Vert {\mathbb{R}}_{n+s}(t)-{\mathbb{R}}_{n}(t)\right\Vert \leq \sum\nolimits_{m = n+1}^{n+s}X_{5}^{j} = \frac{X_{5}^{n+1}-X_{5}^{n+s+1}}{1-X_{5}}, \end{array} \end{equation}$ $

(4.13)

with $ X_{m} = \frac{{\mathcal{H}}(\delta)}{\delta} \kappa^{\delta}\Lambda_{m} < 1 $ by hypothesis. Consequently, the sequences $ \mathbb{S}_{n} $, $ \mathbb{E}_{n} $, $ \mathbb{I}_{n} $, $ \mathbb{Q}_{n} $, and $ \mathbb{R}_{n} $ can be considered as Cauchy sequences in the Banach space $ \mathcal{A}(Y) $. It has been shown that they converge uniformly ^[49].

5. Parameter estimation

Parameter estimation is a fundamental problem in statistical inference, machine learning, and many other fields. It involves estimating the values of unknown parameters in a model based on observed data. The goal of parameter estimation is to find the values of the parameters that best fit the data and allow us to make accurate predictions or draw meaningful conclusions about the system under study. There are many different methods for parameter estimation, ranging from simple techniques like least squares regression to more complex approaches like maximum likelihood estimation or Bayesian inference. The choice of method often depends on the nature of the data, the complexity of the model, and the specific goals of the analysis. However, regardless of the method chosen, parameter estimation is a crucial step in many scientific and engineering applications, and its success or failure can have significant consequences.

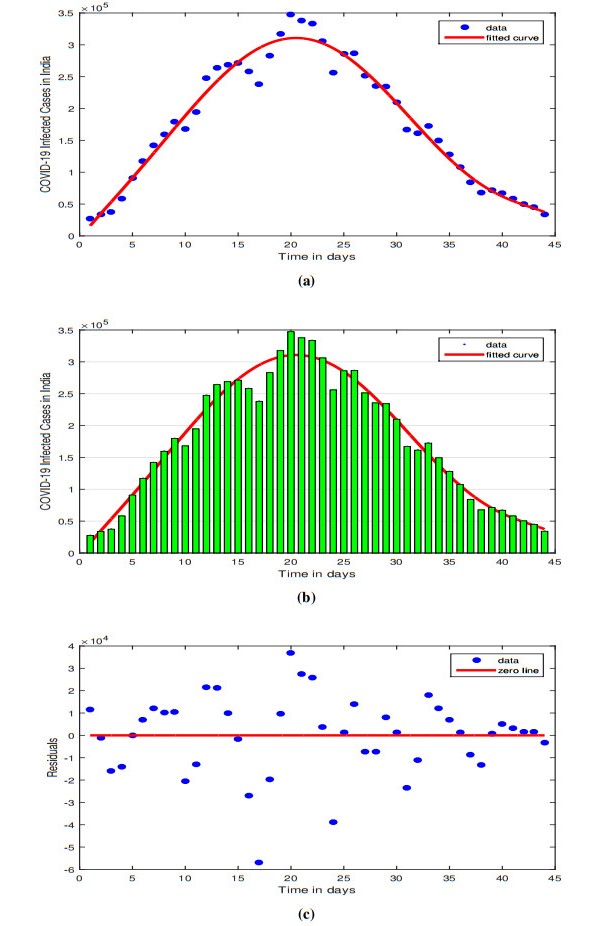
In this part, we used the least square curve fitting methods to analyze the instances of COVID-19 that were reported in India between 13 July 2021 and 25 August 2021 ^[50]. The system's (3.4) estimated parameters are based on India's overall data on conformed events and fatalities. The daily reports' error terms are reduced using the ordinary least square solution (OLS), and the goodness of fit test uses the related relative error.

$\begin{equation} \min\left( \frac{\sum\nolimits_{\iota = 1}^{n}\left( \mathbb{I}_{\iota}-\hat {\mathbb{I}}_{l}\right) ^{2}}{\sum\nolimits_{\iota = 1}^{n}\mathbb{I}_{\iota}^{2} }\right). \end{equation}$ $

(5.1)

6. Sensitivity analysis

Sensitivity analysis plays a crucial role in identifying the parameters that are most effective in controlling the spread of COVID-19. Although forward sensitivity analysis can be laborious for complex biological models, it remains an essential component of phenomena modeling. Ecologists and epidemiologists have shown considerable interest in conducting sensitivity analysis of $ R_0 $.

Definition 4. The normalized forward sensitivity index of $ R_{0} $ that depends on the differentiability of a parameter $ \varkappa $ is described as follows:

$\begin{equation*} \Upsilon_{\varkappa} = \frac{\varkappa}{R_{0}}\frac{\partial R_{0}}{\partial\varkappa}. \end{equation*}$ $

Sensitivity indices, which quantify the contribution of various factors to the output of a model, can be computed in a number of different ways. Direct differentiation, Latin hypercube sampling, and system linearization are three frequently used techniques. The direct differentiation method will be used in this study because it gives analytical expressions for the indices. Using this method, we can compare the variation between the $ R_0 $ parameter and other parameters and analyze the effects of various financial crime-related factors. We can learn vital information about the relative weights of various variables and how they impact the model's output by using sensitivity indices. This knowledge can enhance our comprehension of the dynamics of financial crime and assist in guiding policy decisions. The graphical results are displayed in Figures 2 and 3.

Figure 1. The simulation results for a suggested model of COVID-19 cases in India from January 1 to February 14, 2022 are shown in the figure. The best-fitted curve and its residuals, which represent the variations between the simulated results and the actual daily cumulative cases reported during that time, are displayed on the graph. The curve may serve as a decision-making tool for public health measures and interventions by assisting researchers and decision-makers in better understanding the patterns and trends of the pandemic in India.

DownLoad: Full-Size Img PowerPoint

Figure 2. This plot provides a thorough evaluation of the relative significance of each input parameter by demonstrating the sensitivity of a model's output to changes in multiple input variables at once.

DownLoad: Full-Size Img PowerPoint

Figure 3. The plot represents the sensitivity of various parameters against $ R_0 $.

DownLoad: Full-Size Img PowerPoint

7. Numerical scheme

Consider $ \dot{\mathbb{S}}(t), \dot{{\mathbb{E}}}(t), \dot{{\mathbb{I}}}(t), \dot{{\mathbb{Q}}}(t) $ and $ \dot{{\mathbb{R}}}(t) $ are in the square integrable function space $ L_{2}[0, 1) $, and can be expressed as a Haar series as

$ \dot{\mathbb{S}}(t) = \sum\limits_{p = 1}^{N}\alpha_{p}\mathbb{\tilde{\psi}}_{p} (t),\dot{{\mathbb{E}}}(t) = \sum\limits_{p = 1}^{N}\theta_{p}\mathbb{\tilde{\psi}} _{p}(t),\dot{{\mathbb{I}}}(t) = \sum\limits_{p = 1}^{N}\lambda_{p}\mathbb{\tilde{\psi} }_{p}(t),\dot{{\mathbb{I}}}(t) = \sum\limits_{p = 1}^{N}\vartheta_{p} \mathbb{\tilde{\psi}}_{p}(t)\text{ and }{\mathbb{R}}(\dot{t}) = \sum\limits_{p = 1} ^{N}\sigma_{p}\mathbb{\tilde{\psi}}_{p}(t) $

where $ \alpha_{p} $, $ \theta_{p} $, $ \lambda_{p} $, $ \vartheta_{p} $ and $ \sigma_{p} $ are coefficients of the Haar series and $ \mathbb{\tilde{\psi}}_{p}(t) $ is the discretise Haar function ^[51] with the exposed compartment $ \mathbb{E}_{0} $ includes people who have been infected but are not yet contagious, and the susceptible compartment $ \mathbb{S}_{0} $ represents people who are initially susceptible to the disease at the start of the epidemic. The infectious individuals are housed in the infected compartment $ \mathbb{I}_{0} $, whereas the isolated or hospitalized individuals are housed in the quarantined compartment $ \mathbb{Q}_{0} $. Those who have recovered from the illness and are no longer contagious are included in the recovered compartment $ \mathbb{R}_{0} $. We integrate the equations that describe the movement of people between these compartments in order to model the epidemic's progression over time. The result of this integration is a set of equations that show how the population of each compartment varies over time.

$\begin{equation} \begin{split} & \mathbb{S}(t) = \mathbb{S}_{0}+\sum\limits_{p = 1}^{N}\alpha_{p}\mathcal{G}_{p,1}(t),{\mathbb{E}}(t) = {\mathbb{E}}_{0}+\sum\limits_{p = 1}^{N}\theta_{p} \mathcal{G}_{p,1}(t),{\mathbb{I}}(t) = {\mathbb{I}}_{0}+\sum\limits_{p = 1}^{N}\lambda _{p}\mathcal{G}_{p,1}(t),\\ & {\mathbb{Q}}(t) = {\mathbb{Q}}_{0}+\sum\limits_{p = 1}^{N}\vartheta_{p} \mathcal{G}_{p,1}(t),\quad\text{ and }\quad{\mathbb{R}}(t) = {\mathbb{R}}_{0} +\sum\limits_{p = 1}^{N}\sigma_{p}\mathcal{G}_{p,1}(t) \end{split} \end{equation}$ $

(7.1)

where $ \mathcal{G}_{p, 1}(t) $ is the operational matrix of integration of $ p^{th} $ order ^[51,52].

By using Caputo derivative, we have

$\begin{equation} \left\{ \begin{split} & \frac{1}{\Gamma(n-\delta)}\int_{0}^{t}\mathbb{S}^{(n)} (\vartheta)(t-\vartheta)^{n-\delta-1}d\mathbb{\vartheta } = B-\theta\mathbb{S}{\mathbb{I}}(1+\tau{\mathbb{I}})-(\varepsilon_{1} +\rho+\eta)\mathbb{S}(t),\\ & \frac{1}{\Gamma(n-\delta)}\int_{0}^{t}{\mathbb{E}}^{(n)} (\vartheta)(t-\vartheta)^{n-\delta-1}d\mathbb{\vartheta } = \theta\mathbb{S}{\mathbb{I}}(1+\tau{\mathbb{I}})-(\varepsilon_{2} +\rho+\mathbb{\varphi}){\mathbb{E}}(t),\\ & \frac{1}{\Gamma(n-\delta)}\int_{0}^{t}{\mathbb{I}}^{(n)} (\vartheta)(t-\vartheta)^{n-\delta-1}d\mathbb{\vartheta } = \varphi{\mathbb{E}}(t)-(\lambda+\epsilon+\rho+\varepsilon_{3}){\mathbb{I} }(t),\\ & \frac{1}{\Gamma(n-\delta)}\int_{0}^{t}{\mathbb{Q}}^{(n)} (\vartheta)(t-\vartheta)^{n-\delta-1}d\mathbb{\vartheta } = \varepsilon_{1}\mathbb{S}(t)+\varepsilon_{2}{\mathbb{E}}(t)+\varepsilon _{3}{\mathbb{I}}(t)+-(\rho+\sigma){\mathbb{Q}}(t),\\ & \frac{1}{\Gamma(n-\delta)}\int_{0}^{t}{\mathbb{R}}^{(n)} (\vartheta)(t-\vartheta)^{n-\delta-1}d\mathbb{\vartheta } = \eta\mathbb{S}(t)+\sigma{\mathbb{Q}}(t)+\lambda{\mathbb{I}}(t)-\rho {\mathbb{R}}(t). \end{split} \right. \end{equation}$ $

(7.2)

As we have assumed that $ 0 < \delta < 1 $, therefore $ n = 1 $, and we have

$\begin{equation} \left\{ \begin{split} & \frac{1}{\Gamma(1-\delta)}\int_{0}^{t}\dot{\mathbb{S} }(\vartheta)(t-\vartheta)^{-\delta}d\mathbb{\vartheta } = B-\theta\mathbb{S}{\mathbb{I}}(1+\tau{\mathbb{I}})-(\varepsilon_{1} +\rho+\eta)\mathbb{S}(t),\\ & \frac{1}{\Gamma(1-\delta)}\int_{0}^{t}\dot{{\mathbb{E}} }(\vartheta)(t-\vartheta)^{-\delta}d\mathbb{\vartheta } = \theta\mathbb{S}{\mathbb{I}}(1+\tau{\mathbb{I}})-(\varepsilon_{2} +\rho+\mathbb{\varphi}){\mathbb{E}}(t),\\ & \frac{1}{\Gamma(1-\delta)}\int_{0}^{t}\dot{{\mathbb{I}} }(\vartheta)(t-\vartheta)^{-\delta}d\mathbb{\vartheta } = \varphi{\mathbb{E}}(t)-(\lambda+\epsilon+\rho+\varepsilon_{3}){\mathbb{I} }(t),\\ & \frac{1}{\Gamma(1-\delta)}\int_{0}^{t}\dot{{\mathbb{Q}} }(\vartheta)(t-\vartheta)^{-\delta}d\mathbb{\vartheta } = \varepsilon_{1}{\mathbb{S}}(t)+\varepsilon_{2}{\mathbb{E}}(t)+\varepsilon _{3}\mathbb{I}(t)-(\rho+\sigma){\mathbb{Q}}(t),\\ & \frac{1}{\Gamma(1-\delta)}\int_{0}^{t}\dot{{\mathbb{R}} }(\vartheta)(t-\vartheta)^{-\delta}d\vartheta = \eta\mathbb{S}(t)+\sigma{\mathbb{Q}}(t)+\lambda{\mathbb{I}}(t)-\rho {\mathbb{R}}(t). \end{split} \right. \end{equation}$ $

(7.3)

Haar approximations are used, and we have

$\begin{equation} \begin{split} \frac{1}{\Gamma(1-\delta)}\int_{0}^{t} & \sum\limits_{p = 1}^{N}\alpha _{p}\mathbb{\tilde{\psi}}_{p}(\vartheta)(t-\vartheta )^{-\delta}d\vartheta = B-\theta\left( {\mathbb{I}}_{0} +\sum\limits_{p = 1}^{N}\lambda_{p}\mathcal{G}_{p,1}(t)\right) \left( \mathbb{S} _{0}+\sum\limits_{p = 1}^{N}\alpha_{p}\mathcal{G}_{p,1}(t)\right) \\ & \left( 1+\tau\left( {\mathbb{I}}_{0}+\sum\limits_{p = 1}^{N}\lambda_{p} \mathcal{G}_{p,1}(t)\right) \right) -(\varepsilon_{1}+\rho+\eta)\left( \mathbb{S}_{0}+\sum\limits_{p = 1}^{N}\alpha_{p}\mathcal{G}_{p,1}(t)\right) \end{split} \end{equation}$ $

(7.4)

$\begin{equation} \begin{split} \frac{1}{\Gamma(1-\delta)}\int_{0}^{t} & \sum\limits_{p = 1}^{N}\theta _{p}\mathbb{\tilde{\psi}}_{p}(\vartheta)(t-\vartheta )^{-\delta}d\vartheta = \theta\left( {\mathbb{I}}_{0}+\sum _{p = 1}^{N}\lambda_{p}\mathcal{G}_{p,1}(t)\right) \left( \mathbb{S}_{0} +\sum\limits_{p = 1}^{N}\alpha_{p}\mathcal{G}_{p,1}(t)\right) \\ & \left( 1+\tau\left( {\mathbb{I}}_{0}+\sum\limits_{p = 1}^{N}\lambda_{p} \mathcal{G}_{p,1}(t)\right) \right) -(\varepsilon_{2}+\rho+\varphi)\left( {\mathbb{E}}_{0}+\sum\limits_{p = 1}^{N}\theta_{p}\mathcal{G}_{p,1}(t)\right) \end{split} \end{equation}$ $

(7.5)

$\begin{equation} \begin{split} \frac{1}{\Gamma(1-\delta)}\int_{0}^{t} & \sum\limits_{p = 1}^{N}\lambda _{p}\mathbb{\tilde{\psi}}_{p}(\vartheta)(t-\vartheta )^{-\delta}d\vartheta = \\ & \varphi\left( {\mathbb{E}}_{0}+\sum\limits_{p = 1}^{N}\theta_{p}\vartheta _{p,1}(t)\right) -(\lambda+\epsilon+\rho+d_{1})\left( {\mathbb{I}}_{0} +\sum\limits_{p = 1}^{N}\lambda_{p}\mathcal{G}_{p,1}(t)\right) \end{split} \end{equation}$ $

(7.6)

$\begin{equation} \begin{split} \frac{1}{\Gamma(1-\delta)}\int_{0}^{t} & \sum\limits_{p = 1}^{N} \vartheta_{p}\mathbb{\tilde{\psi}}_{p}(\vartheta)(t-\mathbb{\vartheta })^{-\delta}d\vartheta = \varepsilon_{3}\left( {\mathbb{I}} _{0}+\sum\limits_{p = 1}^{N}\lambda_{p}\mathcal{G}_{p,1}(t)\right) +\varepsilon _{2}\left( {\mathbb{E}}_{0}+\sum\limits_{p = 1}^{N}\theta_{p}\mathcal{G}_{p,1}(t)\right) \\ & +\varepsilon_{1}\left( \mathbb{S}_{0}+\sum\limits_{p = 1}^{N}\alpha_{p} \mathcal{G}_{p,1}(t)\right) -(\rho+\sigma)\left( {\mathbb{Q}}_{0}+\sum _{p = 1}^{N}\vartheta_{p}\mathcal{G}_{p,1}(t)\right) \end{split} \end{equation}$ $

(7.7)

$\begin{equation} \begin{split} \frac{1}{\Gamma(1-\delta)}\int_{0}^{t} & \sum\limits_{p = 1}^{N}\alpha _{p}\mathbb{\tilde{\psi}}_{p}(\vartheta)(t-\vartheta )^{-\delta}d\vartheta = \eta\left( \mathbb{S}_{0}+\sum\limits_{p = 1} ^{N}\alpha_{p}\mathcal{G}_{p,1}(t)\right) \\ & +\sigma\left( {\mathbb{Q}}_{0}+\sum\limits_{p = 1}^{N}\sigma_{p}\vartheta _{p,1}(t)\right) +\lambda\left( {\mathbb{I}}_{0}+\sum\limits_{p = 1}^{N}\lambda _{p}\mathcal{G}_{p,1}(t)\right) +\rho\left( {\mathbb{R}}_{0}+\sum\limits_{p = 1} ^{N}\zeta_{p}\mathcal{G}_{p,1}(t)\right) \end{split} \end{equation}$ $

(7.8)

Upon simplification, we have

$\begin{equation} \left\{ \begin{array} [c]{l} \frac{1}{\Gamma(1-\delta)}\sum\nolimits_{p = 1}^{N}\alpha_{p}\mathbb{\tilde {\psi}}_{p}(\vartheta)(t-\vartheta)^{-\delta }d\vartheta-B+\theta\left( 1+\tau{\mathbb{I}}_{0}\right) \times\\ \\ \left( {\mathbb{I}}_{0}\mathbb{S}_{0}+{\mathbb{I}}_{0}\sum\nolimits_{p = 1}^{N} \alpha_{p}\mathcal{G}_{p,1}(t)+\mathbb{S}_{0}\sum\nolimits_{p = 1}^{N}\theta_{p} \mathcal{G}_{p,1}(t)+\sum\nolimits_{p = 1}^{N}\alpha_{p}\mathcal{G}_{p,1}(t)\sum\nolimits_{p = 1} ^{N}\theta_{p}\mathcal{G}_{p,1}(t)\right) \\ \\ +\theta\left[ {\mathbb{I}}_{0}\mathbb{S}_{0}\tau\sum\nolimits_{p = 1}^{N}\theta _{p}\mathcal{G}_{p,1}(t)+{\mathbb{I}}_{0}\tau\sum\nolimits_{p = 1}^{N}\alpha_{p} \mathcal{G}_{p,1}(t)\sum\nolimits_{p = 1}^{N}\theta_{p}\mathcal{G}_{p,1}(t)+\mathbb{S} _{0}\tau\left( \sum\nolimits_{p = 1}^{N}\theta_{p}\mathcal{G}_{p,1}(t)\right) ^{2}\right. \\ \\ \left. +\tau\sum\nolimits_{p = 1}^{N}\alpha_{p}\mathcal{G}_{p,1}(t)\left( \sum\nolimits_{p = 1} ^{N}\theta_{p}\mathcal{G}_{p,1}(t)\right) ^{2}\right] +(\varepsilon_{1} +\rho+\eta)\mathbb{S}_{0}+(\varepsilon_{1}+\rho+\eta)\sum\nolimits_{p = 1}^{N}\alpha _{p}\mathcal{G}_{p,1}(t) \end{array} \right\} = 0, \end{equation}$ $

(7.9)

$\begin{equation} \left\{ \begin{array} [c]{l} \frac{1}{\Gamma(1-\delta)}\sum\nolimits_{p = 1}^{N}\theta_{p}\mathbb{\tilde {\psi}}_{p}(\vartheta)(t-\vartheta)^{-\delta }d\vartheta+\theta\left( 1+\tau{\mathbb{I}}_{0}\right) \times\\ \\ \left( {\mathbb{I}}_{0}\mathbb{S}_{0}+{\mathbb{I}}_{0}\sum\nolimits_{p = 1}^{N} \alpha_{p}\mathcal{G}_{p,1}(t)+\mathbb{S}_{0}\sum\nolimits_{p = 1}^{N}\theta_{p} \mathcal{G}_{p,1}(t)+\sum\nolimits_{p = 1}^{N}\alpha_{p}\mathcal{G}_{p,1}(t)\sum\nolimits_{p = 1} ^{N}\theta_{p}\mathcal{G}_{p,1}(t)\right) \\ \\ +\theta\left[ {\mathbb{I}}_{0}\mathbb{S}_{0}\tau\sum\nolimits_{p = 1}^{N}\theta _{p}\mathcal{G}_{p,1}(t)+{\mathbb{I}}_{0}\tau\sum\nolimits_{p = 1}^{N}\alpha_{p} \mathcal{G}_{p,1}(t)\sum\nolimits_{p = 1}^{N}\theta_{p}\mathcal{G}_{p,1}(t)+\mathbb{S} _{0}\tau\left( \sum\nolimits_{p = 1}^{N}\theta_{p}\mathcal{G}_{p,1}(t)\right) ^{2}\right. \\ \\ \left. +\tau\sum\nolimits_{p = 1}^{N}\alpha_{p}\mathcal{G}_{p,1}(t)\left( \sum\nolimits_{p = 1} ^{N}\theta_{p}\mathcal{G}_{p,1}(t)\right) ^{2}\right] +(\varepsilon_{2} +\rho+\varphi){\mathbb{E}}_{0}+(\varepsilon_{2}+\rho+\varphi)\sum\nolimits_{p = 1} ^{N}\theta_{p}\mathcal{G}_{p,1}(t) \end{array} \right\} = 0, \end{equation}$ $

(7.10)

$\begin{equation} \begin{split} \frac{1}{\Gamma(1-\delta)}\int_{0}^{t} & \sum\limits_{p = 1}^{N}\lambda _{p}\mathbb{\tilde{\psi}}_{p}(\vartheta)(t-\vartheta )^{-\delta}d\vartheta-\varphi{\mathbb{E}}_{0}-\varphi\left( \sum\limits_{p = 1}^{N}\theta_{p}\mathcal{G}_{p,1}(t)\right) \\ & +(\lambda+\epsilon+\rho+\varepsilon_{3}){\mathbb{I}}_{0}+(\lambda +\epsilon+\rho+\varepsilon_{3})\left( \sum\limits_{p = 1}^{N}\lambda_{p} \mathcal{G}_{p,1}(t)\right) = 0, \end{split} \end{equation}$ $

(7.11)

$\begin{equation} \begin{split} \frac{1}{\Gamma(1-\delta)}\int_{0}^{t} & \sum\limits_{p = 1}^{N} \vartheta_{p}\mathbb{\tilde{\psi}}_{p}(\vartheta)(t-\mathbb{\vartheta })^{-\delta}d\vartheta-\varepsilon_{3}{\mathbb{I}} _{0}-\varepsilon_{3}\left( \sum\limits_{p = 1}^{N}\lambda_{p}\mathcal{G}_{p,1} (t)\right) +\varepsilon_{2}{\mathbb{E}}_{0}+\varepsilon_{2}\left( \sum _{p = 1}^{N}\theta_{p}\mathcal{G}_{p,1}(t)\right) \\ & +\varepsilon_{1}\mathbb{S}_{0}+\varepsilon_{1}\left( \sum\limits_{p = 1}^{N} \alpha_{p}\mathcal{G}_{p,1}(t)\right) +(\rho+\sigma){\mathbb{Q}}_{0} +(\rho+\sigma)\left( \sum\limits_{p = 1}^{N}\vartheta_{p}\vartheta _{p,1}(t)\right) = 0, \end{split} \end{equation}$ $

(7.12)

$\begin{equation} \begin{split} \frac{1}{\Gamma(1-\delta)}\int_{0}^{t} & \sum\limits_{p = 1}^{N}\zeta _{p}\mathbb{\tilde{\psi}}_{p}(\vartheta)(t-\vartheta )^{-\delta}d\vartheta-\eta\mathbb{S}_{0}-\mathbb{S}_{0}\left( \sum\limits_{p = 1}^{N}\alpha_{p}\mathcal{G}_{p,1}(t)\right) -\sigma{\mathbb{Q}}_{0}\\ & -\sigma\left( \sum\limits_{p = 1}^{N}\sigma_{p}\mathcal{G}_{p,1}(t)\right) -\lambda{\mathbb{I}}_{0}-\lambda\left( \sum\limits_{p = 1}^{N}\lambda_{p} \mathcal{G}_{p,1}(t)\right) +\rho{\mathbb{R}}_{0}+\rho\left( \sum\limits_{p = 1} ^{N}\zeta_{p}\mathcal{G}_{p,1}(t)\right) = 0. \end{split} \end{equation}$ $

(7.13)

Applying the Haar integration method ^[53], we can estimate the integral in the aforementioned system as an approximation, given by:

$\begin{equation} \begin{split} \int_{\varkappa}^{\kappa}f(t)dt \approx\frac{\kappa-\varkappa}{N} \sum\limits_{p = 1}^{N}f\left( t_{p}\right) = \sum\limits_{p = 1}^{N}f\left( \varkappa+\frac{(\kappa-\varkappa)(p-0.5)}{N}\right) \end{split} \end{equation}$ $

(7.14)

$\begin{equation} \left\{ \begin{array} [c]{l} \frac{t}{N\Gamma(1-\delta)}\sum\nolimits_{s = 1}^{N}\sum\nolimits_{p = 1}^{N}\alpha _{p}\mathbb{\tilde{\psi}}_{p}\left( \vartheta_{s}\right) \left( t-\vartheta_{s}\right) ^{-\delta}-B+\theta\left( 1+\tau{\mathbb{I}}_{0}\right) \times\\ \\ \left( {\mathbb{I}}_{0}\mathbb{S}_{0}+{\mathbb{I}}_{0}\sum\nolimits_{p = 1}^{N} \alpha_{p}\mathcal{G}_{p,1}(t)+\mathbb{S}_{0}\sum\nolimits_{p = 1}^{N}\theta_{p} \mathcal{G}_{p,1}(t)+\sum\nolimits_{p = 1}^{N}\alpha_{p}\mathcal{G}_{p,1}(t)\sum\nolimits_{p = 1} ^{N}\theta_{p}\mathcal{G}_{p,1}(t)\right) \\ \\ +\theta\left[ {\mathbb{I}}_{0}\mathbb{S}_{0}\tau\sum\nolimits_{p = 1}^{N}\theta _{p}\mathcal{G}_{p,1}(t)+{\mathbb{I}}_{0}\tau\sum\nolimits_{p = 1}^{N}\alpha_{p} \mathcal{G}_{p,1}(t)\sum\nolimits_{p = 1}^{N}\theta_{p}\mathcal{G}_{p,1}(t)+\mathbb{S} _{0}\tau\left( \sum\nolimits_{p = 1}^{N}\theta_{p}\mathcal{G}_{p,1}(t)\right) ^{2}\right. \\ \\ \left. +\tau\sum\nolimits_{p = 1}^{N}\alpha_{p}\mathcal{G}_{p,1}(t)\left( \sum\nolimits_{p = 1} ^{N}\theta_{p}\mathcal{G}_{p,1}(t)\right) ^{2}\right] +(\varepsilon_{1} +\rho+\eta)\mathbb{S}_{0}+(\varepsilon_{1}+\rho+\eta)\sum\nolimits_{p = 1}^{N}\alpha _{p}\mathcal{G}_{p,1}(t) \end{array} \right\} = 0 \end{equation}$ $

(7.15)

$\begin{equation} \left\{ \begin{array} [c]{l} \frac{t}{N\Gamma(1-\delta)}\sum\nolimits_{s = 1}^{N}\sum\nolimits_{p = 1}^{N}\theta _{p}\mathbb{\tilde{\psi}}_{p}\left( \vartheta_{s}\right) \left( t-\vartheta_{s}\right) ^{-\delta}-\theta\left( 1+\tau {\mathbb{I}}_{0}\right) \times\\ \\ \left( {\mathbb{I}}_{0}\mathbb{S}_{0}+{\mathbb{I}}_{0}\sum\nolimits_{p = 1}^{N} \alpha_{p}\mathcal{G}_{p,1}(t)+\mathbb{S}_{0}\sum\nolimits_{p = 1}^{N}\theta_{p} \mathcal{G}_{p,1}(t)+\sum\nolimits_{p = 1}^{N}\alpha_{p}\mathcal{G}_{p,1}(t)\sum\nolimits_{p = 1} ^{N}\theta_{p}\mathcal{G}_{p,1}(t)\right) \\ \\ +\theta\left[ {\mathbb{I}}_{0}\mathbb{S}_{0}\tau\sum\nolimits_{p = 1}^{N}\theta _{p}\mathcal{G}_{p,1}(t)+{\mathbb{I}}_{0}\tau\sum\nolimits_{p = 1}^{N}\alpha_{p} \mathcal{G}_{p,1}(t)\sum\nolimits_{p = 1}^{N}\theta_{p}\mathcal{G}_{p,1}(t)+\mathbb{S} _{0}\tau\left( \sum\nolimits_{p = 1}^{N}\theta_{p}\mathcal{G}_{p,1}(t)\right) ^{2}\right. \\ \\ \left. +\tau\sum\nolimits_{p = 1}^{N}\alpha_{p}\mathcal{G}_{p,1}(t)\left( \sum\nolimits_{p = 1} ^{N}\theta_{p}\mathcal{G}_{p,1}(t)\right) ^{2}\right] +(\varepsilon_{2} +\rho+\varphi){\mathbb{E}}_{0}+(\varepsilon_{2}+\rho+\varphi)\sum\nolimits_{p = 1} ^{N}\theta_{p}\mathcal{G}_{p,1}(t) \end{array} \right\} = 0, \end{equation}$ $

(7.16)

$\begin{equation} \begin{split} \frac{t}{N\Gamma(1-\delta)}\sum\limits_{s = 1}^{N}\sum\limits_{p = 1}^{N} & \lambda_{p}\mathbb{\tilde{\psi}}_{p}\left( \vartheta_{s}\right) \left( t-\vartheta_{s}\right) ^{-\delta}-\varphi{\mathbb{E} }_{0}-\varphi\left( \sum\limits_{p = 1}^{N}\theta_{p}\mathcal{G}_{p,1}(t)\right) \\ & +(\lambda+\epsilon+\rho+\varepsilon_{3}){\mathbb{I}}_{0}+(\lambda +\epsilon+\rho+\varepsilon_{3})\left( \sum\limits_{p = 1}^{N}\lambda_{p} \mathcal{G}_{p,1}(t)\right) = 0, \end{split} \end{equation}$ $

(7.17)

$\begin{equation} \begin{split} \frac{t}{N\Gamma(1-\delta)}\sum\limits_{s = 1}^{N}\sum\limits_{p = 1}^{N} & \vartheta_{p}\mathbb{\tilde{\psi}}_{p}\left( \vartheta _{s}\right) \left( t-\vartheta_{s}\right) ^{-\delta }-\varepsilon_{3}{\mathbb{I}}_{0}-\varepsilon_{3}\left( \sum\limits_{p = 1}^{N} \lambda_{p}\mathcal{G}_{p,1}(t)\right) +\varepsilon_{2}{\mathbb{E}} _{0}+\varepsilon_{2}\left( \sum\limits_{p = 1}^{N}\theta_{p}\mathcal{G}_{p,1}(t)\right) \\ & +\varepsilon_{1}\mathbb{S}_{0}+\varepsilon_{1}\left( \sum\limits_{p = 1}^{N} \alpha_{p}\mathcal{G}_{p,1}(t)\right) +(\rho+\sigma){\mathbb{Q}}_{0} +(\rho+\sigma)\left( \sum\limits_{p = 1}^{N}\vartheta_{p}\vartheta _{p,1}(t)\right) = 0, \end{split} \end{equation}$ $

(7.18)

$\begin{equation} \begin{split} \frac{t}{N\Gamma(1-\delta)}\sum\limits_{s = 1}^{N}\sum\limits_{p = 1}^{N} & \zeta _{p}\mathbb{\tilde{\psi}}_{p}\left( \vartheta_{s}\right) \left( t-\vartheta_{s}\right) ^{-\delta}-\eta\mathbb{S} _{0}-\mathbb{S}_{0}\left( \sum\limits_{p = 1}^{N}\alpha_{p}\mathcal{G}_{p,1}(t)\right) -\sigma{\mathbb{Q}}_{0}\\ & -\sigma\left( \sum\limits_{p = 1}^{N}\sigma_{p}\mathcal{G}_{p,1}(t)\right) -\lambda{\mathbb{I}}_{0}-\lambda\left( \sum\limits_{p = 1}^{N}\lambda_{p} \mathcal{G}_{p,1}(t)\right) +\rho{\mathbb{R}}_{0}+\rho\left( \sum\limits_{p = 1} ^{N}\zeta_{p}\mathcal{G}_{p,1}(t)\right) = 0. \end{split} \end{equation}$ $

(7.19)

Let

$\begin{equation} \Phi_{1,j} = \left\{ \begin{array} [c]{l} \frac{t}{N\Gamma(1-\delta)}\sum\nolimits_{s = 1}^{N}\sum\nolimits_{p = 1}^{N}\alpha _{p}\mathbb{\tilde{\psi}}_{p}\left( \vartheta_{s}\right) \left( t-\vartheta_{s}\right) ^{-\delta}-B+\theta\left( 1+\tau{\mathbb{I}}_{0}\right) \times\\ \\ \left( {\mathbb{I}}_{0}\mathbb{S}_{0}+{\mathbb{I}}_{0}\sum\nolimits_{p = 1}^{N} \alpha_{p}\mathcal{G}_{p,1}(t)+\mathbb{S}_{0}\sum\nolimits_{p = 1}^{N}\theta_{p} \mathcal{G}_{p,1}(t)+\sum\nolimits_{p = 1}^{N}\alpha_{p}\mathcal{G}_{p,1}(t)\sum\nolimits_{p = 1} ^{N}\theta_{p}\mathcal{G}_{p,1}(t)\right) \\ \\ +\theta\left[ {\mathbb{I}}_{0}\mathbb{S}_{0}\tau\sum\nolimits_{p = 1}^{N}\theta _{p}\mathcal{G}_{p,1}(t)+{\mathbb{I}}_{0}\tau\sum\nolimits_{p = 1}^{N}\alpha_{p} \mathcal{G}_{p,1}(t)\sum\nolimits_{p = 1}^{N}\theta_{p}\mathcal{G}_{p,1}(t)+\mathbb{S} _{0}\tau\left( \sum\nolimits_{p = 1}^{N}\theta_{p}\mathcal{G}_{p,1}(t)\right) ^{2}\right. \\ \\ \left. +\tau\sum\nolimits_{p = 1}^{N}\alpha_{p}\mathcal{G}_{p,1}(t)\left( \sum\nolimits_{p = 1} ^{N}\theta_{p}\mathcal{G}_{p,1}(t)\right) ^{2}\right] +(\varepsilon_{1} +\rho+\eta)\mathbb{S}_{0}+(\varepsilon_{1}+\rho+\eta)\sum\nolimits_{p = 1}^{N}\alpha _{p}\mathcal{G}_{p,1}(t). \end{array} \right. \end{equation}$ $

(7.20)

Let

$\begin{equation} \Phi_{2,j} = \left\{ \begin{array} [c]{l} \frac{t}{N\Gamma(1-\delta)}\sum\nolimits_{s = 1}^{N}\sum\nolimits_{p = 1}^{N}\theta _{p}\mathbb{\tilde{\psi}}_{p}\left( \vartheta_{s}\right) \left( t-\vartheta_{s}\right) ^{-\delta}-\theta\left( 1+\tau {\mathbb{I}}_{0}\right) \times\\ \\ \left( {\mathbb{I}}_{0}\mathbb{S}_{0}+{\mathbb{I}}_{0}\sum\nolimits_{p = 1}^{N} \alpha_{p}\mathcal{G}_{p,1}(t)+\mathbb{S}_{0}\sum\nolimits_{p = 1}^{N}\theta_{p} \mathcal{G}_{p,1}(t)+\sum\nolimits_{p = 1}^{N}\alpha_{p}\mathcal{G}_{p,1}(t)\sum\nolimits_{p = 1} ^{N}\theta_{p}\mathcal{G}_{p,1}(t)\right) \\ \\ +\theta\left[ {\mathbb{I}}_{0}\mathbb{S}_{0}\tau\sum\nolimits_{p = 1}^{N}\theta _{p}\mathcal{G}_{p,1}(t)+{\mathbb{I}}_{0}\tau\sum\nolimits_{p = 1}^{N}\alpha_{p} \mathcal{G}_{p,1}(t)\sum\nolimits_{p = 1}^{N}\theta_{p}\mathcal{G}_{p,1}(t)+\mathbb{S} _{0}\tau\left( \sum\nolimits_{p = 1}^{N}\theta_{p}\mathcal{G}_{p,1}(t)\right) ^{2}\right. \\ \\ \left. +\tau\sum\nolimits_{p = 1}^{N}\alpha_{p}\mathcal{G}_{p,1}(t)\left( \sum\nolimits_{p = 1} ^{N}\theta_{p}\mathcal{G}_{p,1}(t)\right) ^{2}\right] +(\varepsilon_{2} +\rho+\varphi){\mathbb{E}}_{0}+(\varepsilon_{2}+\rho+\varphi)\sum\nolimits_{p = 1} ^{N}\theta_{p}\mathcal{G}_{p,1}(t). \end{array} \right. \end{equation}$ $

(7.21)

Let

$\begin{equation} \begin{split} \Phi_{3,j} = \frac{t}{N\Gamma(1-\delta)}\sum\limits_{s = 1}^{N}\sum\limits_{p = 1}^{N} & \lambda_{p}\mathbb{\tilde{\psi}}_{p}\left( \vartheta_{s}\right) \left( t-\vartheta_{s}\right) ^{-\delta}-\varphi{\mathbb{E} }_{0}-\varphi\left( \sum\limits_{p = 1}^{N}\theta_{p}\mathcal{G}_{p,1}(t)\right) \\ & +(\lambda+\epsilon+\rho+\varepsilon_{3}){\mathbb{I}}_{0}+(\lambda +\epsilon+\rho+\varepsilon_{3})\left( \sum\limits_{p = 1}^{N}\lambda_{p} \mathcal{G}_{p,1}(t)\right) . \end{split} \end{equation}$ $

(7.22)

Let

$\begin{equation} \begin{split} \Phi_{4,j} = \frac{t}{N\Gamma(1-\delta)}\sum\limits_{s = 1}^{N}\sum\limits_{p = 1}^{N} & \vartheta_{p}\mathbb{\tilde{\psi}}_{p}\left( \vartheta _{s}\right) \left( t-\vartheta_{s}\right) ^{-\delta }-\varepsilon_{3}{\mathbb{I}}_{0}-\varepsilon_{3}\left( \sum\limits_{p = 1}^{N} \lambda_{p}\mathcal{G}_{p,1}(t)\right) +\varepsilon_{2}{\mathbb{E}} _{0}+\varepsilon_{2}\left( \sum\limits_{p = 1}^{N}\theta_{p}\mathcal{G}_{p,1}(t)\right) \\ & +\varepsilon_{1}\mathbb{S}_{0}+\varepsilon_{1}\left( \sum\limits_{p = 1}^{N} \alpha_{p}\mathcal{G}_{p,1}(t)\right) +(\rho+\sigma){\mathbb{Q}}_{0} +(\rho+\sigma)\left( \sum\limits_{p = 1}^{N}\vartheta_{p}\vartheta _{p,1}(t)\right) . \end{split} \end{equation}$ $

(7.23)

Let

$\begin{equation} \begin{split} \Phi_{5,j} = \frac{t}{N\Gamma(1-\delta)}\sum\limits_{s = 1}^{N}\sum\limits_{p = 1}^{N} & \zeta_{p}\mathbb{\tilde{\psi}}_{p}\left( \vartheta_{s}\right) \left( t-\vartheta_{s}\right) ^{-\delta}-\eta\mathbb{S} _{0}-\mathbb{S}_{0}\left( \sum\limits_{p = 1}^{N}\alpha_{p}\mathcal{G}_{p,1}(t)\right) -\sigma{\mathbb{Q}}_{0}\\ & -\sigma\left( \sum\limits_{p = 1}^{N}\sigma_{p}\mathcal{G}_{p,1}(t)\right) -\lambda{\mathbb{I}}_{0}-\lambda\left( \sum\limits_{p = 1}^{N}\lambda_{p} \mathcal{G}_{p,1}(t)\right) +\rho{\mathbb{R}}_{0}+\rho\left( \sum\limits_{p = 1} ^{N}\zeta_{p}\mathcal{G}_{p,1}(t)\right) . \end{split} \end{equation}$ $

(7.24)

The nonlinear algebraic equations in the system presented below are generated by strategically placing nodal points:

$\begin{equation} \Phi_{1,j} = \left\{ \begin{array} [c]{l} \frac{t_{p}}{N\Gamma(1-\delta)}\sum\nolimits_{s = 1}^{N}\sum\nolimits_{p = 1}^{N}\alpha _{p}\mathbb{\tilde{\psi}}_{p}\left( \vartheta_{s}\right) \left( t_{p}-\vartheta_{s}\right) ^{-\delta}-B+\theta\left( 1+\tau{\mathbb{I}}_{0}\right) \times\\ \\ \left( {\mathbb{I}}_{0}\mathbb{S}_{0}+{\mathbb{I}}_{0}\sum\nolimits_{p = 1}^{N} \alpha_{p}\mathcal{G}_{p,1}(t_{p})+\mathbb{S}_{0}\sum\nolimits_{p = 1}^{N}\theta _{p}\mathcal{G}_{p,1}(t_{p})+\sum\nolimits_{p = 1}^{N}\alpha_{p}\mathcal{G}_{p,1}(t_{p} )\sum\nolimits_{p = 1}^{N}\theta_{p}\mathcal{G}_{p,1}(t_{p})\right) \\ \\ +\theta\left[ {\mathbb{I}}_{0}\mathbb{S}_{0}\tau\sum\nolimits_{p = 1}^{N}\theta _{p}\mathcal{G}_{p,1}(t_{p})+{\mathbb{I}}_{0}\tau\sum\nolimits_{p = 1}^{N}\alpha _{p}\mathcal{G}_{p,1}(t_{p})\sum\nolimits_{p = 1}^{N}\theta_{p}\mathcal{G}_{p,1} (t_{p})\right. \\ \\ \left. +\mathbb{S}_{0}\tau\left( \sum\nolimits_{p = 1}^{N}\theta_{p}\vartheta _{p,1}(t_{p})\right) ^{2}+\tau\sum\nolimits_{p = 1}^{N}\alpha_{p}\mathcal{G}_{p,1} (t_{p})\left( \sum\nolimits_{p = 1}^{N}\theta_{p}\mathcal{G}_{p,1}(t_{p})\right) ^{2}\right] \\ \\ +(\varepsilon_{1}+\rho+\eta)\mathbb{S}_{0}+(\varepsilon_{1}+\rho+\eta )\sum\nolimits_{p = 1}^{N}\alpha_{p}\mathcal{G}_{p,1}(t_{p}) \end{array} ,\right. \end{equation}$ $

(7.25)

$\begin{equation} \Phi_{2,j} = \left\{ \begin{array} [c]{l} \frac{t_{p}}{N\Gamma(1-\delta)}\sum\nolimits_{s = 1}^{N}\sum\nolimits_{p = 1}^{N}\theta _{p}\mathbb{\tilde{\psi}}_{p}\left( \vartheta_{s}\right) \left( t_{p}-\vartheta_{s}\right) ^{-\delta}-\theta\left( 1+\tau{\mathbb{I}}_{0}\right) \times\\ \\ \left( {\mathbb{I}}_{0}\mathbb{S}_{0}+{\mathbb{I}}_{0}\sum\nolimits_{p = 1}^{N} \alpha_{p}\mathcal{G}_{p,1}(t_{p})+\mathbb{S}_{0}\sum\nolimits_{p = 1}^{N}\theta _{p}\mathcal{G}_{p,1}(t_{p})+\sum\nolimits_{p = 1}^{N}\alpha_{p}\mathcal{G}_{p,1}(t_{p} )\sum\nolimits_{p = 1}^{N}\theta_{p}\mathcal{G}_{p,1}(t_{p})\right) \\ \\ +\theta\left[ {\mathbb{I}}_{0}\mathbb{S}_{0}\tau\sum\nolimits_{p = 1}^{N}\theta _{p}\mathcal{G}_{p,1}(t_{p})+{\mathbb{I}}_{0}\tau\sum\nolimits_{p = 1}^{N}\alpha _{p}\mathcal{G}_{p,1}(t_{p})\sum\nolimits_{p = 1}^{N}\theta_{p}\mathcal{G}_{p,1} (t_{p})\right. \\ \\ \left. +\mathbb{S}_{0}\tau\left( \sum\nolimits_{p = 1}^{N}\theta_{p}\vartheta _{p,1}(t_{p})\right) ^{2}+\tau\sum\nolimits_{p = 1}^{N}\alpha_{p}\mathcal{G}_{p,1} (t_{p})\left( \sum\nolimits_{p = 1}^{N}\theta_{p}\mathcal{G}_{p,1}(t_{p})\right) ^{2}\right] \\ \\ +(\varepsilon_{2}+\rho+\varphi){\mathbb{E}}_{0}+(\varepsilon_{2}+\rho +\varphi)\sum\nolimits_{p = 1}^{N}\theta_{p}\mathcal{G}_{p,1}(t_{p}) \end{array} ,\right. \end{equation}$ $

(7.26)

$\begin{equation} \begin{split} \Phi_{3,j} = \frac{t_{p}}{N\Gamma(1-\delta)}\sum\limits_{s = 1}^{N}\sum _{p = 1}^{N} & \lambda_{p}\mathbb{\tilde{\psi}}_{p}\left( \vartheta _{s}\right) \left( t_{p}-\vartheta_{s}\right) ^{-\delta }-\varphi{\mathbb{E}}_{0}-\varphi\left( \sum\limits_{p = 1}^{N}\theta_{p} \mathcal{G}_{p,1}(t_{p})\right) \\ & +(\lambda+\epsilon+\rho+\varepsilon_{3}){\mathbb{I}}_{0}+(\lambda +\epsilon+\rho+\varepsilon_{3})\left( \sum\limits_{p = 1}^{N}\lambda_{p} \mathcal{G}_{p,1}(t_{p})\right) . \end{split} \end{equation}$ $

(7.27)

$\begin{equation} \begin{split} \Phi_{4,j} = \frac{t_{p}}{N\Gamma(1-\delta)}\sum\limits_{s = 1}^{N}\sum _{p = 1}^{N} & \vartheta_{p}\mathbb{\tilde{\psi}}_{p}\left( \vartheta_{s}\right) \left( t_{p}-\vartheta_{s}\right) ^{-\delta}-\varepsilon_{3}{\mathbb{I}}_{0}-\varepsilon_{3}\left( \sum\limits_{p = 1}^{N}\lambda_{p}\mathcal{G}_{p,1}(t_{p})\right) \\ & +\varepsilon_{2}{\mathbb{E}}_{0}+\varepsilon_{2}\left( \sum\limits_{p = 1} ^{N}\theta_{p}\mathcal{G}_{p,1}(t_{p})\right) +\varepsilon_{1}\mathbb{S} _{0}+\varepsilon_{1}\left( \sum\limits_{p = 1}^{N}\alpha_{p}\mathcal{G}_{p,1} (t_{p})\right) \\ & +(\rho+\sigma){\mathbb{Q}}_{0}+(\rho+\sigma)\left( \sum\limits_{p = 1} ^{N}\vartheta_{p}\mathcal{G}_{p,1}(t_{p})\right) . \end{split} \end{equation}$ $

(7.28)

Let

$\begin{equation} \begin{split} \Phi_{5,j} = \frac{t_{p}}{N\Gamma(1-\delta)}\sum\limits_{s = 1}^{N}\sum _{p = 1}^{N} & \zeta_{p}\mathbb{\tilde{\psi}}_{p}\left( \vartheta _{s}\right) \left( t_{p}-\vartheta_{s}\right) ^{-\delta }-\eta\mathbb{S}_{0}-\mathbb{S}_{0}\left( \sum\limits_{p = 1}^{N}\alpha_{p} \mathcal{G}_{p,1}(t_{p})\right) -\sigma{\mathbb{Q}}_{0}\\ & -\sigma\left( \sum\limits_{p = 1}^{N}\sigma_{p}\mathcal{G}_{p,1}(t_{p})\right) -\lambda{\mathbb{I}}_{0}-\lambda\left( \sum\limits_{p = 1}^{N}\lambda_{p} \mathcal{G}_{p,1}(t_{p})\right) +\rho{\mathbb{R}}_{0}\\ & +\rho\left( \sum\limits_{p = 1}^{N}\zeta_{p}\mathcal{G}_{p,1}(t_{p})\right) . \end{split} \end{equation}$ $

(7.29)

Using Broyden's approach, this system can be solved. The Jacobian is given by:

$\begin{equation} \mathbf{J} = \left[ J_{jp}\right] _{5N\times5N} \end{equation}$ $

(7.30)

The Jacobian can be obtained by evaluating the following partial derivatives.

$\begin{equation} \begin{split} &\frac{\partial\Phi_{1,j}}{\partial\alpha_{p}}, \quad \frac{\partial\Phi_{1,j}}{\partial \alpha_{p}}, \quad \frac{\partial\Phi_{1,j}}{\partial \alpha_{p}}, \quad \frac{\partial\Phi_{1,j}}{\partial \alpha_{p}}, \quad \frac{\partial\Phi_{1,j}}{\partial \alpha_{p}},\\ &\frac{\partial\Phi_{2,j}}{\partial\theta_{p}},\quad \frac{\partial\Phi_{2,j}}{\partial\theta_{p}},\quad \frac{\partial\Phi_{2,j}}{\partial\theta_{p}},\quad \frac{\partial\Phi_{2,j}}{\partial \theta_{p}},\quad \frac{\partial\Phi_{2,j}}{\partial \theta_{p}},\\ &\frac{\partial\Phi_{3,j}}{\partial \lambda_{p}},\quad \frac{\partial\Phi_{3,j}}{\partial \lambda_{p}},\quad \frac{\partial\Phi_{3,j}}{\partial \lambda_{p}},\quad \frac{\partial\Phi_{3,j}}{\partial \lambda_{p}},\quad \frac{\partial\Phi_{3,j}}{\partial \lambda_{p}},\\ &\frac{\partial\Phi_{4,j}}{\partial\varrho_{p}},\quad \frac{\partial\Phi_{4,j}}{\partial\varrho_{p}},\quad \frac{\partial\Phi_{4,j}}{\partial\varrho_{p}},\quad \frac{\partial\Phi_{4,j}}{\partial\varrho_{p}},\quad \frac{\partial\Phi_{4,j}}{\partial\varrho_{p}},\\ &\frac{\partial\Phi_{5,j}}{\partial\sigma_{p}},\quad \frac{\partial\Phi_{5,j}}{\partial \sigma_{p}},\quad \frac{\partial\Phi_{5,j}}{\partial \sigma_{p}},\quad \frac{\partial\Phi_{5,j}}{\partial \sigma_{p}},\quad \frac{\partial\Phi_{5,j}}{\partial \sigma_{p}}.\\ \end{split} \end{equation}$ $

(7.31)

This system's solution yields the values of the $ \alpha_{p} $'s, $ \theta_{p} $'s, $ \lambda_{p} $'s, $ \vartheta_{p} $'s, and $ \sigma_{p} $'s unknown coefficients. By entering $ \alpha_{p} $'s, $ \theta_{p} $'s, $ \lambda_{p} $'s, $ \vartheta_{p} $'s, and $ \sigma_{p} $'s into Eq (7.1), it is possible to calculate the necessary solutions $ \mathbb{S}(t), \mathbb{E}(t) $, $ \mathbb{I}(t), \mathbb{Q}(t) $ and $ \mathbb{R}(t) $ at nodal locations. The experimental rate of convergence, denoted by the formula $ r $$ _{\varrho}(N) $ ^[54], can be calculated as follows:

$\begin{equation} \mathbf{r}_{\varrho}(N) = \frac{1}{\log2}\log\left[ \frac{\text{ Maximum absolute error at }\frac{N}{2}}{\text{ Maximum absolute error at }N}\right]. \end{equation}$ $

(7.32)

Next we are going to display the graphical results.

7.1. Graphical results

In this section, we present graphical results that showcase the dynamics of various groups of individuals in the fractional order model (3.4). To solve the model numerically, we adopt the method described in ^[47,55] and rely on the information provided in Table 1. The resulting figures, which include Figures 4–7, offer valuable insights into the behavior of susceptible $ (\mathbb{S}) $, exposed $ (\mathbb{E}) $, infected $ (\mathbb{I}) $, recovered $ (\mathbb{R}) $, and quarantined $ (\mathbb{Q}) $ individuals. Figure 5(a) depicts the fractional-order derivatives of susceptible individuals, which range between $ 0.50 $ and $ 0.90 $, and shows that the number of susceptible individuals decreases as time progresses due to exposure to the virus. This is a typical behavior observed in other epidemiological models. Figure 5(b) presents the population of exposed individuals, which grows steadily and rapidly as the fractional-order derivative approaches the classical value. This increase is attributed to the higher number of susceptible people becoming infected and joining the exposed class in the initial weeks of the outbreak, suggesting an increased transmission risk during the early stages of the epidemic. The number of infected individuals, depicted in Figure 5(c), increases as the fractional order approaches 1 due to the increased sensitivity of the fractional order. Figure 5(d) illustrates how most students in the confined and infectious stages of the virus leave the exposed class a few weeks after exposure. The exposed population's behavior is identical to that of the population under quarantine, and as the fractional-order derivative becomes closer to the integer order, there are more exposed people overall. The number of recovered individuals is shown in Figure 5(e) and it increases continuously as the fractional-order derivative gets closer to the classical value as a result of the recovery of infected people, which helps to confine the disease. Raising the fractional order will hasten the population increase of the restored class.

Table 1. The Table contains descriptions and estimated values for the parameters.

Symbol of parameters	Values of parameters	References
$ B $	$ 60.5089 $	Fitted
$ \theta $	$ 0.0477 $	Estimated
$ \tau $	$ 0.0205 $	Estimated
$ \epsilon $	$ 0.1571 $	Estimated
$ \varepsilon_{1} $	$ 0.0805 $	Estimated
$ \varepsilon_{2} $	$ 0.0176 $	Estimated
$ \varepsilon_{3} $	$ 0.0309 $	Estimated
$ \rho $	$ 0.3506 $	Fitted
$ \eta $	$ 0.1805 $	Estimated
$ \alpha $	$ 0.0059 $	Estimated
$ \sigma $	$ 0.0009 $	Fitted
$ \lambda $	$ 0.0894 $	Estimated

| Show Table

DownLoad: CSV

Figure 4. The figure illustrates how the Caputo fractional model responds to different initial conditions, showcasing the behavior of each state variable for a specific value of $ \delta $, set at 0.8.

DownLoad: Full-Size Img PowerPoint

Figure 5. The figure showcases the distinct behavior of each state variable in the Caputo version of the fractional model, employing the parameter values specified in the graph.

DownLoad: Full-Size Img PowerPoint

Figure 6. The figure shows the behavior of each state variable for the Caputo fractional model under different initial conditions.

DownLoad: Full-Size Img PowerPoint

Figure 7. The behavior of each state variable is fully illustrated in this figure for a particular value of the parameter $ \theta $, i.e. $ \theta = 0.01815 $. The y-axis displays the values of the state variables while the x-axis indicates time. Each state variable exhibits a distinct pattern over time in the plot, which clearly illustrates the dynamics of the system. Understanding the basic mechanisms guiding the system and projecting its future behavior under various circumstances are made possible with the use of this information.

DownLoad: Full-Size Img PowerPoint

8. Conclusions

In conclusion, sensitivity analysis and computational modeling of fractional COVID-19 models by Haar wavelet collocation methods with real data provides valuable insights into the behavior of COVID-19 spread. This method of analysis helps to understand the impact of different variables on the spread of the disease and can be used to make informed decisions about the most effective strategies to mitigate the spread of COVID-19. The use of Haar wavelet collocation methods allows for a more accurate representation of the data, resulting in a more precise and reliable model. This work highlights the importance of using advanced techniques to better understand the dynamics of the COVID-19 pandemic. In this article, we have studied the Covid epidemic model under the fractional derivatives in Caputo sense. The model's existence and uniqueness are established by considering fixed point theory outcomes. To carry out numerical treatment and simulations, we utilize the Haar wavelet collocation method. We also provide parameter estimation for the COVID-19 cases recorded in India from 13 July 2021 to 25 August, 2021. In future, the control parameters may be incorporated into the proposed model by applying optimal control theory to minimize infection among the infected individuals. This would require defining appropriate optimal control variables, as well as Hamiltonian and Lagrangian functions. Another possible modification to the model is to convert it into a stochastic model by introducing a noise term for each class. This could involve incorporating two types of noise: white noise and Levy noise.

Acknowledgments

This research was funded by Deanship of Scientific Research at King Khalid University, Abha, Saudi Arabia, Project under Grant Number RGP.2/27/44. The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University, Abha, Saudi Arabia, for funding this work through the Research Group Project under Grant Number (RGP.2/27/44). The first author appreciates the support provided by Petchra Pra Jom Klao Ph.D. Research Scholarship through grant no (50/2565), by King Mongkut's University of Technology Thonburi, Thailand.

Conflict of interest

The authors declare there is no conflict of interest.

Acknowledgments

This study was partly supported by the Grants-in-Aid for Scientific Research of Exploratory Research JP21656100, JP25630176, JP17K20029, JP16K12524, and Scientific Research (A) JP22246054 of the Japan Society for the Promotion of Science. We would like to thank Editage (www.editage.com) for English language editing.

Conflict of interest

The authors declare that there is no conflict of interest regarding the publication of this paper.

References

[1]	Bonifazi P, Goldin M, Picardo MA, et al. (2009) GABAergic hub neurons orchestrate synchrony in developing hippocampal networks. Science 326: 1419–1424. doi: 10.1126/science.1175509
[2]	Kamimura T, Nakamura K, Yoneda K, et al. (2010) Information communication in brain based on memory loop neural circuit. ICIS2010 & SEDM2010 (appears in IEEE Xplore), Chengdu, June, 23–25.
[3]	Choe Y (2002) Analogical Cascade: A theory on the role of the thalamo-cortical loop in brain function. Neurocomputing 52: 713–719.
[4]	Tamura S, Mizuno-Matsumoto Y, Chen YW, et al. (2009) Association and abstraction on neural circuit loop and coding. IIHMSP 2009 10-07: 546–549 (appears in IEEE Xplore).
[5]	Thorpre S, Fize D, Marlot C (1996) Speed of processing in the human visual system. Nature 381: 520. doi: 10.1038/381520a0
[6]	Cessac B, Paugam-Moisy H, Viéville T (2010) Overview of facts and issues about neural coding by spike. J Physiol-Paris 104: 5–18. doi: 10.1016/j.jphysparis.2009.11.002
[7]	Kliper O, Horn D, Quenet B, et al. (2004) Analysis of spatiotemporal patterns in a model of olfaction. Neurocomputing 58: 1027–1032.
[8]	Fujita K, Kashimori Y, Kambara T (2007) Spatiotemporal burst coding for extracting features of spatiotemporally varying stimuli. Biol Cybern 97: 293–305. doi: 10.1007/s00422-007-0175-z
[9]	Tyukin I, Tyukina T, Van LC (2009) Invariant template matching in systems with spatiotemporal coding: A matter of instability. Neural Networks 22: 425–449. doi: 10.1016/j.neunet.2009.01.014
[10]	Mohemmed A, Schliebs S, Matsuda S, et al. (2013) Training spiking neural networks to associate spatio-temporal input–output spike patterns. Neurocomputing 107: 3–10. doi: 10.1016/j.neucom.2012.08.034
[11]	Olshausen BA, Field DJ (1996) Emergence of simple-cell receptive field properties by learning a sparse code for natural images. Nature 381: 607–609. doi: 10.1038/381607a0
[12]	Bell AJ, Sejnowski TJ (1997) The "independent components" of natural scenes are edge filters. Vision Res 37: 3327–3338. doi: 10.1016/S0042-6989(97)00121-1
[13]	Aviel Y, Horn D, Abeles M (2004) Synfire waves in small balanced networks. Neurocomputing 58–60: 123–127.
[14]	Abeles M (1982) Local Cortical Circuits: An Electrophysiological study, Berlin: Springer.
[15]	Shinozaki T, Câteau H, Urakubo H, et al. (2007) Controlling synfire chain by inhibitory synaptic input. J Phys Soc Jpn 76: 044806.
[16]	Izhikevich EM (2014) Polychronization: Computation with spikes. Neural Comput 18: 245–282.
[17]	Perc M (2007) Fluctuating excitability: A mechanism for self-sustained information flow in excite arrays. Chaos Soliton Fract 32: 1118–1124. doi: 10.1016/j.chaos.2005.11.035
[18]	Zhang H, Wang Q, Perc M, et al. (2013) Synaptic plasticity induced transition of spike propagation in neuronal networks. Commun Nonlinear Sci 18: 601–615. doi: 10.1016/j.cnsns.2012.08.009
[19]	Mizuno-Matsumoto Y, Okazaki K, Kato A, et al. (1999) Visualization of epileptogenic phenomena using crosscorrelation analysis: Localization of epileptic foci and propagation of epileptiform discharges. IEEE Trans Biomed Eng 46: 271–279. doi: 10.1109/10.748980
[20]	Mizuno-Matsumoto Y, Ishijima M, Shinosaki K, et al. (2001) Transient global amnesia (TGA) in a MEG study. Brain Topogr 13: 269–274. doi: 10.1023/A:1011176612377
[21]	Nishitani Y, Hosokawa C, Mizuno-Matsumoto Y, et al. (2012) Detection of M-sequences from spike sequence in neuronal networks. Comput Intell Neurosci 2012: 167–185.
[22]	Nishitani Y, Hosokawa C, Mizuno-Matsumoto Y, et al. (2014) Synchronized code sequences from spike trains in cultured neuronal networks. Int J Eng Ind 5: 13–24.
[23]	Tamura S, Nishitani Y, Hosokawa C, et al. (2016) Simulation of code spectrum and code flow of cultured neuronal networks. Comput Intell Neurosci 2016: 1–12.
[24]	Nishitani Y, Hosokawa C, Mizuno-Matsumoto Y, et al. (2016) Classification of spike wave propagations in a cultured neuronal network: Investigating a brain communication mechanism. AIMS Neurosci 4: 1–13. doi: 10.3934/Neuroscience.2017.1.1
[25]	Nishitani Y, Hosokawa C, Mizuno-Matsumoto Y, et al. (2017) Effect of correlating adjacent neurons for identifying communications: Feasibility experiment in a cultured neuronal network AIMS Neurosci 5: 18–31.
[26]	Ando H (2002) Human Brain Regions Involved in Visual Motion Prediction. Neuro Image Human Brain Mapping 2002 Meeting, 599.
[27]	Rumelhart DE, Hinton GE, Williams RJ (1986) Learning representations by back-propagating errors. Nature 323: 533–536. doi: 10.1038/323533a0

neurosci-06-04-240-s001.pdf

This article has been cited by:

1.	Muhammed Fatih Basoglu, Zihni Zerin, Adnan Kefal, Erkan Oterkus, A computational model of peridynamic theory for deflecting behavior of crack propagation with micro-cracks, 2019, 162, 09270256, 33, 10.1016/j.commatsci.2019.02.032
2.	Mohammad Naqib Rahimi, Adnan Kefal, Mehmet Yildiz, Erkan Oterkus, An ordinary state-based peridynamic model for toughness enhancement of brittle materials through drilling stop-holes, 2020, 182, 00207403, 105773, 10.1016/j.ijmecsci.2020.105773
3.	Selda Oterkus, Bingquan Wang, Erkan Oterkus, Effect of horizon shape in peridynamics, 2020, 28, 24523216, 418, 10.1016/j.prostr.2020.10.049
4.	Yakubu Kasimu Galadima, Erkan Oterkus, Selda Oterkus, Investigation of the effect of shape of inclusions on homogenized properties by using peridynamics, 2020, 28, 24523216, 1094, 10.1016/j.prostr.2020.11.124
5.	Wenxuan Xia, Erkan Oterkus, Selda Oterkus, Peridynamic modelling of periodic microstructured materials, 2020, 28, 24523216, 820, 10.1016/j.prostr.2020.10.096
6.	Wenxuan Xia, Erkan Oterkus, Selda Oterkus, Ordinary state-based peridynamic homogenization of periodic micro-structured materials, 2021, 113, 01678442, 102960, 10.1016/j.tafmec.2021.102960
7.	Yan Gao, Selda Oterkus, Fully coupled thermomechanical analysis of laminated composites by using ordinary state based peridynamic theory, 2019, 207, 02638223, 397, 10.1016/j.compstruct.2018.09.034
8.	Wei Lu, Selda Oterkus, Erkan Oterkus, Peridynamic modelling of Hertzian indentation fracture, 2020, 28, 24523216, 1559, 10.1016/j.prostr.2020.10.128
9.	Xuefeng Liu, Xiaoqiao He, Jinbao Wang, Ligang Sun, Erkan Oterkus, An ordinary state-based peridynamic model for the fracture of zigzag graphene sheets, 2018, 474, 1364-5021, 20180019, 10.1098/rspa.2018.0019
10.	Hanlin Wang, Erkan Oterkus, Selda Oterkus, Peridynamic modelling of fracture in marine lithium-ion batteries, 2018, 151, 00298018, 257, 10.1016/j.oceaneng.2018.01.049
11.	Zhenghao Yang, Selda Oterkus, Erkan Oterkus, Peridynamic formulation for Timoshenko beam, 2020, 28, 24523216, 464, 10.1016/j.prostr.2020.10.055
12.	Olena Karpenko, Selda Oterkus, Erkan Oterkus, Influence of Different Types of Small-Size Defects on Propagation of Macro-cracks in Brittle Materials, 2020, 2, 2522-896X, 289, 10.1007/s42102-020-00032-z
13.	Adem Candaş, Erkan Oterkus, Cevat Erdem İmrak, Dynamic Crack Propagation and Its Interaction With Micro-Cracks in an Impact Problem, 2021, 143, 0094-4289, 10.1115/1.4047746
14.	Erkan Oterkus, Erdogan Madenci, Selda Oterkus, Peridynamic shell membrane formulation, 2020, 28, 24523216, 411, 10.1016/j.prostr.2020.10.048
15.	Bingquan Wang, Selda Oterkus, Erkan Oterkus, Closed-form dispersion relationships in bond-based peridynamics, 2020, 28, 24523216, 482, 10.1016/j.prostr.2020.10.057
16.	Yan Gao, Selda Oterkus, Ordinary state-based peridynamic modelling for fully coupled thermoelastic problems, 2019, 31, 0935-1175, 907, 10.1007/s00161-018-0691-1
17.	Mingyang Li, Selda Oterkus, Erkan Oterkus, Investigation of the effect of porosity on intergranular brittle fracture using peridynamics, 2020, 28, 24523216, 472, 10.1016/j.prostr.2020.10.056
18.	Cong Tien Nguyen, Selda Oterkus, Erkan Oterkus, 2021, 9780128200698, 419, 10.1016/B978-0-12-820069-8.00015-9
19.	Selda Oterkus, Erdogan Madenci, Erkan Oterkus, 2021, 9780128200698, 387, 10.1016/B978-0-12-820069-8.00010-X
20.	Kyutack Hong, Selda Oterkus, Erkan Oterkus, Peridynamic analysis of fatigue crack growth in fillet welded joints, 2021, 235, 00298018, 109348, 10.1016/j.oceaneng.2021.109348
21.	Yakubu Kasimu Galadima, Wenxuan Xia, Erkan Oterkus, Selda Oterkus, Peridynamic computational homogenization theory for materials with evolving microstructure and damage, 2022, 0177-0667, 10.1007/s00366-022-01696-5
22.	Bingquan Wang, Selda Oterkus, Erkan Oterkus, Thermomechanical phase change peridynamic model for welding analysis, 2022, 140, 09557997, 371, 10.1016/j.enganabound.2022.04.030
23.	Selda Oterkus, Erkan Oterkus, Comparison of Peridynamics and Lattice Dynamics Wave Dispersion Relationships, 2022, 2522-896X, 10.1007/s42102-022-00087-0
24.	M. Ozdemir, S. Oterkus, E. Oterkus, I. Amin, C. T. Nguyen, S. Tanaka, A. El-Aassar, H. Shawky, Evaluation of dynamic behaviour of porous media including micro-cracks by ordinary state-based peridynamics, 2021, 0177-0667, 10.1007/s00366-021-01506-4
25.	Adem Candaş, Erkan Oterkus, C. Erdem İmrak, Peridynamic simulation of dynamic fracture in functionally graded materials subjected to impact load, 2021, 0177-0667, 10.1007/s00366-021-01540-2
26.	Malo Valmalle, Antoine Vintache, Benjamin Smaniotto, Florian Gutmann, Mario Spagnuolo, Alessandro Ciallella, François Hild, Local–global DVC analyses confirm theoretical predictions for deformation and damage onset in torsion of pantographic metamaterial, 2022, 172, 01676636, 104379, 10.1016/j.mechmat.2022.104379
27.	Andrew Premchander, Islam Amin, Selda Oterkus, Erkan Oterkus, Nabil Ahmed Shawky Elminshawy, Peridynamic Modelling of Propagation of Cracks in Photovoltaic Panels, 2022, 41, 24523216, 305, 10.1016/j.prostr.2022.05.036
28.	Selda Oterkus, Erkan Oterkus, Peridynamic Surface Elasticity Formulation Based on Modified Core–Shell Model, 2022, 2522-896X, 10.1007/s42102-022-00089-y
29.	Muhammed Fatih Basoglu, Adnan Kefal, Zihni Zerin, Erkan Oterkus, Peridynamic modeling of toughening enhancement in unidirectional fiber-reinforced composites with micro-cracks, 2022, 297, 02638223, 115950, 10.1016/j.compstruct.2022.115950
30.	Wei Lu, Selda Oterkus, Erkan Oterkus, Dagang Zhang, Modelling of cracks with frictional contact based on peridynamics, 2021, 116, 01678442, 103082, 10.1016/j.tafmec.2021.103082
31.	Yakubu Kasimu Galadima, Wenxuan Xia, Erkan Oterkus, Selda Oterkus, A computational homogenization framework for non-ordinary state-based peridynamics, 2022, 0177-0667, 10.1007/s00366-021-01582-6
32.	M. Ozdemir, M. Imachi, S. Tanaka, S. Oterkus, E. Oterkus, A comprehensive investigation on macro–micro crack interactions in functionally graded materials using ordinary-state based peridynamics, 2022, 287, 02638223, 115299, 10.1016/j.compstruct.2022.115299
33.	Francesco dell’Isola, Simon R Eugster, Roberto Fedele, Pierre Seppecher, Second-gradient continua: From Lagrangian to Eulerian and back, 2022, 27, 1081-2865, 2715, 10.1177/10812865221078822
34.	Zhenghao Yang, Chien-Ching Ma, Erkan Oterkus, Selda Oterkus, Konstantin Naumenko, Bozo Vazic, Analytical Solution of the Peridynamic Equation of Motion for a 2-Dimensional Rectangular Membrane, 2022, 2522-896X, 10.1007/s42102-022-00090-5
35.	Yakubu Kasimu Galadima, Erkan Oterkus, Selda Oterkus, Static condensation of peridynamic heat conduction model, 2022, 27, 1081-2865, 2689, 10.1177/10812865221081160
36.	Zhenghao Yang, Chien-Ching Ma, Erkan Oterkus, Selda Oterkus, Konstantin Naumenko, Analytical Solution of 1-Dimensional Peridynamic Equation of Motion, 2022, 2522-896X, 10.1007/s42102-022-00086-1
37.	Yakubu Kasimu Galadima, Selda Oterkus, Erkan Oterkus, Islam Amin, Abdel-Hameed El-Aassar, Hosam Shawky, Modelling of viscoelastic materials using non-ordinary state-based peridynamics, 2023, 0177-0667, 10.1007/s00366-023-01808-9
38.	Zhenghao Yang, Erkan Oterkus, Selda Oterkus, Chien-Ching Ma, Double horizon peridynamics, 2023, 1081-2865, 108128652311736, 10.1177/10812865231173686
39.	Yakubu Kasimu Galadima, Selda Oterkus, Erkan Oterkus, Islam Amin, Abdel-Hameed El-Aassar, Hosam Shawky, A nonlocal method to compute effective properties of viscoelastic composite materials based on peridynamic computational homogenization theory, 2023, 319, 02638223, 117147, 10.1016/j.compstruct.2023.117147
40.	Yakubu Kasimu Galadima, Selda Oterkus, Erkan Oterkus, Islam Amin, Abdel-Hameed El-Aassar, Hosam Shawky, Effect of phase contrast and inclusion shape on the effective response of viscoelastic composites using peridynamic computational homogenization theory, 2023, 1537-6494, 1, 10.1080/15376494.2023.2218364
41.	Bingquan Wang, Selda Oterkus, Erkan Oterkus, Closed-Form Wave Dispersion Relationships for Ordinary State-Based Peridynamics, 2023, 2522-896X, 10.1007/s42102-023-00109-5
42.	Bingquan Wang, Selda Oterkus, Erkan Oterkus, Non-local modelling of multiphase flow wetting and thermo-capillary flow using peridynamic differential operator, 2023, 0177-0667, 10.1007/s00366-023-01888-7
43.	S. Firooz, A. Javili, P. Steinmann, A versatile implicit computational framework for continuum-kinematics-inspired peridynamics, 2023, 0178-7675, 10.1007/s00466-023-02415-7
44.	Hanlin Wang, Satoyuki Tanaka, Selda Oterkus, Erkan Oterkus, Fracture mechanics investigation for 2D orthotropic materials by using ordinary state-based peridynamics, 2023, 02638223, 117757, 10.1016/j.compstruct.2023.117757
45.	Adem Candaş, Erkan Oterkus, C. Erdem Imrak, Ordinary state-based peridynamic modelling of crack propagation in functionally graded materials with micro cracks under impact loading, 2023, 1537-6494, 1, 10.1080/15376494.2023.2287180
46.	Adem CANDAŞ, Erkan OTERKUS, Cevat Erdem İMRAK, Enine darbe yükü altındaki tel halatların peridinamik teorisi ile modellenmesi ve analizi, 2023, 39, 1300-1884, 847, 10.17341/gazimmfd.1225810
47.	Thanh Hai Tuan Tran, Jamila Rahmoun, Hakim Naceur, Incremental alternating algorithm for damage and fracture modeling using phase-field method, 2024, 38, 1738-494X, 1385, 10.1007/s12206-024-0230-x
48.	E. Yousefimiab, M.F. Basoglu, A. Kefal, Peridynamic analysis of thermomechanical effects in fracture toughening mechanisms of stop holes, 2024, 00137944, 110054, 10.1016/j.engfracmech.2024.110054

Reader Comments

Your name:*

Email:*
© 2019 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)