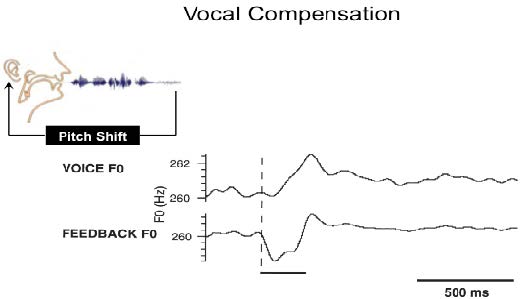
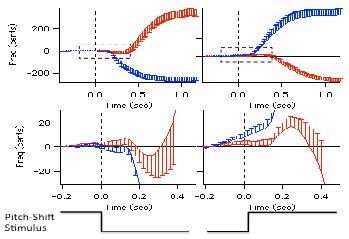
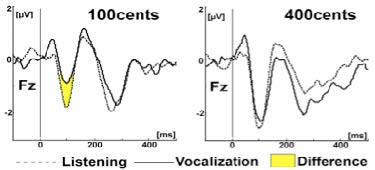
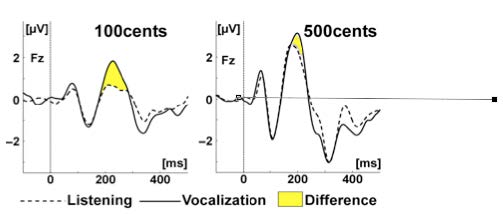
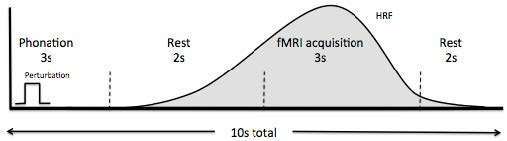
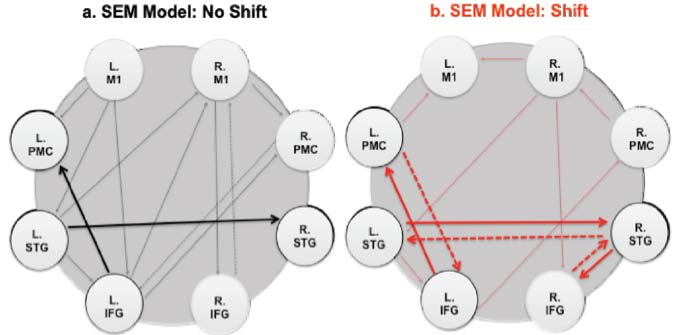
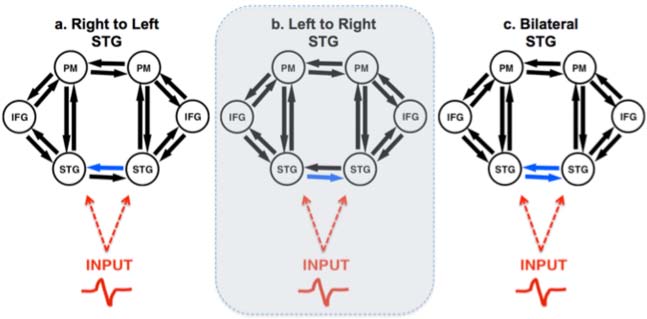
The pitch-shift paradigm has become a widely used method for studying the role of voice pitch auditory feedback in voice control. This paradigm introduces small, brief pitch shifts in voice auditory feedback to vocalizing subjects. The perturbations trigger a reflexive mechanism that counteracts the change in pitch. The underlying mechanisms of the vocal responses are thought to reflect a negative feedback control system that is similar to constructs developed to explain other forms of motor control. Another use of this technique requires subjects to voluntarily change the pitch of their voice when they hear a pitch shift stimulus. Under these conditions, short latency responses are produced that change voice pitch to match that of the stimulus. The pitch-shift technique has been used with magnetoencephalography (MEG) and electroencephalography (EEG) recordings, and has shown that at vocal onset there is normally a suppression of neural activity related to vocalization. However, if a pitch-shift is also presented at voice onset, there is a cancellation of this suppression, which has been interpreted to mean that one way in which a person distinguishes self-vocalization from vocalization of others is by a comparison of the intended voice and the actual voice. Studies of the pitch shift reflex in the fMRI environment show that the superior temporal gyrus (STG) plays an important role in the process of controlling voice F0 based on auditory feedback. Additional studies using fMRI for effective connectivity modeling show that the left and right STG play critical roles in correcting for an error in voice production. While both the left and right STG are involved in this process, a feedback loop develops between left and right STG during perturbations, in which the left to right connection becomes stronger, and a new negative right to left connection emerges along with the emergence of other feedback loops within the cortical network tested.
1.
Introduction
Fractional calculus has emerged as a powerful tool to study complex phenomena in numerous scientific and engineering disciplines such as biology, physics, chemistry, economics, signal and image processing, control theory and so on. Fractional differential equations describe many real world process related to memory and hereditary properties of various materials more accurately as compared to classical order differential equations. For examples and applications see the monographs as [1,2,3,4,5,7,6,8].
In the literature, many authors focused on Riemann-Liouville and Caputo type derivatives in investigating fractional differential equations. A generalization of derivatives of both Riemann-Liouville and Caputo was given by R. Hilfer in [9], the known as the Hilfer fractional derivative of order $ \alpha $ and a type $ \beta\in [0, 1], $ which interpolates between the Riemann-Liouville and Caputo derivative, since it is reduced to the Riemann-Liouville and Caputo fractional derivatives when $ \beta = 0 $ and $ \beta = 1 $, respectively. Some properties and applications of the Hilfer fractional derivative are given in [10,11] and references cited therein.
Initial value problems involving Hilfer fractional derivatives were studied by several authors, see for example [12,13,14,15] and references therein. In [16] the authors initiated the study of nonlocal boundary value problems for Hilfer fractional derivative, by studying boundary value problem of Hilfer-type fractional differential equations with nonlocal integral boundary conditions
where $ ^H\mathfrak{D}^{\alpha, \beta} $ is the Hilfer fractional derivative of order $ \alpha $, $ 1 < \alpha < 2 $ and parameter $ \beta $, $ 0\leq\beta\leq1 $, $ \mathcal{I}^{\varphi_i} $ is the Riemann-Liouville fractional integral of order $ \varphi_i > 0 $, $ \xi_i \in [a, b] $, $ a\geq 0 $ and $ \delta_i \in \mathbb{R}. $ Several existence and uniqueness results were proved by using a variety of fixed point theorems.
In [17] the existence and uniqueness of solutions were studied, for a new class of system of Hilfer-Hadamard sequential fractional differential equations
with two point boundary conditions
where $ _{H}\mathfrak{D}^{\alpha_{i}, \beta_{i}} $ is the Hilfer-Hadamard fractional derivative of order $ \alpha_{i}\in(1, 2] $ and type $ \beta_{i} \in [0, 1] $ for $ i\in\{1, 2\} $, $ k_{1}, k_{2}, A_{1}, A_{2}\in\mathbb{R_{+}} $ and $ f $, $ g:[1, e]\times\mathbb{R}^{2}\to \mathbb{R} $ are given continuous functions.
The fractional derivative with another function, in the Hilfer sense, called $ \psi $-Hilfer fractional derivative, has been introduced in [18]. For some recent results on existence and uniqueness of initial value problems and results on Ulam-Hyers-Rassias stability see [19,20,21,22,23,24,25,26,27,28,29] and references therein. Recently, in [30] the authors extended the results in [16] to $ \psi $-Hilfer nonlocal implicit fractional boundary value problems.
Recently in [31] the existence and uniqueness of solutions were studied, for a new class of boundary value problems of sequential $ \psi $-Hilfer-type fractional differential equations with multi-point boundary conditions of the form
where $ ^H\mathfrak{D}^{\alpha, \beta; \psi} $ is the $ \psi $-Hilfer fractional derivative of order $ \alpha $, $ 1 < \alpha < 2 $ and parameter $ \beta $, $ 0\leq\beta\leq1 $, $ f: [a, b]\times {\mathbb R} \to {\mathbb R} $ is a continuous function, $ a < b, $ $ k, \lambda_i\in {\mathbb R}, \; i = 1, 2, \ldots, m $ and $ a < \theta_1 < \theta_2 < \ldots < \theta_{m} < b. $
In this paper, motivated by the research going on in this direction, we study a new class of boundary value problems of $ \psi $-Hilfer fractional integro-differential equations with mixed nonlocal boundary conditions of the form
where $ {}^{H}\mathfrak{D}_{0^+}^{u, \rho; \psi } $ is $ \psi $-Hilfer fractional derivatives of order $ u = \{\alpha, \mu_k\} $ with $ 1 < \mu_k < \alpha\leq 2 $, $ 0\leq \rho \leq 1 $, $ \mathcal{I}_{0^+}^{v; \psi} $ is $ \psi $-Riemann-Liouville fractional integral of order $ v = \{\phi, \beta_j\}, $ $ \phi, \beta_j > 0 $ for $ j = 1, 2, \ldots, n $, $ \kappa, \delta_i, \omega_j, \lambda_k \in\mathbb{R} $ are given constants, the points $ \eta_i, \theta_j, \xi_k \in J $, $ i = 1, 2, \ldots, m $, $ j = 1, 2, \ldots, n $, $ k = 1, 2, \ldots, r $ and $ f : J\times \mathbb{R}^2 \to \mathbb{R} $ is a given continuous function, and $ J : = [0, T] $, $ T > 0 $. It is imperative to note that the problems addressed in this paper provide more insight into the study of $ \psi $-Hilfer fractional differential equations involving mixed nonlocal boundary conditions. Our results are not only interesting from theoretical point of view, but also helpful in studying the applied problems containing the systems like the ones considered in this paper. Our nonlocal boundary conditions are also useful, since they are the most general mixed type. We emphasize that the mixed nonlocal boundary conditions include multi-point, fractional derivative multi-order and fractional integral multi-order boundary conditions.
This paper is organized as follows: In Section $ 2 $, we present some necessary definitions and preliminaries results that will be used to prove our main results. The existence and uniqueness of the solutions for the problem (1.7) are established in Section $ 3 $. Our methodology for obtaining the desired results is standard, but its application in the framework of the present problem is new. In Section $ 4 $, we discuss the Ulam's stability of the solutions of the problem (1.7) in the frame of Ulam-Hyers ($ \mathbb{UH} $) stability, generalized Ulam-Hyers ($ \mathbb{UH} $) stability, Ulam-Hyers-Rassias ($ \mathbb{UHR} $) stability and generalized Ulam-Hyers-Rassias ($ \mathbb{UHR} $) stability is investigated. Finally, examples are given in Section $ 5 $ to illustrate the theoretical results.
2.
Background material and auxiliary results
In this section, we introduce some notation, spaces, definitions and fundamental lemmas which are useful throughout this paper.
Let $ \mathcal{C} = \mathcal{C}(J, \mathbb{R}) $ denote the Banach space of all continuous functions from $ J $ into $ \mathbb{R} $ with the norm defined by
On the order hand, we have $ n $-times absolutely continuous functions given by
Definition 2.1. [2] Let $ (a, b) $, $ (-\infty \leq a < b \leq \infty) $, be a finite or infinite interval of the half-axis $ \mathbb{R}^+ $ and $ \alpha \in \mathbb{R}^+ $. Also let $ \psi(x) $ be an increasing and positive monotone function on $ (a, b] $, having a continuous derivative $ \psi^{\prime}(x) $ on $ (a, b) $. The $ \psi $-Riemann-Liouville fractional integral of a function $ f $ with respect to another function $ \psi $ on $ [a, b] $ is defined by
where $ \Gamma(\cdot) $ is represent the Gamma function.
Definition 2.2. [2] Let $ \psi^{\prime}(t)\neq 0 $ and $ \alpha > 0 $, $ n \in \mathbb{N} $. The Riemann–Liouville derivatives of a function $ f $ with respect to another function $ \psi $ of order $ \alpha $ correspondent to the Riemann–Liouville, is defined by
where $ n = [\alpha]+1 $, $ [\alpha] $ is represent the integer part of the real number $ \alpha $.
Definition 2.3. [18] Let $ n-1 < \alpha < n $ with $ n \in \mathbb{N} $, $ [a, b] $ is the interval such that $ -\infty \leq a < b \leq \infty $ and $ f, \psi \in \mathcal{C}^n ([a, b], \mathbb{R}) $ two functions such that $ \psi $ is increasing and $ \psi^{\prime}(t)\neq 0 $, for all $ t \in [a, b] $. The $ \psi $-Hilfer fractional derivative of a function $ f $ of order $ \alpha $ and type $ 0\leq\rho\leq1 $, is defined by
where $ n = [\alpha]+1 $, $ [\alpha] $ represents the integer part of the real number $ \alpha $ with $ \gamma = \alpha + \rho(n - \alpha) $.
Lemma 2.4. [2] Let $ \alpha, \beta > 0 $. Then we have the following semigroup property given by,
Next, we present the $ \psi $-fractional integral and derivatives of a power function.
Proposition 2.5. [2,18] Let $ \alpha \geq 0 $, $ \upsilon > 0 $ and $ t > a $. Then, $ \psi $-fractional integral and derivative of a power function are given by
(i) $ \mathcal{I}_{a^+}^{\alpha; \psi}\left(\psi (s)-\psi(a)\right)^{\upsilon -1}(t) = \frac{\Gamma (\upsilon)}{\Gamma (\upsilon +\alpha)} \left(\psi (t)-\psi (a) \right)^{\upsilon +\alpha -1}. $
(ii) $ \mathfrak{D}_{a^+}^{\alpha, \rho; \psi }\left(\psi(s)-\psi(a)\right)^{\upsilon -1}(t) = \frac{\Gamma (\upsilon)}{\Gamma (\upsilon -\alpha)} {{\left(\psi (t)-\psi (a) \right)}^{\upsilon -\alpha -1}}. $
(iii) $ {^{H}\mathfrak{D}}_{a^+}^{\alpha, \rho; \psi } \left(\psi(s)-\psi (a) \right)^{\upsilon -1}(t) = \frac{\Gamma (\upsilon)}{\Gamma (\upsilon -\alpha)} {{\left(\psi (t)-\psi (a) \right)}^{\upsilon -\alpha -1}}, \quad \upsilon > \gamma = \alpha+\rho(2-\alpha) $.
Lemma 2.6. Let $ m-1 < \alpha < m $, $ n-1 < \beta < n $, $ n, m\in\mathbb{N} $, $ n \leq m $, $ 0\leq \rho\leq 1 $ and $ \alpha \geq \beta +\rho (n - \beta) $. If $ h\in {\mathcal{C}^n}(J, \mathbb{R}) $, then
Proof. Let $ \lambda = \beta +\rho (n - \beta) $ with $ n-1 < \lambda < n $, we get
By using Definition $ 2.1 $, we obtain
and
Repeat the above process, we have
which implies that
This completes the proof.
Lemma 2.7. [18] If $ f \in \mathcal{C}^n (J, \mathbb{R}) $, $ n-1 < \alpha < n $, $ 0 \leq \rho \leq 1 $ and $ \gamma = \alpha +\rho(n-\alpha) $ then
for all $ t\in J $, where $ f_{\psi }^{[n]}f(t): = {{\left(\frac{1}{\psi^{\prime}(t)}\frac{d}{dt} \right)}^{n}}f(t) $.
Fixed point theorems play a major role in establishing the existence theory for the problem (1.7). We collect here some well-known fixed point theorems used in this paper.
Lemma 2.8. (Banach contraction principle [32]). Let $ D $ be a non-empty closed subset of a Banach space $ E $. Then any contraction mapping $ T $ from $ D $ into itself has a unique fixed point.
Lemma 2.9. (Krasnosel'ski${\rm{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over i} }}$'s fixed point theorem [33]). Let $ \mathcal{M} $ be a closed, bounded, convex, and nonempty subset of a Banach space. Let $ A, B $ be the operators such that (i) $ Ax+By \in \mathcal{M} $ whenever $ x $, $ y \in \mathcal{M} $; (ii) $ A $ is compact and continuous; (iii) $ B $ is contraction mapping. Then there exists $ z \in \mathcal{M} $ such that $ z = Az+bz $.
Lemma 2.10. (Leray-Schauder nonlinear alternative [32]). Let $ E $ be a Banach space, $ C $ a closed, convex subset of $ E, U $ an open subset of $ C $ and $ 0\in U. $ Suppose that $ \mathcal{D}:\overline{U}\to C $ is a continuous, compact (that is, $ \mathcal{D}(\overline{U}) $ is a relatively compact subset of $ C $) map. Then either
$(i)$ $ \mathcal{D} $ has a fixed point in $ \overline{U}, $ or
$(ii)$ there is a $ x\in\partial U $ (the boundary of $ U $ in $ C $) and $ \nu \in (0, 1) $ with $ x = \nu\mathcal{D}(x). $
In order to transform the problem (1.7) into a fixed point problem, we must convert it into an equivalent Voltera integral equation. We provide the following auxiliary lemma, which is important in our main results and concern a linear variant of the boundary value problem (1.7).
Lemma 2.11. Let $ 1 < \mu_{k} < \alpha \leq 2, $ $ 0 \leq \rho \leq 1 $, $ \gamma = \alpha+\rho(2-\alpha) $, $ k = 1, 2, \ldots, r $ and $ \Omega\ne 0 $. Suppose that $ h \in \mathcal{C}. $ Then $ x\in {\mathcal{C}}^2 $ is a solution of the problem
if and only if $ x $ satisfies the integral equation
where
Proof. Let $ x \in \mathcal{C} $ be a solution of the problem (1.7). By using Lemma 2.7, we have
where $ c_{1}, c_{2}\in\mathbb{R} $ are arbitrary constants.
For $ t = 0 $, we get $ c_{2} = 0, $ and thus
Taking the operators $ {{}^{H}\mathfrak{D}_{0^+}^{\mu_{k}, \rho; \psi} } $ and $ \mathcal{I}_{0^+}^{\beta_j; \psi } $ into (2.10), we obtain
Applying the second boundary condition in (1.7), we have
from which we get
where $ \Omega $ is defined by (2.9). Substituting the value of $ c_1 $ in (2.11), we obtain (2.8).
Conversely, it is easily to shown, by a direct calculation, that the solution $ x $ given by (2.8) satisfies the problem (2.7). The Lemma 2.11 is proved.
3.
Existence and uniqueness results
In this section, we present existence and uniqueness results to the considered problem (1.7).
For the sake of convenience, we use the following notations:
In view of Lemma $ 2.11 $, an operator $ \mathcal{Q}:{\mathcal{C}} \to {\mathcal{C}} $ is defined by
where
Throughout this paper, the expression $ \mathcal{I}_{0^+}^{q, \rho}F_{x}(s)(c) $ means that
where $ u = \{\phi, \beta_{j}\} $ and $ c = \{t, \sigma, \theta_j\} $, $ j = 1, 2, \ldots, n $.
It should be noticed that the problem (1.7) has solutions if and only if the operator $ \mathcal{Q} $ has fixed points.
3.1. Uniqueness result via Banach's fixed point theorem
In the first result, we establish the existence and uniqueness of solutions for the problem (1.7), by applying Banach's fixed point theorem.
Theorem 3.1. Assume that $ f : J\times\mathbb{R}^2 \to \mathbb{R} $ is a continuous function such that:
$ (H_1) $ there exist a constant $ L_1 > 0 $ such that
for any $ u_i $, $ v_i \in \mathbb{R} $, $ i = 1, 2 $ and $ t\in J $.
If
where $ \Lambda_{0} $ and $ \Lambda_{1} $ are given by (3.2) and (3.3) respectively, then the problem (1.7) has a unique solution on $ J $.
Proof. Firstly, we transform the problem (1.7) into a fixed point problem, $ x = \mathcal{Q}x $, where the operator $ \mathcal{Q} $ is defined as in (3.4). Applying the Banach contraction mapping principle, we shall show that the operator $ \mathcal{Q} $ has a unique fixed point, which is the unique solution of the problem (1.7)
Let $ \sup_{t\in J}|f(t, 0, 0)| : = M_1 < \infty. $ Next, we set $ B_{r_1} : = \{x \in \mathcal{C} : {\Vert x \Vert} \leq r_1\} $ with
where $ \Omega $, $ A(T, \gamma-1) $, $ \Lambda_{0} $, $ \Lambda_{1} $ are given by (2.9), (3.1)–(3.3), respectively. Observe that $ B_{r_1} $ is a bounded, closed, and convex subset of $ \mathcal{C} $. The proof is divided into two steps:
Step I. We show that $ \mathcal{Q}B_{r_1} \subset B_{r_1} $.
For any $ x \in B_{r_1} $, we have
We note that
It follows from conditions $ (H_1) $ that
Then we have
which implies that $ \mathcal{Q}B_{r_{1}} \subset B_{r_{1}} $.
Step II. We show that $ \mathcal{Q} : \mathcal{C} \to \mathcal{C} $ is a contraction.
For any $ x $, $ y \in \mathcal{C} $ and for each $ t \in J $, we have
which implies that $ \Vert \mathcal{Q}x-\mathcal{Q}y \Vert \leq \Lambda_0\Lambda_{1}L_{1}\Vert x-y \Vert $. As $ \Lambda_0\Lambda_{1}L_{1} < 1 $, hence, the operator $ \mathcal{Q} $ is a contraction. Therefore, by the Banach contraction mapping principle (Lemma 2.8) the operator $ \mathcal{Q} $ has a fixed point, and hence the problem (1.7) has a unique solution on $ J $. The proof is completed.
3.2. Existence result via Krasnosel'ski${\rm{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over i} }}$'s fixed point theorem
Next, we present an existence theorem by using Krasnosel'ski${\rm{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over i} }}$'s fixed point theorem.
Theorem 3.2. Assume that $ f : J\times\mathbb{R}^2 \to \mathbb{R} $ is a continuous function satisfying $ (H_1) $. In addition, we assume that:
$ (H_2) $ $ |f(t, u, v)| \leq \sigma(t) $, $ \forall (t, u, v) \in J \times \mathbb{R}^2 $, and $ \sigma \in \mathcal{C}(J, \mathbb{R}^+). $
If
where $ \Lambda_{0} $, $ \Lambda_{1} $, $ A(T, \alpha) $ are defined by (3.2), (3.3) and (3.1), respectively, then the problem (1.7) has at least one solution on $ J. $
Proof. Let $ \sup_{t \in J} \vert \sigma(t) \vert = \Vert \sigma \Vert $ and $ B_{r_2}: = \{ x \in \mathcal{C} : \Vert x \Vert \leq r_2\} $, where
We define the operators $ \mathcal{Q}_1 $ and $ \mathcal{Q}_2 $ on $ B_{r_2} $ by
Note that $ \mathcal{Q} = \mathcal{Q}_1+\mathcal{Q}_2 $. For any $ x, y \in B_{r_2} $, we have
This implies that $ \mathcal{Q}_1x+\mathcal{Q}_2x \in B_{r_{2}} $, which satisfies the assumption (i) of Lemma 2.9.
We show that the assumption (ii) of Lemma 2.9 is satisfied.
Let $ x_n $ be a sequence such that $ x_n \to x $ in $ \mathcal{C} $. Then for each $ t \in J $, we have
Since $ f $ is continuous, this implies that the operator $ F_x $ is also continuous. Hence, we obtain
Thus, this shows that the operator $ \mathcal{Q}_1x $ is continuous. Also, the set $ \mathcal{Q}_1B_{r_2} $ is uniformly bounded on $ B_{r_2} $ as
Next, we prove the compactness of the operator $ \mathcal{Q}_1 $. Let $ \sup_{(t, u, v) \in J\times B_{r_{2}}^2} \vert f(t, u, v) \vert = \widehat{f} < \infty $, then for each $ t_1, t_2 \in J $ with $ 0 \leq t_1 < t_2 \leq T $, we obtain
Obviously, the right hand side in the above inequality is independent of $ x $ and tends to zero as $ t_2 \to t_1 $. Therefore, the operator $ \mathcal{Q}_1 $ is equicontinuous. So $ \mathcal{Q}_1 $ is relatively compact on $ B_{r_2} $. Then, by the Arzelá-Ascoli theorem, $ \mathcal{Q}_1 $ is compact on $ B_{r_2} $.
Moreover, it is easy to prove, using condition (3.7), that the operator $ \mathcal{Q}_2 $ is a contraction and thus the assumption (iii) of Lemma 2.9 holds. Thus all the assumptions of Lemma 2.9 are satisfied. So the conclusion of Lemma 2.9 implies that the problem (1.7) has at least one solution on $ J $. The proof is completed.
3.3. Existence result via Leray-Schauder's nonlinear alternative
The Leray-Schauder's nonlinear alternative [32] is used to prove our last existence result.
Theorem 3.3. Assume that:
$ (H_{3}) $ there exist a function $ q\in\mathcal{C}(J, \mathbb{R}^+) $ and a continuous nondecreasing function $ \Phi : [0, \infty) \to [0, \infty) $ which is subhomogeneous (that is, $ \Phi(\mu x)\le \mu \Phi(x), $ for all $ \mu\ge 1 $ and $ x\in \mathcal{C} $), such that
$ (H_{4}) $ there exist a constant $ M_2 > 0 $ such that
with $ \Omega $, $ A(T, \alpha) $ $ \Lambda_0 $ and $ \Lambda_1 $ by (2.9), (3.1), (3.2) and (3.3).
Then, the problem (1.7) has at least one solution on $ J $.
Proof. Let the operator $ \mathcal{Q} $ be defined by (3.4). Firstly, we show that $ \mathcal{Q} $ maps bounded sets (balls) into bounded set in $ \mathcal{C} $. For a constant $ r_3 > 0 $, let $ B_{r_3} = \{x \in \mathcal{C} : \Vert x \Vert \leq r_{3} \} $ be a bounded ball in $ \mathcal{C} $. Then, for $ t\in J $, we obtain
Consequently
Next, we show that the operator $ \mathcal{Q} $ maps bounded sets into equicontinuous sets of $ \mathcal{C} $. Let $ t_1, t_2 \in J $ with $ t_1 < t_2 $ and $ x \in B_{r_3} $. Then we get
As $ t_2 - t_1 \to 0 $, the right hand side of (3.8) tends to zero independently of $ x\in B_{r_3} $. Hence, by the Arzelá-Ascoli theorem, the operator $ \mathcal{Q} $ is completely continuous.
The result will follow from the Leray-Schauder's nonlinear alternative once we have proved the boundedness of the set of all solutions to the equations $ x = \varrho\mathcal{Q}x $ for $ \varrho \in (0, 1) $.
Let $ x $ be a solution. Then, for $ t\in J $, and following calculations similar to the first step, we obtain
which leads to
In view of $ (H_4) $, there exists a constant $ M_2 > 0 $ such that $ \Vert x \Vert \neq M_2 $. Let us set
We see that the operator $ \mathcal{Q} : \overline{K} \to \mathcal{C} $ is continuous and completely continuous. From the choice of $ \overline{K} $, there is no $ x \in \partial K $ such that $ x = \varrho\mathcal{Q}x $ for some $ \varrho \in (0, 1) $. Consequently, by the nonlinear alternative of Leray-Schauder type (Lemma 2.10), we deduce that the operator $ \mathcal{Q} $ has a fixed point $ x \in \overline{K} $ which is a solution of the problem (1.7). The proof is completed.
4.
Stability results
In this section, we are developing some results on the different types of Ulam's stability such as Ulam-Hyers ($ \mathbb{UH} $), generalized Ulam-Hyers ($ \mathbb{UH} $), Ulam-Hyers-Rassias ($ \mathbb{UHR} $) and generalized Ulam-Hyers-Rassias ($ \mathbb{UHR} $) stability for the proposed problem (1.7).
We start with needed definitions. Let $ \epsilon > 0 $ be a positive real number and $ \Theta : J \to \mathbb{R}^+ $ be a continuous function. We consider the following inequalities:
Definition 4.1. [34] The problem (1.7) is said to be $ \mathbb{UH} $ stable if there exists a real number $ M_{f} > 0 $ such that for each $ \epsilon > 0 $ and for each solution $ z\in \mathcal{C} $ of the inequality (4.1), there exists a solution $ x\in \mathcal{C} $ of the problem (1.7) with
Definition 4.2. [34] The problem (1.7) is said to be generalized $ \mathbb{UH} $ stable if there exists a function $ \Theta \in \mathcal{C}(\mathbb{R}^{+}, \mathbb{R}^{+}) $ with $ \Theta(0) = 0 $ such that, for each solution $ z\in \mathcal{C} $ of inequality (4.2), there exists a solution $ x\in \mathcal{C} $ of the problem (1.7) with
Definition 4.3. [34] The problem (1.7) is said to be $ \mathbb{UHR} $ stable with respect to $ \Theta \in \mathcal{C}(J, \mathbb{R}^{+}) $ if there exists a real number $ M_{f, \Theta} > 0 $ such that for each $ \epsilon > 0 $ and for each solution $ z\in \mathcal{C} $ of the inequality (4.2) there exists a solution $ x\in \mathcal{C} $ of the problem (1.7) with
Definition 4.4. [34] The problem (1.7) is said to be generalized $ \mathbb{UHR} $ stable with respect to $ \Theta \in \mathcal{C} (J, \mathbb{R}^{+}) $ if there exists a real number $ M_{f, \Theta} > 0 $ such that for each solution $ z\in \mathcal{C} $ of the inequality (4.3), there exists a solution $ x\in \mathcal{C} $ of the problem (1.7) with
Remark 4.5. It is clear that (i) Definition $ 4.1 $ $ \Rightarrow $ Definition $ 4.2 $; (ii) Definition $ 4.3 $ $ \Rightarrow $ Definition $ 4.4 $; (iii) Definition $ 4.3 $ for $ \Theta(t) = 1 $ $ \Rightarrow $ Definition $ 4.1 $.
Remark 4.6. A function $ z\in \mathcal{C}(J, \mathbb{R}) $ is a solution of the inequality (4.1) if and only if there exists a function $ w\in \mathcal{C}(J, \mathbb{R}) $ (which depends on $ z $) such that:
(i) $ |w(t)|\leq \epsilon $, $ \forall t \in J $.
(ii) $ ^{H}\mathfrak{D}_{0^+}^{\alpha, \rho; \psi }z(t) = F_{z}(t) + w(t) $, $ t\in J $.
Remark 4.7. A function $ z\in \mathcal{C} $ is a solution of the inequality (4.2) if and only if there exists a function $ v\in \mathcal{C} $ (which depends on $ z $) such that:
(i) $ |v(t)|\leq \epsilon \Theta(t) $, $ \forall t \in J $.
(ii) $ ^{H}\mathfrak{D}_{0^+}^{\alpha, \rho; \psi }z(t) = F_{z}(t) + v(t) $, $ t\in J $.
4.1. The $ \mathbb{UH} $ and generalized $ \mathbb{UH} $ stability
Firstly, we present an important lemma that will be used in the proofs of $ \mathbb{UH} $ stability and $ \mathbb{GUH} $ stability.
Lemma 4.8. Let $ \alpha \in (1, 2] $, $ \rho \in[0, 1). $ If $ z \in \mathcal{C} $ is a solution of the inequality (4.1), then $ z $ is a solution of the following inequality
where
and $ \Lambda_{1} $ is given by (3.3).
Proof. Let $ z $ be a solution of the inequality (4.1). So, in view of Remark $ 4.6 $ (ii) and Lemma $ 2.11 $, we have
Thus, the solution of (4.9) will be in the following term
Then, by using Remark $ 4.6 $ (i), it follows that
from which inequality (4.8) is obtained. The proof is completed.
Now, we prove $ \mathbb{UH} $ stability and generalized $ \mathbb{UH} $ stability results for the problem (1.7).
Theorem 4.9. Assume that the function $ f:J\times\mathbb{R}^2 \to \mathbb{R} $ is continuous and $ (H_1) $ holds with $ \Lambda_{0} A(T, \alpha) L_{1} < 1 $. Then the problem (1.7) is $ \mathbb{UH} $ stable on $ J $ and consequently generalized $ \mathbb{UH} $ stable.
Proof. Let $ \epsilon > 0 $ and $ z\in \mathcal{C} $ be any solution of the inequality (4.1). Let $ x \in \mathcal{C} $ be the unique solution of the following problem (1.7)
Using Lemma $ 2.11 $, we obtain
where
On the other hand, if $ x(0) = z(0) $, $ x(\eta_{i}) = z(\eta_{i}) $, $ \mathcal{I}_{0^+}^{\beta_j; \psi }x(s)(\theta_j) = \mathcal{I}_{0^+}^{\beta_j; \psi }z(s)(\theta_j) $ and $ {}^{H}\mathfrak{D}_{0^+}^{\mu_{k}, \rho; \psi}x(s)(\xi_{k}) = {}^{H}\mathfrak{D}_{0^+}^{\mu_{k}, \rho; \psi}z(s)(\xi_{k}) $, then $ \mathcal{R}_{x} = \mathcal{R}_{z}. $ Indeed, we have
Thus $ \mathcal{R}_{x} = \mathcal{R}_{z}. $ Now, by applying the triangle inequality, $ |u-v| \leq |u| + |v| $, and Lemma $ 4.8 $, for any $ t\in J $, we have
This implies that
By setting
we obtain
Hence, the problem (1.7) is $ \mathbb{UH} $ stable. Further, if we set $ \Theta(\epsilon) = M_{f}\epsilon $ and $ \Theta(0) = 0 $ we have
which implies that the solution of the problem (1.7) is generalized $ \mathbb{UH} $ stable. The proof is completed.
4.2. The $ \mathbb{UHR} $ and generalized $ \mathbb{UHR} $ stability
For the proof of our next lemma, we assume the following assumption:
$ (H_3) $ There exists an increasing function $ \Theta\in \mathcal{C}(J, \mathbb{R}^+) $ and there exists $ n_{\Theta} > 0 $, such that, for any $ t\in J $, the following integral inequality
Next, we present an important lemma that will be used in the proofs of $ \mathbb{UHR} $ and generalized $ \mathbb{UHR} $ stability results.
Lemma 4.10. Let $ \alpha \in (1, 2] $, $ \rho\in[0, 1]. $ If $ z \in \mathcal{C} $ is a solution of the inequality (4.2), then $ z $ is a solution of the following inequality
where
Proof. Let $ z $ be a solution of the inequality (4.2). So, in view of Remark $ 4.7 $ (ii) and Lemma $ 2.11 $, the solution of (4.9) can be written by
Then, by using Remark $ 4.7 $ (i) with $ (H_3) $, we have the following estimation
from which inequality (4.11) is obtained. The proof is completed.
Finally, we present $ \mathbb{UHR} $ and generalized $ \mathbb{UHR} $ stability results for the problem (1.7).
Theorem 4.11. Assume that the function $ f:J\times\mathbb{R}^2 \to \mathbb{R} $ is continuous and $ (H_1) $ holds. Then the problem (1.7) is $ \mathbb{UHR} $ stable on $ J $ and consequently generalized $ \mathbb{UHR} $ stable.
Proof. Let $ \epsilon > 0 $ and $ z\in \mathcal{C} $ be the solution of the inequality (4.3). Let $ x \in \mathcal{C} $ be the unique solution of the problem (1.7). By using Lemma $ 2.11 $, we obtain
where
On the other hand, if $ x(0) = z(0) $, $ x(\eta_{i}) = z(\eta_{i}) $, $ \mathcal{I}_{0^+}^{\beta_j; \psi }x(s)(\theta_j) = \mathcal{I}_{0^+}^{\beta_j; \psi }z(s)(\theta_j) $ and $ {}^{H}\mathfrak{D}_{0^+}^{\mu_{k}, \rho; \psi}x(s)(\xi_{k}) = {}^{H}\mathfrak{D}_{0^+}^{\mu_{k}, \rho; \psi}z(s)(\xi_{k}) $, then it is easy to see that $ \mathcal{R}_{x} = \mathcal{R}_{z}. $
Now, by appying $ |u-v| \leq |u| + |v| $ and Lemma $ 4.10 $, for any $ t\in J $, we have
This implies that
By setting
we obtain
Therefore, the problem (1.7) is $ \mathbb{UHR} $ stable. Further, in the same fashion, it is easy to check that the solution of the problem (1.7) is generalized $ \mathbb{UHR} $ stable. This completes the proof.
5.
Some examples
This section presents some examples which illustrate the validity and applicability of our main results.
Example 5.1. Consider the following mixed nonlocal boundary problem of the form:
Here $ \alpha = 8/5 $, $ \rho = 1/4 $, $ \phi = 1/3 $, $ T = 1 $, $ \kappa = 1/2 $, $ m = 3 $, $ n = 2 $, $ r = 4 $, $ \delta_{i} = ((-i)/(i+5))^{(i+1)} $, $ \omega_{j} = (j+1)/(j+2) $, $ \lambda_{k} = ((-k)/(k+2))^k $, $ \eta_i = i/3 $, $ \theta_j = j/2 $, $ \xi_k = k/4 $, $ \beta_j = j/3 $, $ \mu_k = (k+8)/8 $ for $ i = 1, 2, 3 $, $ j = 1, 2 $ and $ k = 1, 2, 3, 4 $. From the given all data, we obtain that $ \Omega \approx 0.5377547471 \neq 0 $, $ \Lambda_{0} \approx 1.96941831 $, $ \Lambda_{1} \approx 2.131548185 $ and $ \Lambda_{2} \approx 6.661728461 $.
(I) Consider the function
For $ x_1 $, $ x_2 $, $ y_1 $, $ y_2\in \mathbb{R} $ and $ t\in [0, 1] $, we have
The assumptions $ (H_1) $ is satisfied with $ L_{1} = 1/9 $. Hence
Since, all the assumptions of Theorem $ 3.1 $ are satisfied, then the problem (5.1) has a unique solution on $ [0, 1] $. Further, we can also compute that
Therefore, by Theorem $ 4.9, $ the problem (5.1) is both $ \mathbb{UH} $ and generalized $ \mathbb{UH} $ stable on $ [0.1] $. In addition, by setting $ \Theta(t) = \psi(t) - \psi(0) $ with Proposition $ 2.5 $ (i), it is easy to calculate that
Thus, the inequality (4.10) is satisfied with $ n_{\Theta} = \frac{4(e^{0.5} - 1)^{\frac{5}{2}} }{15\sqrt{\pi}} > 0 $. It follows that
Hence, by Theorem $ 4.11 $, the problem (5.1), with $ f $ given by (5.2), is both $ \mathbb{UHR} $ and also generalized $ \mathbb{UHR} $ stable on $ [0.1] $.
(II) Consider the function
For $ x_1 $, $ x_2 $, $ y_1 $, $ y_2\in \mathbb{R} $ and $ t\in [0, 1] $, we have
This means that the assumption $ (H_1) $ is satisfied with $ L_{1} = 1/4 $. We obtain
and
which satisfy (3.7) and $ (H_2) $, respectively. Using the Theorem 3.2, the problem (5.1), with $ f $ given by (5.3), has at least one solution on $ [0, 1] $
(III) Consider the function
Also, the nonlinear function can be expressed as
By $ (H_3) $, we set $ q(t) = e^{-t}/(4+t)^2 $ and $ \Phi(u) = u + 1 $, then $ \Vert q \Vert = 1/16 $ and $ \Phi(|x| + |y|) = |x| + |y| + 1. $ Thus, we can compute that there exists a constant $ M_{2} > 1.527092217 $ satisfying inequality in $ (H_4) $. Therefore, all conditions in Theorem $ 3.3 $ are fulfilled. Thus the problem (5.1) with $ f $ given by (5.4) has at least one solution on $ [0, 1] $.
6.
Conclusions
This paper discussed a new class of $ \psi $-Hilfer fractional integro-differential equation supplemented with mixed nonlocal boundary condition which is a combination of multi-point, fractional derivative multi-order and fractional integral multi-order boundary conditions. Existence and uniqueness results are established. The uniqueness result is proved by applying the Banach's fixed point theorem, while the existence results are investigated via Krasnosel'ski${\rm{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over i} }}$'s fixed point theorem and Larey-Schauder nonlinear alternative. Our results are not only new in the given setting but also provide some new special cases by fixing the parameters involved in the problem at hand. For instance, by fixing $ \omega_{j} = 0, \lambda_k = 0 $ for all $ j = 1, 2, \ldots, n, \; k = 1, 2, \ldots, r $ our results correspond to the ones for boundary value problems for $ \psi $-Hilfer nonlinear fractional integro-differential equations supplemented with multi-point boundary conditions. In case we take $ \delta_{i} = 0, \lambda_k = 0 $ for all $ i = 1, 2, \ldots, m, \; k = 1, 2, \ldots, r $ we obtain the results for boundary value problems for $ \psi $-Hilfer nonlinear fractional integro-differential equations equipped with multi-term integral boundary conditions. Further, we studied different kinds of Ulam's stability such as $ \mathbb{UH} $, generalized $ \mathbb{UH} $, $ \mathbb{UHR} $ and generalized $ \mathbb{UHR} $ stability. In the end, we present examples to demonstrate the consistency to the theoretical findings.
The work accomplished in this paper is new and enrich the literature on boundary value problems for nonlinear $ \psi $-Hilfer fractional differential equations.
Acknowledgments
The first author would like to thank King Mongkut's University of Technology North Bangkok and the Center of Excellence in Mathematics (CEM), CHE, Sri Ayutthaya Rd., Bangkok, 10400, Thailand for support this work. The second author would like to thank for funding this work through the Center of Excellence in Mathematics (CEM), CHE, Sri Ayutthaya Rd., Bangkok, 10400, Thailand and Barapha University.
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.













 DownLoad:
DownLoad: