On the viscous Cahn-Hilliard equation with singular potential and inertial term

1.   Introduction

Univalent functions are analytic functions that are one-to-one. Conformal mapping functions are analytic functions that are one-to-one with the angle preserving property. Thus, conformal mapping functions are univalent.

Many conformal mapping problems can be solved using the Szegö kernel, which also satisfies the Kerzman-Stein integral equation ^[1,2]. The Szegö kernel for an annulus has both bilateral series and infinite product representations ^[3,4,5]. The Szegö kernel is closely related to the Ahlfors map. The Ahlfors map of a doubly connected region $ \Omega $ is a branching two-to-one map onto the disk. From the boundary values of the Szegö kernel, the boundary values of the Ahlfors map are completely determined ^[6,7,8]. The Ahlfors map of $ \Omega $ has two zeros, one zero is predetermined which is mapped to zero, the other zero comes from the unique zero of the Szegö kernel. The zero of the Szegö kernel for an annulus has a nice closed formula ^[3]. Computing the zero of the Szegö kernel for $ \Omega $ is an interesting problem in computational complex analysis. A system of nonlinear equations with integrals involving the Szegö kernel and its derivative, satisfied by the zeros of the Szegö kernel for a multiply connected region has been presented by Tegtmeyer ^[8], but did not show any numerical computations of the zeros. In ^[9] the zero of the Szegö kernel of $ \Omega $ has been computed numerically by extending the approach of ^[10]. However, the numerical methods in ^[9] are iterative and require good initial approximation of the zero for convergence. This approximation is obtained by plotting the graph of the absolute value of the Ahlfors map. Additional numerical methods for computing the zeros of the Szegö kernel for doubly connected regions are shown in ^[11]. Since there exists a transformation formula for the Szegö kernel from $ \Omega $ onto an annulus ^[3], the possibility of applying conformal mapping for computing the zero of the Szegö kernel arises, thus, avoiding iterative, and graphing procedures.

There exist many numerical conformal mapping methods in the literature. An introduction to numerical methods for conformal mapping can be found in the books ^[12,13]. For some recent numerical conformal mapping methods, see ^{[14,15,16,17,18]}.

In this paper, by means of conformal mapping, we derive an analytical formula for the zero of the Szegö kernel for $ \Omega $. The conformal mapping of $ \Omega $ onto an annulus is computed numerically based on the boundary integral equation with the generalized Neumann kernel ^[15]. The integral equation is uniquely solvable Fredholm integral equation of the second kind.

The plan of the paper is as follows: In Section 2, some known techniques for calculating the zero of the Szegö kernel for $ \Omega $ are given. In Section 3, the conformal mapping method for computing the zero of the Szegö kernel for $ \Omega $ via integral equation with the generalized Neumann kernel are shown. In Section 4, the numerical implementations of the techniques in Sections 2 and 3 are discussed. In Section 5, seven numerical examples for computing the zeros of the Szegö kernel for various $ \Omega $ are given based on conformal mapping, some comparisons with other techniques of Section 2 are also made. The last Section 6 presents some concluding remarks.

2.   Preliminaries

Let $ \Omega $ be a bounded doubly connected region with the boundary $ \Gamma = \Gamma_{0}\cup\Gamma_{1} $ consists of two smooth Jordan curves with the inner curve $ \Gamma_{1} $ oriented clockwise and outer curve $ \Gamma_{0} $ oriented counterclockwise. Further, we assume $ \alpha $ and $ a $ ($ \alpha\ne a $) are auxiliary given distinct points in the region $ \Omega $ and $ z_0 $ is an auxiliary given point in the simply connected region bounded by $ \Gamma_1 $.

The curve $ \Gamma_j $, $ j = 0, 1 $ is parametrized by a $ 2\pi $-periodic triply continuously differentiable complex-valued functions $ z_j(s) $ with $ z'_j(s)\ne 0, s\in J_j = \left[0, 2\pi\right] $. The total parameter domain $ J = J_0\cup J_1 $ is the disjoint union of two intervals $ J_j = \left[0, 2\pi\right] $. Define a parametrization of the whole boundary $ \Gamma $ as the complex function $ z(s) $ define on $ J $ by

For the special case where $ \Omega $ is an annulus $ D = \left\{z:\rho < |z| < 1\right\} $ bounded by $ C = C_{0}\cup C_{1} $, $ 0 < \rho < 1 $, there exists a bilateral series representation for the Szegö kernel for $ D $ given by ^[3]

It has a unique zero at $ z = -\rho/\overline{a} $ ^[3]. The Szegö kernel for $ D $ has another bilateral series representation ^[4] (in an equivalent form)

The bilateral series (2.2) is actually a basic bilateral series and can be expressed as an infinite product. For $ a\in D $, $ z\in D \cup C $, the Szegö kernel for $ D $ can be represented by the infinite product ^[5]

The infinite product in (2.4) is convergent for $ \rho < 1 $ and $ \rho^2 < \left\vert az \right\vert < 1 $. The zero of $ S_{D}(z, a) $ in $ D $ is equal to $ z = -\rho/\overline{a} $, which is the zero of the factor $ \overline{a}z+\rho $.

For the doubly connected region $ \Omega $, the Szegö kernel $ S_{\Omega}(z, a) $ satisfies the Kerzman-Stein integral equation on $ \Gamma $ ^[3,6,7]

where

and

The Kerzman-Stein kernel $ A(z, w) $ is continuous on $ \Gamma $. In fact the integral equation (2.5) is also valid for an $ n $-connected region for $ n\ge 3 $ ^[6,7]. Using the Cauchy integral formula, the interior values of the Szegö kernel for every $ z\in\Omega $ can be determined by

The derivative of the Szegö kernel on $ \Gamma $ is computed by ^[9]

where

and

The zero of the Szegö kernel $ z^{*} $ for the doubly connected region $ \Omega $ has the explicit formula ^[8]

The boundary values of $ S_{\Omega}(z, a) $ and $ S_{\Omega}'(z, a) $ can be computed by solving the integral equation (2.5) and applying (2.10) respectively. The zero $ z^{*} $ has been computed numerically in ^[11] based on (2.5), (2.10), and (2.11).

The Szegö kernel is closely connected to the Ahlfors function. The Ahlfors function $ g(z) $ is a connected two-to-one analytic function mapping $ \Omega $ onto the unit disk $ E = \left\{w:|w| < 1\right\} $, satisfying $ g(a) = 0 $, $ g'(a) > 0 $. The function $ g(z) $ has another zero from the unique solution of $ S_{\Omega}(z, a) $ = 0. Further, $ g(z) $ maps each component of the boundary of $ \Omega $ one-to-one onto the unit circle. Thus the boundary values of $ g(z) $ are given by

where $ \theta_j(t) $, $ j = 0, 1, $ are the boundary correspondence functions. It can be shown that ^[9]

where $ S_{\Omega}\left({z\left(t \right), a_0 } \right) $ and $ S_{\Omega}'\left({z\left(t \right), a_0 } \right)z'\left(t \right) $ are computed by solving the integral equations (2.5) and (2.10) respectively.

For all $ z\in\Gamma $, the function $ \theta'(t) $ and the zero $ z^{*} $ for the Szegö kernel for $ \Omega $ are related by the nonlinear algebraic equation (by treating $ z^{*} $ as unknown) ^[19]

where $ \theta'(t) $ can be computed using (2.13). Murid et al. ^[11] calculated $ z^{*} $ as follows

where

and

Again $ \theta'(t) $ can be computed using (2.13). By taking imaginary part on both sides of (2.14), it reduces to the equation derived in ^[10], i.e.,

where

is the Neumann kernel. The Newton iterative method and the trapezoidal rule has been used to solve $ z^{*} $ from the nonlinear algebraic equation (2.17) in ^[9].

Theoretically, the Szegö kernel $ S_{\Omega}(z, a) $ for $ \Omega $ can be found using a transformation formula under conformal mapping. If $ \Omega $ is any doubly connected region with smooth boundary $ \Gamma $ and $ f(z) $ is a conformal map of $ \Omega $ onto $ D $, then ^[6]

where $ S_D $ is represented by (2.2). Note that (2.2) contains the inner radius $ \rho $ which needs to be computed.

In the next section, we give another explicit formula for computing zero $ z^{*} $ of $ S_{\Omega}(z, a) $ based on (2.19).

3.   Computing the zero of $ S_{\Omega}(z, a) $ via conformal mapping

Consider the doubly connected region $ \Omega $ with boundary denoted by $ \Gamma $ as described in Section 2. Let $ f(z) $ be a conformal map from $ \Omega $ to the annulus $ D = \left\{w:\rho < |w| < 1\right\} $, where the modulus (or the inner radius) $ \rho $ can be computed by a special method which will be explained later. Consequently $ f^{-1} $ is an inverse map of $ D $ onto $ \Omega $.

Theorem 1. The Szegö kernel for $ \Omega $ can be represented by the bilateral series as

The zero of $ S_{\Omega}(z, a) $ in $ \Omega $ is

Proof. Applying (2.2) to the transformation formula (2.19), yields

Using the fact that $ S_{D}(z, a) $ has a zero at $ z = -\rho/\overline{a} $ in $ D $, the zero $ z^{*} $ of $ S_{\Omega}(z, a) $ for $ \Omega $ satisfies $ f(z^{*})\overline{f(a)} = -\rho $, or $ f(z^{*}) = -\rho/\overline{f(a)} $ which implies $ z^{*} = f^{-1}\left(-\rho/\overline{f(a)}\right) $.

Formula (3.1) is an explicit formula for the zero of $ S_{\Omega}(z, a) $ in terms of $ f $ and $ f^{-1} $. Thus formula (3.1) is applicable provided the mapping functions $ f $ and $ f^{-1} $ are known. These functions are known only for very few special regions. For general region $ \Omega $ we must resort to numerical conformal mapping.

The following theory from ^[16,20] shows an integral equation method with the generalized Neumann kernel to compute the conformal map $ w = f(z) $ from $ \Omega $ onto the annulus $ D $ with normalization

where $ \alpha $ is an auxiliary given point in $ \Omega $.

Denote by $ H $ the space of all functions of the form

where $ \mu_{0}(s) $ and $ \mu_{1}(s) $ are $ 2\pi $-periodic Hölder continuously real functions on $ J_0 $ and $ J_{1} $, respectively. Define a complex function $ B $ on $ \Gamma $ as ^[16,20]

For $ \mu $ and $ \gamma $ in $ H $, consider the following integral equation ^[16,20]

where the integral operators $ {\bf N} $ and $ {\bf M} $ are defined respectively by

and

with the kernels $ N(s, t) $ and $ M(s, t) $ defined respectively as

and

The kernel $ N(s, t) $ is known as the generalized Neumann kernel.

The integral equation (3.5) is uniquely solvable for any real Hölder continuous function $ \gamma\in H $. Additionally, if $ \mu $ is the unique solution of the boundary integral equation (3.5), then the real function $ h $ defined by

is a piecewise constant function on the boundary $ \Gamma $, where $ h_j $ are real constants $ j = 0, 1 $ and $ h(t) = h_j $ for $ z(t)\in\Gamma_j $. Moreover,

are the boundary values of an analytic function $ F $ in the doubly connected region $ \Omega $. For $ z\in \Omega $ the function $ F(z) $ is calculated by the Cauchy integral formula

For more details on the generalized Neumann kernel, see ^[21].

Theorem 2. ^[20] Let the function $ B $ be defined by (3.4), and the function $ \gamma $ be defined by

If $ \mu $ is the unique solution of the boundary integral equation (3.5), and the piecewise constant function $ h $ is given by (3.8), then the function $ F $ with the boundary values (3.9) is analytic in the region $ \Omega $, and the conformal mapping $ f $ is given by

and the modulus $ \rho $ is given by

The inverse mapping function $ f^{-1} $ is analytic and one-to one in the annulus region. If the boundary $ C $ of $ D $ is parametrized by $ \xi(t) $, $ t\in J $, the value of $ z = f^{-1}(w) $ at interior point $ w\in D $ can be computed using the Cauchy integral formula ^[22]

where $ f^{-1}(\xi(t)) = z(t) $ and $ \xi'(t) = f'(z(t))z'(t) $.

4.   Numerical implementations

In this section, we first review some numerical implementations for computing $ z^{*} $, the zero of $ S_{\Omega}(z, a) $, using the formulas (2.11), (2.14), and (2.15). The $ n $ equidistant collocation $ t_i $ is defined by

The integral in (2.11) is discretized using the trapezoidal rule with $ n $ equidistant nodes in each interval $ J_j, \quad j = 0, 1 $. Since all relevant functions are $ 2\pi $-periodic, the trapezoidal rule is the most accurate method to numerically integrate the periodic functions ^[23,24]. Let $ z^{*}_{1, n} $ represents the zero $ z^{*} $ approximated using (2.11), i.e.,

where the integral equation (2.5) is solved numerically to get the approximate values $ S_{\Omega, n}(z(t_i), a) $ of $ S_{\Omega}(z(t_i), a) $, while the approximate values $ S_{\Omega, n}'(z(t_i), a) $ of $ S_{\Omega}'(z(t_i), a) $ are computed using (2.10) (for more details see ^[11]).

The Newton iterative technique with trapezoidal rule can be used to solve for the zero $ z^{*} $ from the nonlinear algebraic equation (2.17), where $ \theta'(t) $ is calculated using Eq (2.13). It is shown that the zero $ z^{*} $ has two unknowns because it is divided into real and imaginary parts (for more details, see ^[9]). Let $ z^{*}_{2, n} $ represents the zero $ z^{*} $ approximated using (2.17).

To evaluate (2.15) for $ z^{*} $ at $ t\in J_0 $, the trapezoidal rule is used to discretize the integral (2.16). The approximation of the zero $ z^{*} $ using (2.15) is denoted by $ z^{*}_{3, n} $, i.e.,

where

where $ q_{0, n}(t_i) $ is the approximation of $ q_{0}(t_i) $ computed numerically using (2.16) (see ^[11] for details).

We next describe a numerical method for computing $ z^{*} $ via conformal mapping using (3.1) and Theorem 2. We use the following algorithm for the computation of $ z^{*} $:

$ (1) $ Solve the integral equation (3.5) with $ \gamma $ given by (3.11) for $ \mu $.

$ (2) $ Calculate the boundary values $ F(z(t)) $ using (3.9).

$ (3) $ Calculate $ F(a), a\in \Omega $, using (3.10).

$ (4) $ Compute $ f(a) $ in (3.1) using (3.12) and $ \rho $ using (3.13).

$ (5) $ Calculate $ f^{-1} $ in (3.1) using (3.14) to compute $ z^{*} $.

The MATLAB function $ \texttt{fbie} $ in ^[18] provides us an efficient method for solving the boundary integral equation (3.5). The function $ \texttt{fbie} $ is based on discretizing the boundary integral (3.5) using the Nyström method with the trapezoidal rule ^[20,23]. This discretization leads to a non-symmetric linear system. Then, the MATLAB function $ \texttt{gmres} $ is used to solve the linear system. The matrix-vector multiplication in the GMRES method is computed using the MATLAB function zfmm2dpart in the toolbox $ \texttt{FMMLIB2D} $ ^[25]. The function $ \texttt{fbie} $ also provides us with approximations to the piecewise constant function $ h $ in (3.8). The computational cost for the overall method is $ \text{O}(n \text{log} n) $ operations where $ n $ (an even positive1 integer) is the number of nodes in each of the intervals $ J_0 $ and $ J_1 $.

To use the MATLAB function $ \texttt{fbie} $, the vectors $ \texttt{z} $, $ \texttt{zp} $, $ \texttt{B} $, and $ \texttt{gam} $ that contain the discretization of the functions $ z(t) $, $ z'(t) $, $ B(t) $, and $ \gamma(t) $, respectively, are stored in MATLAB. Then we call the function

Once the discretization of the two functions $ \mu(t) $ and $ h(t) $ are computed, we use

to find approximations $ F_n $ to the boundary values of the function $ F $. Then approximations $ F_n(z) $ to the values of the function $ F(z) $ for any vector of points $ z\in\Omega $ can be obtained using the Cauchy integral formula (3.10). Numerically we carry out this computation by applying the MATLAB function $ \texttt{fcau} $ ^[18] by calling

In this way, the approximate value of $ f_{n}(a) $ for $ f(a) $ in (3.1) is computed.

The approximate value of $ f_{n}^{-1} $ for $ f^{-1} $ in (3.1) is computed with the help of (3.14). For numerically computing the inverse mapping function $ f^{-1}(w) $, we apply the MATLAB function $ \texttt{fcau} $ ^[18] by calling

where

and

The approximation of zero $ z^{*} $ using (3.1) and Theorem 2 is represented by $ z_{4, n}^{*} $.

The computations presented in this paper were performed on ASUS Laptop with Intel(R) Core(TM) i7-3537H CPU @ 2.00 GHz, 2.50 GHz, 6 Core(s), and 4 GB RAM. We have used Mathematica for computing $ z_{1, n}^{*} $, $ z_{2, n}^{*} $, $ z_{3, n}^{*} $, and MATLAB R2022a for computing $ z_{4, n}^{*} $.

5.   Numerical examples

In this section, we show some examples of conformal mapping using the integral equation with the generalized Neumann kernel to calculate the zero $ z^{*} $ of the Szegö kernel for $ \Omega $ based on (3.1). Numerical comparisons for $ z^{*} $ using (2.11), (2.14), and (2.15) are also given.

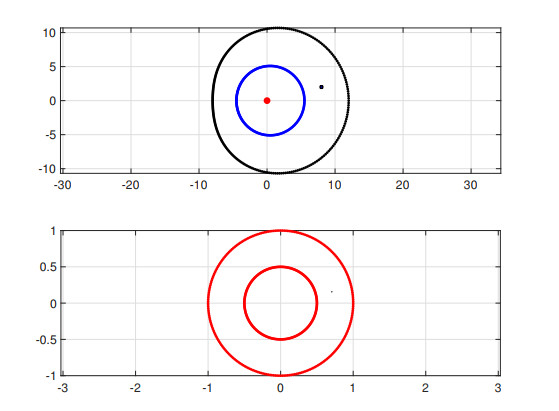
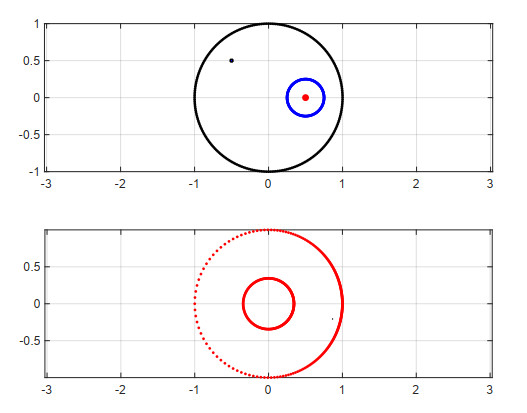
Example 1. Region bounded by circles.

Consider a region $ \Omega $ bounded by the circles

as shown in Figure 1. The exact mapping function that maps $ \Omega $ onto $ D = \left\{w:\rho < |w| < 1\right\} $ is [26, p. A-21]

where

and the exact inner radius is

The inverse mapping function is

Using (3.1) the exact zero of the Szegö kernel $ S_{\Omega}(z, a), $ with $ a\in\Omega $, is

For numerical implementation we have selected $ c = 0.25 $, $ d = 0.75 $, $ a = -0.5-0.5i $, $ z_0 = 0.5 $, and $ \alpha = -0.5 $. The computed exact inner radius $ \rho $ and the exact zero $ z^{*} $ are

and

Table 1 shows that the absolute errors $ \vert z^{*}-z^{*}_{1, n}\vert $, $ \vert z^{*}-z^{*}_{2, n}\vert $, $ \vert z^{*}-z^{*}_{3, n}\vert $, $ \vert z^{*}-z^{*}_{4, n}\vert $, and $ \vert \rho-\rho_n\vert $ are decreasing to zero with increasing number of nodes $ n $. The computation of the zero $ z^{*} $ using (3.1) together with Theorem 2 produces better accuracy than that of the other methods using (2.11), (2.14), and (2.15).

Example 2. Region bounded by limacons.

Consider a region $ \Omega $ bounded by limacons

with $ a_0 = 10, a_1 = 5, b_0 = 2 $, and $ b_1 = 0.25b_0 $, such that

as shown in Figure 2. The exact mapping function that maps $ \Omega $ onto $ D = \left\{w:\rho < |w| < 1\right\} $ and the exact radius are ^[14]

The inverse mapping function is

Using (3.1), the exact zero of the Szegö kernel $ S_{\Omega}(z, a) $, with $ a\in\Omega $, is

For our numerical work, we have chosen $ a = 8+2i $, $ \alpha = 10 $, and $ z_0 = 0 $. The computed exact inner radius $ \rho $ and exact zero $ z^{*} $ are

and

Table 2 shows that the absolute errors $ \vert z^{*}-z^{*}_{1, n}\vert $, $ \vert z^{*}-z^{*}_{2, n}\vert $, $ \vert z^{*}-z^{*}_{3, n}\vert $, $ \vert z^{*}-z^{*}_{4, n}\vert $, and $ \vert \rho-\rho_n\vert $ are decreasing to zero with increasing number of nodes $ n $. The computation of the zero $ z^{*} $ using (3.1) together with Theorem 2 produces better accuracy than that of the other methods using (2.11), (2.14), and (2.15).

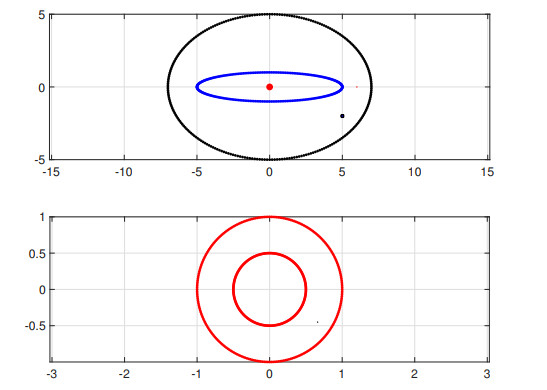
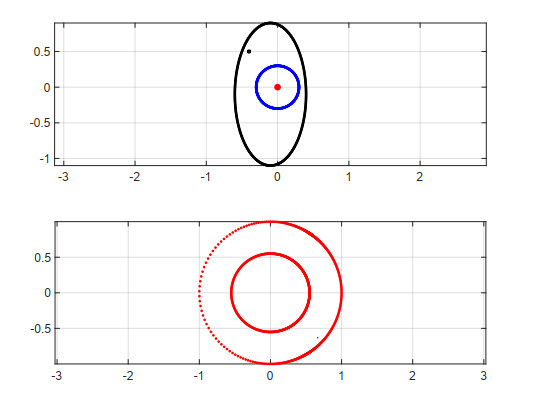
Example 3. Region bounded by ellipses.

Consider a region $ \Omega $ bounded by the ellipses

with $ a_0 = 7, a_1 = 1, b_0 = 5, b_1 = 5 $, such that

as shown in Figure 3. The exact mapping function that maps $ \Omega $ onto $ D = \left\{w:\rho < |w| < 1\right\} $ and the exact radius are ^[14]

The inverse mapping function is

Using (3.1), the exact zero of the Szegö kernel $ S_{\Omega}(z, a) $ is

For our numerical work, we have chosen $ a = 5-2i $, $ \alpha = 6 $, and $ z_0 = 0 $. The computed exact inner radius $ \rho $ and the exact zero $ z^{*} $ are

and

Table 3 shows that the absolute errors $ \vert z^{*}-z^{*}_{1, n}\vert $, $ \vert z^{*}-z^{*}_{2, n}\vert $, $ \vert z^{*}-z^{*}_{3, n}\vert $, $ \vert z^{*}-z^{*}_{4, n}\vert $, and $ \vert \rho-\rho_n\vert $ are decreasing to zero with increasing number of nodes $ n $. The computation of the zero $ z^{*} $ using (3.1) together with Theorem 2 produces better accuracy than that of the other methods using (2.11), (2.14), and (2.15).

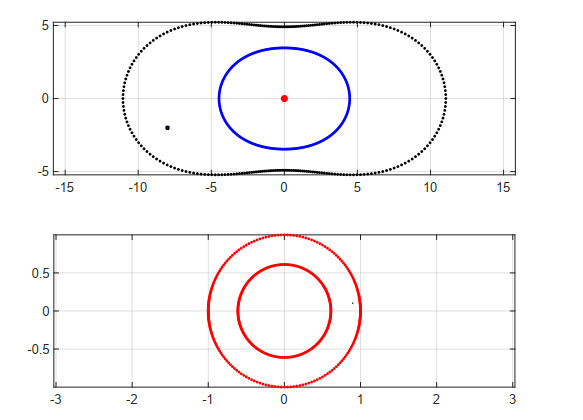
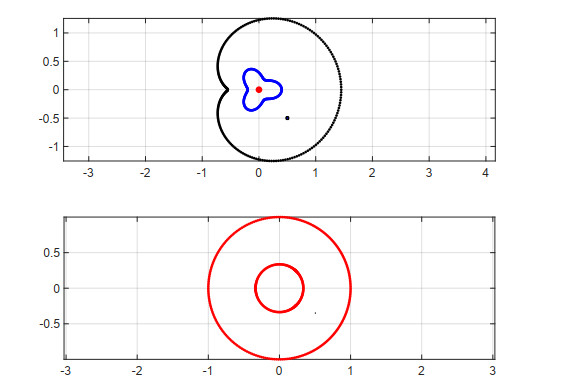
Example 4. Region bounded by ovals of Cassini.

Consider a region $ \Omega $ bounded by the ovals of Cassini

with

and $ a_0 = 8.5488 \text{ (up to 4 decimal places)}, a_1 = 4, b_0 = 7, b_1 = 2 $, such that

as shown in Figure 4. The exact mapping function that maps $ \Omega $ onto $ D = \left\{w:\rho < |w| < 1\right\} $ and the exact radius are ^[14]

and

The inverse mapping function is

Using (3.1), the exact zero of the Szegö kernel $ S_{\Omega}(z, a) $ is

For our numerical work, we have chosen $ a = -8-2i $, $ \alpha = -9 $, and $ z_0 = 0 $. The computed exact radius $ \rho $ and the exact zero $ z^{*} $ are

and

Table 4 shows that the absolute errors $ \vert z^{*}-z^{*}_{1, n}\vert $, $ \vert z^{*}-z^{*}_{2, n}\vert $, $ \vert z^{*}-z^{*}_{3, n}\vert $, $ \vert z^{*}-z^{*}_{4, n}\vert $, and $ \vert \rho-\rho_n\vert $ are decreasing to zero with increasing number of nodes $ n $. The computation of the zero $ z^{*} $ using (3.1) together with Theorem 2 produces better accuracy than that of the other methods using (2.11), (2.14), and (2.15).

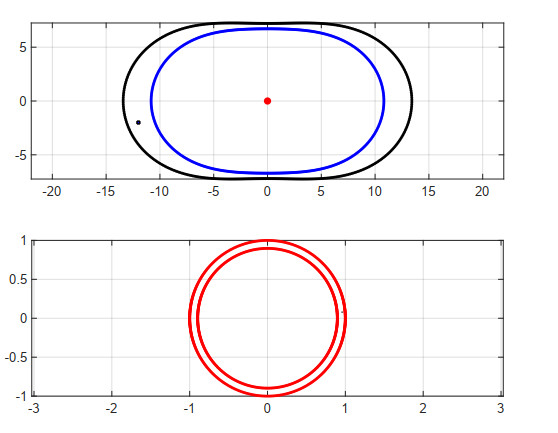
Example 5. Narrow region bounded by ovals of Cassini.

Consider a similar region as in Example 4 with $ a_0 = 10.7703\quad \text{(up to 4 decimal places)} $, $ a_1 = 8, b_0 = 9, b_1 = 6 $, such that

as shown in Figure 5. The region is much narrower than the region shown in Example 4.

For our numerical work, we have chosen $ a = -12-2i $, $ \alpha = -12.5 $, and $ z_0 = 0 $. The computed exact radius $ \rho $ and the exact zero $ z^{*} $ are

and

Table 5 shows that the absolute errors $ |z^{*}-z^{*}_{1, n}| $, $ |z^{*}-z^{*}_{2, n}| $, $ |z^{*}-z^{*}_{3, n}| $ using (2.11), (2.14) and (2.15) respectively produce poor accuracies, while $ |z^{*}-z^{*}_{4, n}| $ and $ |\rho-\rho_n| $ are decreasing to zero with increasing number of nodes $ n $. Table 5 shows the superiority of conformal mapping approach.

Example 6. Consider a region $ \Omega $ bounded by

with $ 0\le t\le 2\pi $, $ a_0 = 0.5-0.5i $, and $ \alpha = -0.50-0.5i $. The region is shown in Figure 6. The exact zero $ z^{*} $, the exact mapping function $ f(z) $, and the inner radius $ \rho $ for this region are unknown.

Since $ S_{\Omega}(z^{*}, a) $ has zero as theoretical value, the accuracy is determined by calculating $ |S_{\Omega}(z^{*}_{1, n}, a)| $, $ |S_{\Omega}(z^{*}_{2, n}, a)| $, $ |S_{\Omega}(z^{*}_{3, n}, a)| $, and $ |S_{\Omega}(z^{*}_{4, n}, a)| $ using (2.9) along with trapezoidal rule. Table 6 shows the numerical results and the conformal mapping approach yields high accuracy.

Example 7. We consider an annulus $ \Omega $ bounded by

with $ 0\le t\le 2\pi $, $ c = -0.1-0.1i $, $ \rho = 0.3 $, $ a_0 = -0.4+0.5i $, and $ \alpha = -0.3-0.5i $. The test region is shown in Figure 7. The exact zero $ z^{*} $, the exact mapping function $ f(z) $, and the inner radius $ \rho $ for this region are unknown.

Since $ S_{\Omega}(z^{*}, a) $ has zero as theoretical value, the accuracy is determined by calculating $ |S_{\Omega}(z^{*}_{1, n}, a)| $, $ |S_{\Omega}(z^{*}_{2, n}, a)| $, $ |S_{\Omega}(z^{*}_{3, n}, a)| $, and $ |S_{\Omega}(z^{*}_{4, n}, a)| $ using (2.9) based on trapezoidal rule with modification ^[27]. Table 7 shows the numerical results and superiority of conformal mapping approach.

The computations above show that the approximations $ z_{1, n}^{*} $ in (4.1) involves trapezoidal rule and approximations $ S_{\Omega, n}(z_0(t_i), a) $, $ S_{\Omega, n}(z_{1}(t_i), a) $, $ S_{\Omega, n}'(z_0(t_i), a) $, and $ S_{\Omega, n}'(z_{1}(t_i), a) $. The approximation $ z_{2, n}^{*} $ involves trapezoidal rule, Newton iterative method and approximations $ \theta_{n}'(t_i) $ based on approximations $ S_{\Omega, n}(z(t), a) $ and $ S_{\Omega, n}'(z(t), a) $. The approximation $ z_{3, n}^{*} $ involved approximations $ q_{0, n}(t_i) $ based on trapezoidal rule and approximation $ \theta_{n}'(t_i) $ which is further based on approximations $ S_{\Omega, n} $ and $ S_{\Omega, n}' $. However, the approximation $ z_{4, n}^{*} $ does not rely on approximations $ S_{\Omega, n} $, $ S_{\Omega, n}' $, and $ \theta_{n}' $ as in previous three methods. This explains why the conformal mapping approach yields better accuracy, even for a narrow region.

6.   Conclusions

Based on conformal mapping, we derived an analytical formula for the zero of the Szegö kernel for a doubly connected region with smooth boundaries. Special cases are the explicit formulas for the zeros of the Szegö kernel for doubly connected regions bounded by circles, limacons, ellipses, and ovals of Cassini. Some MATLAB functions have been used for fast and efficient numerical conformal mapping via the integral equation with the generalized Neumann kernel. The performance and accuracy of the presented conformal mapping method for computing the zeros of the Szegö kernel are compared to analytic solutions or to previous results whenever analytic solutions or previous results are available. Comparisons with previous results show that the conformal mapping approach always yields better accuracy, even for a narrow region. Furthermore, the conformal mapping approach requires only the first and second derivatives of the parametrization of the boundary, while previous methods require up to the third derivative.

The conformal mapping approach presented in this paper can also be extended to doubly connected region with piecewise smooth boundaries with corners. The integral equation (3.5) is valid only at off-corner points ^[22,28]. By means of singularity subtraction ^[29], (3.5) can be written in an alternative form for which the trapezoidal rule with a graded mesh ^[30] can be applied wherein the derivative of the new integrand vanishes at the corner points. See ^{[18,22,28,29,30]} for more details.

Another competitive approach for numerical conformal mapping of doubly connected region with corners is the conjugate function method with the hp-FEM algorithm ^[31,32]. In [21, Example 3.4, p.8], for a square in square region it is found that the computations of the conformal capacity of a condenser, using the integral equation with the generalized Neumann kernel with the trapezoidal rule and graded mesh are not as accurate as the results obtained by the hp-FEM algorithm in ^[32]. Thus, we think computing the zero of the Szegö kernel for a doubly connected region with piecewise smooth boundaries with corners constitutes a good problem for future research.

Acknowledgments

This work was supported by the Ministry of Higher Education Malaysia under Fundamental Research Grant Scheme (FRGS/1/2019/STG06/UTM/02/20). This support is gratefully acknowledged. The first author would also like to acknowledge the Tertiary Education TrustFund (TETFund) Nigeria for overseas scholarship award. The authors thank the referees for their valuable comments and suggestions which improved the presentation of this paper.

Conflict of interest

The authors declare that they have no competing interests.