The historical lepto-variance of the US stock returns

1.   Introduction

The regression tree (RT) is a machine learning model commonly used for explaining a continuous target variable based on various features. RTs are similar to decision trees, being constructed by recursively partitioning the input space into regions and assigning a constant value to each region. Each internal node in a regression tree represents a decision based on a particular feature. The tree structure is hierarchical, with the first decision at the root node and subsequent split decisions at higher depths creating further branching based on the outcomes of previous decisions. For a brief and concise introduction to RTs see Krzywinski and Altman (2017), Torgo (2011), and Elith et al. (2008).

A great advantage of RTs is their interpretability and simple visual representation, which results in a simple-to-understand decision-making process. Additionally, RTs can capture complex, nonlinear relationships in the data. Using the RT methodology, Polimenis (2022) uniquely defined the sample lepto-variance as variance beyond the explanatory power of a RT, and macro-variance as the upper bound of sample variability that may be explained.

Unlike the residual mean squared error (MSE) in a regression that depends on the utilized factors, the lepto-variance is a new type of idiosyncratic sample-specific variability that pertains to the portion of variance that cannot be mitigated by any regression tree, thus providing a measure of inherent variance at a specific tree depth. By establishing an upper boundary on the "resolving power" of RTs for a sample, this statistical concept is valuable as it offers insights into the intrinsic structure of the dataset. At each RT depth level, the overall variance within the dataset is broken into lepto- and macro-variance. This is related to the 1-d clustering problem (Grønlund et al., 2017). The k-means problem in higher dimensions is NP-hard (Aloise et al., 2009). Similar techniques have been used by cartographers to produce so-called choropleth or thematic maps, via the so-called natural breaks introduced by Jenks and Caspall (1971). Data in choropleth maps are categorized using a modification of the Jenks natural breaks classification method. These methods cluster data into groups that minimize the within-group variance and maximize the between-group variance.

Following Polimenis (2022), in this paper, the lepto-regression, lepto-variance, and lepto-ratio concepts are defined and then initially explored by providing simple intuitive examples. Then, 1- and 2-bit lepto-regression analysis for the entire US stock universe is performed utilizing historical daily market return data for the previous 96-year period. The sample comprises 25,272 daily returns from July 1, 1926, to June 30, 2022. We find that the optimal 1-bit RT split is roughly a 30–70 balance. The left and right children subsets are centered roughly around −1% and +0.5%. The 1-bit macro-variance is almost 42% of the total US stock variability, while the residual 58% is structured beyond the resolving power of any 1-bit RT. The 2-bit lepto-variance equals 26.3% of the total, with 42% and 47% the 1-bit lepto-variance of the left and right subtree, respectively.

1.1.   Motivation

The relationship between the total explanatory power and the number of independent variables is complicated. The total explanatory power of a regression model is often assessed using metrics such as the coefficient of determination (${R}^{2}$). R-squared represents the dependent variable variability proportion explained by the independent variables and is a measure of how well the independent variables in a regression model explain dependent variable variation. Adding relevant variables can enhance explanatory power in a linear regression, but careful consideration is needed to avoid overfitting, i.e., a situation of a model fitting the training data closely by capturing noise. Similarly, in a financial regression of stock returns on market-wide factors, the residual (idiosyncratic) variance depends on the factors used in the regression. In general, we can get lower residual variance by adding extra financial factors.

Improving our understanding of the inherent explanatory power of RTs is valuable, as they are a fundamental building block for more advanced ensemble methods, such as random forests and gradient-boosted trees, which combine multiple trees to improve predictive performance and robustness. But, as with linear regression, overfitting the training data is one of the RT challenges, as trees can easily capture noise rather than underlying patterns. Pruning and other regularization techniques are used to address this issue.

1.2.   Motivation from the field of financial risk management

Financial risk management is a large field of academic and practical significance for banking and finance. The key starting point of managing risk is to properly quantify it, which effectively means measuring volatility and correlations for the entire investable asset universe. Understanding the sources of volatility is of great interest. Investors place importance on understanding the factors that contribute to investment return volatility, as it directly affects both risk assessment and the overall decision-making process.

The introduction of a model-free method to analyze return variability has always been of great interest to the academic and financial practitioner communities. For example, the volatility index (VIX) introduced by Whaley (1993) is referred to by some as the market "barometer" and is tradable in CBOE. The index was later calculated via a more model-free method developed by Demeterfi et al. (1999). However, the VIX calculation is neither simple nor intuitive.

1.3.   The role of idiosyncratic financial risk

When utilizing machine learning techniques in financial analysis, we use financial factors as features, being interested in finding the factors that explain a large fraction of the total stock return variance. Stock return variance that cannot be explained by broad market financial factors is considered idiosyncratic for the specific stock. The total risk of investment results from adding risks determined by exposure to market factors (market risks) and idiosyncratic volatility, which represents the risk component specific to the asset and not determined or related (i.e., orthogonal) to any wider market movements. The pricing implications of idiosyncratic volatility are still not well understood (Ang et al., 2006; Campbell et al., 2001).

In conclusion, as investors aim to diversify portfolios and mitigate risk exposure, quantifying variance is crucial. A novel, model-free, and simple statistical method for analyzing total return variability may enable investors to make better decisions, improve risk assessment, and create portfolios that align with their total risk tolerance and investment objectives.

2.   Lepto-regression

In splitting a nominal predictor taking $q$ possible labels (unordered values), there exist ${2}^{q-1}-1$ possible binary partitions of these labels. If all these partitions need to be evaluated, the computation becomes prohibitive for any (except for very small) $q$ values. Various theorems related to the concavity of the underlying impurity function allow the problem to be simplified into a linear search of only $q-1$ partitions, where attribute values are sorted based on their strength of correlation with the target. Most notably, Fisher (1958) showed that for a continuous-valued target Y, the least squares partition of a set is contiguous. Breiman et al. (1984) extended this for a decision tree with binary (2-class) target Y (see the discussion in Ripley, 1996 and Hastie et al., 2009).

The process of constructing a regression tree involves recursively partitioning the sample based on the selected features and split thresholds, with a procedure continuing until a stopping criterion (a maximum depth or a minimum number of samples for the node) is met. At each decision node, the algorithm selects a feature and a threshold to split the data into two subsets with the goal of minimizing the residual target variance within each subset. A constant value is assigned to the instances that reach terminal (or leaf) nodes of the tree.

RTs provide a binary splitting of the sample space with minimization criterion the residual sum of squares (i.e., sum of squared error) $RSS = {\sum }_{i}{\left({y}_{i}-\widehat{y}\left({x}_{i}\right)\right)}^{2}$, with $\widehat{y}\left({x}_{i}\right) = {\widehat{y}}_{i}$ the prediction for ${y}_{i}$ given factor values ${x}_{i}$. RTs predict using the average values ${\widehat{y}}_{i} = {\stackrel{-}{y}}_{i}$ within each subset, as they minimize the residual mean square error $MSE = \frac{1}{n}{\sum }_{i}{\left({y}_{i}-{\stackrel{-}{y}}_{i}\right)}^{2}$.

2.1.   Definition of sample lepto-variance

At each internal tree node $(\#j)$, the RT performs a sorting of the subsample reaching this node $Sj$ using the chosen split factor $xj$ and finds the split point $cj$ that produces the maximum MSE drop from the node to its children $Lj$ and $Rj$. Generally, sorting a sample based on a factor $xj$ will not sort the target $y$. With no loss of generality, assume that the left child L contains the "small" $y$ values (i.e., assume $\stackrel{-}{{y}_{L}} = mean\left\{y\in L\right\} < \stackrel{-}{{y}_{R}} = mean\left\{y\in R\right\}$).

Definition. A binary split of $S$ into $L$ and $R$ is sorted if all target values $y$ in $L$ are smaller than all target values in $R$.

As an extension of the Fisher (1958) theorem on grouping, the following lemma for RTs is shown in Polimenis (2022)

Lemma 1. In terms of minimizing MSE in a RT, when splitting a sample $S$, it is always beneficial to utilize a sorted split. Thus, the best factor to use (in terms of MSE drop) is the dependent variable itself.

Proof. Let's assume an unsorted split of a sample $S$ into $L$ and $R$ (with no loss of generality, assume $\stackrel{-}{{y}_{L}} < \stackrel{-}{{y}_{R}}$). Then, the maximum $y$ value of the left subtree ${u}_{1}$ is larger than the minimum value of the right subtree ${u}_{0}$

But then, we can get a better split by swapping ${u}_{0}$ with ${u}_{1}$ into $L$ and $R$, respectively. Because moving ${u}_{0}$ into $L$ and ${u}_{1}$ into $R$ will move the center of the $L$ subsample to the left and the center of the right subsample to the right, thus producing a larger separation between the left and right subsamples without changing the relative sample sizes. By the law of total variance, a larger between-group variability means a smaller within-group variability and thus a better split.

Since the best binary split is always a sorted split, and regressing the target on itself allows all sorted splits to be evaluated, using the target as a factor will provide an upper bound on the explained variance (or lower bound on residual MSE).

Definition. We call lepto-regression the process of constructing an RT of a target feature on itself, and sample lepto-variance as the residual MSE of the lepto-regression.

We use $\mu {1}^{2}$ and $\lambda {1}^{2}$ to denote the 1-bit macro and lepto-variance, respectively (residual MSE for RTs with depth 1). Total variance equals

3.   The $\boldsymbol{\lambda }{1}^{2}$ lepto-variance of simple examples

To get a better understanding of the novel concept of lepto-variance, a few simple example calculations of $\lambda {1}^{2}$ are presented and discussed.

The simplest case is that of the equiprobable 2-member set. Without loss of generality, assume the set {−0.5, 0.5}. The total variance of this sample is 0.25. In this (degenerate) case, the only split (and thus optimal) is the separation of the two members that produces a variance drop of 0.25 and a residual (lepto) variance remainder equal to zero ${\sigma }^{2} = \mu {1}^{2}$ and $\lambda {1}^{2} = 0$.

Next, consider the {−1, 0, 1} equiprobable set. This will split into {−1} and {0, 1} with its total variance of ${\sigma }^{2} = \frac{2}{3}$ split into macro-variance of $\mu {1}^{2} = \frac{1}{2}$ and lepto-variance of $\lambda {1}^{2} = \frac{1}{6}$

The next case is the equiprobable 4-member set {−1.5, −0.5, 0.5, 1.5}. With no loss of generality, points are chosen to center at zero to help with mental calculations. In this case, the optimal split is the balanced split producing two equiprobable 2-member sets left and right, with residual variance equal to $\lambda {1}^{2} = 0.25$. The two clusters {−1.5, −0.5} and {0.5, 1.5} are centered at −1 and 1, respectively, giving an inter-cluster distance of 2, and a variance drop that equals

Definition. We define the useful concept of lepto ratio $l{R}^{2}$ as the ratio of lepto-variance (at a specific depth) to total sample variance. For the 1-bit case, this equals $l{R1}^{2} = \lambda {1}^{2}/{\sigma }^{2}$.

Using the law of total variance, in the last example, we calculate a total variance of $0.25+1 = 1.25$, and a lepto ratio $l{R1}^{2} = 20\%$ of the total sample variance.

3.1.   A first look at lepto-variance and split balance

From the discussion above for the 2- and 4-member sets, it may seem that the optimal split is always a balanced split. It is significant to note that the optimal split is not always balanced. We may understand some of the concepts related to the split balance (i.e., relative cluster weights) using as an example the 6-member equiprobable sample {−1, 0, 1, 2, 3, 4}. We may think of the entire sample as comprised of two separate clusters, {−1, 0, 1} and {2, 3, 4} centered at 0 and 3, with initial cluster "radius" epsilon equal to 1 and separated by inter-cluster distance delta equal to 3. Total sample variance is thus equal to ${\sigma }^{2} = \frac{{\delta }^{2}}{4}+\frac{2}{3}{ϵ}^{2}$. With epsilon = 1 and delta = 3, this equals $2.9167$ (see Table 1 below).

Separating the sample in the middle gives a residual variance of the two clusters equal to $\lambda {1}^{2} = \frac{2}{3}$ and a variance drop of $\frac{{\delta }^{2}}{4} = \frac{9}{4} = 2.25$. In this case, the balanced split is optimal. For example, if instead the sample is split by isolating −1, there is a var drop equal to only $\frac{1}{6}\times \frac{5}{6}\times {\left(2-\left(-1\right)\right)}^{2} = 1.25$ and there is $1.67 > \lambda {1}^{2}$ var left unexplained. Splitting at {−1, 0} and {1, 2, 3, 4} is better, as it gives a higher var drop equal to $\frac{1}{3}\times \frac{2}{3}\times {\left(2.5 -\left(-0.5\right)\right)}^{2} = 2$ and there is 0.9167 var left unexplained. But this is still inferior to the balanced split.

We want to understand what happens if the two clusters get more spread out. Take, for example (by increasing epsilon to 1.2), the set {−1.2, 0, 1.2, 1.8, 3, 4.2}. Again, the two clusters are centered at 0 and 3 (separated by delta = 3) but they are now more spread out (with higher cluster variance). Total variance is 3.21. Separating the set in the middle gives the expected variance of the two clusters equal to $0.67\times 1.44 = 0.96$ and a variance drop of $0.5\times 0.5\times 9 = 2.25$. The best split is still the balanced split, but now the benefit of the balanced split is less pronounced. For example, splitting the sample by isolating −1.2 gives a var drop equal to only $\frac{1}{6}\times \frac{5}{6}\times {\left(2.04 -\left(-1.2\right)\right)}^{2} = 1.458$ and there is 1.752 var left unexplained. Splitting at {−1.2, 0} and {1.2, 1.8, 3, 4.2} is even better, as it gives a var drop equal to 2.2050 and there is 1.0050 var left unexplained. But this is still inferior to the balanced split. Observe that isolating the "outlier" −1.2 is now more beneficial than in the previous case, as it explains 45.42% of the total var.

As the two clusters get more spread out, as in {−1.3, 0, 1.3, 1.7, 3, 4.3}, the balanced split is not optimal any longer. Again, the two internal clusters are centered at 0 and 3, but they are now more spread out (within cluster variance 1.1267). Total sample variance ${\sigma }^{2}$ is 1.1267 + 2.25 = 3.3767. Separating the sample in the middle again explains $\frac{1}{2}\times \frac{1}{2}\times 9 = 2.25$, but this time represents only 66.63% of the total variance (versus 77.14% in the case of epsilon = 1). The skewed splitting at {−1.3, 0} and {1.3, 1.7, 3, 4.3} is optimal with a var drop equal to $\mu {1}^{2} = \frac{1}{3}\times \frac{2}{3}\times {\left(2.575 -\left(-0.65\right)\right)}^{2} = 2.31125$.

4.   Empirical analysis

4.1.   Estimation of the historical lepto-variance of US stock returns

Here, the concept of lepto-variance of US stock returns is presented and, to provide some perspective, it is compared with the residual variance when two well-known financial factors, size (SMB) and book-to-value (HML), are used to capture return variability. Specifically, historical daily percentage return data for US stock returns starting in 1926 are analyzed. High-quality return data from http://mba.tuck.dartmouth.edu/pages/faculty/ken.french/data_library.html were downloaded on July 30, 2022.¹

¹ Copyright 2022 Kenneth R. French.

Table 2b presents descriptive return stats for daily returns of the entire US stock market and the two Fama-French factors SMB (size) and HML (value) for a 96-year period (in percentage). The variance for the entire sample is approximately 1.167. The average daily US stock return for this period is 4.2 bp (basis points), of which 3 bp is the risk part and 1.2 bp is the risk-free component.

In financial asset pricing, a well-known pricing model is the three-factor model of Fama and French (1993). The three-factor model is based on a time-series linear regression of excess portfolio returns of the type

with $R\left(t\right)$ being the return on a security or portfolio for period $t$, $rf\left(t\right)$ the risk-free return, $Mkt\left(t\right)-rf\left(t\right)$ the excess return on the value-weighted market portfolio above the risk-free asset, $SMB\left(t\right)$ the return on a diversified portfolio of small stocks minus the return on a diversified portfolio of big stocks for the period, and $HML\left(t\right)$ the difference between the returns on diversified portfolios of high and low book-to-market (B/M) ratio stocks. The three-factor linear model above assumes that the sensitivities b, s, and h in (2) capture the most variation in expected returns, and the true value of the alpha intercept in (2) should be near zero for well-priced securities.

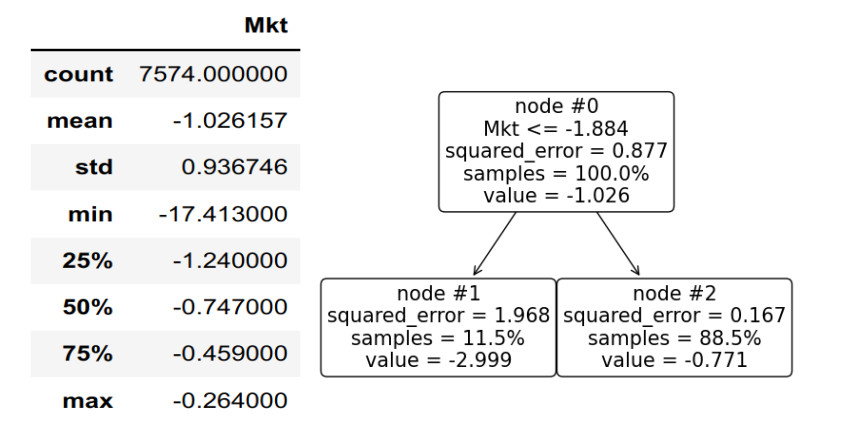
In the Figure below, the optimal depth of one RT when the US stock return vector (Mkt) is lepto-regressed is shown. The optimal split is a 30–70 balance, for a Mkt return less than or equal to −0.264. The two children subsets are centered roughly at −1% and 0.5%. Total sample variance is 1.167.

Sample 1-bit Lepto-variance equals

The 1-bit macro-variance (max variance drop) thus equals

This equals almost 42% of the total US stock variability. This implies a 1-bit lepto-ratio $lR{1}^{2} = 58\%$ comprising structure that cannot be removed by any 1-bit RT. Observe that the macro-variance could also be computed directly as the variance of a δ-scaled Bernoulli distribution with $p = 0.30$ and $\delta = 1.525 = 0.499 - (-1.026)$ via $\mu {1}^{2} = 0.3\times 0.7\times {1.525}^{2}$.

To put the historical 1-bit lepto-ratio of 58% in some perspective, the optimal 1-bit RT when US stock returns are regressed on the two Fama-French SMB and HML factors is also estimated and shown in the Figure below. When using the entire historical sample, HML is more efficient than SMB and thus chosen for the 1-bit RT. The tree is highly skewed and can explain very little of the total historical US stock variability. Residual squared error equals 1.1315 (roughly 97% of total MSE).

An interesting new statistic for any feature then is the percentage $mR{1}^{2}$ of the sample macro-variance that it can capture with a 1-bit RT. Using 1-bit RT, the Fama-French factors can only explain 0.0355 of the total MSE. This is only $mR{1}^{2} = \frac{0.0355}{0.489} = 7.26\%$ of the 1-bit macro-variance, i.e., the maximum MSE that may be explained by 1-bit RTs. Using SMB explains $mR{1}^{2} = \frac{0.025}{0.489} = 5.11\%$ of the 1-bit macro-variance $\mu {1}^{2}$ (see Table 3).

In Table 3 below, the summarized depth 1-bit lepto-regression analysis for 96 years of US stock returns and the two Fama-French factors is shown. Using 1-bit RTs, Fama-French factors explain only a small $mR{1}^{2}$ fraction of the total explainable MSE (sample macro-variance). Overall, HML slightly dominates SMB.

4.2.   The 2-bit historical lepto-structure of US returns

The concept of lepto-variance of a sample may also be defined for trees of a maximum depth larger than 1. As we move deeper down on an RT, there will always be less residual variance. The argument of Lemma 1 will locally still be valid; at any node, the best split is always achieved by the target itself (via a sorted split). But the greediness of the RT may in rare (degenerate) occasions result in a situation where sorting in a split is sub-optimal (Polimenis, 2022).

For the 4-element set {−1, 0, 1, 2}, the greedy 1-bit split correctly splits to {−1, 0} and {1, 2} for a final 1-bit residual MSE $\lambda {1}^{2} = 0.25$, thus explaining 1 out of the 1.25 total variance (i.e., $lR{1}^{2} = 20\%$). But when the greedy 1-bit split is applied on the 4-element set {−1, 0, 1, 4}, it myopically isolates the outlier 4 at the first split, thus explaining $\mu {1}^{2} = 3$ out of the total ${\sigma }^{2} = 3.5$ (i.e., $lR{1}^{2} = 14.3\%$). This is preferable to the balanced 1-bit split into {−1, 0} and {1, 4} that would only explain 2.25 out of the total 3.5 (i.e., $mR{1}^{2} = \frac{2.25}{3} = 75\%$). However, the balanced split would allow a better outcome down the tree, as it could capture the entire variation at the 2-bit split. On the contrary, the myopic isolation of the outlier 4 at the first split limits the 2-bit split, thus resulting in a final 2-bit residual MSE equal to $\frac{1}{8} > 0$.

In Polimenis (2022), it is conjectured that the lepto-regression-based split will still achieve the lowest residual squared error at any average depth. For example, the greedy 2-bit max depth tree in the example has a lower average depth of 1.75 bits and should not be compared with the balanced split resulting in an average depth of 2 bits. Based on this, the lepto-variance ${\lambda j}^{2}$ of a sample at $j$ -bits is defined as the residual variance when the target is lepto-regressed on itself $j$ times and provides the minimum residual MSE for an average depth $j$. In the {−1, 0, 1, 4} case, the 1-bit lepto-variance equals $\lambda {1}^{2} = 0.5$, while $\frac{1}{8}$ is the lepto-variance for 1.75 bits. For practical situations, with large sample sizes (>1K samples) and relatively low-depth trees (less than 3–4 splits), such a situation is highly unlikely to occur, and the distinction between the average and maximum depth of a tree will not matter.

Similarly, $\mu {j}^{2}$ will denote the $j$ -bit macro variance (RTs with depth $j$), thus decomposing total variance into ${\sigma }^{2} = \mu {j}^{2}+\lambda {j}^{2}$.

4.3.   2-bit lepto-regression analysis for historical US stock returns

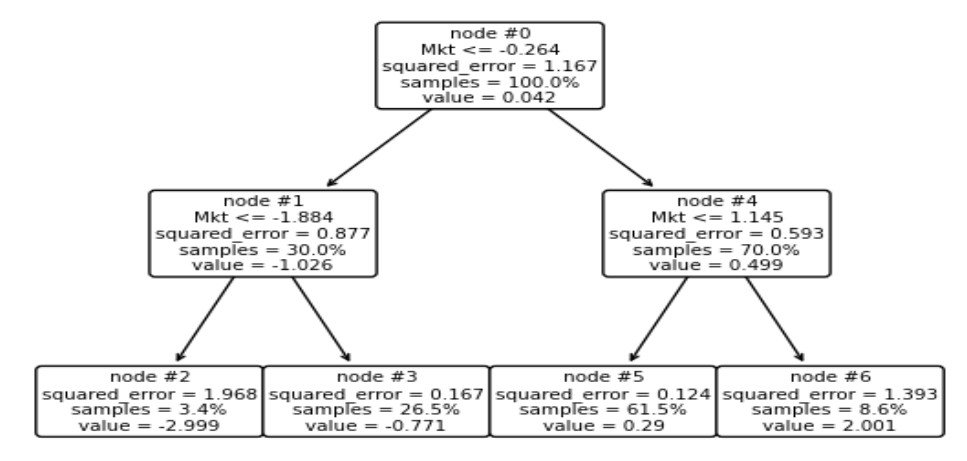
Here, the 2-bit lepto-structure analysis for historical US stock return data is performed following the 1-bit analysis of the previous section. In the Figure below, the descriptive statistics and optimal split for the left subtree of the two optimal-depth RT when US returns are lepto-regressed is depicted. The optimal split point is for returns larger than −1.884, which comprise 88.5% of the total samples reaching the left node. The leftmost child comprises the smallest 3.45% of market returns (11.5% of the initial 30%) with an average −3% return. This is a highly volatile subsection of very negative market returns, with a residual MSE = 1.968. The centermost part of the left child comprises 26.5% (88.5% of the initial 30%) of the total sample (−1.884% < Mkt ≤ −0.264%) and, with a residual MSE = 0.167, it is substantially less volatile. Out of the total MSE of 0.877 that reaches the left subtree, 0.373 is lepto-structure beyond the resolving power of the 2-bit RT. Thus, 42% of the total variability of the left subtree is lepto.

In the Figure below, descriptive statistics and optimal split for the right subtree in the optimal 2-bit RT when the US return vector is lepto-regressed is depicted. The optimal split point is for large returns (larger than 1.145%), which comprise 12.2% of the total samples reaching the intermediate right node, or the highest 8.6% of the entire daily return sample (12.2% of the initial 70%) with an average 2% return. This is a highly volatile subsection of very strong market returns, with a residual MSE = 1.393. The centermost part of the right child is the largest subsection, as it comprises 61.5% (87.8% of the initial 70%) of the total sample (−0.264% < Mkt ≤ 1.145) and, with a residual MSE = 0.124, it is substantially less volatile.

5.   Conclusions

The lepto-regression of a sample is a novel technique defined as the process of constructing an RT by regressing the target on itself. Due to its simplicity, lepto-regression is an interesting model-free technique and has the potential to reveal important properties of sample structure. It has been shown in Polimenis (2022) that, since in a regression tree it is always beneficial to generate a sorted split of a sample S, the lepto-regression provides an upper bound in terms of the variability of a target that can be explained. The variance that cannot be explained via the lepto-regression is called sample lepto-variance. The k-bit lepto-variance ($\lambda {k}^{2}$) of a sample is defined as the residual structure after the sample has been lepto-regressed (up to k times) and is the variance that cannot be explained by any set of features. The k-bit macro-variance is the variance captured by the lepto-regression and thus represents the maximum variance that can be captured by any combination of features. The lepto-variance analysis of the entire 96-year period of US stock market daily returns reveals that the 1-bit macro-variance (variance drop) equals 42% of the total US stock variability, while 58% is structure that cannot be explained by any 1-bit RT. The 2-bit lepto-variance equals 26.3% of the total, with 42% and 47% of the 1-bit lepto-variance of the left and right subtree, respectively.