Prostate cancer is ranked as the fourth most prevalent cancer commonly diagnosed among males over 40 years of age, according to the WHO Cancer Fact Sheet 2020, and it is additionally a leading cause of cancer mortality among males. The incidence of prostate cancer and mortality varied significantly across the globe. Diagnosis of prostate cancer hinders easier management of cases, and prostate-specific antigen (PSA) use for screening of prostate cancer has poor specificity and sensitivity, thereby yielding overdiagnosis and unnecessary biopsies. Radiologically guided (ultrasound/MRI) prostate biopsy, considered the gold standard, is invasive and can miss a significant number of metastatic cancers. Even though mild, other prostate biopsy complications occur on a large scale, and few severe ones are often recorded. Scientists intensify their search for biomarker(s) for non-invasive diagnosis of prostate cancer using proteomics, metabolomics, genomics, and bioinformatics—urinary biomarkers were uniquely on the lookout. Vasoactive intestinal peptide (VIP)/pituitary adenylate cyclase-activating peptide (PACAP) receptor 1 (VPAC1), which is overexpressed (a thousandfold) in prostate cancer at the onset of oncogenesis and is excreted in the urine on tumor cells, is a contender in the prostate cancer biomarker quest. VPAC1 is ubiquitous, expressed by normal and malignant cells, and interwoven in their cell membranes. Therefore, using urine samples limits the possibility of making the wrong diagnosis, since VPAC1 is not normally excreted in the urine. Nevertheless, studying transmembrane receptors is intricate. However, producing monoclonal antibodies against the N-terminal end of VPAC1 can provide a promising target for designing a non-invasive diagnostic assay for early detection of prostate cancer using a urine sample.
Citation: Mansur Aliyu, Ali Akbar Saboor-Yaraghi, Shima Nejati, Behrouz Robat-Jazi. Urinary VPAC1: A potential biomarker in prostate cancer[J]. AIMS Allergy and Immunology, 2022, 6(2): 42-63. doi: 10.3934/Allergy.2022006
| [1] | Ken S. Rosenthal, Daniel H. Zimmerman . J-LEAPS vaccines elicit antigen specific Th1 responses by promoting maturation of type 1 dendritic cells (DC1). AIMS Allergy and Immunology, 2017, 1(2): 89-100. doi: 10.3934/Allergy.2017.2.89 |
| [2] | Johan Garssen, Juandy Jo . Genetically-engineered T cells to treat viral hepatitis-associated liver cancer: is it possible?. AIMS Allergy and Immunology, 2017, 1(1): 43-49. doi: 10.3934/Allergy.2017.1.43 |
| [3] | Robert Cote, Laura Lynn Eggink, J. Kenneth Hoober . CLEC receptors, endocytosis and calcium signaling. AIMS Allergy and Immunology, 2017, 1(4): 207-231. doi: 10.3934/Allergy.2017.4.207 |
| [4] | Michael D. Caponegro, Jeremy Tetsuo Miyauchi, Stella E. Tsirka . Contributions of immune cell populations in the maintenance, progression, and therapeutic modalities of glioma. AIMS Allergy and Immunology, 2018, 2(1): 24-44. doi: 10.3934/Allergy.2018.1.24 |
| [5] | Stefano Regis, Fabio Caliendo, Alessandra Dondero, Francesca Bellora, Beatrice Casu, Cristina Bottino, Roberta Castriconi . Main NK cell receptors and their ligands: regulation by microRNAs. AIMS Allergy and Immunology, 2018, 2(2): 98-112. doi: 10.3934/Allergy.2018.2.98 |
| [6] | Declan P. McKernan . Toll-like receptors and immune cell crosstalk in the intestinal epithelium. AIMS Allergy and Immunology, 2019, 3(1): 13-31. doi: 10.3934/Allergy.2019.1.13 |
| [7] | Kochar Khasro Saleh, Semih Dalkiliç, Lütfiye Kadioğlu Dalkiliç, Bahra Radhaa Hamarashid, Sevda Kirbağ . Targeting cancer cells: from historic methods to modern chimeric antigen receptor (CAR) T-Cell strategies. AIMS Allergy and Immunology, 2020, 4(2): 32-49. doi: 10.3934/Allergy.2020004 |
| [8] | Kazheen Majeed, Hazhmat Ali . Association of low-grade inflammation and oxidative stress with metabolic dysfunction in healthy obese individuals. AIMS Allergy and Immunology, 2025, 9(2): 56-69. doi: 10.3934/Allergy.2025004 |
| [9] | Caterina Marangio, Rosa Molfetta, Erisa Putro, Alessia Carnevale, Rossella Paolini . Exploring the dynamic of NKG2D/NKG2DL axis: A central regulator of NK cell functions. AIMS Allergy and Immunology, 2025, 9(2): 70-88. doi: 10.3934/Allergy.2025005 |
| [10] | Fernanda Costa Brandão Berti, Karen Brajão de Oliveira . IL-10 in cancer: Just a classical immunosuppressive factor or also an immunostimulating one?. AIMS Allergy and Immunology, 2018, 2(2): 88-97. doi: 10.3934/Allergy.2018.2.88 |
Prostate cancer is ranked as the fourth most prevalent cancer commonly diagnosed among males over 40 years of age, according to the WHO Cancer Fact Sheet 2020, and it is additionally a leading cause of cancer mortality among males. The incidence of prostate cancer and mortality varied significantly across the globe. Diagnosis of prostate cancer hinders easier management of cases, and prostate-specific antigen (PSA) use for screening of prostate cancer has poor specificity and sensitivity, thereby yielding overdiagnosis and unnecessary biopsies. Radiologically guided (ultrasound/MRI) prostate biopsy, considered the gold standard, is invasive and can miss a significant number of metastatic cancers. Even though mild, other prostate biopsy complications occur on a large scale, and few severe ones are often recorded. Scientists intensify their search for biomarker(s) for non-invasive diagnosis of prostate cancer using proteomics, metabolomics, genomics, and bioinformatics—urinary biomarkers were uniquely on the lookout. Vasoactive intestinal peptide (VIP)/pituitary adenylate cyclase-activating peptide (PACAP) receptor 1 (VPAC1), which is overexpressed (a thousandfold) in prostate cancer at the onset of oncogenesis and is excreted in the urine on tumor cells, is a contender in the prostate cancer biomarker quest. VPAC1 is ubiquitous, expressed by normal and malignant cells, and interwoven in their cell membranes. Therefore, using urine samples limits the possibility of making the wrong diagnosis, since VPAC1 is not normally excreted in the urine. Nevertheless, studying transmembrane receptors is intricate. However, producing monoclonal antibodies against the N-terminal end of VPAC1 can provide a promising target for designing a non-invasive diagnostic assay for early detection of prostate cancer using a urine sample.
prostate-specific antigen;
vasoactive intestinal peptide;
pituitary adenylate cyclase-activating peptide;
VIP/PACAP receptor 1;
age-standardized rate;
benign prostatic hypertrophy;
5α-dihydrotestosterone;
quantitative reverse transcription polymerase chain reaction;
magnetic resonance imaging;
multiparametric MRI;
dynamic contrast-enhanced MRI;
diffusion-weighted imaging MRI;
trans-rectal ultrasound scan;
enzyme-linked immunosorbent assay;
prostate cancer antigen 3;
transmembrane protease serine 2;
glutathione S-transferase P1;
digital rectal examination;
area under the curve;
hepatocyte growth factor;
insulin-like growth factor binding protein 3;
Plasma osteopontin;
lymph node carcinoma of the prostate;
G protein-coupled receptors;
receptor activity modifying proteins;
seven-transmembrane domain;
extracellular domain;
Chinese hamster ovary;
TATA-box binding protein;
cyclooxygenase-2;
metalloproteinase 9;
urokinase plasminogen activator;
uPA receptor;
4,6-diamidino-2-phenylindole;
adenylyl cyclase;
cAMP response element-binding protein;
phosphokinase A;
inducible nitric oxide synthase;
CREB binding protein;
nuclear factor-κβ;
extracellular signal-regulated kinase;
MAP/ERK kinase (MEK) kinase 1;
IFN regulatory factor-1;
inhibitory κβ kinase;
bombesin-like peptides;
gastrin-releasing peptide receptor;
phospholipase C;
diacylglycerol;
1,4,5-triphosphate;
protein kinase C;
mitogen-activated protein kinase;
mitogen-activated protein kinase kinase;
ETS like-1 protein;
serum response element
Prostate cancer is a highly prevalent neoplastic disease among the male human population [1]. The age-standardized rate (ASR) for prostate cancer varies considerably worldwide [2]. Before the age of 40, prostate cancer exists infrequently, but the ASR rises with age globally, reaching 389.6/100000 among people above 75 years of age [1],[3]. Prostate cancer is routinely diagnosed among males in their sixties and seventies with a 16% lifetime risk [4]. Prostate cancer is the second most typical cause of cancer mortality among men, with a global ASR of 359 deaths per 100000 people [5]. According to the WHO, prostate cancer accounted for 1.41 million out of 10 million cancer deaths in 2020 [6]. Developed and developing countries carry the largest and lowest incidences of prostate cancer, respectively. Also, one-quarter to one-half of the diagnoses in America and Europe occur due to overdiagnosis [7]. Age, race, genetics, and family history are uncontroversial risk factors for prostate cancer development. However, other risk factors like drugs (statins, oral hypoglycemic agents, NSAIDs, and α-reductase inhibitors), diabetes mellitus, obesity, food, and dietary habits have yielded conflicting evidence, as recently reviewed [8]. Of note, no causal relationship exists between benign prostatic hypertrophy (BPH) and prostate cancer [9].
Prostate cancer is predominantly (98%) adenocarcinoma of epithelial origin. Accordingly, prostate cancer malignant transformation is associated with the destruction of extracellular matrix, secondary to loss of adhesion molecules by protease degradation, reorganization of the cytoskeleton, and mesenchymal transition [10]. Testosterone and 5α-dihydrotestosterone (DHT), as androgens, are essential for prostate growth and physiology [11]. Moreover, prostate cancer oncogenesis and progression depend on androgens' stimulation of their nuclear receptor, which functions as a ligand-dependent transcription factor [12]. Conversely, no association was documented between testosterone replacement therapy or testosterone level and prostate cancer [11].
The diagnosis of prostate cancer is still challenging in the 21st century. Although the PSA is a useful marker for monitoring recurrence, despite being used routinely for screening prostate cancer, it is a non-reliable biomarker. The risk of prostate cancer mortality is unaffected by PSA screening; furthermore, it is implicated in overdiagnosis, which leads to excessive prostate biopsies [13]. The PSA is prostate-specific but not prostate cancer-specific; hence, any other prostate condition can affect the PSA serum level [4]. Notwithstanding, scientists have shown that, following the recent decline in PSA usage, the world is now observing a trend of prostate cancer late presentation, with associated increased mortality [14]. Therefore, a more reliable biomarker is needed. Histology of the ultrasound-guided prostate biopsy is assumed to be a gold standard in the absence of one but missed 40% of cancerous lesions with normal ultrasound echo [15].
Clinicians have employed multiparametric magnetic resonance imaging (mp-MRI) that encompasses T1- and T2-weighted imaging, in combination with one or both dynamic contrast-enhanced (DCE)-MRI and diffusion-weighted imaging (DWI)-MRI, for the diagnosis of prostate cancer [16],[17]. The mp-MRI, with a pooled sensitivity of 89% and specificity of 73%, leads to a 27% reduction of primary biopsies, avoids 5% of insignificant tumors, and diagnoses 18% more prostate cancer when combined with trans-rectal ultrasound scan (TRUS) biopsies [18]. The mp-MRI diagnostic power depends on neoplasia location and histology [19]. Several factors limit mp-MRI imaging quality, thereby decreasing its diagnostic power [20]. In this review, we discuss different biomarker candidates for prostate cancer diagnosis. Notably, we point to VPAC1, discuss its role in health and diseases and explain its role as a potential biomarker for prostate cancer.
Researchers have recently renewed their interest in searching for a highly sensitive and specific diagnostic test for prostate cancer, as evidenced in the enormous amount of published literature on this issue across medical journals in the early 21st century. PSA's low specificity has motivated scientists toward an extensive search through proteomics, genomics, and metabolomics for specific and sensitive biomarkers. Studies have also reported on circulating tumor cells, microRNAs, and exosomes, which help in guiding the classification of cancer type (indolent/malignant) and ascertaining the line of therapy [21].
Presently, there is no biomarker clinically recommended for prostate cancer prognosis. Zhao and colleagues reported in a meta-analysis that COX-2, CD147, ALDH1A1, Ki-67, FVIII, and Bcl-2 biomarkers had a statistically significant association with prostate cancer prognosis [22]. Besides, researchers have recently reviewed 20 mutually exclusive, published urinary biomarker assays for a prostate cancer diagnosis, yielding different specificities and sensitivities. However, none of the biomarkers assessed reached the gold standard level, and the authors proposed the enzyme-linked immunosorbent assay (ELISA) laboratory technique as the best way to screen biomarkers. Since ELISA is simple, highly sensitive, and specific, with high throughput, it is used popularly in protein biomarker validation [23].
Urine, a direct blood filtrate that passes within the urethra as it passes through the prostate in the pelvis, can contain essential information regarding prostate health. Additionally, prostate cancer cells have been discovered in urine [24]. Massaging the prostate by the clinician during rectal examination increases prostate cancer cells' yield in the urine. The above reasons make urine an ideal body fluid for the search for prostate cancer biomarkers [24]. Urinary biomarkers at the advanced research stage as candidate biomarkers include prostate cancer antigen 3 (PCA3), transmembrane protease serine 2 (TMPRSS2), and glutathione S-transferase P1 (GSTP1) [25].
PCA3 is expressed by 95% of prostate cancers, at a level that is 66-fold higher than that of a normal prostate [26]. An assay of PCA3 using multiplex gene tests on urine samples yielded statistically significantly higher PCA3 levels after the digital rectal examination (DRE) compared to no DRE. However, several studies reported overtly variable sensitivity and specificity for PCA3, which failed to correlate with the cancer stage [27]. Studies have shown that a PCA3 score cut-off level of 20 yields 72% and 53% sensitivity and specificity, respectively, but can miss close to 2% of high-grade prostate cancers. A cut-off figure of 21 will yield the highest diagnostic value, at an area under the curve (AUC) of 0.81 [27]. Assessment of five urinary methylation biomarkers (C1orf114, RASSF1A, APC, PITX2, and GSTP1) of DNA profiles of cancer cells yielded sensitivities of 60% and 81% if undertaken before and after the prostate massage, respectively [28]. Researchers studying prostate cancer patients found urinary fusion gene TMPRSS2-ERG among 50% of prostate cancers [29].
Sequeiros et al. [30] designed urine multiplexed quantitative reverse transcription-polymerase chain reaction (RT-qPCR) in a pilot study of patients with high-grade prostate intraepithelial neoplasia, an indolent precancerous prostate lesion that requires biopsy. Seven genes were overexpressed in prostate cancer (CDH1, GOLM, KLK3, PCA3, PSGR, PSMA, and SPINK1) and statistically correlate with prostate cancer progression [30]. Combining these genes as a multiplex test leads to a predictive improvement over the weakness of the FDA-approved PCA3 [31]. The multiplex test possesses a specificity of 95% and a sensitivity of 41–58%. Fryczkowski et al. [32] reported hepatocyte growth factor (aHGF) to be associated with angiogenesis, migration, adhesion, and invasion of prostate cancer [32].
While insulin-like growth factor binding protein 3 (IGFBP3) is associated with cellular differentiation, survival, and proliferation [33], both aHGF and IGFBP3 are overexpressed in prostate cancer [23]. Plasma osteopontin (OPN), overexpressed in prostate cancer, is associated with tumorigenesis, metastasis, and apoptosis inhibition [34]. Prager et al. found aHGF and IGFBP3 expression to be statistically significant (diagnostic) in prostate cancer compared to controls, with AUC values of 0.75 and 0.74, respectively, but recommended OPN, with an AUC of 0.68, for delineating prostate cancer patients with the aggressive disease [35]. In sum, the aforementioned genes fall short to serve as prostate cancer biomarkers.
PACAP is a neuropeptide that possesses diverse biological effects with extensive occurrence [36]. Moreover, PACAP plays a role in various cellular and physiological responses as a multifunctional peptide [37]. PACAP, having the ability to stimulate adenylyl cyclase (AC) activity in anterior pituitary cells, was initially isolated from ovine hypothalami, and it belongs to the vasoactive intestinal peptide (VIP)-secretin-glucagon family [38],[39]. PACAP also induces a short-term surge of c-fos gene expression [40] and shares 68% homology with VIP [41]. Although by low affinity, VIP can interact with PAC1, the specific PACAP receptor [42]. Moreover, PACAP performs its tasks through the VPAC1 receptor [43], giving its name VPAC1, VIP-PAC receptor 1, as previously reviewed [44]. PACAP naturally exists as either 27 or 38 amino acid peptides (PACAP27 and PACAP38). VIP and PACAP were shown to have higher affinities for both VPAC1 and VPAC2 compared to PAC1 (PACAP type1); however, PAC1 is only activated by PACAP [45]. VIP and PACAP analogs affect tumor growth in animal tumor study models. Therefore, VIP and PACAP receptors could be considered tumor localization factors and therapeutic targets [46].
A previous study has shown the existence of PAC1, VPAC1, and VPAC2 in healthy and disease prostate tissue and persistence after neoplastic transformation [47]. Immunohistochemical staining of prostatectomy tissue samples of patients with benign, malignant, and healthy prostates revealed high expression of PAC1 by healthy, benign, and malignant prostatic tissues. However, upregulated PAC1 null variant expression was observed among cancerous samples [48]. Another study specifically showed PACAP27 to be upregulated among neoplastic prostate cells compared to benign tissues [49]. PACAP (6–38), a PACAP receptor analogwas shown to inhibit the expression of cAMP and the c-fos gene and retard prostate cancer cell growth [40].
The VPAC receptors (VPAC1 and VPAC2) were named according to the order in which they were identified: VIP-specific receptors in rat lung tissue followed by a homologous receptor from a rat olfactory bulb cDNA library. Hence, the nomenclature of VPAC1 and VPAC2 was first VIP1 and VIP2, respectively [50]. VPAC1, like other GRPRs, can form oligomeric complexes, and this oligomerization affects neither the recognition of ligands nor the function of the receptors. Besides, VPAC1 can form homodimers and heterodimers with VPAC2 or other secretin receptors [51]. VPAC receptors can interact with other “G protein-coupled receptor (GPCR) interacting proteins (GIPs)”, like receptor activity modifying proteins (RAMPs) or PSD-95/Dlg/ZO-1—containing proteins (PDZ-cp), which contain the PDZ domain [51],[52].
VPAC1 is expressed in healthy prostate cells; however, its expression in BPH is relatively low [53]. Despite the role of VPAC1 in signaling at the lower urinary tract, it is only present in the major pelvic ganglia. Nevertheless, urothelium, detrusor smooth muscle, lumbosacral dorsal root ganglia, and lumbosacral spinal cord lack VPAC1 [54]. VPAC1 is the predominant subtype of VIP/PACAP receptors in most prostate cancers [47],[55],[56].
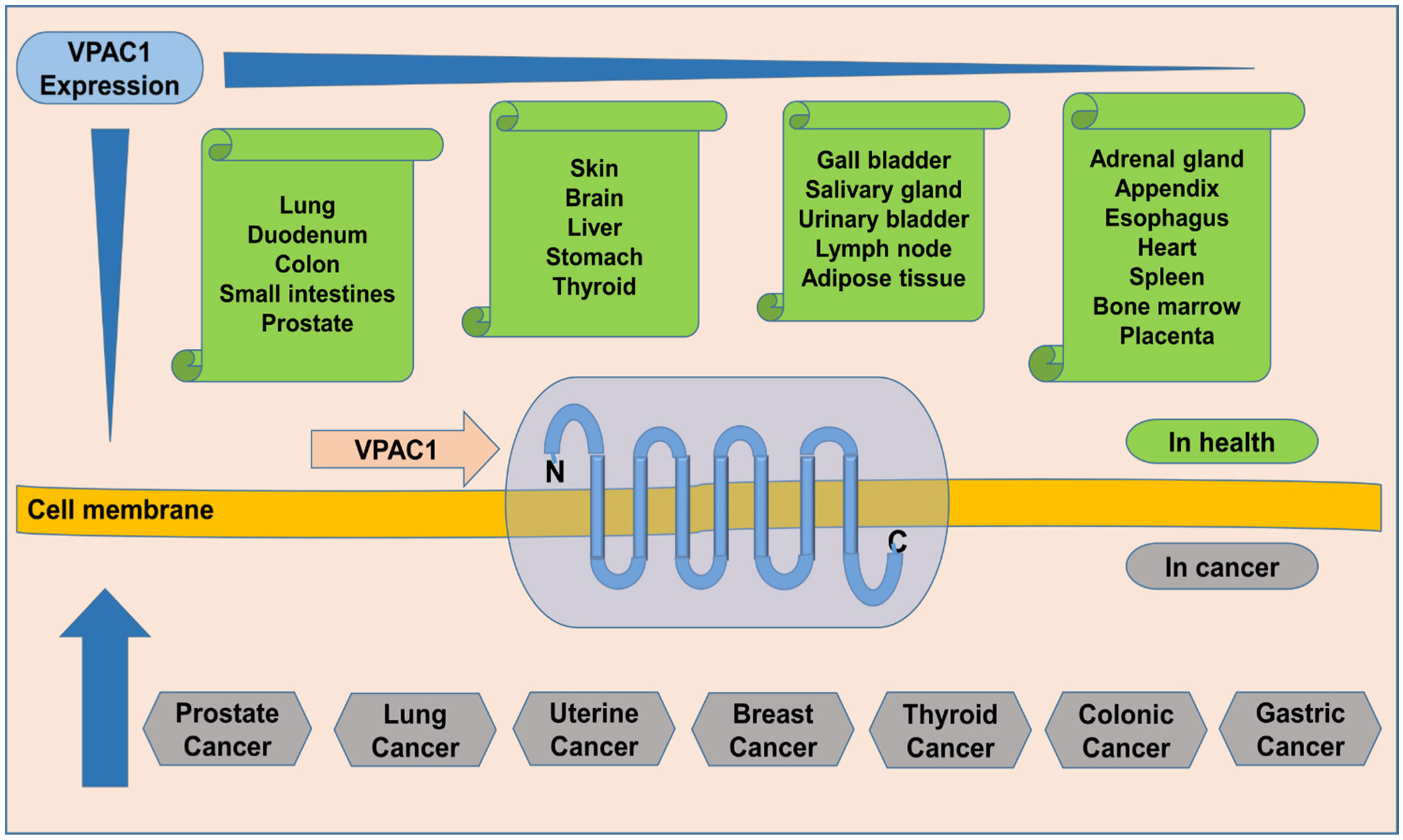
The VPAC1 receptors are widely distributed across various tissues in the human body [57]. Figure 1 below depicts some tissues that express VPAC1 in health and some human cancers. Lung, gastric, colonic, and breast cancers exhibit VPAC1 upregulation [58]–[62]. Genitourinary cancers do overexpress VPAC1 that is detectable in urine on released cancer cells. Despite increased expression in many cancer types, only genitourinary cancers (prostate and urothelial bladder cancers) secrete VPAC1 on cancer cells in the urine [63].
The expression of VPAC1 on immune cells like lymphocytes, monocytes, macrophages, and microglia is constitutive [64], but it is expressed at lower levels and responds poorly to VIP on immune cells in ankylosing spondylitis, rheumatoid arthritis, and osteoarthritis [65].
The GPCRs represent the biggest group of membrane proteins, having close to a thousand members subdivided into five groups [66]. The human VPAC1 gene (Vpr1) is located on chromosome 3 at the p22 region, while that of VPAC2 (Vpr2) occupies region q36.3 of chromosome 7 [64]. The VPAC1 receptor is composed of 427 amino acid residues [67]. VPAC1 interlaces the membrane with alternating extracellular, transmembrane, and intracellular domains linked together as a single receptor [42],[68],[69], which makes studying them outside the membrane a problematic task.
The structure of GPCRs is made up of a seven-transmembrane domain (7-TMD) linked by three intracellular loops ending in the C-terminus and three extracellular loops that end in the N-terminus region (as depicted in Figure 1). The GPCRs are built to recognize a diverse group of ligands [70]. The class B GPCRs that include VPAC1 are composed of 15 members, and each possesses 120–160 and 310–420 amino residues at the N-terminal extracellular domain (ECD) and the 7-TMD, respectively. The class B GPCRs have α-β-β-α three-layered orientation, which is stabilized by disulfide bonds [71].
In humans, two basic amino acid residues of VPAC1 on the second transmembrane helix, Arg188, and Lys195, are essential for ligand recognition and signaling through AC [72]. Ligand binding to class B GPCRs is initiated through recognition by conserved ECD, which allows for onward binding to TMD ligand-binding pockets, initiating the signaling cascade [73],[74]. A crystallographic study has shown that VIP agonists and antagonists interact with different ECDs of VPAC1. The Lys143, Thr144, and Thr147 residues located on the TMD are essential for VPAC1 affinity. The first transmembrane domain of VPAC1 is the first to interact with VIP's first histidine residue [75].
The GPCRs constitute the largest family of receptors encoded by the human genome, and they are involved in the physiology of different organs and the pathophysiology of several diseases. Nevertheless, few biologics were researched successfully to target GPCRs with the desired outcome. Researchers are still intensively searching for the appropriate biologics that target GPCRs. Previous biologics usually failed in the desired specificity, and the complexity arises from the GPCRs being transmembranous. The GPCRs are challenging to study in situ (due to the presence of contaminants). Without the membrane, compromised epitope conformation results, and synthetic GPCRs will be devoid of post-translational modifications [76]. Scientists were able to produce some antibodies against VPAC1 using varied modalities as outlined below.
Peyrassol and colleagues succeeded in identifying monovalent antibodies (nanobodies) with modest affinity to VPAC1, which they obtained through dual animal immunization with subcutaneous Chinese hamster ovary (CHO)-WTA11 cells overexpressing VPAC1 and intradermal injection of the viral vector-transfected with human VPAC1 DNA plasmid [77]. In another study, monoclonal antibody (IgG1), an anti-VPAC1 (antagonist) was obtained secondary to immunization of BALB/c mice with purified human VPAC1. Consequently, injection of the anti-VPAC1 into the study animals inhibited cAMP generation [78]. Herman and co-workers succeeded in producing rabbit α-VPAC1 polyclonal antibody (α-mVPAC1 pAb) through immunization of study rabbits with a complete mouse VPAC1 vector [79]. Monoclonal antibodies to VPAC1 were also generated after immunization with a construct for human VPAC1 to female BALB/c mice potentiated by injection with a culture of CHO cells overexpressing the VPAC1 receptor [80].
The VPAC1 receptor plays a crucial role in transmitting various physiological, immunological, and neoplastic signals upon ligation by VIP in different tissues [42],[60]. Researchers have used agonist and antagonist analogs of VIP and PACAP and have shown that different parts of the receptors' domains are responsible for their selectivities to ligands [81],[82]. The short-term effects of VIP are seen in hormone secretions, muscle relaxation, neurotransmission, and metabolism. The effects of VPAC1 observed in moderate duration include neuroprotection and immune reaction, as well as cell proliferation, cell death inhibition, angiogenesis, invasion, and metastasis of cancer cells [52],[83]–[86]. Long-term effects were observed in fetal growth, learning behavior, and circadian rhythms [42],[87].
When VIP ligates VPAC1, it triggers a signal transduction pathway that leads to the biosynthesis of a neurotransmitter, a cytokine, or a neuroendocrine hormone, depending on the source and the target tissue [88]. The VPAC1 ECD is essential for ligand recognition and subsequent binding. The ECD is structured into a sushi domain stabilized by disulfide bonds and salt bridges. The central α-helix and C-terminal of the ligand peptide (VIP) interact with the sushi domain and cause a conformational change to align the peptide N-terminus with the first transmembrane domain of the receptor, thereby activating the VPAC1 receptor [89]. The interaction of the first histidine residue of the VIP ligand with the VPAC1 Lys143, Thr144, and Thr147 is essential for activating the receptor as described earlier [52].
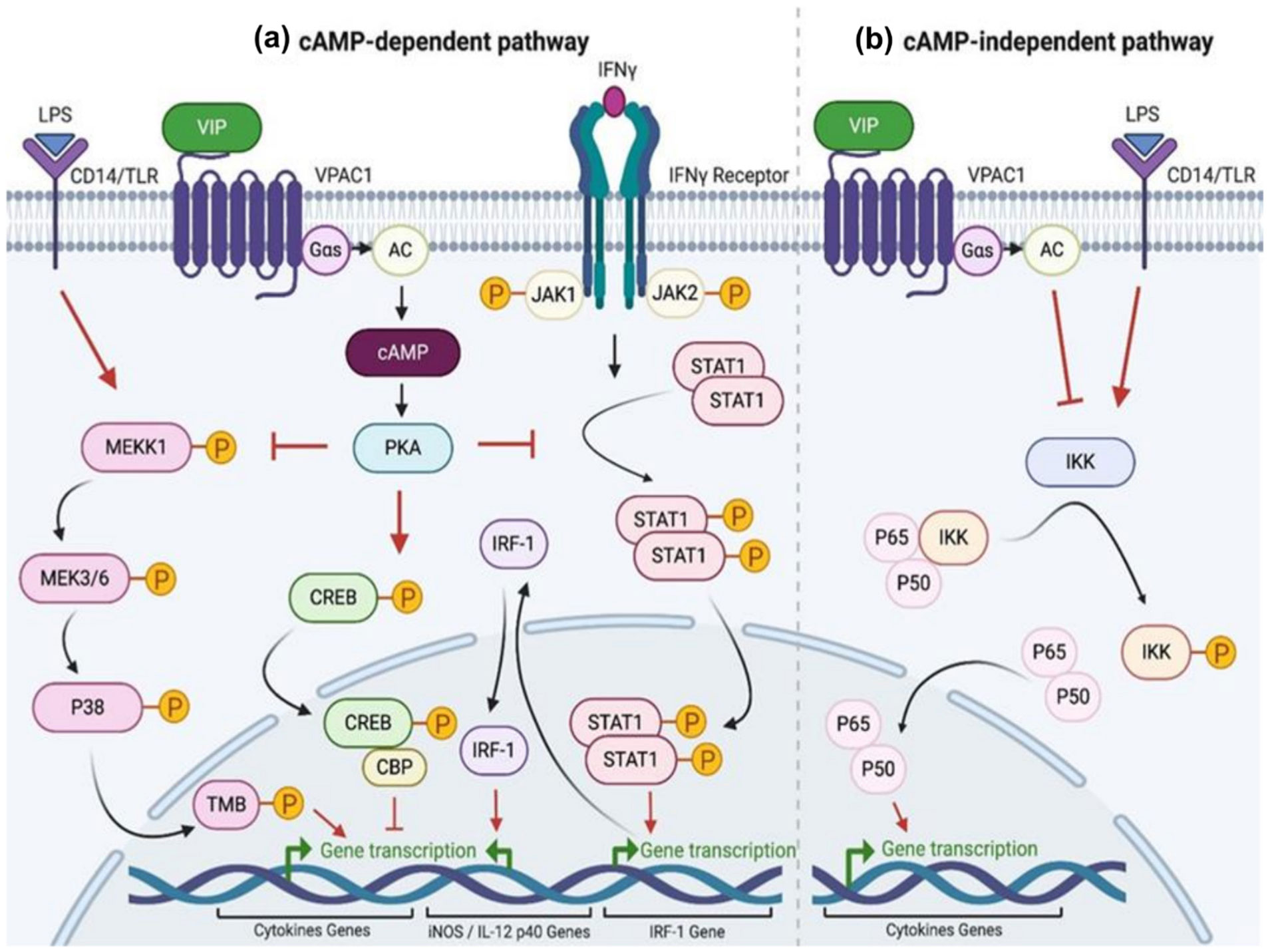
Activation of VPAC1 entails a conversion of GDP to GTP that is linked to Gαs to aid its dissociation from Gβγ with resultant VIP signaling [90]. In a study on mouse macrophages, VIP inhibits the LPS and IFN-γ-induced inflammatory pathways through cAMP-dependent or independent mechanisms. In the cAMP-dependent pathway, when the ligand binds to the VPAC1, it can activate the Gαs protein, which can increase AC activity and results in cAMP production that in turn activates phosphokinase A (PKA) [91],[92]. The PKA inhibits NF-κβ by two different downstream effects: cAMP response element-binding protein (CREB) phosphorylation and inhibition of MAP/ERK kinase phosphorylation [93].
In the first PKA-linked cAMP-dependent pathway, PKA phosphorylates the CREB that is attached to CREB binding protein (CBP): CREB co-factor. CBP blocks CREB interaction with NF-κβ, and as a result, NF-κβ activity is reduced [93],[94]. In the second PKA-linked cAMP-dependent pathway, the PKA inhibits phosphorylation of MAP/ERK kinase (MEK) kinase 1 (MEKK1) and the subsequent cascade of the MEK3/6/p38 pathway. Furthermore, it could inhibit the phosphorylation of TATA-box binding protein (TBP), and the NF-κβ co-factor [93],[95], as shown in Figure 2a.
Apart from the cAMP-dependent pathway effects on NF-κβ inhibition via cAMP, the pathway activation also inhibits phosphorylation of the Janus kinase/signal transducer and activator of transcription (JAK/STAT) and binding of phosphorylated STAT1 to the IFNγ-activated site (Gαs) sequence in the IFN regulatory factor-1 (IRF-1) promoter. As a result, transcription, and synthesis of IFN regulatory factor-1 (IRF-1), which is a transactivator in multiple genes, including inducible nitric oxide synthase (iNOS) and IL-12 p40, are inhibited [92],[93], as shown in Figure 2a.
In the cAMP-independent pathway, the activity of inhibitory κβ kinase (IKK) is inhibited, which stabilizes the Iκβ/NF-κβ complex, thereby preventing Iκβ phosphorylation and resulting in the prevention of nuclear translocation of NF-κβ subunits [93]. So, both inhibition of Iκβ phosphorylation and prevention of nuclear translocation of the p50:p65 dimer are cAMP-independent inhibitory mechanisms of VIP on inflammation [95], as shown in Figure 2b. The above describes the basis of the VPAC1 anti-inflammatory role in the immune system in a healthy state, as shown in Figure 2. Further, VPAC1 activates heterogeneous signaling pathways, which include phospholipase D, calcium channels, tyrosine kinases, MAPK, RhoA GTPases, Src, carbon monoxide [96], and phospholipase C [97].
VPAC1 is the sole VIP receptor overexpressed in all prostate cancer [84]. VPAC1 receptors are coupled to Gαs protein, which activates AC when VIP binds to these membrane receptors in the prostate gland. PKA is activated due to increased cAMP levels, which leads to the CREB phosphorylation as one of the PKA substrates. Phosphorylated CREB results in c-fos, c-jun, and c-myc oncogene expression [98]. The VPAC1 receptor generally caused Gαs to increase intracellular cAMP expression and intracellular calcium production [83]. Notably, intracellular calcium rise is dependent on the activation of both Gαi and Gαq coupled pathways [96].
Furthermore, VPAC receptors enhance [Ca2+]i levels by coupling to the IP3/Ca2+ pathway via Gαq and Gαi proteins. Besides, VPAC1 receptors' ligation by VIP in the human androgen-dependent lymph node carcinoma of the prostate (LNCaP) cell line, an epithelial cell line derived from a human prostate carcinoma, leads to the expression of the angiogenic factor VEGF and neuroendocrine differentiation. Likewise, VIP inhibits apoptosis among androgen-independent prostate cancer cell lines [98]. Further, activation of cAMP results in p50 translocation into the nucleus and VEGF activation [86]. Cumulatively, the above findings in prostate cancer show that VIP promotes carcinogenesis.
NF-κβ is a potent activator of genes responsible for proliferation, survival, and angiogenesis, which are linked to cancer angiogenesis, invasion, and metastasis [99]. NF-κβ is inherently activated in prostate cancer tissue, so nuclear NF-κβ p65 was found to be a poor prognostic factor associated with biochemical reoccurrence and bone metastasis [100]. Fernández-Martínez and co-workers conducted an in vitro study on three prostate cancer cell lines: non-neoplastic human prostatic epithelial cells (RWPE-1), castrate-sensitive prostate cancer cells (LNCaP), and castrate-insensitive prostate cancer cells. They found that VIP signaling through VPAC1 induced increased expression of NF-κβ in all the cell lines (normal and cancerous) through both cAMP activation of PKA and non-PKA dependent cAMP signaling pathways [86].
The VIP signaling through VPAC1 induces the expression of VEGF, cyclooxygenase-2 (COX-2), and neuroendocrine differentiation in castrate-sensitive prostate cancer cell lines. Additionally, it activates EGF-2 phosphorylation, thereby ensuring the survival of castrate-resistant prostate cancer. In sum, VIP signaling favors metastasis in both prostate cancer subtypes [86]. NF-κβ-mediated expression of genes may further contribute to the progression of prostate cancer. Some of these genes, like IL-8 and VEGF, are involved in angiogenesis. Meanwhile, metalloproteinase 9 (MMP9), urokinase plasminogen activator (uPA), and uPA receptor (uPAR) promote prostate cancer invasiveness and metastasis [86].
The healthy prostate, prostate cancer cell lines, and human prostate cancer all secrete VIP. Accordingly, signaling through VPAC1 in prostate cancer cell lines results in the expression of cyclin D1 and cell proliferation [84]. Nevertheless, VPAC1 signaling in normal prostate epithelial cells engrafted into nude athymic mice induces cancerous transformation with associated increased expression of metastasis-prone proteins [10]. Molecular studies reveal a two-fold increase in VIP expression in the prostate cancer tissue compared to healthy prostate tissue [98].
Furthermore, the NF-κβ signaling is implicated in prostate cancer initiation and progression due to several reasons [101],[102]. Firstly, the emergence of castrate-resistant prostate cancer is supported by persistent activation of NF-κβ in androgen-independent prostate cancer. Secondly, increased expression of activated IKK1 portions of NF-κβ protein was demonstrated in prostate cancer sampled tissues. Lastly, NF-κβ induces epithelial-mesenchymal transformation through the regulation of TGF-β [103].
Mammalian bombesin-like peptide (BLP), a 27 amino acid peptide, occurs widely in different systems' tissues. The BLPs are associated with different physiological roles and are also involved in disease processes including cancer. In malignant diseases like small cell lung cancer (SCLC) and prostate cancer, the BLPs are secreted at higher levels, thereby acting in an autocrine manner on their receptors (BnRs) [104]. The class of BnRs has three members, neuromedin B receptor (NMBR:BB1), gastrin-releasing peptide receptor (GRPR) (also known as BB2), and bombesin receptor subtype 3 (BRS-3:BB3), which is an orphan receptor [105]. BB2r is a class A GPCR, overexpressed in prostate cancer [106], unlike BB1 and BB3, which are not expressed in prostate cancer [107].
Furthermore, increased cAMP secondary to activation of VPAC1 causes the release of BLPs from SCLC cells. Hence, studies have shown an abrupt ten-fold rise in cAMP and a three-fold rise in BLPs secondary to VPAC1 ligation by VIP [85]. Similar studies on prostate cancer are lacking, but the same orchestration is likely to explain the dual rise of both VPAC1 and BB2r in prostate cancer cells. As such, more studies are needed in this regard. As outlined in Figure 3, activation of the BLPs leads to intracellular activation of phospholipase C (PLC) [108], Ca2+ release [109], and subsequent activation of the serum response element (SRE) of early oncogenes c-fos and c-jun. The oncogenes form a heterodimer that activates AP-1 on the SCLC growth factor gene, leading to clonal proliferation [85],[109].
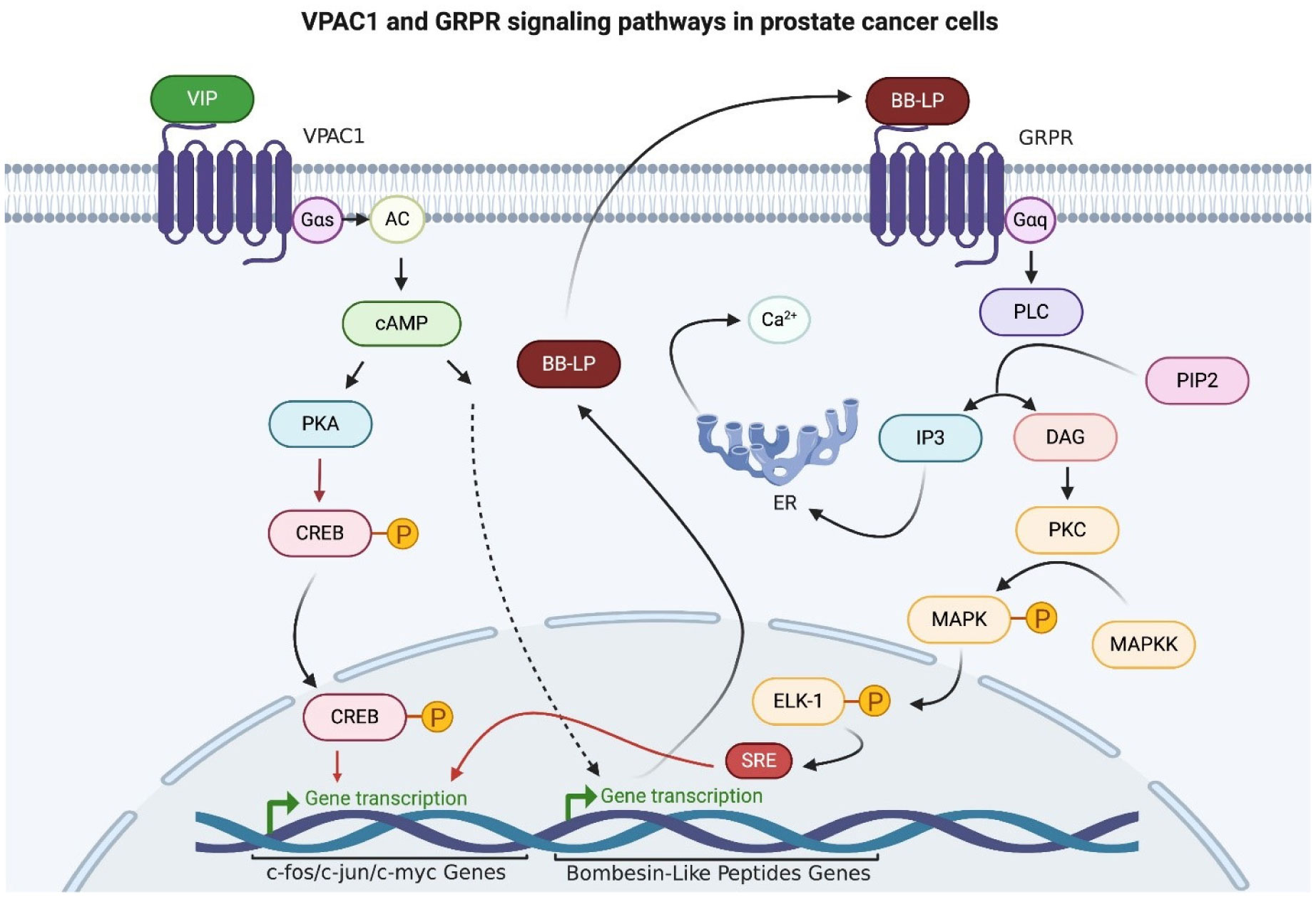
The BB-like peptides activate Raf-MEK-ERK mitogen-activated kinases known to facilitate tumorigenesis, also linked to the emergence of castrate-resistant prostate cancer in an Src-dependent manner. The BB-like peptides are associated with increased IL-8 and VEGF-R2 mRNA expression in prostate cancer cell lines, and transactivation of EGF-R promotes prostate cancer growth [110].
The VPAC1 expression is upregulated in prostate cancer cells compared to BPH and healthy prostate [60]. Fujita and colleagues have shown that urine samples collected after a prostate massage when subjected to multiplex staining and cytology for prostate cancer diagnosis have a specificity of 100% and a sensitivity of 36%. A few milliliters of centrifuged urine from prostate cancer patients contain cancer cells that vary from a few hundred to several thousand. Standard urinary cytopathology scores 15% sensitivity, which is lower than molecular urinary cytology [111]. Scientists are currently extensively searching for a sensitive molecular biomarker for the non-invasive urinary diagnosis of prostate cancer [23],[25],[30],[112],[113].
Truong and colleagues reported remarkable non-invasive prostate cancer positron emission tomography/computerized tomography (PET/CT) targeting VPAC1 with radioactive copper-64 labeled sVPAC1 analog ligands. The scan differentiated benign from malignant prostate cancer [60]. In the last decade, in vivo oncologic imaging of prostate cancer has attracted researchers' interest but with no success on biochemical targets [15]. Scientists designed an in vivo PET scan of prostate cancer using VIP analog TP3939 (Lys12, Nle17 (3-OH3, 4-OH) Phe22, Val26, and Thr28). The TP3939 was linked to radioactive 64Cu to target VPAC1 in prostate cancer. The test successfully diagnosed prostate cancer tissue xenograft in athymic nude mice and spontaneous cancer in transgenic adenocarcinoma of mouse prostate (TRAMP). It correctly diagnosed grade IV intraepithelial neoplasia of the prostate cancer but failed to diagnose grade II intraepithelial neoplasia in the study mice [15].
The PET scan evolution was intended for a minimally invasive, in vivo, specific and sensitive prostate cancer diagnosis. Another study using 64Cu-TP3805 (synthetic VIP conjugated to an N2S2 (diamine dithiol [N2S2-benzoyl]2) at the C-terminus) was carried out on patients that were planned for radical prostatectomy, correctly diagnosed 98% of the cases, and also differentiated cancer and non-cancer tissues, including metastatic tissues in lymph nodes. Furthermore, it revealed a cancerous lesion that was not diagnosed by prostate histology [53]. A significant setback for a 64Cu-TP3805 PET scan is its inability to distinguish high-grade prostate intraepithelial neoplasia (HGPIN) from aggressive prostate cancer. Both 64Cu-TP3805 and 64Cu-TP3939 are excreted mainly in feces, and to a lesser extent kidneys, with renal excretion of <2%, The two analogs are highly stable in humans and mice [60] signifying their safety in human testing.
A recent human study to search for prostate cancer biomarkers incorporated 141 patients diagnosed with prostate cancer, 10 patients with BPH, and 56 as controls in a urology clinic. Participants' collected urine was centrifuged within four hours and treated with 4,6-diamidino-2-phenylindole (DAPI) and fluorophore PSVue 794 linked to TP4303 (VIP analog) to target VPAC1. The test correctly diagnosed 98.6% of the men with prostate cancer, as confirmed by genetic profiling. The pilot study yielded a sensitivity of 99.3% and a specificity of 100% [114].
In the above study, 19.6% of control males, not females, had a VPAC1 positive test but were not confirmed with genetic profiling to have prostate cancer. These individuals might be having the earliest stage of prostate cancer, since increased expression of VPAC1 by the prostate starts at the initial stage of carcinogenesis, before the detectable rise in PSA, as reviewed above. This implies that urinary VPAC1 can provide a possible biomarker for the early diagnosis of prostate cancer [114],[115].
It is crucial how VPAC1 provides an attractive biomarker target for diagnosis and possibly therapy, but, being a GPCR, it is inherently difficult to study, like its cohorts. Additionally, monoclonal antibodies (mAbs), with their inherent advantages, provide a better ligand than small molecules. As reviewed in [76], mAbs were superior to small molecules in affinity and specificity for the target receptors. The mAbs do not readily cross the blood-brain barrier. Therefore, central nervous system adverse effects are not usually found with mAb therapy. Improved immune tolerance and better pharmacokinetics are other advantages of mAbs. Besides, the mAbs alleviate the inherent patient variability. They have a better dosing regimen and an effective plasma half-life. Furthermore, they functionally provide an opportunity for coupling effector mechanisms: for instance, antibody-dependent cellular cytotoxicity (ADCC), complement-dependent cytotoxicity (CDC), and antibody-dependent cellular phagocytosis (ADCP) [116] based on mAbs bi-specificity (Fab and Fc).
The study of the secretin receptor family of GPCRs is difficult, as they interlace the cell membrane with 7-TMDs, which are linked with intracellular and extracellular loops [117],[118]. The GPCRs are also redundant, showing mAb targeting to be better than using small molecules. To produce a specific antibody against an antigen, a pure, preferably intact, and sufficient amount of that antigen is required. However, GPCRs are embedded within a membrane and, if prepared independent of the membrane or extracted using detergents, tend to yield unstable receptors, and some of the relevant epitopes are lost. Studies on the production of recombinant GPCRs recorded some success, so part of the epitopes will be lost. Researchers succeeded in coming up with mAbs against the N-terminal residues of the GPCRs, being an extracellular domain to provide an easy target. Different antigen formats were employed to induce mAbs against the GPCRs; hence, each format has its problems. Generally, the expression of GPCR molecules is usually low; other obstacles are reviewed elsewhere [76],[119].
Recently, the study of VPAC1 ligand analogs yielded promising results, as described above in the diagnosis of solid tumors with the aid of PET scanning and immunofluorescence microscopy of labeled cancer cells in the voided urine. VPAC1 shows promising results in diagnosis, but similar results are lacking in immunotherapy. Previously, researchers were interested in finding a mAb that can be a biomarker for diagnosis and also be used in therapy, but the complexity of GPCRs limits researchers' success.
Prostate cancer is among the significant contributors to global cancer incidence and mortality. Notably, scientists are searching for prostate cancer biomarkers to replace PSA and prostate biopsy due to their unreliability and invasiveness, respectively. Urinary VPAC1 is a promising biomarker, as it is overexpressed on prostate cancer cells from the initial stage of carcinogenesis and released in urine on the cancer cells. A recent study using VPAC1 ligands coupled to a fluorescent molecule in voided urine yielded an encouraging result.
| [1] |
Kimura T, Egawa S (2018) Epidemiology of prostate cancer in Asian countries. Int J Urol 25: 524-531. https://doi.org/10.1111/iju.13593 
|
| [2] |
Pernar CH, Ebot EM, Wilson KM, et al. (2018) The epidemiology of prostate cancer. Cold Spring Harbor Perspect Med 8: a030361-a030380. https://doi.org/10.1101/cshperspect.a030361 
|
| [3] |
Adeloye D, David RA, Aderemi AV, et al. (2016) An estimate of the incidence of prostate cancer in Africa: A systematic review and meta-analysis. PLoS One 11: e0153496. https://doi.org/10.1371/journal.pone.0153496 
|
| [4] |
Kang DY, Li HJ (2015) The effect of testosterone replacement therapy on prostate-specific antigen (PSA) levels in men being treated for hypogonadism: a systematic review and meta-analysis. Medicine 94: e410-e418. https://doi.org/10.1097/MD.0000000000000410 
|
| [5] |
Ferlay J, Colombet M, Soerjomataram I, et al. (2019) Estimating the global cancer incidence and mortality in 2018: GLOBOCAN sources and methods. Int J Cancer 144: 1941-1953. https://doi.org/10.1002/ijc.31937 
|
| [6] | (2018) World Health OrganisationCancer Fact Sheets. WHO. Available from: https://www.who.int/news-room/fact-sheets/detail/cancer |
| [7] |
Taitt HE (2018) Global trends and prostate cancer: a review of incidence, detection, and mortality as influenced by race, ethnicity, and geographic location. Am J Mens Health 12: 1807-1823. https://doi.org/10.1177/1557988318798279 
|
| [8] |
Campi R, Brookman-May SD, Subiela Henriquez JD, et al. (2018) Impact of metabolic diseases, drugs, and dietary factors on prostate cancer risk, recurrence, and survival: A systematic review by the European Association of Urology Section of Oncological Urology. Eur Urol Focus 5: 1029-1057. https://doi.org/10.1016/j.euf.2018.04.001 
|
| [9] |
Miah S, Catto J (2014) BPH and prostate cancer risk. Indian J Urol 30: 214-218. https://doi.org/10.4103/0970-1591.126909 
|
| [10] |
Fernández-Martínez AB, Bajo AM, Arenas ML, et al. (2010) Vasoactive intestinal peptide (VIP) induces malignant transformation of the human prostate epithelial cell line RWPE-1. Cancer Lett 299: 11-21. https://doi.org/10.1016/j.canlet.2010.07.019 
|
| [11] |
Boyle P, Koechlin A, Bota M, et al. (2016) Endogenous and exogenous testosterone and the risk of prostate cancer and increased prostate-specific antigen (PSA) level: a meta-analysis. BJU Int 118: 731-741. https://doi.org/10.1111/bju.13417 
|
| [12] |
Tan ME, Li J, Xu HE, et al. (2015) Androgen receptor: structure, role in prostate cancer and drug discovery. Acta Pharmacol Sin 36: 3-23. https://doi.org/10.1038/aps.2014.18 
|
| [13] |
Lee YJ, Park JE, Jeon BR, et al. (2013) Is prostate-specific antigen effective for population screening of prostate cancer? A systematic review. Ann Lab Med 33: 233-241. https://doi.org/10.3343/alm.2013.33.4.233 
|
| [14] |
Negoita S, Feuer EJ, Mariotto A, et al. (2018) Annual report to the nation on the status of cancer, part II: Recent changes in prostate cancer trends and disease characteristics. Cancer 124: 2801-2814. https://doi.org/10.1002/cncr.31549 
|
| [15] |
Zhang K, Aruva MR, Shanthly N, et al. (2008) PET imaging of VPAC1 expression in experimental and spontaneous prostate cancer. J Nucl Med 49: 112-121. https://doi.org/10.2967/jnumed.107.043703 
|
| [16] |
Litwin MS, Tan HJ (2017) The diagnosis and treatment of prostate cancer: a review. JAMA 317: 2532-2542. https://doi.org/10.1001/jama.2017.7248 
|
| [17] |
Renard-Penna R, Cancel-Tassin G, Comperat E, et al. (2015) Functional magnetic resonance imaging and molecular pathology at the crossroad of the management of early prostate cancer. World J Urol 33: 929-936. https://doi.org/10.1007/s00345-015-1570-z 
|
| [18] |
Ahmed HU, Bosaily ESA, Brown LC, et al. (2017) Diagnostic accuracy of multi-parametric MRI and TRUS biopsy in prostate cancer (PROMIS): a paired validating confirmatory study. Lancet 389: 815-822. https://doi.org/10.1016/S0140-6736(16)32401-1 
|
| [19] | Boesen L (2017) Multiparametric MRI in detection and staging of prostate cancer. Dan Med J 64: B5327. |
| [20] | Sosnowski R, Zagrodzka M, Borkowski T (2016) The limitations of multiparametric magnetic resonance imaging also must be borne in mind. Cent Eur J Urol 69: 22-23. https://doi.org/10.5173/ceju.2016.e113 |
| [21] |
Saini S (2016) PSA and beyond: alternative prostate cancer biomarkers. Cell Oncol 39: 97-106. https://doi.org/10.1007/s13402-016-0268-6 
|
| [22] |
Zhao L, Yu N, Guo T, et al. (2014) Tissue biomarkers for prognosis of prostate cancer: A systematic review and meta-analysis. Cancer Epidem Biomar 23: 1047-1054. https://doi.org/10.1158/1055-9965.EPI-13-0696 
|
| [23] |
Jedinak A, Loughlin KR, Moses MA (2018) Approaches to the discovery of non-invasive urinary biomarkers of prostate cancer. Oncotarget 9: 32534-32550. https://doi.org/10.18632/oncotarget.25946 
|
| [24] |
Wu D, Ni J, Beretov J, et al. (2017) Urinary biomarkers in prostate cancer detection and monitoring progression. Crit Rev Oncol Hemat 118: 15-26. https://doi.org/10.1016/j.critrevonc.2017.08.002 
|
| [25] |
Tosoian JJ, Ross AE, Sokoll LJ, et al. (2016) Urinary biomarkers for prostate cancer. Urol Clin N Am 43: 17-38. https://doi.org/10.1016/j.ucl.2015.08.003 
|
| [26] |
Luo Y, Gou X, Huang P, et al. (2014) The PCA3 test for guiding repeat biopsy of prostate cancer and its cut-off score: a systematic review and meta-analysis. Asian J Androl 16: 487-492. https://doi.org/10.4103/1008-682X.125390 
|
| [27] |
Dijkstra S, Mulders PF, Schalken JA (2014) Clinical use of novel urine and blood based prostate cancer biomarkers: a review. Clin Biochem 47: 889-896. https://doi.org/10.1016/j.clinbiochem.2013.10.023 
|
| [28] |
Larsen LK, Jakobsen JS, Abdul-Al A, et al. (2018) Noninvasive detection of high-grade prostate cancer by DNA methylation analysis of urine cells captured by microfiltration. J Uroly 200: 749-757. https://doi.org/10.1016/j.juro.2018.04.067 
|
| [29] |
Ratz L, Laible M, Kacprzyk LA, et al. (2017) TMPRSS2:ERG gene fusion variants induce TGF-β signaling and epithelial to mesenchymal transition in human prostate cancer cells. Oncotarget 8: 25115-25130. https://doi.org/10.18632/oncotarget.15931 
|
| [30] |
Sequeiros T, Bastarós JM, Sánchez M, et al. (2015) Urinary biomarkers for the detection of prostate cancer in patients with high-grade prostatic intraepithelial neoplasia. Prostate 75: 1102-1113. https://doi.org/10.1002/pros.22995 
|
| [31] |
Mengual L, Lozano JJ, Ingelmo-Torres M, et al. (2016) Using gene expression from urine sediment to diagnose prostate cancer: development of a new multiplex mRNA urine test and validation of current biomarkers. BMC Cancer 16: 76. https://doi.org/10.1186/s12885-016-2127-2 
|
| [32] |
Fryczkowski M, Bułdak R, Hejmo T, et al. (2018) Circulating levels of omentin, leptin, VEGF, and HGF and their clinical relevance with PSA marker in prostate cancer. Dis Markers 2018: 3852401. https://doi.org/10.1155/2018/3852401 
|
| [33] | Dheeraj A, Tailor D, Deep G, et al. (2018) Insulin-like Growth Factor Binding Protein-3 (IGFBP-3) regulates mitochondrial dynamics, EMT, and angiogenesis in progression of prostate cancer. Cancer Res 78: 1095. https://doi.org/10.1158/1538-7445.AM2018-1095 |
| [34] | Wisniewski T, Zyromska A, Makarewicz R, et al. (2019) Osteopontin and angiogenic factors as new biomarkers of prostate cancer. Urol J 16: 134-140. |
| [35] |
Prager AJ, Peng CR, Lita E, et al. (2013) Urinary aHGF, IGFBP3, and OPN as diagnostic and prognostic biomarkers for prostate cancer. Biomarkers Med 7: 831-841. https://doi.org/10.2217/bmm.13.112 
|
| [36] |
Rivnyak A, Kiss P, Tamas A, et al. (2018) Review on PACAP-induced transcriptomic and proteomic changes in neuronal development and repair. Int J Mol Sci 19: 1020. https://doi.org/10.3390/ijms19041020 
|
| [37] |
Ashina M, Martelletti P (2018) Pituitary adenylate-cyclase-activating polypeptide (PACAP): another novel target for treatment of primary headaches?. J Headache Pain 19: 33. https://doi.org/10.1186/s10194-018-0860-4 
|
| [38] |
Johnson GC, Parsons R, May V, et al. (2020) The role of pituitary adenylate cyclase-activating polypeptide (PACAP) signaling in the hippocampal dentate gyrus. Front Cell Neurosci 14: 111. https://doi.org/10.3389/fncel.2020.00111 
|
| [39] |
Hirabayashi T, Nakamachi T, Shioda S (2018) Discovery of PACAP and its receptors in the brain. J Headache Pain 19: 28. https://doi.org/10.1186/s10194-018-0855-1 
|
| [40] |
Leyton J, Coelho T, Coy D, et al. (1998) PACAP (6–38) inhibits the growth of prostate cancer cells. Cancer Lett 125: 131-139. https://doi.org/10.1016/S0304-3835(97)00525-9 
|
| [41] |
Derand R, Montoni A, Bulteau-Pignoux L, et al. (2004) Activation of VPAC1 receptors by VIP and PACAP-27 in human bronchial epithelial cells induces CFTR-dependent chloride secretion. Brit J Pharmacol 141: 698-708. https://doi.org/10.1038/sj.bjp.0705597 
|
| [42] |
Couvineau A, Ceraudo E, Tan YV, et al. (2012) The VPAC1 receptor: structure and function of a class B GPCR prototype. Front Endocrinol 3: 139. https://doi.org/10.3389/fendo.2012.00139 
|
| [43] |
Couvineau A, Tan YV, Ceraudo E, et al. (2013) Strategies for studying the ligand-binding site of GPCRs: Photoaffinity labeling of the VPAC1 receptor, a prototype of class B GPCRs. Method Enzymol 520: 219-237. https://doi.org/10.1016/B978-0-12-391861-1.00010-1 
|
| [44] |
Starr CG, Maderdrut JL, He J, et al. (2018) Pituitary adenylate cyclase-activating polypeptide is a potent broad-spectrum antimicrobial peptide: Structure-activity relationships. Peptides 104: 35-40. https://doi.org/10.1016/j.peptides.2018.04.006 
|
| [45] |
Jayawardena D, Guzman G, Gill RK, et al. (2017) Expression and localization of VPAC1, the major receptor of vasoactive intestinal peptide along the length of the intestine. Am J Physiol-Gastr L 313: G16-G25. https://doi.org/10.1152/ajpgi.00081.2017 
|
| [46] |
Dorsam GP, Benton K, Failing J, et al. (2011) Vasoactive intestinal peptide signaling axis in human leukemia. World J Biol Chem 2: 146-160. https://doi.org/10.4331/wjbc.v2.i6.146 
|
| [47] |
Garcı́a-Fernández MO, Solano RM, Carmena MJ, et al. (2003) Expression of functional PACAP/VIP receptors in human prostate cancer and healthy tissue. Peptides 24: 893-902. https://doi.org/10.1016/S0196-9781(03)00162-1 
|
| [48] |
Moretti C, Mammi C, Frajese GV, et al. (2006) PACAP and type I PACAP receptors in human prostate cancer tissue. Ann NY Acad Sci 1070: 440-449. https://doi.org/10.1196/annals.1317.059 
|
| [49] |
Tamas A, Javorhazy A, Reglodi D, et al. (2016) Examination of PACAP-like immunoreactivity in urogenital tumor samples. J Mol Neurosci 59: 177-183. https://doi.org/10.1007/s12031-015-0652-0 
|
| [50] |
Ibrahim H, Barrow P, Foster N (2011) Transcriptional modulation by VIP: a rational target against inflammatory disease. Clin Epigenet 2: 213-222. https://doi.org/10.1007/s13148-011-0036-4 
|
| [51] |
Gomariz RP, Juarranz Y, Carrión M, et al. (2019) An overview of VPAC receptors in rheumatoid arthritis: biological role and clinical significance. Front Endocrinol 10: 729. https://doi.org/10.3389/fendo.2019.00729 
|
| [52] |
Couvineau A, Laburthe M (2012) VPAC receptors: structure, molecular pharmacology, and interaction with accessory proteins. Brit J Pharmacol 166: 42-50. https://doi.org/10.1111/j.1476-5381.2011.01676.x 
|
| [53] |
Tripathi S, Trabulsi EJ, Gomella L, et al. (2016) VPAC1 targeted (64)Cu-TP3805 positron emission tomography imaging of prostate cancer: preliminary evaluation in man. Urology 88: 111-118. https://doi.org/10.1016/j.urology.2015.10.012 
|
| [54] |
Arms L, Vizzard MA (2011) Neuropeptides in lower urinary tract function. Handbook of Experimental Pharmacology : 395-423. https://doi.org/10.1007/978-3-642-16499-6_19 
|
| [55] |
Inbal U, Alexandraki K, Grozinsky-Glasberg S (2018) Gastrointestinal hormones in cancer. Encyclopedia of Endocrine Diseases . Oxford: Academic Press 579-586. https://doi.org/10.1016/B978-0-12-801238-3.95875-6 
|
| [56] |
Tang B, Yong X, Xie R, et al. (2014) Vasoactive intestinal peptide receptor-based imaging and treatment of tumors (Review). Int J Oncol 44: 1023-1031. https://doi.org/10.3892/ijo.2014.2276 
|
| [57] |
Reubi JC (2000) In vitro evaluation of VIP/PACAP receptors in healthy and diseased human tissues: clinical implications. Ann NY Acad Sci 921: 1-25. https://doi.org/10.1111/j.1749-6632.2000.tb06946.x 
|
| [58] | Thakur ML (2016) Targeting VPAC1 genomic receptors for optical imaging of lung cancer. Eur J Nucl Med Mol Imaging 43: S662-S663. |
| [59] |
Tang B, Wu J, Zhu MX, et al. (2019) VPAC1 couples with TRPV4 channel to promote calcium-dependent gastric cancer progression via a novel autocrine mechanism. Oncogene 38: 3946-3961. https://doi.org/10.1038/s41388-019-0709-6 
|
| [60] |
Truong H, Gomella LG, Thakur ML, et al. (2018) VPAC1-targeted PET/CT scan: improved molecular imaging for the diagnosis of prostate cancer using a novel cell surface antigen. World J Urol 36: 719-726. https://doi.org/10.1007/s00345-018-2263-1 
|
| [61] |
Liu S, Zeng Y, Li Y, et al. (2014) VPAC1 overexpression is associated with poor differentiation in colon cancer. Tumour Biol 35: 6397-6404. https://doi.org/10.1007/s13277-014-1852-x 
|
| [62] | Tang B, Xie R, Xiao YF, et al. (2017) VIP promotes gastric cancer progression via the VPAC1/TRPV4/Ca2+ signaling pathway. J Dig Dis 152: S836. https://doi.org/10.1016/S0016-5085(17)32886-X |
| [63] | Tripathi S, Trabulsi E, Kumar P, et al. (2015) VPAC1 targeted detection of genitourinary cancer: A urinary assay. J Nuclear Med 56: 388. |
| [64] |
Delgado M, Pozo D, Ganea D (2004) The significance of vasoactive intestinal peptide in immunomodulation. Pharmacol Rev 56: 249-290. https://doi.org/10.1124/pr.56.2.7 
|
| [65] |
Ganea D, Hooper KM, Kong W (2015) The neuropeptide vasoactive intestinal peptide: direct effects on immune cells and involvement in inflammatory and autoimmune diseases. Acta Physiol 213: 442-452. https://doi.org/10.1111/apha.12427 
|
| [66] |
Wu F, Song G, de Graaf C, et al. (2017) Structure and function of peptide-binding G protein-coupled receptors. J Mol Biol 429: 2726-2745. https://doi.org/10.1016/j.jmb.2017.06.022 
|
| [67] |
Moody TW (2019) Peptide receptors as cancer drug targets. Ann NY Acad Sci 1455: 141-148. https://doi.org/10.1111/nyas.14100 
|
| [68] |
Latek D, Langer I, Krzysko K, et al. (2019) A molecular dynamics study of vasoactive intestinal peptide receptor 1 and the basis of its therapeutic antagonism. Int J Mol Sci 20: 4348-4369. https://doi.org/10.3390/ijms20184348 
|
| [69] |
Langer I (2012) Conformational switches in the VPAC1 receptor. Brit J Pharmacol 166: 79-84. https://doi.org/10.1111/j.1476-5381.2011.01616.x 
|
| [70] |
Santos R, Ursu O, Gaulton A, et al. (2017) A comprehensive map of molecular drug targets. Nat Rev Drug Discov 16: 19-34. https://doi.org/10.1038/nrd.2016.230 
|
| [71] |
de Graaf C, Song G, Cao C, et al. (2017) Extending the structural view of class B GPCRs. Trends Biochem Sci 42: 946-960. https://doi.org/10.1016/j.tibs.2017.10.003 
|
| [72] |
Solano RM, Langer I, Perret J, et al. (2001) Two basic residues of the h-VPAC1 receptor second transmembrane helix are essential for ligand binding and signal transduction. J Biol Chem 276: 1084-1088. https://doi.org/10.1074/jbc.M007696200 
|
| [73] |
Jazayeri A, Doré AS, Lamb D, et al. (2016) Extra-helical binding site of a glucagon receptor antagonist. Nature 533: 274. https://doi.org/10.1038/nature17414 
|
| [74] |
Parthier C, Reedtz-Runge S, Rudolph R, et al. (2009) Passing the baton in class B GPCRs: peptide hormone activation via helix induction?. Trends Biochem Sci 34: 303-310. https://doi.org/10.1016/j.tibs.2009.02.004 
|
| [75] |
Ceraudo E, Hierso R, Tan YV, et al. (2012) Spatial proximity between the VPAC1 receptor and the amino terminus of agonist and antagonist peptides reveals distinct sites of interaction. FASEB J 26: 2060-2071. https://doi.org/10.1096/fj.11-196444 
|
| [76] |
Hutchings CJ, Koglin M, Olson WC, et al. (2017) Opportunities for therapeutic antibodies directed at G-protein-coupled receptors. Nat Rev Drug Discov 16: 787-810. https://doi.org/10.1038/nrd.2017.91 
|
| [77] |
Peyrassol X, Laeremans T, Lahura V, et al. (2018) Development by genetic immunization of monovalent antibodies against human vasoactive intestinal peptide receptor 1 (VPAC1), new innovative, and versatile tools to study VPAC1 receptor function. Front Endocrinol 9: 153. https://doi.org/10.3389/fendo.2018.00153 
|
| [78] |
Freson K, Peeters K, De Vos R, et al. (2008) PACAP and its receptor VPAC1 regulate megakaryocyte maturation: therapeutic implications. Blood 111: 1885-1893. https://doi.org/10.1182/blood-2007-06-098558 
|
| [79] |
Hermann RJ, Van der Steen T, Vomhof-Dekrey EE, et al. (2012) Characterization and use of a rabbit-anti-mouse VPAC1 antibody by flow cytometry. J Immunol Methods 376: 20-31. https://doi.org/10.1016/j.jim.2011.10.009 
|
| [80] |
Langlet C, Langer I, Vertongen P, et al. (2005) Contribution of the carboxyl terminus of the VPAC1 receptor to agonist-induced receptor phosphorylation, internalization, and recycling. J Biol Chem 280: 28034-28043. https://doi.org/10.1074/jbc.M500449200 
|
| [81] |
Ramos-Álvarez I, Mantey SA, Nakamura T, et al. (2015) A structure-function study of PACAP using conformationally restricted analogs: Identification of PAC1 receptor-selective PACAP agonists. Peptides 66: 26-42. https://doi.org/10.1016/j.peptides.2015.01.009 
|
| [82] |
Van Rampelbergh J, Juarranz MG, Perret J, et al. (2000) Characterization of a novel VPAC1 selective agonist and identification of the receptor domains implicated in the carboxyl-terminal peptide recognition. Brit J Pharmacol 130: 819-826. https://doi.org/10.1038/sj.bjp.0703384 
|
| [83] |
Dickson L, Aramori I, McCulloch J, et al. (2006) A systematic comparison of intracellular cyclic AMP and calcium signalling highlights complexities in human VPAC/PAC receptor pharmacology. Neuropharmacol 51: 1086-1098. https://doi.org/10.1016/j.neuropharm.2006.07.017 
|
| [84] |
Moody TW, Nuche-Berenguer B, Jensen RT (2016) Vasoactive intestinal peptide/pituitary adenylate cyclase-activating polypeptide, and their receptors and cancer. Curr Opin Endocrinol 23: 38-47. https://doi.org/10.1097/MED.0000000000000218 
|
| [85] |
Moody TW, Chan D, Fahrenkrug J, et al. (2003) Neuropeptides as autocrine growth factors in cancer cells. Curr Pharm Design 9: 495-509. https://doi.org/10.2174/1381612033391621 
|
| [86] |
Fernández-Martínez AB, Carmena MJ, Bajo AM, et al. (2015) VIP induces NF-κB1-nuclear localisation through different signalling pathways in human tumour and non-tumour prostate cells. Cell Signal 27: 236-244. https://doi.org/10.1016/j.cellsig.2014.11.005 
|
| [87] |
Iwasaki M, Akiba Y, Kaunitz JD (2019) Recent advances in vasoactive intestinal peptide physiology and pathophysiology: focus on the gastrointestinal system. F1000Research 8: 1629-1642. https://doi.org/10.12688/f1000research.18039.1 
|
| [88] |
Langer I (2012) Mechanisms involved in VPAC receptors activation and regulation: lessons from pharmacological and mutagenesis studies. Front Endocrin 3: 129. https://doi.org/10.3389/fendo.2012.00129 
|
| [89] |
Harmar AJ, Fahrenkrug J, Gozes I, et al. (2012) Pharmacology and functions of receptors for vasoactive intestinal peptide and pituitary adenylate cyclase—activating polypeptide: IUPHAR Review 1. Brit J Pharmacol 166: 4-17. https://doi.org/10.1111/j.1476-5381.2012.01871.x 
|
| [90] |
Langer I, Robberecht P (2007) Molecular mechanisms involved in vasoactive intestinal peptide receptor activation and regulation: current knowledge, similarities to and differences from the A family of G-protein-coupled receptors. Biochem Soc Trans 35: 724-728. https://doi.org/10.1042/BST0350724 
|
| [91] |
Igarashi H, Fujimori N, Ito T, et al. (2011) Vasoactive intestinal peptide (VIP) and VIP receptors-elucidation of structure and function for therapeutic applications. Int J Clin Med 2: 500-508. https://doi.org/10.4236/ijcm.2011.24084 
|
| [92] |
Delgado M, Ganea D (2000) Inhibition of IFN-gamma-induced Janus kinase-1-STAT1 activation in macrophages by vasoactive intestinal peptide and pituitary adenylate cyclase-activating polypeptide. J Immunol 165: 3051-3057. https://doi.org/10.4049/jimmunol.165.6.3051 
|
| [93] |
Smalley SGR, Barrow PA, Foster N (2009) Immunomodulation of innate immune responses by vasoactive intestinal peptide (VIP): its therapeutic potential in inflammatory disease. Clin Exp Immunol 157: 225-234. https://doi.org/10.1111/j.1365-2249.2009.03956.x 
|
| [94] |
Shaywitz AJ, Greenberg ME (1999) CREB: a stimulus-induced transcription factor activated by a diverse array of extracellular signals. Annu Rev Biochem 68: 821-861. https://doi.org/10.1146/annurev.biochem.68.1.821 
|
| [95] |
Delgado M, Ganea D (2001) Vasoactive intestinal peptide and pituitary adenylate cyclase-activating polypeptide inhibit nuclear factor-kappa B-dependent gene activation at multiple levels in the human monocytic cell line THP-1. J Biol Chem 276: 369-380. https://doi.org/10.1074/jbc.M006923200 
|
| [96] |
Dickson L, Finlayson K (2009) VPAC and PAC receptors: From ligands to function. Pharmacol Therapeut 121: 294-316. https://doi.org/10.1016/j.pharmthera.2008.11.006 
|
| [97] |
Laburthe M, Couvineau A, Tan V (2007) Class II G protein-coupled receptors for VIP and PACAP: Structure, models of activation and pharmacology. Peptides 28: 1631-1639. https://doi.org/10.1016/j.peptides.2007.04.026 
|
| [98] |
Collado B, Sánchez MG, Díaz-Laviada I, et al. (2005) Vasoactive intestinal peptide (VIP) induces c-fos expression in LNCaP prostate cancer cells through a mechanism that involves Ca2+ signalling. Implications in angiogenesis and neuroendocrine differentiation. Biochim Biophys Acta Mol Cell Res 1744: 224-233. https://doi.org/10.1016/j.bbamcr.2005.04.009 
|
| [99] |
Park MH, Hong JT (2016) Roles of NF-κB in cancer and inflammatory diseases and their therapeutic approaches. Cells 5: 15. https://doi.org/10.3390/cells5020015 
|
| [100] |
Grosset AA, Ouellet V, Caron C, et al. (2019) Validation of the prognostic value of NF-κB p65 in prostate cancer: A retrospective study using a large multi-institutional cohort of the Canadian Prostate Cancer Biomarker Network. PLoS Med 16: e1002847. https://doi.org/10.1371/journal.pmed.1002847 
|
| [101] |
Staal J, Beyaert R (2018) Inflammation and NF-κB signaling in prostate cancer: mechanisms and clinical implications. Cells 7: 122. https://doi.org/10.3390/cells7090122 
|
| [102] |
Thomas-Jardin SE, Dahl H, Nawas AF, et al. (2020) NF-κB signaling promotes castration-resistant prostate cancer initiation and progression. Pharmacol Therapeut 211: 107538. https://doi.org/10.1016/j.pharmthera.2020.107538 
|
| [103] |
Jain G, Cronauer MV, Schrader M, et al. (2012) NF-kappaB signaling in prostate cancer: a promising therapeutic target?. World J Urol 30: 303-310. https://doi.org/10.1007/s00345-011-0792-y 
|
| [104] |
Moreno P, Ramos-Álvarez I, Moody TW, et al. (2016) Bombesin-related peptides/receptors and their promising therapeutic roles in cancer imaging, targeting, and treatment. Expert Opin Ther Targets 20: 1055-1073. https://doi.org/10.1517/14728222.2016.1164694 
|
| [105] |
Ramos-Álvarez I, Moreno P, Mantey SA, et al. (2015) Insights into bombesin receptors and ligands: Highlighting recent advances. Peptides 72: 128-144. https://doi.org/10.1016/j.peptides.2015.04.026 
|
| [106] |
Baratto L, Jadvar H, Iagaru A (2018) Prostate cancer theranostics targeting gastrin-releasing peptide receptors. Mol Imaging Biol 20: 501-509. https://doi.org/10.1007/s11307-017-1151-1 
|
| [107] |
Moody TW, Ramos-Alvarez I, Jensen RT (2018) Neuropeptide G protein-coupled receptors as oncotargets. Front Endocrinol 9: 345-345. https://doi.org/10.3389/fendo.2018.00345 
|
| [108] | Dai J, Shen R, Sumitomo M, et al. (2002) Synergistic activation of the androgen receptor by bombesin and low-dose androgen. Clin Cancer Res 8: 2399. |
| [109] |
Putney JW, Tomita T (2012) Phospholipase C signaling and calcium influx. Adv Biol Regul 52: 152-164. https://doi.org/10.1016/j.advenzreg.2011.09.005 
|
| [110] |
Weber HC (2009) Regulation and signaling of human bombesin receptors and their biological effects. Curr Opin Endocrinol 16: 66-71. https://doi.org/10.1097/MED.0b013e32831cf5aa 
|
| [111] |
Fujita K, Pavlovich CP, Netto GJ, et al. (2009) Specific detection of prostate cancer cells in urine by multiplex immunofluorescence cytology. Hum Pathol 40: 924-933. https://doi.org/10.1016/j.humpath.2009.01.004 
|
| [112] |
Fujita K, Nonomura N (2018) Urinary biomarkers of prostate cancer. Int J Urol 25: 770-779. https://doi.org/10.1111/iju.13734 
|
| [113] |
Wei JT (2015) Urinary biomarkers for prostate cancer. Curr Opin Urol 25: 77-82. https://doi.org/10.1097/MOU.0000000000000133 
|
| [114] |
Trabulsi EJ, Tripathi SK, Gomella L, et al. (2017) Development of a voided urine assay for detecting prostate cancer non-invasively: a pilot study. BJU Int 119: 885-895. https://doi.org/10.1111/bju.13775 
|
| [115] |
Trabulsi E, Tripathi S, Calvaresi A, et al. (2016) VPAC1 in shed urinary cells—A potential genitourinary cancer biomarker. J Urol 195: e12. https://doi.org/10.1016/j.juro.2016.02.1880 
|
| [116] | Hoepel J (2021) Unraveling the mechanisms of antibody-dependent inflammation [PhD's thesis]. University of Amsterdam, Netherlands . |
| [117] |
Lagerström MC, Schiöth HB (2008) Structural diversity of G protein-coupled receptors and significance for drug discovery. Nat Rev Drug Discov 7: 339-357. https://doi.org/10.1038/nrd2518 
|
| [118] |
Pediani JD, Ward RJ, Marsango S, et al. (2018) Spatial intensity distribution analysis: studies of G protein-coupled receptor oligomerisation. Trends Pharmacol Sci 39: 175-186. https://doi.org/10.1016/j.tips.2017.09.001 
|
| [119] |
Hutchings CJ, Koglin M, Marshall FH (2010) Therapeutic antibodies directed at G protein-coupled receptors. mAbs 2: 594-606. https://doi.org/10.4161/mabs.2.6.13420 
|
| 1. | ATIEH POURBAGHERI-SIGAROODI, FATEMEH FALLAH, MAJID MOMENY, NIMA REZAEI, DAVOOD BASHASH, Unveiling the predictive power of bacterial response-related genes signature in hepatocellular carcinoma: with bioinformatics analyses and experimental approaches, 2024, 48, 1667-5746, 1781, 10.32604/biocell.2024.055848 |