Antibody profiling reveals gender differences in response to SARS-COVID-2 infection

1.   Introduction

The emergence of SARS-CoV-2 resulted in over 243 million (as of October 20, 2021) infections and more than 4.9 million deaths worldwide. A growing body of evidence suggests sex differences in the clinical outcomes of coronavirus disease. Large-scale data analysis of global data suggests that males face higher odds of both intensive therapy unit (ITU) admission and death from COVID-19 compared to females [1],[2]. The situation in country of Georgia is similar to global statistics. According to the available official statistics in Georgia for 1th of July 2021 (https://stopcov.ge/en) the number of SARS-CoV-2 infected females were more than males (58% vs 42%) but the lethality was significantly higher in mans (52.7% vs 47.3%, Chi-squared test P < 2e⁻¹⁴).

In order to elucidate the immune responses against SARS-CoV-2 infection in men and women, we performed antibody profiling of convalescent plasma from patients in country of Georgia. In particular, immunoblot analysis was performed to identify possible associations between gender and the presence of proteins in COVID-19 patients' blood plasma. We have studied the presence of antibodies against the various fragments of spike (S) protein and nucleocapsid protein (NCP). This later one is an internal viral protein and not exposed on the surface of virion particles [3],[4]. Antibodies against NCP thus lack virus neutralizing capacities. However, in recovered patients with severe acute respiratory syndrome (SARS) the antibodies were mainly against NCP [5] and it is suggested that their production might reflect the strength of T-helper cell responses [6].

2.   Materials and methods

A total of 162 subjects were involved in the study, 72 males (44.4%) and 90 females (56.6%). The age of patients varied between 25–70 years. The median age for females was 42 and for males 46. All of them were diagnosed as COVID-19 positive by PCR testing. Blood was drawn and plasma was prepared 6-8 weeks after the initial positive testing. None of the patients were on oxygen supply or artificial ventilation. The patients involved in the study were confirmed as SARS-CoV-2 infected at different stages of the disease. Subsequently, they had different Ct values at the above mentioned moment. The positive status was determined according to manufacturer recommendation which mainly was CT < 35. Meantime, most of them were tested more than once and Ct values varied as well.

Blood was centrifuged for 10000 g for 15 min and plasma incubated at 56 °C for 30 min and centrifuged again. Obtained plasma was diluted 1:100 in PBS for Western immunoblotting experiments.

The mixture of the following proteins was prepared: (1) Recombinant SARS Nucleocapsid protein (Bioss Antibodies Cat.N bs-49002p); (2) Recombinant SARS-CoV-2 spike S1 region (Bioss Antibodies, Cat.No. bs-46004P); (3) Recombinant SARS-CoV-2 spike RBD (Bioss Antibodies, Cat. No. bs-46003P); (4) Recombinant SARS-CoV-2 S2 subunit (Ray Biotech, Cat. No. 230-30163). Polyacrylamide 1.0 mm gels were loaded with 150 ng of proteins on each line. Proteins migrate as bands of the following molecular weights: S1 115–120 kDa, S2 80 kDa, NCP 45–47 kDa and RBD ~40 kDa. For the visualization of loaded recombinant proteins control lines were stained with Coomassie blue (Figure 1a).

The sodium dodecyl sulfate (SDS) gel electrophoresis and Western immunoblotting were carried out as described in our previous studies [7]. After transfer the nitrocellulose membranes were incubated in 3% fat-free milk (1 hour), then in patient's plasma (dilution 1:100, 1 hour), washed three times in PBS-Tween (0.1%), incubated 1 hour with peroxidase labelled monoclonal anti-human IgG (Abcam, ab99759) and exposed to X-ray films with intensifying screen.

2.1.   Statistical analysis

The association between gender and the presence of a protein in the blood was assessed with a two-tailed Fisher exact test, while a two-tailed exact binomial test was used for assessing whether an equal proportion of patients were producing antibodies against NCP proteins or antibodies against fragments of S proteins. All p-values were corrected for multiple testing with the Benjamini–Hochberg method. All analyses were performed with the R statistical software [8].

2.2.   Ethics approval of research

The experimental samples were collected for surveillance purposes and were eligible for further investigation without written consent form. In addition, this study does not include any personal identification information. From a large cohort of patients only those were selected which were diagnosed with COVID-19 with PCR tests. From the selected group patients were selected randomly, in blind that explains unequal representation by gender (see below). The experiments were approved by Ethics committee at the I. Beritashvili Center of Experimental Biomedicine (N 04/04.01.2021).

3.   Results

The representative images of Western immunoblots are shown on Figure 1. There was a great variability in the antibody response amongst the patients studied. Some of them did not reveal any antibodies against tested proteins, while others demonstrated immune response to only NCP or/and S protein fragments (Table 1).

Figure 1.  Representative images of: (a) Coomassie blue stained gel showing the separation of loaded antigens by ascending order: (1) RBD 40 kDa; (2) NCP 45–47 kDa; (3) S2 fragment 80 kDa, and (4) S1 fragment 115–120 kDa. (b–d) Immunoblots of patient's plasma which are treated with different antibodies (lane-B antibodies against S2 and NCP, lane-C antibodies against S1, NCP and RBD and lane-D antibodies only against NCP).

DownLoad: Full-Size Img PowerPoint

Table 1.  Distribution of antibody reactivity by antigens in patients. Some patients produce antibodies against more than one antigen and hence the sum of all positives exceeds the total number of patients studied.

	Number	Gender differences
		M	F
Number of patients	162	72	90
Absence of antibodies	21	13	8
NCP positive	129	52	77
RBD positive	39	11	28
S1 positive	45	12	33
S2 positive	30	10	20

---

 | Show Table

DownLoad: CSV

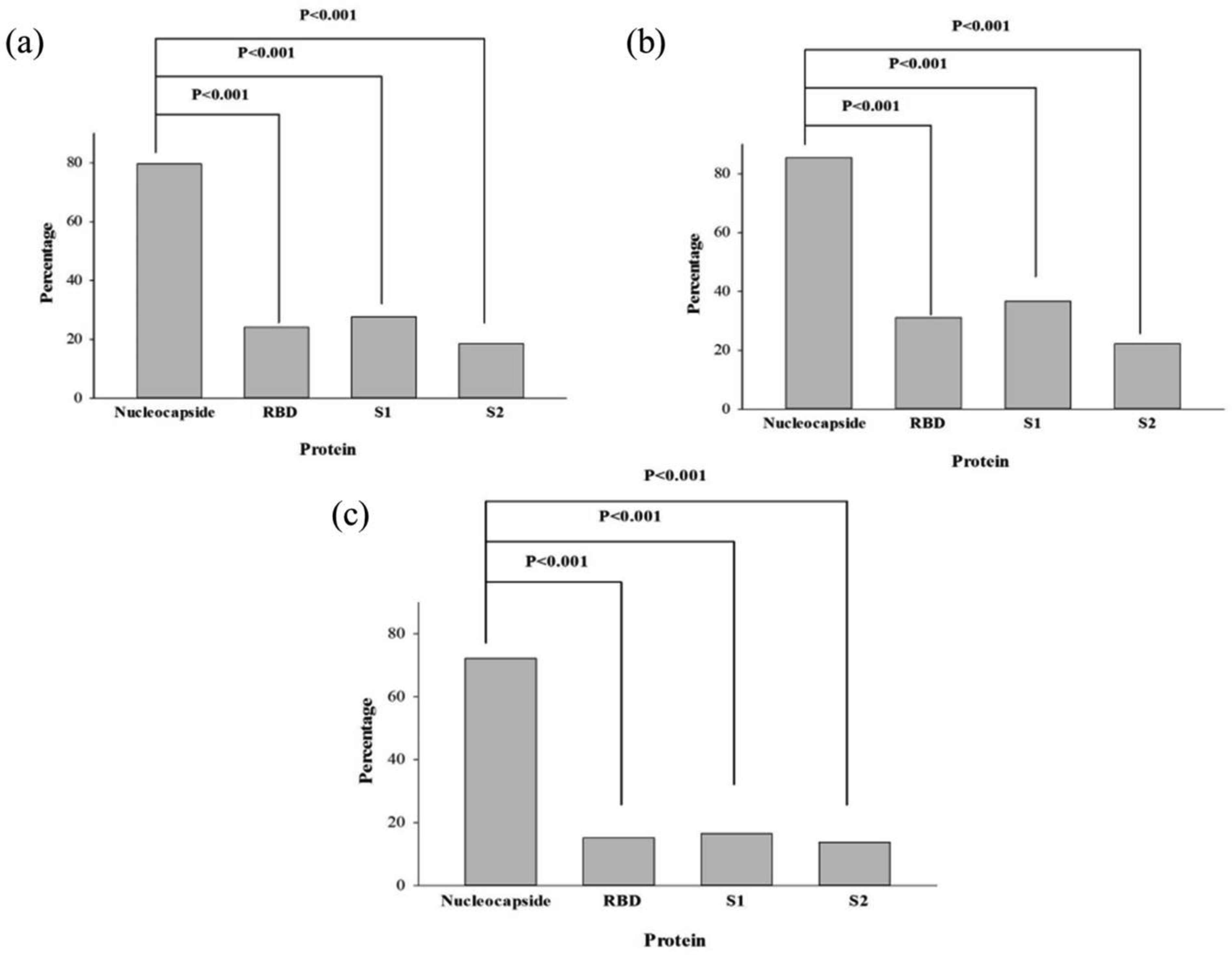
We have found that significantly more patients were producing antibodies against NCP as compared to various fragments of S protein (Figure 2a). This difference was not associated with gender and significant differences were detected both for females (Figure 2b) and males (Figure 2c).

Figure 2.  Percentage of patients producing antibodies against NCP or various fragments of S protein. (a) All patients, (b) females and (c) males. For all cases the antibodies against NCP antibodies are produced in more patients as compared to other antigens studied (adjusted p-value < 0.001).

DownLoad: Full-Size Img PowerPoint

We have compared a gender-specific signature of antibody response to SARS-CoV-2 infection. The percentage of females expressing antibodies to studied antigens in general were higher as compared to males. The presence of the antibodies against S1 fragment is highly associated with gender (corrected P value = 0.02), whereas the gender-specific differences for NCP and RBD are significant on one-tailed test only (for NCP one-tailed P value = 0.038, whereas for RBD P = 0.029), (Figure 3). There are no differences by gender in response to S2 fragment of S protein (P = 0.22).

Figure 3.  The antibody response to NCP and S protein fragments by gender. (a) NCP, (b) RBD, (c) S1 and (d) S2. The significant difference is observed in the case of S1 fragment—higher percentage of females are characterized by the presence of antibodies.

DownLoad: Full-Size Img PowerPoint

The results obtained indicates that: (1) There is a difference in antibody response to viral proteins; significant majority of patients are producing antibodies against NCP, compared to fragments of S-protein; (2) there is a gender difference in antibody response to SARS-CoV-2 at least in patients with a mild conditions: more females as compared to males are producing antibodies against S1 fragment of S protein. This part of S protein contains RBD—essential region for receptor recognition and virus cell entry and thus antibodies recognizing it would have neutralizing capabilities. The distribution of antibodies specifically recognizing only RBD follows the same pattern (Figure 3c).

4.   Discussion and conclusions

SARS-CoV-2 targets angiotensin converting enzyme-2 (ACE-2) for entry into the cell and the serine protease TMPRSS2 for S protein priming [9]. Sex hormones also regulate and influence aspects of viral entry via regulation of expression and activity of ACE2 and TMPRSS2 [10]. Androgens may promote or contribute to infection because transcription of TMPRSS2 is under their positive control [10].

Gender dependent different responses to SARS-Cov-2 infections were also reported for other aspects of immunity rather than antibody production [2]. In patients with moderate disease, without immunomodulatory medications, higher plasma levels of innate immune cytokines (IL8 and IL18) and more robust induction of non-classical monocytes was revealed in males. Female patients were characterized with significantly more robust T cell activation than male patients. A poor T cell response negatively correlated with patients' age and was associated with worse disease outcome in male patients, but not in female patients [2].

It is well known that across species, females tend to develop a stronger innate and adaptive immune response to infections (reviewed in [10]). In male and female mice with SARS, male mice had a 90% mortality rate, while female mice had a mortality rate of 20% and this sex bias is statistically significant [2],[10],[11]. It is supposed that stronger immunity in females increases the reproductive fitness of a species, as mothers are more likely to survive and care for their offspring [10],[11]. In support of this suggestion, in animal species where father is responsible for delivering and supporting offspring, upregulation of immunity is observed in males [12].

In humans females have stronger immune response against viral infections than men [12]. Women possess 2 copies of X chromosomes (maternal and paternal), which leads the silencing of one copy of genes in order to ensure an appropriate gene dosage. X chromosome inactivation is cell specific and some cells express the maternal chromosomal copy whereas others express the paternal copy. In female lymphocytes approximately 15% of X-chromosome genes escape inactivation, leading to biallelic expression with a double dosage [10],[12]–[15]. Biallelic expression has been shown for CXCR3, TLR7, and CD40L [13],[15]. In turn, females possess a diversity of possible immune responses, which provides women with a wider variety of tools with which to fight pathogens [14].

We hypothesize that stronger antibody response in females could account for the significantly less fatality despite higher infectivity of females. Demonstration of such dimorphism in the case of SARS-COV-2 could give basis for the development of selective and efficient therapy separately for mans and women against this viral infection.