Citation: Rosa Molfetta, Beatrice Zitti, Angela Santoni, Rossella Paolini. Ubiquitin and ubiquitin-like modifiers modulate NK cell-mediated recognition and killing of damaged cells[J]. AIMS Allergy and Immunology, 2017, 1(4): 164-180. doi: 10.3934/Allergy.2017.4.164
| [1] | Stefano Regis, Fabio Caliendo, Alessandra Dondero, Francesca Bellora, Beatrice Casu, Cristina Bottino, Roberta Castriconi . Main NK cell receptors and their ligands: regulation by microRNAs. AIMS Allergy and Immunology, 2018, 2(2): 98-112. doi: 10.3934/Allergy.2018.2.98 |
| [2] | Ling Wang, Shunbin Ning . “Toll-free” pathways for production of type I interferons. AIMS Allergy and Immunology, 2017, 1(3): 143-163. doi: 10.3934/Allergy.2017.3.143 |
| [3] | Arosh S. Perera Molligoda Arachchige . A universal CAR-NK cell approach for HIV eradication. AIMS Allergy and Immunology, 2021, 5(3): 192-194. doi: 10.3934/Allergy.2021015 |
| [4] | Amolak S Bansal, Alex Nicholas, Nazira Sumar, Veronica Varney . Mast cells, mediators, and symptomatic activation. AIMS Allergy and Immunology, 2024, 8(1): 34-55. doi: 10.3934/Allergy.2024004 |
| [5] | Issam Tout, Marie Marotel, Isabelle Chemin, Uzma Hasan . HBV and the importance of TLR9 on B cell responses. AIMS Allergy and Immunology, 2017, 1(3): 124-137. doi: 10.3934/Allergy.2017.3.124 |
| [6] | Mansur Aliyu, Fatema Zohora, Ali Akbar Saboor-Yaraghi . Spleen in innate and adaptive immunity regulation. AIMS Allergy and Immunology, 2021, 5(1): 1-17. doi: 10.3934/Allergy.2021001 |
| [7] | Swarna Bale, John Varga, Swati Bhattacharyya . Role of RP105 and A20 in negative regulation of toll-like receptor activity in fibrosis: potential targets for therapeutic intervention. AIMS Allergy and Immunology, 2021, 5(2): 102-126. doi: 10.3934/Allergy.2021009 |
| [8] | Manal Alkan, Fadel Sayes, Abdulraouf Ramadan, Francois Machavoine, Michel Dy, Elke Schneider, Nathalie Thieblemont . Basophil activation through TLR2 and TLR4 signaling pathways. AIMS Allergy and Immunology, 2018, 2(3): 126-140. doi: 10.3934/Allergy.2018.3.126 |
| [9] | Boel De Paepe . A recipe for myositis: nuclear factor κB and nuclear factor of activated T-cells transcription factor pathways spiced up by cytokines. AIMS Allergy and Immunology, 2017, 1(1): 31-42. doi: 10.3934/Allergy.2017.1.31 |
| [10] | Andrey Mamontov, Alexander Polevshchikov, Yulia Desheva . Mast cells in severe respiratory virus infections: insights for treatment and vaccine administration. AIMS Allergy and Immunology, 2023, 7(1): 1-23. doi: 10.3934/Allergy.2023001 |
Natural killer (NK) cells are innate lymphocytes rapidly activated during early stages of viral infections and tumor transformation [1,2]. Their cytolytic function against infected and transformed cells, as well as their ability to secrete cytokines and chemokines, is finely controlled by the integration of signals derived from inhibitory receptors which recognize major histocompatibility complex (MHC) class Ⅰ molecules on healthy cells, and activating receptors, some ligands of which have been only partially characterized [3].
Among activating receptors, natural-killer receptor group 2, member D (NKG2D) and DNAX accessory molecule 1 (DNAM1/CD226) play a crucial role in "induced self" recognition in that their ligands are self-molecules up-regulated upon cellular stress, microbial infection and malignant transformation [4,5,6].
NKG2D is a potent activating C-type lectin receptor expressed on all NK cells but also on CD8+ αβ T cells, γδ T cells, and activated CD4+ αβ T cells [7,8,9].
NKG2D-deficient mice show impaired surveillance towards spontaneous malignancies [10], and enhanced susceptibility to cytomegalovirus (CMV) infection [11], thus supporting a prominent role for NKG2D in NK cell-mediated immune responses.
Human NKG2D forms a hexameric complex with the transmembrane adaptor DNAX activating protein 10 (DAP10), which is required for signal propagation [12]. Ligand engagement promotes the phosphorylation of a tyrosine-based motif (YINM) in DAP10 intracellular domain that allows the recruitment of growth factor receptor-bound protein 2 (Grb2)/Vav1 complex and the activation of phosphatidyl-inositol-3-kinase (PI3K) [12,13]. Together, these signals are responsible for the consequent activation of phospholipase C gamma (PLCγ) 2, leading to cytotoxic granule secretion and cytokine synthesis [14]. A shorter NKG2D isoform that associates with either DAP10 or DAP12 adapters is expressed on activated murine NK cells and can initiate a signalling cascade involving the Syk/LAT pathway thanks to the immune tyrosine-based activation motif (ITAM) present in DAP12 cytoplasmic tail [15,16].
Remarkably, NKG2D can recognize multiple ligands that are all homologous to MHC class Ⅰ molecules. NKG2D binds to two families of polymorphic ligands in humans: MHC class Ⅰ related proteins (MIC) A/B and six UL16 binding proteins (ULBP1-6). MICA and MICB contain α1, α2 and α3 domains similar to MHC molecules and are transmembrane proteins, even though allelic variants of MICA exist that are linked to plasma membrane by a glycosylphosphatidylinositol (GPI) anchor. ULBP proteins possess only α1 and α2 domains and are expressed either as transmembrane (ULBP 4 and 6) or GPI-linked (ULPB1-3 and 5) surface molecules [4,9,17].
Three subfamilies of ligands are known in mice (Rae-1α-ε, MULT1, and H60a–c). All are orthologous to the human ULPB family, and can be expressed as transmembrane (MULT1) or GPI-linked (Rae-1 and some H60 ligands) proteins [4,9,17].
DNAM1 is an immunoglobulin receptor expressed on the majority of NK cells as well as on monocytes, T cells and subsets of B cells [8,18]. It is an adhesion molecule with a clear role in monocyte transendothelial migration [19] but it also contributes to tumor surveillance [20,21] and control of viral infections [22], as demonstrated in DNAM1-deficient mice.
DNAM1-mediated signalling cascade remains poorly defined. Ligand binding promotes the phosphorylation of a cytoplasmic serine by the protein kinase C (PKC) [23]. This phosphorylation allows the association of DNAM1 with the integrin LFA1 that is required for DNAM1-mediated signalling. Indeed, LFA1 crosslinking triggers the phosphorylation of a tyrosine in the DNAM1 cytoplasmic tail that, in turn, propagates intracellular signals required for cytotoxicity and cytokine production [24].
Both in humans and in mice DNAM1 interacts with the Nectin and Nectin-like family members Nectin2/CD112 and Nectin-like5/CD155 also known as poliovirus receptor (PVR) [25,26,27], even though murine DNAM1 binding to Nectin2 is still debated [28]. Nectin2 and PVR share a structure characterized by the presence of three immunoglobulin domains, while they differ in the cytoplasmic domain [27]. Like other members of the Nectin/Nectin-like family, Nectin2 and PVR are involved in cell-cell adhesion through the interaction with other members of the same family. Moreover, Nectin2 is also able to establish homophilic interactions.
NKG2D ligands (NKG2DL) are almost absent in healthy cells but are found on the membrane of several tumors of epithelial and non-epithelial origin, including melanoma, leukemia, lymphoma, glioma, and hepatocellular carcinoma where their expression contributes to render tumor cells susceptible to NK cell-mediated killing [29,30,31,32]. Moreover, epithelial tumors that express MICA and MICB, including carcinomas of the lung, breast, kidney, ovary, prostate, and colon, are efficiently recognized by infiltrating γδ T cells [33].
Differently from NKG2DLs, DNAM1 ligands (DNAM1L) are widely expressed on normal cells, including neuronal, epithelial, endothelial and fibroblastic cells [27]. However, up-regulation of PVR and/or Nectin2 on solid and haematological cancers activates NK cell killing of these tumors in a DNAM1-dependent manner [34,35,36,37,38]. Notably, DNAM1-dependent cytotoxicity is particularly relevant against tumor cells that do not express NKG2DLs [39].
NKG2D and DNAM1 ligands play also a crucial role in infected cell elimination. They are rapidly induced on infected cells to alert the immune system. However, virus-encoded proteins often inhibit their cell surface expression in order to evade NKG2D and DNAM1-mediated NK cell recognition [5,18,40]. Both NKG2D ligands of the MIC and ULBP families are up-regulated on HCMV-infected fibroblasts [41,42,43,44], thus increasing the co-stimulation of CD8+ T cells by NKG2D and inducing NK cell activation. Concomitantly, DNAM1 participates to the NK cell-mediated killing of HCMV-infected cells since PVR is up-regulated upon infection [45]. Similarly to HCMV, HIV infection induces the expression of MICA, ULBP1-2 and PVR on virus-infected T cells rendering these cells susceptible to NK cell cytotoxicity [46,47,48]. ULBP1 and Nectin2 are up-regulated on EBV-infected B cells and activate NK cell cytotoxicity against these cells [49], while the expression of MICB on human macrophages upon infection with Influenza A or Sendai virus induces IFN-γ production in NK cells [50].
Expression of both NKG2D and DNAM-1 ligands is induced by different stress pathways associated with hyper-proliferation, malignant transformation and virus infection [4,5,6]. Notably, ligand expression can be the result of transcriptional, post-transcriptional and post-translational levels of regulation depending on the type of stress and cell context (Figure 1). Therefore, unravelling these different layers of regulation may allow the development of new therapeutic approaches aimed at improving NK cell-mediated immune surveillance.
Figure 1. Regulation of NKG2D and DNAM1 ligand expression in response to stress stimuli. Mechanisms of post-transcriptional regulation include inhibition by microRNAs; mechanisms of post-translational regulations include metalloproteinase-induced shedding from the cell surface, release inside exosomes, and intracellular retention by ubiquitin or SUMO modification. (Figure modified from [6]).Until now, much efforts have been mainly concentrated in the identification of molecular pathways involved in the transcriptional regulation of NK cell activating ligand expression in response to different types of stress. One of the best-characterized pathways is the DNA damage response (DDR), a signalling pathway involved in the maintenance of DNA integrity. In fact, DDR is activated in response to DNA lesions produced during replication or induced by stress-related stimuli including virus infection and genotoxic agents [5]. This pathway is implicated in the induction of MICA and PVR in healthy proliferating T cells [51,52] and in the up-regulation of MICA, ULBP2 and PVR on CD4+ T lymphocytes upon HIV infection [53,54,55]. Several lines of evidence demonstrated that up-regulation of both NKG2D and DNAM1 ligands is mainly driven by the DDR pathway also in cancer cells, further supporting a role for this pathway in alerting immune system against damaged cells [56,57,58,59].
In addition to DDR pathway, stressful stimuli including the heat shock pathway, the oxidative stress pathway and the endoplasmic reticulum stress response, as well as stimulation through Toll-like receptor (TLR) are responsible for NKG2D ligand and PVR transcriptional up-regulation [4,60,61]. In some cases, as during HCMV infection, viral proteins can directly be responsible for transcriptional regulation of these ligands [62]. Among transcription factors involved in NKG2D and DNAM1 ligand regulation, a role for NF-ΚB, AP-1, and E2F has been documented [51,61,63,64,65,66].
As formally demonstrated in the case of NKG2DLs, ligand transcript levels can also be regulated at mRNA level by different endogenous or virus-encoded microRNA [67,68,69,70].
Different post-translational mechanisms, including the release of soluble ligands and the Ubiquitin (Ub) and Ub-like modifications, are also implicated in the regulation of both NKG2D and DNAM1 ligand expression, and will be discussed further below.
The best characterized post-translational mechanism is the production of NKG2DL soluble forms by tumor cells either by metalloproteinase-mediated shedding [31,71,72,73] or by their release on the membrane of exosomes [74,75], nanosized vesicles involved in intracellular communications (Figure 1). Regarding DNAM1Ls, soluble PVR forms, generated by alternative mRNA splicing, have been detected in sera of tumor patients [76]. However, the mechanism through which these soluble forms increase during transformation is largely unknown.
Post-translational mechanisms that repress surface expression of NKG2D and DNAM1 ligands have also been reported upon viral infection. Human CMV-encoded proteins UL16 and UL142 can cause NKG2DL intracellular retention [43,77,78], while UL141 promotes intracellular retention of an immature form of PVR [45] and the constitutive degradation of Nectin2 [79]. Similarly, HIV-Nef induces intracellular retention of PVR [48] and NKG2DLs of ULBP family [46]. Upon HSV-1 infection, MICA is down-modulated from the cell surface without any effect on total protein level [80], suggesting ligand intracellular retention.
These evidences support the conclusion that post-translational regulation of NKG2D and DNAM1 ligands may represent a general viral strategy to evade NK cell recognition.
Additional examples of post-translational regulation of NK cell activating ligands comprise the down-regulation of PVR surface expression and protein degradation in hepatocellular carcinoma upon activation of unfolded protein response (UPR) [81].
Regarding the molecular mechanisms implicated, Ub and small Ub-like modifier (SUMO) pathways appears to be deregulated in damaged cells, including virus infected and transformed cells [82,83,84]. In particular, the enzymes involved in ubiquitination and SUMOylation are often up-regulated in tumor cells, and several viruses exploit these pathways for their replication.
Interestingly, recent evidences reveal a previously unknown role for Ub and Ub-like modifiers as regulators of NKG2D and DNAM1 ligand expression, and provide novel insights in molecular mechanisms underlying expression of innate immune activating ligands on tumor cells [85,86,87,88].
Protein ubiquitination is a dynamic post-translational modification whereby the 76-amino acid protein Ub is covalently attached to a protein substrate. It is involved in nearly all aspects of eukaryotic biology due to the large number of proteins that may be subjected to this modification [89,90]. Ubiquitination, is catalyzed by the consecutive action of three classes of enzymes: the Ub-activating enzyme (E1), the Ub-conjugating enzyme (E2) and the Ub protein ligase (E3) that is responsible for substrate specificity. Once ubiquitinated, the substrate may undergo proteasome-dependent degradation as well as non-degradative fate, depending on the type of ubiquitin modification (Figure 2A). Indeed, Ub possesses seven lysine (K) residues that can be ubiquitinated, thus leading to the formation of different kind of Ub chains. In particular, whether the addition of K48-linked Ub chains signals for proteasomal degradation, modification by single Ub moieties (mono-and multi-ubiquitination) or by K63-linked Ub chains regulates endocytosis and trafficking of membrane proteins [89,91].
Figure 2. Comparison of ubiquitin and SUMO conjugation pathways. (A) The ubiquitin pathway. Attachment of ubiquitin (Ub) to a target protein requires three major enzymatic steps. In the first ATP-dependent step, Ub becomes covalently linked to the ubiquitin-activating enzyme E1 with a thiolester link. The activated Ub is then transferred to ubiquitin-conjugating enzyme (E2), which serves as a carrier protein. Ubiquitin ligase (E3) catalyzes the covalent attachment of Ub to the target substrate by the formation of isopeptide bonds. One or several Ub molecules can be conjugated to a substrate, determining its cellular fate. (B) The SUMO pathway. The conjugation pathway to SUMO is similar to the ubiquitin pathway, but it uses different E1 and E2 enzymes. The second step consists of a thiolester link that conjugates SUMO to Ubc9. This enzyme seems to have some intrinsic ligase activity for SUMO but the E3 protein might serve to increase the affinity between Ubc9 and the substrate allowing SUMOylation to occur at a maximal rate. SUMOylation may affect enzymatic activity, subcellular localization, and the ability to interact with other proteins. (Figure modified from Gasparrini et al., Int Arch Allergy Immunol 156: 16-26; 2011).The first evidence of an NK cell activating ligand modified by ubiquitination came from studies on Kaposi's sarcoma-associated herpesvirus. The viral protein K5, endowed with E3 Ub ligase activity, has been shown to be responsible for MICA ubiquitination on cytoplasmic lysines [85], thus preventing ligand surface expression. However, MICA does not undergo Ub-dependent degradation but instead it is retained in intracellular compartments (Figure 3, left). Interestingly, MICB was shown to be subjected to the same mechanism of down-regulation, while a common MICA allele that lack the cytoplasmic tail (MICA*008) resulted resistant to K5-mediated down-regulation [85].
Figure 3. Model depicting how ubiquitin and/or SUMO modifiers prevent activating ligand surface expression on target cell (left), and provide a signal for internalization and trafficking of activating receptors on NK cell (right).Murine NKG2D ligand MULT-1 has been shown to be constitutively ubiquitinated by the cellular orthologues of the Kaposi herpes virus-encoded Ub ligase on their cytoplasmic lysine residues [86,87]. Notably, MULT1 ubiquitination is responsible for ligand lysosomal degradation under normal conditions, and it is reversed in response to UV radiation and heat shock but not by other stressful stimuli [86], suggesting that only specific stressors impact on post-translational ligand modifications. No evidences are actually available in regard to DNAM1L ubiquitination.
Protein SUMOylation is a modification whereby the Ub-like modifier SUMO is covalently attached to the lysine residues of acceptor proteins. In analogy with Ub modification, SUMOylation occurs in three sequential steps catalyzed by different enzymes: a single E1, a single E2 and a small number of E3 enzymes [92,93]. Upon SUMOylation, target proteins do not necessarily undergo a degradative fate but instead they are subjected to conformational changes that modify their enzymatic activity or their ability to interact with other macromolecules (Figure 2B).
SUMO conjugation to protein substrates is frequently up-regulated in many tumors including breast and lung cancers, glioblastoma and multiple myeloma [92,93].
We have recently reported that this pathway impacts on activating ligand expression, thus impairing tumor cell recognition by NK cells [88]. Focusing on DNAM1Ls, we demonstrated that the SUMO pathway controls PVR, but not Nectin2 surface expression. PVR is directly subjected to SUMOylation, and this modification prevents its surface expression impairing DNAM1-mediated NK cell recognition [88] (Figure 3, left).
Intracellular retention of immature forms of MICA in endoplasmic reticulum followed by constitutive degradation has been observed in melanoma cells, and renders these cells able to evade NKG2D-mediated surveillance [94]. Similar results were obtained for MICB in a panel of tumor cell lines: this ligand is continuously internalized from plasma membrane and retained in intracellular compartments without being degraded [95]. Whether Ub or Ub-like modifications are directly implicated in MICA/B intracellular retention has not been investigated so far.
More recently, a similar behavior has been observed for ULBP1 that is continuously internalized and degraded in proteasome [96], suggesting that Ub or Ub-like modifications also affect GPI-linked molecules.
Altogether, these findings provide novel insights into the molecular mechanisms underlying NKG2D and DNAM1 ligand expression, and confer a role to post-translational modifications in preventing NK cell-mediated recognition and killing.
The efficacy of damaged cell elimination also depends on the presence and relative abundances of activating receptors on the surface of NK cells.
In the case of NKG2D, its surface expression can be modulated under different conditions. For examples, several cytokines, i.e. interleukin-2 (IL-2), IL-7, IL-12 and IL-15, increase NKG2D/DAP10 transcripts and receptor surface expression, whereas others (i.e. TGF-β and IL-21) decrease NKG2D surface expression and promote a selective impairment of NKG2D-mediated cytotoxicity [97,98,99,100,101,102,103,104].
It is now well recognized that persistent exposure to NKG2D ligands also results in a decrease of NKG2D surface expression promoting receptor down-modulation and the consequent impairment of NK cell-mediated effector functions [72,105,106,107,108,109,110,111].
The main mechanism responsible for NKG2D down-modulation is ligand-mediated endocytosis [112]. Both human and murine NKG2D receptors are indeed removed from the plasma membrane by clathrin-dependent internalization [107,110], and then rapidly traffics through endosomal compartment till lysosomes where both NKG2D and its associated adaptor, DAP10, are degraded [105,111,113,114].
Recent findings indicate that ligand-dependent human NKG2D endocytosis requires DAP10 ubiquitination that provides a signal for both receptor internalization from plasma membrane and its sorting through the endocytic compartments to lysosomes for degradation [114] (Figure 3, right). Indeed, a mutated form of DAP10 that does not undergo ubiquitination strongly impairs both NKG2D/DAP10 internalization and lysosomal degradation [114]. Although not formally demonstrated in mouse, it is likely that the Ub pathway is also implicated in murine NKG2D endocytosis. Indeed, NKG2D/DAP10 receptor complex degradation was observed in a murine transgenic model overexpressing a DAP10-Ub fusion molecule [115].
Notably, some NKG2DLs possess intrinsic diverse ability to induce NKG2D endocytosis. In particular, MICA and ULBP2 differ in their capability to phosphorylate the Ub ligase c-Cbl and to activate the Ub pathway, being MICA the most efficient ligand [111]. Whether c-Cbl is the Ub ligase responsible for DAP10 ubiquitination is still unknown; however, these results suggest that the degree of NKG2D/DAP10 ubiquitination dictates the extent of receptor internalization and degradation.
Interestingly, Ub modification has been also previously demonstrated for CD16, the low affinity receptor for IgG responsible for NK cell-mediated antibody-dependent cellular cytotoxicity (ADCC) [116]. Ubiquitination of CD16 ζ subunit and the associated tyrosine kinases promotes endocytosis of engaged receptor complexes and render NK cells impaired in their ability to further perform ADCC [116,117,118,119].
Regarding DNAM1, less is known about the effect of cytokines on receptor surface expression. As in the case of NKG2D, IL-15 up-regulates DNAM1 mRNA level whereas TGF-β has the opposite effect [120]. Upon ligand binding, down-modulation of DNAM1 surface expression was observed on NK cells from patients affected by different tumors, including multiple myeloma, acute myeloid leukemia and ovarian carcinoma, as compared to healthy donors [35,36,121]. Notably, DNAM1 down-modulation leads to an impaired NK cell mediated natural cytotoxicity. The molecular mechanisms responsible for DNAM1 down-modulation have not been clarified yet. In particular, whether DNAM1 may undergo ubiquitination has not been investigated so far.
Altogether these results demonstrate that the Ub pathway may also negatively regulate the functional capability of NK cells by a direct covalent modification and down-regulation of their activating receptors.
Recent findings support a role for Ub and Ub-like pathways in the regulation of NKG2D and DNAM1 ligands. Those ligands undergo ubiquitination or SUMOylation, and are then degraded or subjected to intracellular retention with the consequent reduction of their surface expression. Of note, compared to transcriptional regulation this mechanism offer the opportunity for a much more rapid kind of regulation, since the ligands have been already transduced.
In healthy cells, these modifications may act to prevent ligand membrane expression and a potential dangerous NK cell recognition, while in viral infected or transformed cells may represent a mechanism to evade NK cell surveillance.
Upon contact with ligand-bearing targets, the Ub pathway may also contribute to down-regulate the surface expression of engaged activating NK cell receptors, as formally demonstrated for CD16 and NKG2D.
Altogether, these findings support the conclusion that post-translational regulation of NK cell activating receptors and their ligands may rapidly regulate the strength of NK cell-target interaction, and impair the ability of NK cells to eliminate dangerous cells.
Work in our laboratory is supported by grants from the Italian Association for Cancer Research (AIRC), the Italian Ministry for University and Research (MIUR-FIRB; PRIN/20103FMJEN/AngelaSantoni), and the Center of Excellence (BEMM).
All authors declare that they have no conflict of interest in this paper.
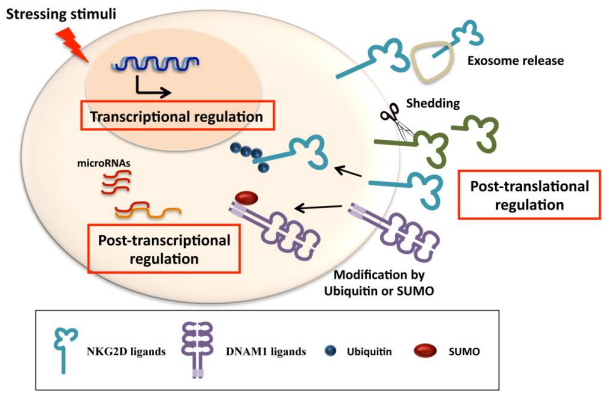
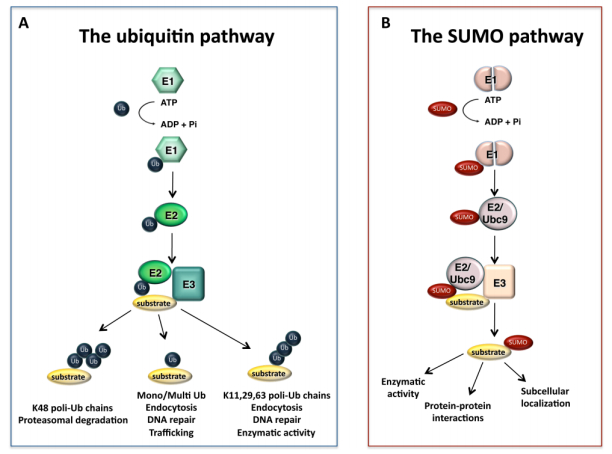
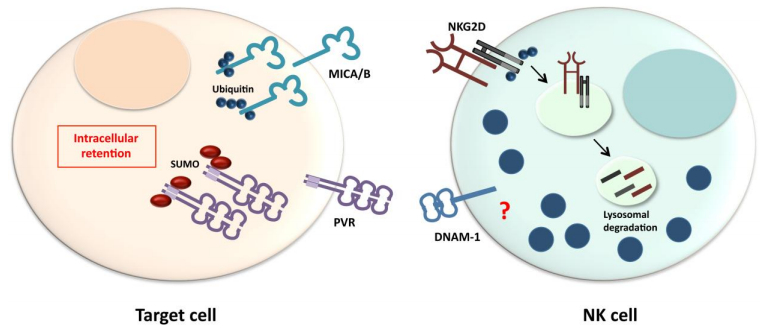
| [1] |
Caligiuri MA (2008) Human natural killer cells. Blood 112: 461–469. doi: 10.1182/blood-2007-09-077438
|
| [2] | Morvan MG, Lanier LL (2016) NK cells and cancer: you can teach innate cells new tricks. Nat Rev Cancer 16: 7–19. |
| [3] |
Long EO, Kim HS, Liu D, et al. (2013) Controlling natural killer cell responses: integration of signals for activation and inhibition. Annu Rev Immunol 31: 227–258. doi: 10.1146/annurev-immunol-020711-075005
|
| [4] |
Raulet DH, Gasser S, Gowen BG, et al. (2013) Regulation of ligands for the NKG2D activating receptor. Annu Rev Immunol 31: 413–441. doi: 10.1146/annurev-immunol-032712-095951
|
| [5] | Cerboni C, Fionda C, Soriani A, et al. (2014) The DNA damage response: a common pathway in the regulation of NKG2D and DNAM-1 ligand expression in normal, infected, and cancer cells. Front Immunol 4: 508. |
| [6] |
Chan CJ, Smyth MJ, Martinet L (2014) Molecular mechanisms of natural killer cell activation in response to cellular stress. Cell Death Differ 21: 5–14. doi: 10.1038/cdd.2013.26
|
| [7] |
Ullrich E, Koch J, Cerwenka A, et al. (2013) New prospects on the NKG2D/NKG2DL system for oncology. Oncoimmunology 2: e26097. doi: 10.4161/onci.26097
|
| [8] |
Marcus A, Gowen BG, Thompson TW, et al. (2014) Recognition of tumors by the innate immune system and natural killer cells. Adv Immunol 122: 91–128. doi: 10.1016/B978-0-12-800267-4.00003-1
|
| [9] |
Lanier LL (2015) NKG2D receptor and its ligands in host defense. Cancer Immunol Res 3: 575–582. doi: 10.1158/2326-6066.CIR-15-0098
|
| [10] |
Guerra N, Joncker NT, Choy A, et al. (2008) NKG2D-deficient mice are defective in tumor surveillance in models of spontaneous malignancy. Immunity 28: 571–580. doi: 10.1016/j.immuni.2008.02.016
|
| [11] |
Zafirova B, Mandarić S, Antulov R, et al. (2009) Altered NK cell development and enhanced NK cell-mediated resistance to mouse cytomegalovirus in NKG2D-deficient mice. Immunity 31: 270–282. doi: 10.1016/j.immuni.2009.06.017
|
| [12] |
Bauer S, Groh V, Wu J, et al. (1999) Activation of NK cells and T cells by NKG2D, a receptor for stress-inducible MICA. Science 285: 727–729. doi: 10.1126/science.285.5428.727
|
| [13] |
Wu J, Song Y, Bakker AB, et al. (1999) An activating immunoreceptor complex formed by NKG2D and DAP10. Science 285: 730–732. doi: 10.1126/science.285.5428.730
|
| [14] |
Upshaw JL, Leibson PJ (2006) NKG2D-mediated activation of cytotoxic lymphocytes: unique signaling pathways and distinct functional outcomes. Semin Immunol 18: 167–175. doi: 10.1016/j.smim.2006.03.001
|
| [15] |
Diefenbach A, Tomasello E, Lucas M, et al. (2002) Selective associations with signaling proteins determine stimulatory versus costimulatory activity of NKG2D. Nat Immunol 3: 1142–1149. doi: 10.1038/ni858
|
| [16] |
Gilfillan S, Ho EL, Cella M, et al. (2002) NKG2D recruits two distinct adapters to trigger NK cell activation and costimulation. Nat Immunol 3: 1150–1155. doi: 10.1038/ni857
|
| [17] |
Eagle RA, Trowsdale J (2007) Promiscuity and the single receptor: NKG2D. Nat Rev Immunol 7: 737–744. doi: 10.1038/nri2144
|
| [18] | de Andrade LF, Smyth MJ, Martinet L (2013) DNAM-1 control of natural killer cells functions through nectin and nectin-like proteins. Immunol Cell Biol 92: 237–244. |
| [19] |
Reymond N, Imbert AM, Devilard E, et al. (2004) DNAM-1 and PVR regulate monocyte migration through endothelial junctions. J Exp Med 199: 1331–1341. doi: 10.1084/jem.20032206
|
| [20] |
Iguchi-Manaka A, Kai H, Yamashita Y, et al. (2008) Accelerated tumor growth in mice deficient in DNAM-1 receptor. J Exp Med 205: 2959–2964. doi: 10.1084/jem.20081611
|
| [21] |
Gilfillan S, Chan CJ, Cella M, et al. (2008) DNAM-1 promotes activation of cytotoxic lymphocytes by nonprofessional antigen-presenting cells and tumors. J Exp Med 205: 2965–2973. doi: 10.1084/jem.20081752
|
| [22] |
Welch MJ, Teijaro JR, Lewicki HA, et al. (2012) CD8 T cell defect of TNF-α and IL-2 in DNAM-1 deficient mice delays clearance in vivo of a persistent virus infection. Virology 429: 163–170. doi: 10.1016/j.virol.2012.04.006
|
| [23] | Shibuya A, Lanier LL, Phillips JH (1998) Protein kinase C is involved in the regulation of both signaling and adhesion mediated by DNAX accessory molecule-1 receptor. J Immunol 161: 1671–1676. |
| [24] |
Shibuya K, Lanier LL, Phillips JH, et al. (1999) Physical and functional association of LFA-1 with DNAM-1 adhesion molecule. Immunity 11: 615–623. doi: 10.1016/S1074-7613(00)80136-3
|
| [25] |
Bottino C, Castriconi R, Pende D, et al. (2003) Identification of PVR (CD155) and Nectin-2 (CD112) as cell surface ligands for the human DNAM-1 (CD226) activating molecule. J Exp Med 198: 557–567. doi: 10.1084/jem.20030788
|
| [26] |
Tahara-Hanaoka S, Shibuya K, Onoda Y, et al. (2004) Functional characterization of DNAM-1 (CD226) interaction with its ligands PVR (CD155) and nectin-2 (PRR-2/CD112). Int Immunol 16: 533–538. doi: 10.1093/intimm/dxh059
|
| [27] |
Fuchs A, Colonna M (2006) The role of NK cell recognition of nectin and nectin-like proteins in tumor immunosurveillance. Semin Cancer Biol 16: 359–366. doi: 10.1016/j.semcancer.2006.07.002
|
| [28] |
Stanietsky N, Rovis TL, Glasner A, et al. (2013) Mouse TIGIT inhibits NK-cell cytotoxicity upon interaction with PVR. Eur J Immunol 43: 2138–2150. doi: 10.1002/eji.201243072
|
| [29] |
Pende D, Cantoni C, Rivera P, et al. (2001) Role of NKG2D in tumor cell lysis mediated by human NK cells: cooperation with natural cytotoxicity receptors and capability of recognizing tumors of nonepithelial origin. Eur J Immunol 31: 1076–1086. doi: 10.1002/1521-4141(200104)31:4<1076::AID-IMMU1076>3.0.CO;2-Y
|
| [30] |
Jinushi M, Takehara T, Tatsumi T, et al. (2003) Expression and role of MICA and MICB in human hepatocellular carcinomas and their regulation by retinoic acid. Int J Cancer 104: 354–361. doi: 10.1002/ijc.10966
|
| [31] |
Salih HR, Antropius H, Gieseke F, et al. (2003) Functional expression and release of ligands for the activating immunoreceptor NKG2D in leukemia. Blood 102: 1389–1396. doi: 10.1182/blood-2003-01-0019
|
| [32] | Friese MA, Platten M, Lutz SZ, et al. (2003) MICA/NKG2D-mediated immunogene therapy of experimental gliomas. Cancer Res 63: 8996–9006. |
| [33] |
Groh V, Rhinehart R, Secrist H, et al. (1999) Broad tumor-associated expression and recognition by tumor-derived gamma delta T cells of MICA and MICB. Proc Natl Acad Sci USA 96: 6879–6884. doi: 10.1073/pnas.96.12.6879
|
| [34] |
Pende D, Spaggiari GM, Marcenaro S, et al. (2005) Analysis of the receptor-ligand interactions in the natural killer-mediated lysis of freshly isolated myeloid or lymphoblastic leukemias: evidence for the involvement of the Poliovirus receptor (CD155) and Nectin-2 (CD112). Blood 105: 2066–2073. doi: 10.1182/blood-2004-09-3548
|
| [35] |
Carlsten M, Björkström NK, Norell H, et al. (2007) DNAX accessory molecule-1 mediated recognition of freshly isolated ovarian carcinoma by resting natural killer cells. Cancer Res 67: 1317–1325. doi: 10.1158/0008-5472.CAN-06-2264
|
| [36] |
El-Sherbiny YM, Meade JL, Holmes TD, et al. (2007) The requirement for DNAM-1, NKG2D, and NKp46 in the natural killer cell-mediated killing of myeloma cells. Cancer Res 67: 8444–8449. doi: 10.1158/0008-5472.CAN-06-4230
|
| [37] |
Lakshmikanth T, Burke S, Ali TH, et al. (2009) NCRs and DNAM-1 mediate NK cell recognition and lysis of human and mouse melanoma cell lines in vitro and in vivo. J Clin Invest 119: 1251–1263. doi: 10.1172/JCI36022
|
| [38] |
Torelli GF, Peragine N, Raponi S, et al. (2014) Recognition of adult and pediatric acute lymphoblastic leukemia blasts by natural killer cells. Haematologica 99: 1248–1254. doi: 10.3324/haematol.2013.101931
|
| [39] |
Chan CJ, Andrews DM, McLaughlin NM, et al. (2010) DNAM-1/CD155 interactions promote cytokine and NK cell-mediated suppression of poorly immunogenic melanoma metastases. J Immunol 184: 902–911. doi: 10.4049/jimmunol.0903225
|
| [40] | Paolini R, Bernardini G, Molfetta R, et al. (2015) NK cells and interferons. Cytokine Growth F R 2: 113–120. |
| [41] |
Groh V, Rhinehart R, Randolph-Habecker J, et al. (2001) Costimulation of CD8alphabeta T cells by NKG2D via engagement by MIC induced on virus-infected cells. Nat Immunol 2: 255–260. doi: 10.1038/85321
|
| [42] |
Cosman D, Müllberg J, Sutherland CL, et al. (2001) ULBPs, novel MHC class I-related molecules, bind to CMV glycoprotein UL16 and stimulate NK cytotoxicity through the NKG2D receptor. Immunity 14: 123–133. doi: 10.1016/S1074-7613(01)00095-4
|
| [43] |
Welte SA, Sinzger C, Lutz SZ, et al. (2003) Selective intracellular retention of virally induced NKG2D ligands by the human cytomegalovirus UL16 glycoprotein. Eur J Immunol 33: 194–203. doi: 10.1002/immu.200390022
|
| [44] |
Rölle A, Mousavi-Jazi M, Eriksson M, et al. (2003) Effects of human cytomegalovirus infection on ligands for the activating NKG2D receptor of NK cells: up-regulation of UL16-binding protein (ULBP)1 and ULBP2 is counteracted by the viral UL16 protein. J Immunol 171: 902–908. doi: 10.4049/jimmunol.171.2.902
|
| [45] | Tomasec P, Wang EC, Davison AJ, et al. (2005) Downregulation of natural killer cell-activating ligand CD155 by human cytomegalovirus UL141. Nat Immunol 6: 181–188. |
| [46] |
Cerboni C, Neri F, Casartelli N, et al. (2007) Human immunodeficiency virus 1 Nef protein downmodulates the ligands of the activating receptor NKG2D and inhibits natural killer cell-mediated cytotoxicity. J Gen Virol 88: 242–250. doi: 10.1099/vir.0.82125-0
|
| [47] |
Ward J, Bonaparte M, Sacks J, et al. (2007) HIV modulates the expression of ligands important in triggering natural killer cell cytotoxic responses on infected primary T-cell blasts. Blood 110: 1207–1214. doi: 10.1182/blood-2006-06-028175
|
| [48] |
Matusali G, Potestà M, Santoni A, et al. (2012) The human immunodeficiency virus type 1 Nef and Vpu proteins downregulate the natural killer cell-activating ligand PVR. J Virol 86: 4496–4504. doi: 10.1128/JVI.05788-11
|
| [49] |
Pappworth IY, Wang EC, Rowe M (2007) The switch from latent to productive infection in epstein-barr virus-infected B cells is associated with sensitization to NK cell killing. J Virol 81: 474–482. doi: 10.1128/JVI.01777-06
|
| [50] |
Sirén J, Sareneva T, Pirhonen J, et al. (2004) Cytokine and contact-dependent activation of natural killer cells by influenza A or Sendai virus-infected macrophages. J Gen Virol 85: 2357–2364. doi: 10.1099/vir.0.80105-0
|
| [51] |
Cerboni C, Zingoni A, Cippitelli M, et al. (2007) Antigen-activated human T lymphocytes express cell-surface NKG2D ligands via an ATM/ATR-dependent mechanism and become susceptible to autologous NK-cell lysis. Blood 110: 606–615. doi: 10.1182/blood-2006-10-052720
|
| [52] |
Ardolino M, Zingoni A, Cerboni C, et al. (2011) DNAM-1 ligand expression on Ag-stimulated T lymphocytes is mediated by ROS-dependent activation of DNA-damage response: relevance for NK-T cell interaction. Blood 117: 4778–4786. doi: 10.1182/blood-2010-08-300954
|
| [53] |
Ward J, Davis Z, DeHart J, et al. (2009) HIV-1 Vpr triggers natural killer cell-mediated lysis of infected cells through activation of the ATR-mediated DNA damage response. PLoS Pathog 5: e1000613. doi: 10.1371/journal.ppat.1000613
|
| [54] |
Richard J, Sindhu S, Pham TN, et al. (2010) HIV-1 Vpr up-regulates expression of ligands for the activating NKG2D receptor and promotes NK cell-mediated killing. Blood 115: 1354–1363. doi: 10.1182/blood-2009-08-237370
|
| [55] |
Vassena L, Giuliani E, Matusali G, et al. (2013) The human immunodeficiency virus type 1 Vpr protein upregulates PVR via activation of the ATR-mediated DNA damage response pathway. J Gen Virol 94: 2664–2669. doi: 10.1099/vir.0.055541-0
|
| [56] |
Gasser S, Orsulic S, Brown EJ, et al. (2005) The DNA damage pathway regulates innate immune system ligands of the NKG2D receptor. Nature 436: 1186–1190. doi: 10.1038/nature03884
|
| [57] |
Soriani A, Zingoni A, Cerboni C, et al. (2009) ATM-ATR-dependent up-regulation of DNAM-1 and NKG2D ligands on multiple myeloma cells by therapeutic agents results in enhanced NK-cell susceptibility and is associated with a senescent phenotype. Blood 113: 3503–3511. doi: 10.1182/blood-2008-08-173914
|
| [58] |
Croxford JL, Tang ML, Pan MF, et al. (2013) ATM-dependent spontaneous regression of early Eμ-myc-induced murine B-cell leukemia depends on natural killer and T cells. Blood 121: 2512–2521. doi: 10.1182/blood-2012-08-449025
|
| [59] |
Fionda C, Abruzzese MP, Zingoni AS, et al. (2015) Nitric oxide donors increase PVR/CD155 DNAM-1 ligand expression in multiple myeloma cells: role of DNA damage response activation. BMC Cancer 15: 17. doi: 10.1186/s12885-015-1023-5
|
| [60] |
Champsaur M, Lanier LL (2010) Effect of NKG2D ligand expression on host immune responses. Immunol Rev 235: 267–285. doi: 10.1111/j.0105-2896.2010.00893.x
|
| [61] |
Kamran N, Takai Y, Miyoshi J, et al. (2013) Toll-like receptor ligands induce expression of the costimulatory molecule CD155 on antigen-presenting cells. PLoS One 8: e54406. doi: 10.1371/journal.pone.0054406
|
| [62] |
Pignoloni B, Fionda C, Dell'Oste V, et al. (2016) Distinct roles for human cytomegalovirus immediate early proteins IE1 and IE2 in the transcriptional regulation of MICA and PVR/CD155 Expression. J Immunol 197: 4066–4078. doi: 10.4049/jimmunol.1502527
|
| [63] |
Solecki DJ, Gromeier M, Mueller S, et al. (2002) Expression of the human poliovirus receptor/CD155 gene is activated by sonic hedgehog. Biol Chem 277: 25697–25702. doi: 10.1074/jbc.M201378200
|
| [64] |
Hirota T, Irie K, Okamoto R, et al. (2005) Transcriptional activation of the mouse Necl-5/Tage4/PVR/CD155 gene by fibroblast growth factor or oncogenic Ras through the Raf-MEK-ERK-AP-1 pathway. Oncogene 24: 2229–2235. doi: 10.1038/sj.onc.1208409
|
| [65] |
Jung H, Hsiung B, Pestal K, et al. (2012) RAE-1 ligands for the NKG2D receptor are regulated by E2F transcription factors, which control cell cycle entry. J Exp Med 209: 2409–2422. doi: 10.1084/jem.20120565
|
| [66] |
Soriani A, Iannitto ML, Ricci B, et al. (2014) Reactive oxygen species- and DNA damage response-dependent NK cell activating ligand upregulation occurs at transcriptional levels and requires the transcriptional factor E2F1. J Immunol 193: 950–960. doi: 10.4049/jimmunol.1400271
|
| [67] |
Stern-Ginossar N, Gur C, Biton M, et al. (2008) Human microRNAs regulate stress-induced immune responses mediated by the receptor NKG2D. Nat Immunol 9: 1065–1073. doi: 10.1038/ni.1642
|
| [68] |
Yadav D, Ngolab J, Lim RS, et al. (2009) Cutting edge: down-regulation of MHC class I-related chain A on tumor cells by IFN-gamma-induced microRNA. J Immunol 182: 39–43. doi: 10.4049/jimmunol.182.1.39
|
| [69] |
Nachmani D, Stern-Ginossar N, Sarid R, et al. (2009) Diverse herpesvirus microRNAs target the stress-induced immune ligand MICB to escape recognition by natural killer cells. Cell Host Microbe 5: 376–385. doi: 10.1016/j.chom.2009.03.003
|
| [70] |
Heinemann A, Zhao F, Pechlivanis S, et al. (2012) Tumor suppressive microRNAs miR-34a/c control cancer cell expression of ULBP2, a stress-induced ligand of the natural killer cell receptor NKG2D. Cancer Res 72: 460–471. doi: 10.1158/0008-5472.CAN-11-1977
|
| [71] |
Boutet P, Agüera-González S, Atkinson S, et al. (2009) Cutting edge: the metalloproteinase ADAM17/TNF-alpha-converting enzyme regulates proteolytic shedding of the MHC class I-related chain B protein. J Immunol 182: 49–53. doi: 10.4049/jimmunol.182.1.49
|
| [72] |
Waldhauer I, Steinle A (2006) Proteolytic release of soluble UL16-binding protein 2 from tumor cells. Cancer Res 66: 2520–2526. doi: 10.1158/0008-5472.CAN-05-2520
|
| [73] |
Zingoni A, Cecere F, Vulpis E, et al. (2015) Genotoxic stress induces senescence-associated ADAM10-dependent release of NKG2D MIC ligands in multiple myeloma cells. J Immunol 195: 736–748. doi: 10.4049/jimmunol.1402643
|
| [74] |
Ashiru O, Boutet P, Fernández-Messina L, et al. (2010) Natural killer cell cytotoxicity is suppressed by exposure to the human NKG2D ligand MICA*008 that is shed by tumor cells in exosomes. Cancer Res 70: 481–489. doi: 10.1158/0008-5472.CAN-09-1688
|
| [75] |
Fernández-Messina L, Ashiru O, Boutet P, et al. (2010) Differential mechanisms of shedding of the glycosylphosphatidylinositol (GPI)-anchored NKG2D ligands. J Biol Chem 285: 8543–8551. doi: 10.1074/jbc.M109.045906
|
| [76] |
Iguchi-Manaka A, Okumura G, Kojima H, et al. (2016) Increased soluble CD155 in the serum of cancer patients. PLoS One 11: e0152982. doi: 10.1371/journal.pone.0152982
|
| [77] |
Ashiru O, Bennett NJ, Boyle LH, et al. (2009) NKG2D ligand MICA is retained in the cis-Golgi apparatus by human cytomegalovirus protein UL142. J Virol 83: 12345–12354. doi: 10.1128/JVI.01175-09
|
| [78] |
Bennett NJ, Ashiru O, Morgan FJ, et al. (2010) Intracellular sequestration of the NKG2D ligand ULBP3 by human cytomegalovirus. J Immunol 185: 1093–10102. doi: 10.4049/jimmunol.1000789
|
| [79] |
Prod'Homme V, Sugrue DM, Stanton RJ, et al. (2010) Human cytomegalovirus UL141 promotes efficient downregulation of the natural killer cell activating ligand CD112. J Gen Virol 91: 2034–2039. doi: 10.1099/vir.0.021931-0
|
| [80] |
Schepis D, D'Amato M, Studahl M, et al. (2009) Herpes simplex virus infection downmodulates NKG2D ligand expression. Scand J Immunol 69: 429–436. doi: 10.1111/j.1365-3083.2009.02241.x
|
| [81] |
Gong J, Fang L, Liu R, et al. (2014) UPR decreases CD226 ligand CD155 expression and sensitivity to NK cell-mediated cytotoxicity in hepatoma cells. Eur J Immunol 44: 3758–3767. doi: 10.1002/eji.201444574
|
| [82] | Bologna S, Ferrari S (2013) It takes two to tango: ubiquitin and SUMO in the DNA damage response. Front Genet 4: 106. |
| [83] |
Wimmer P, Schreiner S (2015) Viral mimicry to usurp ubiquitin and SUMO host pathways. Viruses 7: 4854–4872. doi: 10.3390/v7092849
|
| [84] |
Ardorisio S, Fierabracci A, Muscari I, et al. (2017) SUMO proteins: guardians of immune system. J Autoimmun 84: 21–28. doi: 10.1016/j.jaut.2017.09.001
|
| [85] |
Thomas M, Boname JM, Field S, et al. (2008) Down-regulation of NKG2D and NKp80 ligands by Kaposi's sarcoma-associated herpesvirus K5 protects against NK cell cytotoxicity. Proc Natl Acad Sci USA 105: 1656–1661. doi: 10.1073/pnas.0707883105
|
| [86] |
Nice TJ, Coscoy L, Raulet DH (2009) Posttranslational regulation of the NKG2D ligand Mult1 in response to cell stress. J Exp Med 206: 287–298. doi: 10.1084/jem.20081335
|
| [87] |
Nice TJ, Deng W, Coscoy L, et al. (2010) Stress-regulated targeting of the NKG2D ligand Mult1 by a membrane-associated RING-CH family E3 ligase. J Immunol 185: 5369–7536. doi: 10.4049/jimmunol.1000247
|
| [88] |
Zitti B, Molfetta R, Fionda C, et al. (2017) Innate immune activating ligand SUMOylation affects tumor cell recognition by NK cells. Sci Rep 7: 10445. doi: 10.1038/s41598-017-10403-0
|
| [89] |
Komander D, Rape M (2012) The ubiquitin code. Annu Rev Biochem 81: 203–229. doi: 10.1146/annurev-biochem-060310-170328
|
| [90] |
Varshavsky A (2017) The ubiquitin system, autophagy, and regulated protein degradation. Annu Rev Biochem 86: 123–128. doi: 10.1146/annurev-biochem-061516-044859
|
| [91] |
Molfetta R, Gasparrini F, Santoni A, et al. (2010) Ubiquitination and endocytosis of the high affinity receptor for IgE. Mol Immunol 47: 2427–2434. doi: 10.1016/j.molimm.2010.06.003
|
| [92] |
Wilkinson KA, Henley JM (2010) Mechanisms, regulation and consequences of protein SUMOylation. Biochem J 428: 133–145. doi: 10.1042/BJ20100158
|
| [93] |
Flotho A, Melchior F (2013) Sumoylation: a regulatory protein modification in health and disease. Annu Rev Biochem 82: 357–385. doi: 10.1146/annurev-biochem-061909-093311
|
| [94] |
Fuertes MB, Girart MV, Molinero LL, et al. (2008) Intracellular retention of the NKG2D ligand MHC class I chain-related gene A in human melanomas confers immune privilege and prevents NK cell-mediated cytotoxicity. J Immunol 180: 4606–4614. doi: 10.4049/jimmunol.180.7.4606
|
| [95] |
Agüera-González S, Boutet P, Reyburn HT, et al. (2009) Brief residence at the plasma membrane of the MHC class I-related chain B is due to clathrin-mediated cholesterol-dependent endocytosis and shedding. J Immunol 182: 4800–4908. doi: 10.4049/jimmunol.0800713
|
| [96] |
Fernández-Messina L, Reyburn HT, Valés-Gómez M (2016) A short half-life of ULBP1 at the cell surface due to internalization and proteosomal degradation. Immunol Cell Biol 94: 479–485. doi: 10.1038/icb.2016.2
|
| [97] |
Castriconi R, Cantoni C, Della CM, et al. (2003) Transforming growth factor beta 1 inhibits expression of NKp30 and NKG2D receptors: consequences for the NK-mediated killing of dendritic cells. Proc Natl Acad Sci USA 100: 4120–4125. doi: 10.1073/pnas.0730640100
|
| [98] |
Lee JC, Lee KM, Kim DW, et al. (2004) Elevated TGF-beta1 secretion and down-modulation of NKG2D underlies impaired NK cytotoxicity in cancer patients. J Immunol 172: 7335–7340. doi: 10.4049/jimmunol.172.12.7335
|
| [99] |
Dasgupta S, Bhattacharya-Chatterjee M, Jr OB, et al. (2005) Inhibition of NK cell activity through TGF-beta 1 by down-regulation of NKG2D in a murine model of head and neck cancer. J Immunol 175: 5541–5550. doi: 10.4049/jimmunol.175.8.5541
|
| [100] |
Burgess SJ, Marusina AI, Pathmanathan I, et al. (2006) IL-21 down-regulates NKG2D/DAP10 expression on human NK and CD8+ T cells. J Immunol 176: 1490–1497. doi: 10.4049/jimmunol.176.3.1490
|
| [101] |
Zhang C, Zhang J, Niu J, et al. (2008) Interleukin-12 improves cytotoxicity of natural killer cells via upregulated expression of NKG2D. Hum Immunol 69: 490–500. doi: 10.1016/j.humimm.2008.06.004
|
| [102] |
Crane CA, Han SJ, Barry JJ, et al. (2010) TGF-beta downregulates the activating receptor NKG2D on NK cells and CD8+ T cells in glioma patients. Neuro Oncol 12: 7–13. doi: 10.1093/neuonc/nop009
|
| [103] |
Muntasell A, Magri G, Pende D, et al. (2010) Inhibition of NKG2D expression in NK cells by cytokines secreted in response to human cytomegalovirus infection. Blood 115: 5170–5179. doi: 10.1182/blood-2009-11-256479
|
| [104] |
Park YP, Choi SC, Kiesler P, et al. (2011) Complex regulation of human NKG2D-DAP10 cell surface expression: opposing roles of the γc cytokines and TGF-β1. Blood 118: 3019–3027. doi: 10.1182/blood-2011-04-346825
|
| [105] |
Groh V, Wu J, Yee C, et al. (2002) Tumor-derived soluble MIC ligands impair expression of NKG2D and T-cell activation. Nature 419: 734–738. doi: 10.1038/nature01112
|
| [106] |
Doubrovina ES, Doubrovin MM, Vider E, et al. (2003) Evasion from NK cell immunity by MHC class I chain-related molecules expressing colon adenocarcinoma. J Immunol 171: 6891–6899. doi: 10.4049/jimmunol.171.12.6891
|
| [107] |
Ogasawara K, Hamerman JA, Hsin H, et al. (2003) Impairment of NK cell function by NKG2D modulation in NOD mice. Immunity 18: 41–51. doi: 10.1016/S1074-7613(02)00505-8
|
| [108] |
Oppenheim DE, Roberts SJ, Clarke SL, et al. (2005) Sustained localized expression of ligand for the activating NKG2D receptor impairs natural cytotoxicity in vivo and reduces tumor immunosurveillance. Nat Immunol 6: 928–937. doi: 10.1038/ni1239
|
| [109] |
Wiemann K, Mittrücker HW, Feger U, et al. (2005) Systemic NKG2D down-regulation impairs NK and CD8 T cell responses in vivo. J Immunol 175: 720–729. doi: 10.4049/jimmunol.175.2.720
|
| [110] |
Cerboni C, Ardolino M, Santoni A, et al. (2009) Detuning CD8+ T lymphocytes by down-regulation of the activating receptor NKG2D: role of NKG2D ligands released by activated T cells. Blood 113: 2955–2964. doi: 10.1182/blood-2008-06-165944
|
| [111] |
Molfetta R, Quatrini L, Capuano C, et al. (2014) c-Cbl regulates MICA- but not ULBP2-induced NKG2D down-modulation in human NK cells. Eur J Immunol 44: 2761–2770. doi: 10.1002/eji.201444512
|
| [112] |
Molfetta R, Quatrini L, Zitti B, et al. (2016) Regulation of NKG2D expression and signaling by endocytosis. Trends Immunol 37: 790–802. doi: 10.1016/j.it.2016.08.015
|
| [113] |
Roda-Navarro P, Reyburn HT (2009) The traffic of the NKG2D/Dap10 receptor complex during natural killer (NK) cell activation. J Biol Chem 284: 16463–16472. doi: 10.1074/jbc.M808561200
|
| [114] |
Quatrini L, Molfetta R, Zitti B, et al. (2015) Ubiquitin-dependent endocytosis of NKG2D-DAP10 receptor complexes activates signaling and functions in human NK cells. Sci Signal 8: ra108. doi: 10.1126/scisignal.aab2724
|
| [115] |
Horng T, Bezbradica JS, Medzhitov R (2007) NKG2D signaling is coupled to the interleukin 15 receptor signaling pathway. Nat Immunol 8: 1345–1352. doi: 10.1038/ni1524
|
| [116] |
Paolini R, Serra A, Molfetta R, et al. (1999) Tyrosine kinase-dependent ubiquitination of CD16 zeta subunit in human NK cells following receptor engagement. Eur J Immunol 29: 3179–3187. doi: 10.1002/(SICI)1521-4141(199910)29:10<3179::AID-IMMU3179>3.0.CO;2-9
|
| [117] |
Paolini R, Molfetta R, Piccoli M, et al. (2001) Ubiquitination and degradation of Syk and ZAP-70 protein tyrosine kinases in human NK cells upon CD16 engagement. Proc Natl Acad Sci USA 98: 9611–9616. doi: 10.1073/pnas.161298098
|
| [118] |
Capuano C, Romanelli M, Pighi C, et al. (2015) Anti-CD20 therapy acts via FcγRIIIA to diminish responsiveness of human natural killer cells. Cancer Res 75: 4097–4108. doi: 10.1158/0008-5472.CAN-15-0781
|
| [119] |
Capuano C, Pighi C, Molfetta R, et al. (2017) Obinutuzumab-mediated high-affinity ligation of FcγRIIIA/CD16 primes NK cells for IFNγ production. Oncoimmunology 6: e1290037. doi: 10.1080/2162402X.2017.1290037
|
| [120] |
Wilson EB, El-Jawhari JJ, Neilson AL, et al. (2011) Human tumour immune evasion via TGF-β blocks NK cell activation but not survival allowing therapeutic restoration of anti-tumour activity. PLoS One 6: e22842. doi: 10.1371/journal.pone.0022842
|
| [121] |
Sanchez-Correa B, Gayoso I, Bergua JM, et al. (2012) Decreased expression of DNAM-1 on NK cells from acute myeloid leukemia patients. Immunol Cell Biol 90: 109–115. doi: 10.1038/icb.2011.15
|
Rosa Molfetta, Beatrice Zitti, Angela Santoni, Rossella Paolini. Ubiquitin and ubiquitin-like modifiers modulate NK cell-mediated recognition and killing of damaged cells[J]. AIMS Allergy and Immunology, 2017, 1(4): 164-180. doi: 10.3934/Allergy.2017.4.164
DownLoad: 
