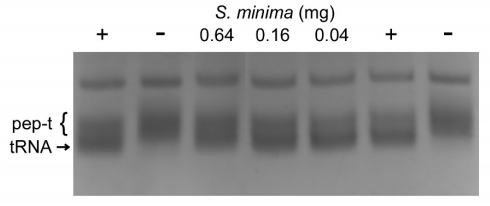
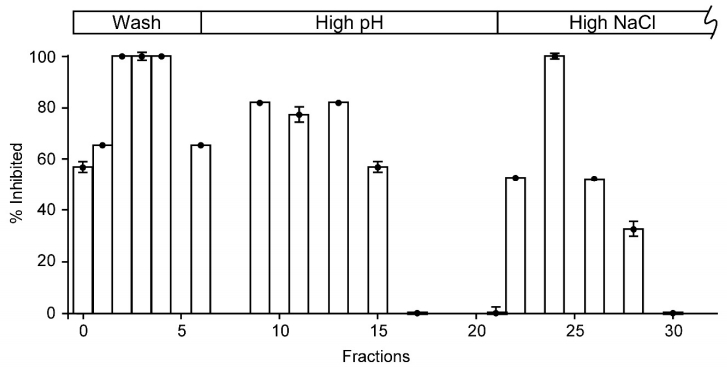
New antibiotics and new antibiotic targets are needed to counter the development of bacterial drug resistance that threatens to return the human population to the pre-antibiotic era. Bacterial peptidyl-tRNA hydrolase (Pth1) is a promising new antibiotic target in the early stages of development. While inhibitory activity has been observed in a variety of natural products, bioactive fractionation has been a bottleneck for inhibitor isolation. To expedite the isolation of inhibitory compounds from complex mixtures, we constructed a Pth1 affinity column and used it to isolate inhibitory compounds from crude natural products. Recombinantly produced S. typhimurium Pth1 was covalently attached to a column matrix and the inhibitory activity isolated from ethanol extracts of Salvinia minima. The procedure reported here demonstrates that isolation of Pth1 inhibitory compounds from complex natural product extracts can be greatly expedited over traditional bioactive fractionation, decreasing time and expense. The approach is generally applicable to Pth1s from other bacterial species and opens an avenue to advance and accelerate inhibitor development against this promising antimicrobial target.
1.
Introduction
Protein is very important for the human body. Some of these proteins can interact with DNA and are called DNA-binding proteins (DBPs). These are very important for gene-related life activities. For example, in DNA replication and repair functions, origins of replication sites [1] is the location where genomic DNA replication begins, and is important for the study of the DNA replication process. In transcription and regulatory functions, RNA is an important molecule in the cell. Messenger RNA passes genetic information to DNA and acts as a template for protein synthesis, while only 2% of RNA molecules in proteins act as templates, the rest being a molecule called MicroRNA, which plays an important regulatory role in biological processes. Identifying molecules of MicroRNA [2] helps to understand the whole regulatory process, while some other functions are single-stranded DNA binding and separation functions, chromatin formation functions and cell development functions [3,4]. In addition, research into drug target proteins [5,6] and DNA expression genetics are also quite popular, as drug target proteins are closely related to human diseases, while DNA expression genetics include DNA N4-methylcytosine [7,8], histone modification, RNA interference, etc. The main study in this paper is DNA binding proteins. Identification of DBPs can help us better understand how proteins interact with DNA, thus promoting the development of life science.
Although the traditional method based on biological experiments can obtain high-precision results, it needs large quantities of time and human effort. In addition, with the advent of the post-genome era, Web-lab methods cannot keep up with the growth rate of protein sequences. By contrast, computational approach reduces the resources and manpower required and enables simple and efficient identification of DBPs from many protein sequences. Thus, for the development of bioinformatics, the use of computational methods to predict DBPs is of great value.
In the past decade, machine learning based algorithms are already getting a lot of attention, and researchers have also proposed several research algorithms. In general, DNA-binding proteins can be identified by two computational methods, one based on structure and the other on sequence. Gao et al. [9] proposed a knowledge-based method called DBD-Hunter. This method uses protein structural alignment and statistical potential energy assessment to predict DBPs. Nimrod et al. [10] used the 3D structure of proteins to predict DBPs. They used a random forest classifier to determine whether a protein was a DBP based on features obtained from the protein's evolutionary profile. Zhao et al. [11] Identification of DBPs proteins using 3D structures generated based on HHblits [12]. However, structure-based approaches rely on predicted or natural 3D protein structures, and obtaining these structures is difficult. As a result, many sequence-based methods have been developed. Kumar et al. [13] developed a random forest approach called DNA-Prot to identify DBPs from protein sequences. Liu et al. [14] developed a predictor called iDNAPro-PseAAC, which relies only on protein sequence information. They applied PseAAC [15,16] to support vector machines to identify DBPs. Wei et al. [17] used the features extracted from the local PSE-PSSM (pseudo location-specific scoring matrix) in combination with a random forest classifier and to identify DBPs. Mishra et al. [18] proposed a method called StackDPPred, which uses features extracted from PSSM and residue-specific contact energy to help train a stacking-based machine learning method that can effectively predict DNA-binding proteins. Nanni et al. [19] in order to build an optimal and most general classification system for DNA-binding proteins, features were experimentally extracted from proteins and trained and evaluated in a separate support vector machine, while the matrix of proteins was fine-tuned using convolutional neural networks with different parameter settings, and the decisions were fused with the support vector machine using weights and rules for predicting DBPs. In recent years, deep learning has proven to be very effective in image and natural language processing. Therefore, researchers gradually began to apply deep learning in bioinformatics. Deep learning methods need only to input raw data and do not need to manually extract features, as does machine learning. For example, Qu et al. [20] used a combination of LSTM and CNN and extracted features from protein sequences to predict DBPs. Shadab et al. [21] proposed two methods, DeepDBP-ANN and DeepDBP-CNN, by using deep learning methods, the first by generating a set of features through traditional neural network training and the second by means of pre-learned embedding and convolutional neural networks, both of which have fetched good results. Some other methods, such as DeepDRBP-2L [22], iDRBP_MMC [23], and PDBP-Fusion [24], also improved the predictive performance of DBP by using deep learning.
2.
Methods
2.1. The framework of DBPs prediction based on deep transfer learning
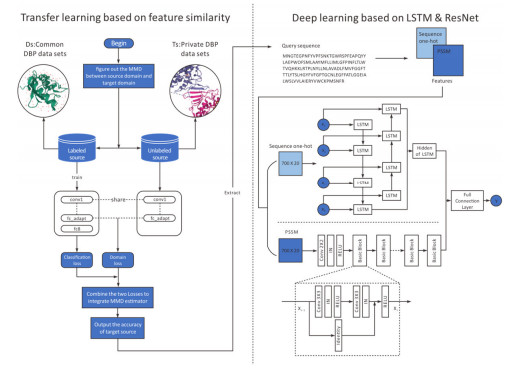
In the experiments of this study, the main approach to prediction was to use a conjunction of transfer learning and deep learning. First, the transfer learning algorithm was used to extract the data set S, which was related to the target sample, but not completely distributed based on sample similarity. Then the sequence and PSSM [25] features of data set S were extracted, in a deep network with an attention mechanism, the features are input and trained.
In the deep learning part of this method, the sequence and PSSM features were entered into LSTM [26] and CNN [27] respectively. In subsequent improvements, ResNet [28] was used to replace CNN, and better results were obtained. The final prediction results of these two parts also need to go through the fully connected layer. Figure 1 shows an overall prediction framework, mainly based on the DBP [29,30] prediction framework of deep transfer learning.
2.2. Transfer learning used in this paper
Many machine learning and data mining algorithms can now achieve positive results, but this is based on data sets with the same distribution [31]. In practice, this is often not true. The performance of traditional machine learning is likely to degrade when the distribution of the datasets used is different. When researchers are interested in a data domain, it is very expensive to re-label new data, and the labeled data will become outdated over time. For example, the search data on a Web site will be updated every once in a while, and the labeled data will become outdated at that time [32].
The situation described above makes it necessary to train a powerful learning classifier from the relevant data domain. In processing related data domains and test data, the classifier can divide data with the same distribution. This is the principle of transfer learning.
In fact, machine transfer learning is closely related to human behavior. For example, once we learned to ride a bike when we were young, it was much easier to use an electric bike or a motorcycle [33]. After we learn the knowledge needed for riding a bi-cycle, when riding electric bikes and motorcycles, part of the technical knowledge can be shared. This means that we can quickly master the technology of riding electric bikes and motorcycles. This is human transfer learning, and machines can also master this learning mode. By using this model, machines can achieve faster learning and better results when faced with differently distributed data sets.
In transfer learning, there are generally two pairs of concepts, collectively referred to as two domains and two tasks, with two domains referring to the source and target domains and two tasks referring to the source and target tasks [33]. A domain can generally be thought of as a data set consisting mainly of a feature space and an edge probability distribution, which can be expressed as D = {x, P(X)}, where x = {x1, ..., xn} ∈ x. The two domains can be represented using Ds (source domain) and Dt (target domain) respectively. A task is simply the work to be performed and consists mainly of a label space and a target prediction function, usually denoted by T = {y, ƒ(X)}. The two tasks are represented by Ts (source task) and Tt (target task) respectively.
With defined Ds and Ts and Dt and Ts, the main goal of using transfer learning is to acquire knowledge in Ds and Ts and finally learn the prediction function ft(·), but with the requirement that Ds ≠ Dt or Ts ≠ Tt [33].
Users of transfer learning must be clear about three things: 1) what transfer actually means; 2) how users make the transfer; and 3) when the transfer occurs [33].
To address the first point, "what to transfer", the first step is to clarify what kinds of problems need to be solved. The effect of transfer learning is better in classification and regression problems. As for the second point, "how to transfer", the only caveat is to choose simple and effective methods. There is no need to stick to a fixed algorithm because the algorithm is constantly changing and improving. As long as the algorithm has good results, it can be used. As for the third point, "when to transfer", although many studies have discussed the first two points, the third point is often more important. The aim of transfer learning is to optimize Tt. However, in real transfers, researchers often encounter a negative transfer effect, where the effect of transfer learning is not as good as that of learning without transfer. This requires a weighing and evaluation of how to avoid negative transfer.
There are four main approaches to achieving transfer learning: sample transfer, feature transfer, model transfer and relationship transfer. In sample-based transfer, the main task is to find data that are akin to the target domain in the Ds, and then to match the obtained data with the Dt data after corresponding operations. In feature-based transfer, the main task is to find similarities in the data from the two domains and to quantify these similarities using features. In model-based transfer, the trained model is directly migrated to the new domain. The advantage of this transfer is that deep learning can be used in conjunction with it. In the relational model, applying the network of logical relations learned in Ds to Dt is the main task.
There are many classical transfer-learning algorithms, which include learning to learn, knowledge transfer, lifelong learning, multi-task learning, meta learning, and context-sensitive learning. The experiments in [34] used TrAdaBoost [35], the pioneering work based on sample transfer in transfer learning. In addition, there are many ways deep learning can be integrated with transfer learning. Large amounts of annotated data are needed by deep learning, but pre-training + fine-tuning a training model and parameter sharing require only a small fraction of labeled data. In the experiments in this study, deep domain confusion [36] (an algorithm combining deep learning and transfer learning) was also used to migrate source domain samples based on features.
2.3. Introduction to transfer learning algorithm
Considering that only slightly more than 1000 internationals standard DBP samples for deep learning training are available, too few data sets will have an impact on the effectiveness of deep learning. To increase the number of training samples, two migration algorithms, DDC and TrAdaBoost, were used in this study to migrate data sets, and appropriate data were selected for experimental testing and comparison.
2.3.1. Deep domain confusion
The general strategy for using deep learning with an insufficient number of data samples is to use fine-tuned networks, but testing with this paper's own samples did not work well. More layers may need to be fine-tuned to achieve better results, which requires many more samples. With little or no label data, there is no way to identify new samples through fine-tuning networks.
This study used the deep domain confusion approach. For each new sample, the dispersion of the data in the two domains is calculated and a layer is added between their adaptive layers and a domain is added to the confusion function. Next, the distance distribution is optimized using a convolutional neural network to reduce the distance between these scattered parts of the source and target domains. Finally, the problem was resolved un-der the condition of small samples of labels or no labels to identify problems. Table 1 shows the specific algorithm process.
The DDC algorithm in its essence involves looking for similar characteristics in two fields to maximize similar characteristics [36] by means of optimization loss. There are two main parts to the loss, the classification of the source domain is one part of the loss and the other part is used for the confusion loss of the two domains. To optimize the two losses, it is necessary to make the two domains close enough to the characteristics of the distribution [37]. In the end, the two domains will be indistinguishable.
In the DDC experiment, the data from the two domains are first mapped into a reproducing kernel Hilbert space, in which the average difference between the two domains is calculated as the distance between their distributions. According to Eq (2), the empirical estimate of MMD [38] is calculated, and the value of MMD obtained is used as the test statistic, which is entered into the deep network for training.
This network is an improved CNN architecture. Traditionally, for monitoring a source domain (labeled data), the loss is trained through the network. However, for a target domain without labels, data loss cannot be used for monitoring. Therefore, the model parameters used for source domain training are shared with the target domain, and an adaptive layer is added to one of the architecture layers.
It is well known that a deep network is gradually more proprietary from the bottom to the top. However, in order to share the characteristics of the two domains, there is no need to be proprietary, and therefore this layer is usually selected at the top. In deep domain obfuscation, the next step is to improve domain invariance as much as possible by choosing the adaptation layer as the seventh layer of the deep network.
Finally, classification loss and domain loss are combined according to Eq (4). Regularization hyper-parameters should be set to make the target mainly weighted classification and avoid over-fitting. Finally, the model trained from the source do-main must also achieve good results in the target domain through deep network back-tracking.
2.3.2. TrAdaBoost
The distribution of training and test data is the same in traditional machine learning, but in practice, the two data sets are usually distributed differently. Old data may be out of date, and the cost of re-labeling new data to learn new data is huge. Often, old data have parts worth using.
To meet this need, the TrAdaBoost algorithm was used. Identically distributed training data refers to a small number of new data points, and differentially distributed training data refers to data points where the distribution of the training set differs from the distribution of the test set. With each iteration of the algorithm, the weights of the training data are thus adjusted. If a different distribution of training data points is incorrectly classified, then the target data is different from this sample, and the data weights in the sample will be reduced as a result. On the contrary, if a sample with the same distribution is misclassified, this will result in an increase in the weight of that sample and the algorithm will next focus on training a weak classifier, in line with the idea of the AdaBoost algorithm. Table 2 shows the specific algorithm process.
Table 2 clearly shows that during each iteration, the data weights are updated. The weight of the last data point is multiplied by a value that is greater than 0 and less than 1, so that the weight of wrong samples in the auxiliary training samples will be reduced in the next training round, and the weight of the wrong samples will be in-creased. Finally, a strong classifier is obtained by voting with a 1/2 base learner.
2.4. Attention mechanism to improve prediction effect
To improve prediction accuracy, an attention mechanism was added to the model [39]. As information increases, the model also becomes complex. However, for the time being, the strength of the computational power remains an important constraint on the development of neural networks. Meanwhile, LSTM can only alleviate the problem of long-range dependence in recurrent neural networks (RNNs) to a certain extent, but its information memory capacity remains weak. Therefore, an attention mechanism was added to the model. In natural language processing tasks, attention mechanisms are often used, especially sequence to sequence tasks [40].
The main purpose of the attention mechanism is to let machines learn to have the same focus as humans. The nature of a query mapping to a series of key-value pairs can be referred to as an attention mechanism function. If attention needs to be computed, then three main steps are required. The first step is to calculate the similarity between each key from one query to another, and getting the similarity is equivalent to getting the weights. Then, the second step is to use a SoftMax [41] function to normalize each weight. The final step is attention, which focuses on weighting and summing the weights and the corresponding key values.
Compared with CNN and RNN, the complexity and the number of parameters when using an attention mechanism are smaller, and therefore the computing power requirements are smaller. In addition, the attention mechanism can solve parallel computing problems that cannot be solved by RNN and can obtain extremely fast computing speeds. Therefore, adding an attention mechanism can greatly improve the efficiency and accuracy of predictions in this field.
2.5. Feature construction
At present, in the field of biology, the main methods for feature extraction are those based on feature representation and those based on sequence information [42], both of which are relatively common extraction methods, and there are many other methods. For DNA-binding protein feature extraction methods, there are also many methods to draw on. For example, PsePSSM, PSSM-DWT, PSSM-AB and other methods [43,44]. In this paper, the One-Hot coding and PSSM methods are mainly used for protein feature extraction.
2.5.1. One-hot
One-hot coding was used in this study to process the original protein sequence [45]. The one-hot code can be used to represent each residue in the protein sequence. Due to the fact that there are only 20 amino acids in nature, a 20-dimensional vector is used to represent all amino acid residues. A 20-dimensional vector consists of 19 zeros and 1 one, and then, a 20-dimensional vector is corresponded to a one-hot encoding, so a 20-dimensional vector can be used to represent an amino acid in the protein sequence index.
2.5.2. PSSM
The PSSM is an extremely important spectrum of information in the evolution of proteins [30]. It is generated by a scoring strategy with different amino acid occurrence frequencies at the same locus and their background frequency information in the results of protein multi-sequence alignment [46], and therefore contains information on protein evolution. It is the most commonly used evolutionary information spectrum in protein structure and function recognition. In a defined protein sequence, The L × 20 matrix can be used to identify the PSSM matrix and the length of the protein sequence can be represented by L. When the matrix is a positive integer, it means that the amino acids at the corresponding site in the protein sequence are more likely to mutate to the 20 amino acids on the corresponding horizontal coordinate during the substitution process, and the larger the value, the higher the probability of substitution here. The opposite is true when the value is a negative integer, where a larger value indicates that it is less likely to change.
2.6. Training process
2.6.1. Neural network architecture
The paper for this research initially chose to use a neural network architecture combining LSTM and CNN, with ResNet added later as an improvement. LSTM, as an improved recurrent neural network, is not only able to solve the problem that RNNs cannot handle long-range dependencies, but also solves some common problems associated with gradients in neural networks. LSTM usually performs better than RNNs and hidden Markov models (HMM). In addition, LSTM has excellent performance in handwriting and speech recognition. In the method proposed here, LSTM is mainly used to deal with one-hot sequences.
In general, the depth in a neural network has a significant impact on model performance. Networks that need to extract more complex feature patterns need to increase the number of network layers, and when the appropriate number of layers is reached, theoretically better results can be obtained. However, it has been found that increasing the network depth may lead to the degradation problem: in other words, as the depth of the network increases and reaches a certain point, this will lead to saturation or even a decrease in accuracy. He et al. [47] proposed ResNets, which use residual learning to solve this degradation issue. ResNet uses a residual network structure, which allows the network layers to be added very deeply and ultimately results in better classification. Each output of the residual block can be represented by Eq (5).
The weight of the basic block of the t-th residual can be expressed as Wt. The function f is the activation function, and in the method proposed here, ReLU [48] is chosen as the activation function. In this study, ResNet was used to process the PSSM matrix. Use of ResNet can make the gradient flow more smoothly, which makes it possible to train the neural network with great depth.
2.6.2. Implementation of the method
The proposed method was trained under the Adam optimizer and implemented in Pytorch [49,50], along with a learning rate of 1e-3 and a cross-entropy loss for 40 epochs. Due to the limitations of GPU memory, when using LSTM and ResNet with relatively few layers, a batch size of 64 was used. For ResNet with very many layers, a batch size of 32 was used.
2.6.3. Evaluation indexes
The method has four main evaluation metrics, the first being Accuracy (ACC), the second being Matthew's Correlation Coefficient (MCC), the third being Sensitivity (SN) and the fourth being Specificity (Spec). The calculation formulas for the ACC, MCC, SN, and Spec indicators are shown as Eqs (6) to (9):
Where TP refers to a positive case identified correctly, TN refers to a negative case identified correctly, FN refers to a negative case identified incorrectly and FP refers to a positive case identified incorrectly.
3.
Experiments
3.1. Introduction to the dataset
In this work, baseline data sets (PDB186 and PDB1075) that recognize DNA binding proteins were used [14,51]. Each protein sequence in the benchmark data sets was derived from the PDB [52] (http://www.rcsb.org/pdb/home/home.do). The training set PDB1075 was originally extracted by Liu et al. in 2014 and the test set PDB186 was compiled by Lou in 2014. Each sequence was no more than 25% similar to other sequences in the dataset and did not contain irregular amino acids ('X'). The positive and negative sample counts for PDB1075 and PDB186 are shown in Table 3.
To carry out transfer learning, additional datasets PDB14189 and PDB2272 were used as source domains. These two datasets are from Du et al. [53] on the article published in 2019, while the two datasets also come from PDB Bank. The sequence similarity in PDB14189 was no more than 40%, the sequence similarity in PDB2272 was no more than 25%, and neither contained irregular amino acids ('X'). The positive and negative sample sizes for PDB14189 and PDB2272 are shown in Table 3.
3.2. Experimental comparison of different network models for deep learning
The deep learning experiments reported in this paper mainly used a network model combining CNN and LSTM. To examine the effects of different depths and types of models on experimental performance, a comparison of the results using several common deep learning models is presented in Figure 2 and Table 4. The neural net-work models involved in the comparison included different kinds of ResNet. All these methods used the Adam optimizer with cross-entropy loss.
The data show that different depths and types of models affected the experimental results. When using ResNet18 (a network with 18 convolution and linear layers), the evaluation was slightly lower than the original. However, when using ResNet with more layers, the experimental performance was significantly improved.
3.3. Experimental comparison of different network models for transfer learning
Similarly, the different model depths and types used above were applied to the PDB186 data set obtained through the transfer learning algorithm. Comparison through extensive experimental data, the performance obtained by adding the transfer data to the training sample was greatly improved. Specific experimental data are shown in Figure 3, and detailed results are given in Table 4.
3.3.1. DDC Experiment
In the experiments using DDC, datasets from the PDB14189 source domain and PDB2272 target domain were used, as transfer learning presupposes similarity between the two domains, which would otherwise lead to negative transfer.
According to the results of the DDC experiment, after the 20th training epoch, the supervised training accuracy of the data in the source domain was only 88.24%, whereas the accuracy of the classifier obtained when acting on the target domain was 71.55%. However, after the 100th training epoch, the classification accuracy of the source do-main data was 99.82%, and that of the target domain data was 74.24%.
In this paper the classifier is considered good enough for both domains and the results of the 100th round of classification are used.
3.3.2. TrAdaBoost Experiment
Tradaboost as a transfer learning algorithm, we used PDB14189 as the source domain and PDB2272 as the target domain for migration learning. The features used in the migration learning process were PSSM matrices, after learning using a decision tree classifier, and 50 iterations were selected.
It is known that TrAdaBoost algorithm adjusts the weight of each data in each iteration. In the last iteration, the classification weight result of the classifier was recorded, and the average weight obtained was 7.047713017125943E-05. Through weight comparison, 12,541 migration results that met the classification were selected.
In the actual experiment, the DDC algorithm trains the network by supervised learning from the Ds and uses unsupervised learning from the Dt to train the network, and then fine-tunes the network model. The implementation cycle of this process is relatively long, and the trained model is too complex, leading to a model accuracy of only 74.24% on the test sample after 100 iterations, which is not ideal. The TrAdaBoost algorithm can quickly distinguish sample classification through sample-based migration, achieving faster execution and better effect.
3.4. Comparison of deep transfer learning methods and traditional methods
In traditional machine learning, the training and test sets are equally distributed and the datasets are already labelled, in which case they tend to show better performance. However, the number of samples available for the PDB186 dataset is relatively small and the data accuracy is not satisfactory. Therefore, the model was changed by adding transfer learning to determine the best model. The transfer learning model using LSTM and CNN demonstrated the best performance.
In order to achieve an objective and fair evaluation, experiments will be conducted using several other up-to-date methods and the results obtained will be compared with the methods in this paper. The proposed method is mainly covered in comparative experiments with other advanced methods. The results of various predictors on PDB186 are shown in Table 5 and Figure 4. In Table 5, the ACC, MCC, and Spec values from the proposed method on PDB186 exceed those from the other prediction methods. The experiments conclusively show that the approach used achieves excellent results in terms of performance and model robustness on the PDB186 independent dataset.
Experimental comparisons show that by using transfer learning, the number of training samples can be supplemented to some extent and fewer labelled samples can be used. This means that the method used here has better results than other DBP predictors.
4.
Conclusions
The prediction of DNA-Binding Proteins has a long history of development in the field of structural biology and is currently a popular research topic, while the prediction of DNA-Binding Proteins continues to drive the development of the pharmaceutical industry. However, as far as the current traditional method is concerned, it is a serious drain on time and resources. In this paper, we excluded irregular amino acids ('X') in the samples, adopted transfer learning, and added attention mechanism to the deep neural network, which achieved better performance than traditional machine learning methods. But we didn't take into account the noise samples in the experiment. We will continue to investigate this in future research to continuously increase the predictive accuracy of the DBP.
Acknowledgments
This paper is supported by the National Natural Science Foundation of China (61902272, 62073231, 62176175, 61876217, 61902271), National Research Project (2020YFC2006602), Provincial Key Laboratory for Computer Information Processing Technology, Soochow University (KJS2166), Opening Topic Fund of Big Data Intelligent Engineering Laboratory of Jiangsu Province (SDGC2157), the Municipal Government of Quzhou (Grant Number 2020D003 and 2021D004).
Conflict of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad: