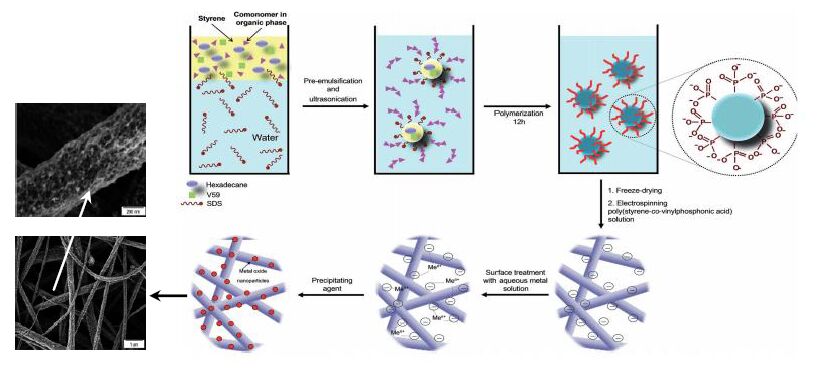
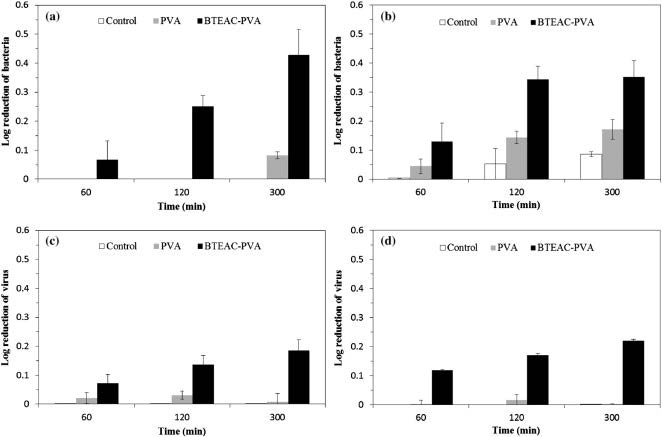
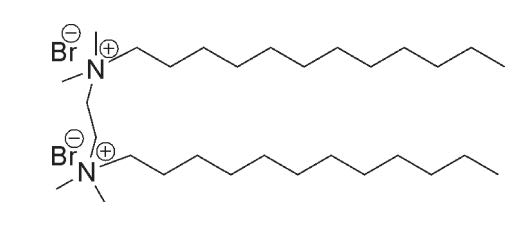
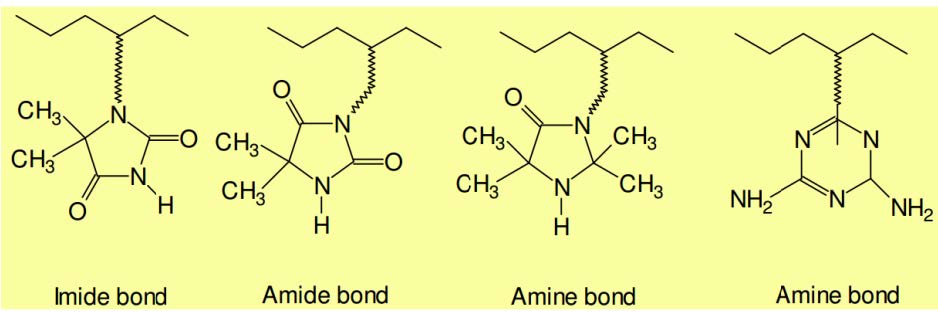
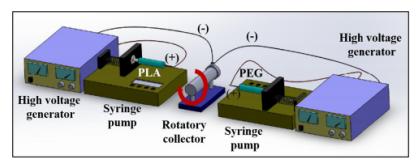
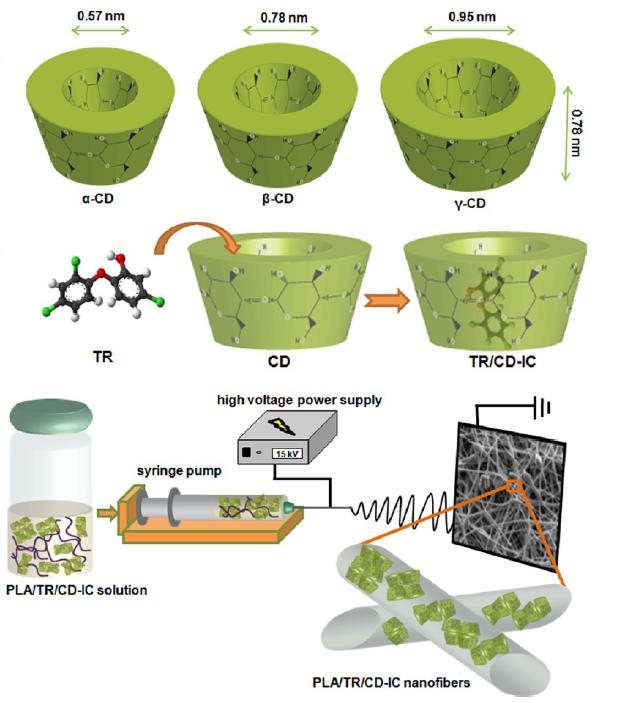
Development of materials with an antimicrobial activity is fundamental for different sectors, including medicine and health care, water and air treatment, and food packaging. Electrospinning is a versatile and economic technique that allows the incorporation of different natural, industrial, and clinical agents into a wide variety of polymers and blends in the form of micro/nanofibers. Furthermore, the technique is versatile since different constructs (e.g. those derived from single electrospinning, co-electrospinning, coaxial electrospinning, and miniemulsion electrospinning) can be obtained to influence the ability to load agents with different characteristics and stability and to modify the release behaviour. Furthermore, antimicrobial agents can be loaded during the electrospinning process or by a subsequent coating process. In order to the mitigate burst release effect, it is possible to encapsulate the selected drug into inorganic nanotubes and nanoparticles, as well as in organic cyclodextrine polysaccharides. In the same way, processes that involve covalent linkage of bactericide agents during surface treatment of electrospun samples may also be considered.
The present review is focused on more recent works concerning the electrospinning of antimicrobial polymers. These include chitosan and common biodegradable polymers with activity caused by the specific load of agents such as metal and metal oxide particles, quaternary ammonium compounds, hydantoin compounds, antibiotics, common organic bactericides, and bacteriophages.
1.
Introduction
Nutrients and substrates play a pivotal role in the sustenance and proliferation of living organisms, and therefore, evolutionary forces have constrained organisms to detect their availability. Cells reproduce quickly in a nutrient and substrate-rich environment and reduce proliferation when those resources become scarce. Availability of both energy rich substrates and starting materials for biomass production control this balance of growth and starvation [41].
Energy is produced in heterotrophic organisms by degrading organic compounds into products with low free energy. As per the second law of thermodynamics, no process can be fully efficient. So, a part of the free energy is used up to drive the reaction itself and the rest is stored into ATPs, the cell's energy currency. When more than one process is available for such conversions, there usually occurs a trade-off between rate (kinetic efficiency) versus yield (thermodynamic efficiency). This is true for fermentation and oxidative phosphorylation (OP) [34].
Fermentation yields 2-4 moles of ATP per mole of glucose whereas OP produces about 30 ATPs (the actual number may vary with the organism). In contrast, the rate of fermentation can reach about two orders of magnitude higher than the rate of OP [34,44].
Many organisms can utilize both pathways in the presence of oxygen and substrate [26], but OP is not feasible in the absence of oxygen. A direct consequence of this is seen in a phenomenon, first observed in cancer cells [45], called the Warburg effect, where cells utilize the fermentation pathways much more than the OP in presence of ample substrate and even oxygen [34]. A similar phenomenon can be seen across a broad range of cell types and organisms. Many yeast variants (in which the same phenomenon is called the Crabtree effect [7]) and bacteria (where it is called overflow metabolism [1]) exhibit this behavior. Other than the cells undergoing growth, lymphocytes and Kupffer cells (upon activation), fast twitch muscle fibers and microglial cells, also display this effect in the human body [34,41]. Most of the work on the Warburg effect has been concentrated on cancer cells, and for bacterial metabolism, the phenomenon has been well studied in Escherichia coli [49].
This behavior can appear to be paradoxical in that a less efficient pathway is utilized even when a more efficient one is available. Given that substrate limitation is a major environmental constraint, the properties of these two pathways must have been under intense selection. Such a behavior, therefore, should confer some additional biological advantage, and a number of explanations and modeling frameworks have been suggested accordingly [34].
Several game theory models have been proposed describing a population using a common resource (glucose in most cases), and the two metabolic pathways (i.e., OP and fermentation) as alternate strategies based on a kinetic-thermodynamic trade-off. A tragedy of the commons scenario sometimes emerges [16,26]. Prisoner's dilemma and Nash equilibria (based on relative enzymatic/protein costs of the two pathways) were also used to describe the dynamics of this system [13,34].
For a similar trade-off between investment in protein synthesis and metabolic yield, a medium-scale kinetic model has also been proposed [22]. Such a model explains the increase in ribosomal content observed with increasing growth rate and related characteristics in bacteria [34].
Another family of models that has been used extensively to explain this behavior belongs to a framework called Flux Balance analysis (FBA) [10,28,32]. In such an analysis, linear maximization is utilized to determine optimal values of reaction rates at a steady state condition where a linear combination of rates attain a maximized value. There has been some controversy on whether the criterion for optimality should be based on rate or yield in these models [34]. A branch-off from this family of models, called FBA with macromolecular crowding (FBAwmc), incorporates the areal and volumetric needs of the enzymes constrained by the cell membrane space and cytoplasm, respectively [49]. Some studies looked at maximization of biomass production using this framework [37].
Some of the models discussed above focus on one specific behavior seen in the Warburg effect but avoid other behaviors that are part of the same process, thus preventing study of interactions among the observed behaviors. Among notable ones, Pfeiffer et al. [26] use the rate-efficiency trade-off to explore the problem and delve into origins of multicellularity. Kareva [16] uses efficiency of the two pathways (respiration and fermentation) and the effect of lactic acid produced from fermenting cells, on neighbouring cells but it looks at cancer cells in specific.
In many other cases, the work utilizes more than one trade-offs, especially using the FBA regime [3,34,37,42,49]. Vazquez et al. [42] focuses on cancer cells, and uses constraints on maximal glucose uptake, enzyme efficiency and total cellular volume, in order to maximize ATP production. Their model considers not only the stoichiometry of glycolysis and oxidative phosphyrylation but also the enzyme-volumetric costs of activating these pathways. A comparable idea of constraints on enzyme-volumetric costs was used in a work focusing on Escherichia coli to explain overflow metabolism [3]. Yet another work which used a similar concept was that of Shlomi et al. [37], which focuses on cancer cells in specific. For this class of models, a consistent criticism has been that, despite its overwhelming success, these models fail to explain overflow metabolism from first principles, that is, without imposing multiple measured fluxes as constraints on the models [22]. In comparison, a slightly different approach was taken in the work by Molenaar et al. [22], where they focus on trade-offs between investments in enzyme synthesis and metabolic yields for different catabolic pathways, in order to maximize growth rate. Zhuang et al. [49] uses the constraint on membrane occupancy to explore the effects on fermentation and respiration, via a transformed FBA.
Given this large body of work on modeling the Warburg effect, yet another model may seem to be a futile exercise, but if one looks closely, most of the models either focus on cancer cells or dive only into the biochemical aspect of the problem. This leaves the ecological implications of the Warburg effect to be modeled, specifically in bacteria. None of the models discussed above take into account the effects associated with size and shape of the bacterial cell on the overall metabolism of the organism, especially considering the wide variability in both those physical characteristics. Moreover, predicting overflow metabolism from first principles has always been a challenge without invoking a large number of boundary conditions [22].
In this work, we attend to the three major trade-offs involved in the Warburg effect, specifically in the case of a bacterial cell. We seek to incorporate only the necessary details, both from a physical and a biochemical viewpoint, to retain model simplicity and usability in an ecological context (Table 1).
Our aim here is to predict size and shape dependence of growth rate in bacteria across a range of substrate concentrations, in addition to estimating the proportions of OP and fermentation (hereafter denoted AG, for aerobic glycolysis in presence of oxygen) for respiration and metabolism. We also seek to explain overflow metabolism in our model as a direct consequence of energy production and consumption trade-off, through first principles. Unlike the previous models on the Warburg effect, we explore more of the ecological ramifications though the model, in addition to the basic biochemical effects. In turn, we limit ourselves to a single bacterial cell as the model system and glucose as the substrate.
2.
The model
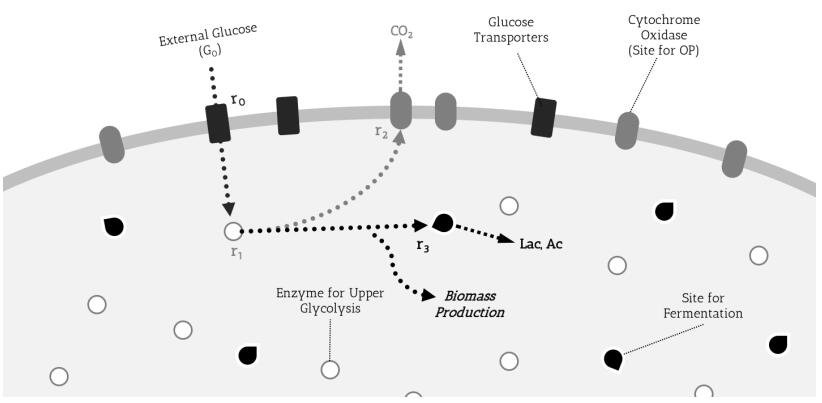
The model assumes a bacterial cell, with glucose transporter proteins (responsible for importing glucose into the cell) and cytochrome oxidase enzymes (where OP occurs) embedded in the cell membrane as trans-membrane proteins [49]. In contrast, the (upper) glycolytic enzymes, which convert glucose to pyruvate, and the fermentation enzyme pathways function in the cytoplasm [34]. Thus OP should scale as a function of the surface area of the cell whereas fermentation processes should scale as a function of cell volume. A schematic representation of the model is illustrated in Figure 1.
The rate of glucose input into the cell ($r_0$) can be represented as,
where t is time, r is position, $G_{cell}$ is the cellular concentration glucose, $G_0$ is the concentration of glucose in the environment around the cell, $\beta$ is the areal density of glucose transporter sites on the cell membrane, A is area of the cell membrane (as a function of the semi-major axis of the cell, $a_{cell}$), and $k_\beta$ is normalized efficiency of the transporters (we define normalized efficiency as the ratio of molecules transported relative to the total number present on the outer/source side per unit time). We assume a uniform $G_0$ in the environment around the cell here and therefore, inside it ($G_{cell}$).
This glucose imported into the cell goes into the upper glycolysis pathway, whose enzymes are located in the bacterial cytoplasm. In bacteria, there are two well known pathways for this: Embden-Meyerhof-Parnas (EMP) pathway and Entner-Doudoroff (ED) pathway, which differ in both their output of ATP (2 mol in EMP versus 1 mol in ED for every mol of glucose consumed) and their enzyme costs (the EMP enzyme costs can be 3.5 to 5 fold higher than ED pathway enzymes) [11]. The end product is pyruvate in both the cases, and the rate of conversion ($r_1$) can be written as:
where $\kappa_{EMP}$ and $\kappa_{ED}$ are the volume density of EMP and ED enzyme sites respectively, $k_{EMP}$ and $k_{ED}$ are normalized efficiencies of the pathways, and $V$ is the volume of the cell. $\delta_{EMP}$ and $\delta_{ED}$ indicate presence of EMP and/or ED pathway in the organism under scrutiny, taking a value 1 if present and 0 if absent; else if both are present, it denotes the fraction out of 1 which is occupied by either pathway such that $\delta_{EMP}+\delta_{ED} = 1$. About 43% of the prokaryotic cells use just EMP pathway, 13% use just the ED pathway, 14% use both pathways, and in about 30% of the cases, the pathway is not known [11].
The relative usage of the EMP and ED pathways can be calculated on the basis of protein cost, kinetics and the efficiency of the enzymes involved in both the pathways at any given glucose concentration as well as the thermodynamic constraints [11]. To put it in simpler terms, the ED pathway is about 3-5 times faster than EMP pathway, but EMP produces 2 ATP molecules whereas ED produces 1 per molecule of glucose [11]. So, in the case of OP, a difference of one ATP is not of much significance because the total production of ATP is high, but in cases of fermentation, one ATP is a substantial difference. Thus, we would expect to see mostly EMP in anaerobes versus ED in aerobes. Anaerobic bacteria have predominantly only EMP (97%), whereas some facultative anaerobes and aerobes have ED only (10% and 21% respectively), others have both ED and EMP (19% and 21% respectively), and more than half have only EMP [11]. Here we seek to model aerobic heterotrophic bacteria, so we can expect that the ED pathway is prevalent when the metabolism is predominantly aerobic (OP) while EMP is prevalent when it is anaerobic (fermentation).
Next, this $r_1(t)$ flux of products from upper glycolysis goes to either the oxidative phosphorylation (OP) pathway ($r_2(t)$) or to the fermentation pathway ($r_3(t)$). This splitting of the flux forms the basis of the three trade-offs on which we focus: yield vs rate, surface area vs volume, and biomass production (Table 1). The rates for $r_2$ and $r_3$, can be written as:
and
where $\gamma_{Cyo}$ and $\gamma_{CydII}$ are the areal density of the two cytochrome complexes Cyo and Cyd-Ⅱ respectively, $k_{Cyo}$ and $k_{CydII}$ are normalized efficiency of the complexes, $\sigma$ is the volume density of the fermentation enzymes (sites), and $k_{\sigma}$ is the normalized efficiency of the fermentation enzymes (sites). Here, normalized efficiency is defined as the ratio of products formed by the enzyme site relative to the total substrate that was present, per unit time. As a part of the simplification in the model, we have only considered the cytochrome complexes Cyo and Cyd-Ⅱ as a part of the model leaving behind the Cyd-Ⅰ complex.
For maintenance of the cellular membrane structure in prokaryotes, the protein-to-lipid ratio is kept within certain bounds [22]. At high rates of catabolism, the surface area available to proteins can become saturated and proteins might need to 'compete' for expression [49]. Both substrate transporters (in this case, glucose transporters) and OP enzymes are located on the membrane, and thus, compete for the available space for expression. Thus, we can write:
where, we assume a constant maximal value.
In previous literature, the relative membrane cost of an enzyme has been inversely related to its turnover rate [2] and hence at high catabolic rate one would expect the faster and inefficient Cyd-Ⅱ to be preferred over efficient but slower Cyd [2]. The relative cost of moderately efficient Cyd-Ⅰ is similar to Cyo under completely aerobic conditions, but under low concentration of oxygen, the cost becomes much less due to the high affinity of Cyd-Ⅰ to $O_2$ [40,49].
Summarizing the model, the net energy production rate can be written as
where $e_{r_2}$ is the energy produced through $r_2$ (via OP) and $e_{r_3}$ is the energy produced through $r_3$ (via fermentation (F) or in presence of oxygen, termed as aerobic glycolysis). $\left \langle \epsilon_{OP} \right \rangle$ and $\left \langle \epsilon_{OP} \right \rangle(t)$ are the weighted average efficiencies of ATP production from OP (via Cyo and Cyd-Ⅱ), and F respectively. For simplicity, each of these process averages also include a term regarding the overall efficacy of the upper glycolysis (as a function of the proportion of EMP and ED pathways). In other words, the two averages mentioned above involve the efficiency from the point of upper glycolysis to the end of their respective processes.
A main function of unregulated glycolysis in proliferating cells is to maintain the supply of intermediates required to support biosynthesis [20,41]. Interestingly, in such rapidly proliferating cells, most of the glucose is converted into lactate (or other fermentation products) and excreted. However, an increased lactate excretion is correlated with increased growth [1,20,41]. Such a seemingly inefficient high glycolytic flux to fermentation products and low flux to biosynthesis actually helps in regulation of biomass production during growth [20,41]. The branching of a low flux process (biosynthesis) from a high flux one (fermentation) would render the former extremely sensitive to the latter [20,25]. Comprehending the exact role of such processes in biomass production would need a thorough study of carbon metabolism (for details please see [20]). However, given the dependence, one can certainly assume a simple linear relationship between biomass synthesis and fermentation. Here onwards, we explain biomass production in terms of $r_3$ flux and thus, the rate of biomass addition $\Lambda$, can be given by:
where $g$ is the conversion constant relating the products of fermentation pathway to biomass. The process of biomass production also involves energy usage (along with the need for other resources such as nitrogen and phosphorus, which have been assumed to be present in sufficient quantity for this model).
The energy consumption rate can thus, be given by:
where $e_{b}$ is the basal energy requirement of the cell and $\epsilon_{g}$ is the energy required per unit conversion for biomass production from base materials.
Most metabolic networks operate in a steady state [34]. Thus, here we tried to optimize the energy production and growth using linear programming, adhering to the following relations:
The first inequality states that the total glucose processing that takes place in OP and fermentation is constrained by the total glucose input into the cell. The next relation describes the fact that the total energy production in the cell has a lower bound of the basal metabolic rate of the cell ($e_b$). Below this level, the cell may cease to function properly or shut down entirely [17]. The third relation is an equation which is modified and combined form of Equations (3) and (4). The way to look at it is that both the terms in Equation (10) simplify to $r_1$, as is evident from Equations (3) and (4).
Let us also define an additional parameter called $Z$ denoting the ratio of surface area-to-volume of a cell. From (11), it is evident that $Z$ controls the distribution of $r_1$ into $r_2$ and $r_3$ by controlling the total number of sites available for those processes. A low value of $Z$ denotes either a spherical cell and/or a large cell size; and a high value of Z represents an elongated/deformed cell shape and/or a small cell size.
These conditions can be used for linear programming and the point in solution space having the highest value of $r_3$ will give the optimal values of $(r_2, r_3)$ at a given set of steady state conditions. This accords with our assumption that only $r_3$ related processes directly help in biomass production, and any organism would maximize its biomass production in a given set of conditions, provided its basal needs are satisfied. All other parameters are considered to be constants for finding the optimal solution for a given iteration.
3.
Results
Given the number of model parameters, it is pragmatic to focus on a few important ones, which would enable us to predict and investigate broad-scale natural phenomena from an improved viewpoint. In this work, we primarily focus on changing the substrate concentration and the surface area-to-volume ratio of bacterial cells to gain insights from the model and explore the Warburg effect (overflow metabolism) in bacterial cells.
3.1. Dependence on substrate concentration
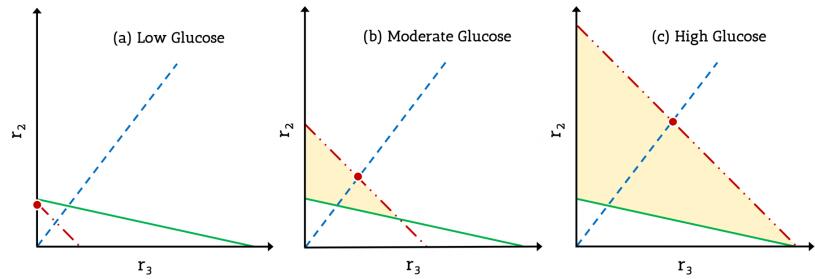
$r_0$ is the rate of substrate input from the environment, and is representative of the external substrate concentration. Figure 2 plots the results of the applying the maximization criterion for $r_3$ constrained by (9)-(11), on changing the value of $r_0$. Three important regimes of substrate concentration are considered: glucose starved (low $r_0$), moderate glucose availability (moderate $r_0$), and glucose rich environment (high $r_0$).
When (9) and (10) do not have a common solution space, i.e., when the substrate availability is not sufficient to sustain all basic metabolic activities, but is high enough not to cause complete dormancy [17], the maximized solution is $(0, r_0)$ in the $(r_2, r_3)$ space. This suggests that under a substrate-poor scenario there exists a need for high efficiency in substrate conversion, without much consideration for its rate of production or cellular growth.
Increasing $r_0$ enables high rates of $r_3$ due to fulfillment of basal metabolic processes and a need to increase biomass output for growth. This points at the higher growth rates associated with nutrient and substrate rich environments [41]. At extremely high glucose concentrations, the value of $\beta$ would saturate (to its highest value in order to keep the protein-to-lipid ratio of the membrane intact) and $k_\beta$ would decrease (as only a specific maximal number of glucose molecules can be transported into the cell constrained by the protein efficiency) in Equation (1). These two features make the value of $r_0$ constant above a certain threshold of $G_{0}$. Thus, beyond this threshold value, growth (which is proportional to $r_3$) would not depend upon $G_{0}$ explicitly, but only on the available $r_0$. Such a behavior is observed in E. coli along with an increase in expected growth rate with increasing $G_{0}$ until the threshold concentration (maximal value of $r_0$) is reached [35].
Such an overall pattern of starvation metabolism in environments with scarce substrate environments and proliferative metabolism in environments with abundant substrate is seen in all unicellular organisms [41].
3.2. Dependence on cellular size and shape
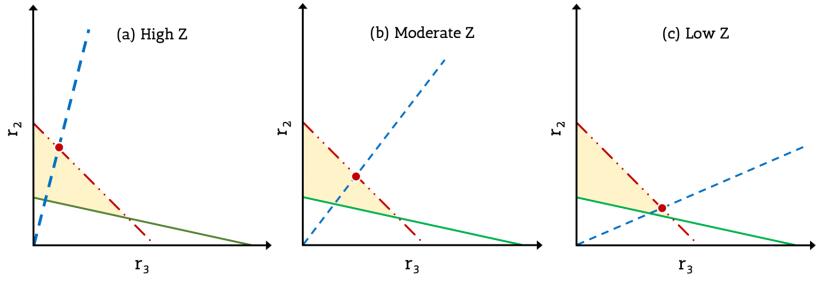
The solutions of the constraint equations (9)-(11) for three differing regimes of $Z$ are plotted in Figure 3. The value of $r_0$ has been kept constant in the three cases for clarity. As mentioned previously, a low value of $Z$ refers to either a spherical cell and/or a large cell size; and a high value of $Z$ points to an elongated/deformed cell shape and/or a small cell size.
Large values of $Z$ enable higher efficiency for energy conversion processes but trade off for slower growth, which may be typical for substrate poor environments. Low values of $Z$ sacrifice efficiency for a higher rate of energy and biomass production, and would be expected in conditions where substrate is abundant. This shape and size based control of metabolic strategies is quite commonly seen in different types of bacteria [48]. Numerous previous works and experiments support the predictions from our model regarding the interdependence of metabolism, growth, shape and size. These cases have been analyzed in the discussion section.
3.3. Overflow metabolism and bacterial metabolic regime
The Warburg effect is termed overflow metabolism in bacteria, due to the cellular excretion (or overflow) of excess metabolites like lactate, acetate, or ethanol after incomplete oxidation of glucose. Acetate overflow metabolism has been well documented in E. coli [49], but the process is not clearly understood [43].
During the process of conversion of $r_3$ products into biomass, energy consumption is involved as in Equation (8). If the value of $\epsilon_g\cdot g > \epsilon_F$, then the energy gained from $r_3$ alone is insufficient to convert substrate into biomass and the cell would depend upon more efficient $r_2$ for energy. But, if the value of $r_3$ is high enough $e_+$ (Equation 6) would be insufficient to sustain $e_-$ (Equation 8), i.e., $e_- > e_+$. In such a case, the excess $r_3$ products would be dumped outside the cell and the rest would be used for biomass production. The maximum value of $r_3$ for which all substrate would be converted into biomass, is given by the relation:
The solution for (9) and (12) would give us the maximal value of $r_3$ beyond which export of excess $r_3$ products will occur. Additionally in such a high flux regime, we would need to invoke Equation (5), which describes the maximum rate of OP, in order not to destabilize the protein-lipid ratio of the bacterial membrane.
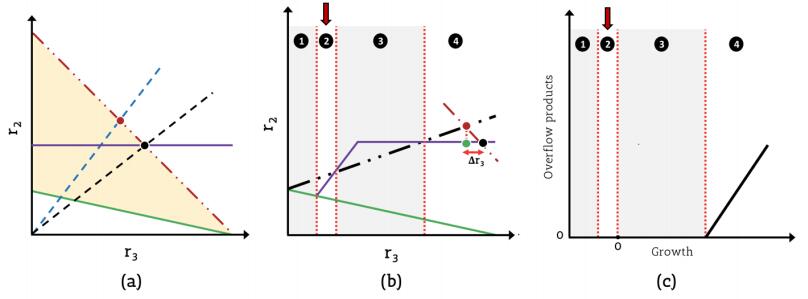
In such a scenario, the fermentation related enzymes are up-regulated [20], resulting in changes to the slope of Equation (11), even though the value of $Z$ remains unchanged. This occurs because the number of OP enzymes ($\gamma$s) remaining constant whereas that of fermentation ($\sigma$) increasing in value. This decreases the slope of the line- a shift to match the intersection of Equations (5) and (9), i.e., in order to process the remaining glucose influx (shown in Figure 4a via the black dot, which is the final solution for Equations (5), (9)-(11)).
Furthermore, the intersections of the line representing final solutions of (5), (9)-(11) with the line representing (12), provides us with three different regimes of bacterial metabolism (denoted by regime 2-4 in Figure 4b). We also find an additional regime of metabolism arising from the part of the phase space where there is no solution for (5), (9)-(11) (denoted by regime 1 in Figure 4b). This leads us to a total of four such scenarios (as seen in Figure 4b). We discuss these regimes in brief before delving into overflow metabolism in detail again.
As discussed in section 3.1, regime 1 in Figure 4b, c, is characterized by substrate concentrations that are insufficient to fulfill all the basic metabolic requirements of the cell. Thus, the cell resorts to limited activity and uses only OP to extract as much energy as possible from the substrate for sustainence.
Regime 2 is more interesting and is denoted by an arrow in Figures 4b, c. Here, the substrate flux is enough to maintain the basic cellular metabolic requirements, but does not produce enough energy for biomass production (i.e., $e_+ \geq e_b$ but $<\epsilon_g\cdot g \cdot r_3$). In such a case, even though it is a low substrate scenario, $r_3$ products are in excess. According to a previous model [23], in such a regime, excess $r_3$ products might be converted back to pyruvate ($r_1$ product) and reused for OP to keep the respiration at full capacity. Unfortunately, a direct prediction of this could not be obtained from our model, but it predicts excess $r_3$ products that is definitely not known to be excreted away (see data in [1]).
Once enough energy can be produced for the cell to start proliferating (the first intersection of the solid purple line and the dot dashed black line in Figure 4b), the cell not only has enough energy to sustain basic metabolic activities but also for biomass production. In this case, there are no overflow products. This scenario continues till the second intersection of the aforementioned lines in Figure 4b. Above this limit, overflow metabolism takes place, because $e_+ \ngtr e_-$ and thus the excess products are excreted. There are several other reasons for non-reduction of $r_3$ processes even though they seem wasteful and they can be found in relevant reviews [20].
In Figure 4b, the difference ($\Delta r_3$) in the final solution of $r_3$ value for the solutions of (7), (9)-(11) with (12) will give an estimate of the overflow metabolism. In this fourth regime, $\Delta r_3$ can be plotted against growth/biomass production rate (Equation (7)) to obtain Figure 4c. The prediction of this relation matches numerous laboratory observations of overflow metabolism in multiple strains of bacteria [1].
3.4. Further considerations and applications
As represented in Equation (7), the bacterial growth rate $R$ can be given by:
where $r_{3, max}$ is the final solution for (5), (9)-(12) (symbolized by the purple line in Figure 4b) and $\Lambda_0$ is the biomass ($\Lambda$) required to make a new cell. This growth rate, $R$, can then be incorporated into a regular Lotka-Volterra equation system to find the population size $N_i$ of a species $i$ directly as a function of substrate concentration through $R$, given by:
where $R_i$ is the growth rate of species $i$, $N_i$ is the number of individuals of species $i$, $\alpha_{ij}$ is the competition coefficient between species $i$ and $j$ and $K_i$ is the carrying capacity of species $i$.
Our model can be extrapolated to include multiple substrates using a vector to symbolize $r_0$, in order to estimate $R$. We can then use the independent experimental data for growth and substrate preference in individual species to calculate $\alpha_{ij}$ [39], in order to obtain all the parameters in (13).
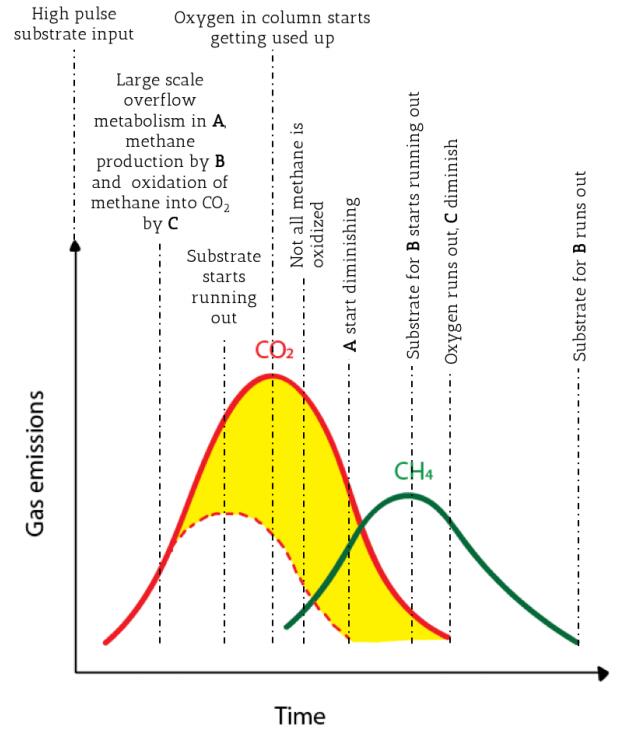
In addition to the direct estimation of populations, we can use the same technique of vectorization of resources and then species in the model to calculate the magnitude of overflow metabolism. This understanding can then be used in the context of many modern and paleo-ecosystems where spatio-temporal change in substrate concentration is significant and would result in interactions between various communities. Such usage is not possible from any of the earlier models because they do not estimate overflow metabolism from first-principles [22], and further, most the FBA models are specific to a particular species. Temperate wetlands are one such example of an ecosystem with spatio-temporal change in substrate concentration. Our model can be extrapolated to predict and estimate the gas fluxes ($CO_2$ and methane), and further to account for phenomena such as aerobic methanogenesis.
In temperate zone wetlands, the fall season can be seen as a pulse of high concentration of substrate and resources. Due to the Warburg effect, an increased concentration of substrates would not result in higher carbon dioxide fluxes, but rather in production of secondary metabolites like lactate and acetate, and a sudden proliferation of bacterial populations. This can not only affect the amount of carbon dioxide released but also the amount of substrate that is available to methanogens. Acetate is produced by heterotrophic bacteria through overflow metabolism [1] and can be utilized by the acetate-based methanogens, which form a large part of the methanogen community in the wetlands. Moreover, lactate is also formed during the process [41] and can be used by the syntropic relations of hydrogen-based methanogens and sulfate-reducing bacteria [21].
This methane produced by the methanogens, using the metabolites from the Warburg effect (overflow metabolism), is then oxidized by the methanotrophs, which use the oxygen from the water column (of the small water bodies in these wetlands) above the methanogens, thus producing carbon dioxide. We illustrate this idea in Figure 5 where the bold red line is the total $CO_2$ production and the dotted red line represents the $CO_2$ emitted from the heterotrophic bacteria. So, even though the total $CO_2$ emissions increase, it is actually the increase in methane production and its subsequent oxidation that is fueling this rise.
Once the initial substrates start depleting, the water column becomes anoxic due to oxygen usage by both the methanotrophs, whose population rises because of increased methane availability, and by the already large aerobic heterotrophic community, fueled by the initial pulse of substrates. After a certain degree of anoxia is reached, the aerobic heterotrophs start declining due to lower oxygen and lower substrate availability. Only the anaerobic heterotrophs remain plentiful, but in reduced abundance as easily available resources have been depleted, and they have to process the less usable ones. During this time the total $CO_2$ production falls, and due to the lack of sufficient oxygen, not all of the methane gets oxidized. This results in a net release of methane from the system.
Now as the process continues, the methane flux rises to a maximum, where the metabolites for methanogenesis are still available (from the accumulated overflow metabolism of the heterotrophs) but are getting depleted. After a certain tipping point, the methane flux also decreases, and the column becomes completely anoxic. In previous literature [5], such a rough pattern has been observed and the time frame for the whole process sums up to about one year. Seasonal rainfall mixes the anoxic waters with atmospheric oxygen well, and the cycle starts again by provision of pulsed high substrate input in the next fall. The process has been visualized in Figure 5.
4.
Discussion
Here we considered the three major trade-offs of Warburg effect in a bacterial cell through linear equations and inequalities with the goal of improving the understanding of the ecological consequences of bacterial metabolism.
4.1. Comparison with previous work
Most previous modeling of the Warburg effect comes from the family of models called FBA (Flux Balance Analysis), which was briefly discussed in the introduction of this work [22,23,34,37,42,49]. These models use the knowledge of constructed biochemical networks, in particular the genome-scale metabolic network reconstructions [22]. These networks consist of most identified metabolic reactions in a given organism and the genes that encode each enzyme. The model estimates the flow of metabolites through this network, thus predicting the growth rate of an organism or rate of production of a given metabolite. These networks are specific to organisms and making a generalized model network for all aerobic heterotrophic bacteria would be an immense task. Calculations over such networks are also computationally intensive.
In contrast, we try to generate a very simple model using linear relations. The parameters that are used in the model can be inferred from experiments and are usable for any aerobic heterotrophic bacterial species. In addition, one can look at the growth and other estimates that are predicted by the model, and explore how they change as functions of the parameter values. Disadvantages of our approach are that we cannot predict the flux of other metabolites that are not encoded in our model and we cannot take protein costs and related terms into account.
Consequently, our model reflects the classic trade-off between generalizability and specificity. Because our aim was to study the ecology of these organisms, we chose a more general model that helps us explore the Warburg effect in this class of organisms broadly, rather than obtaining highly resolved pathways and fluxes. This simple formulation allowed us to incorporate the volume and surface area of the cell, leading to parameterization of shape and size of the cell. Exploration of how cellular metabolism and growth depend on cell shape and size (in addition to substrate concentration) is a novel feature of our model as compared to previous studies [22,23,34,37,42].
Even though this family of FBA models has been noticeably successful in estimating fluxes, it is unable to explain overflow metabolism from first principles [22]. Only when using measured fluxes like maximal oxygen uptake rates or other pathway capacities as auxiliary constraints do FBA models predict the use of fermentation or other inefficient routes [22]. Such a method does not seem adequate, as these constraints act like fitted parameters and the models do not fully explain why organisms simply do not increase the capacity of the efficient routes by producing more enzymes [22]. We note, however, that Zhuang et al. [49] incorporated membrane crowding and an upper limit on the number of respiratory enzymes in order to add a physical constraint on the model (FBAwmc).
In comparison, our model has a physical constraint similar to Zhuang et al. [49], but unlike them, we use a generalized model instead of a specific organism's metabolic network. We take into consideration the facts that, as a component of the maintenance of cellular membrane structure in prokaryotes, the protein-to-lipid ratio is kept within certain bounds [22] and that at high rates of catabolism, the surface area available to proteins can become saturated and proteins (such as glucose transporters and OP enzymes) might 'compete' for expression [49].
Molenaar et al. [22] used constraints of membrane structure maintenance and a maximal cellular density of proteins to construct their model. That work introduced a shape parameter but did not develop it further as the primary focus was to optimize enzyme systems in order to maximize growth. But even their model, which overcame some of the shortcomings of FBA, did not consider the minimal energy requirement of the cell.
Though minimal energy requirements for bacterial cells have been known for some time [17], they were not directly incorporated in the models mentioned above. Our incorporation of such a constraint helped us to classify different metabolic regimes in bacteria, something that has not been done in many previous studies [22,34,37,42]. Vazquez et al. [42] sought to identify dynamic regimes but ended up making two very strict ones: one with only OP and one with mixed metabolism (fermentation and OP). Moller et al. [23] aimed to classify dynamical regimes but did not take minimal energy requirements into consideration and did not address overflow metabolism.
Our adoption of a minimum energy constraint equation leads directly to the four regimes in metabolism, as described in the Results and Figure 4. These regimes stretch all the way from low substrate conditions to very high substrate concentrations. Even more, the same set of equations give us a direct estimate of overflow metabolism products. Understanding this set of regimes is crucial for many biotechnological applications which may utilize bacterial culture under different conditions.
4.2. Support from previous studies and experiments
There are numerous studies and experiments that follow the predictions outlined in our work - especially regarding the shape and size dependence of bacterial metabolism and growth.
In substrate poor conditions, it has been observed that E. coli reduces its $Z$ by becoming much smaller to allow for more efficiency [18]. In a similar note, certain strains of E. coli grew to become much larger than undiluted cells within a few generations [4] on serial dilution with fresh growth media.
A comparable result was shown in a long term evolutionary experiment in the same organism, where the mean cell volume increased in serial dilutions over 10,000 generations [19]. The increase in cell volume was also accompanied by an increase in relative fitness, which can be taken as a measure of $r_3$, implying a lower $Z$ has a higher $r_3$, as predicted from our model. Such a general trend of higher fitness being associated with larger size was shown in about 40 species of obligate heterotrophic bacteria in another work [6].
In a set of classic experiments, Salmonella enterica serovar Typhimurium produced wider cells (lower $Z$) in resource rich medium than when grown in minimal medium, and slow growing cells (low $r_3$) were smaller than fast growing cells (high $r_3$) [33]. The latter was been also demonstrated in E. coli, where faster growing cells (high $r_3$) are significantly wider (high $Z$) [24].
Geobacter sulfurreducens has a capacity to process acetate more efficiently than a similar iron-reducer Rhodoferax ferrireducens [9,29,49] due to its smaller size (and thus, larger $Z$). Similarly, living in energy-starved environments Dehalococcus spp. may have evolved its disc shape to maximize the dechlorination rate (given that the process has a low thermodynamic efficiency) [15].
When grown in nutrient-limiting conditions, certain Streptococcus isolates grew as true filaments instead of as cocci [12,31]. In a similar way, Pseudomonas aeruginosa, Pseudomonas putida and Pseudomonas fluorescens elongate into thin slim cells in nutrient poor environment, unlike the short rods observed in normal media [36,38].
A cell cannot increase its $Z$ indefinitely by change in cell shape, hence another strategy would be to use subsidiary filaments to increase surface area (and $Z$). When deprived of certain substrates, Actinomyces israelii grows branched filamentous roads (high $Z$) and returns to its normal morphology once those substrates are added back [27]. Nutrient-poor conditions also enhance filamentation in Arthobacter globiforms [8,14] and Clostridiium welchii [46,47].
4.3. Further comments
As outlined in the Results, we can use a vectorized version of our model to understand the wetland gas emission dynamics via estimation of overflow metabolism. As a further speculation, we note that a similar process may have happened over longer geological timescales. In the past, events involving heavy releases of methane such as the end-Permian mass extinction [30] might also be explainable to some extent using our formulation. High primary productivity and substrate availability due to increased $CO_2$ and weathering processes might have triggered overflow metabolism in the heterotrophic microbes leading to a large scale production of metabolites such as acetate and lactate. These substrates can then be utilized by methanogens, especially acetate, which has been linked to the massive methanogenic burst at end-Permian [30].
Although simple, our work provides a fairly straightforward way to look at ecological trends in systems of bacterial taxa. This is an added benefit which extends beyond the main results concerning overflow metabolism and the relative dynamics of respiration and fermentation. Not only are these trends supported by previous studies and experiments, but even more importantly they provide simple predictions, which can be tested in the lab.
Acknowledgments
WFF was partially supported by the U.S. Army Research Laboratory and the U.S. Army Research Office under Grant W911NF-14-1-0490.
Conflict of interest
The authors declare there is no conflict of intetest.









 DownLoad:
DownLoad: